Нейросети в трейдинге: Адаптивная периодическая сегментация (Создание токенов)

Введение

В предыдущей статье мы подробно рассмотрели теоретические основы фреймворка LightGTS (Lightweight General Time Series Forecasting) — одного из наиболее прогрессивных и инженерно продуманных подходов к прогнозированию временных рядов на сегодняшний день, который был представлен в работе "LightGTS: A Lightweight General Time Series Forecasting Model". Его концепция строится на глубоком понимании природы периодичности, характерной для финансовых и экономических данных, а также на вдумчивом переосмыслении архитектуры Transformer под специфические задачи обработки временных структур. Основное внимание мы уделили тому, как LightGTS работает с периодическими шаблонами, минимизируя издержки на обучение и обеспечивая устойчивую генерализацию даже на разнотипных и шумных данных.

Фреймворк начинается с так называемого Period Patching — механизма, в котором временной ряд разбивается на сегменты, соответствующие внутренней частоте исследуемого сигнала. Эта частота не задаётся вручную, а определяется моделью на основании анализа частотного спектра, полученного с помощью быстрого преобразования Фурье. Каждый выделенный патч представляет собой один цикл, содержащий значимые локальные закономерности. И именно такой фрагмент преобразуется в токен посредством проекции. И здесь возникает первая архитектурная инновация — Flex Projection Layer, позволяющая обрабатывать патчи переменной длины при помощи гибкой линейной трансформации весов. Эта проекция не просто масштабирует данные, а сохраняет эквивалентность токенов при переходе между различными шкалами и частотами.

В блоке Энкодера используется Rotary Positional Encoding (RoPE), обеспечивающий компактное и устойчивое представление относительных позиций токенов. Это особенно важно для финансовых рядов, где абсолютное положение часто гораздо менее значимо, чем взаимное расположение элементов внутри последовательности. После этого токены обрабатываются классическим стеком Transformer-блоков, каждый из которых состоит из многоголовой Self-Attentiom и модуль Feed-Forward.

Одним из наиболее оригинальных решений, предложенных авторами LightGTS, стал механизм Periodical Parallel Decoding, концептуально противоположный авторегрессионным стратегиям. Вместо поэтапного прогнозирования последовательности, модель использует последний токен скрытого представления (который аккумулирует всю информацию о предыдущем ряде) и на его основе одновременно генерирует сразу всю выходную последовательность, реплицируя его с последующим позиционным взвешиванием. Такой подход позволяет не только ускорить прогнозирование, но и сохранить периодическую согласованность во временной структуре на выходе модели.

В завершении, фреймворк применяет Flex-resize к проекционному слою Декодера — тем самым обеспечивая соответствие предсказаний реальной длине прогнозируемого сигнала. Всё обучение модели сводится к минимизации классической MSE-функции между предсказанными значениями и целевым рядом.

Таким образом, LightGTS — это не просто модифицированный Transformer. Это продуманная архитектура, в которой каждый компонент адаптирован под особенности временных рядов: от обработки периодичности до отказа от авторегрессии в пользу полной параллельной генерации. Именно благодаря этой глубокой адаптации, фреймворк демонстрирует высокую точность при низкой вычислительной стоимости.

Авторская визуализация фреймворка LightGTS представлена ниже.

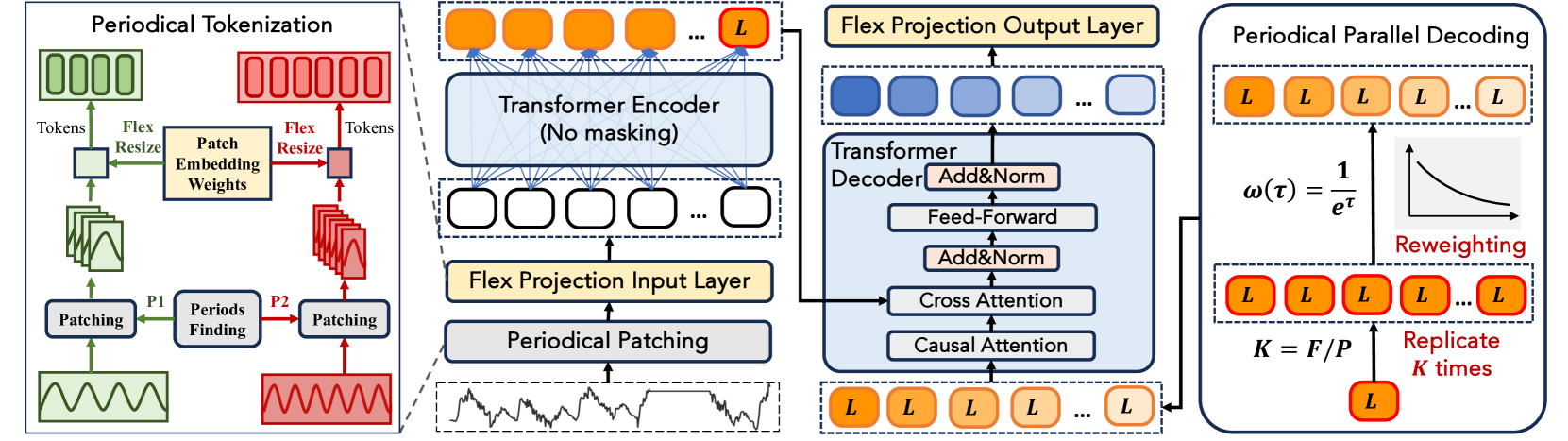
В практической части предыдущей статьи мы приступили к построению алгоритма адаптивного периодического патчинга — одного из ключевых элементов архитектуры LightGTS. Были подробно рассмотрены ограничения, связанные с невозможностью использовать динамическое распределение памяти в среде исполнения, характерной для MQL5 и OpenCL. Эти ограничения вынудили нас отказаться от идеи произвольного количества токенов на выходе.

Вместо этого, мы приняли стратегически взвешенное решение: зафиксировать количество патчей и использовать их перекрытие в качестве инструмента для компенсации изменения длины отдельных сегментов. Таким образом, нам удалось найти компромисс между адаптивностью (модель остается чувствительной к реальной периодичности временного ряда) и вычислительной стабильностью, необходимой для эффективного использования аппаратных ресурсов. Этот подход позволил сохранить как точность отражения циклических структур анализируемых данных, так и предсказуемость в управлении памятью, что критично для высокочастотных торговых моделей и реализации в условиях ограниченного контекста исполнения.

Алгоритм выбора доминирующей частоты мы уже реализовали — он эффективно извлекает основную периодичность для каждой унитарной последовательности входного временного ряда. Это позволит нам указать базовый масштаб для последующей сегментации данных. Сегодня же мы продолжим начатую работу и сделаем следующий шаг — реализуем алгоритм генерации токенов на стороне OpenCL-контекста.

Наша задача — разбить каждую временную последовательность на фиксированное количество фрагментов, где размер сегмента задается в соответствии с выявленной доминирующей частотой, а перекрытие регулирует адаптацию под длину окна. Всё это должно быть выполнено в условиях строгой параллельности, используя GPU-совместимый код, где каждый поток будет отвечать за формирование одного токена в одной из унитарных компонент анализируемой последовательности.

Построение OpenCL-кернелов

После выделения доминирующей частоты на основе быстрого преобразования Фурье, мы с вами вплотную приблизились к ключевому этапу — построению механизма генерации токенов, то есть, фрагментов временного ряда, соответствующих выявленной периодичности. Напомним, в рамках предыдущей части мы сосредоточились на важной задаче: совместить адаптацию модели к текущей рыночной частоте с необходимостью фиксированного числа выходных патчей, что особенно важно для работы в среде MQL5, ограниченной в плане динамического распределения памяти.

Наш подход основывается на принципе: пусть количество токенов (патчей) остаётся постоянным, но их длина адаптируется под текущую частоту, а перекрытие регулируется таким образом, чтобы обеспечить полное покрытие анализируемого временного ряда. Это позволяет эффективно сочетать гибкость и контроль ресурсов. Однако тут скрыта техническая загвоздка: если окно свёртки меняется, значит и матрица весов, по логике, должна адаптироваться — либо перестраиваться каждый раз, либо проецироваться на новое пространство.

В оригинальной статье авторы фреймворка LightGTS предложили решение: матрица весов обучается на фиксированном размере окна (определённом статистикой обучающей выборки), а затем при каждом новом размере окна происходит проекция весов с использованием псевдообратной матрицыМура–Пенроуза. Математически элегантно, но практически — громоздко.

Реальные финансовые рынки неумолимы: цикл сегодня — это не цикл завтра. Периодичность плавает, и адаптация требует гибкости. Вычислять псевдообратную матрицу на лету, особенно в условиях онлайн-обработки или высокочастотной торговли, — значит пожертвовать скоростью и ресурсоэффективностью ради строгости формализма. А это непозволительная роскошь.

Наше решение гораздо более практичное. Вместо постоянной перестройки весов, мы пошли другим путём: используем матрицу максимального допустимого размера, в которой просто игнорируем ненужные веса за счёт нулевого паддинга. То есть, если фрагмент данных не попадает в активное окно — он умножается на ноль, а соответствующий вес не влияет на результат. Просто и эффективно.

Такой подход позволяет:

• сохранить фиксированную структуру матрицы весов, избегая дорогостоящих операций;
• динамически варьировать размер окна и шаг между патчами;
• адаптироваться к частотным колебаниям рынка на лету, без остановки модели или пересчёта параметров.

Всё это реализуется на стороне OpenCL-контекста в кернеле FeedForwardAdaptConv, где каждый поток отвечает за конкретную пару сегмент–фильтр для одной из унитарных последовательностей.

__kernel void FeedForwardAdaptConv(__global const float *matrix_w,
                                   __global const float *matrix_i,
                                   __global float *matrix_o,
                                   __global const float *main_freq,
                                   const int inputs,
                                   const int window_in,
                                   const int activation
                                  )
  {
   const size_t u = get_global_id(0);
   const size_t f = get_global_id(1);
   const size_t v = get_global_id(2);
   const size_t units = get_global_size(0);
   const size_t filters = get_global_size(1);
   const size_t variables = get_global_size(2);

В теле кернела мы сначала определяем номера потоков операций в трёхмерном пространстве задач. Затем, по идентификатору унитарной последовательности v, извлекаем из глобального буфера main_freq доминирующую частоту анализируемой переменной.

const int freq = main_freq[v];
int window = (inputs / variables + freq - 1) / freq;

На её основе вычисляется размер окна, с поправками на шаг и границы фрагментации. Тут же мы определяем размер шага окна анализа, исходя из размера тензора исходных данных и количества создаваемых токенов. Задача — покрыть всю последовательность равномерно, без потерь.

const int step = (int)(inputs / variables + units + 1) / (units + 2);
if(window < step)
   window = (int)((step + window - 1) / window) * window;
if(window > window_in)
   window = window_in;

Далее следует ключевой момент. Нам важно, чтобы окно не оказалось меньше шага, иначе часть данных может быть не охвачена. Поэтому, если найденный период оказывается слишком мал, мы кратно увеличиваем окно, доводя его до значения не менее шага, но не превышающего максимально допустимое.

После этого определяются смещения во входных и выходных массивах, а также в матрице весов. Это необходимо для корректной адресации данных внутри глобальных буферов

const int shift_in = (u < (units - 1) ? u * step : inputs / variables - window);
const int shift_in_var =  v * inputs / variables;
const int shift_out = (u + v * units) * filters + f;
const int shift_weight = (v * filters + f) * (window_in + 1);

Тут стоит отметить важный нюанс: нам необходимо покрыть всю входную последовательность, включая её хвостовую часть. Если сегментация осуществляется с фиксированным шагом, а длина каждого окна определяется динамически, то последние несколько элементов могут остаться вне анализа. Поэтому, чтобы гарантировать полное покрытие всей входной последовательности, начальную точку последнего сегмента мы рассчитываем как разницу между полной длиной анализируемого последовательности и размером окна. Это позволяет сместить последнее окно таким образом, чтобы оно обязательно захватило финальные данные последовательности, даже если его размер был определён динамически и оказался меньше максимально допустимого.

Затем начинается главная вычислительная часть — операция свёртки, в рамках которой формируется итоговое значение для каждого токена. На первом этапе мы берём базовое значение, соответствующее bias-компоненте, которая извлекается из матрицы весов с помощью предварительно рассчитанного смещения. Этот элемент выступает в роли стартовой точки для накопления вклада от каждого элемента окна анализа.

float sum = matrix_w[shift_weight + window_in];
for(int i = 0; i < window; i++)
   if((shift_in + i) < (inputs / variables))
      sum += IsNaNOrInf(matrix_i[shift_in_var + shift_in + i], 0) *
             matrix_w[shift_weight + i];

Затем, начинается проход по каждому элементу окна анализа. Именно здесь проявляется ключевая особенность нашей реализации — стратегия с нулевым паддингом. Если элемент последовательности находится за пределами фактически рассчитанного окна, он просто исключается из расчётов. Это позволяет избежать искажений сигнала, которые могли бы возникнуть при включении нерелевантных данных. Такая техника обеспечивает стабильность результатов и позволяет добиться корректных вычислений, независимо от текущего размера окна. Кроме того, нулевой паддинг облегчает поддержку фиксированной размерности весовой матрицы, поскольку мы можем гарантировать, что все пустые позиции будут компенсированы нулями, не влияющими на итоговую сумму.

В завершение применяем выбранную функцию активации и сохраняем результат в буфер выходных значений.

 matrix_o[shift_out] = Activation(sum, activation);
}

Таким образом, мы получаем эмбеддинги, адаптированные к текущей рыночной частоте, с чётким локальным контекстом и готовностью к подаче в Transformer-блоки. Всё это — без дорогостоящих операций, с минимальными затратами ресурсов и в полной гармонии с ограничениями среды MQL5.

Прежде чем мы запустим полученные токены в омут Transformer-блоков, надо позаботиться о том, чтобы сама модель не сдалась с первого шага и умела учиться. Для этого нам нужен полноценный обратный проход (backpropagation) — тот самый этап, на котором вычисляются градиенты, позволяющие нам подправлять свёрточные адаптивные фильтры. Без него всё, что мы сделали в прямом ходе, превратится в стагнацию: фильтры окажутся застывшими в случайных состояниях, а модель попросту не сможет адаптироваться к новым броскам рынка, замораживаясь в своих ошибках.

Запуск обратного прохода — это как дать оркестру обратный отклик: если один инструмент сбился, звуковую волну нужно вернуть назад и точно подсказать, что исправить. В мире адаптивной свёртки с переменными окнами это задача не из простых: каждое исходное значение могло участвовать сразу в нескольких токенах, и все они требуют распределения ошибки обратно к своим источникам.

Именно для этой цели мы создали OpenCL-кернел CalcHiddenGradientAdaptConv. Он работает в двумерном пространстве: по оси inp у нас позиции в исходных унитарных последовательностях, а по оси v — разные каналы (унитарные последовательности). Такой расклад гарантирует, что каждый элемент анализируемых данных получит свой точный градиент.

__kernel void CalcHiddenGradientAdaptConv(__global const float *matrix_w,
                                          __global const float *matrix_i,
                                          __global float *matrix_ig,
                                          __global const float *matrix_og,
                                          __global const float *main_freq,
                                          const int outputs,
                                          const int window_in,
                                          const int window_out,
                                          const int activation
                                         )
  {
   const size_t inp = get_global_id(0);
   const size_t v = get_global_id(1);
   const size_t inputs = get_global_size(0);
   const size_t variables = get_global_size(1);

Внутри кернела сначала включается радар — мы идентифицируем текущий поток по всем измерениям пространства задач. А затем, аналогично кернелу прямого прохода, определяем размер сегмента индивидуально для каждой унитарной последовательности и его шага.

const int units = outputs / (window_out * variables);
const int freq = main_freq[v];
int window = (inputs / variables + freq - 1) / freq;
const int step = (int)(inputs + units + 1) / (units + 2);
if(window < step)
   window = (int)((step + window - 1) / window) * window;
if(window > window_in)
   window = window_in;

И потом определяем смещения в буферах данных до необходимых элементов.

const int shift_in = v * inputs + inp;
int u = inp / step;
int shift_out_var = v * (outputs / variables);
int shift_weight_var = (v * window_out) * (window_in + 1);

Далее мы переходим к основному процессу распределения градиента ошибки. Здесь мы сначала определяем, при формировании какого токена использовался текущий элемент буфера исходных данных, и собираем градиент ошибки со всех элементов полученного токена с учетом вклада анализируемого элемента.

Однако следует обратить внимание, что использование перекрывающихся сегментов приводит к возможности использования одного элемента исходных данных при формировании нескольких токенов на разных позициях. Поэтому операцию сбора градиентов ошибки мы оборачиваем в цикл.

float sum = 0;
while(u * step <= inp && u < (units - 1))
  {
   int pos = inp - u * step;
   if(pos >= window)
     {
      u++;
      continue;
     }
   int shift_out = u * window_out;
   int shift_weight = pos + shift_weight_var;
   for(int out = 0; out < window_out; out++)
     {
      if((shift_out + out) >= (outputs / variables))
         continue;
      sum += IsNaNOrInf(matrix_og[shift_out_var + shift_out + out] *
                        matrix_w[shift_weight + out * (window_in + 1)], 0);
     }
   u++;
  }

Не стоит забывать и об особенностях формирования последнего сегмента. В алгоритме распределения градиента ошибки мы вынесем его отдельным блоком.

if(inp >= (inputs - window))
  {
   int pos = inp + window - inputs;
   int shift_out = (units - 1) * window_out;
   int shift_weight = pos + shift_weight_var;
   for(int out = 0; out < window_out; out++)
     {
      if((shift_out + out) >= (outputs / variables))
         continue;
      sum += IsNaNOrInf(matrix_og[shift_out_var + shift_out + out] *
                        matrix_w[shift_weight + out * (window_in + 1)], 0);
     }
  }

И последний штрих — аккумулированную сумму градиентов ошибки корректируем на производную сумму активации и сохраняем в соответствующем элементе глобального буфера данных.

 matrix_ig[shift_in] = Deactivation(sum, matrix_i[shift_in], activation);
}

Такой подход с циклом по токенам гарантирует, что каждый бит исходных данных получит свой заслуженный градиент ошибки, даже если его голос звучал сразу в нескольких токенах. Это позволяет нашим адаптивным фильтрам учиться не по вырванным фразам, а по целым партиям рыночных данных.

Однако распределение градиента ошибки — это лишь середина пути. Настоящая магия происходит далее, когда мы используем эти градиенты для обновления параметров модели. Представьте себе садовника, который после сбора урожая решает, какие деревья подстричь, а какие подкормить, чтобы в следующем сезоне ветви давали ещё более обильный плод. Точно так же наши алгоритмы оптимизации принимают на вооружение вычисленные градиенты, чтобы скорректировать веса в сторону минимизации общей ошибки прогнозирования.

В нашем случае обновление параметров модели реализовано внутри OpenCL-кернела UpdateWeightsAdaptConvAdam. Это не просто технический шаг, а кульминация всего процесса обратного распространения ошибки — момент, когда модель делает выводы из своих ошибок и делает шаг к улучшению.

__kernel void UpdateWeightsAdaptConvAdam(__global float *matrix_w,
                                         __global const float *matrix_og,
                                         __global const float *matrix_i,
                                         __global float *matrix_m,
                                         __global float *matrix_v,
                                         __global float *main_freq,
                                         const int inputs,
                                         const int outputs,
                                         const float l,
                                         const float b1,
                                         const float b2
                                        )
  {
   const size_t id_in = get_global_id(0);    // input shift
   const size_t id_out = get_global_id(1);   // filter shift
   const size_t id_v = get_global_id(2);     // variable
   const size_t window_in = get_global_size(0) - 1;
   const size_t window_out = get_global_size(1);
   const size_t variables = get_global_size(2);

Алгоритм работы кернела устроен как многоуровневая сцена с тремя координатными осями, каждая из которых берёт на себя чётко определённую роль в вычислительном процессе. Первая ось — это позиция внутри анализируемого окна (сегмента) исходных данных (id_in), вторая — номер фильтра или, иначе говоря, конкретная позиция в токене на выходе объекта (id_out), а третья — индекс унитарной последовательности (id_v), что означает отдельный канал исходных данных.

Такое трёхмерное распределение вычислений — не просто архитектурное удобство, а стратегический замысел. Оно обеспечивает полную декомпозицию задачи: каждый обучаемый параметр матрицы весов применяется строго в контексте соответствующего фрагмента входной последовательности и привязан к конкретному фильтру и каналу. Представьте, что каждый фильтр — это отдельный аналитик, работающий со своей диаграммой и ни с кем не путающий бумаги. Это позволяет не смешивать сигналы между временными рядами, избегая перекрёстных искажений, которые особенно критичны при работе с финансовыми данными, где шум и неустойчивость — повседневная реальность.

Такой подход формирует своего рода микроскоп с независимыми линзами: каждый фильтр сфокусирован на уникальном фрагменте данных, обеспечивая высокоточную настройку на мельчайшие колебания сигнала. Если один канал содержит бурные, стремительные колебания, а другой — устойчивый, но вялотекущий тренд, алгоритм сумеет справиться с каждым из них, не теряя резкости восприятия. Фактически, каждый вес обучается индивидуально под свою локальную задачу, как если бы это была отдельная модель внутри большой системы.

В теле кернела мы сразу идентифицируем поток в трехмерном пространстве задач, что позволит нам выделить один элемент из матрицы обучаемых параметров для выполнения дальнейших операций.

Сразу после этого, опираясь на доминирующую частоту main_freq[id_v], вычисляем текущий размер сегмента window, на котором этот вес будет применяться.

const int units = outputs / (window_out * variables);
const int freq = main_freq[id_v];
int window = (inputs / variables + freq - 1) / freq;
const int step = (int)(inputs / variables + units + 1) / (units + 2);
if(window < step)
   window = (int)((step + window - 1) / window) * window;
if(window > window_in)
   window = window_in;

Такой подход обеспечивает:

• изоляцию параметров — каждый вес работает только с теми исходными данными, к которым он привязан;
• полную параллельность — потоки не мешают друг другу, так как работают с разными элементами весовой матрицы;
• точность — фильтр синхронизирован с частотой данных и обрабатывает только релевантные сегменты.

Нельзя забывать, что все наши вычисления ведутся над универсальной рамкой — матрицей весов, рассчитанной на максимально возможное окно анализируемых данных. Но в реальности каждый конкретный сегмент зачастую оказывается меньше этого предельного размера. Чтобы не тратить драгоценное время и энергию GPU на бесполезную работу, мы в самом начале каждого потока проверяем принадлежность параметра к текущему сегменту и мгновенно завершаем работу лишних потоков.

if(id_in != window_in &&
   id_in >= window)
   return;

В результате, общая производительность резко возрастает, а модель работает ощутимо быстрее — как ориентированный по целям гонщик, который сразу отбрасывает все ненужные повороты и едет по самому прямому маршруту к финишу.

Следующим шагом идёт определение смещений в глобальных буферах данных — без этого ни один поток не сможет найти нужные элементы.

const int shift_in_var = id_v * inputs / variables;
const int shift_out_var = id_v * outputs / variables;
const int shift_weight = (id_v * window_out + id_out) *
                         (window_in + 1) + id_in;
const bool bias = (id_in == window_in);

Этот простой, но крайне важный приём гарантирует, что каждый параметр фильтра в единицу времени работает только со своей порцией данных, повышая эффективность и предсказуемость всей модели.

Далее мы переходим к одной из самых ответственных частей — вычислению градиента ошибки для выбранного параметра. Градиент — это не абстрактная величина, а настоящий маяк, который подсказывает, в каком направлении и насколько стоит скорректировать вес, чтобы модель прогнозировала точнее.

С целью получения истинного вклада анализируемого параметра, мы пробегаем по всей унитарной последовательности и аккумулируем все его отклики в выходных токенах.

float grad = 0;
for(int u = 0; u < (units - 1); u++)
  {
   const int shift_in_loc = id_in + u * step;
   if(shift_in_loc >= (inputs / variables))
      continue;
   float inp = (bias ? 1 : IsNaNOrInf(matrix_i[shift_in_var + shift_in_loc], 0));
   grad += IsNaNOrInf(inp * matrix_og[shift_out_var + u * window_out + id_out], 0);
  }

Не забываем про особенности формирования последнего сегмента. Его мы вынесли отдельным блоком.

{
 const int shift_in_loc = id_in + inputs / variables - window;
 if(shift_in_loc < (inputs / variables))
   {
    float inp = (bias ? 1 : IsNaNOrInf(matrix_i[shift_in_var + shift_in_loc], 0));
    grad += IsNaNOrInf(inp * matrix_og[shift_out_var + (units - 1) * window_out + id_out], 0);
   }
}

Такой метод сбора градиента — тщательный и исчерпывающий. Мы не упускаем ни одного отклика исходных данных и, следовательно, получаем максимально точный вектор направления для корректировки веса. Именно эта педантичная обратная трассировка — залог того, что модель не застрянет в локальных ошибках, а будет надёжно и плавно адаптироваться к изменчивому ритму финансового рынка.

Затем включается алгоритм Adam — адаптивный метод оптимизации, сочетающий в себе преимущества градиентного сглаживания (Momentum) и нормализации дисперсии (RMSProp). Он использует два вспомогательных массива: matrix_m для первого момента (накопленного градиента) и matrix_v для второго момента (накопленной квадратичной ошибки).

float mt = IsNaNOrInf(clamp(b1 * matrix_m[shift_weight] + (1 - b1) * grad, -1.0e5f, 1.0e5f), 0);
float vt = IsNaNOrInf(clamp(b2 * matrix_v[shift_weight] + (1 - b2) * pow(grad, 2), 1.0e-6f, 1.0e6f), 1.0e-6f);
float weight = clamp(matrix_w[shift_weight] + IsNaNOrInf(l * mt / sqrt(vt), 0), -MAX_WEIGHT, MAX_WEIGHT);

Значение параметра корректируется с учётом как направления (mt), так и стабильности (vt) изменения. Обновлённые значения записываются обратно в глобальные буферы данных.

 matrix_w[shift_weight] = weight;
 matrix_m[shift_weight] = mt;
 matrix_v[shift_weight] = vt;
}

Таким образом, каждый параметр фильтра адаптируется, опираясь на богатый контекст своих прошлых обновлений. Это позволяет модели не только быстро реагировать на локальные ошибки, но и избегать скачкообразных колебаний параметров, обеспечивая плавную и устойчивую адаптацию к данным. Такая тонкая настройка особенно важна в условиях нестабильных финансовых временных рядов, где каждый лишний импульс может привести к переобучению или потере обобщающей способности.

На этом мы завершаем работу на стороне OpenCL-программы. Польный её код представлен во вложении к статье.

Создание объекта

Мы рассмотрели, как в кернелах OpenCL-программы по шагам реализуется адаптивная свёртка с переменным окном, динамическое формирование токенов, градиентный расчёт и обновление весов. Однако, одна лишь вычислительная логика — это только половина дела. Чтобы эта архитектура заработала в реальном времени и в рамках полноценной модели, её нужно грамотно встроить в основную программу.

И вот здесь начинается самое интересное — интеграция. Как и в хорошем оркестре, важен не только талант солистов (кернелов), но и чёткая работа дирижёра — того, кто запускает нужные процессы в нужный момент, управляет их взаимодействием и следит за целостностью всей композиции.

В нашем случае дирижёром выступает класс CNeuronAdaptConv. Именно он координирует всё: от анализа доминантных частот до запуска адаптивной свёртки, от обратного распространения ошибки до обновления весов оптимизатором Adam. Это не просто обёртка над OpenCL-программой, а полноценный управляющий модуль, который принимает решения, связывает между собой этапы вычислений и обеспечивает сохранность состояния между итерациями.

Структура нового объекта представлена ниже.

class CNeuronAdaptConv    :  public CNeuronConvOCL
  {
protected:
   CBufferFloat      bMainFreq;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im,
                         CBufferFloat *out_re, CBufferFloat *out_im, 
                         uint variables, bool reverse = false);
   virtual bool      PeriodsFinding(CBufferFloat *inp_re, CBufferFloat *inp_im, 
                                    CBufferFloat *main_freq, uint variables);
   virtual bool      AdaptiveConvolution(CNeuronBaseOCL *NeuronOCL, CBufferFloat *main_freq);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronAdaptConv(void) {};
                    ~CNeuronAdaptConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window,
                          uint window_out, uint units_count, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override const  {  return defNeuronAdaptConv;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj)   override;
  };

Как можно заметить, внутри CNeuronAdaptConv объявляется лишь один собственный буфер — bMainFreq для хранения доминирующих частот. Все остальные необходимые для работы объекты унаследованы от родительского класса сверточного слоя CNeuronConvOCL, что обеспечивает переиспользование общей логики и снижает дублирование кода.

Буфер bMainFreq объявлен статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Процесс инициализации данного буфера и всех унаследованных объектов организован в методе Init, в параметрах которого мы получаем ряд констант, позволяющих однозначно интерпретировать архитектуру создаваемого объекта.

bool CNeuronAdaptConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_out, uint units_count, uint variables,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, window, window_out,
                                    units_count, variables, optimization_type, batch))
      return false;

Алгоритм метода довольно прост. Вначале мы делегируем всю проверку и инициализацию базовой логике родительского класса, словно доверяем наставнику, который уже знает, с какими параметрами и буферами нужно работать. Это освобождает наш код от лишней рутины. А затем, нам остается лишь инициализировать буфер доминирующих частот.

   bMainFreq.BufferFree();
   if(!bMainFreq.BufferInit(iVariables, 1) ||
      !bMainFreq.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

И возвращаем логический результат работы метода вызывающей программе.

Надо сказать, что большая часть методов нового объекта является лишь обертками для организации работы по постановке в очередь выполнения соответствующих кернелов, построенных по уже знакомому вам алгоритму:

• FFT — разложение временного ряда на частотные компоненты с помощью быстрого преобразования Фурье;
• PeriodsFinding — поиск доминирующей частоты;
• AdaptiveConvolution — прямой проход адаптивной свертки.

Так как быстрое преобразование Фурье и алгоритм поиска доминирующей частоты не используют обучаемых параметров и не требуют распределения градиента ошибки, то и методы обратного прохода превращаются в соответствующие обертки. На их фоне явно выделяется метод прямого прохода feedForward, который объединяет несколько итераций.

bool CNeuronAdaptConv::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

В параметрах метода получаем указатель на объект исходных данных, актуальность которого сразу проверяем. Далее мы разложим полученные данные на частотные составляющие путем вызова метода FFT.

if(!FFT(NeuronOCL.getOutput(), NULL, Output, PrevOutput, iVariables, false))
   return false;

Из полученного спектра выделяем доминирующие частоты для каждой унитарной последовательности.

if(!PeriodsFinding(Output, PrevOutput, GetPointer(bMainFreq), iVariables))
   return false;

И в завершении вызываем метод адаптивной свертки, который и сгенерирует необходимые нам токены.

 return AdaptiveConvolution(NeuronOCL, GetPointer(bMainFreq));
}

Логический результат выполнения операций возвращаем вызывающей программе.

Таким образом, класс CNeuronAdaptConv выступает настоящим «маэстро» вычислительного конвейера: нет у него громоздких реализаций, зато есть идеальное умение дирижировать и синхронизировать все этапы работы, передавая управление там, где это действительно нужно.

Заключение

В этой статье мы завершили формирование полноценного конвейера обработки временных рядов, совмещающего спектральный анализ и адаптивную свёртку в одном целостном алгоритме. Мы показали, как при помощи FFT и поиска доминирующей частоты можно определить ритм каждого канала данных, а затем, опираясь на эту информацию, гибко настраивать ширину сегмента, сохраняя при этом фиксированное число токенов на выходе объекта.

Особое внимание было уделено практической реализации в среде MQL5 и OpenCL. Мы прошли все этапы: от разбора спектра и нарезки патчей, до обратного распространения ошибки и обновления весов оптимизатором Adam. Каждая фаза оформлена в виде небольшого, но самостоятельного кернела, а управляющий класс CNeuronAdaptConv дисциплинирует и синхронизирует их работу, выступая в роли дирижёра вычислительного оркестра.

Благодаря тщательно продуманной архитектуре, где каждый поток GPU обрабатывает только свой вес и свой фрагмент данных, нам удалось достичь впечатляющей параллельности без взаимных блокировок. Нулевой паддинг и жёсткая система смещений гарантируют, что никакая информация не потеряется и не перемешается между каналами. А адаптивный Adam-оптимизатор, аккуратно учитывая моменты первого и второго порядка, обеспечивает плавное и стабильное обучение модели.

В следующей статье мы поговорим об использовании полученных токенов в модифицированном стеке Transformer.

Ссылки

• LightGTS: A Lightweight General Time Series Forecasting Model
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы