
Нейросети — это просто (Часть 28): Policy gradient алгоритм
Содержание
- Введение
- 1. Особенности применения policy gradient
- 2. Принципы обучения модели политики
- 3. Реализация обучения модели
- 4. Тестирование обученной модели в тестере стратегий
- Заключение
- Ссылки
- Программы, используемые в статье
Введение
Мы продолжаем погружение в методы обучения с подкреплением. В предыдущей статье мы познакомились с методом глубокого Q-обучения. Напомню, метод аппроксимирует функцию полезности действия с использованием нейронной сети. В результате мы получаем инструмент прогнозирования ожидаемого вознаграждения при совершении конкретного действия в том или ином состоянии системы. И далее агент совершает действие основываясь заложенной политике и размере ожидаемого вознаграждения. Мы не обсуждали явно использование политики, но предполагали выбор действия с максимальной ожидаемой наградой. Это следует из формулы Беллмана и общей цели обучения с подкреплением. Которая заключается в максимизации вознаграждения за анализируемую сессию.
И заметьте, при изучении методов обучения с подкреплением мы ни разу не упоминали об переобучении модели. На самом деле, если посмотреть на модель обучения с подкреплением, то цель агента как можно лучше изучить среду. И в таком случае, чем лучше агент знает среду, тем успешнее будет его результативность.
Но когда мы имеем дело с изменчивой средой, какой является рынок, то порой понимаешь, что нет предела его вариативности. В нем нет 2-х одинаковых состояний. И даже из похожих состояний мы попадаем в абсолютно противоположные состояния на следующем шаге.
Аппроксимация Q-функции нам даёт лишь ожидаемое среднее вознаграждение без учета разброса значений и вероятности появления положительного вознаграждения. А использование жадной стратегии с выбором максимального вознаграждения всегда дает однозначный выбор действия. С одной стороны, это облегчает работу нашего агента. Но такая стратегия дает плоды только пока наш агент не находится в некоем противостоянии со средой. В таком случае его действия становятся предсказуемые для среды, и она может выработать шаги противодействия действиям агента и изменить политику наград. А агент будет продолжать пользоваться ранее аппроксимированной Q-функцией, которая уже будет не соответствовать изменившейся среде.
Для решения подобных задач были предложены методы, которые не аппроксимируют политику вознаграждения среды. А вырабатывают свою стратегию поведения. Именно к таким методам относится policy gradient, с которым я предлагаю познакомиться сегодня.
1. Особенности применения policy gradient
Начиная изучение методов обучения с подкреплением, мы говорили, что Агент взаимодействует со средой и совершает действия в соответствии со своей стратегией. В результате чего осуществляется переход из одного состояния в другое. И за каждый переход агент получает от среды некое вознаграждение, по размеру которого агент может оценить полезность совершенного действия. Метод policy gradient предполагает выработку стратегии поведения агента.
Разумеется, мы не будем явно задавать стратегию агента, как это можно проследить в DQN. Мы лишь делаем допущение о существовании некой математической функции политики P. Которая оценивает текущее состояние среды и возвращает лучшее действие, которое совершает агент. Как можно заметить, такой подход позволяет нам позабыть обо всех трудностях аппроксимирования Q-функции. А вместе с тем и об указании явной политики поведения агента, как-то выбор действия с максимальной ожидаемой наградой (жадная стратегия).
Конечно, за все надо платить. И вместо аппроксимации Q-функции нам придется аппроксимировать P-функцию политики нашего агента. В данной статье речь пойдет о стохастическом методе policy gradient. Он предполагает, что наша функция политики при оценке текущего состояния среды возвращает вероятностное распределение получения положительного вознаграждении при совершении соответствующего действия.
При этом мы предполагаем, что действия нашего агента распределены равномерно. И для выбора конкретного действия агенту достаточно семплировать значение из нормального распределения з заданными вероятностями. Разумеется, можно воспользоваться жадной стратегией и выбрать действие с максимальной вероятностью. Но именно семплирование добавляет вариативность в поведение нашего агента. А большая вероятность повышает частоту выбора именно этого действия.
Помните, ранее при обучении моделей с подкреплением мы вводили гиперпараметр, отвечающий за баланс исследования и эксплуатации. В случае же использования метода стохастического policy gradient данный баланс регулируется моделью в процессе обучения именно благодаря использованию семплированию действий агента с заданной вероятностью. В начале обучения модели вероятности всех действий практически равны. Что позволяет модели максимально исследовать изучаемую среду. В процессе изучения среды мы повышаем вероятности действий, ведущих к максимизации доходности. И снижаем вероятности выбора для остальных действий. Таким образом изменяется баланс исследования и эксплуатации в пользу выбора наиболее прибыльных действий, что позволяет выстроить стратегию с максимальной доходностью.
Для аппроксимации P-функции политики агента мы будем использовать нейронную сеть. И, как можно догадаться, раз нам нужно по исходным данным текущего состояния среды определить наилучшее действие агента, то можно рассматривать данную задачу как задачу классификации. Где каждое действие является отдельным классов исходных состояний. И тут, как уже упоминалось ранее, нам необходимо получить на выходе нейронного слоя вероятностное представление отнесения состояния среды к тому или иному состоянию.
Вероятностное представление накладывает некоторые ограничение на результирующее значение. Они должны быть нормализованы в диапазоне от 0% до 100%. И сумма всех вероятностей должна составлять 100%. В области машинного обучения принято вместо процентов использовать доли единицы. И в таком представлении мы имеем ограничение диапазона значений от 0 до 1 и сумма всех значений равна 1. Добиться такого результата нам позволяет использование функции SoftMax, которая имеет следующую математическую формулу.
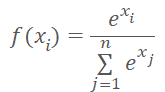
Ранее мы уже знакомились с этой функцией, при знакомстве с методами кластеризации данных. Но если при изучении методов обучения без учителя мы искали сходства в исходных данных для определения класса. То сейчас мы будем распределять состояния среды на действия (классы) в зависимости от получаемого вознаграждения. И функция SoftMax полностью удовлетворяет нашим требованиям. Она полностью позволяет перевести результаты работы нейронной сети в область вероятностей и дифференцируема на всем протяжении значений. Что очень важно для обучения нашей модели.
2. Принципы обучения модели политики
Теперь давайте немного поговорим о принципах обучения модели аппроксимации функции политики. Дело в том, что при обучении модели DQN на каждом новом состоянии среда возвращала нам вознаграждение. И мы обучали модель на прогнозирование ожидаемого вознаграждения с минимальной ошибкой. Что мало чем отличалось от используемых ранее подходов при обучении с учителем.
В случае же аппроксимации P-функции политики агента на каждом новом состоянии мы также получаем от среды вознаграждение. Но мы же хотим прогнозировать лучшее действие, а не вознаграждение. Знак вознаграждения нам может только показать влияние текущего действия на результат. И мы будем обучать модель на увеличение вероятности выбора действия с положительной наградой и снижения вероятности выбора действия с отрицательной наградой.
И тут надо вспомнить, что мы обучаем модель прогнозирования вероятностей. Как было сказано выше, значения предсказанных вероятностей ограничены диапазоном от 0 до 1. Что совсем не сопоставимо с получаемым вознаграждением. Оно может быть как положительным, так и отрицательным. Здесь мы используем следующую логику. Так как нам нужно максимизировать вероятность выбора действий с положительной наградой, то для таких действий мы будем устанавливать целевое значение равным "1". Таким образом, ошибка модели будет определяться как отклонение прогнозной вероятности действия от 1. Использование отклонения позволяет нам эксплуатировать уже построенный метод градиентного спуска для обучения нашей модели аппроксимации функции политики, так как минимизируя отклонения от 1 мы максимизируем вероятность выбора действия с положительным вознаграждением.
Также надо обратить внимание на выбор функции потерь нашей модели. Здесь мы также можем обратиться к методам обучения с учителем и вспомнить, что для задач классификации используется функция кросс-энтропии.
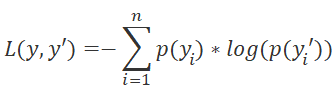
где p(y) — истинные значения распределения, а p(y') — прогнозные значения нашей модели.
Использование логарифма также имеет большое значение для прогнозирования последовательных событий. Из теории вероятности мы знаем, что вероятность наступления двух последовательных событий равна произведению вероятностей этих событий. А для всех логарифмов верно свойство.
![]()
Это позволяет нам перейти от произведения вероятностей к сумме их логарифмов. Что делает обучение нашей модели более стабильным.
Как и в случае обучения DQN, для получения наград наш агент проходит полностью сессию с фиксированными параметрами. Сохраняем в буфер состояния, действия и награды. И делаем обратный проход модели по с использованием накопленных данных.
Обратите внимание, так как мы не имеем функции полезности действий, мы заменяем её суммой значений, полученных в процессе прохода сессии. Для каждого состояния значением Q-функции является сумма последующих вознаграждений до конца сессии.
Обучение модели повторяется до достижения желаемого уровня ошибки или максимального количества сессий обучения.
3. Реализация обучения модели
После изучения теоретических аспектов работы метода мы переходим к его реализации средствами MQL5. Для начала мы реализуем функцию SoftMax. Ранее мы не реализовывали её в качестве функции активации, ввиду особенностей её работы. Сейчас же, чтобы не вносить кардинальных правок в ранее созданные объекты я предлагаю реализовать её отдельным слоем нашей модели.
3.1 Реализация SoftMax
С этой целью мы создадим новый класс CNeuronSoftMaxOCL наследником от базового класса нейронов CNeuronBaseOCL.
class CNeuronSoftMaxOCL : public CNeuronBaseOCL { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; } public: CNeuronSoftMaxOCL(void) {}; ~CNeuronSoftMaxOCL(void) {}; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool calcOutputGradients(CArrayFloat *Target, float error) override; //--- virtual int Type(void) override const { return defNeuronSoftMaxOCL; } };
Новый класс не требует создание отдельных буферов. Более того, он не использует все буфера родительского класса, о чем мы поговорим чуть позже. Поэтому конструктор и деструктор класса остаются пустыми. По этой же причине мы не будем переопределять метод инициализации нашего класса. По существу, нам нужно будет переопределить только методы прямого прохода feedForward и распределения градиента ошибки calcOutputGradients.
Так же в связи с использованием новой функции потерь мы переопределим метод расчета ошибки модели и её градиента calcOutputGradients.
И, конечно, переопределим метод идентификации класса Type.
Начнем мы работу с организации процесса прямого прохода. Как и ранее все вычислительные операции мы будем осуществлять в многопоточном режиме с использованием технологии OpenCL. А значит, сначала мы создадим новый кернел SoftMax_FeedForward в программе OpenCL. В параметрах кернела мы будем передавать указатели на буфера исходных данных и результатов. А также размер этих буферов. Вычисление функции не требует каких-либо дополнительных параметров.
В теле кернела мы, как всегда, определяем идентификатор потока, который служит нам указателем на соответствующий элемент массива исходных данных и результатов. Так как это является реализацией функции активации, то размер буфера исходных данных и результатов равны. И, соответственно, указатель на элементы обоих буферов будет один и тот же.
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs, const ulong total) { uint i = (uint)get_global_id(0); uint l = (uint)get_local_id(0); uint ls = min((uint)get_local_size(0), (uint)256); //--- __local float temp[256];
Следует обратить внимание, что вычисление функции SoftMax требует определение суммы экспоненциальных значений всех элементов буфера исходных данных. Мы бы не хотели повторять вычисления данного значения в каждом потоке. Более того, мы бы хотели распределить процесс вычисления данного значения между несколькими потоками. Но здесь есть проблема синхронизации работы нескольких потоков и обмена данными между ними. Технология OpenCL не даёт возможности отправки данных из одного потока в другой. Но позволяет в рамках отдельных рабочих групп создавать общие переменные и массивы в локальной памяти. А для синхронизации работы потоков в рамках рабочей группы предусмотрена функция barrier(CLK_LOCAL_MEM_FENCE). Этим инструментарием мы и воспользуемся.
Поэтому, одновременно с определением идентификатора потока в глобальном пространстве задач мы определим идентификатор потока в рабочей группе. И сразу объявим массив в локальной памяти. Его мы будем использовать для обмена данными между потоками рабочей группы при вычислении общей суммы экспоненциальных значений.
Сложность заключается в том, что OpenCL не позволяет использовать динамические массивы в локальной памяти. И мы вынуждены определять размер массива на стадии создания кернела. Этим размером мы ограничиваем количество потоков, участвующих в суммировании экспоненциальных значений.
Непосредственно процесс суммирования экспоненциальных значений организован из 2-х последовательных циклов. В теле первого цикла каждый поток, из участвующих в процессе суммирования пройдется по всему вектору исходных значений с шагом равным количеству потоков суммирования и соберет свою часть суммы экспоненциальных значений. Таким образом, весь процесс суммирования мы равномерно распределим между всеми потоками. И каждый из них сохранит свое значение в соответствующий элемент локального массива.
uint count = 0; if(l < 256) do { uint shift = count * ls + l; temp[l] = (count > 0 ? temp[l] : 0) + (count * ls + l < total ? exp(inputs[shift]) : 0); count++; } while((count * ls + l) < total); barrier(CLK_LOCAL_MEM_FENCE);
На данном этапе мы синхронизируем потоки после завершения итераций цикла.
Далее нам нужно собрать в единое значение сумму всех элементов локального массива. Для этого мы организуем второй цикл. Здесь мы разделим размер локального массива пополам и попарно сложим значения. Разумеется, каждую операцию сложения 2-х значений выполнит отдельный поток. После этого мы повторяем итерации цикла: деление количества элементов пополам и попарное сложение элементов. Итерации цикла повторяются пока мы не получим общую сумму значений в элементе массива с индексом "0".
count = ls; do { count = (count + 1) / 2; if(l < 256) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
Как можно заметить, каждая новая итерация цикла может начаться только после завершения операций всех участвующих потоков. Поэтому синхронизацию мы осуществляем после каждой итерации цикла.
Здесь надо обратить внимание, что архитектурой OpenCL предусмотрена только полная синхронизация потоков. И все элементы рабочей группы должны дойти до соответствующего оператора barrier. В противном случае выполнение программы "зависнет". Поэтому, при организации программы нужно очень аккуратно подходить к точкам синхронизации потоков. Их крайне не рекомендуется устанавливать в теле условных операторов, когда алгоритм программы позволит обойти точки синхронизации хотя бы одному потоку.
После завершения итераций вышеуказанных циклов мы получили сумму всех экспоненциальных значений исходных данных и можем завершить процесс нормализации данных. Для этого мы организуем ещё один цикл, в котором и заполним буфер исходных данных соответствующими значениями.
float sum = temp[0]; if(sum != 0) { count = 0; while((count * ls + l) < total) { uint shift = count * ls + l; outputs[shift] = exp(inputs[shift]) / (sum + 1e-37f); count++; } } }
На этом мы завершаем работу над кернелом прямого прохода и переходим к созданию кернелов обратного прохода.
Начнем мы создание кернелов обратного прохода с распределения градиента через функцию SoftMax. Здесь следует обратить внимание, что основной особенностью данной функции является нормализация суммы всех значений результатов в "1". Следовательно, изменение только одного значения на входе в функцию активации ведет к пересчету всех значений вектора результатов. Аналогично, при распределении градиента ошибки каждый элемент исходных данных должен получить свою долю ошибки от каждого элемента вектора результатов. Математическая формула влияние каждого элемента исходных данных на результат представлены ниже. Её нам и предстоит реализовать в кернеле SoftMax_HiddenGradient.
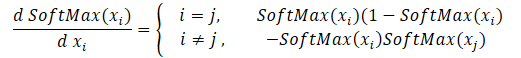
В параметрах кернел получает указатели на 3 буфера данных. Буферы результатов после прямого прохода, градиентов от предыдущего слоя или от функции потерь. А также буфер градиентов предыдущего слоя, в который будем записывать результаты работы данного кернела.
В теле кернела мы определяем идентификатор потока и общее количество запущенных потоков. Которые нам укажут на элемент массива для записи результата работы текущего потока и размеры буферов.
Дале мы подготовим 2 частные переменные. В одну мы скопируем значение соответствующего элемента вектора результатов прямого прохода. А вторую мы объявим для сбора результатов работы текущего потока. Использование частных переменных обусловлено особенностями архитектуры OpenCL устройств. Обращение к частным переменным осуществляется гораздо быстрее аналогичных операций с буферами в глобальной памяти. Поэтому такой подход позволяет повысить общую производительность работы кернела.
Затем мы в цикле соберем градиент ошибки со всех элементов результатов в соответствии с указанной выше формулой. После завершения операций цикла мы передаем накопленное значение градиента в соответствующий элемент буфера градиентов предыдущего слоя и завершаем работу кернела.
__kernel void SoftMax_HiddenGradient(__global float* outputs, __global float* output_gr, __global float* input_gr) { size_t i = get_global_id(0); size_t outputs_total = get_global_size(0); float output = outputs[i]; float result = 0; for(int j = 0; j < outputs_total; j++) result += outputs[j] * output_gr[j] * ((float)(i == j ? 1 : 0) - output); input_gr[i] = result; }
Теперь нам осталось реализовать кернел определения градиента ошибки функции потерь SoftMax_OutputGradient. Напомню, что в данном случае мы используем LogLoss в качестве функции потерь.
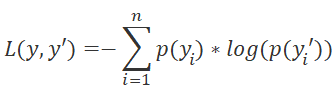
Так как мы распределяем градиенты на элементы соответствующего действия, то мы и производную будем считать поэлементно. Это позволяет нам разделить расчет градиента ошибки по потокам. Из школьного курса математики мы знаем, что производная логарифма равна отношению 1 к аргументу функции. Таким образом, производная нашей функции потерь примет следующий вид.
![]()
Нам остается лишь реализовать приведенную выше математическую формулу в кернел программы OpenCL. Его код довольно прост и умещается в 2 строки, приведенные ниже.
__kernel void SoftMax_OutputGradient(__global float* outputs, __global float* targets, __global float* output_gr) { size_t i = get_global_id(0); output_gr[i] = -targets[i] / (outputs[i] + 1e-37f); }
На этом мы завершаем работу на стороне OpenCL программы и переходим к работе на стороне основной программы. Здесь мы добавляем константы для работы с новыми кернелами, добавляем объявление новых кернелов и создаем методы их вызовов.
#define def_k_SoftMax_FeedForward 36 #define def_k_softmaxff_inputs 0 #define def_k_softmaxff_outputs 1 #define def_k_softmaxff_total 2 //--- #define def_k_SoftMax_HiddenGradient 37 #define def_k_softmaxhg_outputs 0 #define def_k_softmaxhg_output_gr 1 #define def_k_softmaxhg_input_gr 2 //--- #define def_k_SoftMax_OutputGradient 38 #define def_k_softmaxog_outputs 0 #define def_k_softmaxog_targets 1 #define def_k_softmaxog_output_gr 2
Методы вызова кернелов полностью повторяют используемые ранее алгоритмы аналогичных методов. С их полным кодом можно ознакомиться во вложении.
Поле реализации недостающей функции SoftMax мы можем приступить к реализации советника для реализации и обучения модели policy gradient.
3.2 Строим советник для обучения модели
Для обучения модели аппроксимации функции политики поведения агента мы создадим новый советник в фале "REINFORCE.mq5". Основной функционал данного советника будет заимствован из "Q-learning.mq5", который мы создали в прошлой статье для обучения модели DQN. Надо отметить, что в отличии от модели DQN в новом советнике мы используем только одну нейронную сеть. Но для корректной реализации алгоритма нам потребуется создание трех стеков: состояний среды, совершенных действий и полученных вознаграждений.
CNet StudyNet; CArrayObj States; vectorf vActions; vectorf vRewards;
Далее мы немного изменили внешние параметры советника в соответствии с требованиями алгоритма.
input int SesionSize = 24 * 22; input int Iterations = 1000; input double DiscountFactor = 0.999;
Метод инициализации советника остался практически без изменений. Мы лишь добавили инициализацию стеков для накопления выполняемых действий и полученных вознаграждений.
if(!vActions.Resize(SesionSize) || !vRewards.Resize(SesionSize)) return INIT_FAILED;
Сам же процесс обучения построен в функции Train. Её я и предлагаю рассмотреть подробнее.
В начале функции, как и ранее, мы определяем диапазон обучающей выборки в соответствии с заданными внешними параметрами.
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time);
После определения периода обучения мы загружаем обучающую выборку.
int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); //--- int total = bars - (int)(HistoryBars + 2 * SesionSize);
Указанные выше операции не отличаются от используемых в ранее советниках. Далее же следует система циклов обучения модели. В ней и реализованы основные подходы обучения модели.
Внешний цикл отвечает за перебор сессий обучения модели. И в начале цикла мы случайным образом определяем бар начала сессии в общем пуле загруженной истории.
CBufferFloat* State; for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int error_code; int shift = (int)(fmin(fabs(Math::MathRandomNormal(0,1,error_code)),1) * (total) + SesionSize); States.Clear();
Затем мы организовываем цикл, в котором наш агент шаг за шагом полностью проходит сессию. В теле цикла мы сначала заполняем буфер текущего состояния системы историческими данными на анализируемый период. Аналогичную операцию мы осуществляли при обучении предыдущих моделей перед каждым прямым проходом.
for(int batch = 0; batch < SesionSize; batch++) { int i = shift - batch; State = new CBufferFloat(); if(!State) { ExpertRemove(); return; } int r = i + (int)HistoryBars; if(r > bars) continue; for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = r - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) || !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) || !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign)) break; }
И осуществляем прямой проход нашей модели.
if(IsStopped()) { ExpertRemove(); return; } if(State.Total() < (int)HistoryBars * 12) continue; if(!StudyNet.feedForward(GetPointer(State), 12, true)) { ExpertRemove(); return; }
По результатам прямого прохода мы получаем вероятностное распределение действий и семплируем очередное действие из нормального распределения с учетом полученного вероятностного распределения. Непосредственно семплирование осуществляется отдельной функцией GetAction, в параметрах которой передается вероятностное распределение.
StudyNet.getResults(TempData); int action = GetAction(TempData); if(action < 0) { ExpertRemove(); return; }
После семплирования действия мы определяем вознаграждение для выбранного действия по размеру следующей свечи. Политику вознаграждения мы используем принятую в прошлой статье.
double reward = Rates[i - 1].close - Rates[i - 1].open; switch(action) { case 0: if(reward < 0) reward *= -2; break; case 1: if(reward > 0) reward *= -2; else reward *= -1; break; default: reward = -fabs(reward); break; }
И сохраняем весь набор данных в стек. Здесь надо сказать, что состояния и действия мы просто добавляем в стеки. А вот вознаграждения мы сохраняем с учетом фактора дисконтирования. И тут надо определить на стадии проектирования каким образом мы будем дисконтировать вознаграждения. Здесь есть 2 варианта дисконтирования. Мы можем дисконтировать первые награды, предоставляя больше значимости последующим вознаграждениям. Такой подход чаще всего используется, когда в процессе прохода по сессии агент получает промежуточные вознаграждения. Но основная задача агента добраться до конца сессии, где он получит максимальное вознаграждение.
Второй подход обратный, когда больше значимости дается первым наградам. А последующие вознаграждения дисконтируются. Этот вариант приемлем, когда мы стремимся к максимальному и быстрому вознаграждению. Именно такой подход использовал я. Ведь нам важна сразу получить максимальную прибыль, а не пересиживать убытки в ожидании разворота рынка после совершения сделки.
И ещё один момент. После завершения прохода сессии нам предстоит посчитать комулятивное вознаграждение от каждого состояния до конца сессии. Векторные операции MQL5 позволяют посчитать только прямую кумулятивную сумму. Поэтому, мы просто и сохраним все значения вознаграждений в вектор в обратном порядке. А после завершения цикла воспользуемся векторной операцией для подсчета кумулятивной суммы.
if(!States.Add(State)) { ExpertRemove(); return; } vActions[batch] = (float)action; vRewards[SessionSize - batch - 1] = (float)(reward * pow(DiscountFactor, (double)batch)); vProbs[SessionSize - batch - 1] = TempData.At(action); //--- }
После сохранения данных мы переходим к следующий итерации цикла. Таким образом мы собираем данные за всю сессию.
По завершению всех итераций цикла мы посчитаем суммарное вознаграждение за сессию с учетом дисконтирования, вектор кумулятивных сумм вознаграждения от каждого состояния до конца сессии и значение функции потерь.
Тут же мы сохраним текущую модель, но только при условии обновления максимального вознаграждения.
float cum_reward = vRewards.Sum(); vRewards = vRewards.CumSum(); vRewards = vRewards / fmax(vRewards.Max(), fabs(vRewards.Min())); float loss = (vRewards * MathLog(vProbs) * (-1)).Sum(); if(MaxProfit < cum_reward) { if(!StudyNet.Save(FileName + ".nnw", loss, 0, 0, Rates[shift - SessionSize].time, false)) return; MaxProfit = cum_reward; }
Теперь, когда у нас есть значения вознаграждений по всему пути прохождения агентом сессии мы можем организовать цикл обучения модели функции политики. Для этого мы организуем еще один цикл. В нём мы поочередно будем извлекать состояния среды из нашего буфера и осуществлять прямой проход модели. Это необходимо для восстановления всех внутренних значений модели для соответствующего состояния среды.
Затем мы подготовим вектор эталонных значений для текущего состояния среды. Напомню, мы будем максимизировать вероятности выбора действия с положительным вознаграждением и минимизировать вероятности других. Поэтому, если при выполнении действия мы получили положительное значение мы заполняем вектор эталонных вероятностей нулевыми значениями. И только для совершенного действия установим вероятность 1. В случае получения отрицательного вознаграждения мы заполним вектор эталонных вероятностей единицами. И только для выбранного действия установим нулевую вероятность.
for(int batch = 0; batch < SessionSize; batch++) { State = States.At(batch); if(!StudyNet.feedForward(State)) { ExpertRemove(); return; } if((vRewards[SessionSize - batch - 1] >= 0 ? (!TempData.BufferInit(Actions, 0) || !TempData.Update((int)vActions[batch], 1)) : (!TempData.BufferInit(Actions, 1) || !TempData.Update((int)vActions[batch], 0)) )) { ExpertRemove(); return; } if(!StudyNet.backProp(TempData)) { ExpertRemove(); return; } }
И выполним обратный проход для обновления весовых коэффициентов нашей модели. Итерации повторяем для всех сохраненных состояний среды.
После выполнения всех итераций цикла мы выводим информационное сообщение в журнал и переходим к следующей сессии.
PrintFormat("Iteration %d, Cummulative reward %.5f, loss %.5f", iter, cum_reward, loss); } Comment(""); //--- ExpertRemove(); }
Не забываем на каждом шаге контролировать процесс выполнения операций. И после успешного выполнения всех итераций мы выходим из функции и генерируем событие закрытия терминала. С полным кодом советника можно ознакомиться во вложении.
Ещё надо сказать, что для аппроксимации функции политики нашей модели мы использовали нейронную сеть с архитектурой аналогичной обучению Q-функции из прошлой статьи. Более того, мы взяли обученную модель из прошлой статьи и заменили в ней блок принятия решений с добавления SoftMax последним слое нейронной сети для нормализации данных.
Процесс обучения модели полностью аналогичен процессу обучению любой другой модели. Таких примеров много в каждой статье этой серии. И для подведения итогов работы в этой статье я решил немного отступить от уже шаблонного формата статьи. Вместо этого я предлагаю посмотреть на работу обученных моделей в тестере стратегий.
4. Тестирование обученной модели в тестере стратегий
В предыдущей статье мы обучили DQN модель. В этой мы создали и обучили модель policy gradient. И я предлагаю создать тестовых советников, с помощью которых мы сможем посмотреть на работу моделей в тестере стратегий. Для этого мы создадим 2 советника "Q-learning-test.mq5" и "REINFORCE-test.mq5". По названию файлов легко догадаться какую модель тестирует каждый советник.
Структура построения советников абсолютно одинакова. Поэтому мы рассмотрим только один. А с полным кодом обоих советников можно ознакомиться во вложении.
Новый советник "REINFORCE-test.mq5" построен на базе рассмотренного выше советника "REINFORCE.mq5". Но так как советник не будет обучать модель мы удалили функцию Train. При этом основной функционал мы перенести в функцию OnTick, которая обрабатывает каждое событие появления нового тика.
Наша обученная модель оценивает состояния среды по закрытым свечам. Поэтому, в теле функции OnTick мы проверяем открытие новой свечи. И только при появлении новой свечи будут выполнять остальные операции функции.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if(lastBar >= iTime(Symb.Name(), TimeFrame, 0)) return;
При появлении новой свечи мы загружаем последние исторические данные и заполняем буфер описания состояния системы.
int bars = CopyRates(Symb.Name(), TimeFrame, 0, HistoryBars+1, Rates); if(!ArraySetAsSeries(Rates, true)) return; RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); //--- State1.Clear(); for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = (int)HistoryBars - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) || !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) || !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign)) break; }
Затем мы проверяем корректность заполнения данных и вызываем прямой проход нашей модели.
if(State1.Total() < (int)(HistoryBars * 12)) return; if(!StudyNet.feedForward(GetPointer(State1), 12, true)) return; StudyNet.getResults(TempData); if(!TempData) return;
В результате прямого прохода мы получаем вероятностное распределение возможных действий, из которого мы семплируем случайное действие.
lastBar = Rates[0].time; int action = GetAction(TempData); delete TempData;
Далее нам предстоит совершить выбранное действие. Но прежде, чем перейти к открытию новой сделки мы проверим наличие уже открытых позиций. Для этого мы определим 2 флага: Buy и Sell. При объявлении переменных мы укажем им значение false.
После этого мы организуем цикл с перебором всех значений. И при нахождении открытой позиции по анализируемому символу мы изменим значение соответствующего флага.
bool Buy = false; bool Sell = false; for(int i = 0; i < PositionsTotal(); i++) { if(PositionGetSymbol(i) != Symb.Name()) continue; switch((ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE)) { case POSITION_TYPE_BUY: Buy = true; break; case POSITION_TYPE_SELL: Sell = true; break; } }
Далее следует блок совершения торговых операций. Здесь мы используем оператор switch для разветвления алгоритма блока в зависимости от совершаемого действия. Если выбор пал на открытие новой позиции, мы проверяем флаги открытых позиций. В случае, когда уже открыта позиция в соответствующем направлении мы просто оставляем её в рынке и ожидаем открытия новой свечи.
Если же на момент принятия решения открыта противоположная позиция, мы сначала закрываем открытую позицию и лишь потом открываем новую.
switch(action) { case 0: if(!Buy) { if((Sell && !Trade.PositionClose(Symb.Name())) || !Trade.Buy(Symb.LotsMin(), Symb.Name())) { lastBar = 0; return; } } break; case 1: if(!Sell) { if((Buy && !Trade.PositionClose(Symb.Name())) || !Trade.Sell(Symb.LotsMin(), Symb.Name())) { lastBar = 0; return; } } break; case 2: if(Buy || Sell) if(!Trade.PositionClose(Symb.Name())) { lastBar = 0; return; } break; } //--- }
Если же агенту необходимо закрыть все позиции, то мы вызываем функцию закрытия позиций по текущему символу. Вызов функции осуществляется только при наличии открытой хотя бы одной позиции.
И, конечно, не забываем контролировать процесс выполнения операций на каждом шаге.
С полным кодом советника можно ознакомиться во вложении.
Первой мы протестировали модель DQN. И здесь нас ждал неожиданный сюрприз. Модель получила прибыль. Но при этом совершила только одну торговую операцию, которая была открыта на протяжении всего теста. График инструмента с совершенной сделкой представлен ниже.
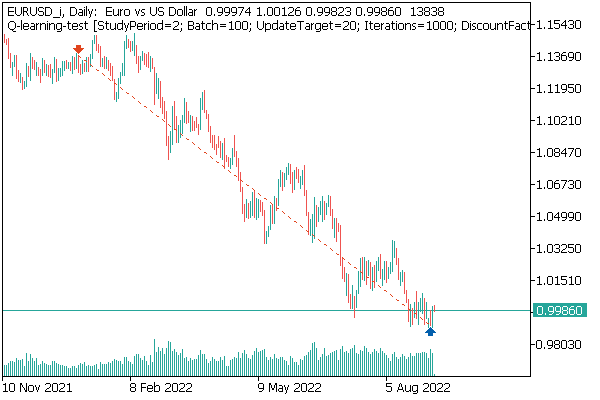
Оценивая сделку на графике инструмента, нельзя не согласиться, что модель четко определила глобальный тренд и открыла сделку в его направлении. Сделка прибыльная, но открыт вопрос — сможет ли модель вовремя закрыть такую сделку? На самом деле мы обучали модель на исторических данных за 2 последних года. И все 2 года на рынке преобладает медвежий тренд по анализируемому инструменту. Поэтому возникает вопрос, сможет ли модель вовремя закрыть сделку.
И тут надо сказать, что при использовании жадной стратегии модель policy gradient дает схожие результаты. А помните, начиная изучение методов обучения с подкреплением, я неоднократно акцентировал внимание на необходимости правильного выбора политики вознаграждения. И тут я решил поэкспериментировать с политикой вознаграждения. В частности, чтобы исключить пересиживание в позиции убытков было принято решением о повышении штрафов за убыточность позиций. И, соответственно, дообучил модель policy gradient с учетом новой политик наград. После нескольких экспериментов с гиперпараметрами модели мне удалось добиться 60% прибыльных операций. График тестирования представлен ниже.
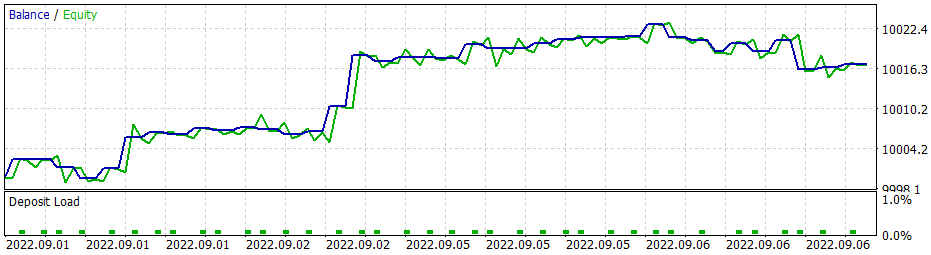
Среднее время удержания позиции составляет 1 час 40 минут.
Заключение
В данной статье мы изучили еще один алгоритм из методов обучения с подкреплением. Мы создали и обучили модель методом policy gradient.
В отличии от других статей этой серии, в данной статье мы обучили и протестировали модели в тестере стратегий. По результатам тестирования можно сделать вывод, что модели вполне способны генерировать сигналы для совершения прибыльных торговых операций. Вместе с тем, стоит ещё раз отметить важность правильного выбора политики вознаграждения и функции потерь для достижения желаемого результата.
Ссылки
- Нейросети — это просто (Часть 25): Практикум Transfer Learning
- Нейросети — это просто (Часть 26): Обучение с подкреплением
- Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | REINFORCE.mq5 | Советник | Советник для обучения модели |
| 2 | REINFORCE-test.mq5 | Советник | Советник для тестирования модели в тестере стратегий |
| 1 | Q-learning-test.mq5 | Советник | Советник для тестирования модели DQN в тестере стратегий |
| 2 | NeuroNet.mqh | Библиотека классов | Библиотека для организации моделей нейронных сетей |
| 3 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL для организации моделей нейронных сетей |
…
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торговой системы на основе индикатора Force Index
Разработка торговой системы на основе индикатора Force Index
 Возможности Мастера MQL5, которые вам нужно знать (Часть 02): Карты Кохонена
Возможности Мастера MQL5, которые вам нужно знать (Часть 02): Карты Кохонена
 Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
Нейросети — это просто (Часть 27): Глубокое Q-обучение (DQN)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Я попробовал напрямую в файле VAE.mqh добавить строку #include <Math\Stat\Normal.mqh> Но это не дало результата. Компилятор всё равно пишет 'MathRandomNormal' - undeclared identifier VAE.mqh 92 8. При этом если эту функцию стереть и начать набирать заново, то появляется всплывающая подсказка с этой функцией, что как я понимаю , говорит о том что по идее она видна с файла VAE.mqh.
Вообще я уэе попробовал на другом компе с другой даже версией винды, и результат тот же - не видит функцию и не компилируется. мт5 последней версии бетта 3420 от 5 сентября 2022.
Дмитрий а у вас никаких настроек в редакторе не включено?
Я попробовал напрямую в файле VAE.mqh добавить строку #include <Math\Stat\Normal.mqh> Но это не дало результата. Компилятор всё равно пишет 'MathRandomNormal' - undeclared identifier VAE.mqh 92 8. При этом если эту функцию стереть и начать набирать заново, то появляется всплывающая подсказка с этой функцией, что как я понимаю , говорит о том что по идее она видна с файла VAE.mqh.
Вообще я уэе попробовал на другом компе с другой даже версией винды, и результат тот же - не видит функцию и не компилируется. мт5 последней версии бетта 3420 от 5 сентября 2022.
Дмитрий а у вас никаких настроек в редакторе не включено?
Попробуйте закомментировать строку "namespace Math"
Дмитрий у меня терминал версии 3391 от 5 августа 2022 (последняя стабильная версия). Сейчас попробовал обновиться до бетта версии 3420 от 5 сентября 2022. Ошибка с values.Assign ушла. А вот с MathRandomNormal не уходит. Библиотечка с этой функцией есть у меня по пути как вы написали. Но в файле VAE.mqh у вас нет ссылки на эту библиотечку, а в файле NeuroNet.mqh у вас указывается эта библиотечка так:
namespace Math
{
#include <Math\Stat\Normal.mqh>
}
Но так оно у меня не собирается. :(
PS: Если напрямую в файл VAE.mqh указать путь на библиотечку. Так можно сделать? Я не очень понимаю как у вас задана библиотечка в файле NeuroNet.mqh, не будет ли конфликта?
3445 от 23 сентября - тоже самое.
Нужен совет :) Только присоединился после переустановки терминал, хочу провести обучение и выдает ошибку
Здравствуйте.
Нужен совет :) Только присоединился после переустановки терминал, хочу провести обучение и выдает ошибку