Нейросети в трейдинге: Вероятностное прогнозирование временных рядов (K2VAE)

Введение

В последние годы анализ временных рядов сделал настоящий прорыв. Задачи обнаружения аномалий, классификации и восстановления пропущенных значений теперь решаются точнее и быстрее. Однако, для финансовых рынков куда важнее вероятностное прогнозирование: не просто предсказать цену актива, а оценить диапазон возможных сценариев. Такие оценки помогают трейдерам и аналитикам выстраивать гибкие стратегии, управлять рисками и принимать обоснованные решения.

Классические модели отлично справляются с краткосрочными прогнозами. Но стоит заглянуть дальше, и ошибки начинают накапливаться, волатильность раздувает неточности, а вычислительные затраты стремительно растут. Особенно на финансовых рынках, где каждое событие (отчёт компании или геополитический сюрприз) вносит нелинейность и меняет правила игры.

В качестве одного из возможных вариантов решения подобной задачи в работе "K²VAE: A Koopman-Kalman Enhanced Variational AutoEncoder for Probabilistic Time Series Forecasting" был предложен новый фреймворк, опирающийся на две фундаментальные идеи. Во‑первых, теория Купмана переводит нелинейные процессы в линейную форму. Представьте, что вы смотрите на график цены акции через специальные линзы, и он превращается в прямую линию — такой подход упрощает понимание динамики. Во‑вторых, классический фильтр Калмана аккуратно перерабатывает новые данные, корректируя прогноз каждый раз, когда приходит свежая информация: отчёт о прибыли, изменение процентных ставок или неожиданное событие.

Авторы работы объединили эти идеи в фреймворк K²VAE — лёгкую и быструю систему на базе вариационного автоэнкодера. Сначала KoopmanNetнакладывает линейную структуру на исторические котировки и индикаторы. Затем KalmanNet, построенная на подходах фильтра Калмана, шаг за шагом уточняет оценку возможных движений и их неопределённость. Такая архитектура позволяет прогнозировать на краткосрочном и долгосрочном горизонтах, сохраняя высокую точность и устойчивость.

Важные преимущества фреймворка K²VAE:

• прозрачность модели. Линейная часть даёт трейдерам понятные сигналы, а не чёрный ящик;
• гибкость прогнозов. Можно быстро получить сценарии для разных активов: валютных пар, индексов, сырьевых товаров;
• управление рисками. Адаптивное уточнение доверительного интервала помогает вовремя снижать риск больших убытков.

В результате K²VAE становится универсальным решением для краткосрочных и долгосрочных прогнозов, позволяя не ограничиваться одним сценарием, а сразу оценивать весь спектр возможных движений рынка. Это существенно повышает эффективность управления портфелем и надёжность автоматических торговых стратегий — вы видите не просто точечный прогноз, а картину потенциальных рисков и возможностей.

Алгоритм K²VAE

В динамике финансовых рынков мы часто сталкиваемся с кажущимся хаосом — колебания цен, внезапные всплески волатильности, влияние новостных сообщений. Теория Купмана предлагает взгляд изнутри: вместо того чтобы пытаться напрямую приручить нелинейность, мы переводим нашу систему в особое измерительное пространство. Здесь каждый вектор состояния xₖ (например, корзина котировок или набор экономических индикаторов) через функцию ψ превращается в некое измерение, где эволюция описывается линейным оператором 𝒦. Проще говоря, сложный график цен мы расстилаем так, чтобы он лег по прямой, и благодаря этому оказывается значительно проще анализировать и прогнозировать основную динамику временного ряда. Такой приём помогает отделить долгосрочную тенденцию от краткосрочных шумов.

Однако даже с линейным представлением мы остаёмся в плену неопределённости: котировки меняются каждую секунду, приходят новые экономические отчёты, центральные банки корректируют ставку. Именно здесь на сцену выходит фильтр Калмана. Этот алгоритм работает по простому, но мощному принципу Прогноз – Корректировка: сначала мы прогнозируем текущее состояние системы и оцениваем нашу уверенность в прогнозе (матрица Pₖ), а затем, получив фактическое измерение (цену, объём торгов или макроэкономический индикатор) вычисляем коэффициент Калмана Kₖ. С его помощью подминаем первоначальный прогноз под реальность и обновляем оценку неопределённости. Для трейдера это эквивалент оперативного обучения модели на свежих данных: отчёты компаний, изменение ликвидности или внезапные геополитические события мгновенно интегрируются в прогноз, минимизируя отставание модели от живого рынка.

Объединив линейное развёртывание системы и адаптивную фильтрацию, мы получаем прочный фундамент для вероятностного прогноза. Но чтобы не ограничиваться одним-единственным сценарием, мы добавляем мощь вариационного автоэнкодера. VAE превращает задачу в условную генерацию: на входе — исторические данные X (T последних наблюдений по N активам), на выходе — не один вектор будущих значений, а распределение возможных траекторий Y. Ключевой момент — латентная переменная Z, отвечающая за скрытые рыночные факторы: корреляции, циклы, неожиданные шоки. Оптимизация ведётся через нижнюю границу лог-правдоподобия. Первый компонент штрафует модель за плохую генерацию, а второй — за уход латентного распределения в крайние области, далекие от наших априорных ожиданий.

В фреймворке K²VAE эти три элемента (KoopmanNet, KalmanNet и VAE) не просто уживаются рядом, а органично дополняют друг друга. В целом, архитектура K²VAE выстроена по чёткой многоступенчатой схеме, в которой каждая компонента отвечает за свой этап превращения анализируемых данных в понятную динамическую модель.

Сначала модуль Input Token Embedding разбивает исходный временной ряд на токены — небольшие фрагменты истории цен или показателей ликвидности. Этот приём похож на то, как аналитик делит график котировок на отрезки с ключевыми уровнями поддержки и сопротивления: он делает данные более осмысленными.

Далее KoopmanNet переводит эти токены в так называемое измерительноепространство. Здесь сложная нелинейность временных рядов (корреляции между активами, краткосрочные всплески волатильности) раскладывается на простые линейные компоненты. С помощью процедуры обучения мы подбираем линейный оператор Купмана, который при итерации по первому токену строит модель эволюции. Разумеется, идеального измерительного пространства, делающего систему абсолютно линейной, не существует — отсюда и смещение в прогнозах.

После этого вступает в игру KalmanNet. По аналогии с фильтром Калмана он получает линейный прогноз и дообучается на новых данных, уточняя ковариацию многомерного состояния и тем самым формируя вариационный постериор Q(Z|X) с прозрачной семантикой. Для финансов это критически важно: мы не просто строим базовую траекторию движения цены, а сразу оцениваем диапазон её возможных отклонений — от внезапных гэпов до разворотов в ответ на важные новости.

Наконец, декодер выполняет функцию обратного измерения (ψ⁻¹), возвращая полученные образцы из латентного пространства в привычный формат временного ряда. Он же отвечает за моделирование финального распределения P(Y|Z,X) на горизонте планирования. Таким образом, мы получаем готовый к использованию сценарий будущих котировок — и не один, а множество вероятностных траекторий, каждая со своей оценкой риска и доверия.

В итоге K²VAE превращает необработанные финансовые данные в стройную линейно-динамическую модель с адаптивным уточнением неопределённости и генерацией полного спектра возможных движений рынка. Это мощный инструмент для планирования портфеля, оценки рисков и создания надёжных алгоритмических стратегий.

Разбиение временного ряда на патчи (patches) — это гораздо больше, чем техническая уловка. В финансовом анализе это сродни переходу от отдельных тиковых котировок к пятиминутным или получасовым свечам, которые сразу демонстрируют и тренд, и ключевые всплески волатильности. В фреймворке K²VAE предварительная обработка данных строится на аналогичной идее, но идет дальше привычной канальнонезависимой архитектуры, где каждый канал обрабатывается отдельно. Вместо этого, авторы фреймворка объединяют все переменные (цены разных активов, объёмы торгов, технические индикаторы) в одном патче, что позволяет модели естественным образом учитывать перекрестные влияния между ними.

Изначально, контекстный временной ряд X, представляющий собой матрицу из N переменных за T временных шагов, разбивается на несколько равных непересекающихся фрагментов длиной s. Каждый из этих патчей содержит одновременно данные всех N показателей за s временных точек, что дает срез рыночной ситуации за данный промежуток. После этого вытягиваем каждый фрагмент в вектор размерности N·s и пропускаем через линейную проекцию, которая сжимает полученную информацию в компактное embedding-представление размером d. Благодаря такой операции, модель не просто учится заглядывать внутрь каждого патча, но и автоматически выявляет наиболее значимые сочетания переменных: будь то корреляция между акциями технологического сектора и полупроводниковыми акциям, или синхронные всплески объёмов торгов в разных сегментах рынка.

Такой едва ли не взрывной переход от разрозненных каналов к многомерным токенам дает сразу несколько преимуществ. Во‑первых, модель мгновенно фиксирует кластерные явления, когда волатильность или ценовые тренды охватывают несколько активов одновременно. Во‑вторых, локальные шумы и случайные джиттеры внутри одного патча выравниваются, что значительно уменьшает количество ложных сигналов. И в-третьих, благодаря более обширному охвату переменных, внутри каждого токена становятся заметнее скрытые циклы и долгосрочные закономерности, которые при традиционном подходе могли бы остаться незамеченными или исказиться при независимой обработке каналов.

Таким образом, K²VAE получает на вход не набор отдельных признаков, а готовый к анализу комплексный срез рыночной обстановки за каждый интервал s. Это и становится отправной точкой для последующих этапов.

В реальных финансовых рядах мы сталкиваемся сразу с несколькими проявлениями нелинейности: фазы ценовых циклов могут смещаться друг относительно друга, статистические характеристики меняются при выходе важных отчётов, а внезапные новости разрывают привычные закономерности. Чтобы приручить эту сложность, авторы фреймворка K²VAEнадевали линзы Купмана — то есть переводили токены из зоны хаотичных колебаний в пространство, где их эволюция оказывается простой и прямолинейной.

На практике это выглядит так. Сначала каждый сглаженный embedding‑вектор патча X′ᴾ проходит через небольшой, но мощный MLP, исполняющий роль измерительной функции ψ. Проще говоря, мы перевариваем сложные взаимосвязи цен и индикаторов в новый вектор xᴾᵢ*, где скрытая динамика становится более разборчивой.

Собрав все такие векторы, получаем матрицу X*ᴾ, в которой каждая строка — это уже линейно читаемая проекция одного патча. Но одного взгляда на это мало. Чтобы понять, как система движется от шага к шагу, мы используем метод eDMD (extended Dynamic Mode Decomposition), вытаскивая из X*ᴾ пару предыдущее–следующее и вычисляя оператор 𝒦loc, минимизирующий расхождение между ними. Он обучается так, чтобы первая колонка X*ᴾ, умноженная на 𝒦loc, как можно точнее воспроизводила вторую, и так далее, до конца ряда. Такой приём позволяет локально выстраивать правила перехода шаг за шагом.

Переходя от локального к глобальному, мы добавляем второй, обучаемый компонент 𝒦glo. В сумме они образуют полный Koopman‑оператор 𝒦 = 𝒦loc + 𝒦glo. Именно он позволяет не только реконструировать исторические патчи, но и смело заглянуть в будущее, умножая первую проекцию x₁ᴾ* на 𝒦ⁿ, 𝒦ⁿ⁺¹ и так далее. При этом m = L/s патчей в измерительном пространстве однозначно соответствует L шагам в исходных рядах.

В результате даже самые запутанные взаимодействия между ценами акций, объёмами торгов и техническими индикаторами оказываются выпрямленными. K²VAE получает возможность быстро и точно строить прогнозы на любой горизонт — от ближайших минут до месяцев вперёд. При этом прозрачность модели сохраняется: мы видим и локальные правила перехода, и глобальные тренды, а линейная оболочка даёт возможность трейдерам и риск‑менеджерам понимать, за счёт чего формируется тот или иной сценарий.

После того как KoopmanNetвыпрямил основные тренды и реконструировал контекстную последовательность, неизбежно остаются небольшие промахи — разница между истинными проекциями патчей и их линейной аппроксимацией. Авторы фреймворка K²VAE не игнорируют эти остатки, а, наоборот, собирают их в единый информационный поток разностей, которые показывают, где и насколько линейная модель недотянула.

Этот матричный список жалоб учитывает любые неожиданности: внезапные гэпы, резкие скачки объёма или новостные шоки, которые пока ещё не успели найти отражение в операторе Купмана.

Затем, лёгкий Transformer‑интегратор берёт на себя роль мудрого советчика: он анализирует всю эту накопленную нелинейность и превращает её в серию управляющих импульсов U = [u₁, …, uₘ]. Каждый вектор uₖ служит сигналом, в каком направлении следует подтянуть прогноз на шаге k. Благодаря способности Transformer учитывать взаимосвязи между разными временными точками, модель учится перераспределять информацию об ошибках и корректировать их наиболее эффективным образом.

Получив управляющие команды, мы строим классическую процессную модель.

Где A отвечает за базовый переход шаг за шагом, B — за влияние импульса, а wₖ добавляет нотку случайного шума, отражающего непредсказуемые рыночные факторы. Начальное состояние z₀ мы берём из последнего истинного патча, чтобы модель стартовала с максимально точной точки.

Далее смотрим на полученный прогноз через призму наблюдательной модели.

Здесь H переводит внутреннее состояние в формат прогноза, а vₖ добавляет шум измерения, напоминающий о неточностях самой линейной части модели. В качестве приоритетного наблюдения мы принимаем ранее сгенерированный KoopmanNet прогноз для горизонта.

Традиционный цикл Прогноз–Корректировка позволяет KalmanNet динамично балансировать между линейным прогнозами и информацией об ошибках. Сначала мы получаем предварительный прогноз ẑₖ и матрицу ковариации P̂ₖ, оценивающую уверенность модели.

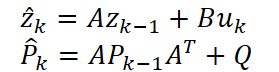
Затем, сравнивая его с наблюдением, вычисляем коэффициент Калмана Kₖ. После чего уточняем состояние и ковариацию.

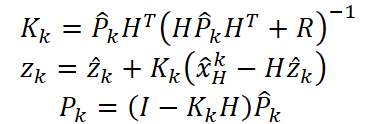
Так модель не просто реструктурирует прогноз, но и на каждом шаге чётко показывает, насколько ей понятен рынок, а где она всё ещё требует дополнительного подтверждения.

Чтобы не терять накопленной информации об ошибках, авторы фреймворка соединяют окончательные состояния с импульсами через skip‑connection.

Это гарантирует, что вплоть до тех пор, пока KoopmanNet и KalmanNet не освоят все нюансы, модель будет использовать весь объём доступной информации. По мере обучения величина U стремится к нулю — значит, линейная динамика становится всё более самодостаточной.

В итоге фреймворк K²VAE получает не просто прогноз цен, а сразу две связанные оценки: само значение и степень уверенности в нём. Для трейдера и риск‑менеджера это бесценный двойной сигнал: прогноз позволяет планировать сделки, а ковариация указывает, где стоит действовать осторожнее, а где можно рискнуть. Такой подход превращает алгоритмическую торговлю из слепой гонки за точечными предсказаниями во взвешенную стратегию управления рисками.

Наконец, мы переходим к завершающему этапу генерации вероятностного прогноза. На этом шаге у нас уже есть два ключевых результата: скорректированные латентные состояния Z' и ковариационные матрицы P, описывающие нашу уверенность на каждом этапе прогноза. Именно они и задают вариационное распределение из которого мы будем извлекать случайные семплы будущих сценариев.

Чтобы градиенты могли пробиваться сквозь случайную выборку, авторы фреймворка применяют привычный трюк с репараметризацией. Вместо того, чтобы напрямую тянутьZ из N(Z',P), они генерируют стандартный нормальный шум ϵ∈N(0,1) и строят:

Где L — нижнетреугольная матрица из разложения P = LLᵀ. Таким образом, сам процесс дифференцируем, и градиенты свободно текут от функции потерь к параметрам как KalmanNet, так и KoopmanNet.

Далее авторы K²VAEвозвращают полученные латентные векторы Zsample обратно в привычный формат временных рядов с помощью декодера — двух симметричных MLP, зеркально отражающих исходный Koopman‑Encoderψ. Первый MLP, который мы обозначим ψ⁻¹μ, прогнозирует вектор средних значений μ, а второй, ψ⁻¹σ, — вектор стандартных отклонений σ.

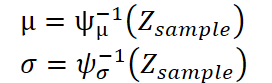
В итоге каждый полученный семпл генерирует вектор будущих значений вместе с оценкой разброса — то есть, мы сразу видим не только наиболее вероятную траекторию, но и границы доверительного интервала.

Чтобы дополнительно закрепить качество обратного преобразования, авторы фреймворка также подают в ψ⁻¹μ реконструированную последовательность X̂C.

Получаем XRec, по которой вычисляем ошибку реконструкции LRec. Это стимулирует измерительную функцию ψ строить действительно линейную систему, а декодер — точно возвращать данные в исходное пространство цен и индикаторов.

Наконец, собрав всё вместе, мы определяем распределение прогноза.

Для каждого семпла Декодер выдаёт вектор μ и вектор σ, из которых строится полнофункциональный вероятностный прогноз: медиана, доверительные интервалы, экстремальные сценарии.

На практике это означает, что трейдер или риск‑менеджер получает сразу развернутую картину возможных движений рынка — от консервативного скольжения в минимальном диапазоне до агрессивных выстрелов в сопровождении повышенной волатильности. Благодаря репараметризации и синхронному обучению всех компонентов (KoopmanNet, KalmanNet и Decoder), K²VAE обеспечивает гладкий, дифференцируемый пайплайн, где каждая итерация улучшает не только точность среднего прогноза, но и надёжность оценки рисков.

В сердце обучения K²VAE лежит дуэт из двух взаимодополняющих функций потерь, которые вместе формируют мощный механизм самосовершенствования модели. Первой из них выступает классическая ELBO‑цель (Evidence Lower Bound), где модель стремится одновременно достичь двух вещей: убедиться, что сгенерированные траектории Y подчиняются ожидаемому распределению, и не позволить латентному пространству Zубежать слишком далеко от наших априорных представлений.

Первый член — это штраф за плохую генерацию будущих сценариев: чем хуже декодер воспроизводит распределение Y из сэмплов Z, тем больше он нас накажет. Второй член — KL‑дивергенция между нашим вариационным апостериорным Q(Z|X) и простой нулевой априорой P(Z|X)=N(0,I). Благодаря этому, мы заставляем латентное пространство не разгоняться выше разумных пределов и плавно сходиться к стабильному состоянию, где линейная система в измерительном пространстве становится устойчивой.

Но ELBO само по себе не гарантирует, что наше измерительное пространство действительно будет вести себя линейно. Здесь на сцену выходит второй важнейший компонент — ошибка реконструкции.

Авторы фреймворка сравнивают фактическую исходную последовательность X с её восстановлением XRec, преобразованным через Декодер из реконструированной Koopman‑выходной цепочки. Чем точнее модель умеет возвращать данные в изначальное пространство, тем более правильно и чисто она выстраивает линейную динамику в измерительном слое. Эта функция потерь словно подпирает основание модели, не давая измерительной функции ψ сбиться с пути линейности.

В итоге, полная цель обучения — это просто сумма двух частей.

ELBO отвечает за правильную генерацию и аккуратное латентное пространство, а ошибка реконструкции — за строгость линейного приближения и качество обратного преобразования. Вместе они заставляют K²VAE не только учиться создавать правдоподобные сценарии развития рынка, но и формировать удобочитаемую, интерпретируемую линейно‑динамическую оболочку, устойчивую к выбросам волатильности и неожиданным рыночным всплескам. Это даёт трейдерам и риск‑менеджерам не просто прогноз, а полный, прозрачный и надёжный инструмент для принятия решений.

Авторская визуализация фреймворка K²VAE представлена ниже.

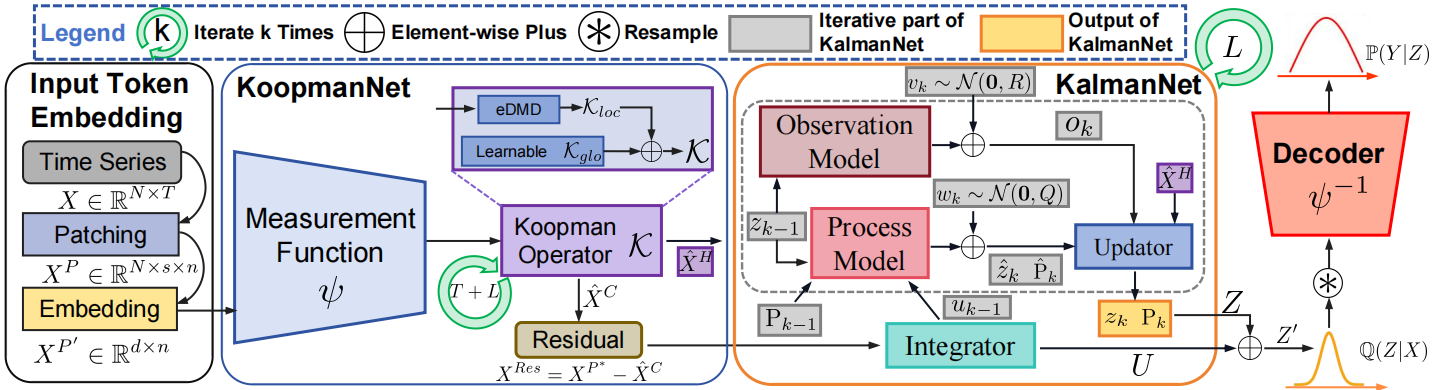
Реализация средствами MQL5

Теперь, когда мы подробно разобрали все ключевые компоненты фреймворка K²VAE — от линейного выпрямления динамики KoopmanNet до адаптивного уточнения неопределённости KalmanNet и завершающего VAE‑декодера — пора перенести теорию в реальность. В практической части нашей работы мы последовательно покажем, как реализовать каждый из этих модулей прямо в среде MQL5: от подготовки исходных данных и формирования патчей до обучения параметров модели и вывода готового результата. Такое практическое руководство позволит вам шаг за шагом воплотить K²VAE в собственных алгоритмических стратегиях, сохраняя всю гибкость и прозрачность предложенной архитектуры.

Как вы уже могли заметить, ядро K²VAE строится вокруг нескольких ключевых матриц — оператор Купмана, матрицы перехода и управления в KalmanNet, а также весовые проекции в энкодере и декодере. И в отличие от привычной иерархии Свертка → Активация → Свертка в стандартных нейросетях, тут одни и те же параметры участвуют сразу в нескольких местах пайплайна. Если бы мы просто скопировали эту идею как есть, нам пришлось бы объявлять по отдельным слоям MLP для каждого шага и, соответственно, дублировать веса, что не только замедлит работу и усложнит код, но и исказит задумку единого линейного оператора.

Поэтому нам необходимо найти альтернативное решение, которое позволит сохранить концепцию общих параметров, но при этом встроить их в существующий механизм обучения. И здесь стоит вспомнить старый, проверенный подход, к которому мы уже прибегали в других проектах, когда сталкивались с необходимостью обучаемых матриц вне стандартной иерархии нейронных слоёв.

Речь идёт о том, чтобы реализовать обучаемую матрицу в виде двухслойного MLP (Multi-Layer Perceptron). Первый слой подаёт одно фиксированное значение — 1.0, а второй — раскрывает из него всю нужную матрицу параметров. Эта хитрая конструкция позволяет использовать стандартные средства обратного распространения ошибки и обновления весов даже для таких внеструктурных параметров.

То есть, по сути, мы создаём псевдослой, задача которого — не обрабатывать исходные данные, а просто генерировать параметрическую матрицу. В первом приближении он бесполезен с точки зрения вычислений, но именно через него протекает градиент, который обучает второй слой — а это уже и есть наши матрицы A, B, K, H или, скажем, ψ.

Преимущество такого подхода в том, что он позволяет сохранять совместимость с общей структурой обучения нейросетей. У нас нет необходимости городить отдельный механизм оптимизации или вручную обновлять веса. Всё работает по правилам стандартного механизма: прямой проход → ошибка → распределение градиента → обновление параметров.

Таким образом, даже такие особенные элементы, как операторы Купмана или ковариационные матрицы KalmanNet, могут быть встроены в архитектуру с полной поддержкой обучения.

Когда в задаче требуется лишь одна параметризованная матрица, то реализация небольшой MLP внутри одного объекта вполне уместна. Мы просто добавляем в структуру пару внутренних слоёв, подаём константу на вход, и получаем на выходе нужную матрицу, которую далее используем в вычислениях. Всё просто, прозрачно и не требует дополнительной архитектуры.

Однако в рамках алгоритма KoopmanNet и KalmanNet ситуация иная: здесь нам необходим целый арсенал таких матриц. Использовать обособленные реализации для каждой — значит рисковать захламлением архитектуры и потерей читаемости.

Поэтому мы приняли более универсальное и масштабируемое решение — вынести логику генерации обучаемых матриц в отдельный класс, назовём его CParams. Такой класс берёт на себя всю работу по инициализации, хранению и обновлению весов, а также выдаче нужной матрицы в нужный момент. Это позволяет:

• централизованно управлять параметрами,
• легко масштабировать архитектуру при добавлении новых матриц,
• использовать единый интерфейс генерации,
• упрощает отладку и визуализацию.

Структура нового объекта представлена ниже и включает в себя минимальный, но функционально завершённый каркас для интеграции в любую нейросетевую схему.

class CParams  :  public   CNeuronBaseOCL
  {
protected:
   CNeuronBaseOCL    cOne;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override
                        { return FeedForward(); }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override
                        { return UpdateInputWeights(); }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override  { return true; }
   virtual bool      calcHiddenGradients(CNeuronBaseOCL *NeuronOCL) override { return true; }

public:
                     CParams(void) {};
                    ~CParams(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   virtual bool      Identity(const int rows, const int cols);
   //---
   virtual bool      FeedForward(void);
   virtual bool      UpdateInputWeights(void);
   //---
   virtual bool      Save(const int file_handle) override;
   virtual bool      Load(const int file_handle) override;
   //---
   virtual int       Type(void) override const  {  return defParams; }
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
  }; 

Ключевая особенность реализации — использование фиктивного входа cOne, заполненного единичными значениями, который подаётся на обучаемый слой. Таким образом, результирующая матрица, формируемая на выходе, становится единственным объектом, содержащим нужные параметры, пригодные для прямого использования.

Под капотомCParams наследуется от базового нейронного слоя CNeuronBaseOCL, что делает его полностью совместимым с остальной частью фреймворка. Основная логика работы сосредоточена в методах FeedForward и UpdateInputWeights, которые реализованы через вызов унаследованных одноименных методов с входом от cOne.

Инициализация объекта осуществляется через вызов метода Init, в котором создаются необходимые интерфейсы и производится настройка связей между компонентами.

bool CParams::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons,
                                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch))
      return false;
   if(!cOne.Init(numNeurons, 0, OpenCL, 1, optimization, iBatch))
      return false;
   cOne.SetActivationFunction(None);
   if(!cOne.getOutput().Fill(1))
      return false;
//---
   return true;
  }

Аккуратная реализация даёт нам возможность полностью скрыть все сложности, связанные с поддержкой прямого и обратного проходов, оптимизации параметров и буферов в OpenCL-контексте, оставляя пользователю только декларативное указание формы и назначения матрицы.

Финальный результат — универсальный, масштабируемый и переиспользуемый блок обучаемых параметров, пригодный для сложных графов вычислений. Иными словами, мы получаем гибкий аналог nn.Parameter из PyTorch, только в условиях MQL5 с поддержкой OpenCL.

Стоит особо отметить важную деталь: операции прямого прохода (FeedForward) в объекте CParams выполняются исключительно в процессе обучения. Это логично — ведь именно в этот момент матрица весов должна быть адаптирована к ошибкам модели и скорректирована с учётом обратного распространения.

bool CParams::FeedForward(void)
  {
   if(!bTrain)
      return true;
//---
   return CNeuronBaseOCL::feedForward(cOne.AsObject());
  }

Однако в режиме эксплуатации, то есть при использовании обученной модели для прогнозов или принятия решений, необходимость в перерасчёте матрицы отпадает. Полученная обучением матрица становится статичным параметром — она больше не изменяется и не требует выполнения лишних операций, особенно ресурсоёмких вызовов OpenCL-ядер.

Таким образом, при переходе в боевой режим мы фактически фиксируем параметры и можем смело отключить прямой проход, избавив систему от ненужных вычислений. Это снижает нагрузку на вычислительный ресурс, ускоряет работу модели и повышает её стабильность.

Такой подход — классический пример разделения вычислительных фаз, где обучение и использование строго разграничены по логике и по нагрузке. Это делает архитектуру не только более понятной и гибкой, но и более предсказуемой в эксплуатации, что особенно важно в системах реального времени.

Полный код объекта CParams и всех его методов представлен во вложении.

Мы уже проделали колоссальную работу: разобрали теоретические основы фреймворка K²VAE, детально рассмотрели ключевые модули, и даже реализовали объект CParams — универсальный генератор параметризованных матриц, незаменимый в архитектуре модели. Теперь перед нами стоит более масштабная задача — выстроить чёткую и согласованную логику всего фреймворка, где каждая деталь является важным компонентом в хорошо отлаженном механизме.

Но спешка здесь ни к чему. Настройка такой системы требует ясного ума, внимательности и свежего взгляда. Именно поэтому мы берём паузу до следующей статьи и возвращаемся с новыми силами и свежим вдохновением.

Заключение

В этой статье мы познакомились с мощным и многообещающим фреймворком K²VAE, сочетающим в себе преимущества линейной динамики, вариационного вывода и обучаемой фильтрации. Его главная сила — в умении линейно аппроксимировать сложные нелинейные процессы в латентном измерительном пространстве, оставаясь при этом устойчивым к шумам и системным отклонениям. Это даёт не просто модель, а инструмент с высокой степенью интерпретируемости, гибкости и точности — особенно актуальный для задач анализа временных рядов и прогнозирования рыночной динамики.

Мы лишь начали распутывать клубок идей, лежащих в основе фреймворка K²VAE. В этой статье были сделаны первые шаги — от теоретических оснований до реализации ключевых компонентов, таких как параметризованные матрицы и универсальный класс CParams, взявший на себя всю тяжесть управления весами вне стандартной нейросетевой архитектуры. Это стало важным этапом в подготовке к построению полной логики модели.

Однако, впереди ещё больше работы. Нам предстоит объединить разрозненные элементы в единую, стройную систему: реализовать механизмы фильтрации, организовать вероятностную динамику в латентном пространстве, собрать в одно целое архитектуру Энкодера, Интегратора, KalmanNet и Декодера. Задача непростая, но именно она позволит модели стать по-настоящему интеллектуальной системой принятия решений.

Мы не подводим итог — мы лишь наметили траекторию. Основное развитие событий ещё впереди. Поэтому логично сделать небольшую паузу, чтобы с новыми силами продолжить путь в следующей части.

Ссылки

• K²VAE: A Koopman-Kalman Enhanced Variational AutoEncoder for Probabilistic Time Series Forecasting
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы