Торгуем опционы без опционов (Часть 1): Основы теории и эмуляция через базовые активы

Введение

Финансовый инструмент под названием опцион вызывает все больший интерес среди участников биржевых торгов. Достаточно сказать, что последние несколько лет, когда московская биржа MOEX проводила соревнования среди частных инвесторов — ЛЧИ, торговцы опционами неизменно занимали на срочной секции конкурса призовые места. И это в условиях повышенной конкуренции при проведении конкурса.

Математическая теория опционов относительно сложна и нетривиальна для понимания и расчетов вручную, но существует достаточно большое число так называемых опционных калькуляторов — программ, которые позволяют просчитать любое сочетание опционов. Как правило, торгуется набор опционов с разными параметрами — опционные конструкции. Но об этом — в следующих статьях.

В этой статье описывается эмуляция опционов через покупку/продажу базового актива. Такой способ позволяет создать (эмулировать) синтетический опцион с любыми нужными параметрами (в том числе не существующий на реальном рынке). Например, создать такой экзотический инструмент, как опцион на опцион, или опцион на спред и другие виды реальных или синтетических базовых активов.

Основы теории опционов

• 1. Определения

Опцион — производный финансовый инструмент, так называемый дериватив (от английского слова "derivative"), дающий право (но не обязанность) участнику торгов:

• купить базовый актив — Call-опцион
• продать базовый актив — Put-опцион
  

Для продавца опциона (он же является контрагентом покупателя) договоренность является не правом, а обязательством совершить сделку (если опцион Call, то продать базовый актив покупателю, если опцион Put — купить базовый актив у покупателя), за что он получает премию от покупателя.

Покупка (или продажа) базового актива происходит по фиксированной цене в заранее определённую дату в будущем — дату экспирации или до наступления даты экспирации. После исполнения (экспирации) опциона, участник торгов получает на своем счете соответствующее количество купленного (проданного) базового актива (акции, фьючерсы, валюту) — для поставочных опционов, либо денежный эквивалент (результат исполнения опциона) — для расчетных опционов.

• 2. Термины

Базовый актив — акция, индекс, валюта, товар или другой инструмент, на который выпущен опцион.

Страйк — оговоренная заранее цена, по которой базовый актив может быть куплен или продан, она же цена исполнения опциона (от английского слова "strike").

Премия — стоимость опциона, которую покупатель платит продавцу за приобретение права купить или продать базовый актив по определенной цене в определенный момент.

Экспирация — дата истечения срока действия опциона (от английского слова "expiration"), дата до которой покупатель может воспользоваться своим правом покупки/продажи базового актива.

• 3. Виды опционов

• 3.1. По возможности исполнения

Американские  — можно исполнить в любой день до экспирации (обычно стоят дороже европейских);

Европейские  — можно исполнить только в дату экспирации;

Бермудские — исполнение в определенные даты.

• 3.2. По типу расчетов

Поставочные  — поставка базового актива;

Расчетные  — денежный расчет.

• 3.3. По торгуемому рынку

Биржевые  — стандартизированные, торгуются на биржах (например, CBOE, MOEX);

Внебиржевые (OTC) — индивидуальные условия между контрагентами.

• 4. Суть инструмента опцион

Опцион это хорошее средство хеджирования (от английского слова hedge — ограда, изгородь), то есть защиты вложений. Цена опциона (премия опциона) определяет, сколько вы готовы заплатить за устранение (частичное или полное) риска. Например, вы решили защитить (захеджировать) рублевый актив от рисков роста курса рубля к американскому доллару, причем, на срок в полгода. Предположим, вам через полгода понадобится определенная сумма в рублях на крупную покупку.

Один из вариантов хеджирования — можно купить непосредственно сам базовый актив, доллары за рубли. Но здесь возникают новые риски — если за эти полгода рубль начнет укрепляться к доллару, то вы потеряете на обратной конвертации в рубли, возможно, существенную сумму. Например, курс изменился со 100 руб/доллар до 80 руб/доллар — получится, что вы потеряете 20% от исходной рублевой суммы.

Второй вариант хеджирования — покупка опциона Put на актив RUB/USD со сроком экспирации полгода и страйком, примерно равным текущему курсу рубля к доллару (допустим, 100 руб/долл). Заплатив премию за опцион, мы сможем в течение полугода продать наш опцион Put и получить базовый актив (рубли) по курсу 100руб/долл. Даже если к тому времени рубль укрепится до, страшно представить, 50 руб/долл. В результате, мы заплатим только премию за опцион.

Аналогично, можно защитить свой рублёвый актив от девальвации (обесценивания) рубля. Здесь нужно купить опцион Call со страйком, примерно равным текущему курсу рубля к доллару.

• 5. Модель опционов Блэка-Шоулза

Модель Блэка-Шоулза (Black-Scholes) — это математическая формула, разработанная в 1973 году Фишером Блэком, Майроном Шоулзом и (косвенно) Робертом Мертоном для расчета справедливой цены европейских опционов. Справедливая цена, в данном случае, это  цена, которая устраивает как покупателя, так и продавца опциона. За эту работу Шоулз и Мертон получили Нобелевскую премию по экономике в 1997 году (Фишер Блэк умер раньше и не был награждён).

Цена (премия) опциона Call:

Цена (премия) опциона Put:

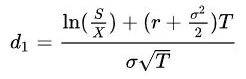
где:

• S - текущая цена базового актива
• X - цена страйк опциона
• r - без рисковая процентная ставка (непрерывно начисляемая)
• T - время до экспирации (в годах)
• N(d) - кумулятивная функция стандартного нормального распределения
• σ - волатильность базового актива

Модель строится на нескольких допущениях:

1. рынок абсолютно эффективен — отсутствие возможности арбитража;
2. безрисковая процентная ставка — постоянна и известна;
3. волатильность базового актива — постоянна;
4. отсутствие дивидендов — позже модель была доработана;
5. логнормальное распределение цен актива — цены не могут быть отрицательными;
6. непрерывное время — торговля идет без перерывов;
7. отсутствие комиссий и налогов.

Основные недостатки модели следуют из приведенных выше допущений:

• рынок не является эффективным — с некоторым приближением можно таковыми считать только наиболее ликвидные инструменты;
• волатильность базового актива меняется слишком часто и непрерывно, чтобы считать ее постоянной;
• распределение далеко от логнормального — реальные рынки имеют "тяжелые хвосты" (краш-риски), также игнорируются скачкообразные движения цен;
• не подходит для американских опционов.

Существуют альтернативные модели ценообразования опционов, учитывающие некоторые факторы, перечисленные выше:

• модель Хестона (стохастическая волатильность)
• модель Бэйеса (учет макрофакторов)
• методы машинного обучения (нейросети для прогнозирования опционных цен).

• 6. "Греки"

Так называемые "греки" это статистические показатели чувствительности цены опциона к изменению различных параметров: цены страйк, волатильности, текущей цены базового актива, даты истечения и т.д. Математически, "греки" — это частные производные от формулы Блэка-Шоулза. По смыслу, используют следующие основные показатели:

• Дельта (Delta) — показывает, как изменяется стоимость опциона при изменении цены базового актива. Рассчитывается как отношение изменения стоимости опциона к изменению стоимости актива. Если значение дельты отрицательно, значит, при повышении стоимости актива, стоимость опциона будет падать. Для опционов Call дельта положительная, для опционов Put — отрицательная. Это самый важный показатель, который будет использоваться при эмуляции опционов.
• Гамма (Gamma) — показывает, как изменяется значение дельты при изменении цены базового актива. По сути, она является второй производной цены опциона по цене базового актива. У опционов, до истечения которых еще много времени, гамма является минимальной. Ее значение растет при приближении экспирации.
• Тэта (Teta) — показывает, как изменяется стоимость опциона в зависимости от близости времени экспирации. Рассчитывается как отношение изменения стоимости опциона к изменению времени до экспирации. Значение тэты всегда показывается как отрицательное, поскольку оно снижает стоимость опциона.
• Вега (Vega) — показывает, как изменяется стоимость опциона при изменении ожидаемой волатильности. Рассчитывается как отношение изменения стоимости опциона к изменению ожидаемой волатильности. Самое высокое значение веги имеют опционы с ценой страйк, находящейся наиболее близко к текущей рыночной цене актива. Такие опционы наиболее чувствительные к изменению ожидаемой волатильности. Значение веги уменьшается с приближением даты экспирации опциона.
• Подразумеваемая волатильность (Implied Volatility - IV) — важный показатель, который не относится к "грекам", но используется в формуле Блэка-Шоулза. Рассчитывается на базе реальных сделок по конкретным опционным контрактам. Причем, волатильность можно считать разными способами: методом подгонки под формулу Блэка-Шоулза, только в центральном страйке, взвешивая ее по разным страйкам, с учетом и без учета заявок и т.п. При эмуляции, мы будем исходить из того, что у базового актива нет реальных опционов и заявок по ним, или они нам недоступны.

Поэтому, вместо подразумеваемой волатильности, мы будем использовать историческую волатильность (Historical Volatility - HV), рассчитанную для интервалов: день, неделя, месяц. Интервал зависит от периода времени до экспирации опциона. С математической точки зрения историческая волатильность — это статистический показатель разброса данных относительно их среднего значения за определённый период времени. Он рассчитывается как стандартное отклонение, умноженное на квадратный корень из количества периодов времени T. Для наших целей целесообразно использовать период времени день, неделя, месяц.

Эмуляция опционов

• 1. Необходимость эмуляции

Необходимость эмуляции диктуется несколькими факторами, перечисленными ниже:

• Физическое отсутствие опциона на нужный базовый актив. Например, на криптобирже Bybit торгуются опционы только на три спот-актива: BTC, ETH и SOL. Также, до недавнего времени на московской бирже MOEX отсутствовали опционы на акции.
• Неподходящий тип опциона по времени экспирации. Например, на MOEX для опционов на акции есть только европейские опционы — с исполнением только в последний день. Это сужает диапазон стратегий опционной торговли, отсекая спекулятивные.
• Недостаточная ликвидность для открытия/досрочного закрытия опционов. На MOEX только опционы на наиболее ликвидные фьючерсы/акции позволяют быстро открыть/закрыть опционную позицию. Это может привести как к потере прибыли, так и к получению несистемного убытка. Также, этот фактор затрудняет использование скальперских стратегий, в которых решающее значение имеет скорость открытия/закрытия опционных позиций.

• 2. Сравнение реальных и виртуальных опционов

Критерий сравнения	Реальный опцион	Виртуальный опцион
Уплата стоимости (премии) при покупке опциона	Есть плата	Нет платы
Получение премии при продаже опциона	Есть премия	Нет премии
Наличие временного распада опциона по мере приближения даты экспирации	Есть временной распад	Нет временного распада
Влияние "автершоков" и новостного фона	Не влияет в общем случае	Влияет на качество эмуляции опционов
Гибкость в выборе времени экспирации	Отсутствует. Задается биржей	Задается пользователем
Возможность использовать малые времена экспирации (сутки, несколько часов, десятки минут)	Отсутствует	Любое время экспирации
Необходимость постоянного мониторинга позиций	Не нужен в общем случае	Требуется постоянный мониторинг

Жирным текстом выделены положительные качества варианта. Как видно из таблицы, оба варианта опционов имеют свои положительные и свои отрицательные стороны. Как и следовало ожидать — ничего идеального в нашем реальном мире нет.

• 3. Требования к торговым условиям для использования эмуляции опционов

Поскольку для эмуляции опционов используется проведение сделок с базовым активом, то желательно минимизировать комиссии и прочие торговые накладные расходы, такие как: проскальзывание, большие спреды, свопы для открытых позиций. Все они ухудшают качество виртуального опциона, особенно при малых периодах экспирации. В остальном, особых требований к торговым условиям нет.

Чтобы утверждать, что позиция в базовом активе  эквивалентна опциону, нужно понимать, что в каждый момент времени опцион имеет определенную дельту (Delta). Если количество базового актива совпадает с дельтой опциона, то такие позиции будут эквивалентными в данный момент времени, то есть, приносить одинаковые прибыль-убыток.
 
Разберем более подробно как построить эмуляцию.

Пусть нужно купить-продать опцион или несколько опционов на один базовый актив. Подсчитаем сначала (это можно сделать, например, на сайте московской биржи MOEX - если речь идёт о биржевых опционах) дельту этой позиции, как если бы мы её создали через опционы.
Рассмотрим пример. Пусть, мы планируем купить 100 опционов Call в деньгах, чтобы поучаствовать в росте с плечом и ограниченным риском. Дельта одного опциона составляет 0.5. Суммарная дельта портфеля из 100 опционов будет составлять 0.5 * 100 = 50. Чтобы создать эквивалентный портфель, нужно всего лишь купить 50 единиц базового актива. Тогда у обоих портфелей дельта будет совпадать и равняться 50.

Однако, купив опцион, про него можно, в общем случае, забыть до самой экспирации. С эмуляцией же всё немного по-другому. Здесь, на протяжении всего срока её жизни, необходимо обеспечивать эквивалентность опционному портфелю — поскольку рыночная цена все время меняется. Поэтому потребуются корректировки (ребалансировки), то есть, купля/продажа недостающего/избыточного числа единиц базового актива. Как часто и в какой момент времени проводить ребалансировки? Можно это делать с определенным временным шагом (раз в час, раз в день), а можно с шагом по дельте (при изменении дельты на +/-1, +/-2 и т.п.). Также существуют и другие варианты.

Рассмотрим далее наш пример. Был создан портфель из 50 купленных единиц базового актива, то есть из 100 опционов Call. К вечеру рынок немного прибавил, и дельта одного опциона Call выросла до 0.53, дельта портфеля увеличилась до 0.53 * 100 = 53. Тогда, для сохранения эквивалентности, мы должны докупить 3 единицы базового актива. Если котировки на следующий день откатятся ниже уровня входа, и дельта опциона уменьшится, скажем, до 0.48, нам придется продать 5 единиц базового актива. Таким образом, поддерживается эквивалентность портфелей.

Почему профиль имитированной опционной позиции будет повторять профиль купленных опционов? Потому что при росте дельта увеличивается, и трейдер докупает базовый актив. Чем дальше опцион входит «в деньги», тем больше купленных единиц базового актива мы имеем в портфеле, тем самым оказываясь в прибыли при росте, подобно купленному опциону Call. Если цена пойдёт вниз, то будем продавать базовый актив, будем избавляться от него вплоть до нулевой позиции. Этим обеспечивается ограниченность убытков при падении, как и у опциона Call .

Теперь детальней о ребалансировке. Это основной момент в эмуляции. От этих сделок, собственно, и зависит финальный результат. Корректировки должны проводиться систематически, следуя заранее принятому алгоритму, в противном случае, возможны непредвиденные убытки. Например, если котировка ушла резко вверх с дельты 0.5 до дельты 0.6, и была пропущена ребалансировка, т. е. не было куплено 10 единиц базового актива, то базовый актив, в худшем случае, может до экспирации и не вернуться в эту зону. На следующий день дельта может быть уже 0.65, и мы будем вынуждены покупать 15 единиц при дельте 0.65, вместо того, чтобы купить 10 единиц при дельте 0.6 и 5 при дельте 0.65. Естественно, что нужно использовать торгового робота для осуществления эмуляции опциона.

Идеальным является вариант, если фьючерс торгуется круглосуточно, и осуществлять корректировку можно постоянно. Однако, достаточно частые корректировки могут приводить к лишним, на первый взгляд, абсолютно ненужным убыткам. Если рынок по дельте двигался за три дня: 0.50, 0.55, 0.50, то, следуя алгоритму ребалансировки, нам нужно будет сначала купить 5 единиц при дельте 0.55, а на следующий день продать 5 единиц при дельте 0.50, чем мы, естественно, зафиксируем убытки. Поэтому, если трейдером была по какой-то причине пропущена корректировка на второй день, то ничего страшного не произошло — цена не изменилась. Но рынок мог двигаться и монотонно в одну из сторон, поэтому ребалансировку нужно делать регулярно.

Минусом «ребалансировок по времени» является наличие резких движений цены, когда рынок за короткий промежуток вырастает или падает на несколько процентов. С этим успешно борются методы корректировок «по шагу дельты», однако иногда и у них бывают проколы, когда чисто физически нельзя успеть осуществить сделку по намеченной цене, из-за очень резкого движения и большого проскальзывания. Тут  выручают торговые роботы, которые быстрее и точнее «подправляют» позицию при «выносах» рынка.

Очевидно, что при флуктуациях базового актива вверх-вниз мы своими ребалансировками лишь фиксируем каждый раз небольшой убыток. В самом деле, в примере по покупке опциона Call трейдер покупает базовый актив дорого, а продаёт  дёшево. Если базовый актив за время жизни позиции так никуда и не уйдёт, стратегия будет убыточной за счет поддержания дельты. Но ведь и при покупке опциона за него взимается премия. А если он не выходит «в деньги», то премия также сгорает. Временной распад разъедает опцион, при эмуляции убытки может приносить ребалансировка.

Покупки-продажи базового актива для поддержания дельты это небольшие убыточные сделки, общий размер убытков по которым за всё время приближённо равен премии опциона. Ясно, что премия зависит от волатильности IV при покупке. Чем выше IV, тем, как предполагают трейдеры, чаще будет «гулять» рынок. Чем выше IV, тем дороже опцион. Также и с эмуляцией: чем чаще рынок колебался, тем он был волатильней, тем дороже вышла эмуляция. Чем сильнее блуждания, тем больше потери, подобно увеличению стоимости опциона при возрастании волатильности.

Эмуляция оправдывает себя, если за время жизни опциона базовый актив был маловолатильным, и нам редко приходилось делать ребалансировки, либо размер потерь от них был небольшим. Тогда эмулировать опцион выгодней, чем покупать его на бирже с дорогой IV. Ведь волатильность за время жизни портфеля реализовалось гораздо меньше, чем IV. Здесь тоже уместна аналогия с проданным опционом. Например, если вы продали опцион по 52%-ой волатильности, а реализуется 60%-ая, то из-за поддержания дельта-нейтральности результат отрицателен. Если же реализуется 45%-ая волатильность, то продажа становится выгодной, так как затраты на ребалансировку меньше премии.

Эмуляция уступает прямой покупке опциона, если реализуется волатильность, превосходящая IV на момент создания портфеля. Ведь частые корректировки из-за высокой нервозности рынка превысят величину премии опциона. Напротив, если эмулировать короткий опцион, то при большей реализованной волатильности эмуляция оказывается выгодней прямой продажи опциона.

Что ещё необходимо знать при создании опциона искусственным путём?  Вспомним, что ценообразование опциона определяется, в основном, тремя факторами: временем до экспирации, стоимостью базового актива, подразумеваемой волатильностью. При прочих равных, каждый из этих факторов по-своему действует на опцион. Можно сказать, что стоимость обычного опциона есть функция трёх переменных. Эмулированный же опцион состоит только из базового актива, цена которого не зависит от уровня подразумеваемой волатильности и от времени. Цена «искусственного» опциона есть функция только стоимости базового актива.  Хорошо это или плохо?  Очевидно, что данное обстоятельство может сыграть как в плюс, так и в минус.

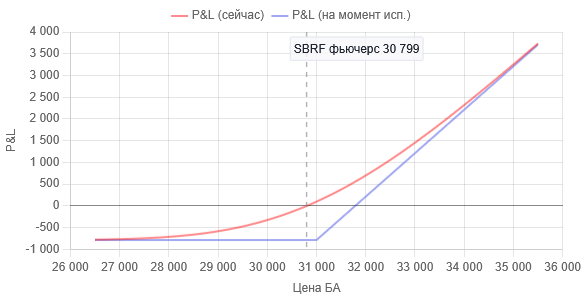
Прежде чем реализовывать эмуляцию, рассмотрим практические моменты алгоритма. Для этого построим графики зависимости дельты опциона и P&L (прибыль/убытки) от цены базового актива. Данные графики получены с сайта MOEX для опциона на фьючерс SBRF со страйком 31000 и временем экспирации 18.06.2025г. Графики актуальны на дату 22.05.2025г. Текущая цена (соответствует вертикальной пунктирной линии) на тот момент была равна 30800.

Рис.1 Зависимость прибыли/убытка (P&L) купленного опциона Call со страйком 31000 от цены базового актива. P&L выражен в рублях для одного опциона. Вертикальный пунктир — момент времени построения графиков. Для этого момента времени P&L отрицательна и равна - 23.92 руб.

Красная линия — для текущего момента времени (22.05.2025г.), синяя линия — на момент экспирации (18.06.2025г.), т.е. когда T = 1 в формуле Блэка-Шоулза.

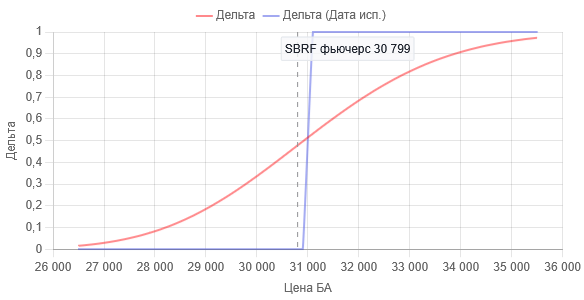
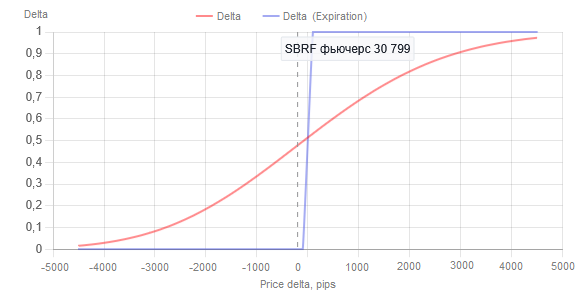
Рис.2 Зависимость значения Delta купленного опциона Call со страйком 31000 от цены базового актива для одного опциона. Вертикальный пунктир — момент времени построения графиков. Для этого момента времени Delta равна 0.48.

Красная линия — для текущего момента времени (22.05.2025г.), синяя линия — на момент экспирации (18.06.2025г.), т.е. когда T = 1 в формуле Блэка-Шоулза.

Показанные выше графики непосредственно следуют из формулы Блэка-Шоулза. Как видно из графика на рис.1, при покупке опциона Call мы уплачиваем премию продавцу в размере около 789 руб за контракт. То есть, мы сразу оказываемся в минусе. В отличие от эмулируемого опциона (комиссией за покупку базового актива, в первом приближении, можно пренебречь). Но есть и хорошая новость — при любом падении цены базового актива, свыше значения премии наши убытки не уйдут в бесконечный минус. В этом принципиальное различие между покупкой опциона Call и покупкой, например, акции — во втором случае, при падении цены убытки ничем не ограничены.

Разрабатываем эмуляцию опционов на MQL5

Из рис. 2 видно, что Deltaменяется (для одного контракта купленного опциона Call) в диапазоне от 0 до +1. Перейдем для оси X графика Delta от абсолютных цен к приращениям в пунктах. Для этого, вычтем из цен цену страйка — в данном случае, 31000. Полученный график будут выглядеть так:

Рис.3 Зависимость значения Delta купленного опциона Call со страйком 31000 от изменения цены базового актива относительно страйка для одного опциона. Вертикальный пунктир — момент времени построения графиков. Для этого момента времени Delta равна 0.48.

Красная линия — для текущего момента времени (22.05.2025г.), синяя линия — на момент экспирации (18.06.2025г.), т.е. когда T = 1 в формуле Блэка-Шоулза.

Естественно, полученный график качественно ничем не отличается от исходного, кроме шкалы по оси X. Поскольку в формуле Блэка-Шоулза фигурирует подразумеваемая волатильность (IV), а нам она, в общем случае, неизвестна, то единственный подходящий вариант —это использовать вместо нее историческую волатильность (HV). Для месячных опционов это будет средняя HV за месяц, для недельных —средняя HV за неделю и т.д.

Для удобства сопоставления графиков с различными базовыми активами и для получения возможности создания опционов на синтетические инструменты (портфель, состоящий из разных активов), будет целесообразно использовать  относительные приращения цен, нормировав эти приращения на рассчитанную историческую волатильность HV.

Тогда относительное приращение от цены price выражается следующим соотношением: Relative Price(price) = (price - Strike) / HV.

Предположим, что для периода экспирации мы рассчитали HV = 5000. В принципе, это видно из рис.3. Получим график следующего вида:

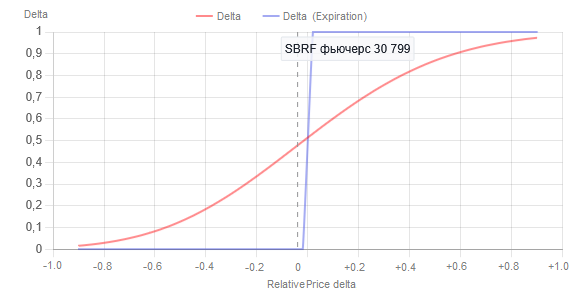
Рис.4 Зависимость значения Delta купленного опциона Call со страйком 31000 от относительного изменения цены, нормированного на историческую волатильность базового актива для одного опциона. Вертикальный пунктир — момент времени построения графиков. Для этого момента времени Delta равна 0.48.

Красная линия — для текущего момента времени (22.05.2025г.), синяя линия — на момент экспирации (18.06.2025г.), т.е. когда T = 1 в формуле Блэка-Шоулза.

Видно, что при цене, равной strike, Delta равна 0.5. График дельты, показанный красной линией, есть не что иное, как известный в математике и машинном обучении сигмоид вида: 1 \ (1 + exp(-K \ (x - S))), где S = 0, а K в общем случае неизвестен и подбирается экспериментально. По смыслу, коэффициент K зависит от периода экспирации. Зная значение дельты в данный момент времени (0.48) при текущей цене базового актива (30800), мы можем вычислить значение K — для данного момента времени оно равно 2 и будет меняться (увеличиваться) с приближением к экспирации опциона.

Для целей эмуляции будем игнорировать временной распад опциона и изменение K — он будет постоянным во все время жизни опциона. Это положительно скажется на P&L купленного опциона Call и отрицательно — на P&L купленного опциона Put. В целом, на P&L портфеля опционов большого влияния не будет.

Если приравнять параметр S в сигмоиде 1 \ (1 + exp(-K \ (x - S))) к 0.5, то график зависимости дельты от относительного изменения цены сдвинется по оси X  вправо на величину S, и мы получим в нуле значение, близкое к нулю — сигмоид асимптотически стремится к 0 и к 1. Такой вид более удобен для целей эмуляции и нормировки на диапазон волатильности, чем мы воспользуемся уже при разработке эксперта на MQL.

Итак, у нас есть все исходные данные для написания кода на MQL5 для эмуляции опциона на произвольный базовый актив. А именно: формула функции эмуляции, цена страйка, историческая волатильность и понимание процессов, происходящих в идеальном рынке Блэка-Шоулза.

• 1. Базовый класс

Будем эмулировать следующие типы опционов:

• покупка права купить базовый актив — Long Call-опцион
• покупка права продать базовый актив — Long Put-опцион
• продажа права купить базовый актив — Short Call-опцион
• продажа права продать базовый актив — Short Put-опцион

Определим все поддерживаемые типы опционов в виде перечисления:

// ---------------------------------------------------------------------
//  Тип опциона:
// ---------------------------------------------------------------------
enum ENUM_OPTION_TYPE
{
   ENUM_OPTION_CALL_LONG,                 // Long Call
   ENUM_OPTION_CALL_SHORT,                // Short Call
   ENUM_OPTION_PUT_LONG,                  // Long Put
   ENUM_OPTION_PUT_SHORT,                 // Short Put
};

Базовый класс порожден от стандартного MQL-класса 'CObject'. Это сделано для того, чтобы можно было легко использовать стандартные MQL-списки 'CList' для манипуляций объектами и создания опционных конструкций любой сложности. Об этом будет рассказано в следующей статье цикла.

Основные члены-данные базового класса:

• тип опциона — поле 'type_enum'
• цена страйк — поле 'strike'
• текущее значение дельты опциона — поле 'delta'
• цена для нормировки опциона на волатильность — поле 'norm_price'

Также, есть ряд вспомогательных полей, потребующихся в классах-потомках базового класса. Базовый класс является абстрактным, с обязательным определением в классах-потомках метода 'GetSigmoidValue'. Данный метод различен для разных типов опционов в рамках модели Блэка-Шоулза. Также, такой подход позволит в дальнейшем добавить другие типы опционов, например, с использованием методов машинного обучения и/или других моделей ценообразования.

// =====================================================================
// Базовый класс опциона - порожден от 'CObject', чтобы можно было
// помещать в списки.
// =====================================================================
class TOptionBase : public CObject
{
protected:
   ENUM_OPTION_TYPE  type_enum;
   double  strike;
   double  shift;
   double  koeff_K;
   double  koeff_S;
   int     digits;
   double  norm_price;
   double  delta;

   double  norm_koeff;
   bool    range_inited_Flag;

public:
   // ---------------------------------------------------------------------
   //  Конструктор:
   // ---------------------------------------------------------------------
   TOptionBase(const ENUM_OPTION_TYPE _type, const double _k, const double _s, const int _digits)
   :
   CObject(),
   type_enum(_type),
   strike(0.0),
   shift(0.0),
   koeff_K(_k),
   koeff_S(_s),
   digits(_digits),
   range_inited_Flag(false),
   delta(0.0),
   norm_koeff(0.0)
   {
   }

public:
   // ---------------------------------------------------------------------
   //  Установить диапазон нормировки дельты для центрального страйка:
   // ---------------------------------------------------------------------
   void SetRange(const double _strike, const double _norm_price)
   {
     this.strike = _strike;
     this.norm_price = _norm_price;
     this.norm_koeff = 1.0 / (this.norm_price - this.strike);
     this.range_inited_Flag = true;
   }
   // ---------------------------------------------------------------------
   //  Рассчитать значение нормированной дельты для заданной цены:
   // ---------------------------------------------------------------------
   double UpdateDelta(const double _price)
   {
     if(this.range_inited_Flag == false)
     {
       this.delta = 0.0;
     }
     else
     {
       this.delta = NormalizeDouble(this.GetSigmoidValue((_price - this.strike) * this.norm_koeff), 5);
     }

     return(this.delta);
   }
   // ---------------------------------------------------------------------
   //  Получить значение вычисленной ранее нормированной дельты:
   // ---------------------------------------------------------------------
   double Delta()
   {
     return(this.delta);
   }
   // ---------------------------------------------------------------------
   //  Получить флаг инциализации диапазона для дельты:
   // ---------------------------------------------------------------------
   bool    IsRangeInited()
   {
     return(this.range_inited_Flag);
   }
protected:
   // ---------------------------------------------------------------------
   //  Получить значение нормированной дельты:
   // ---------------------------------------------------------------------
   virtual double GetSigmoidValue(const double _x) = 0;
};
// ---------------------------------------------------------------------

• 2. Особенности работы в реальных условиях

При эмуляции опциона мы должны выбрать: при каком изменении дельты, надо производить ребалансировку позиций. Это ограничит точность эмуляции с одной стороны, но, с другой — позволит контролировать расходы на комиссии при открытии/закрытии позиций. Мы используем параметры базового актива — Vmin_size (минимальный объем открываемой позиции) и Vmin_delta_size (минимальное изменение объема позиции).

Также, зададим число ребалансировок позиций при изменении дельты в диапазоне (по модулю) - |0.0...1.0|. Это число ребалансировок N будем задавать в качестве внешнего параметра. Тогда суммарный объем позиций будет меняться от 0 до (Vmin_size + Vmin_delta_size * (N - 1)).

Как правило, Vmin_sizeравноVmin_deltasize, но это не обязательно так. По умолчанию, примем число ребалансировок равным десяти в диапазоне дельты |0.0...1.0|.

• 3. Опцион Long Call

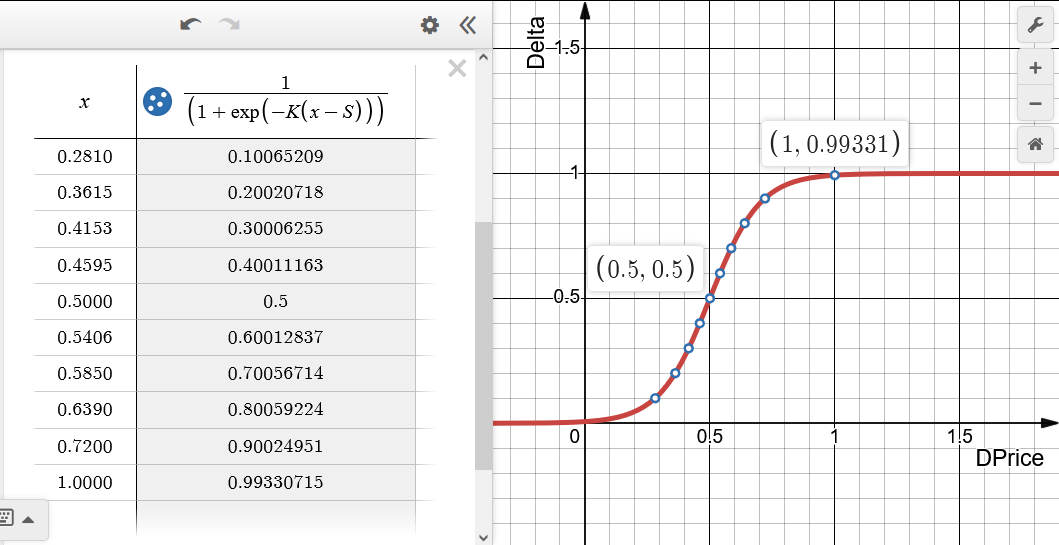
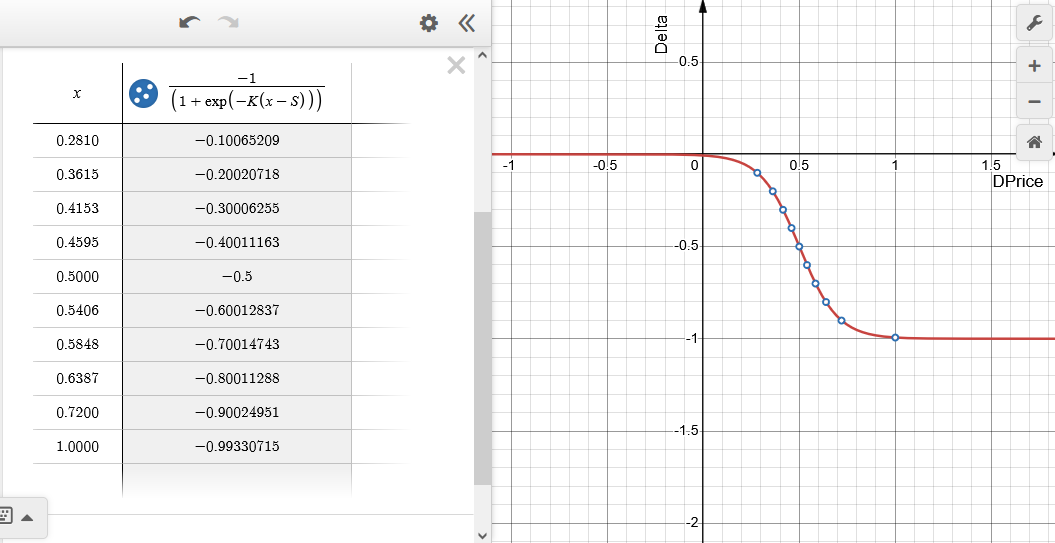
Рис.5 Зависимость значения дельты Delta от относительного изменения цены DPrice (x - в таблице) для эмулируемого опциона Long Call (покупка Call). S = 0.5, K = 10. Диапазон по дельте разбит на десять равных частей.

Цене страйк соответствует нулевая точка DPrice = 0. При значении дельты, близкой к единице, говорят, что опцион находится "глубоко в деньгах" — при этом, он ведет себя как купленная позиция по базовому активу максимальной величины. При приближении к цене страйк, объем позиции по базовому активу сокращается и становится равным нулю, когда опцион находится "вне денег", то есть дельта близка к нулю. Реальный опцион при этом уходит в минус на величину премии.

// =====================================================================
//    Класс опциона типа 'Long Call'
// =====================================================================
class OptionLongCall : public TOptionBase
{
public:
    // ---------------------------------------------------------------------
    //    Конструктор:
    // ---------------------------------------------------------------------
    OptionLongCall(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_CALL_LONG, _k, _s, _digits)
    {
    }

protected:
    // ---------------------------------------------------------------------
    //    Получить значение нормированной дельты:
    // ---------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(1.0 / (1.0 + MathExp(-this.koeff_K * (_x - this.koeff_S))));
    }
};
// ---------------------------------------------------------------------

• 4. Опцион Long Put

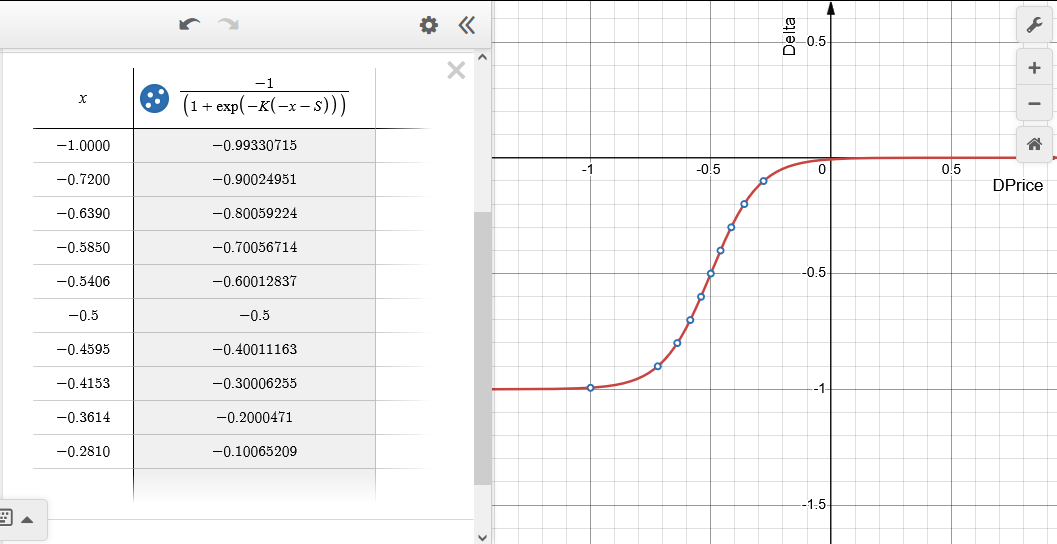
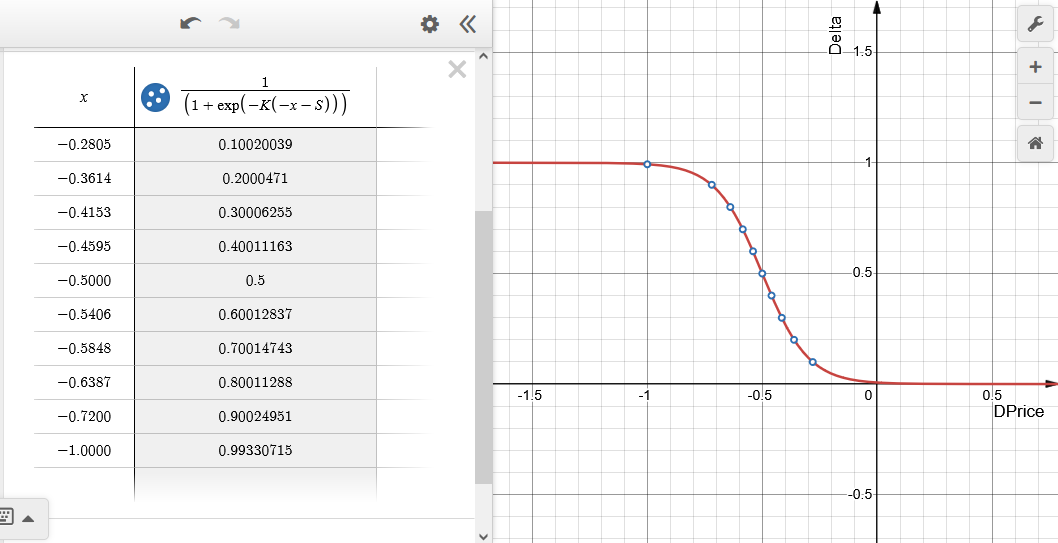
Рис.6 Зависимость значения дельты Delta от относительного изменения цены DPrice (x - в таблице) для эмулируемого опциона Long Put (покупка Put). S = 0.5, K = 10. Диапазон по дельте разбит на десять равных частей.

Цене страйк соответствует нулевая точка DPrice= 0. При значении дельты, близкой к минус единице, говорят, что опцион находится "глубоко в деньгах" — при этом, он ведет себя как проданная позиция по базовому активу максимальной величины. При приближении к цене страйк, объем позиции по базовому активу сокращается и становится равным нулю, когда опцион находится "вне денег", то есть дельта близка к нулю. Реальный опцион при этом уходит в минус на величину премии.

// =====================================================================
//    Класс опциона типа 'Long Put'
// =====================================================================
class OptionLongPut : public TOptionBase
{
public:
    // ---------------------------------------------------------------------
    //    Конструктор:
    // ---------------------------------------------------------------------
    OptionLongPut(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_PUT_LONG, _k, _s, _digits)
    {
    }

protected:
    // ---------------------------------------------------------------------
    //    Получить значение нормированной дельты:
    // ---------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(-1.0 / (1.0 + MathExp(-this.koeff_K * (-_x - this.koeff_S))));
    }
};
// ---------------------------------------------------------------------

• 5. Опцион Short Call

Рис.7 Зависимость значения дельты Delta от относительного изменения цены DPrice (x - в таблице) для эмулируемого опциона Short Call (продажа Call). S = 0.5, K = 10. Диапазон по дельте разбит на десять равных частей.

Цене страйк соответствует нулевая точка DPrice= 0. При значении дельты, близкой к минус единице, говорят, что опцион находится "глубоко в деньгах" — при этом, он ведет себя как проданная позиция по базовому активу максимальной величины. При приближении к цене страйк объем позиции по базовому активу сокращается и становится равным нулю, когда опцион находится "вне денег", то есть дельта близка к нулю. Реальный опцион при этом уходит в плюс на величину премии.

// =====================================================================
//    Класс опциона типа 'Short Call'
// =====================================================================
class OptionShortCall : public TOptionBase
{
public:
    // ---------------------------------------------------------------------
    //    Конструктор:
    // ---------------------------------------------------------------------
    OptionShortCall(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_CALL_SHORT, _k, _s, _digits)
    {
    }

protected:
    // ---------------------------------------------------------------------
    //    Получить значение нормированной дельты:
    // ---------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(-1.0 / (1.0 + MathExp(-this.koeff_K * (_x - this.koeff_S))));
    }
};
// ---------------------------------------------------------------------

• 6. Опцион Short Put

Рис.8 Зависимость значения дельты Delta от относительного изменения цены DPrice (x - в таблице) для эмулируемого опциона Short Put (продажа Put). S = 0.5, K = 10. Диапазон по дельте разбит на десять равных частей.

Цене страйк соответствует нулевая точка DPrice= 0. При значении дельты, близкой к единице, говорят, что опцион находится "глубоко в деньгах" — при этом, он ведет себя как проданная позиция по базовому активу максимальной величины. При приближении к цене страйк объем позиции по базовому активу сокращается и становится равным нулю, когда опцион находится "вне денег", то есть дельта близка к нулю. Реальный опцион при этом уходит в плюс на величину премии.

// =====================================================================
//    Класс опциона типа 'Short Put'
// =====================================================================
class OptionShortPut : public TOptionBase
{
public:
    // ---------------------------------------------------------------------
    //    Конструктор:
    // ---------------------------------------------------------------------
    OptionShortPut(const double _k, const double _s, const int _digits)
    :
    TOptionBase(ENUM_OPTION_PUT_SHORT, _k, _s, _digits)
    {
    }

protected:
    // ---------------------------------------------------------------------
    //    Получить значение нормированной дельты:
    // ---------------------------------------------------------------------
    double GetSigmoidValue(const double _x) override
    {
        return(1.0 / (1.0 + MathExp(-this.koeff_K * (-_x - this.koeff_S))));
    }
};
// ---------------------------------------------------------------------

• 7. Особенности расчета объема позиции по базовому активу

Для расчета объема позиции, нам нужно перевести значение дельты из диапазона |0.0...1.0| в диапазон целых значений |0...10|. А уже это целое значение будем умножать на объем минимального изменения лота и получать требуемое значение объема позиции. 

Предположим, что число "поддиапазонов" дельты равно десяти. Просто умножив дельту на  десять и преобразовав результат к целому типу, мы не достигнем цели. Так как при колебании дельты около любой границы "поддиапазона", объем будет также колебаться синхронно с дельтой. Поясним примером: пусть дельта равна 0.090 (объем тогда равен (int)(0.090 * 10) = 0 (то есть, позиция отсутствует) и затем выросла до 0.101 (объем тогда равен (int)(0.101 * 10) = 1, затем, на следующем тике через короткое время снова уменьшилась до 0.090 —объем опять стал равным 0. То есть, мы, фактически, купили и почти тут же продали позицию,  — получается бессмысленная ребалансировка позиции, которая может так повториться много раз за несколько секунд. Это так называемый "дребезг" сигнала.

Поэтому, при переводе дельты в требуемый объем, должен быть некий "гистерезис" ребалансировки позиции. Это достигается путем различения направления ребалансировки — что требуется: уменьшить или увеличить текущую позицию в базовом активе и учет предыдущего значения объема позиции.

Введем понятие — уровень эмуляции опциона. Пояснение: если задано соответствие |0.0...1.0| -> |0...10| (см. пояснения выше), то будем считать, что уровень эмуляции опциона меняется от нуля, до десяти. Число уровней задается как внешний по отношению к методу расчета параметр N. Уровень эмуляции, как и дельту будем брать по модулю. И отдельно будем использовать знак уровня эмуляции опциона — {0, +1, -1}. Если 0, то позиция закрыта.

• 8. Расчет объема позиции по базовому активу на MQL5

Способ реализации "гистерезиса" при расчете текущего уровня эмуляции опциона — табличный через использование двух массивов:

• IncreaseLevel_Array — определяет уровень эмуляции опциона при его увеличении.
• DecreaseLevel_Array — определяет уровень эмуляции опциона при его уменьшении.

Это делается в методе UpdateOptionLevel, который принимает два входных параметра:

• _delta — текущая дельта опциона.
• _curr_level — текущий уровень эмуляции опциона, рассчитанный ранее. Либо 0, если это первый вызов метода.

Конструктор класса OptionContractsVolume в качестве параметров принимает два аргумента:

• _ZeroDelta — значение дельты, соответствующее нулевому уровню эмуляции опциона. Может меняться от 0.001 до 0.099.
• _LevelsNumber — число уровней эмуляции опциона. Чем больше уровней, тем плавнее и точнее эмуляция, но тем больше торгуемый лот в базовом активе (из-за дискретности его изменения).

В конструкторе заполняются массивы IncreaseLevel_Arrayи DecreaseLevel_Array и инициализируются различные вспомогательные переменные (см. исходный код с комментариями).

// =====================================================================
//      Класс расчета объема контракта базового актива для опциона:
// =====================================================================
class OptionContractsVolume
{
  int IncreaseLevel_Array[];          // уровень эмуляции опциона при его увеличении
  int DecreaseLevel_Array[];          // уровень эмуляции опциона при его уменьшении
  // ---------------------------------------------------------------------
protected:
  double  ZeroDelta;                  // значение дельты, соответствующее нулевому уровню уровню эмуляции опциона
  int     LevelsNumber;               // число уровней эмуляции опциона
  // ---------------------------------------------------------------------
  int     zero_delta;                 // целое значение дельты, соответствующее нулевому уровню эмуляции опциона
  int     curr_option_level_sign;     // текуший знак уровня эмуляции опциона
  int     curr_option_level;          // текуший уровень эмуляции опциона
  // ---------------------------------------------------------------------
  int     curr_inc_level;
  int     curr_dec_level;
  // ---------------------------------------------------------------------
  int     curr_contracts_index;
  // ---------------------------------------------------------------------
  bool    is_contracts_updated_Flag;

public:
  // ---------------------------------------------------------------------
  //  Конструктор:
  // ---------------------------------------------------------------------
  OptionContractsVolume(const double _ZeroDelta, const int _levels_number)
  :
  ZeroDelta(_ZeroDelta),
  LevelsNumber(_levels_number),
  curr_option_level_sign(0),
  curr_option_level(0),
  curr_inc_level(0),
  curr_dec_level(0),
  is_contracts_updated_Flag(false)
  {
    this.zero_delta = (int)(NormalizeDouble(this.ZeroDelta, 3) * 1000.0);

    // Выделим память для массивов, хранящих уровни эмуляции:
    ArrayResize(this.IncreaseLevel_Array, (this.LevelsNumber + 1) * 100 + 1);
    ArrayResize(this.DecreaseLevel_Array, (this.LevelsNumber + 1) * 100 + 1);

    // Заполним массив в сторону увеличения:
    for(int i = 0; i < this.LevelsNumber + 1; i++)
    {
      ArrayFill(this.IncreaseLevel_Array, i * this.LevelsNumber * 100, this.LevelsNumber * 100, i);
    }
    ArrayFill(this.IncreaseLevel_Array, (this.LevelsNumber + 1) * 100, 1, this.LevelsNumber);

    // Заполним массив в сторону уменьшения:
    ArrayFill(this.DecreaseLevel_Array, 0,    zero_delta,  0);
    ArrayFill(this.DecreaseLevel_Array, zero_delta,  this.LevelsNumber * 100 - zero_delta + 1,  1);
    for(int i = 2; i < this.LevelsNumber + 1; i++)
    {
      ArrayFill(this.DecreaseLevel_Array, i * this.LevelsNumber * 100,  this.LevelsNumber * 100,  i);
    }
    ArrayFill(this.DecreaseLevel_Array, (this.LevelsNumber + 1) * 100, 1, this.LevelsNumber);
  }
  // ---------------------------------------------------------------------
  //  Рассчитать уровень эмуляции опциона для заданной дельты:
  // ---------------------------------------------------------------------
  //  - если произошло изменении уровня, возвращает 'true'.
  // ---------------------------------------------------------------------
  bool  UpdateOptionLevel(const double _delta, const int _curr_level)
  {
    this.is_contracts_updated_Flag = false;

    //  Определим направление торговли:
    int delta_int = (int)(NormalizeDouble(_delta, 3) * 1000.0);
    this.curr_option_level_sign = 0;
    if(delta_int > zero_delta / 2)
    {
      this.curr_option_level_sign = 1;
    }
    else if(delta_int < -zero_delta / 2)
    {
      this.curr_option_level_sign = -1;
    }

    //  Текущий индекс для массивов, исходя из 'Delta' с точностью 3 знака после запятой:
    this.curr_contracts_index = (int)MathAbs(delta_int);
    if(this.curr_contracts_index > ((this.LevelsNumber + 1) * 100))
    {
      //  Индекс не должен превыщать размер массива (здесь опцион глубоко в деньгах):
      this.curr_contracts_index = (this.LevelsNumber + 1) * 100;
    }

    //  Текущий уровень эмуляции опционов (0...N) в сторону УВЕЛИЧЕНИЯ:
    this.curr_inc_level = this.IncreaseLevel_Array[this.curr_contracts_index];

    //  Текущий уровень эмуляции опционов (0...N) в сторону УМЕНЬШЕНИЯ:
    this.curr_dec_level = this.DecreaseLevel_Array[this.curr_contracts_index];

    //  Если уровень эмуляции опционов (0...N) по сравнению с текущим, УВЕЛИЧИЛСЯ:
    if(this.curr_inc_level > _curr_level)
    {
      this.curr_option_level = this.curr_inc_level;
      this.is_contracts_updated_Flag = true;
      return(true);
    }

    //  Если, уровень эмуляции опционов (0...N) по сравнению с текущим УМЕНЬШИЛСЯ:
    if(this.curr_dec_level < _curr_level)
    {
      this.curr_option_level = this.curr_dec_level;

      this.is_contracts_updated_Flag = true;
      return(true);
    }

    return(false);
  }
};
// ---------------------------------------------------------------------

Полный текст кода содержится в файле OptionEmulatorA1.mqh в приложении к данной статье.

Заключение 

Итак, мы рассмотрели вариант эмуляции опционов через базовый актив — это относительно сложный и мощный инструмент, который:

• позволяет создавать сложные и не стандартные опционные стратегии;
• дает больше гибкости, чем стандартные опционы;
• требует глубокого понимания математических моделей;
• эффективен при правильном управлении рисками.

Этот метод особенно полезен, когда требуется:

• хеджирование больших портфелей,
• создание экзотических опционных стратегий,
• торговля на рынках с низкой ликвидностью опционов.

Далее будет рассмотрена практическая часть — ведение/ребалансировка позиций в базовом активе с использованием торговых функций MQL5.