Нейросети в трейдинге: Эффективное извлечение признаков для точной классификации (Mantis)

Введение

В мире, где миллисекунды и малейшие колебания цены имеют решающее значение, трейдеры стремятся к инструментам, способным не просто прогнозировать дальнейшее движение, но и точно классифицировать сложнейшие паттерны на графиках. В этом контексте фундаментальная (foundation) модель Mantis, предложенная в статье "Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification", открывает новую страницу в анализе временных рядов. Своей лёгкостью, продуманной архитектурой и превосходной калибровкой Mantis позволяет быстро интегрировать классификатор в торговые системы и получать надёжные доверительные интервалы для риск-менеджмента.

Авторы отмечают, что классические подходы, обученные прогнозированию последующих значений, часто оказываются слишком инертными: им требуется тщательная перенастройка под каждую новую стратегию, а крупные скачки волатильности могут существенно исказить их работу. При этом, в последние годы foundation-модели для прогнозирования ряда показали впечатляющие результаты, но они по сути заточены под регрессию, а не классификацию режимов рынка. Именно эту пустоту заполнили авторы фреймворка, предложив фреймворк Mantis с контрастным предварительным обучением.

Идея проста и элегантна: разбить временной ряд на серию патчей и затем, подобно Vision Transformer в компьютерном зрении, применить многогранное внимание. При этом классический механизм глобального внимания квадратичен по сложности, что для высокочастотных данных становится узким горлышком. Чтобы смягчить этот эффект, Mantis одновременно использует локальные токены, получаемые через свёртки и пулинг по небольшим окнам, и глобальные токены, аккумулирующие информацию о трендах за весь отрезок. Такое сочетание даёт почти линейную масштабируемость по длине ряда и сохраняет способность улавливать как мелкие флуктуации, так и долгосрочные паттерны.

Контрастное предварительное обучение в Mantis стало тем секретным соусом, который объединяет разные аугментации одного и того же временного фрагмента и при этом отталкивает кардинально различные ряды. В результате, эмбеддинги одного и того же паттерна с разными вариациями стягиваются в пространстве, а разные события — расходятся. Такая стратегия позволяет модели выучить устойчивые признаки различных паттернов, несмотря на то, что пики и впадины могут смещаться по амплитуде и времени.

Важнейшим аспектом для трейдера является оценка безопасности открытия позиции: не достаточно лишь сказать «это разворот тренда», нужно понимать, насколько модель уверена в своём выводе. Mantis решает эту задачу встроенным модулем температурного шкалирования: он корректирует на выходе логиты таким образом, чтобы апостериорные вероятности действительно отражали частоту попадания в класс. Благодаря этому, при пометке «80% вероятность разворота» трейдер может рассчитывать, что примерно в четырёх случаях из пяти сигнал окажется верным.

Особое внимание авторы уделили и мультимодальному анализу: в алгоритмическом трейдинге часто используются десятки индикаторов одновременно (скользящие средние, RSI, объёмы, корреляции валютных пар и т. д.). Простое объединение всех каналов в один, высокой размерности, влечёт за собой взрыв числа параметров и рост требований к памяти, а анализ унитарных последовательностей лишает информации о межканальных зависимостях. Поэтому авторы фреймворка встроили лёгкие адаптеры, которые сжимают межканальные взаимодействия в компактное пространство, не теряя при этом информации о взаимосвязях между разными индикаторами.

Чтобы иллюстрировать практическую пользу Mantis, представьте себе сценарий «flash crash» на рынке криптовалют: в течение секунды цена обваливается на несколько процентов, а затем так же стремительно отскакивает. Классическая модель может воспринять эту аномалию как шум и проигнорировать сигнал входа. Mantis, благодаря предварительному обучению на миллионах реальных и синтетических примеров, понимает, что подобные события бывают «ложными» и «истинными»: она выдает метку «кратковременная аномалия» или «настоящий разворот» с разными доверительными интервалами, позволяя трейдеру выработать адекватную стратегию защиты капитала.

Ещё один живой кейс — классификация режимов рынка акций технологических компаний. При фазе роста, цены движутся практически синхронно из-за общего новостного фона, а в режиме коррекции — каждый актив ведёт себя по-своему. Mantis, благодаря адаптерам, улавливает эти межканальные рассогласования: низкая корреляция между подобными активами становится сигналом начала коррекционного цикла, о чём модель уведомляет с оценкой уверенности.

Алгоритм Mantis

Фреймворк Mantis демонстрирует, как продуманная архитектура и тщательное обучение превращают набор идей в надёжный инструмент. Представленный авторами фреймворка foundation-подход опирается на четыре ключевых столпа: токенизацию временных рядов, гибридное внимание, адаптеры для многомерности и Self-Supervised контрастивное предварительное обучение с последующей калибровкой.

Главная идея Mantis заключается в отказе от традиционного разбиения временного ряда на фиксированные окна. Вместо этого, используется разбиение на фиксированное число патчей, что обеспечивает независимость от длины входной последовательности и стабилизирует вычислительные затраты. Например, ряды длиной 1024 и 2048 будут преобразованы в одинаковое количество патчей — 32. Такой подход критически важен при массовой обработке гетерогенных временных рядов.

Формирование эмбеддинга осуществляется в несколько этапов. Сначала применяется сверточный слой с 256 выходными каналами. Этот слой преобразует временной ряд в более компактное пространственное представление. Затем, каждый из 32 патчей агрегируется при помощи операции усреднения (mean pooling), в результате чего получается тензор размерности (32, 256). Каждый патч кодирует локальные характеристики временного ряда, включая пики, колебания и микроструктуру ценового движения.

Параллельно создаётся второй поток данных — дифференциальный. Он строится на основе разностей первого порядка между соседними значениями временного ряда. Это преобразование помогает устранить долгосрочные тренды и усилить сигналы, связанные с краткосрочной динамикой. Оно особенно полезно в ситуациях, когда интерес представляют отклонения от стабильного уровня или резкие движения вблизи уровней поддержки и сопротивления.

Оба потока проходят через одинаковую процедуру обработки: свёртка, усреднение, нормализация. На выходе получаются два набора патчей, каждый по 32 токена размерности 256. Это обеспечивает модель равноправной информацией как о форме сигнала, так и о его изменениях во времени.

Дополнительно извлекается ещё два вида информации: масштабы и волатильность. Для этого временной ряд разбивается на 32 равных окна, в каждом из которых вычисляются среднее значение и стандартное отклонение. Эти статистики кодируются с помощью Multi-Scaled Scalar Encoder, позволяющего передать модели представление о фоновых характеристиках сигнала. Таким образом, модель получает сразу четыре потока: нормализованные значения, дифференциалы, средние значения и стандартные отклонения.

Четыре полученных потока данных объединяются путем конкатенации. Перед этим они пропускаются через индивидуальные линейные проекторы для выравнивания размерности. Затем, объединённые эмбеддинги проходят слой прекции с последующим применением Layer Normalization, формируя итоговое представление временного ряда в виде 32 токенов размерности 256. Эти токены являются универсальными контейнерами, содержащими поведенческую и статистическую информацию о рынке.

Следующим шагом в архитектуре становится добавление класс-токена — обучаемого вектора, задача которого агрегировать информацию со всех токенов. Это позволяет модели формировать итоговое представление ряда, учитывая как локальные, так и глобальные закономерности. Чтобы сохранить информацию о порядке патчей, применяется синусоидальное позиционное кодирование, после чего, данные поступают в блок Transformer.

Transformer включает 6 слоёв. Каждый слой содержит Multi-Head Attention с 8 головами, слой нормализации и двухслойный блок Feed-Forward с GELU-активацией. На этапе предварительного обучения применяется dropout с вероятностью 10%, что помогает избежать переобучения. После прохождения всех слоёв, используется выходной вектор класс-токена, который и формирует итоговый эмбеддинг последовательности.

Mantis обучается в Self-Supervised парадигме с использованием контрастивного обучения. Модель применяет множество аугментаций временного ряда исходных данных. В частности, метод RandomCropResize: случайно удаляется от 0 до 20% последовательности, а оставшаяся часть растягивается обратно до исходной длины. Это сохраняет общую структуру сигнала, не нарушая порядок событий.

Для каждого примера xi из батча случайно выбираются две аугментации. Полученные представления пропускаются через проекционную голову и сравниваются по косинусному сходству.

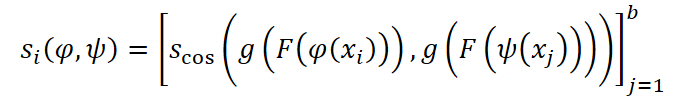
После чего, вычисляется кросс-энтропийная функция потерь.

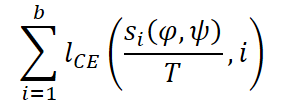
Авторы фреймворка в своей работе проводили предварительное обучение модели на объединённой выборке из 10 датасетов, объёмом более 7 миллионов временных рядов. Обучение длилось 100 эпох. Использовался батч 2048 и четыре GPU Tesla V100-32GB.

На этапе дообучения к эмбеддингу была подключена классификационная голова. Полученные прогнозные значения проходят температурную калибровку (temperature scaling), позволяющую минимизировать ожидаемую калибровочную ошибку и интерпретировать результаты модели в вероятностной форме.

Однако, мультивариантная природа временных рядов остаётся одним из главных вызовов. Разные задачи могут включать разные числа каналов, что требует адаптации модели. Подобно другим фундаментальным моделям, Mantis обучается в унивариантной форме и применяет один и тот же механизм к каждому каналу. Это не только увеличивает нагрузку на вычислительные ресурсы, но и игнорирует межканальные корреляции.

Для решения этих ограничений авторы фреймворка предлагают использовать адаптер каналов — это функция a, преобразующая исходные d каналов в dnew. Такой подход позволяет адаптировать исходные данные под вычислительный бюджет, сохранить временную структуру и обеспечить совместимость с любой моделью.

Здесь авторы фреймворка Mantis рассматривают пять вариантов адаптеров. Первые четыре — классические методы уменьшения размерности:

• PCA (Principal Component Analysis): находит ортогональное пространство, где максимум дисперсии сосредоточен в меньшем числе компонент;
• Truncated SVD: аналогичен PCA, но работает с нескорректированной матрицей;
• Random Projection: случайное линейное отображение в пространство меньшей размерности;
• Variance-Based Selector: выбор наиболее вариативных каналов.

Данные для этих адаптеров приводятся к форме (n*t, d), где n — число примеров. Искомая матрица W реализует проекцию каналов.

Пятый адаптер — Differentiable Linear Combiner (LComb) — обучается вместе с основной моделью путем корректировки параметров в процессе обратного прохода. Это позволяет учесть контекст задачи и добиться более высокой точности.

В результате, Mantis становится пригодным для широкого круга задач, не теряя при этом временную структуру данных и межканальные взаимосвязи. Модель остаётся универсальной и производительной, даже в условиях реальных мультивариантных сценариев.

Авторская визуализация фреймворка Mantis представлена ниже.

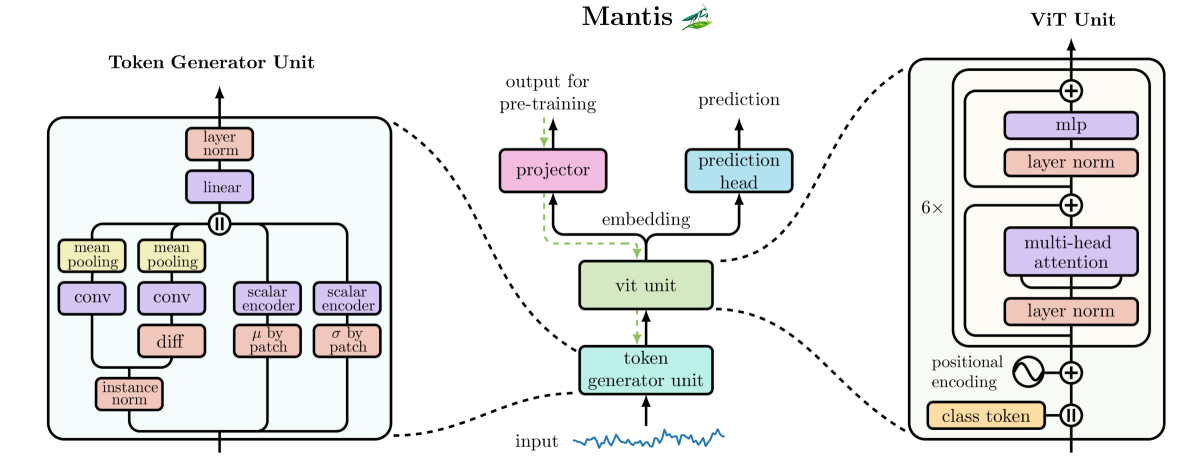
Реализация средствами MQL5

После глубокого анализа теоретических аспектов фреймворка Mantis, приходит время перейти к самому интересному — его практической реализации. Именно здесь, в недрах реального кода, идеи обретают форму, а абстрактные принципы начинают приносить пользу. В центре нашего внимания — программная реализация ключевых архитектурных решений фреймворка средствами языка MQL5. Несмотря на высокую сложность концепций, перед нами стоит чёткая и амбициозная задача: построить модель, способную эффективно обрабатывать реальные рыночные данные, адаптироваться к волатильности и при этом оставаться максимально экономной по ресурсам.

Обсуждение подходов

Прежде чем приступить к написанию кода, как и положено в инженерной практике, необходимо разработать стратегию. Без чёткого плана ни одна архитектура не выдержит давления реального рынка. Наш путь начинается с системного осмысления: что именно мы хотим реализовать, каковы роли отдельных компонентов, и где могут скрываться потенциальные узкие места. Важно не просто переписать идеи авторов, а адаптировать их к нашей задаче и условиям MQL5, которые имеют свои ограничения и особенности.

В центре реализации — формирование токенов. Именно здесь закладываются основы будущего успеха модели, ведь Transformer не может эффективно работать с сырыми данными. Ему необходим вход в виде последовательностей токенов, каждый из которых несёт сжатое, но выразительное представление участка временного ряда.

Оригинальная архитектура Mantis предлагает использовать многоканальную схему, включая ряды отклонений, средние значения и стандартные отклонения сегментов. Однако в условиях нормализованных входов, с которыми чаще всего работают наши модели, снижается информативность потоков средних значений и стандартных отклонений. Мы сознательно отказываемся от этих каналов, делая ставку на два ключевых потока: оригинальный временной ряд и его первую разность. Такая комбинация позволяет одновременно учитывать как глобальные уровни, так и локальные изменения — своего рода компромисс между стабильностью и чувствительностью.

Процесс подготовки этих потоков начинается с нормализации исходного временного ряда. Это важный этап, позволяющий сгладить масштабные колебания и повысить устойчивость модели к выбросам. Далее применяется операция дифференцирования, с помощью которой вычисляется разность между соседними наблюдениями. Полученный ряд отличается повышенной реакцией на резкие изменения, что особенно ценно при попытке уловить импульсы или развороты рынка. После этого, оба ряда объединяются в тензор с двумя каналами, где каждый канал представляет собой отдельный информационный поток.

Однако, одного объединения недостаточно. Несмотря на богатство информации, заключённой в многоканальном временном ряде, модели критически не хватает сведений о временном контексте. Трансформеры, как известно, не обладают встроенной способностью понимать порядок элементов в исходной последовательности, а потому нуждаются в дополнительной информации, описывающей расположение каждого наблюдения относительно других.

В оригинальной реализации Mantis эту задачу решали путём добавления синусоидального позиционного кодирования, аналогичного тому, что было предложено в статье Attention is All You Need. Такой подход удобен своей универсальностью и переносимостью: он не требует обучения и хорошо работает на задачах различной природы. При этом, кодирование добавляется уже после объединения каналов и сегментации на патчи.

Однако мы предлагаем иной путь. Прежде чем разрезать последовательность на фрагменты, мы вводим временное кодирование, аналогично фреймворку Mamba4Cast. Это кодирование не просто обозначает положение точки во временной сетке, но и передаёт информацию о темпоральной структуре ряда — позволяет модели уловить скрытую сезонность, повторяющиеся шаблоны, асимметрии и ритмику рыночных данных. В отличие от синусоидального, временное кодирование более чувствительно к микроструктуре рынка и может захватывать закономерности, простирающиеся за пределы текущего анализируемого окна.

Лишь после добавления такого кодирования, мы можем переходить к следующему логическому этапу — сегментации каналов. Этот шаг играет роль своеобразного фильтра, который превращает темпорально обогащённую информацию в удобную для модели форму. Иными словами, к этому моменту данные уже несут в себе не только значение и производную, но и дополнительный слой контекста, раскрывающий их поведенческую динамику во времени. Это значительно облегчает задачу модели по выделению сложных зависимостей и делает её работу более устойчивой к рыночному шуму.

Об изменениях в алгоритме сегментации я предлагаю поговорить немного позже, когда подойдем непосредственно к его реализации. Мы пока сознательно оставляем в стороне описание остальных блоков, чтобы сосредоточиться на фундаменте — преобразовании временного ряда в информативную, стандартизированную и структурированную последовательность. Именно на этом этапе закладывается успех всей модели. Хорошо подготовленные данные позволяют эффективно выявлять закономерности, корректно учитывать порядок событий и различать важные паттерны поведения рынка.

Теперь, когда концептуальная основа выстроена, и дорожная карта обозначена, пора переходить от слов к делу. На этом этапе начинается непосредственная реализация модели — тот самый момент, когда теория трансформируется в строки кода. Начнём мы с самой базовой и при этом крайне важной части — предварительной обработки временного ряда, на выходе которой формируется многоканальное представление данных. Именно здесь происходит первичное извлечение признаков, которое впоследствии определит, что увидит и как интерпретирует Transformer. Задача — извлечь два потока: оригинальный ряд и его первую разность, а затем объединить их в единый тензор. Всё это мы реализуем средствами OpenCL.

Изменения в OpenCL-программе

Использование OpenCL обусловлено необходимостью ускорения вычислений, особенно при работе с большим количеством временных рядов. GPU позволяет параллелизировать операции над множеством переменных и ускорить подготовку данных без загрузки основного процессора. Поэтому первым делом мы реализуем специализированный кернел ConcatDiff. Его задача — одновременно вычислить первую разность и сконкатенировать полученный результат с оригинальными данными, формируя тем самым тензор с двумя каналами на каждый временной отрезок.

В параметрах данного кернела передаются всего два указателя на буферы данных — минимализм, проверенный временем. Первый — это входной массив data, содержащий анализируемые временные ряды, а второй — выходной буфер output, в который сохраняются результаты вычислений. Такой подход делает интерфейс кернела максимально простым и понятным, избавляя от лишней нагрузки.

Дополнительным параметром выступает константа step — шаг, с которым рассчитывается разность. Это нововведение значительно расширяет универсальность алгоритма. Теперь мы можем рассчитывать как классическую первую разность (между соседними точками), так и, например, разность между значением «сейчас» и «через пять шагов». Последнее может быть особенно полезно в финансовом контексте: такой параметр позволяет подготовить признаки, отражающие изменения с различным временным горизонтом.

__kernel void ConcatDiff(__global const float* data,
                         __global float* output,
                         const int step)
  {
   const size_t i = get_global_id(0);
   const size_t v = get_local_id(1);
   const size_t inputs = get_local_size(0);
   const size_t variables = get_local_size(1);

Каждый поток операций получает уникальную пару индексов — временной индекс i и индекс унитарной последовательности v. Таким образом, каждый поток отвечает за обработку одного конкретного значения в матрице исходных данных.

Массив исходных данных data представляет собой нормализованный временной ряд, представленный в линейной форме — с разложением по времени и каналам.

Далее внутри кернела мы вычисляем shift — смещение в массиве data, соответствующее текущему временно-переменному положению.

const int shift = i * variables;
const float d = data[shift + v];

Получив оригинальное значение d, мы переходим к вычислению его первой разности по оси времени. Для этого берётся разность между текущим значением и расположенным на step шагов далее. Такая схема ориентирована на подготовку целевых признаков, которые отражают локальную динамику: рост или падение, ускорение или замедление изменения. При этом, обязательно проверяется корректность индекса: мы не должны выйти за пределы массива.

float diff = 0;
if(step > 0 && (i + step) < inputs)
   diff = IsNaNOrInf(d - data[shift + step * variables + v], 0);

Вычисление разности завершается защитной функцией IsNaNOrInf, которая обнуляет результат в случае появления NaN или бесконечностей — это особенно важно при наличии пропущенных значений или сбоев в данных.

Затем наступает ключевой этап — формирование выходного массива output. Здесь происходит интересная операция: данные записываются попарно. Вначале записывается оригинальное значение, а следом — соответствующее значение первой разности. Поскольку мы используем удвоенный сдвиг по переменным (в два раза больше каналов), итоговый тензор для каждой временной точки содержит два значения на каждую переменную. Таким образом, структура output становится размером (T * 2 * V), где T — количество временных шагов, V — количество переменных.

 output[2 * shift + v] = d;
 output[2 * shift + v + variables] = diff;
}

Это решение позволяет сразу в одном проходе подготовить данные к подаче в модель: тензор уже содержит как статические, так и динамические характеристики рынка.

Применение OpenCL в данном случае даёт двукратный выигрыш: экономится время (за счёт параллельной обработки) и упрощается логика кода, поскольку вся работа с индексами и массивами осуществляется внутри кернела. Вместо громоздких циклов на стороне CPU, мы имеем компактный и эффективный блок, легко масштабируемый под данные любой длины и ширины.

Этот модуль становится первым кирпичиком в фундаменте всей модели. Он реализует ключевую идею: первичная декомпозиция временного ряда на два взаимодополняющих потока. Оригинальные значения позволяют видеть уровни и тренды, тогда как первая разность обеспечивает чувствительность к изменению — своего рода производная, которая сигнализирует о поворотных моментах. Совместно они создают сбалансированное представление, устойчивое к шуму и адаптивное к быстрым изменениям.

Здесь стоит особо подчеркнуть архитектурную особенность данного этапа: в кернеле ConcatDiff отсутствуют какие-либо обучаемые параметры. Его задача исключительно функциональна — произвести простейшие линейные операции (извлечение значений и их разности) и объединить результаты в единый массив. Всё это делает его исключительно подходящим для реализации на стороне OpenCL, где особенно эффективны операции массовой параллельной обработки без сложной логики состояния.

Более того, сами исходные данные, с учётом специфики финансовых временных рядов, вполне логично рассматривать как константные в пределах одной итерации подготовки. Именно поэтому, в данном случае, мы не реализуем кернелы для обратного распространения градиента ошибки или обновления параметров. Такие задачи актуальны лишь для обучаемых слоёв, которые формируют модель. Здесь же мы имеем дело с предварительной обработкой — этапом, где важна скорость, надёжность и полная детерминированность вычислений.

Полный код OpenCL-программы представлен во вложении.

Объект вычисления разности

Следующим шагом нашей работы становится интеграция кернела ConcatDiff в структуру основной программы. Для этого мы создаём специализированный объект, реализованный в виде класса CNeuronConcatDiff. Этот объект играет роль интерфейса между логикой высокоуровневой нейросетевой модели и низкоуровневым OpenCL-кодом, отвечая за корректную подготовку параметров, запуск кернела и приём результата.

class CNeuronConcatDiff:  public CNeuronBaseOCL
  {
protected:
   uint              iUnits;
   uint              iVariables;
   uint              iStep;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override   { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronConcatDiff(void) :  iUnits(0), iVariables(1), iStep(1) {  activation = None; }
                    ~CNeuronConcatDiff(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units_count, uint step, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override  const   {  return defNeuronConcatDiff;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
  };

Сам класс включает несколько ключевых переменных:

• iUnits — количество временных шагов,
• iVariables — количество каналов или переменных в исходных данных,
• iStep — параметр сдвига, задающий шаг для вычисления разности. Это значение делает компонент универсальным — его можно адаптировать под произвольную ширину временного окна или частоту отсчётов.

Конструктор класса инициализирует ключевые параметры по умолчанию: один канал (iVariables = 1), шаг равный единице (iStep = 1) и отключённую функцию активации (activation = None), что логично — ведь наш компонент работает на уровне предварительной обработки и не должен вносить нелинейности.

Также в классе реализован метод инициализации объекта Init, в параметрах которого предаются константы, позволяющие однозначно интерпретировать архитектуру создаваемого объекта.

bool CNeuronConcatDiff::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                             uint units_count, uint step, uint variables,
                             ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * variables, optimization_type, batch))
      return false;
   if(step<=0 || step >= units_count)
      return false;
//---
   iUnits = units_count;
   iVariables = variables;
   iStep = step;
//---
   return true;
  }

Логика метода Init максимально проста и лаконична. В его теле вызывается одноимённая функция родительского класса с учётом особенностей структуры данных. Так как мы объединяем в выходном массиве исходные данные и значения первой разности, то объём выходного буфера должен быть увеличен в два раза.

После инициализации родительской части, все параметры, полученные на вход, сохраняются во внутренние переменные класса. Это позволяет использовать их при формировании параметров для OpenCL-кернела.

Такой подход делает объект гибким, независимым и повторно используемым.

Особое внимание уделяется виртуальному методу feedForward, который отвечает за прямой проход и, соответственно, вызов OpenCL-кернела.

В параметрах метода получаем указатель на объект исходных данных и сразу осуществляем контроль его актуальности. 

bool CNeuronConcatDiff::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!OpenCL || !NeuronOCL || !Output)
      return false;
   if(getOutputIndex() < 0)
      return false;

После успешного прохождения блока контролей, осуществляется постановка в очередь выполнения кернела ConcatDiff. Здесь используется уже знакомый вам алгоритм. Сохраненные ранее во внутренних переменных значения используются для указания размерности пространства задач. 

{
 uint global_work_offset[2] = {0};
 uint global_work_size[2] = {iUnits, iVariables};
 const int kernel = def_k_ConcatDiff;
 if(!OpenCL.SetArgumentBuffer(kernel, def_k_concdiff_data, NeuronOCL.getOutputIndex()))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel),
                                                               GetLastError(), __LINE__);
    return false;
   }
 if(!OpenCL.SetArgumentBuffer(kernel, def_k_concdiff_output, getOutputIndex()))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
 if(!OpenCL.SetArgument(kernel, def_k_concdiff_step, iStep))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
 //---
 if(!OpenCL.Execute(kernel, global_work_size.Size(), global_work_offset, global_work_size))
   {
    printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                               GetLastError(), __LINE__);
    return false;
   }
}

Однако, на этом работа метода feedForward не завершается. Следующим шагом выполняется нормализация сформированного тензора — по сути, приведение данных к единому масштабу, что критически важно при обучении нейросети. Причём, здесь реализована раздельная нормализация по признакам (нормализуются исходные значения переменных) и разностям (отдельно обрабатываются значения первой разности). Это позволяет сохранить чувствительность модели к резким изменениям во временном ряду, не теряя при этом устойчивость к масштабным колебаниям.

     {
      uint global_work_offset[1] = {0};
      uint global_work_size[1] = {2 * iUnits};
      const int kernel = def_k_Normilize;
      if(!OpenCL.SetArgumentBuffer(kernel, def_k_norm_buffer, getOutputIndex()))
        {
         printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel),
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.SetArgument(kernel, def_k_norm_dimension, iVariables))
        {
         printf("Error of set parameter kernel %s: %d; line %d", OpenCL.GetKernelName(kernel), 
                                                                    GetLastError(), __LINE__);
         return false;
        }
      if(!OpenCL.Execute(kernel, global_work_size.Size(), global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s: %d -> %s", OpenCL.GetKernelName(kernel), 
                                                                GetLastError(), error);
         return false;
        }
     }
//---
   return true;
  }

Подобная постобработка позволяет значительно повысить стабильность обучения и ускорить сходимость модели за счёт унификации диапазона входных значений.

Несколько слов стоит сказать и о методе распределения градиента ошибки — calcInputGradients. Несмотря на то, что для данного слоя мы не создаём кернела обратного прохода, соответствующий метод всё же реализован.

Зачем? Ответ прост. Это позволяет нам встраивать данный объект на любом уровне модели, не опасаясь нарушения цепочки обратного распространения ошибки. Даже если вычисление собственных градиентов этому слою не требуется, он должен корректно передавать сигнал ошибки дальше — на уровень предыдущих объектов. Иначе обучение всей модели может обрываться именно на нём, что приведёт к стагнации градиентного потока и, как следствие, к невозможности оптимизации параметров нижележащих уровней.

Алгоритм метода — простой и надёжный. Получаем указатель на объект исходных данных (NeuronOCL) и сразу проверяем его актуальность.

bool CNeuronConcatDiff::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Перенаправляем градиент ошибки по прямому информационному потоку исходных данных, накопленный в текущем объекте, в качестве сигнала для предыдущего слоя. Этот процесс — чистая деконкатенация без каких-либо вычислительных изысков.

if(!DeConcat(NeuronOCL.getGradient(), getPrevOutput(), getGradient(), iVariables, iVariables, iUnits))
   return false;

При необходимости (в зависимости от архитектуры) градиент ошибки может быть скорректирован на производную функции активации.

   if(NeuronOCL.Activation() != None)
      if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(),
                                                                       NeuronOCL.Activation()))
         return false;
//---
   return true;
  }

Такой подход обеспечивает совместимость и гибкость архитектуры. Объект CNeuronConcatDiff не мешает распространению градиентов и может использоваться в составе сложных моделей — как на нижних уровнях (рядом с входом), так и глубоко внутри вычислительного графа.

На этом мы завершаем рассмотрение алгоритмов построения методов класса CNeuronConcatDiff. С полным кодом данного класса и всех его методов можно ознакомиться во вложении.

Постепенно мы подошли к границам разумного объёма текущей статьи. Несмотря на это, основная часть работы ещё впереди. Мы лишь заложили фундамент. Однако, на этом история не заканчивается. Чтобы не перегружать читателя и сохранить читаемость материала, сделаем небольшой перерыв и продолжим реализацию в следующей статье данной серии. Там нас ждёт не менее интересный и технически насыщенный этап.

Заключение

В данной статье мы познакомились с фреймворком Mantis, который сочетает в себе лёгкость и высокую точность. Авторы фреймворка предложили инновационный подход к формированию токенов, основывающийся на свёртке и mean-pooling, что позволяет эффективно представлять временные ряды в виде 32 токенов размерностью 256, снижая вычислительные затраты по сравнению с традиционными методами. Контрастное предварительное обучение на примерах из разнообразных датасетов обеспечило устойчивое и переносимое представление признаков, превосходя аналоги в zero-shot и fine-tuning режимах и достигая рекордно низкой ошибки калибровки.

В практической части представлена реализация ключевого слоя предварительной обработки данных средствами OpenCL и MQL5, обеспечив параллельную и детерминированную подготовку входных тензоров. В следующей статье мы продолжим реализацию собственного видения подходов, предложенных авторами фреймворка Mantis.

Ссылки

• Mantis: Lightweight Calibrated Foundation Model for User-Friendly Time Series Classification
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	StudyContrast.mq5	Советник	Советник контрастивного обучения Энкодера
4	Study.mq5	Советник	Советник офлайн обучения моделей
5	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
6	Test.mq5	Советник	Советник для тестирования модели
7	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
8	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
9	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы