Нейросети в трейдинге: Обобщение временных рядов без привязки к данным (Mamba4Cast)

Введение

Рынок — вещь упрямая и капризная. Он не даёт второй попытки тем, кто ошибается в оценке сигналов. Особенно в наш век — когда новостной поток разносится быстрее, чем вспыхивает свеча на минутном графике. Современный трейдер работает не с прошлым, а с тем, что ещё только зарождается в потоке данных. Предугадать зарождение паттерна раньше других — значит получить преимущество. Поэтому запрос к современным алгоритмам один: прогнозировать прежде, чем стало очевидным. И при этом, желательно, не утонуть в технических сложностях настройки и поддержки модели.

В этой гонке традиционные модели, вроде рекуррентных архитектур, уже начинают ощутимо буксовать. Они отлично справляются с повторяющимися шаблонами, хорошо помнят последовательности, но нередко теряются в хаотичном поведении реального рынка. Им трудно ловить импульсы, они не любят разрывы, плохо справляются с выбросами и требуют настройки под каждую новую среду. Сегодня рынок требует более гибкого и предиктивного инструмента.

Архитектуры на основе Transformer добавили интеллектуальности и точности, особенно в задачах с длинными временными рядами. Однако вместе с этим они принесли вычислительную сложность и архитектурную громоздкость. С ростом объёма данных и увеличением длины горизонта планирования эти модели становятся всё менее подходящими для задач реального времени. На практике это означает — больше ресурсов, больше времени и больше хлопот.

На этом фоне появляется фреймворк Mamba4Cast, представленный в работе "Mamba4Cast: Efficient Zero-Shot Time Series Forecasting with State Space Models". Он выглядит как глоток свежего воздуха и базируется на двух ключевых идеях: лёгкой, но выразительной архитектуре Mamba и революционной концепции Prior-data Fitted Networks (PFNs). Вместе они образуют фундамент для новой волны подходов к прогнозированию временных рядов — особенно в таких динамичных отраслях как трейдинг.

Концепция PFN — это переворот в мышлении. В отличие от классических подходов, где модель сначала предобучается на одном датасете, а потом долго дообучается на другом, PFNs предлагают заранее обучить модель на синтетически сгенерированных задачах. То есть вместо одной реальной задачи, модель обучается на миллионе разных, пусть и неидеальных. Это делает её по-настоящему универсальной и устойчивой к новому. В трейдинге это означает, что модель не привязана к конкретному инструменту или временным рамкам — она способна адаптироваться на лету.

Фреймворк Mamba4Cast применяет PFN-подход в полной мере. Используя синтетически сгенерированные данные, охватывающие разнообразные сценарии он формирует у модели широкий поведенческий охват. Благодаря этому, модель обладает своеобразной интуицией — умением обобщать закономерности даже в условиях высокой волатильности и нестабильной динамики.

Вторая фундаментальная особенность — это архитектура Mamba, отличающаяся линейной вычислительной сложностью по длине последовательности. В отличие от трансформеров, Mamba не требует квадратичных операций с матрицами внимания, и поэтому способна обрабатывать длинные последовательности исходных данных быстро и экономно. Что особенно важно для трейдера — Mamba4Cast может прогнозировать целое окно будущих значений за один проход. Это резко снижает ошибки, возникающие при авторегрессионном прогнозировании, и даёт возможность быстрее реагировать на изменения рыночной картины.

Кроме того, благодаря построению прогнозов сразу на несколько шагов вперёд модель идеально подходит для создания комплексных торговых стратегий: от анализа сигнала до прямого принятия торгового решения. Mamba4Cast может стать не просто ориентиром, а полноценным ядром прогнозирующего модуля в автоматизированной торговой системе.

Алгоритм фреймворка Mamba4Cast

Фреймворк Mamba4Cast — это смелый и многообещающий шаг в эволюции систем прогнозирования временных рядов. В его основе лежит сочетание строгой математической базы и гибких алгоритмов глубокого обучения, способных рассматривать рынок как сложную экосистему, где прошлое, настоящее и будущее сплетены в единую картину.

В традиционном подходе модели обучаются на исторических данных одного актива и затем повторяют усвоенные закономерности. Этот путь дал отличные результаты в свое время, но сегодня он сталкивается с ограничениями: рынки становятся более динамичными, а события — менее предсказуемыми. Mamba4Cast предлагает другой путь: вместо запоминания конкретных временных рядов используется методика PFN (Prior-data Fitted Networks). Представьте, что вы тренируете аналитика не на реальных котировках отдельно взятой акции, а на бесчисленном множестве синтетических сценариев: вот тренд, здесь флэт, там затишье перед бурей, а затем новостной взрыв. Таким образом формируется универсальный рыночный интеллект, готовый действовать «из коробки» на любом инструменте.

Сердце этой системы — архитектура Mamba, основанная на State Space Modeling. В отличие от громоздких Self-Attention слоев трансформеров, Mamba работает линейно по длине последовательности, что позволяет ей обрабатывать сотни и тысячи временных точек без взрывного роста вычислительных затрат. Такая эффективность не просто ускоряет расчёты — она открывает двери для оперативного анализа данных в реальном времени, где каждая миллисекунда на счету. Такое решение позволяет экономить ресурсы и делает систему подходящей для обработки потоков данных реального времени в условиях высокой волатильности.

На первом этапе происходит масштабирование исходного временного ряда. Для этого применяется стандартная Min-Max нормализация, при которой каждое значение xt преобразуется по формуле:

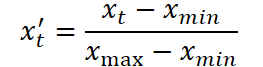
где xmin и xmax определяются по диапазону внутри обучающей выборки. Это устраняет дисбаланс между различными по шкале признаками и подготавливает данные для эффективного обучения.

Затем начинается ключевая часть предварительной обработки — позиционное кодирование. Временные метки, такие как минута, час, день недели, день месяца, месяц и год, выделяются отдельно и преобразуются в векторные представления. Здесь используется синусоидальная схема кодирования, аналогичная трансформерам, но адаптированная под периодические компоненты временных рядов. Для каждой компоненты времени вычисляются несколько гармоник синусов и косинусов от произведения периода и степеней двойки:

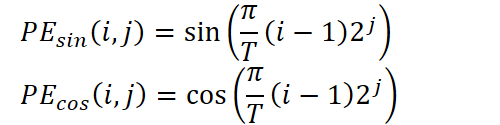
где T — период соответствующей компоненты, i — индекс временной точки, а j — индекс частоты в спектре.

Эти векторы кодируют временные зависимости на множестве масштабов, позволяя модели почувствовать суточную цикличность, сезонность и макроэкономические фазы.

После этого они конкатенируются с нормализованными значениями самих рядов. Полученный вектор представляет собой эмбеддинг временной точки.

Следующим шагом является обработка последовательности с использованием набора причинных свёрточных слоёв. Несколько параллельных свёрток с уникальными окнами позволяют охватить различные временные масштабы. Каждая свёртка улавливает информацию на своём уровне: от самых локальных колебаний до долгосрочных трендов. Результаты работы этих слоёв объединяются, формируя обогащённое представление для каждой временной точки. Это особенно важно в контексте финансовых данных, где одна и та же свеча может нести как краткосрочный импульс, так и быть частью широкой рыночной тенденции.

Затем применяется проекция в пространство высокой размерности, что позволяет подготовить данные к передаче в основной блок модели. Здесь также подключается модифицированный inception-слой, который сочетает свёртки разных размеров, объединяя локальные и глобальные характеристики. Итоговая активация в точке времени содержит информацию с разных уровней обобщения, сохраняя при этом размерность выхода и обеспечивая устойчивость к пропускам и шуму.

Сердцем архитектуры являются блоки на базе модуля Mamba — инновационной реализации State Space Models (SSM) с линейной сложностью по длине последовательности. Каждый блок реализует обобщённую SSM-структуру, где скрытое состояние обновляется через матрицы A, B, C, D, обучаемые совместно с другими параметрами модели:

Таким образом, каждый момент времени зависит от предыдущего состояния и текущего входа. Это обеспечивает стабильную долгосрочную память и гибкую адаптацию к текущему контексту. После каждого такого слоя применяется Layer Normalization, устраняющая смещения и нормализующая распределение активаций, что делает обучение более стабильным. За этим следует очередной causal-свёрточный слой, поддерживающий поток информации вдоль временной оси.

Количество таких блоков в стеке может варьироваться в зависимости от требуемой глубины обобщения. Нижние уровни специализируются на захвате коротких паттернов — быстрых откатов, импульсов, колебаний на новостях. Верхние блоки формируют представление о рыночных циклах, сезонных движениях, повторяющихся формациях. Стек работает как нейронный спектр, где каждый уровень отвечает за свой диапазон временной частоты.

Завершающий этап — декодирование. Все полученные активации проецируются линейным слоем в один или несколько каналов выхода. Если требуется дополнительно оценить неопределённость, используется отдельная голова, прогнозирующая дисперсию в логарифмическом масштабе:

Для задач классификации используется SoftMax-голова, выдающая вероятности анализируемых классов.

Особенность Mamba4Cast — его способность к Zero-Shot обобщению. Чтобы этого добиться, авторы предложили уникальный этап предобучения на обширном синтетическом датасете. В него входят временные ряды, сгенерированные по стохастическим дифференциальным уравнениям (SDE), вручную заданным паттернам (развороты, консолидации, импульсы) и даже случайным генеративным правилам.

Модель обучается сразу по нескольким функциям потерь: среднеквадратичная ошибка, отрицательное логарифмическое правдоподобие, кросс-энтропия по смене режима. Это позволяет сформировать устойчивое универсальное представление рыночных закономерностей, способное адаптироваться к новым активам и временным масштабам.

Всё это делает Mamba4Cast не просто экспериментальной моделью, а полноценной основой для построения прогнозных торговых систем, алгоритмов оценки рыночных фаз и прогнозирования волатильности.

Авторская визуализация фреймворка Mamba4Cast представлена ниже.

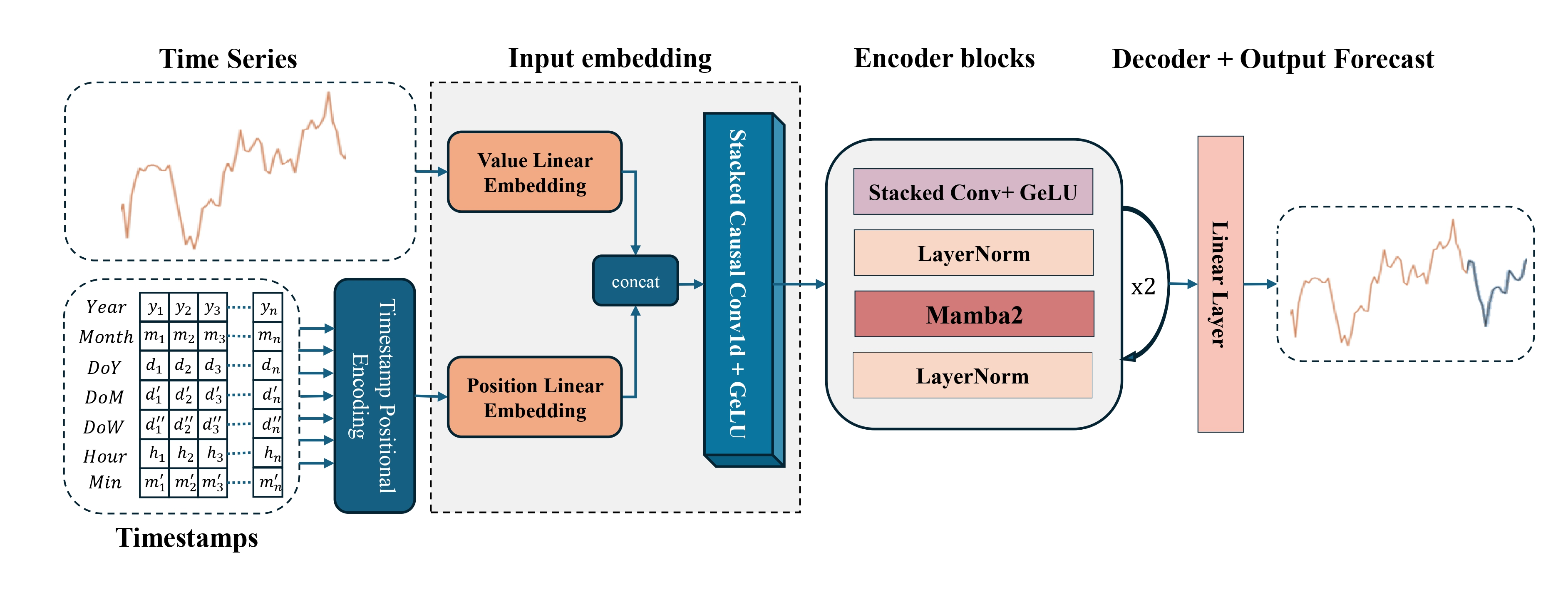
Реализация средствами MQL5

После фундаментального погружения в архитектуру Mamba4Cast мы переходим к самой боевой части — практической реализации ключевых блоков фреймворка средствами MQL5. И первым делом нам предстоит разобраться с объектом позиционного кодирования, без которого ни одна современная прогностическая модель не сможет корректно воспринимать анализируемую последовательность как истинную временную шкалу.

В нашей библиотеке уже существуют классические реализации позиционных эмбеддингов — от простых синусо-косинусных до обучаемых таблиц, — но все они смотрят на временной ряд как на набор подряд идущих элементов, не принимая во внимание время получения данных от окружающей среды. Между тем авторы Mamba4Cast настаивают на том, что каждый шаг должен кодироваться с учётом реального периода: минута, час, день недели, день месяца, месяц и даже год — всё это влияет на динамику рынка. Их подход заключается в том, чтобы для каждой временной компоненты построить собственное синусоидальное разложение, — и именно этому глубинному учёту времени мы и посвятим первый блок практической работы.

Этот шаг по-настоящему определяет, как модель будет видеть время: не просто последовательность баров, а живой поток событий с чётко обозначенными моментами. Без точного учёта временных меток даже самый продвинутый алгоритм потеряет смысл — ведь рынок реагирует на минуту, на час и на день совсем по-разному.

Временное кодирование на стороне OpenCL

В своей реализации вместо крутого, но громоздкого подхода с предварительно вычисленными таблицами гармонических функций мы задействуем OpenCL-ядро для мгновенного вычисления позиционного кодирования на основе реальных меток времени. Это решение убирает необходимость держать в памяти большие массивы значений синусов и косинусов, устраняет ступеньки при переходе от одной точки к другой и максимально упрощает логику советника.

В нашем подходе каждый временной шаг приходит в ядро OpenCL сразу с двумя наборами информации: числовыми признаками (цена, объём, индикаторы) и временем события. Именно этот момент мы превращаем в вектор, который рассказывает модели о том, когда он произошёл: в разгаре сессии или в полуденную тишину выходного дня, в начале месяца или в преддверии года.

Преимущества этого метода ощущаются сразу же. Во‑первых, мы получаем абсолютно гладкое позиционное кодирование: никакие скачки между соседними индексами не нарушат целостность embeddings. Во‑вторых, отсутствие таблиц означает меньше кода, меньше ошибок синхронизации и меньше памяти, выделяемой в платформе. В‑третьих, вычисление на лету делает embedding ещё более актуальным: не нужно пересобирать таблицы при смене настроек или периодов — достаточно изменить значения периодов и модель моментально адаптируется к новым требованиям.

Алгоритм добавления временного кодирования в анализируемые данные на стороне OpenCL‑ядра заключается в том, чтобы каждый бар окружить собственным вектором гармоник, отражающим, в какой точке каждого из циклов он сформировался. В параметрах кернела TSPositionEncoder передаются указатели на три массива:

• исходные данные data,
• массив временных меток time,
• массив периодов period, задающий длину каждого календарного цикла.

__kernel void TSPositonEncoder(__global const float2* __attribute__((aligned(8))) data,
                               __global const float* time,
                               __global float2* __attribute__((aligned(8))) output,
                               __global const float* period
                              )
  {
   const int id = get_global_id(0);
   const int freq = get_global_id(1);
   const int p = get_global_id(2);
   const int total = get_global_size(0);
   const int freqs = get_global_size(1);
   const int periods = get_global_size(2);

Данный кернел мы планируем запускать в трехмерном пространстве задач:

• размер анализируемой последовательности (количество временных шагов),
• количество гармоник для каждого периода,
• количество периодов.

И в теле кернела сразу идентифицируем текущий поток операций во всех измерениях пространства задач.

Сначала для каждой точки времени (индекс id) и для каждой гармоники (freq) в периоде (p) ядро вычисляет координату внутри периода: реальное время делится на длину цикла, превращая абсолютное значение time[id] в число полных периодов, а дробную часть мы умножаем на π и на степень двойки 2^(freq+1). Это позволяет получить аргумент val для синуса и косинуса, где первая гармоника охватывает весь цикл, вторая — делит его пополам, третья — на четверти и так далее.

   const int shift = id * freqs + freq;
   const float2 d = data[shift * periods + p];
   const float t = time[id] / period[p];
   float val = M_PI_F * t * pow(2.0f, freq + 1);

Далее это значение добавляется к исходному эмбеддингу: OpenCL‑поток загружает пару чисел из data, соответствующую текущему времени, гармонике и циклу, а затем увеличивает первую половину этой пары на sin(val), вторую — на cos(val). Получившийся вектор сохраняется в буфер output. Именно такая операция окрашивает каждую точку временного ряда дополнительными признаками, чётко указывающими на её положение в календарных паттернах.

   output[shift * periods + p] = (float2)(d.s0 + sin(val), d.s1 + cos(val));
  }

Преимущество такого подхода заключается в том, что вычисление осуществляется на лету, прямо в GPU‑ядре, без обращений к большим таблицам и без логики на стороне CPU. Любые изменения — например, добавление нового периода или увеличение количества гармоник — сводятся к корректировке размеров трёхмерной сетки потоков и значений в массиве period. При этом мы сохраняем абсолютную плавность: синус и косинус гарантируют непрерывное представление времени, а GPU‑параллелизм позволяет обрабатывать сразу большое количество точек без задержек.

В результате каждое событие получает свой собственный, уникальный embedding: с учётом не только цены или объёма, но и точного момента, когда это событие произошло. Это даёт Mamba4Cast всю глубину контекста и делает алгоритм прогнозирования по-настоящему осознанным в отношении времени.

Поскольку временные метки событий в нашем приложении не являются обучаемыми параметрами, для их обработки достаточно реализовать только прямой проход — шаг вычисления embedding‑векторов в OpenCL‑ядре. Нам не нужно распределять градиенты ошибки по времени или обновлять сами метки. Это позволяет исключить процессы обратного прохода, максимально упростив архитектуру, и свести расчёт позиционного кодирования к чисто детерминированной функции от времени.

Объект временного кодирования

На стороне основной программы алгоритмы временного кодирования анализируемой последовательности реализованы в классе CNeuronTSPositionEncoder, структура которого представлена ниже.

class CNeuronTSPositionEncoder   :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL             cProjection;
   CNeuronBatchNormOCL        cNorm;
   CBufferFloat               cPeriods;
   //---
   virtual bool               AddPE(CBufferFloat *time);
   //---
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool               feedForward(CNeuronBaseOCL *NeuronOCL,
                                          CBufferFloat *SecondInput) override;
   virtual bool               updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool               calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTSPositionEncoder(void) {};
                    ~CNeuronTSPositionEncoder(void) {};
   //---
   virtual bool               Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                   uint window, uint units_count, uint &periods[], uint freqs,
                                   ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int                Type(void) override  const   {  return defNeuronTSPositionEncoder;   }
   //---
   virtual bool               Save(int const file_handle) override;
   virtual bool               Load(int const file_handle) override;
   //---
   virtual bool               WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void               SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual uint               GetWindow(void) const { return cProjection.GetWindow(); }
   virtual uint               GetWindowOut(void) const { return cProjection.GetFilters(); }
   virtual uint               GetUnits(void) const { return cProjection.GetUnits(); }
  };

В представленной структуре сразу бросается в глаза три внутренних объекта, которые, казалось бы, избыточны с учетом выполнения временного кодирования на стороне OpenCL. Тем не менее именно они отвечают за то, чтобы любая последовательность анализируемых данных оказалась аккуратно упакована и выровнена по масштабу до того, как ей будет добавлен временной контекст.

Во-первых, cProjection принимает на вход абсолютно любые массивы признаков, которые приходят из предыдущего слоя нейронной сети, и превращает их в ровные векторы фиксированной размерности. Благодаря этому остальные части кода могут не задумываться о том, сколько внутри данных признаков и как они сгруппированы — выход из cProjection всегда имеет прогнозируемую форму, готовую к батч‑нормализации и позиционному кодированию.

Во-вторых, cNorm выполняет роль гаранта стабильности. На практике цены, объёмы и любые стохастические сигналы могут прыгать по диапазону значений. Если сразу после проекции мы подмешаем к ним синусо‑косинусные значения в диапазоне [-1,1], часть информации рискует быть потерянной. Чтобы этого не произошло, мы прогоняем выход cProjection сквозь батч‑норму, приводя среднее к нулю и дисперсию к единице. Только после этого впускаем гармоники времени. Именно в этом порядке получается, что временные признаки становятся органичной надстройкой над уже обработанными данными, а не хаотичным шумом.

Наконец, cPeriods хранит постоянный набор периодичности временных циклов.

Именно такое разделение ответственности делает класс одновременно гибким (он принимает любые входные данные), устойчивым (он всегда выравнивает всё к стабильному виду) и точным (с допуском абсолютной непрерывности временного кодирования).

Чтобы превратить класс CNeuronTSPositionEncoder из декларативной конструкции в реальный рабочий узел, необходимо корректно инициализировать все его внутренние компоненты. Именно эту задачу решает метод Init.

bool CNeuronTSPositionEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint units_count, uint &periods[], uint freqs,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * freqs * periods.Size(),
                                                                         optimization_type, batch))
      return false;

Метод строго следует описанной ранее логике архитектуры: проекция → нормализация → добавление временных признаков.

На первом этапе вызываем одноименный метод родительского класса. В нем задаются общие параметры объекта. Обратите внимание, что при указании размера тензора результатов мы умножаем произведение полученных параметров на 2. Причина тому — представление каждой гармоники времени в виде двух компонент: синуса и косинуса.

Затем инициализируется буфер временных циклов. Их периодичность задается в секундах.

   cPeriods.BufferFree();
   if(!cPeriods.AssignArray(periods) ||
      !cPeriods.BufferCreate(OpenCL))
      return false;

Следующим инициализируем слой проекции исходных данных в фиксированное пространство размерности: 2 × частот × периодов. Этот размер соответствует количеству каналов, которые мы хотим снабдить временными признаками. По сути, мы настраиваем фильтры, которые будут подготавливать каждый фрагмент временного ряда к добавлению временных фаз.

   int index = 0;
   if(!cProjection.Init(0, index, OpenCL, window, window, 2 * freqs * cPeriods.Total(), units_count,
                                                                           1, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(TANH);

Использование функции активации TANH на этапе проекции — это не просто стилистический выбор, а практический способ ограничить амплитуду выходных значений в диапазоне [-1;1]. И это даёт сразу несколько важных преимуществ.

Если исходные данные содержат шум, скачки, экстремумы — TANH действует как мягкий ограничитель, сглаживая сильные отклонения и делая поведение модели более устойчивым. Это особенно важно в условиях финансовых временных рядов, где внезапные свечи или всплески объёмов могут дезориентировать всю сеть.

Кроме того, функция TANH обеспечивает плавную производную на всём диапазоне входов, что важно при дальнейшем распространении градиента. Это снижает риск залипания нейрона и способствует более стабильной и быстрой сходимости.

Как только свёртка завершена, её результат передаётся в cNorm, где выравниваются средние значения и масштаб. Это защищает от утопления синусо-косинусных сигналов в слишком больших амплитудах и обеспечивает надёжность временного кодирования.

   index++;
   if(!cNorm.Init(0, index, OpenCL, cProjection.Neurons(), iBatch, optimization))
      return false;
   cNorm.SetActivationFunction(None);

Завершающий штрих: поскольку временное кодирование не является обучаемым узлом в классическом смысле, мы отключаем общую активацию и просто прокидываем градиенты от внешних интерфейсов к cNorm.

   SetActivationFunction(None);
   if(!SetGradient(cNorm.getGradient(), true))
      return false;
//---
   return true;
  } 

Переходя к реализации прямого прохода в классе CNeuronTSPositionEncoder, стоит подчеркнуть, что данный этап является логическим завершением всей процедуры временного кодирования. Именно здесь происходит объединение проецированной и нормализованной информации об исходной последовательности с детализированной временной структурой в виде гармоник, рассчитанных по реальному времени поступления данных.

Метод feedForward аккуратно разбивает процесс на три последовательные стадии. При этом обратите внимание, что в параметрах метода передаются указатели на 2 источника данных. По основному информационному потоку представлена анализируемая последовательность, а по второму — временные метки.

bool CNeuronTSPositionEncoder::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

Вначале вызывается метод прямого прохода слоя проекции исходных данных. На этом этапе исходные данные любой размерности сводятся к заданному числу признаков, обеспечивая согласование размерностей для последующего наложения заданного количества гармоник временной информации.

Затем полученные проекции проходят через слой нормализации.

   if(!cNorm.FeedForward(cProjection.AsObject()))
      return false;

Задача нормализации — сгладить статистические различия между признаками анализируемых данных и подготовить их к сложению с временными гармониками.

И, наконец, завершающий шаг — вызов метода-оберкти выше описанного кернела временного кодирования, который в реальном времени для каждого временного шага и каждой заданной частоты рассчитывает синусо-косинусные гармоники на основании текущего значения временной метки и набора заданных периодов.

   return AddPE(SecondInput);
  }

Эта операция не зависит от параметров, подлежащих обучению, и не требует распространения градиента, поскольку время — это внешний, детерминированный фактор.

В результате на выходе мы получаем богатое представление, сочетающее в себе как содержательные особенности данных, так и точный контекст времени, в который эти данные поступили — не по порядковому номеру, а по фактическому ритму событий.

Процессы обратного прохода в классе CNeuronTSPositionEncoder предельно лаконичны по своей структуре, но не теряют при этом важности. Все вычисления сводятся к классической схеме распространения градиента ошибки на уровень исходных данных. При этом основной поток вычислений проходит через два ключевых компонента: слой проекции (cProjection) и слой нормализации (cNorm). Каждый из них содержит обучаемые параметры и требует соответствующей оптимизации.

На практике это означает, что при вызове методов updateInputWeights и calcInputGradients наш объект лишь последовательно делегирует управление соответствующим методам внутренних компонентов.

Такой подход обеспечивает модульность и повторяемость логики: изменения в механизме обучения конкретного слоя автоматически распространяются на всю систему без необходимости переписывать код верхнего уровня. Это особенно важно в контексте масштабируемых нейросетевых архитектур.

Однако, здесь следует сделать одно важное замечание. Несмотря на то, что метод прямого прохода feedForward принимает два информационных потока: основную исходную последовательность и массив временных меток. В процессе обратного распространения ошибки участвует только основной информационный поток. И это абсолютно оправдано.

Причина в том, что временное кодирование в CNeuronTSPositionEncoder не имеет обучаемых параметров. Оно представляет собой фиксированную, детерминированную операцию над временной меткой. Более того, мы сознательно не распространяем градиент ошибки на уровень временных меток. Эти значения являются внешними по отношению к модели и не должны изменяться в результате оптимизации.

Эта логика делает архитектуру не только чистой и стабильной, но и логически непротиворечивой: данные времени используются для контекстуализации, но не для обучения.

Полный код данного класса и всех его методов представлен во вложении.

Мы плавно подошли к разумным пределам формата статьи. Основные компоненты временного кодирования разобраны, ключевые идеи реализованы, а архитектура слоя получила чёткое, стройное воплощение в коде. Но, как говорится, не всё сразу.

Наша реализация ещё не завершена. Впереди много работы, которая требует спокойного, вдумчивого подхода. Сделаем небольшую паузу, переведём дух и продолжим в следующей статье.

Заключение

В данной статье мы познакомились с фреймворком Mamba4Cast, призванным решить одну из фундаментальных задач в анализе временных рядов — построение гибкой и масштабируемой модели, способной учитывать сложную структуру динамических временных рядов. Мы увидели, как авторы фреймворка обошли традиционные ограничения классических моделей, интегрировав новейшие архитектурные подходы, включая State Space Models (SSM), расширенные механизмом Causal Convolution, и дополнив их точным позиционным кодированием на основе реальных временных меток.

Постепенно погружаясь в структуру фреймворка, мы детально разобрали логику формирования временных признаков. Поняли, как с помощью простых, но мощных гармонических функций можно превратить голые метки времени в осмысленные эмбеддинги, отражающие циклическую природу рыночных процессов. На примере реализации в OpenCL мы рассмотрели, как такие эмбеддинги могут быть эффективно получены прямо в вычислительном ядре, без дополнительных таблиц и задержек.

Но наша работа ещё не завершена и мы продолжим её в следующей статье, где покажем, как временные эмбеддинги взаимодействуют с архитектурными блоками модели, обеспечивая целостность анализа и повышая точность прогнозов.

Ссылки

• Mamba4Cast: Efficient Zero-Shot Time Series Forecasting with State Space Models
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник офлайн обучения моделей
4	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы