
Нейросети в трейдинге: Единый взгляд на пространство и время (Extralonger)
Введение
Прогнозирование динамики сложных систем традиционно является одной из ключевых задач анализа данных. От качества и глубины прогнозов зависит не только академический интерес исследователей, но и вполне практические результаты: оптимизация потоков, снижение издержек, управление рисками. Наиболее ярко эта проблема проявляется в двух, казалось бы, далеких друг от друга сферах — в интеллектуальных транспортных системах и на финансовых рынках. На первый взгляд, дороги с их потоками автомобилей и биржевые площадки с потоками ордеров имеют мало общего. Однако внимательное рассмотрение обнаруживает глубокое структурное сходство.
В транспортных исследованиях данные представляют собой сеть, в которой узлы — это станции мониторинга, а рёбра отражают их взаимосвязь. В финансовом мире аналогичную роль играют активы, биржи, брокеры, торговые платформы, между которыми непрерывно циркулирует информация и капитал. Если в дорожной сети сигналом выступает трафик автомобилей, то в финансовых системах таким сигналом являются цены, объёмы, ликвидность и поведение участников торгов. В обоих случаях задача заключается в том, чтобы на основе изучения исторических данных найти закономерности пространственно-временной динамики и построить прогноз на будущее.
Традиционные подходы к решению подобных задач опирались на раздельное рассмотрение пространственной и временной составляющих. В транспортных исследованиях это означало анализ временных рядов трафика отдельно от топологии дорожной сети. В финансах же, аналогичные методы сосредотачивались либо на временной динамике ценовых рядов, либо на структурных корреляциях между активами. Подобный разрыв между пространством и временем порождает серьёзные ограничения: алгоритмы становятся чрезмерно ресурсоёмкими, а их способность к долгосрочному прогнозированию резко снижается.
Основная трудность заключается в том, что обработка временных признаков требует повторных итераций по пространственным связям. В то же время анализ структурных зависимостей между узлами — многократных проходов по временной оси. В результате сложность вычислений возрастает на порядок выше, чем в задачах чистого прогнозирования временных рядов. Если к этому добавить быстро растущие объёмы данных, свойственные транспортным системам и финансовым рынкам, становится очевидным, что без принципиально нового подхода продвинуться дальше горизонта в несколько часов или нескольких шагов практически невозможно.
Один из вариантов решения указанной проблемы предложили авторы работы "Extralonger: Toward a Unified Perspective of Spatial-Temporal Factors for Extra-Long-Term Traffic Forecasting". Авторы черпают вдохновение в идеях Альберта Эйнштейна о неразрывности пространства и времени, утверждая, что пространственные и временные факторы должны рассматриваться нераздельно и одновременно. Эта мысль воплощается в концепции Unified Spatial-Temporal Representation — единого пространственно-временного представления, которое устраняет необходимость искусственного разделения данных на временные и пространственные компоненты. Пространственная информация включается в каждый временной шаг, а временная — в каждый узел сети.
В транспортных системах такой подход позволил впервые в истории расширить прогнозный горизонт с привычных 2–4 часов до целой недели. Для финансовых рынков потенциал ещё более впечатляющий. Представьте модель, которая способна не только реагировать на краткосрочные импульсы, но и строить осмысленные прогнозы на горизонтах, значимых для стратегической торговли, риск-менеджмента и инвестиционного планирования. В условиях, где даже небольшое преимущество в понимании будущей динамики цен может привести к значительным финансовым результатам, возможность прогнозировать с опорой на единое пространственно-временное представление открывает принципиально новые горизонты.
Кроме того, унификация пространства и времени радикально снижает вычислительные затраты. Если в классической постановке сложность алгоритмов стремительно росла и фактически ограничивала исследователей рамками короткого горизонта, то Extralonger демонстрирует сокращение сложности на порядок. Это означает более быструю работу алгоритмов и возможность их применения в реальных условиях, где важны скорость отклика и эффективность использования ресурсов. В результате обучение моделей ускоряется в сотни раз, а потребление памяти снижается до величин, делающих возможным долгосрочное прогнозирование даже в условиях ограниченной инфраструктуры.
Для финансовых рынков это обстоятельство имеет особое значение. Ведь рынок — это не только огромные массивы исторических данных, но и непрерывный поток новых сигналов, требующих обработки в режиме реального времени. Традиционные архитектуры часто спотыкались именно на этом этапе. Избыточная сложность мешала им справляться с задачами длинного горизонта планирования и приходилось жертвовать скоростью или надёжностью. А порой и тем, и другим. Фреймворк Extralonger демонстрирует, что подобные компромиссы больше не обязательны.
Алгоритм Extralonger
Большинство существующих моделей прогнозирования строятся на так называемом классическом представлении данных.
![]()
где T — длина временного окна, N — количество узлов сети, C — число исходных признаков, а D — размерность преобразованного признакового пространства.
На практике это означает, что данные сначала линейно проецируются в пространство фиксированной размерности, а затем обрабатываются модулями, отвечающими за извлечение временной и пространственной информации.
Классическая архитектура обычно включает два типа модулей: временной и пространственный. Их можно комбинировать в разном порядке — сначала анализировать время, затем пространство. Или наоборот, пытаться обрабатывать оба измерения одновременно. Однако на деле любое такое разбиение имело один и тот же недостаток — обработка признаков по одной оси требовала многократных итераций по другой. В результате вычислительная сложность быстро возрастала. Например, для механизмов Self-Attention она достигала порядка O(NT2 + TN2) с аналогичным ростом потребления памяти. Для финансовых рынков это означает, что прогнозирование на длинном горизонте становится крайне ресурсоёмким. Большие массивы исторических котировок и взаимосвязей между инструментами попросту перегружают систему.
Попытки обойти эти ограничения предпринимались и ранее. В том числе с помощью сверточных моделей (CNN). В этом случае данные обрабатывались как изображение, где одна ось соответствует времени, а другая — множеству узлов. Такой подход действительно позволяет рассматривать пространство и время одновременно, но имеет ограничения. Сверточное окно не позволяет охватить всю картину целиком, а лишь локальные участки. Кроме того, сложность алгоритма при этом выражалась как O(k2TN), где k — размер ядра свертки, что всё равно ограничивало возможности расширения горизонта.
Фреймворк Extralonger радикально меняет эту ситуацию за счёт введения Unified Spatial-Temporal Representation — единого пространственно-временного представления. Суть идеи проста: пространство и время не разделяются, а описываются единым образом. Для этого исходное представление X∈RT×N×C сначала сжимается по признаковому измерению, после чего применяются две линейные проекции: одна по пространству, другая по времени. В итоге формируются два набора представлений:
- Et ∈ RT×D — каждый временной шаг содержит информацию обо всех узлах сети,
- Es ∈ RN×D — каждый узел аккумулирует данные обо всех временных шагах.
Таким образом, каждое наблюдение начинает нести в себе полную пространственно-временную картину, а не только локальный срез. Это и есть принципиальное отличие: если классическое представление опиралось на частные признаки, то новое обеспечивает целостный охват.
Данный подход имеет сразу несколько фундаментальных преимуществ. Во-первых, снижение сложности. За счёт устранения избыточных итераций, временные и пространственные зависимости теперь обрабатываются совместно, и сложность алгоритма сокращается до O(T2 + N2). Это дает возможность строить прогнозы на десятки и сотни шагов вперёд, не упираясь в потолок вычислительных ресурсов.
Во-вторых, одновременная агрегация. Если классические методы вынуждены были двигаться вдоль одной оси, постепенно догружая информацию с другой, то Extralonger позволяет каждому узлу быть связанным сразу со всеми остальными на любом временном шаге. Следовательно, алгоритм способен учитывать одновременно взаимодействие между разными инструментами и динамику их изменения во времени, что крайне важно для комплексного анализа корреляций и межрыночных связей.
И наконец, в-третьих, полный рецептивный охват. Используя Self-Attention в рамках единого представления, Extralonger обеспечивает связь каждого узла с любым другим узлом во все моменты времени. Это даёт модели возможность фиксировать самые длинные зависимости — от дневных и недельных циклов до более сложных паттернов, связанных, например, с сезонностью на фондовом рынке или многодневными фазами тренда. Для сравнения: в RNN, Attention или классических Transformer-моделях агрегация идёт по отдельным измерениям, а CNN ограничены локальным окном восприятия.
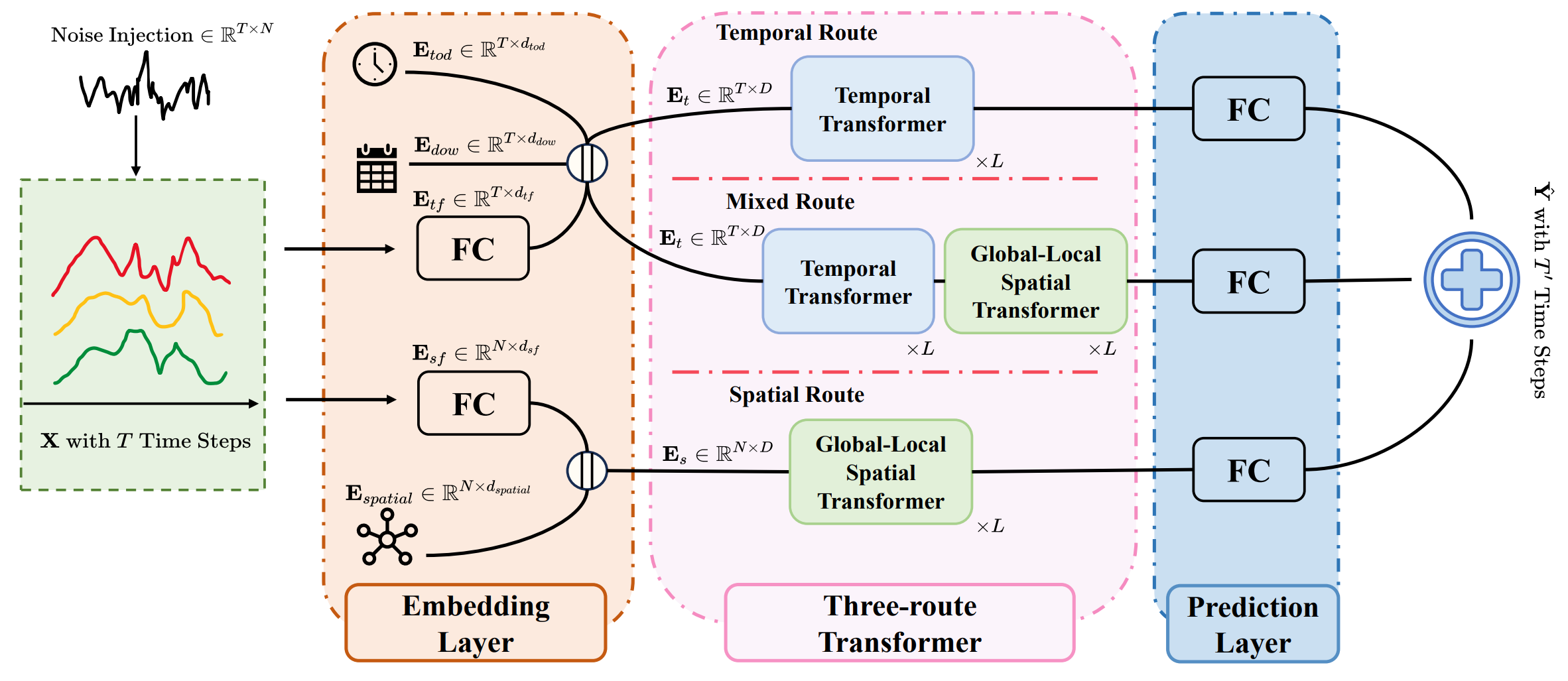
Архитектура Extralonger состоит из трёх основных компонентов:
- слоя эмбеддинга (embedding layer),
- трёхмаршрутного Transformer-модуля (three-route Transformer)
- слоя прогнозирования (prediction layer).
Слой эмбеддинга преобразует исходные данные во внутреннее представление, которое включает два ключевых элемента — пространственное Es и временное Et представления. Особенность архитектуры заключается в том, что ещё на входе данные подвергаются предварительной обработке. В массив исходных данных X вводится обучаемый шум, что помогает повысить устойчивость модели к рыночным шумовым колебаниям.
Затем применяются две полносвязные линейные проекции: одна формирует временные признаки Etf∈RT×dtf, другая — пространственные Esf∈RN×dsf.
С целью уловить цикличность, свойственную реальным процессам, в архитектуру Extralonger добавлены обучаемые эмбеддинги периодичности. Для временной оси используется встраивание timestamp-of-dayEtod∈RT×d_tod, которое отражает суточный цикл, и day-of-weekEdow∈RT×d_dow, моделирующее недельную сезонность. Аналогично, для пространственного измерения вводится обучаемое встраивание Espatial∈RN×d_spatial, позволяющее уловить устойчивые пространственные закономерности.
Финальные представления получаются конкатенацией этих эмбеддингов:
- временное представление Et = Etf ‖ Etod ‖ Edow ∈ RT×D,
- пространственное представление Es = Esf ‖ Espatial ∈ RN×D.
Таким образом, ещё на этапе формирования признаков в модель закладываются фундаментальные циклы и пространственные связи. Для финансовых рынков это особенно ценно: ежедневные колебания ликвидности, недельные ритмы активности, корреляции между инструментами и торговыми площадками сразу находят отражение в структуре данных.
Сердцем системы является трёхмаршрутный Transformer, в котором параллельно работают три пути: временной, пространственный и смешанный. Благодаря использованию единого пространственно-временного представления, все три маршрута способны одновременно учитывать как временную, так и пространственную структуру данных. При этом каждый маршрут делает акцент на своей задаче. Временной Transformer в чисто временном и в смешанном пути реализован как стандартный Transformer-энкодер, тогда как пространственный маршрут и смешанный маршрут дополнены специальным модулем — Global-Local Spatial Transformer, позволяющим эффективно фиксировать как локальные, так и глобальные связи.
В отличие от стандартного механизма Self-Attention, где все узлы сети обрабатываются одинаковым образом и без учёта их реальной структуры, Global-Local Spatial Transformer специально создан для использования топологических особенностей исследуемой системы. В транспортной задаче это дорожная сеть, где одни станции соединены напрямую, а другие лишь опосредованно. В мире финансов аналогичная структура проявляется в виде графа активов: одни бумаги жёстко коррелируют между собой, а другие связаны лишь через глобальные рыночные тренды.
Традиционный Transformer рассматривает все связи как равнозначные. Это позволяет фиксировать общую картину, но в то же время приводит к размытию локальных особенностей. И наоборот, модели, которые концентрируются исключительно на локальных связях, хорошо улавливают детали, но теряют способность видеть дальнодействующие зависимости. Именно здесь возникает необходимость в балансе — учёте глобальных и локальных закономерностей одновременно.
Модуль GLST реализует эту идею напрямую, соединяя два механизма внимания — глобальный и локальный. На первом этапе из пространственного представления Es строятся матрицы Query, Key и Value. На их основе вычисляются коэффициенты глобального внимания.
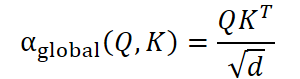
Эта матрица отражает силу взаимосвязей между всеми узлами сразу. В финансовом контексте это можно понимать, как матрицу кросс-корреляций между инструментами.
Далее в игру вступает локальное внимание. Для его формирования используется матрица смежности A, которая задаёт структуру реальных связей. В транспортных задачах A кодирует дорожные соединения, в финансах же, в качестве такой матрицы может выступать граф устойчивых корреляций или сеть взаимных влияний между инструментами. Применение A ограничивает внимание только соседними узлами, создавая локальную компоненту.
![]()
где ⊙ — поэлементное произведение.
Таким образом, глобальная часть фиксирует широкие зависимости, а локальная удерживает внимание на наиболее близких и значимых связях.
Обе матрицы проходят через SoftMax-нормализацию и объединяются в единое выражение.
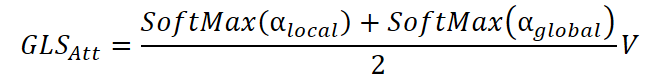
Результат — это сбалансированная агрегация, в которой каждый узел получает одновременно информацию о всей системе и ближайших связях.
После этого, в духе классического Transformer, применяется слой нормализации, остаточные связи (skip-connection) и сеть Feed-Forward. Эти шаги формируют окончательное обновлённое пространственное представление Ês.
Важно подчеркнуть, что для финансовых рынков этот модуль особенно естественен. Корреляции между активами меняются со временем, связи между инструментами бывают устойчивыми или динамическими. Использование глобально-локального внимания даёт модели гибкость: она может подстраиваться под текущую структуру рынка, различать прочные зависимости и временные, а значит, формировать более надёжный прогноз.
В результате, Global-Local Spatial Transformer становится своеобразным мостом между микро- и макроуровнями анализа. На микроуровне он отслеживает локальные рыночные сигналы и краткосрочные взаимосвязи. На макроуровне — видит глобальные тренды и долгосрочные корреляции. Слияние этих двух перспектив делает модель мощной с точки зрения теории и применимой в реальной торговле, где именно сочетание деталей и глобального контекста определяет успешность стратегий.
После того как трёх маршрутный Transformer завершает обработку данных и формирует пространственно-временные представления, наступает заключительный этап — прогнозирование. Его задача состоит в том, чтобы преобразовать абстрактные эмбеддинги в конкретные прогнозные значения на заданном горизонте планирования.
Для этого используются линейные проекции, которые переводят выходные тензоры из скрытого пространства обратно в формат прогнозов. Поскольку постановка задачи в Extralonger является асимметричной (T → T′), то есть длина исторического окна T и длина прогнозируемого интервала T′ не совпадают, необходимо явно спроецировать выходы Transformer на размерность T′. Другими словами, из исторического фрагмента фиксированной длины мы получаем прогноз на более длинный или более короткий горизонт, что особенно важно для финансовых рынков, где размер окна может адаптироваться в зависимости от стратегии.
После проекции результаты всех трёх маршрутов (временного, пространственного и смешанного) объединяются. Здесь авторы фреймворка используют не автоматическое обучение весов, а заранее заданную комбинацию — ручная настройка весовых коэффициентов. Такой подход позволяет явно регулировать вклад каждого маршрута в итоговый прогноз: при желании можно усилить роль временной компоненты для рынков с выраженными трендами, или наоборот, акцентировать пространственные зависимости, если важнее структура корреляций между активами.
В совокупности предложенная архитектура превращает Extralonger в мощный инструмент, где каждый модуль усиливает другой. Временной маршрут фиксирует протяжённые динамики котировок и объёмов, пространственный — взаимозависимости между активами и рынками, а смешанный объединяет оба аспекта, создавая целостное восприятие рыночной картины.
Авторская визуализация фреймворка Extralonger представлена ниже.
Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка Extralonger, мы переходим к практической части нашей работы, где попробуем воссоздать один из возможных вариантов реализации его алгоритмов средствами MQL5. Удобство предлагаемой авторами архитектуры состоит в её модульности. Каждый компонент можно выделить отдельно, протестировать и, при необходимости, заменить или доработать. Это особенно ценно для трейдинговых систем, где важна гибкость и возможность адаптации к специфике конкретных рынков. В нашем случае мы также пойдём путём поэтапного построения — модуль за модулем, максимально используя ранее разработанный набор объектов, чтобы избежать дублирования функционала.
Как было отмечено в теоретической части, обработка исходных данных начинается с добавления обучаемого шума. При этом важно подчеркнуть, что под шумом здесь понимается не традиционная случайная компонента, формируемая генераторами псевдослучайных чисел. Напротив, это матрица обучаемых параметров, играющая роль дополнительного смещения. Иными словами, это не хаотическое искажение, а целенаправленное расширение признакового пространства, позволяющее модели захватывать скрытые зависимости, которые неочевидны в исходных данных.
Если провести аналогию с классическими архитектурами, то подобный слой выполняет ту же функцию, что и обучаемое позиционное кодирование в Transformer-моделях. Там он позволяет модели различать позиции во временной последовательности, здесь же — добавляет возможность смещать данные в направлении, благоприятном для последующего извлечения закономерностей. И именно это качество делает подход особенно ценным для финансовых рынков: такие смещения могут фактически кодировать устойчивые сезонные паттерны или слабые корреляции, которые не выражены напрямую в ценовых рядах.
В нашей библиотеке уже имеется объект CNeuronLearnabledPE, выполняющий подобный функционал. Его предназначение заключается в добавлении обучаемого позиционного смещения к исходным данным, и в контексте реализации фреймворка Extralonger он идеально ложится на задачу обучаемого шума. По сути, мы можем воспользоваться готовым решением, проверенным временем, без необходимости изобретать новый компонент.
Это не только экономит усилия, но и гарантирует стабильность, поскольку объект прошёл проверку в предыдущих экспериментах.
Следующим этапом после добавления обучаемого смещения, идёт формирование проекций во временной и пространственной плоскостях. В теоретическом описании фреймворка Extralonger для этого используются два полносвязных слоя, которые, работая параллельно, создают два набора эмбеддингов.
В нашей реализации мы можем возложить эту задачу на объекты сверточного слоя CNeuronConvOCL. Это решение естественно и удобно. Сверточные операции уже хорошо зарекомендовали себя в качестве универсального инструмента для преобразования исходных массивов. Они позволяют легко управлять числом входных и выходных каналов, задавая размер ядра. Следовательно, формирование временных и пространственных проекций может быть реализовано как два параллельных сверточных слоя: первый работает по оси времени и формирует Et, второй — по оси узлов и формирует Es. Это полностью соответствует идее авторов Extralonger и при этом сохраняет унифицированность нашей реализации.
Добавление пространственных эмбеддингов
Далее следует этап добавления эмбеддингов пространства и времени. На первый взгляд, здесь нет особых сложностей. Мы уже сталкивались с подобными операциями. Создание пространственного эмбединга в условиях фиксированной структуры данных похоже на предыдущий шаг с добавлением обучаемого шума. Только на этом этапе мы не суммируем тензоры, а конкатенируем их, соединяя информацию из разных источников. Процесс организован в новом объекте CNeuronSpatialEmbedding, который наследует базовую функциональность от CNeuronBaseOCL и расширяет её под наши задачи.
class CNeuronSpatialEmbedding : public CNeuronBaseOCL { protected: uint iWindow; uint iUnits; uint iEmbeddingDim; CParams cEmbedding; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSpatialEmbedding(void) {}; ~CNeuronSpatialEmbedding(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint embed_dim, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSpatialEmbedding; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; virtual void SetActivationFunction(ENUM_ACTIVATION value) override { }; };
Архитектура нейрона формируется в методе инициализации Init. Именно здесь задаются его ключевые параметры: количество унитарных последовательностей, размер каждой из них и размерность эмбеддинга.
bool CNeuronSpatialEmbedding::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint embed_dim, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, (window + embed_dim)*units, optimization_type, batch)) return false; activation = None;
Внутри метода сначала вызывается инициализация родительского класса нейрона с поддержкой OpenCL. Размерность тензора результатов рассчитывается как сумма длины представления унитарной последовательности и эмбеддинга, умноженная на число таких последовательностей. Если базовая инициализация не удалась, метод корректно завершает работу, возвращая сигнал об ошибке.
Далее нейрон настраивает функцию активации — для самого нейрона она пока не используется.
Затем инициализируем объект формирования эмбеддингов. И здесь мы уже используем гиперболический тангенс TANH в качестве функции активации, который придаёт нелинейность и ограничивает значения в диапазоне [-1, 1]. Это помогает модели формировать более устойчивые представления рыночных закономерностей и предотвращает чрезмерное влияние экстремальных значений на процесс обучения.
if(!cEmbedding.Init(0, 0, OpenCL, embed_dim * units, optimization, iBatch)) return false; cEmbedding.SetActivationFunction(TANH); //--- iUnits = units; iWindow = window; iEmbeddingDim = embed_dim; //--- return true; }
Затем сохраняются параметры нейрона для последующих операций прямого и обратного проходов.
В результате метод Init плавно соединяет теорию с практикой. Нейрон становится полностью готовым к обработке данных, конкатенации эмбеддингов и передаче структурированной информации дальше. Это создаёт надёжный фундамент для построения торговых моделей, которые могут анализировать рыночные сигналы с разных временных горизонтов и выявлять скрытые зависимости, важные для принятия обоснованных торговых решений.
В методе feedForward построен алгоритм прямого прохода данных через нейрон — от входов к выходам. В финансовом контексте это похоже на то, как трейдер последовательно анализирует исторические данные и формирует интегральное представление текущей рыночной ситуации.
Сначала проверяется актуальность переданного указателя на предыдущий нейрон NeuronOCL. Если его нет, метод сразу возвращает false. Это важно. Без исходных данных прямой проход невозможен, как без рыночных котировок невозможно принимать решения.
bool CNeuronSpatialEmbedding::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Далее, если нейрон находится в режиме обучения (bTrain=true), вызывается прямой проход для объекта cEmbedding. Здесь формируются пространственные эмбеддинги, которые кодируют ключевые зависимости рынка в выбранном окне данных. Если эта операция не удалась, метод возвращает false, чтобы сигнализировать о проблеме в создании эмбеддингов.
if(bTrain) if(!cEmbedding.FeedForward()) return false;
Обратите внимание, что операция выполняется только в процессе обучения. Ведь в данном случае эмбеддинги не зависят от исходных данных, а только кодируют позиции последовательностей. Следовательно, в процессе эксплуатации значения остаются фиксированными, и мы исключаем излишние операции, что позволит повысить скорость принятия решения.
После формирования эмбеддингов наступает ключевой шаг — конкатенация исходных данных с эмбеддингами. Метод Concat объединяет выходы предыдущего нейрона и эмбеддинга в единый тензор Output, учитывая размер представления каждой унитарной последовательности и размерность эмбеддинга.
if(!Concat(NeuronOCL.getOutput(), cEmbedding.getOutput(), Output, iWindow, iEmbeddingDim, iUnits)) return false; //--- return true; }
Наконец, если все операции прошли успешно, метод возвращает true, сигнализируя, что прямой проход нейрона выполнен корректно и тензор результатов готов к передаче следующему слою модели.
Как можно заметить, алгоритм метода прямого прохода довольно прост и линейно организован. Он последовательно проверяет входные данные, формирует пространственные эмбеддинги и конкатенирует их с выходами предыдущего слоя, создавая готовый к передаче тензор. Аналогично устроены и методы обратного прохода, повторяя ту же структуру, но в обратном направлении. Благодаря такой ясной и последовательной организации, оба метода легко воспринимаются и позволяют сосредоточиться на ключевых особенностях работы нейрона с временными рядами финансовых данных.
Для более глубокого изучения предлагается самостоятельно ознакомиться с реализацией обратного прохода. Полный код класса CNeuronSpatialEmbedding и всех его методов представлен во вложении, что даёт возможность проследить работу нейрона от инициализации до формирования эмбеддингов и передачи информации в модель.
Временной эмбеддинг
С временными эмбеддингами ситуация оказывается чуть сложнее. Во-первых, их несколько, и каждый кодирует различные временные циклы. Авторы фреймворка предлагают использовать два уровня: внутридневной и внутринедельный. Задача знакомая нам по предыдущим экспериментам с темпоральным энкодером фреймворка HimNet, где мы тоже формировали эмбеддинги временных рядов. Тогда использовались рекуррентные блоки, и на каждом шаге тензор исходных данных получал лишь эмбеддинги анализируемого состояния.
Теперь задача немного сложнее. На каждом проходе нейрона анализируется целая временная последовательность, и каждый её временной шаг должен получить свои собственные эмбеддинги. Это напоминает работу трейдера, который не просто смотрит на текущую цену или индикатор, а одновременно оценивает весь ряд исторических сигналов, чтобы выявить скрытые циклы и закономерности.
Мы, конечно, будем использовать наработки из HimNet, но адаптируем их под новую архитектуру, где временные эмбеддинги формируются для всех шагов последовательности одновременно, что позволяет модели точнее улавливать динамику рынка и более корректно реагировать на её изменения.
Работу над построением алгоритма временных эмбеддингов мы начинаем на стороне OpenCL-программы, где создаём кернел ConcatByLabel. Этот кернел решает задачу конкатенации исходных данных с несколькими уровнями эмбеддингов — в нашем случае это два временных эмбеддинга, соответствующих внутридневным и внутри недельным циклам. В финансовом контексте это похоже на анализ нескольких временных горизонтов одновременно: краткосрочные колебания и более длинные циклы влияют на прогноз, и модель должна учитывать их все.
Кернел использует трёхмерную сетку глобальных идентификаторов: row_id, col_id и buffer_id. Это позволяет нам одновременно обрабатывать строки и столбцы исходного тензора, а также выбирать, с каким буфером мы работаем — исходными данными или одним из эмбеддингов.
__kernel void ConcatByLabel(__global const float* data, __global const float* label, __global const float* embedding1, __global const float* embedding2, __global float *output, const int dimension_data, const int dimension_emb1, const int dimension_emb2, const int frame1, const int frame2, const int period1, const int period2 ) { const size_t row_id = get_global_id(0); const size_t col_id = get_global_id(1); const size_t buffer_id = get_global_id(2); const size_t total_rows = get_global_size(0); const size_t total_cols = get_global_size(1); const size_t total_buffers = get_global_size(2);
Сначала каждому потоку операций присваиваются глобальные идентификаторы:
- row_id — индекс строки, соответствует временной отметке или шагу временного ряда;
- col_id — индекс столбца, соответствует конкретной переменной или признаку;
- buffer_id — выбирает, с каким буфером работает данный поток: исходные данные, первый или второй эмбеддинг.
Глобальные размеры пространства задач определяют общую сетку потоков. Здесь важно понимать, что total_buffers определяет, сколько разных наборов данных мы конкатенируем. В зависимости от этого, определяется итоговая размерность выходного вектора.
__global const float *buffer; int dimension_in, dimension_out; int shift_in, shift_out; //--- switch(total_buffers) { case 1: dimension_out = dimension_data; break; case 2: dimension_out = dimension_data + dimension_emb1; break; case 3: dimension_out = dimension_data + dimension_emb1 + dimension_emb2; break; default: return; }
Если буферов больше трёх, кернел просто завершает работу, что предотвращает некорректное использование.
Следующий шаг — выбор конкретного буфера, вычисление смещений для чтения и записи данных.
switch(buffer_id) { case 0: buffer = data; dimension_in = dimension_data; shift_in = RCtoFlat(row_id, col_id, total_rows, dimension_in, 0); shift_out = RCtoFlat(row_id, col_id, total_rows, dimension_out, 0); break; case 1: buffer = embedding1; dimension_in = dimension_emb1; shift_in = ((int)IsNaNOrInf(label[row_id] / frame1, 0)) % period1; shift_in = RCtoFlat(shift_in, col_id, period1, dimension_in, 0); shift_out = RCtoFlat(row_id, dimension_data + col_id, total_rows, dimension_out, 0); break; case 2: buffer = embedding2; dimension_in = dimension_emb2; shift_in = ((int)IsNaNOrInf(label[row_id] / frame2, 0)) % period2; shift_in = RCtoFlat(shift_in, col_id, period2, dimension_in, 0); shift_out = RCtoFlat(row_id, dimension_data + dimension_emb1 + col_id, total_rows, dimension_out, 0); break; }
Для исходных данных shift_in и shift_out вычисляются напрямую через функцию RCtoFlat, которая преобразует двумерные индексы строки и столбца в линейный индекс глобального буфера.
Для эмбеддингов shift_in зависит от значения верменной метки отдельного шага последовательности label[row_id], делённой на период (frame1 или frame2). Это позволяет циклически выбирать эмбеддинг, соответствующий конкретной фазе временного цикла, что особенно важно для финансовых данных с повторяющимися внутридневными и внутринедельными паттернами.
После выполнения подготовительной работы выполняется запись соответствующих данных в буфер результатов.
if(col_id < dimension_in) output[shift_out] = IsNaNOrInf(buffer[shift_in], 0); }
Здесь следует обратить внимание, что мы предполагаем использование различных размерностей исходных данных и эмбеддингов. При постановке кернела в очередь выполнения планируется использование максимального параметра, поэтому, перед выполнением операций обращения к буферам, осуществляем проверку индекса столбца на соответствие используемому буферу. Кроме того, данные очищаются от некорректных значений (NaN или Inf), чтобы не нарушать последующие вычисления.
В результате кернел формирует полностью конкатенированный тензор, который учитывает все заданные эмбеддинги и исходные данные. Каждый временной шаг получает собственный набор эмбеддингов, что позволяет модели видеть всю динамику рынка одновременно, включая краткосрочные флуктуации и более длинные циклы, улучшая качество прогнозов и устойчивость торговых моделей.
После построения алгоритма прямого прохода, естественным следующим шагом становится организация процесса обратного распространения ошибки. Если прямой проход формирует эмбеддинги и объединяет их с исходными данными, то обратный проход отвечает за корректировку весов и улучшение качества представления информации. В финансовом контексте это похоже на работу трейдера, который, оценивая последствия прошлых решений, корректирует стратегию для следующего шага. Ошибки прогноза на предыдущих временных шагах позволяют модели подтянуть эмбеддинги, чтобы лучше отражать динамику рынка.
Обратное распространение в данном случае осуществляется между исходными данными и соответствующими эмбеддингами. И организовано в кернеле ConcatByLabelGrad. По сути, это шаг, на котором сеть возвращает ошибки к каждому компоненту, позволяя скорректировать веса и улучшить прогноз.
__kernel void ConcatByLabelGrad(__global float* data_gr, __global const float* label, __global float* embedding1_gr, __global float* embedding2_gr, __global float *output_gr, const int dimension_data, const int dimension_emb1, const int dimension_emb2, const int frame1, const int frame2, const int period1, const int period2, const int units ) { const size_t row_id = get_global_id(0); const size_t col_id = get_global_id(1); const size_t buffer_id = get_global_id(2); const size_t total_rows = get_global_size(0); const size_t total_cols = get_global_size(1); const size_t total_buffers = get_global_size(2); //--- __global float *buffer; int dimension_in, dimension_out; int shift_in, shift_out, shift_col; int period, frame, rows;
Вначале каждый поток идентифицируется в трехмерном пространстве задач. Это позволяет отдельному потоку обрабатывать конкретное сочетание временного шага, признака и буфера.
Далее определяется итоговая размерность тензора результатов, в данном случае градиентов ошибки.
switch(total_buffers) { case 1: dimension_out = dimension_data; break; case 2: dimension_out = dimension_data + dimension_emb1; break; case 3: dimension_out = dimension_data + dimension_emb1 + dimension_emb2; break; default: return; }
Думаю вы заметили повтор операций кернела прямого прохода. Однако, далее нас ждут отличия. Если обрабатываемый буфер — исходные данные (buffer_id == 0), то градиенты просто копируются напрямую из буфера градиентов ошибки на уровне результатов. После чего завершаем работу кернела.
switch(buffer_id) { case 0: if(col_id < dimension_data && row_id<units) { shift_in = RCtoFlat(row_id, col_id, total_rows, dimension_in, 0); shift_out = RCtoFlat(row_id, col_id, total_rows, dimension_out, 0); data_gr[shift_in] = IsNaNOrInf(output_gr[shift_out], 0); } return;
А вот в случае эмбеддингов (buffer_id == 1 или 2) алгоритм немного сложнее. Здесь вначале определяем для какого периода и с каким смещением будем собирать градиенты.
case 1: rows = period1; buffer = embedding1_gr; dimension_in = dimension_emb1; shift_in = RCtoFlat(row_id, col_id, period1, dimension_in, 0); shift_col = dimension_data; period = period1; frame = frame1; break; case 2: rows = period2; buffer = embedding2_gr; dimension_in = dimension_emb2; shift_in = RCtoFlat(row_id, col_id, period2, dimension_in, 0); shift_col = dimension_data + dimension_emb1; period = period2; frame = frame2; break; }
Затем мы проверяем попадание текущего потока в размерности соответствующего эмбеддинга по размерности представления и периодичности данных. И только после этого организуем цикл, который проходит по всем временным шагам тензора градиентов ошибки на уровне результатов и аккумулирует вклад ошибки для каждого эмбеддинга.
if(row_id >= rows || col_id >= dimension_in) return; float grad = 0; for(uint r = 0; r < total_rows; r ++) { int row = ((int)IsNaNOrInf(label[r] / frame, 0)) % period; if(row != row_id) continue; shift_out = RCtoFlat(r, shift_col + col_id, total_rows, dimension_out, 0); grad += IsNaNOrInf(output_gr[shift_out], 0); } buffer[shift_in] = IsNaNOrInf(grad, 0); }
В теле цикла сначала вычисляем к какому объекту периодичности относится текущий шаг, чтобы градиенты аккумулировались по соответствующему фазовому положению временного цикла. И только при соответствии полученного значения анализируемому элементу суммируем ошибки на уровне результатов.
Накопленный градиент ошибки записывается в глобальный буфер градиентов соответствующего эмбеддинга. При этом не забываем очистить полученный результат от некорректных значений (NaN или Inf).
В результате, кернел ConcatByLabelGrad аккуратно распределяет ошибки между исходными данными и эмбеддингами, обеспечивая корректное обновление весов на всех уровнях временной последовательности. Это позволяет модели адаптироваться к сложным циклам финансовых временных рядов, улучшая точность прогнозов и устойчивость к шуму.
Мы проделали значительную работу, и статья уже выглядит весьма содержательно. Предлагаю сделать небольшой перерыв, чтобы информация устоялась, и её можно было воспринимать спокойно. Начатую реализацию мы продолжим и подробно разберём в следующей статье.
Заключение
В данной статье мы познакомились с фреймворком Extralonger, который объединяет пространственные и временные факторы в единую модель для прогнозирования временных рядов. Такой подход позволяет существенно снизить вычислительную сложность и требования к памяти по сравнению с классическими методами. Это расширяет горизонты прогнозирования до рекордных масштабов.
Особая ценность подхода заключается в передаче каждому элемент временной последовательности своего эмбеддинга, что позволяет модели одновременно учитывать краткосрочные колебания и долгосрочные закономерности. Этот принцип может быть адаптирован для решения различных задач, где важны взаимодействия пространственных и временных факторов — от финансовых рынков до планирования городской инфраструктуры или прогнозирования погодных условий.
Extralonger открывает новый путь для построения эффективных моделей прогнозирования на основе пространственно-временных данных, сочетая высокую точность, экономию ресурсов и масштабируемость на большие горизонты времени.
Ссылки
- Extralonger: Toward a Unified Perspective of Spatial-Temporal Factors for Extra-Long-Term Traffic Forecasting
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Переходим на MQL5 Algo Forge (Часть 2): Работа с несколькими репозиториями
Переходим на MQL5 Algo Forge (Часть 2): Работа с несколькими репозиториями
 От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (III) — Анализ индикаторов
От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (III) — Анализ индикаторов
 От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (IV) - Анализ рынка локально размещенными моделями с использованием ИИ
От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (IV) - Анализ рынка локально размещенными моделями с использованием ИИ
 Торговый робот на языковой GPT-модели
Торговый робот на языковой GPT-модели
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования