Neural networks made easy (Part 30): Genetic algorithms

Contents

• Introduction
• 1. Evolutionary optimization methods
• 2. Implementation using MQL5
• 3. Testing
• Conclusion
• List of references
• Programs used in the article

Introduction

We continue to study model training algorithms. All the previously considered algorithms used an analytical method for determining the direction and strength of changes in model parameters during the learning process. This sets the main requirement for all models: the model function must be differentiable over the entire range of values. This property enabled the use of the gradient descent method. It also allowed us to determine the influence of each model parameter on the overall result and to correct weight coefficients towards the error reduction.

However, there are quite a few problems when it is not possible to differentiate the original function. These may be non-differentiable functions or a model exhibiting explosive or decaying gradient problems. While the methods to solve these problems turn to be inefficient. In such cases, we resort to evolutionary optimization methods.

1. Evolutionary optimization methods

Evolutionary optimization methods are referred to as gradientless methods. They allow the optimizing of models that cannot be optimized by previously considered methods. However, there are also many other application ways. Sometimes it is interesting to observe how a model is trained using the evolutionary method and using another method which implies the application of the error gradient descent algorithms.

The main ideas of the method are borrowed from natural science. In particular, from Darwin's theory of evolution. According to this theory, any population of living organisms is fertile enough to create offspring and to grow the population. But the limited resources available for life limit the population growth. This is where natural selection plays a key role. This means the survival of the fittest. I.e., those most adapted to the environment survive. Thus, with each generation, the population develops and adapts better to the environment. The members of the population develop new properties and abilities that help them survive. Also, they forget everything that is irrelevant.

But this highly concise description of the theory does not contain any mathematics. Of course, one can calculate the maximum possible population size based on the total number of available resources and their consumption. However, this does not affect the general principles of the theory.

Exactly this theory served as the prototype for creating a whole family of evolutionary methods. In this article, I propose to get acquainted with the genetic optimization algorithm. It is one of the basic algorithms of evolutionary methods. The algorithm is based on two main postulates of Darwin's theory of evolution: heredity and natural selection.

The essence of the method is to observe each generation of the population and to select its best representatives. But first things first.

Since we are observing the population as a whole, the basic requirement is the finiteness of the life of each generation. Similar to the previously considered reinforcement learning algorithms, the process here must be finite. So, here we will use the same approaches. In particular, a session will be limited in time.

As mentioned above, we will observe the entire population. Therefore, unlike the algorithms discussed earlier, we create not one model, but an entire population. The population "lives" simultaneously in the same conditions. The population size is a hyperparameter, which determines the ability of the population to explore the environment. Each member of the population performs actions in accordance with its individual policy. Accordingly, the larger the observed population, the more different strategies we observe. Accordingly, the better the environment is studied.

This process can be compared to the repeated random selection of agent actions in the same state during reinforcement learning. But now we use several agents at the same time, each of them makes its own selection.

The use of independent population members is convenient for parallelizing the optimization process. Very often, in order to reduce the optimal model search time, the optimization process is run in parallel on several machines, using all available resources. In this case, each member of the population "lives" in its own microprocessor thread. The whole optimization process is controlled and processed by the node machine, which evaluates each agent's results and generates a new population.

Natural selection is executed after the end of the session of one generation. This process selects the best representatives from the entire population, which then produce the offspring. It means they generate a new generation of the population. The number of best representatives is a hyperparameter and is most often indicated as a share of the total population size.

The criteria for selecting the best representatives depend on the architecture of the optimization process. For example, they can use the rewards, as we did in reinforcement learning. Optionally, they can use a loss function as with supervised learning. Accordingly, we will choose agents with the maximum total reward or the minimum value of the loss function.

Note that we are not using an error gradient. Therefore, we can use a non-differentiable function for selecting the best representatives.

After selecting parents for the future offspring, we need to create a new generation of the population. To do this, we randomly select a couple of models from the selected best representatives — they will serve as the parents of the new model. Isn't it symbolic to choose a pair to create a new model?

In the process of creating a new model, all its parameters are considered as chromosome. Each separate weight is a separate gene that is inherited from one of the parents.

Inheritance algorithms may be different, but they are all based on two rules:

• Each gene does not change its place
• The parent for each gene is selected randomly

We can randomly choose parents for each member of the population of the new generation or we can create a pair of agents with mirror inheritance of genes.

The process is repeated cyclically until the new generation of the population is completely filled. Previously selected parents are not included in the new generation of the population. They are deleted after producing the offspring.

For the new generation, we start a new session and repeat the optimization process.

Pay attention that I deliberately say "optimization" instead of "learning". The process described above bears little resemblance to learning. This is pure natural selection in the process of evolution. As you know, there are various mutations in the process of evolutions, which however are not very often. But they are an integral part of the evolutionary process. Therefore, we will also add some uncertainty into our optimization process.

This may sound strange. In the optimization process, almost everything is based on random selection. First, we randomly generate the first population. Then we randomly select parents. And finally, we randomly copy model parameters. But there is no novelty behind all this randomness. So, we are adding the novelty through mutation.

Let us add another hyperparameter in the optimization process, which will be responsible for some mutation. It will indicate the probability with which we will add random genes into the new offspring, instead of copying. In other words, instead of inheriting from parents, each new member of the population receives a random gene with the probability of the Mutation parameter. Thus, in addition to inheritance from parents, something new will be introduced in each new generation. This is the maximum similarity to our development.

2. Implementation using MQL5

After considering the theoretical aspects of the algorithms, let us move on to the practical part of our article. We will implement the considered algorithm using MQL5. Of course, there is practically no mathematics in the presented algorithm. But it has something else — a clear built algorithm of actions. This is what we are going to implement.

The model that we have previously built is not suitable for solving such problems. When building our CNet class for working with neural networks, we expected the use of single only linear models. This time, we need to implement the parallel operation of several linear models. There are 2 ways to solve this problem.

The first one is less labor-intensive for the programmer but is more resource-intensive: we can simply create a dynamic array of objects in which we create several identical models. Then we will alternately extract models from the array and process them one by one. In this variant, all the work of each individual model will be implemented within the framework of the existing functionality. We will only need to implement the methods of selecting parents and generating a new generation, as well as the agent selection process.

The disadvantages of this method include high resource consumption and the necessity to create a large number of extra objects. For each agent, we need to create a separate instance of the class for working with the OpenCL context. Along with this, we create a separate context, a copy of the program and objects of all kernels. This is acceptable when using several computing devices in parallel. Otherwise, the creation of extra objects leads to an inefficient use of resources and severely limits the size of the population. This in turn has a negative impact on the results of the optimization process.

Therefore, I decided to modify our class for working with neural network models. But in order not to break the workflow, I create a new class CNetGenetic with public inheritance from the CNet class.

class CNetGenetic : public CNet
  {
protected:
   uint              i_PopulationSize;
   vector            v_Probability;
   vector            v_Rewards;
   matrixf           m_Weights;
   matrixf           m_WeightsConv;

   //---
   bool              CreatePopulation(void);
   int               GetAction(CBufferFloat * probability);
   bool              GetWeights(uint layer);
   float             NextGenerationWeight(matrixf &array, uint shift, vector &probability);
   float             GenerateWeight(uint total);

public:
                     CNetGenetic();
                    ~CNetGenetic();
   //---
   bool              Create(CArrayObj *Description, uint population_size);
   bool              SetPopulationSize(uint size);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true);
   bool              Rewards(CArrayFloat *targetVals);
   bool              NextGeneration(double quantile, double mutation, double &average, double &mamximum);
   bool              Load(string file_name, uint population_size, bool common = true);
   bool              SaveModel(string file_name, int model, bool common = true);
   //---
   bool              CopyModel(CArrayLayer *source, uint model);
   bool              Detach(void);
  };

I will provide the explanation of the method purposes along with their implementation. Now let's look at the variables:

• i_PopulationSize — population size
• v_Probability — vector of probabilities of selecting a model as a parent
• v_Rewards — vector of total rewards accumulated by each individual model
• m_Weights — matrix for recording the parameters of all models
• m_WeightsConv — a similar matrix for recording all parameters of convolutional neural layers

In the class constructor, we only initialize the above variables. Here we set the default population size and call the method for changing the corresponding variables.

CNetGenetic::CNetGenetic() :  i_PopulationSize(100)
  {
   SetPopulationSize(i_PopulationSize);
  }

This class does not use instances of other objects. Therefore, the class destructor remains empty.

We have already mentioned the method for specifying the SetPopulationSize population size. Its algorithm is very simple. In the parameters, the method receives the size of the population. In the body of the method, we save the received value in the corresponding variable and initialize the vector of probabilities and rewards with zero values.

bool CNetGenetic::SetPopulationSize(uint size)
  {
   i_PopulationSize = size;
   v_Probability = vector::Zeros(i_PopulationSize);
   v_Rewards = vector::Zeros(i_PopulationSize);
//---
   return true;
  }

Next, let us have a look at the Create class object initialization method. By analogy with a similar method of the parent class, the method receives in the parameters a pointer to the description object of one agent. We also add the population size.

bool CNetGenetic::Create(CArrayObj *Description, uint population_size)
  {
   if(CheckPointer(Description) == POINTER_INVALID)
      return false;
//---
   if(!SetPopulationSize(population_size))
      return false;
   CNet::Create(Description);
   return CreatePopulation();
  }

In the method body, we first check the validity of the received pointer to the model architecture description object. After successful validation, call the already known method for specifying the population size.

Next, call a similar method of the parent class, in which one agent will be created according to the received description and in which all additional objects will be initialized.

And finally, call the population creation method CreatePopulation, in which the population is populated by copying the previously created model. Let's take a closer look at the algorithm of this method.

At the beginning of the method, we check the number of neural layers in the created model. There must be at least two layers.

bool CNetGenetic::CreatePopulation(void)
  {
   if(!layers || layers.Total() < 2)
      return false;

Next, save the pointer to the source data neural layer into a local variable.

   CLayer *layer = layers.At(0);
   if(!layer || !layer.At(0))
      return false;
//---
   CNeuronBaseOCL *neuron_ocl = layer.At(0);
   int prev_count = neuron_ocl.Neurons();

Pay attention that the first neural layer is used only to record the source data. All agents of our population will work with the same source data. Therefore, it makes no sense to copy the layer of source data by the number of agents in the population. The duplication of neural layers starts from the next neural layer with index 1.

Let's recall the structure of the objects of our neural networks. The CNet class is responsible for organizing the work of the model at the top level. It contains an instance of the CArrayLayer object of a dynamic array of neural layers. In this dynamic array, we store pointers to objects of nested dynamic arrays directly from the CLayer neural layer. There we will write the pointers to neuron objects CNeuronBaseOCL and others.

CNet -> CArrayLayer -> CLayer -> CNeuronBaseOCL

This structure was created originally, when we implemented the calculation processes using MQL5 on the CPU. Each individual neuron was a separate object. Later, when we moved calculations to the GPU using the OpenCL technology, we were forced to use data buffers. Actually, each neural layer was expressed in one CNeuronBaseOCL neuron, which performed the functionality of the neural layer. The same applies to the use of other types of neurons.

Thus, each object of the CLayer neural layer now contains only one neuron object. Previously, we did not change the data storage architecture to maintain compatibility with previous versions. This fact has another importance now. We will simply add to the CLayer dynamic array the required number of objects to store the whole population of our agents. Thus, within one model we have parallel objects of neural layers of all agents of our population. So, we only need to implement their work according to the corresponding agent index.

Following this logic, we then create a loop to duplicate neural layers. In this loop, we will iterate through all the neural layers of our model and add the required number of neurons similar to the first neuron created earlier in each layer.

In the loop body, we first check the validity of the pointer to the previously created neural layer.

   for(int i = 1; i < layers.Total(); i++)
     {
      layer = layers.At(i);
      if(!layer || !layer.At(0))
         return false;
      //---

Then get a description of the neuron architecture.

      neuron_ocl = layer.At(0);
      CLayerDescription *desc = neuron_ocl.GetLayerInfo();
      int outputs = neuron_ocl.getConnections();

Create similar objects and fill the neural layer to the required population size. For this purpose we need to create another nested loop.

      for(uint n = layer.Total(); n < i_PopulationSize; n++)
        {
         CNeuronConvOCL *neuron_conv_ocl = NULL;
         CNeuronProofOCL *neuron_proof_ocl = NULL;
         CNeuronAttentionOCL *neuron_attention_ocl = NULL;
         CNeuronMLMHAttentionOCL *neuron_mlattention_ocl = NULL;
         CNeuronDropoutOCL *dropout = NULL;
         CNeuronBatchNormOCL *batch = NULL;
         CVAE *vae = NULL;
         CNeuronLSTMOCL *lstm = NULL;
         switch(layer.At(0).Type())
           {

            case defNeuron:
            case defNeuronBaseOCL:
               neuron_ocl = new CNeuronBaseOCL();
               if(CheckPointer(neuron_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_ocl.Init(outputs, n, opencl, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_ocl))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl = NULL;
               break;

            case defNeuronConvOCL:
               neuron_conv_ocl = new CNeuronConvOCL();
               if(CheckPointer(neuron_conv_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_conv_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.window_out,
                                                           desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_conv_ocl))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl = NULL;
               break;

            case defNeuronProofOCL:
               neuron_proof_ocl = new CNeuronProofOCL();
               if(!neuron_proof_ocl)
                  return false;
               if(!neuron_proof_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.count,
                                                                   desc.optimization, desc.batch))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_proof_ocl))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl = NULL;
               break;

            case defNeuronAttentionOCL:
               neuron_attention_ocl = new CNeuronAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMHAttentionOCL:
               neuron_attention_ocl = new CNeuronMHAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMLMHAttentionOCL:
               neuron_mlattention_ocl = new CNeuronMLMHAttentionOCL();
               if(CheckPointer(neuron_mlattention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_mlattention_ocl.Init(outputs, n, opencl, desc.window, desc.window_out,
                                               desc.step, desc.count, desc.layers, desc.optimization, desc.batch))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_mlattention_ocl))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl = NULL;
               break;

The algorithm for adding objects is similar to creating a new object in the parent class.

Once all elements of the population of one neural network have been added, align the layer size with the population size and delete the neuron description object.

        }
      if(layer.Total() > (int)i_PopulationSize)
         layer.Resize(i_PopulationSize);
      delete desc;
     }
//---
   return true;
  }

Once all iterations of the loop system have completed, we will get the full population within our single model instance and exit the method with a positive result.

The full code of this method and of the entire class is available in the attachment.

After finishing with the methods initializing the CNetGenetic class objects, mode on to describing the feed forward method. Its name and parameters repeat this used in the parent class method. It contains a pointer to the dynamic array object of the source data, as well as parameters for creating source data timestamps

In the method body, check the validity of the received pointer and of used internal objects.

bool CNetGenetic::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
  {
   if(CheckPointer(layers) == POINTER_INVALID || CheckPointer(inputVals) == POINTER_INVALID || layers.Total() <= 1)
      return false;

Prepare local variables.

   CLayer *previous = NULL;
   CLayer *current = layers.At(0);
   int total = MathMin(current.Total(), inputVals.Total());
   CNeuronBase *neuron = NULL;
   if(CheckPointer(opencl) == POINTER_INVALID)
      return false;
   CNeuronBaseOCL *neuron_ocl = current.At(0);
   CBufferFloat *inputs = neuron_ocl.getOutput();
   int total_data = inputVals.Total();
   if(!inputs.Resize(total_data))
      return false;

Move source data to the source data layer buffer and write them to the OpenCL context. If necessary, add timestamps.

   for(int d = 0; d < total_data; d++)
     {
      int pos = d;
      int dim = 0;
      if(window > 1)
        {
         dim = d % window;
         pos = (d - dim) / window;
        }
      float value = pos / pow(10000, (2 * dim + 1) / (float)(window + 1));
      value = (float)(tem ? (dim % 2 == 0 ? sin(value) : cos(value)) : 0);
      value += inputVals.At(d);
      if(!inputs.Update(d, value))
         return false;
     }
   if(!inputs.BufferWrite())
      return false;

After that, create a system of loops to implement the feed forward pass for all agents of the analyzed population. The outer loop will iterate through the neural layers in ascending order. The nested loop will iterate through the agents.

Please note that when specifying the neuron of the previous layer, we must clearly control the correspondence of agents. Each agent operates in its own vertical of neurons, which is determined by the serial number of the neuron in the layer. At the same time, we didn't duplicate the original data layer. Therefore, when specifying the index of the corresponding neuron of the previous layer, we first check the serial number of the neural layer itself. For the source data layer, the serial number of the previous layer neuron will always be 0. For all other layers, it will correspond to the agent's serial number.

Since all agents are absolutely independent, we can perform operations for all agents simultaneously.

   for(int l = 1; l < layers.Total(); l++)
     {
      previous = current;
      current = layers.At(l);
      if(CheckPointer(current) == POINTER_INVALID)
         return false;
      //---
      for(uint n = 0; n < i_PopulationSize; n++)
        {
         CNeuronBaseOCL *current_ocl = current.At(n);
         if(!current_ocl.FeedForward(previous.At(l == 1 ? 0 : n)))
            return false;
         continue;
        }
     }
//---
   return true;
  }

Of course, the use of a loop does not provide the full parallelism of calculations. But at the same time, we will sequentially implement similar iterations for all agents, one after another. This will enable the use of generated source data for all agents. This in turn will reduce costs when preparing the source data for each separate agent.

Do not forget to control the results at each step. Once all iterations of the system of nested loops are completed, exit the method.

There is no backpropagation with error gradient in the genetic algorithm. However, we need to evaluate the performance of the models. In this article, I will optimize the agent from the previous article, which we trained using the policy gradient algorithm. To optimize the performance of the models, we will maximize the total reward of the model per session. Therefore, we must return to each agent its reward after each action. As you remember, the reward depends on the chosen action. Each agent performs its own action. Previously, we received from the agent the probability distribution of performing actions, sampled one action from this distribution and returned the relevant reward to the agent. Now we have many such agents. In order not to repeat these iterations for each individual agent in the external program, let us wrap it in a separate Rewards method. The external program (environment) will pass the reward for all possible actions in its parameters. This approach allows us to evaluate each action only once, regardless of the number of agents used.

In the method body, first check the validity of pointers to the reward vector received in the parameters and the dynamic array of our neural layers.

bool CNetGenetic::Rewards(CArrayFloat *rewards)
  {
   if(!rewards || !layers || layers.Total() < 2)
      return false;

Next, extract a pointer to the agent results layer from the dynamic array and check the validity of the received pointer.

   CLayer *output = layers.At(layers.Total() - 1);
   if(!output)
      return false;

After that, create a loop iterating and interrogating all agents of our population. For each agent, we sample one action from the corresponding distribution. Depending on the selected action, the agent receives its reward, which is added to the rewards received earlier in the v_Rewards vector under the agent index.

   for(int i = 0; i < output.Total(); i++)
     {
      CNeuronBaseOCL *neuron = output.At(i);
      if(!neuron)
         return false;
      int action = GetAction(neuron.getOutput());
      if(action < 0)
         return false;
      v_Rewards[i] += rewards.At(action);
     }

Based on the agents' assessment results, we can make a probability distribution of agents getting into the number of parents of the next generation.

   v_Probability = v_Rewards - v_Rewards.Min();
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
//---
   return true;
  }

Then exit the method with a positive result. The complete code of all methods and classes is available in the attachment below.

The created functionality is enough to implement each individual session for the analyzed population and to evaluate agent actions. Once the session ends, we need to select the best representatives and generate a new generation of our population. This functionality will be implemented in the NextGeneration method. In the parameters of this method, we will pass two hyperparameters: the proportion of individuals to be removed and the mutation parameter. In addition, the method parameters contain two variables, in which we will return the average and maximum rewards of the selected agents.

In the method body, we first set to zero the probabilities of choosing agents that are not among the selected ones. And calculate the maximum rewards and the weighted average for the selected candidates.

bool CNetGenetic::NextGeneration(double quantile, double mutation, double &average, double &maximum)
  {
   maximum = v_Rewards.Max();
   v_Probability = v_Rewards - v_Rewards.Quantile(quantile);
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
   average = v_Rewards.Average(v_Probability);

Pay attention that we are using the recently added vector operations. Thanks to them, we do not have to use loops and the program code has been reduced. The vector::Max() method allows determining the maximum value of the entire vector in just one line. The vector::Quantile(...) method returns the value of the specified quantile for the vector. We use this value to remove weak agents. And after the vector subtraction operation, their probabilities will become negative.

Using the vector::Clip(0, vector::Max()) function, reset all negative values of the vector to zero.

Also, elegantly, in one line, we normalize all the vector values in the range between 0 and 1 with the total value of all elements being 1.

v_Probability = v_Probability / v_Probability.Sum();

Operation vector::Average(weights) determines the weighted average value of the vector. The weights vector contains the weights of each element of the vector. Earlier, we have set the probabilities of weak agents to zero, so their values will not be taken into account when calculating the weighted average of the vector.

Thus, the use of vector operations considerably reduces the program code and facilitates the programmer's work. Special thanks to the MetaQuotes team for these possibilities! For detailed information about vector and matrix operations please refer to the relevant section of Documentation.

But back to our method. We have determined the candidates and their probabilities. Now let us add the proportion of mutations to the distribution and recalculate the probabilities.

   if(!v_Probability.Resize(i_PopulationSize + 1))
      return false;
   v_Probability[i_PopulationSize] = mutation;
   v_Probability = (v_Probability / (1 + mutation)).CumSum();

At this stage, we have a probability distribution of the use of agents as parents of the next generation. Now we can move on directly to generating a new population. For this purpose, we implement a loop in which we will generate each neural layer of the new population. At each level of the neural layer we will generate weight matrices for all agents at once. We will do it layer by layer.

But in order not to create new objects, we will simply overwrite the weight matrices of existing agents. Therefore, before proceeding to update the weights of the next neural layer, we first call the GetWeights method, in which we copy the parameters of the current neural layer of all agents into specially created m_Weights and m_WeightsConv matrices. Here we indicate only the weight matrices of the fully connected and convolutional layers, since they are the only ones used in the architecture of the model being optimized. When using other neural layer architectures, you will need to add appropriate matrices to temporarily store parameters.

   for(int l = 1; l < layers.Total(); l++)
     {
      if(!GetWeights(l))
        {
         PrintFormat("Error of load weights from layer %d", l);
         return false;
        }

After receiving a copy of the model parameters, we can start editing the parameters in the objects. First, we get a pointer to the neural layer object. Then we implement a nested loop through all our agents. In this loop, we extract a pointer to the weight matrix of the corresponding agent.

      CLayer* layer = layers.At(l);
      for(uint i = 0; i < i_PopulationSize; i++)
        {
         CNeuronBaseOCL* neuron = layer.At(i);
         CBufferFloat* weights = neuron.getWeights();

And if the obtained pointer is valid, we implement another nested loop in which we will iterate through all the elements of the weight matrix and replace them with the corresponding parameters of the parents.

         if(!!weights)
           {
            for(int w = 0; w < weights.Total(); w++)
               if(!weights.Update(w, NextGenerationWeight(m_Weights, w, v_Probability)))
                 {
                  Print("Error of update weights");
                  return false;
                 }
            weights.BufferWrite();
           }

Please note that this slightly digresses from the basic algorithm. We didn't randomly extract a pair of parents. Instead, we will randomly take weights from all selected agents at once in accordance with their probability distribution. The weights are sampled in the NextGenerationWeight method.

After generating the values of the next data buffer, copy its values to the OpenCL context.

If necessary, repeat the operations for the matrix of the convolutional layer.

         if(neuron.Type() != defNeuronConvOCL)
            continue;
         CNeuronConvOCL* temp = neuron;
         weights = temp.GetWeightsConv();
         for(int w = 0; w < weights.Total(); w++)
            if(!weights.Update(w, NextGenerationWeight(m_WeightsConv, w, v_Probability)))
              {
               Print("Error of update weights");
               return false;
              }
         weights.BufferWrite();
        }
     }

After updating the parameters of all agents, we reset the value of the reward accumulation vector to zero in order to correctly determine the profitability of the new generation. Then exit the method with a positive result.

   v_Rewards.Fill(0);
//---
   return true;
  }

We have considered the algorithm of the main class methods, which form the basis of the genetic algorithm. However, there are also several helper methods. Their algorithm is not complicated, and you can see them in the attachment. I would like to draw your attention to the model saving method. The point is that the parent class saving method will save all agents. You can use it to continue the optimization further. But it is not applicable to save a single agent. However, the goal of the optimization is to find the optimal agent. Therefore, to save one best agent, we will create the SaveModel method. In the method parameters we will pass the name of the file to save the model to, the agent's serial number and the flag for writing to the Common directory.

In the body of the method, we first check the agent's serial number. If it does not satisfy the number of active agents, replace it with the number of the agent with the maximum probability. Which is also the agent with the highest profit.

bool CNetGenetic::SaveModel(string file_name, int model, bool common = true)
  {
   if(model < 0 || model >= (int)i_PopulationSize)
      model = (int)v_Probability.ArgMax();

Next, create an instance of a new model object and copy the parameters of the required model into it.

   CNetGenetic *new_model = new CNetGenetic();
   if(!new_model)
      return false;
   if(!new_model.CopyModel(layers, model))
     {
      new_model.Detach();
      delete new_model;
      return false;
     }

Now we can simply call the parent class saving method for the new model.

   bool result = new_model.Save(file_name, 0, 0, 0, 0, common);

After saving the model, before exiting the method, we must delete the newly created object. However, when copying the data, we did not create new neural layer objects, but simply used pointers to them. Therefore, if we delete a model object, we will also delete all the objects of the saved agent in our general model. To avoid this, we first use the method Detach, which will detach the objects of neural layers from the saved model. After that we can easily create the model object created in this method.

   new_model.Detach();
   delete new_model;
//---
   return result;
  }

The full code of all methods of this class is available in the attachment below. Now, let us move on to creating the Genetic.mq5 EA in which we will implement the model optimization process. The new EA will be created on the basis of the Actor_Critic.mq5 EA from the previous article.

Let's add hyperparameters in the EA's external parameters, to organize the new process.

input int                  PopulationSize =  50;
input int                  Generations = 1000;
input double               Quantile =  0.5;
input double               Mutation = 0.01;

Also, replace the working object if the model.

CNetGenetic          Models;

The model initialization in the EA is organized similarly to the parent model initialization in the previously considered EA.

int OnInit()
  {
//---
.............
.............
//---
   if(!Models.Load(MODEL + ".nnw", PopulationSize, false))
      return INIT_FAILED;
//---
   if(!Models.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   Models.getResults(TempData);
   if(TempData.Total() != Actions)
      return INIT_PARAMETERS_INCORRECT;
//---
   bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init");
//---
   return(INIT_SUCCEEDED);
  }

As always, the optimization process is implemented in the Train function. At the beginning of the function, similarly to the previously considered EA, we determine the optimization (training) period.

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

Load the training sample.

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

After generating the initial data, prepare the local variables. We exclude the last month from the training sample — it will be used to test the performance of the optimized model on new data.

   CBufferFloat* State = new CBufferFloat();
   float loss = 0;
   uint count = 0;
   uint total = bars - HistoryBars - 1;
   ulong ticks = GetTickCount64();
   uint test_size=22*24;

Next, create a system of nested loops to organize the optimization process. The outer loop is responsible for counting optimization generations. The nested loop will count optimization iterations. In this case, I used complete iteration of the training sample by all agents. However, to reduce the time it takes to complete one session, you can use random sampling. In this case, you should make sure the sample is sufficient for assessing the main tendencies of the training sample. Of course, in this case, the optimization accuracy may decrease. An important factor here is the balance between the accuracy of the results and model optimization costs.

   for(int gen = 0; (gen < Generations && !IsStopped()); gen ++)
     {
      for(uint i = total; i > test_size; i--)
        {
         uint r = i + HistoryBars;
         if(r > (uint)bars)
            continue;

In the body of the nested loop, we define the boundaries of the current pattern and create a source data buffer.

         State.Clear();
         for(uint b = 0; b < HistoryBars; b++)
           {
            uint bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) ||
               !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) ||
               !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign))
               break;
           }
         if(IsStopped())
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(State.Total() < (int)HistoryBars * 12)
            continue;

Now, call the feed forward method for our optimized population.

         if(!Models.feedForward(State, 12, true))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

As you can see, this process is similar to the operations performed earlier when training models. Because all the differences in the processes are implemented in the libraries. The interface of the methods has not changed. Now we will call forward pass for one model. In the body of the CNetGenetic class, we have feed forward implemented for all active agents of the population.

Next, we need to transfer the current reward to agents. As mentioned above, here we will not poll all agents. Instead, we will create a buffer in which we specify a reward for each action in the given state. The buffer is passed in the parameters of the following method. 

         double reward = Rates[i - 1].close - Rates[i - 1].open;
         TempData.Clear();
         if(!TempData.Add((float)(reward < 0 ? 20 * reward : reward)) ||
            !TempData.Add((float)(reward > 0 ? -reward * 20 : -reward)) ||
            !TempData.Add((float) - fabs(reward)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(!Models.Rewards(TempData))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

We use the original reward policy without any change. This will allow us to evaluate the impact of the optimization process on the overall result.

Once iterations of the loop processing one system state complete, we will plot the relevant information for visual control of the process and move on to the next iteration of the loop.

         if(GetTickCount64() - ticks > 250)
           {
            uint x = total - i;
            double perc = x * 100.0 / (total - test_size);
            Comment(StringFormat("%d from %d -> %.2f%% from %.2f%%", x, total - test_size, perc, 100));
            ticks = GetTickCount64();
           }
        }

After the end of a session, save the parameters of the best agent.

      Models.SaveModel(MODEL+".nnw", -1, false);

Next, move on to creating a new generation. This is done by calling one method — CNetGenetic::NextGeneration. Remember to control the execution of operations.

      double average, maximum;
      if(!Models.NextGeneration(Quantile, Mutation, average, maximum))
        {
         PrintFormat("Error of create next generation: %d", GetLastError());
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      //---
      PrintFormat("Genegation %d, Average Cumulative reward %.5f, Max Reward %.5f", gen, average, maximum);
     }

In conclusion, print information about the achieved results in the journal and proceed to the assessment of the new generation of the analyzed population in a new iteration of the loop.

After the completion of the optimization process, clear the data and complete the EA operation.

   delete State;
   Comment("");
//---
   ExpertRemove();
  }

As you can see, this arrangement of the class has greatly simplified the work on the side of the main program. In practice, the optimization process consists in the sequential call of 3 methods of the class. This is comparable to training models using gradient descent methods. This also significantly reduces the total number of transactions within a single agent.

3. Testing

The optimization process was tested with all previously used parameters. The training sample is the EURUSD H1 historical data. For the optimization process, I used the history for the last 2 years. The EA was used with default parameters. As a model for testing, I used architectures from the previous article with the search for the optimal probability distribution of decision making. This approach enables the substitution of the optimized model into the "REINFORCE-test.mq5" Expert Advisor used earlier. As you can see, this is the third approach in the process of training a model of the same architecture. Previously, we have already trained a similar model using the Policy Gradient and Actor-Critic algorithms. So, it is even more interesting to observe the optimization results.

When optimizing the model, we did not use the last-month data. Thus, we left some data for testing the optimized model. The optimized model was run in the Strategy Tester. It generated the following result.

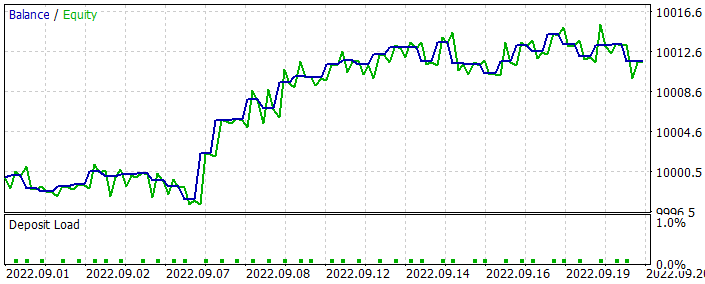
As you can see from the presented graph, we got a growing balance graph. But its profitability is a bit lower than that obtained when training a similar model using the Actor-Critic method. It also executed less trading operations. Actually, the number of trades decreased by two times.

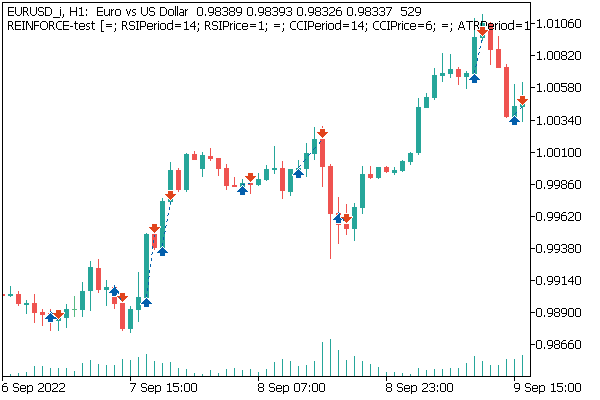
If you look at the symbol chart with executed trades, you can clearly see that the model tried to trade with the trend. I think this is an interesting result. When training a similar model using gradient methods, the model tried to execute a trade on most movements. Quite often, this was rather chaotic. This time we see a certain logic which is consonant with the well-known postulates in trading.

Or does it only seem to me? Are all my conclusions "far-fetched"? Perform your experiments — it will be interesting to observe the results.

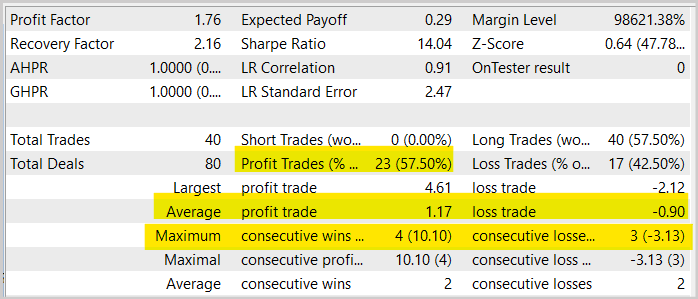
In general, we see an increase in the share of profitable trades by almost 1.5% compared to a similar test of the model trained by the Actor-Critic method. But the number of trades us reduced by 2 times. At the same time, we also see a decrease in the average profit and loss per operation. All this leads to a general decrease in the trading turnover, as well as in the total profitability for the period. However, please note that testing during the 1st month cannot be assessed as presentable for the EA operation over a long time period. Therefore, once again recommend performing thorough and comprehensive testing of your models before using them for real trading.

Conclusion

In this article, we got acquainted with the genetic method for optimizing models. It can be used to optimize any parametric models. One of the main advantages of this method is the possibility of using it to optimize non-differentiable models. This is impossible when training models with gradient methods, including different variations of the gradient descent method.

The article also contains the algorithm implementation in MQL5. We even optimized the tested model and observed its results in the Strategy Tester.

Based on the testing results, we can say that the model showed quite good results. So, the method can be used to optimize trading models. But before you decide to use the model on a real account, you must test it thoroughly and comprehensively.

List of references

1. Neural networks made easy (Part 26): Reinforcement learning
2. Neural networks made easy (Part 27): Deep Q-Learning (DQN)
3. Neural networks made easy (Part 28): Policy gradient algorithm
4. Neural networks made easy (Part 29): Advantage actor-critic algorithm

Programs used in the article

#	Name	Type	Description
1	Genetic.mq5	EA	EA for optimizing the model
2	NetGenetic.mqh	Class library	Library for implementing a genetic algorithm
3	REINFORCE-test.mq5	EA	An Expert Advisor to test the model in the Strategy Tester
4	NeuroNet.mqh	Class library	Library for creating neural network models
5	NeuroNet.cl	Code Base	OpenCL program code library to create neural network models