ニューラルネットワークが簡単に（第30部）：遺伝的アルゴリズム

MetaTrader 5 — トレーディングシステム | 10 1月 2023, 14:57

265

Dmitriy Gizlyk

内容

はじめに

モデル訓練アルゴリズムの研究も続けます。これまでに検討されたすべてのアルゴリズムでは、学習過程におけるモデルパラメータの変化の方向と強さを決定するために解析的な手法が用いられていました。これにより、モデル関数が値の全範囲にわたって微分可能でなければならないという、すべてのモデルの主要な要件が設定されます。この特性により、勾配降下法の利用が可能になりました。また、各モデルパラメータが全体の結果に与える影響を判断し、誤差低減に向けた重み係数の補正をおこなうことができました。

しかし、元の関数を微分できない問題が結構あります。これらは、微分不可能な関数や、爆発的または減衰的な勾配問題を示すモデルかもしれません。しかし、これらの問題を解決する方法は、非効率的であることが判明しました。そのような場合、進化的最適化手法に頼ることになります。

1.進化的最適化手法

進化的最適化手法は勾配なし手法と呼ばれ、これまで考えられてきた手法では最適化できないようなモデルの最適化を可能にします。しかし、それ以外にもさまざまな応用方法があります。進化的手法と、誤差勾配降下アルゴリズムの適用を意味する別の手法で、モデルの学習方法を観察することは、時に興味深いものです。

この手法の主要な考え方は、自然科学から借用したものです。特に、ダーウィンの進化論からです。この理論によれば、生物の集団は、どんなものでも子孫を残し、集団を大きくするために十分な繁殖力をもっていることになります。ただし、生命に利用できる資源は限られているため、人口増加には限界があります。そこで重要な役割を果たすのが、自然選択です。これは適者生存を意味します。つまり、環境に最も適応したものが生き残るのです。こうして、世代を重ねるごとに、集団は発展し、環境に適応していきます。集団のメンバーは、生き残るために新しい特性や能力を身につけます。また、関係ないことはすべて忘れてしまいます。

しかし、この極めて簡潔な理論の記述には、数学は一切含まれていません。もちろん、利用可能な資源の総数とその消費量から、可能な人口の最大サイズを算出することもできます。しかし、これは理論の一般的な原理には影響しません。

まさにこの理論が、進化論の一群を生み出す原型となったのです。今回は、遺伝的最適化アルゴリズムについて学ぶことを提案します。これは、進化法の基本的なアルゴリズムの1つです。このアルゴリズムは、ダーウィンの進化論の2つの主要な仮定、すなわち遺伝と自然選択に基づいています。

この方法の本質は、母集団の各世代を観察し、その最適な代表者を選択することです。まず必要なことから始めていきます。

集団全体を観察するわけですから、各世代の生命の有限性が基本的な条件となります。先に検討した強化学習アルゴリズムと同様に、ここでの処理も有限であることが求められます。そこで、ここでも同じような方法をとります。特に、セッションは時間的に制限されます。

前述したように、母集団全体を観察することになります。そのため、先に述べたアルゴリズムとは異なり、1つのモデルではなく、母集団全体を作成することになります。母集団は同じ条件の中で同時に「生きて」います。母集団の大きさはハイパーパラメータであり、母集団が環境を探索する能力を決定します。母集団の各メンバーは、それぞれのポリシーに従って行動をとります。したがって、観測される母集団が大きければ大きいほど、さまざまな戦略が観測されることになります。従って、環境が研究されればより良くなります。

この過程は、強化学習において同じ状態のエージェント行動をランダムに繰り返し選択することに例えることができますが、今は複数のエージェントを同時に使い、それぞれが独自の選択をしています。

独立した母集団を使用することで、最適化処理の並列化に便利です。最適なモデルの探索時間を短縮するために、利用可能なすべてのリソースを使用して、複数のマシンで最適化処理を並行して実行することが非常によくあります。この場合、母集団の各メンバーは、それぞれのマイクロプロセッサのスレッドに「住んで」いることになります。最適化の過程全体はノードマシンが制御処理し、各エージェントの結果を評価して新しい母集団を生成します。

自然選択は、1世代のセッションが終了した後に実行されます。この過程により、母集団全体から最適な代表が選ばれ、その代表が子孫を残すのです。これは、新しい世代の母集団を生み出すということです。最良の代表の数はハイパーパラメータであり、ほとんどの場合、全母集団のサイズに対する割合で示されます。

最適な代表を選ぶ基準は、最適化過程のアーキテクチャに依存します。例えば、強化学習でおこなったように、報酬を使うことができます。オプションとして、教師あり学習と同様に損失関数を使用することも可能です。したがって、総報酬が最大になるエージェント、あるいは損失関数の値が最小になるエージェントを選択することになります。

なお、誤差勾配は使っていません。したがって、最適な代表を選択するために、非微分化関数を用いることができます。

将来の子孫のために親を選択した後、新しい世代の集団を作る必要があります。そのために、選択された最良の代表からランダムに2、3のモデルを選択します。これが新しいモデルの親となります。新しいモデルを作るためにペアを選ぶというのは、象徴的なことではないでしょうか。

新しいモデルを作る過程では、そのすべてのパラメータを染色体として考えます。それぞれの別々の重さは、両親のどちらかから受け継いだ別々の遺伝子です。

継承のアルゴリズムは様々だが、いずれも2つのルールに基づいています。

各遺伝子はその場所を変えません。
各遺伝子の親はランダムに選択されます。

新世代の母集団の各メンバーの親をランダムに選ぶか、遺伝子を鏡面継承させたエージェントのペアを作ることができます。

この過程は、新しい世代の母集団が完全に埋まるまで周期的に繰り返されます。以前に選ばれた親は、新しい世代の母集団には含まれません。子孫を残した後、削除されます。

新しい世代では、新しいセッションを開始し、最適化の過程を繰り返します。

私が「学習」ではなく、あえて「最適化」と言っていることに注意してください。上記のような過程は、学習とは似ても似つきません。これは、進化の過程における純粋な自然選択です。ご存知のように、進化の過程ではさまざまな突然変異が起こります。その頻度は高くはありませんが、それらは進化の過程で不可欠なものです。したがって、最適化の過程にも不確実性を加えることになります。

不思議に思うかもしれません。最適化の過程では、ほとんどすべてがランダムな選択に基づいています。まず、最初の母集団をランダムに生成してから、ランダムに親を選びます。そして最後に、モデルのパラメータをランダムにコピーしますが、このランダム性の裏には、何の目新しさもないのです。つまり、突然変異で新しさを加えているわけです。

最適化の過程で、もう1つのハイパーパラメータを追加して、何らかの突然変異を起こすようにしましょう。これは、コピーではなく、ランダムな遺伝子を新しい子孫に加える確率を示します。つまり、親から遺伝するのではなく、母集団の各新メンバーがMutationパラメータに応じた確率でランダムに遺伝子を受け取るのです。このように、親からの継承に加えて、新しい世代ごとに新しいものが導入されます。これが、私たちの開発との最大の類似点です。

2.MQL5を使用した実装

アルゴリズムの理論的な側面を考慮した上で、実用的な部分に話を移しましょう。検討したアルゴリズムをMQL5を用いて実装します。もちろん、このアルゴリズムに数学は一切含まれていませんが、それ以外のものがあります。それは、明確に構築されている行動のアルゴリズムです。これがここで実装するものです。

このような問題を解決するには、これまで構築してきたモデルは適していません。ニューラルネットワークを扱うクラスを作る際にCNetを構築する際、単一の線形モデルのみを使用することを想定していました。今回は、複数の線形モデルの並列演算を実装する必要があります。解決策は2種類あります。

1つ目は、プログラマーの労力は少ないが、リソースを多く消費します。単純にオブジェクトの動的配列を作成し、その中に同一のモデルを複数作成すれば良いのです。そして、配列から交互にモデルを取り出して、1つずつ処理していきます。このバリエーションでは、個々のモデルのすべての作業は、既存の機能の枠組みの中で実施されます。親を選んで新世代を生成する手法と、エージェントの選択処理だけを実装すればよいことになります。

この手法の欠点は、リソースを多く消費することと、余分なオブジェクトを大量に作成する必要があることです。各エージェントに対して、OpenCLコンテキストで動作するためのクラスのインスタンスを個別に作成する必要があります。これに伴い、別コンテキスト、プログラムのコピー、全カーネルのオブジェクトを作成します。複数のコンピューティングデバイスを並行して使用する場合は許容範囲内です。そうでなければ、余分なオブジェクトの作成は資源の非効率的な使用につながり、母集団の大きさを著しく制限することになります。これは、ひいては最適化過程の結果に悪影響を及ぼします。

そこで、ニューラルネットワークモデルを扱うために、クラスを修正することにしました。ただし、ワークフローを壊さないために、新しいクラスを作成します。CNetGeneticをpublicに継承したCNetクラスです。

class CNetGenetic : public CNet
  {
protected:
   uint              i_PopulationSize;
   vector            v_Probability;
   vector            v_Rewards;
   matrixf           m_Weights;
   matrixf           m_WeightsConv;

   //---
   bool              CreatePopulation(void);
   int               GetAction(CBufferFloat * probability);
   bool              GetWeights(uint layer);
   float             NextGenerationWeight(matrixf &array, uint shift, vector &probability);
   float             GenerateWeight(uint total);

public:
                     CNetGenetic();
                    ~CNetGenetic();
   //---
   bool              Create(CArrayObj *Description, uint population_size);
   bool              SetPopulationSize(uint size);
   bool              feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true);
   bool              Rewards(CArrayFloat *targetVals);
   bool              NextGeneration(double quantile, double mutation, double &average, double &mamximum);
   bool              Load(string file_name, uint population_size, bool common = true);
   bool              SaveModel(string file_name, int model, bool common = true);
   //---
   bool              CopyModel(CArrayLayer *source, uint model);
   bool              Detach(void);
  };

メソッドの目的とその使用法について説明します。では、変数を見てみましょう。

i_PopulationSize-母集団の大きさ
v_Probability - あるモデルを親として選択する確率のベクトル
v_Rewards - 各モデルが蓄積した総報酬のベクトル
m_Weights - 全モデルのパラメータを記録するための行列
m_WeightsConv -畳み込みニューラルネットワーク層の全パラメータを記録するための類似の行列

クラスのコンストラクタでは、上記の変数を初期化するだけです。ここでは、デフォルトの母集団サイズを設定し、対応する変数を変更するためのメソッドを呼び出します。

CNetGenetic::CNetGenetic() :  i_PopulationSize(100)
  {
   SetPopulationSize(i_PopulationSize);
  }

このクラスは、他のオブジェクトのインスタンスを使用しません。そのため、クラスのデストラクタは空のままです。

母集団の大きさを指定するメソッドについては、すでに述べたとおりです。母集団の大きさの設定を指定するメソッドについて説明しました。そのアルゴリズムは非常にシンプルです。パラメータで、このメソッドは母集団の大きさを受け取ります。メソッド本体では、受け取った値を対応する変数に保存し、確率と報酬のベクトルをゼロ値で初期化します。

bool CNetGenetic::SetPopulationSize(uint size)
  {
   i_PopulationSize = size;
   v_Probability = vector::Zeros(i_PopulationSize);
   v_Rewards = vector::Zeros(i_PopulationSize);
//---
   return true;
  }

次にCreateクラスオブジェクトの初期化メソッドを見てみましょう。親クラスの同様のメソッドと同様に、このメソッドはパラメータとして1つのエージェントの記述オブジェクトへのポインタを受け取ります。また、母集団の大きさも加えています。

bool CNetGenetic::Create(CArrayObj *Description, uint population_size)
  {
   if(CheckPointer(Description) == POINTER_INVALID)
      return false;
//---
   if(!SetPopulationSize(population_size))
      return false;
   CNet::Create(Description);
   return CreatePopulation();
  }

メソッド本体では、まず、受け取ったモデルアーキテクチャ記述オブジェクトへのポインタの有効性を確認します。検証に成功したら、すでに知られている母集団の大きさを指定するメソッドを呼び出します。

次に、親クラスの同様のメソッドを呼び出します。このメソッドでは、受け取った説明に従って1つのエージェントが作成され、すべての追加オブジェクトが初期化されます。

そして最後に、母集団作成メソッドであるCreatePopulationを呼び出します。このメソッドでは、以前に作成されたモデルをコピーすることによって母集団を生成します。このメソッドのアルゴリズムをもう少し詳しく見てみましょう。

メソッドの冒頭で、作成したモデルのニューラル層の数を確認します。最低でも2層は必要です。

bool CNetGenetic::CreatePopulation(void)
  {
   if(!layers || layers.Total() < 2)
      return false;

次に、ソースデータのニューラル層へのポインタをローカル変数に保存します。

   CLayer *layer = layers.At(0);
   if(!layer || !layer.At(0))
      return false;
//---
   CNeuronBaseOCL *neuron_ocl = layer.At(0);
   int prev_count = neuron_ocl.Neurons();

最初のニューラル層は、ソースデータの記録のみに使用されることに注意してください。私たちの母集団のすべてのエージェントは、同じソースデータで作業します。したがって、母集団のエージェント数でソースデータの層をコピーするのは意味がありません。ニューラル層の複製は、インデックス1の次のニューラル層から開始されます。

ニューラルネットワークのオブジェクトの構造を思い出してみましょう。CNetクラスは、トップレベルでモデルの作業を整理する役割を担っています。ニューラル層の動的配列であるCArrayLayerオブジェクトのインスタンスが含まれます。この動的配列に、CLayerニューラル層から直接、ネストした動的配列のオブジェクトへのポインタを格納します。そこにニューロンオブジェクトへのポインタCNeuronBaseOCLなどへのポインタを記述します。

CNet -> CArrayLayer -> CLayer -> CNeuronBaseOCL

この構造体は、CPUでMQL5を使った計算処理を実装した際に、独自に作成したものです。.個々のニューラル細胞は、それぞれ別のオブジェクトでした。その後、OpenCL技術を使ってGPUに計算を移すと、データバッファを使うことを余儀なくされました。実際には、各ニューラル層は1つのCNeuronBaseOCLニューロンで表現され、そのニューロンはニューラル層の機能を実行します。また、他の種類のニューロンを使用する場合も同様です。

よって、CLayerニューラル層の各オブジェクトにはニューロンオブジェクトが1つだけ含まれるようになりました。従来は、旧バージョンとの互換性を保つために、データストレージのアーキテクチャを変更しませんでした。この事実にはもう1つの重要性があります。CLayerの動的配列に必要な数のオブジェクトを追加するだけで、エージェントの全個数を格納することができます。このように、1つのモデルの中に、母集団のすべてのエージェントのニューラル層を並列に持つことができるため、対応するエージェントインデックスに従って、その作業を実施すればよいのです。

このロジックに従って、ニューラル層を複製するループを作成します。このループでは、モデルのすべてのニューラル層を繰り返し、各層に先に作成した最初のニューロンと同様のニューロンを必要数追加していきます。

ループ本体では、まず、先に作成したニューラル層へのポインタの有効性を確認します。

   for(int i = 1; i < layers.Total(); i++)
     {
      layer = layers.At(i);
      if(!layer || !layer.At(0))
         return false;
      //---

そして、ニューロンアーキテクチャの説明を受けます。

      neuron_ocl = layer.At(0);
      CLayerDescription *desc = neuron_ocl.GetLayerInfo();
      int outputs = neuron_ocl.getConnections();

同様のオブジェクトを作成し、必要な母集団の大きさまでニューラル層を埋めます。この目的のために、もう1つ入れ子のループを作る必要があります。

      for(uint n = layer.Total(); n < i_PopulationSize; n++)
        {
         CNeuronConvOCL *neuron_conv_ocl = NULL;
         CNeuronProofOCL *neuron_proof_ocl = NULL;
         CNeuronAttentionOCL *neuron_attention_ocl = NULL;
         CNeuronMLMHAttentionOCL *neuron_mlattention_ocl = NULL;
         CNeuronDropoutOCL *dropout = NULL;
         CNeuronBatchNormOCL *batch = NULL;
         CVAE *vae = NULL;
         CNeuronLSTMOCL *lstm = NULL;
         switch(layer.At(0).Type())
           {

            case defNeuron:
            case defNeuronBaseOCL:
               neuron_ocl = new CNeuronBaseOCL();
               if(CheckPointer(neuron_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_ocl.Init(outputs, n, opencl, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_ocl))
                 {
                  delete neuron_ocl;
                  return false;
                 }
               neuron_ocl = NULL;
               break;

            case defNeuronConvOCL:
               neuron_conv_ocl = new CNeuronConvOCL();
               if(CheckPointer(neuron_conv_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_conv_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.window_out,
                                                           desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_conv_ocl))
                 {
                  delete neuron_conv_ocl;
                  return false;
                 }
               neuron_conv_ocl = NULL;
               break;

            case defNeuronProofOCL:
               neuron_proof_ocl = new CNeuronProofOCL();
               if(!neuron_proof_ocl)
                  return false;
               if(!neuron_proof_ocl.Init(outputs, n, opencl, desc.window, desc.step, desc.count,
                                                                   desc.optimization, desc.batch))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_proof_ocl))
                 {
                  delete neuron_proof_ocl;
                  return false;
                 }
               neuron_proof_ocl = NULL;
               break;

            case defNeuronAttentionOCL:
               neuron_attention_ocl = new CNeuronAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMHAttentionOCL:
               neuron_attention_ocl = new CNeuronMHAttentionOCL();
               if(CheckPointer(neuron_attention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_attention_ocl.Init(outputs, n, opencl, desc.window, desc.count, desc.optimization, desc.batch))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_attention_ocl))
                 {
                  delete neuron_attention_ocl;
                  return false;
                 }
               neuron_attention_ocl = NULL;
               break;

            case defNeuronMLMHAttentionOCL:
               neuron_mlattention_ocl = new CNeuronMLMHAttentionOCL();
               if(CheckPointer(neuron_mlattention_ocl) == POINTER_INVALID)
                  return false;
               if(!neuron_mlattention_ocl.Init(outputs, n, opencl, desc.window, desc.window_out,
                                               desc.step, desc.count, desc.layers, desc.optimization, desc.batch))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl.SetActivationFunction(desc.activation);
               if(!layer.Add(neuron_mlattention_ocl))
                 {
                  delete neuron_mlattention_ocl;
                  return false;
                 }
               neuron_mlattention_ocl = NULL;
               break;

オブジェクトを追加するアルゴリズムは、親クラスで新しいオブジェクトを作成するのと似ています。

1つのニューラルネットワークの母集団の全要素を追加したら、層サイズを母集団サイズに合わせ、ニューロン記述オブジェクトを削除します。

        }
      if(layer.Total() > (int)i_PopulationSize)
         layer.Resize(i_PopulationSize);
      delete desc;
     }
//---
   return true;
  }

ループシステムのすべての反復が完了したら、1つのモデルインスタンス内の全母集団を取得し、肯定的な結果でこのメソッドを終了します。

このメソッドとクラス全体の完全なコードは、添付ファイルにあります。

クラスオブジェクトを初期化するメソッドを終了した後CNetGeneticクラスオブジェクトを初期化するメソッドを終えたら、フィードフォワードメソッドを説明するモードに進みます。このメソッドの名前とパラメータは、親クラスのメソッドで使用されているものと同じです。ソースデータの動的配列オブジェクトへのポインタと、ソースデータのタイムスタンプを作成するためのパラメータが含まれます。

メソッド本体で、受け取ったポインタと使用した内部オブジェクトの有効性を確認します。

bool CNetGenetic::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true)
  {
   if(CheckPointer(layers) == POINTER_INVALID || CheckPointer(inputVals) == POINTER_INVALID || layers.Total() <= 1)
      return false;

ローカル変数を用意します。

   CLayer *previous = NULL;
   CLayer *current = layers.At(0);
   int total = MathMin(current.Total(), inputVals.Total());
   CNeuronBase *neuron = NULL;
   if(CheckPointer(opencl) == POINTER_INVALID)
      return false;
   CNeuronBaseOCL *neuron_ocl = current.At(0);
   CBufferFloat *inputs = neuron_ocl.getOutput();
   int total_data = inputVals.Total();
   if(!inputs.Resize(total_data))
      return false;

ソースデータをソースデータ層バッファに移動し、書き込む。OpenCLのコンテキストに書き込みます。必要であれば、タイムスタンプを追加します。

   for(int d = 0; d < total_data; d++)
     {
      int pos = d;
      int dim = 0;
      if(window > 1)
        {
         dim = d % window;
         pos = (d - dim) / window;
        }
      float value = pos / pow(10000, (2 * dim + 1) / (float)(window + 1));
      value = (float)(tem ? (dim % 2 == 0 ? sin(value) : cos(value)) : 0);
      value += inputVals.At(d);
      if(!inputs.Update(d, value))
         return false;
     }
   if(!inputs.BufferWrite())
      return false;

その後、分析母集団のすべてのエージェントに対してフィードフォワードパスを実行するループのシステムを作成します。外側のループでは、ニューラル層を昇順に繰り返し処理します。ネストされたループは、エージェントを繰り返し処理します。

なお、前の層のニューロンを指定する際には、エージェントの対応を明確に制御する必要があります。各エージェントは、ニューロンの垂直方向で動作し、その垂直方向は層内のニューロンの通し番号で決定されます。同時に、元のデータ層を重複させないようにしました。そのため、前の層の対応するニューロンのインデックスを指定する際には、まずニューラル層自体の通し番号を確認します。ソースデータ層では、前の層のニューロンの通し番号は常に0になります。それ以外の層の場合は、エージェントのシリアル番号に対応します。

すべてのエージェントは絶対的に独立しているので、すべてのエージェントに対して同時に操作を実行することができます。

   for(int l = 1; l < layers.Total(); l++)
     {
      previous = current;
      current = layers.At(l);
      if(CheckPointer(current) == POINTER_INVALID)
         return false;
      //---
      for(uint n = 0; n < i_PopulationSize; n++)
        {
         CNeuronBaseOCL *current_ocl = current.At(n);
         if(!current_ocl.FeedForward(previous.At(l == 1 ? 0 : n)))
            return false;
         continue;
        }
     }
//---
   return true;
  }

もちろん、ループを使っても完全な並列計算ができるわけではありません。しかし同時に、すべてのエージェントに対して、同様の繰り返しを順次、実施していくことになります。これにより、すべてのエージェントで生成されたソースデータを使用することが可能になります。これにより、各エージェントのソースデータを準備する際のコストを削減することができます。

各ステップで結果を制御することを忘れないでください。ネストされたループのシステムのすべての反復が完了したら、メソッドを終了します。

遺伝的アルゴリズムには誤差勾配を伴うバックプロパゲーションは存在しません。ただし、モデルの性能を評価する必要があります。今回は、前回、政策勾配アルゴリズムを用いて学習させたエージェントを最適化することにします。モデルの性能を最適化するために、1セッションあたりのモデルの総報酬を最大化します。したがって、各エージェントが行動するたびにその報酬を返さなければなりません。覚えているように、報酬は選んだ行動によって異なります。各エージェントはそれぞれ自分の行動を実行します。これまでは、エージェントから行動を起こす確率分布を受け取り、その分布から1つの行動をサンプリングして、該当する報酬をエージェントに返していました。今ではそのようなエージェントは多数あります。外部プログラムの個々のエージェントに対して，このような繰り返しをしないようにするために，別の報酬メソッドにまとめましょう。外部プログラム（環境）は、そのパラメータに、すべての可能な行動に対する報酬を渡します。この手法により、使用するエージェントの数に関わらず、各行動の評価を1回で済ませることができます。

メソッド本体では、まず、パラメータで受け取った報酬ベクトルへのポインタと、ニューラル層の動的配列の妥当性を確認します。

bool CNetGenetic::Rewards(CArrayFloat *rewards)
  {
   if(!rewards || !layers || layers.Total() < 2)
      return false;

次に、動的配列からエージェント結果層へのポインタを取り出し、受け取ったポインタの有効性を確認します。

   CLayer *output = layers.At(layers.Total() - 1);
   if(!output)
      return false;

その後、母集団のすべてのエージェントを反復して尋問するループを作成します。各エージェントに対して、対応する分布から1つの行動をサンプリングします。選択された行動に応じて、エージェントはその報酬を受け取り、それはエージェントインデックスの下のv_Rewardsベクトルで先に受け取った報酬に追加されます。

   for(int i = 0; i < output.Total(); i++)
     {
      CNeuronBaseOCL *neuron = output.At(i);
      if(!neuron)
         return false;
      int action = GetAction(neuron.getOutput());
      if(action < 0)
         return false;
      v_Rewards[i] += rewards.At(action);
     }

エージェントの評価結果に基づいて、エージェントが次世代の親の数に入る確率分布を作ることができます。

   v_Probability = v_Rewards - v_Rewards.Min();
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
//---
   return true;
  }

次に、メソッドをtrueで終了します。すべてのメソッドとクラスの完全なコードは、以下の添付ファイルにあります。

作成された機能は、分析された母集団の個々のセッションを実装し、エージェントの行動を評価するのに十分なものです。セッションが終了したら、最も優れた代表者を選び、新しい世代の母集団を生成する必要があります。この機能は、NextGenerationメソッドに実装される予定です。このメソッドのパラメータには、除去する個体の割合と突然変異のパラメータの2つのハイパーパラメータを渡すことにします。さらに、メソッドのパラメータには2つの変数があり、選択されたエージェントの平均報酬と最大報酬を返すことになります。

メソッド本体では、まず、選択されたエージェントの中に入っていないエージェントを選択する確率をゼロに設定します。そして、選ばれた候補者の最大報酬と加重平均を計算します。

bool CNetGenetic::NextGeneration(double quantile, double mutation, double &average, double &maximum)
  {
   maximum = v_Rewards.Max();
   v_Probability = v_Rewards - v_Rewards.Quantile(quantile);
   if(!v_Probability.Clip(0, v_Probability.Max()))
      return false;
   v_Probability = v_Probability / v_Probability.Sum();
   average = v_Rewards.Average(v_Probability);

最近追加されたベクトル演算を使用していることに注意してください。そのおかげで、ループを使う必要がなくなり、プログラムコードも削減されました。vector::Max()メソッドを使えば、たった1行でベクトル全体の最大値を決定することができます。このvector::Quantile(...)メソッドは、ベクトルの指定された分位数の値を返します。この値を使って、弱いエージェントを排除しています。そして、ベクトルの引き算の操作の後、それらの確率は負になります。

vector::Clip(0,vector::Max())関数を使用して、ベクトルのすべての負の値をゼロにリセットします。

また、エレガントなことに、1行で、0から1の間の範囲にすべてのベクトル値を正規化して、すべての要素の合計値が1になります。

v_Probability = v_Probability / v_Probability.Sum();

操作vector::Average(weights)でベクトルの加重平均値を求めます。重みベクトルには、ベクトルの各要素の重みが含まれています。先に、弱いエージェントの確率を0にしたので、ベクトルの加重平均を計算するときに、その値は考慮されません。

このように、ベクトル演算を利用することで、プログラムコードを大幅に削減し、プログラマーの作業を容易にすることができます。このような可能性を与えてくれたMetaQuotesチームに感謝します。ベクトルや行列の操作の詳細については、ドキュメントの該当箇所を参照してください。

さて、私たちの手法に話を戻します。候補とその確率を決定しました。ここで、突然変異の割合を分布に加え、確率を再計算してみましょう。

   if(!v_Probability.Resize(i_PopulationSize + 1))
      return false;
   v_Probability[i_PopulationSize] = mutation;
   v_Probability = (v_Probability / (1 + mutation)).CumSum();

この段階で、次世代の親としてエージェントを使用する確率分布が得られています。これで、新しい母集団を生成することに直接的に移行できます。そのために、新しい母集団の各ニューラル層を生成するループを実装します。ニューラル層の各レベルで、すべてのエージェントの重み行列を一度に生成します。1層ずつやっていきます。

しかし、新しいオブジェクトを作らないために、既存のエージェントの重み行列を単純に上書きします。したがって、次のニューラル層の重みの更新に進む前に、最初にGetWeightsメソッドを呼び出します。このメソッドでは、すべてのエージェントの現在のニューラルレイヤのパラメータを、特別に作成されたm_Weightsとm_WeightsConv行列にコピーします。ここでは、最適化されるモデルのアーキテクチャで使用されるのは完全接続層と畳み込み層の重み行列のみであるため、完全接続層と畳み込み層の重み行列を示します。他のニューラル層アーキテクチャを使用する場合は、パラメータを一時的に格納するために適切なマトリクスを追加する必要があります。

   for(int l = 1; l < layers.Total(); l++)
     {
      if(!GetWeights(l))
        {
         PrintFormat("Error of load weights from layer %d", l);
         return false;
        }

モデルパラメータのコピーを受け取った後で、オブジェクト内のパラメータの編集を開始します。まず、ニューラル層オブジェクトへのポインタを取得します。そして、すべてのエージェントに対してネストしたループを実装します。このループの中で、対応するエージェントの重み行列へのポインタを抽出します。

      CLayer* layer = layers.At(l);
      for(uint i = 0; i < i_PopulationSize; i++)
        {
         CNeuronBaseOCL* neuron = layer.At(i);
         CBufferFloat* weights = neuron.getWeights();

そして，得られたポインタが有効であれば，重み行列の全要素を繰り返し，親の対応するパラメータに置き換える，別の入れ子型ループを実装します。

         if(!!weights)
           {
            for(int w = 0; w < weights.Total(); w++)
               if(!weights.Update(w, NextGenerationWeight(m_Weights, w, v_Probability)))
                 {
                  Print("Error of update weights");
                  return false;
                 }
            weights.BufferWrite();
           }

基本的なアルゴリズムから若干脱線することをご了承ください。無作為に両親のペアを抽出したわけではありません。その代わり、選択されたすべてのエージェントから、その確率分布に従ってランダムに一度に重みを取ることにします。重みのサンプリングはNextGenerationWeightメソッドを使用します。

次のデータバッファの値を生成した後、その値をOpenCLコンテキストにコピーします。

必要であれば、畳み込み層の行列に対してこの操作を繰り返します。

         if(neuron.Type() != defNeuronConvOCL)
            continue;
         CNeuronConvOCL* temp = neuron;
         weights = temp.GetWeightsConv();
         for(int w = 0; w < weights.Total(); w++)
            if(!weights.Update(w, NextGenerationWeight(m_WeightsConv, w, v_Probability)))
              {
               Print("Error of update weights");
               return false;
              }
         weights.BufferWrite();
        }
     }

全エージェントのパラメータを更新した後、新世代の収益性を正しく判断するために、報酬蓄積ベクトルの値をゼロにリセットします。次に、メソッドをtrueで終了します。

   v_Rewards.Fill(0);
//---
   return true;
  }

遺伝的アルゴリズムの基礎となる主なクラスメソッドのアルゴリズムを考えてみました。ただし、いくつかのヘルパーメソッドも用意されています。そのアルゴリズムは複雑なものではなく、添付ファイルで確認することができます。モデル保存方式に注目してください。ポイントは、親クラスの保存メソッドですべてのエージェントを保存することです。それを使って、さらに最適化を続けることができますが、単一のエージェントを保存するには適用できません。ただし、最適化の目的は、最適なエージェントを見つけることです。したがって、1つの最適なエージェントを保存するためにSaveModelメソッドを使用します。メソッドのパラメータには、モデルを保存するファイル名、エージェントのシリアル番号、Commonディレクトリへの書き込みのフラグを渡します。

メソッドの本文では、まずエージェントのシリアルナンバーを確認します。アクティブなエージェントの数を満たさない場合、最大の確率を持つエージェントの数に置き換えます。また、最も利益の高いエージェントでもあります。

bool CNetGenetic::SaveModel(string file_name, int model, bool common = true)
  {
   if(model < 0 || model >= (int)i_PopulationSize)
      model = (int)v_Probability.ArgMax();

次に、新しいモデルオブジェクトのインスタンスを作成し、必要なモデルのパラメータをその中にコピーします。

   CNetGenetic *new_model = new CNetGenetic();
   if(!new_model)
      return false;
   if(!new_model.CopyModel(layers, model))
     {
      new_model.Detach();
      delete new_model;
      return false;
     }

これで、新しいモデルに対して親クラスの保存メソッドを単純に呼び出すことができます。

   bool result = new_model.Save(file_name, 0, 0, 0, 0, common);

モデルを保存した後、メソッドを終了する前に、新しく作成されたオブジェクトを削除する必要があります。ただし、データをコピーする際には、新しいニューラル層オブジェクトは作らず、単にそのポインタを利用しました。したがって、モデルオブジェクトを削除すると、保存されたエージェントのオブジェクトも一般モデルですべて削除されることになります。これを避けるために、まずDetachというメソッドを使い、保存されたモデルからニューラル層のオブジェクトを切り離します。この後、このメソッドで作成したモデルオブジェクトを簡単に作成することができます。

   new_model.Detach();
   delete new_model;
//---
   return result;
  }

このクラスのすべてのメソッドのコード全体は、以下の添付ファイルにあります。では、次にモデル最適化処理を実装するジェネティック.mq5EAを作成することにしましょう。新しいEAは、前回の記事で紹介したActor_Critic.mq5EAを基に作成します。

EAの外部パラメータにハイパーパラメータを追加して、新しい処理を整理してみましょう。

input int                  PopulationSize =  50;
input int                  Generations = 1000;
input double               Quantile =  0.5;
input double               Mutation = 0.01;

また、モデルの場合は、作業オブジェクトを置き換えます。

CNetGenetic          Models;

EAにおけるモデルの初期化は、先に検討したEAにおける親モデルの初期化と同様の構成です。

int OnInit()
  {
//---
.............
.............
//---
   if(!Models.Load(MODEL + ".nnw", PopulationSize, false))
      return INIT_FAILED;
//---
   if(!Models.GetLayerOutput(0, TempData))
      return INIT_FAILED;
   HistoryBars = TempData.Total() / 12;
   Models.getResults(TempData);
   if(TempData.Total() != Actions)
      return INIT_PARAMETERS_INCORRECT;
//---
   bEventStudy = EventChartCustom(ChartID(), 1, 0, 0, "Init");
//---
   return(INIT_SUCCEEDED);
  }

いつものように、最適化処理を実装するのは電車関数で実行されます。関数の冒頭で、先に考えたEAと同様に、最適化（訓練）期間を決めます。

void Train(void)
  {
//---
   MqlDateTime start_time;
   TimeCurrent(start_time);
   start_time.year -= StudyPeriod;
   if(start_time.year <= 0)
      start_time.year = 1900;
   datetime st_time = StructToTime(start_time);

訓練用サンプルを読み込みます。

   int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates);
   if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars))
     {
      ExpertRemove();
      return;
     }
   if(!ArraySetAsSeries(Rates, true))
     {
      ExpertRemove();
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

初期データを生成したら、ローカル変数を用意します。最後の月は、新しいデータで最適化されたモデルのパフォーマンスをテストするために使用されるため、訓練サンプルからは除外します。

   CBufferFloat* State = new CBufferFloat();
   float loss = 0;
   uint count = 0;
   uint total = bars - HistoryBars - 1;
   ulong ticks = GetTickCount64();
   uint test_size=22*24;

次に、最適化過程を整理するために、ネストされたループのシステムを作成します。外側のループは、最適化の世代をカウントする役割を担っています。ネストされたループは、最適化の反復をカウントします。この場合、全エージェントによる訓練サンプルの完全な反復を使用しました。しかし、1回のセッションにかかる時間を短縮するために、ランダムサンプリングを使用することができます。この場合、訓練サンプルの主な傾向を評価するのに十分なサンプルであることを確認する必要があります。もちろん、この場合、最適化の精度が低下する可能性があります。ここで重要なのは、結果の精度とモデルの最適化コストとのバランスです。

   for(int gen = 0; (gen < Generations && !IsStopped()); gen ++)
     {
      for(uint i = total; i > test_size; i--)
        {
         uint r = i + HistoryBars;
         if(r > (uint)bars)
            continue;

ネストされたループの本体では、現在のパターンの境界を定義し、ソースデータバッファを作成します。

         State.Clear();
         for(uint b = 0; b < HistoryBars; b++)
           {
            uint bar_t = r - b;
            float open = (float)Rates[bar_t].open;
            TimeToStruct(Rates[bar_t].time, sTime);
            float rsi = (float)RSI.Main(bar_t);
            float cci = (float)CCI.Main(bar_t);
            float atr = (float)ATR.Main(bar_t);
            float macd = (float)MACD.Main(bar_t);
            float sign = (float)MACD.Signal(bar_t);
            if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
               continue;
            //---
            if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) ||
               !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) ||
               !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) ||
               !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign))
               break;
           }
         if(IsStopped())
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(State.Total() < (int)HistoryBars * 12)
            continue;

ここで、最適化された母集団に対してフィードフォワード法を呼び出します。

         if(!Models.feedForward(State, 12, true))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

見ての通り、この作業は先ほどのモデル訓練時の操作と似ています。なぜなら、過程の違いはすべてライブラリに実装されているからです。メソッドのインターフェイスは変更されていません。ここで、1つのモデルについてフォワードパスを呼び出します。CNetGeneticクラスの本体では、母集団のすべてのアクティブなエージェントに対してフィードフォワードを実装しています。

次に、現在の報酬をエージェントに転送する必要があります。前述の通り、ここではすべてのエージェントにポーリングをおこなうわけではありません。その代わり、与えられた状態での各行動に対する報酬を指定するバッファを作成します。バッファは以下のメソッドのパラメータで渡されます。

         double reward = Rates[i - 1].close - Rates[i - 1].open;
         TempData.Clear();
         if(!TempData.Add((float)(reward < 0 ? 20 * reward : reward)) ||
            !TempData.Add((float)(reward > 0 ? -reward * 20 : -reward)) ||
            !TempData.Add((float) - fabs(reward)))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }
         if(!Models.Rewards(TempData))
           {
            PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
            break;
           }

元の報酬ポリシーをそのまま使用しています。これにより、最適化過程が全体の結果に与える影響を評価することができます。

一つのシステム状態を処理するループの反復が完了したら、過程の視覚的な制御のために関連情報をプロットし、次のループの反復に移ることになります。

         if(GetTickCount64() - ticks > 250)
           {
            uint x = total - i;
            double perc = x * 100.0 / (total - test_size);
            Comment(StringFormat("%d from %d -> %.2f%% from %.2f%%", x, total - test_size, perc, 100));
            ticks = GetTickCount64();
           }
        }

セッションの終了後、最適なエージェントのパラメータを保存します。

      Models.SaveModel(MODEL+".nnw", -1, false);

次に、新しい世代の作成に移ります。これは、1つのメソッドCNetGenetic::NextGenerationを呼び出すことで行われます。操作の実行を制御することを忘れないでください。

      double average, maximum;
      if(!Models.NextGeneration(Quantile, Mutation, average, maximum))
        {
         PrintFormat("Error of create next generation: %d", GetLastError());
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
      //---
      PrintFormat("Genegation %d, Average Cumulative reward %.5f, Max Reward %.5f", gen, average, maximum);
     }

最後に、達成された結果に関する情報を操作ログに出力し、ループの新しい反復で分析された集団の新しい世代の評価に進みます。

最適化処理終了後、データをクリアしてEA操作を完了します。

   delete State;
   Comment("");
//---
   ExpertRemove();
  }

このように、クラスをアレンジすることで、メインプログラム側の作業が大幅に簡略化されました。実際には、3つのメソッドを順次呼び出すことで最適化をおこないます。これは、勾配降下法を用いたモデルの訓練に匹敵するものです。これにより、1つのエージェント内のトランザクションの総数も大幅に削減されます。

3.テスト

最適化過程は、以前に使用したすべてのパラメータでテストされました。訓練サンプルはEURUSDH1のヒストリカルデータです。最適化処理には、過去2年分の履歴を使いました。EAはデフォルトのパラメータで使用しました。テストのモデルとして、前回の記事から意思決定の最適な確率分布の探索でアーキテクチャを使用しました。この方法により、最適化されたモデルを、先に使用したExpertAdvisor「REINFORCE-test.mq5」に代入することができます。このように、同じアーキテクチャのモデルを訓練させる過程では、3つ目のアプローチとなります。以前、我々はすでにPolicyGradientとActor-Criticアルゴリズムを用いて同様のモデルを訓練しました。最適化の結果を観察するのは、さらに興味深いことです。

モデルを最適化する際、前月のデータは使用しませんでした。そのため、最適化されたモデルをテストするためのデータを残しています。最適化されたモデルは、ストラテジーテスターで実行されました。その結果、次のような結果が得られました。

最適化されたモデルテストグラフ

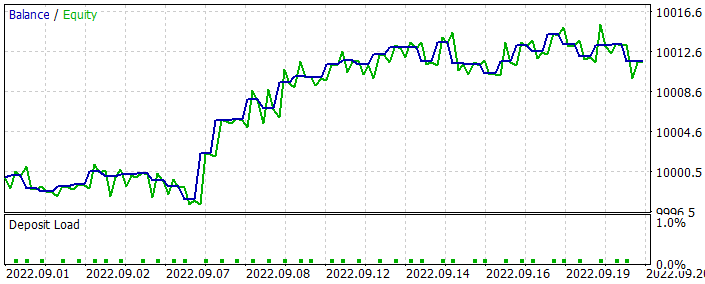
提示されたグラフからわかるように、成長するバランスグラフを得ることができました。しかし、アクタークリティック法で同様のモデルを訓練させた場合と比べて、収益性はやや低くなります。また、取引操作も減少しました。実際、取引件数は2分の1に減少しました。

モデル取引履歴のチャート

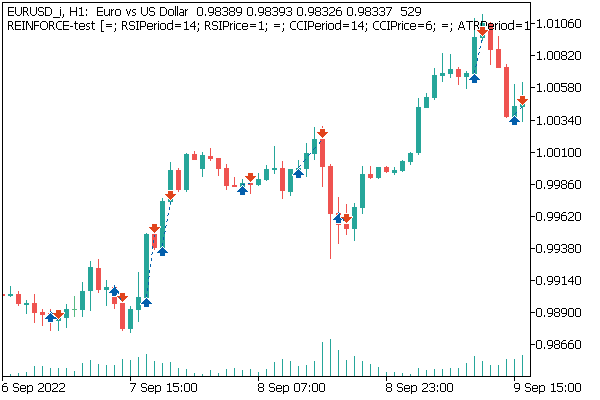
売買が成立した銘柄チャートを見ると、モデルがトレンドに沿った売買をしようとしていることがよくわかります。これは面白い結果だと思います。勾配法を用いて同様のモデルを訓練させたところ、ほとんどの動きで取引を実行しようとしました。かなり、カオスな状態でした。今回は、取引のポスチュレートとしてよく知られる、ある種のロジックを見ることができます。

それとも、私にだけそう見えるのでしょうか。私の結論はすべて「奇想天外」なのでしょうか。ご自分で実験をして、その結果を観察するのも面白いでしょう。

テスト結果一覧

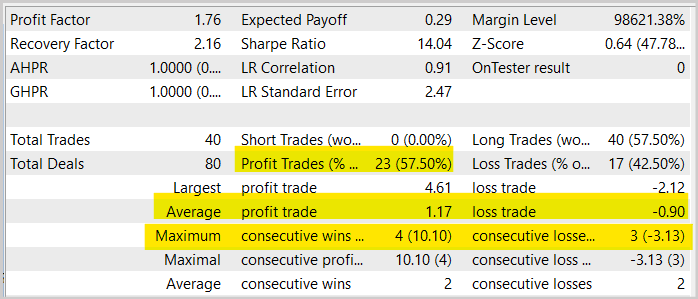
一般に、Actor-Critic法で学習させたモデルの同様のテストと比較して、利益をもたらす取引のシェアがほぼ1.5%増加していることがわかります。ただし、取引回数は2分の1に減りました。同時に、1回の操作あたりの平均損益も減少していることがわかります。このため、売上高および期間全体の収益性は概して低下しました。ただし、1ヶ月目のテストは、長期間のEA運用に耐えうるものであるとは評価できませんので、ご注意ください。したがって、実際の取引に使用する前に、モデルの徹底的かつ包括的なテストを実施することを再度お勧めします。

結論

今回は、モデルを最適化するための遺伝的手法に迫りました。あらゆるパラメトリックモデルの最適化に利用できます。この手法の主な利点の1つは、微分不可能なモデルの最適化に使用できる可能性があることです。これは、勾配降下法のさまざまなバリエーションを含む勾配法を用いてモデルを訓練する場合には不可能です。

また、MQL5によるアルゴリズムの実装も掲載されています。テストしたモデルを最適化し、StrategyTesterでその結果を観察することもおこないました。

テスト結果から、このモデルはかなり良い結果を示したと言えるでしょう。そのため、この手法は取引モデルの最適化に利用することができますが、実際の口座でそのモデルを使うことを決める前に、徹底的に包括的にテストする必要があります。

参考文献リスト

記事で使用されているプログラム

#	名前	タイプ	詳細
1	Genetic.mq5	EA	モデルを最適化するためのEA
2	NetGenetic.mqh	クラスライブラリ	遺伝的アルゴリズムを実装するためのライブラリ
3	REINFORCE-test.mq5	EA	ストラテジーテスターでモデルをテストするためのEA
4	NeuroNet.mqh	クラスライブラリ	ニューラルネットワークモデルを作成するためのライブラリ
5	NeuroNet.cl	コードベース	ニューラルネットワークモデルを作成するためのOpenCLプログラムコードライブラリ

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/11489

添付されたファイル |

ZIPをダウンロード

MQL5.zip (680.14 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

DoEasy-コントロール（第19部）：TabControl、WinFormsオブジェクトイベントでのタブのスクロール

この記事では、スクロールボタンを使用してTabControlでタブヘッダーをスクロールする機能を作成します。この機能は、コントロールの両方側からタブヘッダーを1行に配置するためのものです。

一からの取引エキスパートアドバイザーの開発（第31部）：未来に向かって(IV)

引き続きEAから分離した部分を取り除きます。本連載は今回で最終回です。そして、最後に取り除くのがサウンドシステムです。この連載をご覧になっていない方には、少し分かりにくいかもしれません。

知っておくべきMQL5ウィザードのテクニック（第03回）：シャノンのエントロピー

今日のトレーダーは哲学者であり、ほとんどの場合、新しいアイデアを探し、試し、変更するか破棄するかを選択します。これは、かなりの労力を要する探索的プロセスです。この連載では、MQL5ウィザードがトレーダーの主力であるべきであることを示します。

アクセラレーターオシレーター（Accelerator Oscillator）による取引システムの設計方法を学ぶ

最も人気のあるテクニカル指標によって取引システムを設計する方法についての連載の新しい記事へようこそ。今回は、新しい指標であるアクセラレーターオシレーター（Accelerator Oscillator、AC）について学び、それを使った取引システムを設計する方法を学びます。