Нейросети в трейдинге: Модель адаптивной графовой диффузии (Окончание)
Введение
Сегодня мы завершаем работу по реализации подходов, предложенных авторами фреймворка SAGDFN. Авторы фреймворка предложили один из вариантов решения самой острой проблемы пространственно-временного прогнозирования — неумолимо растущей сложности обработки больших графов. Традиционные модели графовых нейронных сетей (GNN) страдают от избыточности связей: чем больше узлов, тем выше вероятность того, что значимая информация тонет в потоке малосущественных взаимодействий. Попытка обрабатывать все связи подряд приводит к квадратичному росту вычислительной нагрузки и падению обобщающей способности модели. Авторы SAGDFN предложили разорвать этот порочный круг, сфокусировавшись лишь на действительно значимых связях и отсекая лишнее ещё на ранних стадиях обработки данных.
Модуль Significant Neighbors Sampling (SNS) стал первым кирпичиком в этой концепции. Его задача — выделить для каждого узла набор значимых соседей, которые несут максимальную прогностическую ценность. В классическом подходе графовые модели либо берут всех соседей подряд, либо жёстко ограничиваются фиксированной структурой. SNS пошёл дальше: он динамически формирует набор связей, анализируя как ближайших кандидатов по метрике сходства, так и случайно выбранные элементы для поддержания диверсификации. Это не только уменьшает размерность графа, но и снижает риск переобучения, ведь модель не запирается на заранее заданной структуре, а учится адаптивно строить карту важности связей.
После того как каркас графа сформирован, вступает в игру Sparse Spatial Multi-Head Attention (SSMHA) — адаптивнный механизм внимания, который работает с разреженной структурой, полученной на предыдущем этапе. Этот модуль выполняет сразу две ключевые функции: перераспределяет весовые коэффициенты между соседями и позволяет каждому узлу учитывать различные аспекты контекста за счёт многоголового внимания. В отличие от классического SoftMax, где сумма всех весов всегда строго нормирована, в SAGDFN применялся α-Entmax, позволяющий более жёстко обнулять несущественные связи. При α=1 эта функция сводится к обычному SoftMax, а при α=2 — к Sparse-SoftMax, где незначимые элементы фактически исключаются из вычислений. Это даёт модели гибкость. Она может оставаться чувствительной к слабым сигналам, когда это важно. И в то же время концентрироваться на действительно значимых узлах, когда плотность графа становится чрезмерной.
Не менее важным элементом является и OneStepFastGConv — оптимизированная графовая свёртка, которая выполняет преобразование пространственных признаков за один шаг, избегая избыточных каскадов операций. Вместо последовательного наложения нескольких слоёв, каждый из которых выполняет лишь небольшое преобразование, здесь применяется одномоментное агрегирование, что ускоряет обучение и снижает требования к памяти. Этот подход особенно важен для задач реального времени, где каждая миллисекунда обработки данных имеет значение.
Совместная работа этих модулей напоминает слаженную работу оркестра: SNS выбирает ключевых музыкантов, SSMHA распределяет роли и акценты между ними, а FastGConv превращает эту какофонию сигналов в стройную мелодию прогноза. Причём все элементы изначально были задуманы как масштабируемые. То есть способные эффективно работать с относительно компактными графами и с крупными структурами, насчитывающими тысячи узлов и миллионы потенциальных связей.
Авторская визуализация фреймворка SAGDFN представлена ниже.
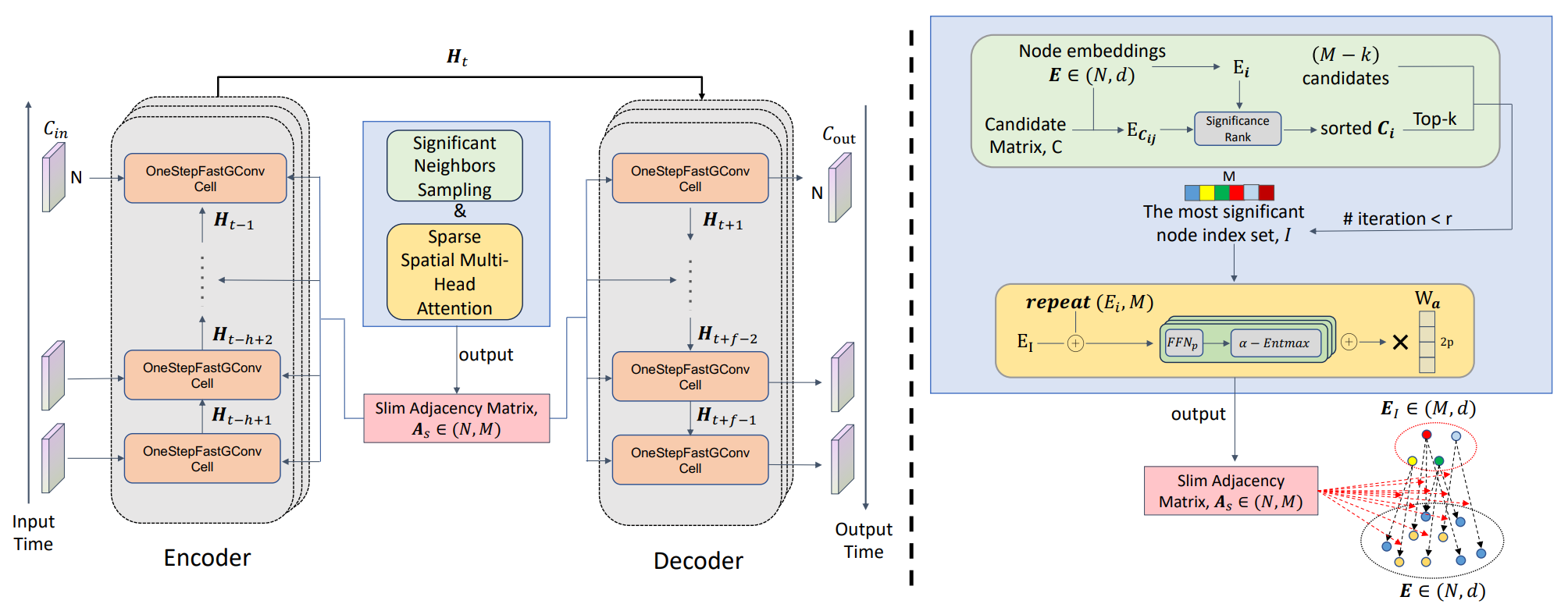
В предыдущих статьях мы последовательно разобрали ключевые строительные блоки фреймворка. Шаг за шагом реализовав модули Significant Neighbors Sampling и Sparse Spatial Multi-Head Attention средствами MQL5 и OpenCL. В этом процессе мы не ограничились буквальным повторением исходного алгоритма — напротив, внесли ряд важных оптимизаций, направленных на повышение вычислительной эффективности и устойчивости модели. Так, вместо итеративной функции α-Entmax, требующей значительных ресурсов из-за поиска оптимального параметра τ, мы применили более лёгкий и стабильный Sparse-SoftMax. Это позволило сохранить концепцию избирательного отсеивания малозначимых элементов и снизить нагрузку на процессор. Дополнительно была усовершенствована процедура формирования связей в модуле отбора соседей. Мы организовали параллельную оценку ранее отобранных и случайных кандидатов, что позволило повысить разнообразие связей и уменьшить вероятность потери потенциально полезной информации.
Теперь, когда механизмы построения графа и распределения весов между его узлами налажены, настало время перейти к следующему логическому шагу — построению модуля OneStepFastGConv. Этот компонент играет особую роль в архитектуре SAGDFN, ведь именно он отвечает за агрегирование пространственной информации и формирование признаков, на которых будет базироваться финальный прогноз.
Рекуррентный объект графовой свертки
Продолжая логическую линию предыдущего материала, где мы уже собрали каркас графа (Significant Neighbors Sampling) и научились аккуратно распределять веса между ключевыми связями (Sparse Spatial Multi-Head Attention), переходим к сердцу рекуррентного блока — быстрой графовой свёртке. Это не первый наш визит в мир рекуррентных графовых модулей: в HimNet мы использовали GСRU, и он отлично показал себя на плотных структурах. Но в SAGDFN — иной ландшафт. Мы сознательно работаем с разреженной матрицей взаимозависимостей, и именно эта разрежённость диктует иной алгоритмический уклад. Чтобы не строить дом на песке, начнём с базовой операции, на которой затем будет держаться OneStepFastGConv — эффективного умножения разреженной матрицы на плотную.
Этот этап является ключевым, поскольку именно он позволит нам эффективно интегрировать разреженную структуру взаимосвязей, полученную ранее, в общий контекст обработки данных. Для этого мы создаем кернел на стороне OpenCL-программы, который выполняет данную операцию максимально просто и в то же время с акцентом на производительность и экономию памяти.
__kernel void SparseMatMult(__global const float *sparse_index, __global const float *sparse_data, __global const float *full, __global float *result, const int full_rows ) { const size_t sparse_row = get_global_id(0); const size_t sparse_col = get_local_id(1); const size_t full_col = get_global_id(2); const size_t sparse_rows = get_global_size(0); const size_t sparse_cols = get_local_size(1); const size_t full_cols = get_global_size(2); //--- __local float Temp[LOCAL_ARRAY_SIZE];
В самом начале работы кернел определяет координаты выполняемой задачи: индексы строки и столбца разреженной матрицы, последние объединены в локальные группы. А так же индекс столбца полной матрицы. Эти параметры формируют своеобразную тройку координат, которая позволяет каждому потоку точно знать, за какой участок данных он отвечает. Далее определяются размеры всех измерений. Они необходимы для корректной адресации элементов.
После этого выделяется локальный массив Temp, используемый для синхронизации и суммирования промежуточных значений внутри рабочей группы.
Следующим этапом каждый поток определяет сдвиг в памяти для текущего элемента разреженной матрицы и извлекает индекс соответствующей строки полной матрицы.
const int shift_sparse = RCtoFlat(sparse_row, sparse_col, sparse_rows, sparse_cols, 0); const int full_row = sparse_index[shift_sparse]; const int shift_full = RCtoFlat(full_row, full_col, full_rows, full_cols, 0);
Если этот индекс находится в допустимых пределах, происходит вычисление произведения коэффициента разреженной матрицы на элемент полной матрицы. В противном случае используется нулевое значение, что позволяет избежать некорректных операций.
float res = (full_row >= 0 && full_row < full_rows ? IsNaNOrInf(sparse_data[shift_sparse] * full[shift_full], 0) : 0); res = LocalSum(res, 1, Temp);
Полученное частичное произведение передается в локальную процедуру суммирования, которая аккумулирует результаты от всех потоков рабочей группы. Как только суммирование завершено, первый поток в каждой группе (имеющий локальный индекс столбца, равный нулю) записывает итоговое значение в результирующую матрицу. Таким образом достигается баланс между параллелизмом вычислений и контролем над записью данных, предотвращая конфликты доступа.
if(sparse_col == 0) { const int shift_result = RCtoFlat(sparse_row, full_col, sparse_rows, full_cols, 0); result[shift_result] = res; } }
Такой подход обеспечивает оптимальное использование ресурсов GPU. Каждый поток выполняет лишь свою часть работы, а коллективное суммирование гарантирует точность и согласованность конечного результата.
После того как мы реализовали прямой проход и научились аккуратно собирать вклад соседей в результирующие признаки, следующим шагом становится обратный проход — корректное распределение градиента ошибки по всем участвующим элементам. Алгоритм реализован в кернеле SparseMatMultGrad, который получает на вход:
- индексы и веса разрежённой матрицы,
- буфер для градиентов по этим весам,
- плотную матрицу и её буфер градиентов,
- массив градиентов результата,
- размеры всех измерений.
__kernel void SparseMatMultGrad(__global const float *sparse_index, __global const float *sparse_data, __global float *sparse_gr, __global const float *full, __global float *full_gr, __global const float *result_gr, const int sparse_rows, const int sparse_cols, const int full_rows, const int full_cols ) { const size_t row_id = get_global_id(0); const size_t local_id = get_local_id(1); const size_t col_id = get_global_id(2); const size_t total_rows = get_global_size(0); const size_t total_local = get_local_size(1); const size_t total_cols = get_global_size(2); //--- __local float Temp[LOCAL_ARRAY_SIZE];
В теле кернела каждый поток получает свои координаты в пространстве задач:
- row_id — строка, по которой идёт обработка матрицы;
- local_id — локальный идентификатор внутри группы;
- col_id — колонка матрицы.
Буфер локальной памяти Temp выделяется для редукций и передачи небольших порций данных между потоками одной рабочей группы. Это главный инструмент для координации — через него потоки обмениваются промежуточными результатами и синхронизируются.
Здесь следует обратить внимание, что в данном кернеле нам предстоит распределить градиенты ошибок между двумя матрицами различного размера. И идентификаторы строки и столбца являются ориентирами именно по матрице-получателе градиентов. С этой целью, при постановке кернела в очередь выполнения мы планируем использовать максимальные значения от обеих матриц. А лишние потоки отсеиваются внутри кернела.
Первым следует блок расчета градиентов ошибки по весам разрежённой матрицы. Мы сначала страхуем индекс: если текущая позиция лежит в допустимом диапазоне, поток вычисляет shift_sparse — плоский сдвиг в массивах индексов и данных разреженной матрицы.
//--- Calce sparse gradient if(row_id < sparse_rows && col_id < sparse_cols) { float grad = 0; int shift_sparse = 0; if(local_id == 0) { shift_sparse = RCtoFlat(row_id, col_id, sparse_rows, sparse_cols, 0); Temp[0] = sparse_index[shift_sparse]; } BarrierLoc; uint full_row = (uint)Temp[0];
Поток с local_id равным 0 читает соответствующий индекс и кладёт его в первый элемент буфера локальной памяти, чтобы остальные потоки могли воспользоваться этим значением без дополнительных глобальных обращений.
После барьера все потоки рабочей группы знают индекс строки плотной матрицы.
Пожалуйста, обратите внимание: важно проверить корректность полученного индекса строки. А после успешного прохождения блока контроля, каждый поток идёт по своим позициям признакового измерения и аккумулирует вклад элемента.
if(full_row < (uint)full_rows) for(int i = local_id; i < full_cols; i += total_local) { int shift_result = RCtoFlat(row_id, i, sparse_rows, full_cols, 0); int shift_full = RCtoFlat(full_row, i, full_rows, full_cols, 0); grad += IsNaNOrInf(result_gr[shift_result] * full[shift_full], 0); }
Это классический скалярный добор по признакам: берем градиент результата по каждому признаку и умножаем его на значение соответствующей ячейки полной матрицы, суммируя по всем признакам.
После завершения локального обхода выполняется редукция по потокам рабочей группы, чтобы получить суммарный вклад для данной пары (row_id, col_id).
grad = LocalSum(grad, 1, Temp); if(local_id == 0) sparse_gr[shift_sparse] = grad; }
И только один поток записывает итоговый результат рабочей группы в соответствующий элемент глобального буфера sparse_gr.
Переходя ко второй большой части (вычислению градиента по плотной матрице) мы сталкиваемся с обратной задачей. Для каждого элемента плотной матрицы нужно аккуратно просуммировать вклад в результат работы блока. Однако здесь мы сталкиваемся с проблемой отсутствия явной привязки к элементам разреженной матрицы. Поэтому нам придется просканировать всю матрицу индексов разреженной матрицы в поиске необходимых указателей. Именно эту задачу мы и возложим на потоки локальной группы.
Сначала мы организуем цикл перебора строк матрицы индексов градиентов ошибки. Напомню, что количество строк в тензоре градиентов ошибки и разреженной матрице одинаково.
//--- Calce full gradient if(row_id < full_rows && col_id < full_cols) { float grad = 0; for(int r = 0; r < sparse_rows; r ++) { float s = 0; for(int c = local_id; c < sparse_cols; c += total_local) { int shift_sparse = RCtoFlat(r, c, sparse_rows, sparse_cols, 0); if((int)sparse_index[shift_sparse] == (int)row_id) { s = sparse_data[shift_sparse]; break; } }
Внутри цикла мы пытаемся найти указатель на текущую строку плотной матрицы среди индексов разреженной матрицы. Для эффективного параллелизма каждый поток локальной группы обходит лишь часть столбцов разреженной матрицы, и при первом совпадении берёт коэффициент внимания и прерывает поиск.
Напомню, что в процессе отбора наиболее близких соседей мы внедрили механизм исключения дубликатов. И поэтому не ожидаем наличие связей более одного раза в каждой строке разреженной матрицы.
Затем с помощью LocalSum собираем информацию о коэффициентах внимания из всех потоков рабочей группы.
s = LocalSum(s, 1, Temp); if(s != 0 && local_id == 0) { int shift_result = RCtoFlat(r, col_id, sparse_rows, full_cols, 0); grad += IsNaNOrInf(s * result_gr[shift_result], 0); } }
Если сумма оказалась ненулевой, то первый поток рабочей группы умножает полученный вес на значение соответствующего элемента из буфера градиентов ошибки блока и аккумулирует в переменной grad.
После завершения всех итераций системы циклов и сбора суммарного градиента ошибки от всех зависимых элементов, первый поток рабочей группы записывает накопленное значение в глобальный буфер full_gr.
if(local_id == 0) { int shift_full = RCtoFlat(row_id, col_id, full_rows, full_cols, 0); full_gr[shift_full] = grad; } } }
После завершения подготовительной работы, переходим к практической реализации рекуррентного блока OneStepFastGConv на стороне основной программы. Здесь мы реализуем предложенные подходы в рамках класса CNeuronFastGConv, задуманного как компактный контейнер для всех промежуточных буферов и логики. Структура класса представлена ниже.
class CNeuronFastGConv : public CNeuronBaseOCL { protected: CNeuronBaseOCL cInpAndHidden; CNeuronBaseOCL cNormAttention; CNeuronBaseOCL cInvDiag; CNeuronBaseOCL cAX; CNeuronBaseOCL cAXplusX; CNeuronBaseOCL cNormAXplusX; CNeuronConvOCL cZ_R; CNeuronBaseOCL cZ; CNeuronBaseOCL cR; CNeuronBaseOCL cCandidate; CNeuronConvOCL cHC; //--- virtual bool RandomWalk(CBufferFloat* data, CBufferFloat* normal, CBufferFloat* inv_diag, const int rows, const int cols ); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override { return false; }; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None ) override { return false; } //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronFastGConv(void) {}; ~CNeuronFastGConv(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint sparse_dimension, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool FeedForward(CNeuronBaseOCL *SourceData, CNeuronSNSMHAttention *SparseAttent); virtual bool CalcInputGradients(CNeuronBaseOCL *SourceData, CNeuronSNSMHAttention *SparseAttent); //--- virtual int Type(void) const { return defNeuronFastGConv; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; virtual void SetActivationFunction(ENUM_ACTIVATION value) override { }; //--- virtual uint GetCount(void) const { return (uint)cInvDiag.Neurons(); } virtual uint GetSparseDimension(void) const { return (uint)cNormAttention.Neurons() / GetCount(); } virtual uint GetWindow(void) const { return (uint)Neurons() / GetCount(); } };
В структуре нового класса мы видим довольно большое количество внутренних объектов. Однако все они объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Весь алгоритм настройки архитектуры объекта перенесен в метод инициализации Init.
bool CNeuronFastGConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint units, uint window, uint sparse_dimension, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units * window, optimization_type, batch)) return false; activation = None;
Первая строка внутри метода передает управление родительскому классу. Это базовая привязка слоя к OpenCL-контексту и создание всех унаследованных интерфейсов, необходимых для работы модуля внутри модели. Если эта инициализация не удаётся, дальнейший смысл метода теряется, поэтому мы сразу возвращаем false. Такой ранний выход защищает от дальнейших ошибок и лишних аллокаций.
Сразу после этого мы явно отключаем функцию активации. Это логично: сам блок управляет активациями в компонентах (сигмоиды для гейтов, tanh для кандидатов), и внешняя общая активация здесь не нужна.
Далее идёт процесс инициализации внутренних компонентов. Первый объект предназначен для конкатенации предыдущего скрытого состояния и исходных данных.
int index = 0; if(!cInpAndHidden.Init(0, index, OpenCL, 2 * units * window, optimization, iBatch)) return false;
Следующей строчкой создаётся cNormAttention. Это место для хранения slim-матрицы внимания As после нормировки. Он будет принимать веса от модуля Sparse Attention.
index++; if(!cNormAttention.Init(0, index, OpenCL, units * sparse_dimension, optimization, iBatch)) return false; index++; if(!cInvDiag.Init(0, index, OpenCL, units, optimization, iBatch)) return false;
Переходим к cInvDiag — вектор инверсий диагонали, который будет умножать строки результата диффузии при нормировке.
Следующим создаётся cAX. Этот буфер хранит результат SpMM. Его размер взят из cInpAndHidden, что гарантирует совместимость по размерам с последующими шагами.
index++; if(!cAX.Init(0, index, OpenCL, cInpAndHidden.Neurons(), optimization, iBatch)) return false; index++; if(!cAXplusX.Init(0, index, OpenCL, cInpAndHidden.Neurons(), optimization, iBatch)) return false; index++; if(!cNormAXplusX.Init(0, index, OpenCL, cInpAndHidden.Neurons(), optimization, iBatch)) return false;
За cAX следует cAXplusX — буфер для суммы AX + X. Здесь мы явно сохраняем промежуточный результат, прежде чем применить инверсию диагонали. Такой явный буфер облегчает отладку и даёт контроль над порядком операций.
Затем создаётся cNormAXplusX — итоговый нормированный тензор (D+I)-1(AX + X). Он подаётся далее в GRU-подобный блок. Если его нет, механика update-гейтов ломается, поэтому опять же проверка критична.
Дальше инициализируется cZ_R. Это компактный сверточный слой, который будет одновременно формировать логиты для gейтов Z и R. В качестве фунцкции активации здесь мы используем сигмоиду. Такой приём — прост и надёжен: гейты всегда в диапазоне [0,1].
index++; if(!cZ_R.Init(0, index, OpenCL, 2 * window, 2 * window, 2 * window, units, 1, optimization, iBatch)) return false; cZ_R.SetActivationFunction(SIGMOID); index++; if(!cZ.Init(0, index, OpenCL, window * units, optimization, iBatch)) return false; index++; if(!cR.Init(0, index, OpenCL, window * units, optimization, iBatch)) return false;
Следующие два буфера cZ и cR создаются для разделения значений гейтов. Наличие отдельных буферов упрощает пошаговую логику обновления скрытого состояния.
Инициализация cCandidate создаёт буфер для промежуточного конкатенированного входа в блок кандидатов.
index++; if(!cCandidate.Init(0, index, OpenCL, 2 * window * units, optimization, iBatch)) return false; index++; if(!cHC.Init(0, index, OpenCL, 2 * window, 2 * window, window, units, 1, optimization, iBatch)) return false; cHC.SetActivationFunction(TANH); //--- return true; }
Блок cHC — это собственно расчёт Candidate Hidden State. Использование для него TANH в качестве функции активации — это стандарт, который делает кандидатов ограниченными и стабильными по масштабу.
Когда все вызовы внутри метода Init отработали успешно, в самом конце возвращаем true, сигнализируя, что слой сконфигурирован и готов к работе.
Плавно переходим от инициализации к исполнению. Теперь, когда всё выделено и настроено, метод FeedForward — это живой поток данных через OneStepFastGConv.
bool CNeuronFastGConv::FeedForward(CNeuronBaseOCL *SourceData, CNeuronSNSMHAttention *SparseAttent) { if(!SourceData || !SparseAttent) return false; //--- const uint units = GetCount(); const uint window = GetWindow(); const uint sparse = GetSparseDimension();
Сначала метод проверяет входы актуальность полученных указателей на объекты исходных данных. Это простая, но необходимая защита — если нет источника данных или модуля разреженного внимания, дальше работать нельзя. Такой ранний выход предотвращает неконтролируемые сбои и даёт предсказуемую диагностику.
Далее мы извлекаем конфигурационные параметры слоя. Очень удобно иметь эти переменные локально: чтение из методов класса в горячем цикле медленнее и менее наглядно.
Следующая строка запускает RandomWalk. Это предварительная обработка матрицы внимания. RandomWalk собирает статистику по строкам slim-матрицы и выполняет гладкую нормировку. После чего записывает cNormAttention (N×M) и cInvDiag (N) — инверсии диагоналей для последующей нормировки. Здесь важно, что RandomWalk работает в параллельном режиме на GPU, аккуратно суммируя по M и возвращая стабильные inv_diag. Если этот шаг терпит неудачу, лучше прервать выполнение — далее зависимы все нормировки.
if(!RandomWalk(SparseAttent.getOutput(), cNormAttention.getOutput(), cInvDiag.getOutput(), window, sparse)) return false; if(!SwapOutputs()) return false; if(!Concat(SourceData.getOutput(), PrevOutput, cInpAndHidden.getOutput(), window, window, units)) return false;
После этого выполняется SwapOutputs. Это внутренний механизм слоя, который меняет указатели на предыдущий/текущий выход (rolling buffer). Своп обеспечивает, что PrevOutput содержит Ht-1, а текущий Output свободен для записи.
Далее собирается вход для SpMM/GRU. Здесь происходит конкатенация вдоль канального измерения: для каждой строки формируется вектор, который объединяет текущий наблюдаемый фрагмент Xt и предыдущее скрытое состояние Ht-1.
После завершения подготовительной работы, осуществляется ключевая операция — умножение разреженной матрицы внимания на ранее подготовленную полную матрицу конкатенированных исходных данных и скрытого состояния.
if(!SparseMatMul(SparseAttent.GetIndexes(), cNormAttention.getOutput(), cInpAndHidden.getOutput(), cAX.getOutput(), units, sparse, units, 2 * window)) return false; if(!SumAndNormilize(cAX.getOutput(), cInpAndHidden.getOutput(), cAXplusX.getOutput(), 2 * window, false, 0, 0, 0, 1)) return false;
Далее выполняют сумму с Self-Loop. Здесь мы складываем AX+X.
Следующий шаг — применение диагональной нормировки.
if(!DiagMatMul(cInvDiag.getOutput(), cAXplusX.getOutput(), cNormAXplusX.getOutput(), units, 2 * window, 1, None)) return false;
Это простое поканальное умножение строк на предварительно вычисленный inv_diag.
Далее вычисляются логиты гейтов. Сверточный слой cZ_R получает нормированные агрегированные признаки и возвращает вектор в 2×hidden (логиты для Z и R). Поскольку активацию SIGMOID устанавливали на этапе инициализации, в результате выполнения данной операции получаем значения в диапазоне [0,1].
if(!cZ_R.FeedForward(cNormAXplusX.AsObject())) return false; if(!DeConcat(cZ.getOutput(), cR.getOutput(), cZ_R.getOutput(), window, window, units)) return false;
Затем разделяем полученные логиты на отдельные буферы.
Сразу после этого идёт элементное умножение Reset-гейта на предыдущее скрытое состояние. Здесь формируется R⊙Ht-1. Результат используется далее, как модифицированная версия скрытого состояния для формирования кандидатов.
if(!ElementMult(cR.getOutput(), PrevOutput, cR.getPrevOutput())) return false;
Дальше формируется вход кандидатов — конкатенируем R⊙Ht-1 вместе с текущим Xt.
if(!Concat(SourceData.getOutput(), cR.getPrevOutput(), cCandidate.getOutput(), window, window, units)) return false; if(!cHC.FeedForward(cCandidate.AsObject())) return false; if(!GateElementMult(PrevOutput, cHC.getOutput(), cZ.getOutput(), Output)) return false; //--- return true; }
Вызов метода прямого прохода сверточного слоя cHC выполняет нелинейную трансформацию и применяет tanh, возвращая кандидатское скрытое состояние. И финальная композиция формирует новое скрытое состояния.
От описания прямого прохода переходим к обратной линийке — теперь нам нужно аккуратно разобрать, как ошибка течёт назад через все звенья OneStepFastGConv. Процесс организован в методе CalcInputGradients.
bool CNeuronFastGConv::CalcInputGradients(CNeuronBaseOCL *SourceData, CNeuronSNSMHAttention *SparseAttent) { if(!SourceData || !SparseAttent) return false; //--- const uint units = GetCount(); const uint window = GetWindow(); const uint sparse = GetSparseDimension();
Сразу же метод страхуется: если нет актуальных указателей на объекты исходных данных, то выполняться нечему. И мы корректно завершаем работу с результатом false. Это простая, но необходимая проверка — лучше прервать обучающий проход на ранней стадии, чем получить загадочные NaN-ы дальше.
Далее вытаскиваются конфигурационные параметры. Эти числа задают форму всех градиентных тензоров и нужны для корректной адресации.
Первый реальный вызов — GateElementMultGrad. Это разворот финальной композиции Ht = Z⊙Ht-1+(1−Z)⊙H̃.
if(!GateElementMultGrad(PrevOutput, cInpAndHidden.getGradient(), cHC.getOutput(), cHC.getGradient(), cZ.getOutput(), cZ.getGradient(), Gradient, None, cHC.Activation(), cZ_R.Activation())) return false;
Функция считает три вещи одновременно: градиент по H̃ (кандидаты), по Z (Update-Gate) и по Ht-1 (предыдущему скрытому состоянию), аккуратно раскладывая общий градиент на компоненты.
После этого проводим градиент ошибки через сверточный слой формирования кандидатов.
if(!cCandidate.CalcHiddenGradients(cHC.AsObject())) return false; if(!DeConcat(SourceData.getGradient(), cR.getPrevOutput(), cCandidate.getGradient(), window, window, units)) return false;
Дальше мы разделим полученные градиенты на две части — влияние исходных данных и R⊙Ht-1.
Затем ElementMultGrad распределяет вклад Reset-гейта и предыдущего скрытого состояния.
if(!ElementMultGrad(cR.getOutput(), cR.getGradient(), PrevOutput, cInpAndHidden.getGradient(), cR.getPrevOutput(), cZ_R.Activation(), None)) return false;
Следующий шаг — собираем локальные градиенты Z и R обратно в плоский вектор логитов, который подаём в cZ_R для обратного распространения слоя.
if(!Concat(cZ.getGradient(), cR.getGradient(), cZ_R.getGradient(), window, window, units)) return false; if(!cNormAXplusX.CalcHiddenGradients(cZ_R.AsObject())) return false; if(!DiagMatMulGrad(cInvDiag.getOutput(), cInvDiag.getGradient(), cAXplusX.getOutput(), cAX.getGradient(), cNormAXplusX.getGradient(), units, 2 * window, 1)) return false; if(!SparseMatMulGrad(SparseAttent.GetIndexes(), cNormAttention.getOutput(), cNormAttention.getGradient(), cInpAndHidden.getOutput(), cInpAndHidden.getGradient(), cAX.getGradient(), units, sparse, units, 2 * window)) return false;
Затем запускаем обратный проход через сверточный слой формирования логитов гейтов. В результате получим градиент по cNormAXplusX — то есть, по нормированному агрегированному входу.
Дальше идёт ряд итераций распределения градиентов ошибки между конкатенированным тензором исходных данных нормированными коэффициентами внимания. Вначале разворачиваем градиент через диагональную нормировку. А затем раскручиваем SpMM и распределяем градиенты на нормированные веса внимания и конкатенированные признаки.
Важно отметить, что после выполнения SparseMatMulGrad нам необходимо суммировать градиент ошибки конкатенированного тензора признаков от 2 информационных потоков.
if(!SumAndNormilize(cAX.getGradient(), cInpAndHidden.getGradient(), cInpAndHidden.getGradient(), 2 * window, false, 0, 0, 0, 1)) return false;
Далее нам необходимо собрать градиенты ошибок на уровне исходных данных. Здесь надо вспомнить, что исходные данные мы использовали в 2 информационных потоках: первичная конкатенация признаков и конкатенация тензора для кандидатов. Со второго информационного потока мы уже передали градиент ошибки. Теперь нам необходимо выделить значения по второму информационному потоку и суммировать с ранее полученными значениями.
if(!DeConcat(cAXplusX.getGradient(), cAXplusX.getPrevOutput(), cInpAndHidden.getGradient(), window, window, units)) return false; if(!SumAndNormilize(SourceData.getGradient(), cAXplusX.getGradient(), SourceData.getGradient(), window, false, 0, 0, 0, 1)) return false; if(SourceData.Activation() != None) if(!DeActivation(SourceData.getOutput(), SourceData.getGradient(), SourceData.getGradient(), SourceData.Activation())) return false;
И не забываем проверить наличие функции активации тензора исходных данных. При необходимости корректируем полученные значения на её производную.
Последний значимый шаг — передача градиента ошибки с нормированной матрицы внимание cNormAttention на её первоначальное состояния SparseAttent. В прямом проходе мы делали нормировку и теперь проводим градиенты через этот диагональный шаг обратно в форму, которую ожидает модуль SparseAttent.
if(!DiagMatMul(cInvDiag.getOutput(), cNormAttention.getGradient(), SparseAttent.getGradient(), units, sparse, 1, None)) return false; //--- return true; }
В конце метод возвращает true, что означает: все градиенты правильно прошли путь назад и аккуратно сложены по соответствующим входам и внутренним параметрам.
На этом мы завершаем рассмотрение алгоритмов построения методов класса CNeuronFastGConv. Полный код данного объекта и всех его методов представлен во вложении.
Верхнеуровневый объект SAGDFN
После построения объекта одного рекуррентного блока, мы переходим к верхнему уровню — обёртке, которая связывает Энкодер и Декодер в единую систему. Класс CNeuronSAGDFN — это не просто контейнер: он организует поток данных, контролирует совместное использование одной и той же slim-матрицы смежности и обеспечивает согласованность временных и пространственных преобразований по всей модели.
class CNeuronSAGDFN : public CNeuronTransposeOCL { protected: CNeuronTransposeOCL cTranspose; CLayer cEmbedding; CNeuronSNSMHAttention cAttention; CLayer cGCRU; CLayer cProjection; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSAGDFN(void) {}; ~CNeuronSAGDFN(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_steps, uint variables, uint embedding_dim, uint emb_layers, uint sparse_dimension, uint heads, float sparse, uint gcru_layers, uint forecast, uint forec_layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronSAGDFN; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; virtual void SetActivationFunction(ENUM_ACTIVATION value) override {}; };
При организации работы класса CNeuronSAGDFN следует обратить внимание, что фреймворк SAGDFN построен на выявлении ключевых пространственных зависимостей, который анализирует корреляции унитарных последовательностей мультимодального временного ряда. Мы же, обычно, работаем с временными последовательностями. Поэтому в рамках объекта мы организовали транспонирование тензора исходных данных и обратное транспонирование тензора результатов.
Для выполнения первой операции объявляем соответствующий внутренний объект, а последнюю планируем выполнять средствами родительского класса CNeuronTransposeOCL. Это решение упрощает задачи подготовки данных перед подачей в модуль и облегчает интеграцию модели в существующий пайплайн.
Кроме того, мы предусмотрели возможность динамического изменения архитектуры объекта. Для этого было включено 3 динамических массива:
- cEmbedding — мини-модель формирования эмбедингов заданного размера из исходных данных;
- cGCRU — набор последовательных GCRU (Graph-Convolutional Recurrent Unit), который агрегирует последовательность OneStepFastGConv блоков;
- cProjection — проекционный блок, который в декодере преобразует скрытые представления в целевые прогнозы.
Такой подход делает возможным гибко наращивать глубину рекуррентного стека и экспериментировать с количеством шагов диффузии. CNeuronSAGDFN связывает транспозицию входов, embedding, общий Attention и стек GCRU в единый Энкодер-Декодер. Он управляет тем, как одна и та же slim-матрица смежности используется повторно по всему стеку, обеспечивает совместимость форматов данных и служит центральным оркестратором при обучении.
Непосредственное построение архитектуры нового объекта осуществляется в методе Init.
bool CNeuronSAGDFN::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_steps, uint variables, uint embedding_dim, uint emb_layers, uint sparse_dimension, uint heads, float sparse, uint gcru_layers, uint forecast, uint forec_layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(emb_layers <= 0 || gcru_layers <= 0 || forec_layers <= 0) return false;
В теле метода сначала осуществляется простая валидация полученных параметров — если число слоёв любого из блоков равняется нулю, инициализация немедленно прерывается. Это честный и полезный чек: лучше отказать на входных данных, чем продолжать собирать некорректную структуру.
Далее передается управление одноименному методу родительского класса, который задаёт общую форму нейрона и резервирует базовые ресурсы. Если этот шаг не прошёл — мы так же аккуратно возвращаем false, потому что всё последующее зависит от корректного базового контекста.
if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, variables, forecast, optimization_type, batch)) return false;
Далее инициализируем объект транспонирования тензора исходных данных в ожидаемый формат.
uint index = 0; if(!cTranspose.Init(0, index, OpenCL, time_steps, variables, optimization, iBatch)) return false;
Затем начинаем собирать мини-модель эмбеддинга. Очищаем контейнер и привязываем OpenCL-контекст. Первый свёрточный блок изменяет размерность данных до заданного уровня. Мы добавляем его в контейнер cEmbedding и назначаем ему SoftPlus в качестве функции активации.
//--- Embedding cEmbedding.Clear(); cEmbedding.SetOpenCL(OpenCL); index++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, time_steps, time_steps, embedding_dim, variables, 1, optimization, iBatch) || !cEmbedding.Add(conv)) { DeleteObj(conv); return false; } conv.SetActivationFunction(SoftPlus); for(uint i = 1; i < emb_layers; i++) { index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, embedding_dim, embedding_dim, embedding_dim, variables, 1, optimization, iBatch) || !cEmbedding.Add(conv)) { DeleteObj(conv); return false; } conv.SetActivationFunction(SoftPlus); }
Далее, в цикле по emb_layers, мы добавляем дополнительные сверточные слои с активацией SoftPlus. Это даёт вам стек глубокого эмбеддинга с одинаковой шириной каналов.
После свёрток добавляем BatchNorm — отдельный объект, который нормализует выход последнего сверточного слоя.
CNeuronBatchNormOCL *norm = new CNeuronBatchNormOCL(); index++; if(!norm || !norm.Init(0, index, OpenCL, conv.Neurons(), iBatch, optimization) || !cEmbedding.Add(norm)) { DeleteObj(norm); return false; } norm.SetActivationFunction(None);
Дальше готовим GCRU-блоки. Очищаем контейнер cGCRU, привязываем OpenCL и сразу инициализируем cAttention.
//--- GCRUs cGCRU.Clear(); cGCRU.SetOpenCL(OpenCL); index++; if(!cAttention.Init(0, index, OpenCL, variables, embedding_dim, heads, sparse_dimension, sparse, optimization, iBatch)) return false;
Обратите внимание: cAttention инициализируется до создания gcru-объектов — это намеренно и правильно, потому что все GCRU будут читать одну и ту же slim-матрицу смежности. Если инициализация attention терпит неудачу, мы останавливаемся и сигнализируем об этом.
Затем в цикле создаём требуемое число CNeuronFastGConv. Если какой-то gcru не создаётся, мы его удаляем и возвращаем false. Таким образом формируется стек рекуррентных графовых блоков, все они будут совместно оперировать матрицей, созданной cAttention.
CNeuronFastGConv *gcru = NULL; for(uint i = 0; i < gcru_layers; i++) { index++; gcru = new CNeuronFastGConv(); if(!gcru || !gcru.Init(0, index, OpenCL, variables, embedding_dim, sparse_dimension, optimization, iBatch) || !cGCRU.Add(gcru)) { DeleteObj(gcru); return false; } }
После этого строится проекционный блок cProjection. Первый сверточный слой преобразует данные из размерности эмбеддинга в пространство прогноза forecast на каждую переменную.
//--- Forecast cProjection.Clear(); cProjection.SetOpenCL(OpenCL); index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, embedding_dim, embedding_dim, forecast, variables, 1, optimization, iBatch) || !cProjection.Add(conv)) { DeleteObj(conv); return false; } conv.SetActivationFunction(SoftPlus); for(uint i = 1; i < forec_layers; i++) { index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, forecast, forecast, forecast, variables, 1, optimization, iBatch) || !cProjection.Add(conv)) { DeleteObj(conv); return false; } conv.SetActivationFunction(SoftPlus); } norm = new CNeuronBatchNormOCL(); index++; if(!norm || !norm.Init(0, index, OpenCL, conv.Neurons(), iBatch, optimization) || !cProjection.Add(norm)) { DeleteObj(norm); return false; } norm.SetActivationFunction(None); //--- return true; }
Затем в цикле добавляем дополнительные сверточные слои. В конце мини-модели добавляем BatchNorm без внешней активации, как это делали в стеке эмбеддингов. Если все добавления прошли успешно, Init возвращает true, и архитектура собрана.
Плавно переходя от устройства слоёв к их исполнению, давайте пройдёмся по методу feedForward и посмотрим, что именно происходит в рантайме — какие буферы двигаются, какие проверки спасают от падений и где подстерегают тонкие места.
bool CNeuronSAGDFN::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTranspose.FeedForward(NeuronOCL)) return false;
Метод стартует с транспонирования исходных данных. Это тот самый момент, когда мы переходим от представления мультимодального временного ряда в набор унитарных последовательностей. Если операция не прошла, дальнейший конвейер бессмысленен — мы аккуратно выходим.
После этого создаем локальные переменные указателей на внутренние объекты. Простая, но ключевая операция, которая позволяет повторно использовать один и тот же блок кода с различными объектами.
CNeuronBaseOCL *inputs = cTranspose.AsObject();
CNeuronBaseOCL *current = NULL;
Вначале выполняется эмбеддинг. Мы итерируем по всем компонентам контейнера cEmbedding в цикле. На каждой итерации получаем следующий слой в переменную current и тут же защищённо вызываем его метод прямого прохода. Это означает, что каждое звено эмбеддинга последовательно преобразует исходные данные и отдаёт результат следующему.
//--- Embedding for(int i = 0; i < cEmbedding.Total(); i++) { current = cEmbedding[i]; if(!current || !current.FeedForward(inputs)) return false; inputs = current; }
После успешного выполнения, изменяем указатель в переменной inputs — то есть перекладываем роль исходных данных на только что полученный результат. И переходим к следующей итерации цикла.
В итоге после выполнения всех итераций цикла, указатель в переменной inputs ссылается на последний слой эмбеддинга — готовое плотное представление анализируемого временного окна.
Следующий этап — GCRU-стек. Сначала мы формируем slim-матрицу As (индексы и веса) на основе текущих представлений. Если attention не сработал, лучше остановиться и не пробовать дальше.
//--- GCRUs if(!cAttention.FeedForward(inputs)) return false; CNeuronFastGConv *gcru = NULL; for(int i = 0; i < cGCRU.Total(); i++) { gcru = cGCRU[i]; if(!gcru || !gcru.FeedForward(inputs, cAttention.AsObject())) return false; inputs = gcru; }
Затем в цикле по контейнеру cGCRU мы по очереди берём каждый элемент и запускаем его метод прямого прохода.
Обратите внимание: в данном случае передаётся два аргумента — текущий тензор и ссылка на объект attention, из которого GCRU возьмёт индексы и веса As. После каждого успешного шага мы снова меняем указатель в локальной переменной исходных данных и переходим к следующей итерации.
В результате стек GCRU работает последовательно: каждый блок читает одну и ту же slim-матрицу, но применяет её к своему состоянию и возвращает обновлённое скрытое представление.
Когда стек рекуррентных блоков отработал, мы переходим к проекционному блоку прогноза. Цикл по контейнеру cProjection повторяет ту же логику: берем следующий проекционный слой и вызываем метод прямого прохода с последующим изменением указателя на объект исходных данных.
//--- Forecast for(int i = 0; i < cProjection.Total(); i++) { current = cProjection[i]; if(!current || !current.FeedForward(inputs)) return false; inputs = current; } //--- result return CNeuronTransposeOCL::feedforward(inputs); }
Концептуально, это преобразование скрытого представления в финальную форму прогноза для каждой переменной.
Наконец, мы возвращаем данные в исходный формат средствами родительского класса. Это обратная транспозиция: теперь прогнозы возвращаются в формат, ожидаемый остальной системой. Если последний шаг успешен, метод вернёт true, и вся цепочка прямого прохода завершится корректно.
Метод feedForward реализован линейно и прозрачно: данные проходят через транспозицию, затем через стек эмбеддинга, получают общую slim-матрицу внимания, последовательно обрабатываются GCRU-блоками, проецируются в прогноз и возвращаются в исходный формат. Такой поток легко отлаживать и расширять — стоит лишь следить за аккуратностью указателей и эффективностью промежуточных преобразований.
Аналогичным образом построены и методы обратного прохода. Поэтому предлагаю не останавливаться на их детальном рассмотрении. Полный код класса CNeuronSAGDFN и всех его методов представлен во вложении и доступен для самостоятельного изучения.
Тестирование
Обучение модели напоминает хорошо спланированную экспедицию: прежде чем отправиться в открытое море реального рынка, мы основательно потренировались в тихой гавани истории. Этот первый, офлайн-этап, был выстроен на данных валютной пары EURUSD с таймфреймом H1 за весь 2024 год — периода, богатого на контрасты. Здесь нашлись и спокойные, почти зеркальные воды боковиков, и бурные штормы резких трендовых движений, и неожиданные порывы новостной волатильности. Такое многообразие рыночных сценариев позволило модели выработать устойчивую навигацию, научиться распознавать как привычные, так и редкие картины движения цены, не теряя ориентира даже в сложных условиях.
Когда эта подготовка была завершена, пришло время выйти из учебного дока и испытать корабль на течениях настоящего рынка. Второй этап — онлайн-настройка — проводился уже в боевых условиях тестера стратегий MetaTrader 5. Здесь данные поступали последовательно, свеча за свечой, а модель училась не только анализировать потоковую информацию, но и сохранять устойчивость в водоворотах шума, на зыбких отмелях низкой ликвидности и во время неожиданных новостных шквалов. Этот этап сыграл роль ювелирной подстройки: он не ломал уже выстроенный каркас, но помогал отшлифовать его под реальность, повышая адаптивность и снижая риск переобучения.
Финальная проверка стала настоящим крещением огнём. Мы взяли данные Января 2025 года — абсолютно новые, не затронутые предыдущими экспериментами, и без единого изменения загрузили все ранее выработанные параметры. Это был принципиальный момент: никакой подгонки, никаких дополнительных коррекций — только чистый тест, отражающий реальную способность модели к обобщению.
Результаты тестирования приведены ниже.
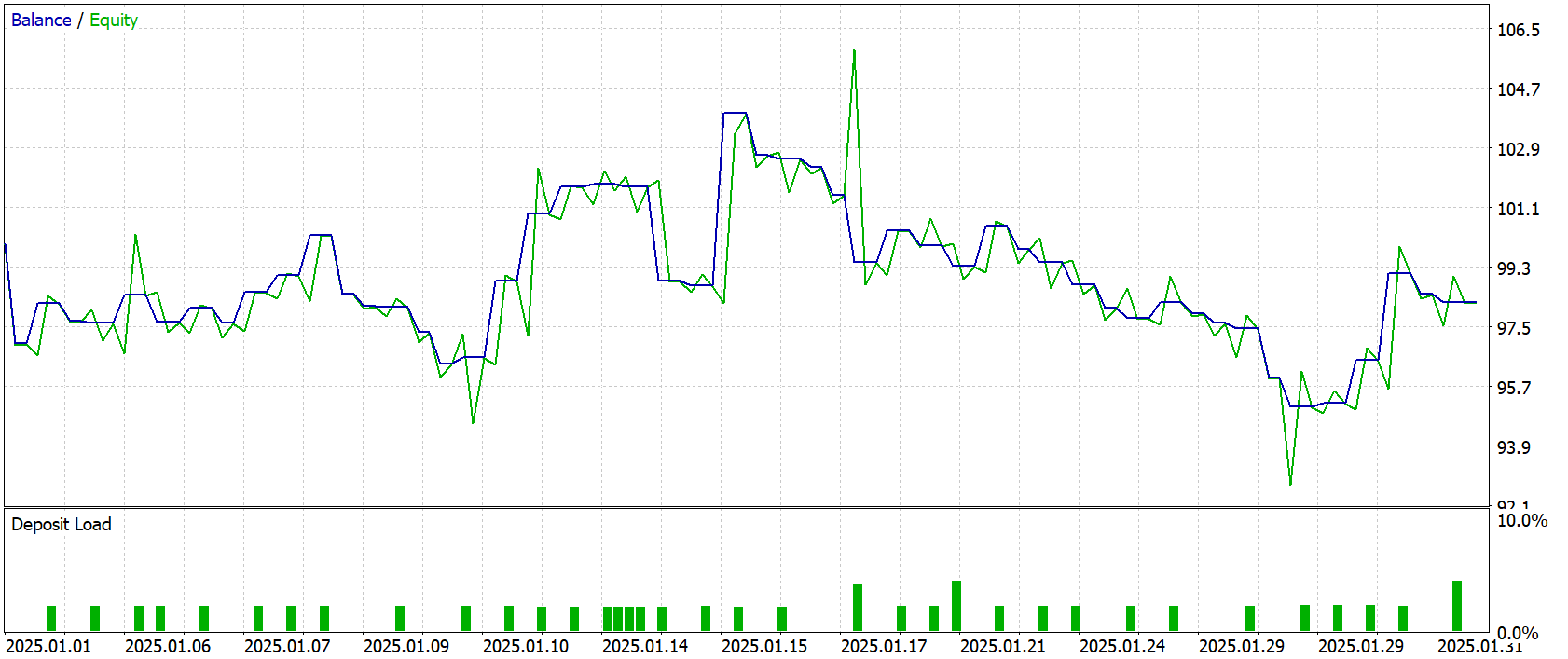
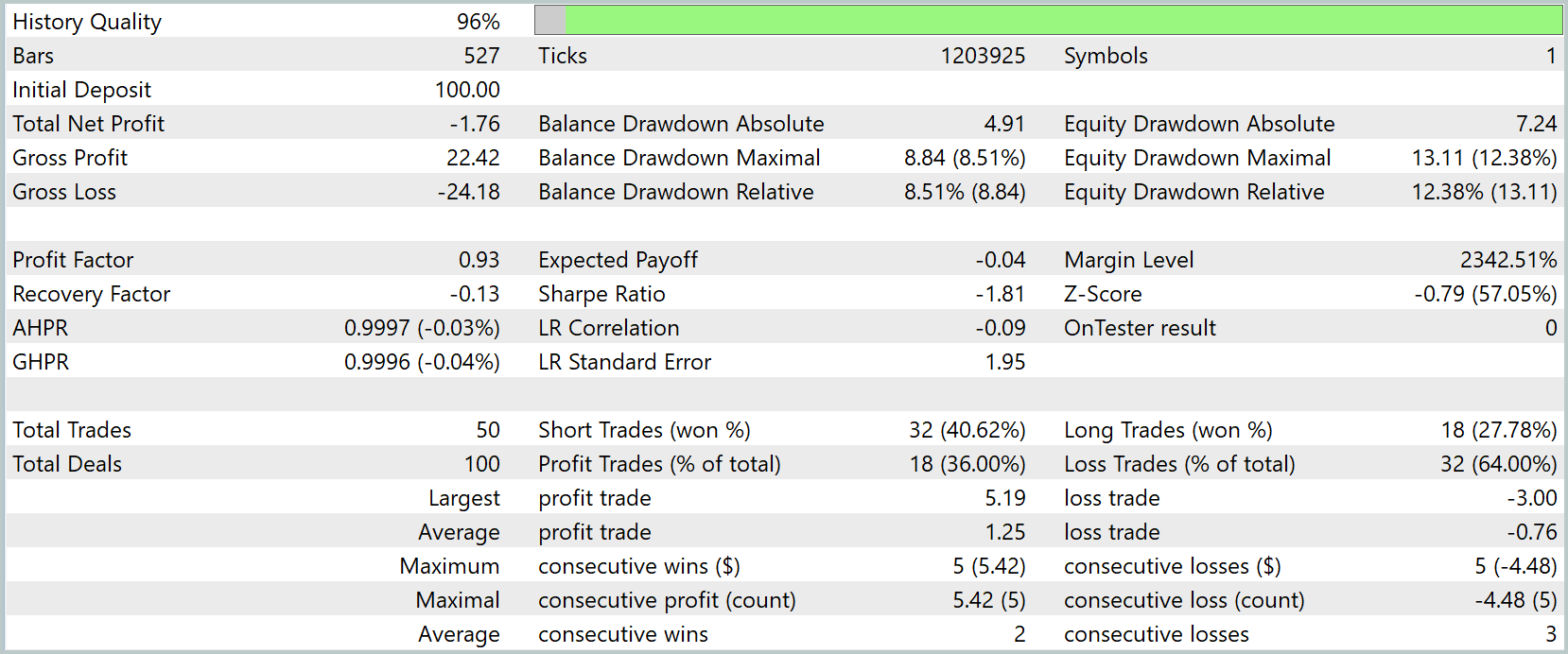
Результаты тестирования продемонстрировали, что модель повела себя сдержанно и достаточно предсказуемо. Хотя итоговая доходность оказалась отрицательной — -1.76USD от стартового депозита 100.0USD. Суммарная прибыль составила 22.42USD, но убытки перекрыли её, достигнув 24.18USD. Это отразилось и на ключевых метриках — фактор прибыли зафиксировался на уровне 0.93, что указывает на незначительное преобладание убыточных сделок. Коэффициент восстановления также ушёл в отрицательную зону, составив -0.13.
По распределению сделок видно, что модель открыла 50 ордеров, из которых 32 пришлись на короткие позиции с результативностью около 40%, а длинных сделок было всего 18, и их успешность составила чуть менее 28%. Прибыльных операций оказалось 18, то есть 36% от общего числа, тогда как убыток зафиксирован по 32 сделкам. Максимальная серия прибыли была относительно скромной — пять последовательных сделок, давших прирост около 5.42USD, тогда как серия убытков также достигала пяти сделок с просадкой -4.48USD.
График баланса и эквити показывает, что стратегия вела себя волнообразно, с периодами умеренного роста и последующими снижениями, без резких обвалов, но и без устойчивого восходящего тренда. После стартовой адаптации наблюдался краткосрочный подъём, который, однако, не был закреплён, и баланс постепенно сползал к отрицательной области, колеблясь вокруг стартовой отметки до конца тестового периода. Это говорит о том, что алгоритм пока не обрел устойчивого преимущества на рассматриваемом временном интервале, но и не продемонстрировал катастрофических сбоев — просадка оставалась в пределах 8.5% по балансу и около 12% по эквити.
В целом, результаты тестирования можно охарактеризовать как промежуточные и показатель того, что модель требует дальнейшей настройки и, возможно, расширения обучающей выборки для повышения обобщающей способности. Она не склонна к агрессивным просадкам, но пока не демонстрирует стабильной прибыли, что делает её поведение скорее консервативным и осторожным, чем рискованным.
Заключение
В завершение проделанной работы можно констатировать: проведённое тестирование позволило объективно оценить текущее состояние разработанного подхода и выявить его сильные и слабые стороны. Модель продемонстрировала устойчивость к резким рыночным колебаниям и умеренный уровень просадок, сохранив контроль над рисками даже в неблагоприятных сценариях. Однако итоговая доходность пока остаётся отрицательной, а соотношение прибыльных и убыточных сделок указывает на необходимость дополнительной оптимизации параметров и, вероятно, расширения объёма обучающих данных.
Эти результаты не являются поражением — напротив, они очерчивают границы текущей реализации и задают направления дальнейшего развития. Следующие шаги должны быть направлены на доработку механизма принятия решений, усиление фильтрации шумов и повышение точности прогнозирования в условиях изменчивого рынка. Таким образом, представленный фреймворк уже сегодня демонстрирует рабочую устойчивую основу, но его потенциал раскрывается лишь частично, оставляя простор для последующих улучшений и практической адаптации под реальные торговые задачи.
Ссылки
- SAGDFN: A Scalable Adaptive Graph Diffusion Forecasting Network for Multivariate Time Series Forecasting
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 2 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 3 | Test.mq5 | Советник | Советник для тестирования модели |
| 4 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 5 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 6 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Передовые методы управления и оптимизации памяти в MQL5
Передовые методы управления и оптимизации памяти в MQL5
 Переосмысливаем классические стратегии (Часть 13): Минимизация задержки при пересечении скользящих средних
Переосмысливаем классические стратегии (Часть 13): Минимизация задержки при пересечении скользящих средних
 От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (II)
От новичка до эксперта: Создание анимированного советника для новостей в MQL5 (II)
 Разработка инструментария для анализа движения цен (Часть 6): Возврат к среднему значению
Разработка инструментария для анализа движения цен (Часть 6): Возврат к среднему значению
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования