神经网络变得轻松（第二十八部分）：政策梯度算法
576
0
内容
概述
我们继续研究不同的强化学习方法。 在上一篇文章中，我们领略了深度 Q-学习方法。 此方法运用神经网络近似于动作功用函数。 结果就是，我们得到了一个工具，可预测在特定系统状态下执行特定动作时的预期奖励。 之后，代理者根据政策和预期奖励的金额执行动过。 我们没有明确讨论政策的应用，但假设选择了具有最高预期奖励的行动。 这遵循贝尔曼（Bellman）公式和强化学习的总体目标，即分析场次的最大化奖励。
另请注意，在研究强化学习方法时，我们从未提到模型过度拟合。 事实上，如果您看一下强化学习模型，那么代理者的目标是尽可能最好地学习环境。 代理者对环境了解得越透彻，其性能就越好。
但是，当我们处理不断变化的环境（即市场）时，有时您会意识到其变化是无限的。 市场上没有两个雷同的状态。 即使存在类似的状态，下一步中我们也有可能遇到完全相反的状态。
Q-函数的近似仅提供预期的平均奖励，而未考虑数值的扩散和正奖励的概率。 使用贪婪策略，并选择最大奖励，总能给出明确的动作选择。 一方面，这使代理者工作更容易。 但只当我们的代理者不与环境发生某种对立时，这种策略才会产生预期的结果。 在这种情况下，其动作对于环境来说是可预测的，且它能展开步骤来对抗代理的操作，并更改奖励政策。 不过，代理者将继续使用以前近似的 Q-函数，而该函数已不再对应于变化的环境。
解决这类问题的方法可以使用无近似的环境奖励政策，但它们会发展自己的动作策略。 方法之一是政策梯度，我们将在本文中讨论。
1. 政策梯度应用特点
开始学习强化学习方法之时，我们曾提到代理者与环境交互，并根据其策略执行动作。 结果会从一种状态过渡到另一种状态。 对于每次转换，代理者都会从环境中获得一定的奖励。 依据奖励值，代理者可以评估所采取的动作的功用。 政策梯度方法意味着代理者行为策略的开发。
当然，我们并没有明确地设置代理者的策略，这在 DQN 中可以看出。 我们只假设政策 P 存在某个数学函数，该函数评估环境的当前状态，并返回代理者采取的最佳动作。 这种方法剔除了近似 Q-函数的所有困难，以及需要指定显式代理者行为政策，例如选择具有最大期望奖励的动作（贪婪策略）。
当然，一切都有其价值。 取代近似 Q 函数，我们近似代理者政策的 P 函数。 本文将重点关注随机政策梯度法。 它推测我们的政策函数，当评估环境的当前状态时，返执行相应动作时获得正奖励的概率分布。
同时，我们假设代理者的动过分布是均匀的。 为了选择特定动作，代理者只需从具有给定概率的正态分布中采样一个数值。 当然，也可能使用贪婪策略，并选择最高概率的动作。 但正是采样增加了代理者行为的可变性。 概率越大，则提升选择此特定操作的频率。
请记住，早前，在模型的强化学习中，我们引入了一个负责探索和开发之间平衡的超参数。 现在，当使用随机政策梯度方法时，平衡调节则由模型在学习过程中基于代理者动作采样的概率。 在模型训练开始时，所有动作的概率近乎相等。 这样能够最全面地探索环境。 在研究环境的过程中，导致盈利能力最大化的动作概率增加。 选择其它动作的概率降低。 因此，探索和开发之间的平衡发生了变化，偏向选择最有利可图的动作，这样就可以构建拥有最大盈利能力的策略。
为了近似代理者政策 P-函数，我们将运用神经网络。 由于我们需要根据当前环境状态的初始数据判定代理者的最佳动作，此任务可考虑当作分类问题。 每个动作都是一个单独的初始状态类。 如早前所述，神经层输出应提供一个概率表示，即环境状态所属的特定状态。
概率表示对结果值施加了一些限制。 结果必须在 0% 到 100% 的范围内进行常规化。 所有概率的总和必须等于 100%。 在机器学习中，通常使用分数，替代百分比。 因此，数值的范围应为 0 到 1，而所有数值的总和应为 1。 此结果可以通过调用 SoftMax 函数获得，该函数具有以下数学公式。
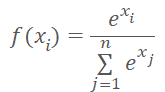
我们之前在研究数据聚类方法时已见过这个函数。 但在研究无监督学习方法时，我们查看了源数据的相似性来判别类。 这一次，我们将根据收到的奖励将环境状态派分到动作（类）之中。 SoftMax 函数完全满足这些需求。 它能够将神经网络操作结果完全转移到概率域中，并可通过数值区分。 这对于模型训练非常重要。
2. 政策模型学习原则
现在我们来谈谈训练政策函数近似模型的原则。 在每个新状态上训练 DQN 模型时，环境会返回奖励。 我们所训练的模型以最小误差预测预期奖励。 这与以前采用的监督学习方法没有太大区别。
当在每个新状态上近似代理者政策 P-函数时，我们还会收到来自环境的奖励。 但我们打算预测的是最好的行动，而不是奖励。 奖励符号只能显示当前动作对结果的影响。 我们将训练模型来增加选择具有正奖励动过的概率，并降低选择具有负奖励动作的概率。
但是我们训练模型来预测概率。 如上所述，预测概率的值限制在 0 到 1 的范围内。 但这与收到的奖励无法相提并论，后者即可是正值，也可是负值。 我们在此采用以下逻辑。 由于我们需要选择具有最大化正奖励的动作的概率，因此此类动作的目标值为 1。 模型误差将定义为动作预测概率与 1 的偏差。 使用偏差/方差允许利用已经构建的梯度下降方法来训练政策函数近似模型，因为最小化距 1 的方差，我们可将最大化选择具有正奖励动作的概率。
请注意模型的损失函数选择。 在此，我们也可以回到监督学习方法，并记住交叉熵函数用于分类问题。
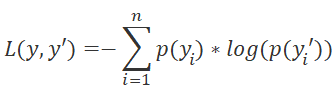
其中 p(y) 是真实的分布值，且 p(y') 是模型的预测值。
对数的使用对于预测连续事件也非常重要。 我们从概率论中知道，两个连续事件发生的概率等于事件概率的乘积。 以下对数是正确的
这允许从概率的乘积转移到它们的对数之和。 这将令模型训练更加稳定。
类似于 DQN 训练，为了得到奖励，代理者会传递具有固定参数的场次。 将状态、动作和奖励保存到缓冲区。 然后采用累积的数据执行反向传播验算。
请注意，由于我们没有动作功用函数，因此我们将其替换为场次验算期间所获值的总和。 对于每个状态，Q-函数的值是后续直至场次结束的奖励总和。
重复模型训练，直至达到所需的误差级别，或最大场景训练次数。
3. 实现模型训练
我们已讨论了理论层面，现在我们继续利用 MQL5 实现它。 我们先从 SoftMax 函数开始。 由于其操作特殊，我们之前并未将其作为激活函数实现。 因此，为了避免针对以前创建的对象进行基础修改，我们将它实现为模型的单独层。
3.1 实现 SoftMax
那么，创建一个新的类 CNeuronSoftMaxOCL，该类派生自神经元的基类 CNeuronBaseOCL。
class CNeuronSoftMaxOCL : public CNeuronBaseOCL { protected: virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return true; } public: CNeuronSoftMaxOCL(void) {}; ~CNeuronSoftMaxOCL(void) {}; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL); virtual bool calcOutputGradients(CArrayFloat *Target, float error) override; //--- virtual int Type(void) override const { return defNeuronSoftMaxOCL; } };
新类不需要创建单独的缓冲区。 甚至，它不会用到父类的所有缓冲区，这个我们将在稍后讨论。 这就是为什么构造函数和析构函数是空的。 出于同样的原因，没有必要重写我们的类初始化方法。 实际上，我们只需要覆盖 feedForward 前馈验算和 calcOutputGradients 误差梯度方法。
此外，由于我们使用了一个新的损失函数，因此有必要覆盖模型误差和梯度计算方法 calcOutputGradients。
当然，我们将覆盖类标识方法 Type。
我们从实现前馈验算过程开始。 再次，所有计算操作都将利用 OpenCL 在多线程模式下执行。 那么，我们在 OpenCL 中创建新的内核 SoftMax_FeedForward。 在内核参数中，我们将传递指向初始数据和结果缓冲区的指针，以及缓冲区大小。 函数计算不需要任何其它参数。
在内核主体中，定义线程标识符，该标识符用作指向初始数据和结果数组的相应元素的指针。 由于这是激活函数的实现，因此初始数据缓冲区和结果缓冲区的大小相等。 因此，指向这两个缓冲区的元素指针也是相同的。
__kernel void SoftMax_FeedForward(__global float *inputs, __global float *outputs, const ulong total) { uint i = (uint)get_global_id(0); uint l = (uint)get_local_id(0); uint ls = min((uint)get_local_size(0), (uint)256); //--- __local float temp[256];
请注意，为了计算 SoftMax 函数，必须判定输入数据缓冲区所有元素的指数值之和。 在每个线程上重复计算此数值是不明智的。 甚而，最好在多个线程之间派发参数计算过程。 不过，在此我们遇到了同步多个线程的工作，并在它们之间交换数据的问题。 OpenCL 技术不允许从一个线程发送数据到另一个线程。 但它允许在单独的工作群内的局部内存中创建公共变量和数组。 为了同步工作群内线程的工作，有一个专门的函数 barrier(CLK_LOCAL_MEM_FENCE)。 这就是我们将要用到的。
因此，除了在全局任务空间中定义线程 ID 外，我们还将在群中定义线程 ID。 此外，我们将在局部内存中声明一个数组。 在计算指数值的总和时，它将用于在工作群线程之间交换数据。
这里的困难部分是 OpenCL 不允许在局部内存中使用动态数组。 因而，应在内核创建阶段确定数组大小。 此大小限制了计算指数值求和的线程数量。
计算指数值求和的进程由 2 个连续循环组成。 在第一个循环的主体中，参与求和进程的每个线程在遍历整个初始值向量，步长等于求和线程的数量，并将收集其指数值总和中的部分。 因此，我们将在所有线程之间均匀分配整个求和进程。 它们中的每一个都将将其值存储在局部数组的相应元素当中。
uint count = 0; if(l < 256) do { uint shift = count * ls + l; temp[l] = (count > 0 ? temp[l] : 0) + (count * ls + l < total ? exp(inputs[shift]) : 0); count++; } while((count * ls + l) < total); barrier(CLK_LOCAL_MEM_FENCE);
在此阶段，我们在循环迭代完毕成后同步线程。
接下来，我们需要将局部数组的所有元素的总和收集到单个值中。 这将在第二个循环中实现。 在此，我们将局部数组的大小切分成两半，并将数值加入数据对。 与添加两个值相关的每个操作将由单独的线程执行。 之后，重复循环迭代：将元素数切分成两半，并将元素加入数据对。 重复循环迭代，直到我们在索引为 0 的数组元素中得到总和值。
count = ls; do { count = (count + 1) / 2; if(l < 256) temp[l] += (l < count && (l + count) < total ? temp[l + count] : 0); barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
如您所见，循环的每个新迭代只能在所有参与的线程完成其操作后启动。 因此，在循环的每次迭代后执行同步。
请注意，OpenCL 架构仅提供线程的完全同步。 因此，工作群中的所有元素都必须到达相关的“分界”操作符。 否则，程序将冻结。 因此，在组织程序时，需要非常小心线程的同步点。 当程序算法允许至少一个线程绕过同步点时，不建议在条件运算符的主体中实现它们。
一旦上述循环的迭代完成，我们得到原始数据所有指数值的总和，之后就可以完成数据归一化过程。 为此，我们将创建另一个循环，其中初始数据缓冲区将填充相应的数值。
float sum = temp[0]; if(sum != 0) { count = 0; while((count * ls + l) < total) { uint shift = count * ls + l; outputs[shift] = exp(inputs[shift]) / (sum + 1e-37f); count++; } } }
前馈内核的操作至此完毕。 接下来，我们继续创建反向传播内核。
我们将从创建反向传播内核开始，通过 softmax 函数派发梯度。 请注意，此函数的主要功能是将所有结果值的总和归一化规范化为 1。 因此，激活函数的输入处只要有一个值变化，就会导致重新计算结果向量的所有值。 与此类似，在传播误差梯度时，输入数据的每个元素必须从结果向量的每个元素接收其误差份额。 下面给出了每个初始数据元素对结果影响的数学公式。 这就是我们将在内核 SoftMax_HiddenGradient 中实现的内容。
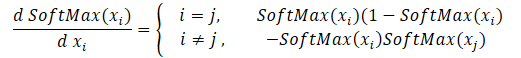
在参数中，内核接收指向 3 个数据缓冲区的指针：前馈验算后的结果、来自前一层、或损失函数的梯度。 此外，它接收前一层的梯度缓冲区，我们将在其中写入该内核的结果。
在内核主体中，定义线程标识符，以及正在运行的线程总数。 它们将指向一个数组元素来记录当前线程的结果和缓冲区大小。
接下来，我们需要准备两个私密变量。 将前馈结果向量的相应元素的值复制到它们其中之一。 第二个应声明为收集当前线程操作结果。 由于 OpenCL 设备的特定架构，我们需使用私密变量。 访问私密变量比在全局内存缓冲区中的类似操作要快得多。 因此，这种方式提高了内核的整体性能。
然后我们循环遍历所有结果元素，根据上述公式收集误差梯度。 完成循环操作后，将累积的梯度值传递给前一层梯度缓冲区的相应元素，然后关闭内核。
__kernel void SoftMax_HiddenGradient(__global float* outputs, __global float* output_gr, __global float* input_gr) { size_t i = get_global_id(0); size_t outputs_total = get_global_size(0); float output = outputs[i]; float result = 0; for(int j = 0; j < outputs_total; j++) result += outputs[j] * output_gr[j] * ((float)(i == j ? 1 : 0) - output); input_gr[i] = result; }
还有最后一个内核 — 判定损失函数 SoftMax_OutputGradient 误差梯度的内核。 在本文中，我们使用 LogLoss 作为损失函数。
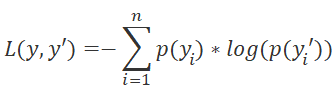
由于梯度分布在相应的动作元素上，因此也将逐个元素计算导数。 这允许跨线程拆分误差梯度。 从学校的数学课程中，我们知道对数的导数等于 1 与函数参数的比率。 因此，损失函数的导数如下。
现在，我们需要在 OpenCL 程序内核中实现上述数学公式。 它的代码非常简单，仅占用两行。
__kernel void SoftMax_OutputGradient(__global float* outputs, __global float* targets, __global float* output_gr) { size_t i = get_global_id(0); output_gr[i] = -targets[i] / (outputs[i] + 1e-37f); }
这样 OpenCL 程序端的操作就完成了。 现在，我们可以进入主程序操控。 我们需要添加用于处理新内核的常量，添加新内核的声明，并创建调用它们的方法。
#define def_k_SoftMax_FeedForward 36 #define def_k_softmaxff_inputs 0 #define def_k_softmaxff_outputs 1 #define def_k_softmaxff_total 2 //--- #define def_k_SoftMax_HiddenGradient 37 #define def_k_softmaxhg_outputs 0 #define def_k_softmaxhg_output_gr 1 #define def_k_softmaxhg_input_gr 2 //--- #define def_k_SoftMax_OutputGradient 38 #define def_k_softmaxog_outputs 0 #define def_k_softmaxog_targets 1 #define def_k_softmaxog_output_gr 2
内核调用方法的算法完全照搬以前所用的类似方法。 它们的完整代码可以在附件中找到。
缺失的 SoftMax 函数现在已经准备就绪，我们可以开始进入智能系统，在其中我们将实现并训练政策梯度模型。
3.2 构建一款 EA 来训练模型
为了训练代理者政策函数近似模型，我们将在 REINFORCE.mq5 文件中创建一个新的智能系统。 基本功能继承自我们在上一篇文章中创建的用于训练 DQN 模型的 Q-learning.mq5。 然而，与 DQN 模型不同的是，新的智能系统只会用到一个神经网络。 为了正确实现算法，我们需要创建三个堆栈：环境状态、采取的动作、和收到的奖励。
CNet StudyNet; CArrayObj States; vectorf vActions; vectorf vRewards;
根据算法的需求，EA 的外部参数略有变化。
input int SesionSize = 24 * 22; input int Iterations = 1000; input double DiscountFactor = 0.999;
EA 初始化方法几乎相同。 我们只添加了堆栈初始化，来累积执行的操作和获得的奖励。
if(!vActions.Resize(SesionSize) || !vRewards.Resize(SesionSize)) return INIT_FAILED;
训练过程在 Train 函数中实现。 我们更详尽地研究一下。
像往常一样，在函数开始时，我们根据给定的外部参数来判定训练样本范围。
void Train(void) { //--- MqlDateTime start_time; TimeCurrent(start_time); start_time.year -= StudyPeriod; if(start_time.year <= 0) start_time.year = 1900; datetime st_time = StructToTime(start_time);
判定训练周期后，加载训练样本。
int bars = CopyRates(Symb.Name(), TimeFrame, st_time, TimeCurrent(), Rates); if(!RSI.BufferResize(bars) || !CCI.BufferResize(bars) || !ATR.BufferResize(bars) || !MACD.BufferResize(bars)) { ExpertRemove(); return; } if(!ArraySetAsSeries(Rates, true)) { ExpertRemove(); return; } //--- RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); //--- int total = bars - (int)(HistoryBars + 2 * SesionSize);
上述操作与早期 EA 中所用没有区别。 接下来是模型训练循环系统。 该系统实现了模型训练的主要方式。
外部循环负责迭代模型训练场次。 在环路开始时，我们随机判定场次在已加载历史记录的常规池中的开始柱线。
CBufferFloat* State; for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int error_code; int shift = (int)(fmin(fabs(Math::MathRandomNormal(0,1,error_code)),1) * (total) + SesionSize); States.Clear();
然后实现一个循环，其中我们的代理者逐步完全贯穿场次。 在循环主体中，首先取所分析周期的历史数据填充当前系统状态的缓冲区。 在每次直接验算之前，在训练以前的模型时，都会执行类似的操作。
for(int batch = 0; batch < SesionSize; batch++) { int i = shift - batch; State = new CBufferFloat(); if(!State) { ExpertRemove(); return; } int r = i + (int)HistoryBars; if(r > bars) continue; for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = r - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State.Add((float)Rates[bar_t].close - open) || !State.Add((float)Rates[bar_t].high - open) || !State.Add((float)Rates[bar_t].low - open) || !State.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State.Add(sTime.hour) || !State.Add(sTime.day_of_week) || !State.Add(sTime.mon) || !State.Add(rsi) || !State.Add(cci) || !State.Add(atr) || !State.Add(macd) || !State.Add(sign)) break; }
接下来，实现模型前馈验算。
if(IsStopped()) { ExpertRemove(); return; } if(State.Total() < (int)HistoryBars * 12) continue; if(!StudyNet.feedForward(GetPointer(State), 12, true)) { ExpertRemove(); return; }
根据前馈验算的结果，我们得到动作的概率分布，并从正态分布中抽取下一个动作，同时考虑获得的概率分布。 采样由单独的函数 GetAction 执行；概率分布在其参数中传递。
StudyNet.getResults(TempData); int action = GetAction(TempData); if(action < 0) { ExpertRemove(); return; }
动作采样之后，根据下一根烛条的大小判定所选动作的奖励。 奖励政策是我们在上一篇文章中采用的政策。
double reward = Rates[i - 1].close - Rates[i - 1].open; switch(action) { case 0: if(reward < 0) reward *= -2; break; case 1: if(reward > 0) reward *= -2; else reward *= -1; break; default: reward = -fabs(reward); break; }
将整体采样保存到堆栈。 请注意，状态和动作都简单地只是添加到堆栈中。 但是考虑到折扣因子，奖励也会被保存。 因此，在设计步骤中，我们需要判定奖励如何打折。 有两种折扣选项。 我们可以为后期奖励提供更多价值来实现早期奖励的打折。 当代理者在贯穿场次中获得中间奖励时，通常会采用此方式。 但是代理者的主要任务是到达场次的末尾，在那里它将获得最大的奖励。
第二种方式正好相反：给予先期奖励更多的权重。 后续奖励则相对打折。 若我们瞄准的是最大和最快的奖励时，此选项是可以接受的。 我采用第二种方式，因为重要的是立即获得最大利润，而不会在成交后于市场逆转时等待亏损。
再等一下。 完成场次贯通后，我们必须计算每个状态的累积奖励，直到场次结束。 MQL5 向量运算仅允许计算直接累积和。 因此，我们简单地把所有奖励值以逆反的顺序存储到一个向量中。 循环结束后，使用向量运算计算累积和。
if(!States.Add(State)) { ExpertRemove(); return; } vActions[batch] = (float)action; vRewards[SessionSize - batch - 1] = (float)(reward * pow(DiscountFactor, (double)batch)); vProbs[SessionSize - batch - 1] = TempData.At(action); //--- }
保存数据后，继续循环的下一次迭代。 因此，我们收集整体场次的数据。
在循环的所有迭代之后，计算考虑了折扣的场次总奖励、从每个状态到场次结束的累积奖励向量，以及损失函数的值。
此外，保存当前模型，但前提是仅更新了最大奖励。
float cum_reward = vRewards.Sum(); vRewards = vRewards.CumSum(); vRewards = vRewards / fmax(vRewards.Max(), fabs(vRewards.Min())); float loss = (vRewards * MathLog(vProbs) * (-1)).Sum(); if(MaxProfit < cum_reward) { if(!StudyNet.Save(FileName + ".nnw", loss, 0, 0, Rates[shift - SessionSize].time, false)) return; MaxProfit = cum_reward; }
现在我们有了代理者顺场次路径的奖励值，我们可以为政策函数模型实现一个训练循环。 这将在另一个循环中实现。 在此循环中，我们从缓冲区中提取环境状态，并执行模型前馈验算。 这对于恢复环境的相应状态，保存模型的所有内部数值是必需的。
此后，为环境的当前状态准备参考值向量。 您还记得，我们选择具有正奖励行动的最大化概率，并最小化其它的概率。 因此，如果在动作执行后我们收到一个正值，则用零值填充参考概率向量。 并且仅针对已执行的动作，设置概率为 1。 如果返回负奖励，则用 1 填充参考概率向量。 在这种情况下，为已执行动作设置零值。
for(int batch = 0; batch < SessionSize; batch++) { State = States.At(batch); if(!StudyNet.feedForward(State)) { ExpertRemove(); return; } if((vRewards[SessionSize - batch - 1] >= 0 ? (!TempData.BufferInit(Actions, 0) || !TempData.Update((int)vActions[batch], 1)) : (!TempData.BufferInit(Actions, 1) || !TempData.Update((int)vActions[batch], 0)) )) { ExpertRemove(); return; } if(!StudyNet.backProp(TempData)) { ExpertRemove(); return; } }
接下来，运行反向传播验算，从而更新模型权重。 针对所有保存的环境状态重复迭代。
循环的所有迭代完成后，将消息打印到日志，并移到下一个场次。
PrintFormat("Iteration %d, Cummulative reward %.5f, loss %.5f", iter, cum_reward, loss); } Comment(""); //--- ExpertRemove(); }
不要忘记检查每一步的操作结果。 所有迭代成功完成后，退出函数，并生成终端关闭事件。 完整的 EA 代码可在附件中找到。
另请注意，为了近似模型的政策函数，我们采用的神经网络架构类似于上一篇文章中的 Q-函数训练。 甚至，我们使用上一篇文章中已训练模型，并添加 SoftMax 作为神经网络的最后一层，替换其中的决策模块，来常规化数据。
模型训练过程与训练任何其它模型完全相似。 本系列的每篇文章中都有很多示例。 如此，总结完结的工作，我决定偏离常用的文章形式。 取而代之，我们看看训练好的模型如何在策略测试器中运行。
4. 在策略测试器中测试训练好的模型
在上一篇文章中，我们训练了一个 DQN 模型。 在本文中，我们创建并训练了一个政策梯度模型。 我拟议创建测试用的智能系统，据其我们可以查看模型在策略测试器中的表现。 为此，我们创建两个 EA：Q-learning-test.mq5 和 REINFORCE-test.mq5。 顾名思义，其反映出每个 EA 测试的模型。
EA 具有相同的结构。 因此，我们来看看其中之一。 无论如何，两个 EA 的完整代码都可以在附件中找到。
新的 EA “REINFORCE-test.mq5” 是在上面讨论的 REINFORCE.mq5 EA 的基础上构建的。 但由于 EA 并不训练模型，因此 Train 函数已被删除。 基本功能已移至 OnTick 函数，其在每次新跳价事件时进行处理。
经过训练的模型根据已收盘烛条评估环境状态。 因此，在 OnTick 函数的主体中，应检查有新蜡烛开盘。 仅当出现新烛条时，才会执行函数的其余操作。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { if(lastBar >= iTime(Symb.Name(), TimeFrame, 0)) return;
当出现新烛条时，加载最新的历史数据，并填写系统状态描述缓冲区。
int bars = CopyRates(Symb.Name(), TimeFrame, 0, HistoryBars+1, Rates); if(!ArraySetAsSeries(Rates, true)) return; RSI.Refresh(); CCI.Refresh(); ATR.Refresh(); MACD.Refresh(); //--- State1.Clear(); for(int b = 0; b < (int)HistoryBars; b++) { int bar_t = (int)HistoryBars - b; float open = (float)Rates[bar_t].open; TimeToStruct(Rates[bar_t].time, sTime); float rsi = (float)RSI.Main(bar_t); float cci = (float)CCI.Main(bar_t); float atr = (float)ATR.Main(bar_t); float macd = (float)MACD.Main(bar_t); float sign = (float)MACD.Signal(bar_t); if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE) continue; //--- if(!State1.Add((float)Rates[bar_t].close - open) || !State1.Add((float)Rates[bar_t].high - open) || !State1.Add((float)Rates[bar_t].low - open) || !State1.Add((float)Rates[bar_t].tick_volume / 1000.0f) || !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) || !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign)) break; }
接着，检查数据是否正确填充，并实现模型前馈验算。
if(State1.Total() < (int)(HistoryBars * 12)) return; if(!StudyNet.feedForward(GetPointer(State1), 12, true)) return; StudyNet.getResults(TempData); if(!TempData) return;
作为前馈验算的结果，我们得到了可能动作的概率分布，从中我们对抽取一个随机动作。
lastBar = Rates[0].time; int action = GetAction(TempData); delete TempData;
接下来，应执行所选动作。 但在继续开立新成交之前，要检查是否已有持仓。 为此，定义 2 个标志：买入和卖出。 声明变量时，将其设置为 false。
之后，实现循环遍历所有数值。 如果找到所分析品种的持仓，则更改相应标志的值。
bool Buy = false; bool Sell = false; for(int i = 0; i < PositionsTotal(); i++) { if(PositionGetSymbol(i) != Symb.Name()) continue; switch((ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE)) { case POSITION_TYPE_BUY: Buy = true; break; case POSITION_TYPE_SELL: Sell = true; break; } }
接下来是交易模块。 在此，我们使用 'switch' 语句根据正在采取的动作将模块算法导入分支。 如果是开新仓，则检查开仓标志。 如果在相关方向上存在持仓，简单地继续持有，并等待新烛条的开盘。
如果在做出决定时，发现一笔相反开仓，则先平仓，然后再开一笔新仓位。
switch(action) { case 0: if(!Buy) { if((Sell && !Trade.PositionClose(Symb.Name())) || !Trade.Buy(Symb.LotsMin(), Symb.Name())) { lastBar = 0; return; } } break; case 1: if(!Sell) { if((Buy && !Trade.PositionClose(Symb.Name())) || !Trade.Sell(Symb.LotsMin(), Symb.Name())) { lastBar = 0; return; } } break; case 2: if(Buy || Sell) if(!Trade.PositionClose(Symb.Name())) { lastBar = 0; return; } break; } //--- }
如果代理者需要全部平仓，则调用当前交易品种的平仓函数。 仅当至少有一笔持仓时，才会调用该函数。
不要忘记控制每一步的结果。
完整的 EA 代码可在附件中找到。
第一个已测试模型是 DQN。 它展现出意想不到的惊喜。 该模型产生了盈利。 但它仅执行了一个交易操作，持仓会贯穿整个测试过程。 已执行成交的品种图表如下所示。
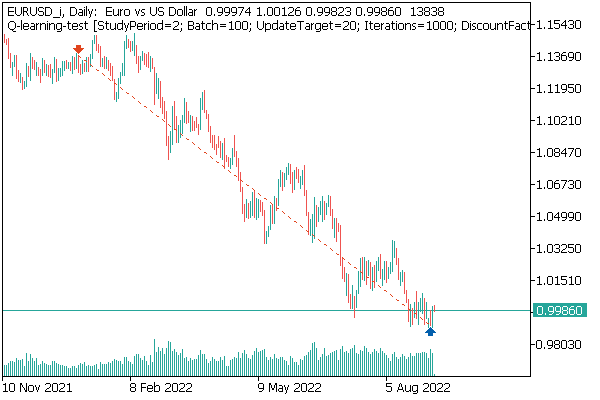
评估品种图表上的成交，您可以看到该模型清楚地识别出全局趋势，并顺着其方向开仓成交。 这笔成交是可盈利的，但问题是该模型是否能够及时了结这样的一笔成交？ 事实上，我们基于过去 2 年的历史数据训练了模型。 在过去的 2 年中，所分析金融产品的行情一直由看跌趋势所主导。 这就是为什么我们想知道该模型是否可以及时了结成交。
若采用贪婪策略，政策梯度模型给出类似的结果。 请记住，当我们开始研究强化学习方法时，我反复强调正确选择奖励政策的重要性。 如此，我决定试验奖励政策。 特别是，为了避免亏损持仓持有的时间过长，我决定增加对无盈利持仓的处罚。 为此，我还采用新的奖励政策训练了政策梯度模型。 针对模型超参数进行的一些试验，我设法达成了 60% 的盈利操作。 测试图如下所示。
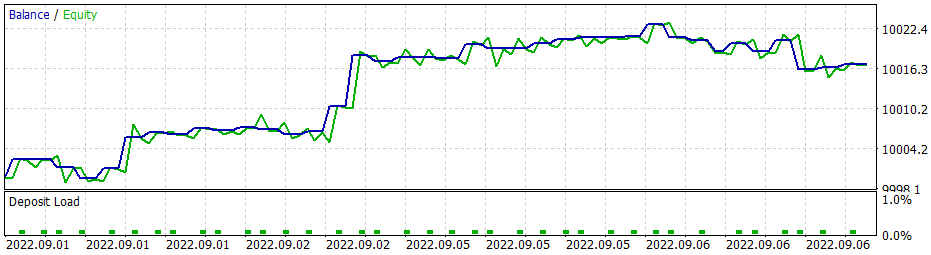
平均持仓时间为 1 小时 40 分钟。
结束语
在本文中，我们讨论了另一种强化学习方法的算法。 我们遵照政策梯度方法创建并训练了一个模型。
与本系列中的其它文章不同，在本文中，我们在策略测试器中训练和测试了模型。 根据测试结果，我们可以得出结论，模型生成的信号，据其执行可实现盈利交易操作。 与此同时，我要再次强调，选择正确的奖励政策和损失函数，从而达到预期的结果非常重要。
参考文献列表
本文中用到的程序
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | REINFORCE.mq5 | EA | 训练模型的智能系统 |
| 2 | REINFORCE-test.mq5 | EA | 在策略测试器中测试模型的智能系统 |
| 1 | Q-learning-test.mq5 | EA | 在策略测试器中测试 DQN 模型的智能系统 |
| 2 | NeuroNet.mqh | 类库 | 创建神经网络模型的类库 |
| 3 | NeuroNet.cl | 代码库 | 创建神经网络模型的 OpenCL 程序代码库 |
…
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11392
学习如何基于 VIDYA 设计交易系统
DoEasy. 控件 (第 17 部分): 裁剪对象不可见部分、辅助箭头按钮 WinForms 对象
神经网络变得轻松（第二十七部分）：深度 Q-学习（DQN）
