Тенденции и традиции: Использование функций Радемахера в трейдинге

Введение

Современный трейдинг требует высокой скорости, точности и способности к адаптации. Из-за этого значительно возрастает потребность в усовершенствованных методах анализа данных. Но традиционные подходы часто оказываются недостаточно эффективными для извлечения полезной информации из зашумленных и нелинейных финансовых временных рядов. В этой статье мы исследуем возможности функций Радемахера — мощных математических инструментов, хорошо зарекомендовавших себя в области обработки сигналов и анализа данных, но пока еще недостаточно используемых в трейдинге.

В этой статье мы попробуем применить эти функции для решения следующих задач:

• фильтрация шума и выделение значимых трендов;
• поиск закономерностей в изменении цен;
• прогнозирование временных рядов;
• адаптация к изменяющимся рыночным условиям и разработка торговых стратегий, способных гибко реагировать на рыночные изменения.

Основная цель статьи — продемонстрировать, как использование функций Радемахера может помочь трейдерам и разработчикам торговых систем в решении этих проблем.

Ожидаемые результаты включают:

• оценку эффективности функций Радемахера для анализа и обработки рыночных данных;
• конкретные примеры применения этих функций в трейдинге, включая алгоритмы фильтрации, прогнозирования и адаптации к рыночным условиям;
• проверку этих алгоритмов на исторических данных и примеры торговых стратегий, построенных на этих функциях.

Я надеюсь, что вы уже изучили вводную статью, посвященную функциям Радемахера и Уолша. Текущая статья послужит отправной точкой для более широкого внедрения этих функций в практику трейдинга и поможет создавать более совершенные и адаптивные торговые системы.

Ограничения функций Радемахера и их возможности

Если мы зададимся вопросом: сколько способов обработки и анализа временных рядов существует на сегодняшний день, то самым близким к истине ответом будет — очень много. Однако, прежде чем применять их на практике, желательно ознакомиться с их ограничениями и недостатками. Для примера возьмем системы функций Радемахера. Первый их недостаток — они являются неполными. Это означает, что с их помощью невозможно точно восстановить исходный сигнал. Еще один недостаток этих функций — их строго заданная периодичность. Период функций может быть равен только какой-либо степени числа 2. Все эти недостатки могут ограничивать применение этих функций на практике.

Но как известно, наши достоинства являются продолжением наших недостатков. И этот тезис мы можем легко доказать с помощью функций Радемахера. Эти функции являются неполными только потому, что для их построения используется нечетная функция синус. Но линейный тренд также может быть выражен через нечетную функцию.

А это означает, что с помощью функций Радемахера можно довольно точно описать линейные тренды, и это их несомненное достоинство. Трейдеры любят тренды.

Теперь, давайте обсудим период функций Радемахера. Предположим, что я решил построить систему 2 порядка. При классическом подходе период всех функций будет равен 4. Допустим, что я решил удвоить период (пример не совсем удачный, но пусть будет так). Никаких препятствий этому нет. А что даст такое удвоение? Наиболее сильно оно скажется на функции самого высокого порядка. В классической системе эта функция является чередованием +1 и -1. Она будет хорошо работать только при явно выраженном тренде. После удвоения коэффициенты этой функции станут выглядеть так: +1,+1,-1,-1 и т.д. Таким образом я смогу сгладить эту функцию, и она станет менее чувствительной к шумам и выбросам.

Примечание: если вас завтра пригласят на международную конференцию по цифровой обработке сигналов, то не рассказывайте там об этом подходе, ваше предложение воспримут неоднозначно. А если вы посетите местный клуб трейдеров, то эта идея им понравится.

Теперь давайте посмотрим, как можно реализовать такой подход на практике. Сначала нам нужно задать порядок системы функций P. Потом зададим параметр масштаба M. Тогда период функций можно рассчитать по формуле:

Конечно же, период индикатора не может быть произвольным, но некоторая свобода выбора у нас все-таки появилась. Расчет коэффициентов функций остается прежним.

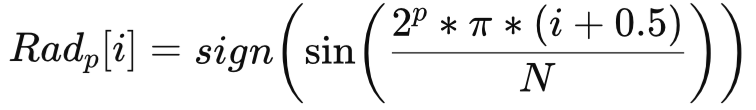
Давайте посмотрим, как будет вести себя индикатор, построенный по этому методу. Для примера, я взял параметры P и M равными 3. Индикатор разбивает весь диапазон цены на 8 уровней длиной по 3 бара каждый.

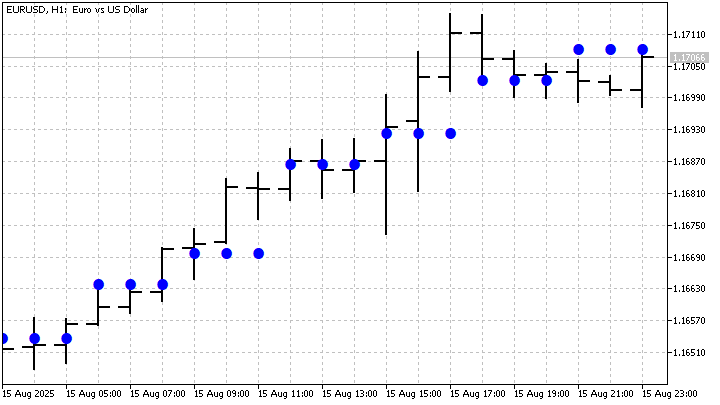
Каждый из этих уровней предлагает свое локальное сглаживание цен. Но, для нас наибольший интерес представляет тот факт, что в формировании каждого уровня участвуют все цены одновременно. Поэтому, мы можем рассматривать их как своеобразные уровни поддержки и сопротивления. Пусть, L – количество цен, лежащих ниже данного уровня. Тогда силу его сопротивления можно рассчитать так:

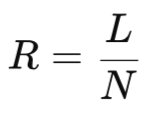
Чем больше сопротивление, тем слабее поддержка этого уровня, и наоборот. В более привычном виде такой индикатор будет выглядеть так:

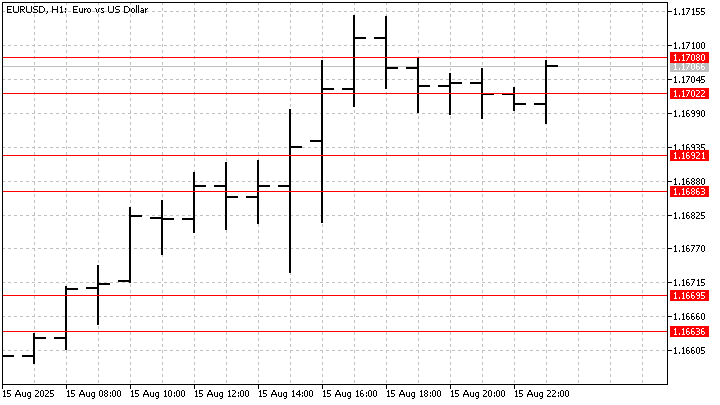
Главное отличие этих уровней заключается в том, что они построены на трендовых функциях. Это означает, что на них влияют не только цены, но и порядок их следования друг за другом. Можно поменять местами всего 2 цены, и значения уровней могут измениться весьма значительно. Такой индикатор можно использовать в качестве фильтра. Ну а мы попробуем более сложные варианты использования функций Радемахера.

Прогнозирование с помощью функций Радемахера

До этого момента мы имели дело с системой функций. И при этом мы не обращали внимания на поведение каждой функции в отдельности. Давайте посмотрим, какие значения может принимать та или иная функция на исторических данных. Для примера я возьму функцию Радемахера 1 порядка. При сборе статистики я не буду нормировать значения функции, а полученные результаты буду переводить в пункты. Так я смогу получить целые числа, а работать с ними очень легко и приятно. Меня интересует, какие значения может принимать функция, и как часто эти значения встречаются в истории. В результате у меня получится эмпирическая функция плотности вероятности (PDF), которая в данном случае выглядит так.

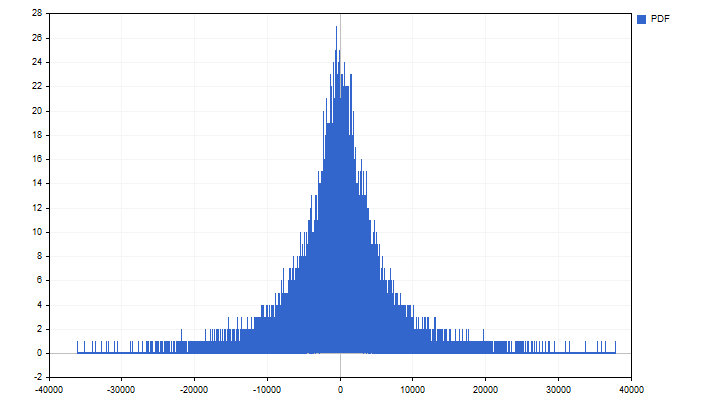
На основе собранной статистики уже можно делать какие-то выводы. Как вы можете видеть, одни значения встречаются чаще, другие реже. И первый вывод, который мы можем сделать — большие тренды встречаются реже, чем маленькие. Также, на основе PDF мы можем построить кумулятивную функцию вероятности (CDF). С математической точки зрения CDF представляет собой сумму вероятностей текущего значения со всеми значениями меньше текущего. Как правило, она принимает вид S-образной кривой, растущей от 0 до 1. 

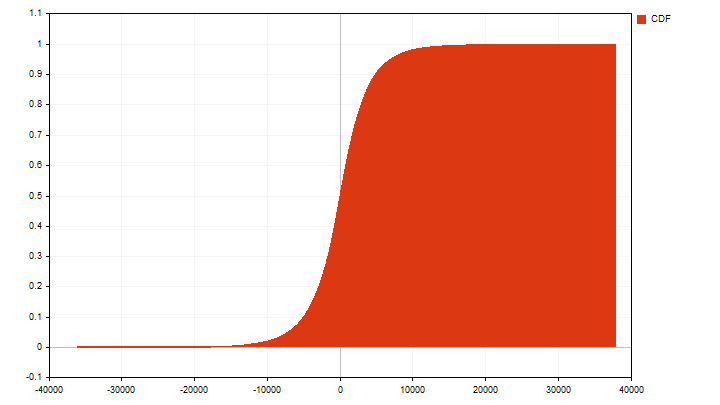
Главная особенность CDF заключается в том, что она показывает вероятность того, что величина примет значение меньшее или равное заданному. Эту особенность уже можно использовать в трейдинге. Например, если текущее значение CDF близко к 0 или 1, то это может служить сигналом об окончании тренда и возможной смене его направления. А пересечение 0.5 может служить подтверждением тренда.

Давайте посмотрим, как можно использовать эти функции на практике. Предположим, что вы используете SMA с периодом N. Текущее значение этого индикатора вам известно. А каким оно будет через N баров? Ответ на этот вопрос не так сложен, как кажется на первый взгляд. Вначале нам нужно узнать, как вообще меняются значения SMA во времени. Для этого нам нужно собрать статистику вида:

А теперь давайте вспомним, что коэффициенты SMA определяются следующим образом:

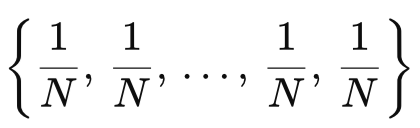
Если мы уберем нормирующий множитель, то разность двух SMA превратится в функцию Радемахера 1 порядка с периодом 2*N. А как собирать статистику для таких функций мы уже знаем. Итак, порядок наших действий будет таким:

• зададим период SMA и желаемую точность прогноза;
• рассчитываем коэффициенты функции Радемахера 1 порядка с удвоенным периодом:
• собираем статистику для этой функции и строим CDF;
• по CDF находим минимальное и максимальное значения, которые будут соответствовать требуемой точности прогноза;
• находим текущее значение SMA. Используя это значение, а также минимум и максимум из предыдущего шага, делаем прогноз.

Индикатор, построенный по этому алгоритму, выглядит так:

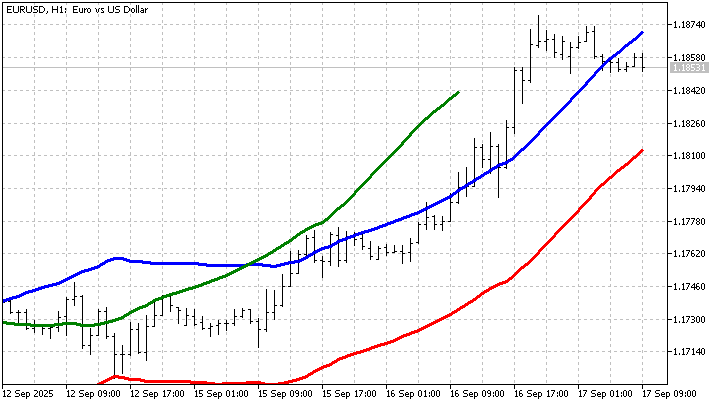
С вероятностью 50% будущее значение SMA будет лежать между красной и синей линиями. Зеленая линия показывает будущее значение SMA на момент расчета прогноза. Индикатор, конечно же ошибается, но ведь и будущее не предопределено.

Усложняем модель

Оценка будущих уровней SMA дело хорошее. Но гораздо более привлекательной выглядит возможность прогнозирования будущего значения тренда. Согласитесь, если я скажу вам, что в течение N баров цена будет расти, то такой прогноз будет более предпочтительным, чем какие-то уровни. Но чтобы получить возможность делать такой прогноз, нам придется приложить немного усилий.

Сначала нам нужно построить осциллятор, на основе функций Радемахера. Он будет немного отличаться от классических осцилляторов. Давайте посмотрим, в чем заключается это отличие. Например, мы решили построить осциллятор на основе SMA. Все что нам нужно в этом случае —рассчитать разность между текущей ценой и значением SMA.

А функции Радемахера оконные. Изменение последней цены приводит к изменению всех значений функций на всем их периоде. С одной стороны, это может быть недостатком — трейдеры скажут, что индикатор перерисовывается. А с другой стороны, это достоинство этих функций — они гибко реагируют на текущую обстановку на рынке.

Для построения осциллятора я воспользуюсь способностью этих функций сглаживать тренды. Алгоритм расчета осциллятора будет таким. Сначала я найду значения всех функций Радемахера. После этого я найду разности между текущей ценой и значениями этих функций. Сумма этих разностей и будет текущим значением осциллятора. В результате у меня получится модель изменения тренда.

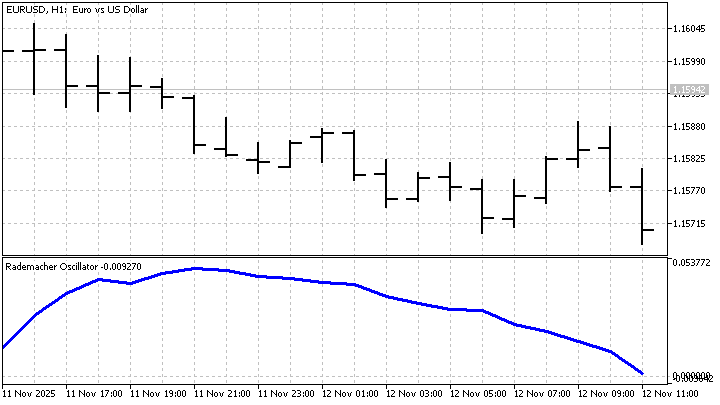
Теперь передо мной стоит вопрос: как из этой модели можно получить прогноз значения тренда? Для построения прогноза я воспользуюсь марковскими цепями. Эти цепи были впервые рассмотрены А. Марковым в 1906 г. в статье "О предельном распределении одного класса связанных случайных величин". Суть этих цепей заключается в том, что с их помощью можно прогнозировать вероятность перехода какого-либо процесса из одного состояния в другое.

Предположим, что я различаю 3 состояния рынка — тренд вверх, флет и тренд вниз. По историческим данным я могу отследить, как менялись эти состояния и вывести вероятность перехода рынка из одного состояния в другое. Удобнее всего эти вероятности представить в виде матрицы.

	тренд вверх	флет	тренд вниз
тренд вверх	0.4	0.3	0.3
флет	0.3	0.4	0.3
тренд вниз	0.2	0.4	0.4

В левом столбце этой матрицы показаны возможные текущие состояния рынка. В верхней строке — состояния рынка на следующем шаге. В ячейках таблицы показаны вероятности перехода из одного состояния в другое.

Это переходная матрица цепи Маркова. С помощью этой матрицы я могу прогнозировать будущее состояние рынка. Прогноз на 1 шаг вперед дает сама матрица. А что делать, если я хочу получить прогноз на 2 шага вперед? Для этого мне нужно умножить переходную матрицу на саму себя.

Далее я хочу посмотреть, что будет на 3 шаге. Нет проблем. Мне нужно только умножить полученную матрицу на переходную.

Как вы уже догадались, продолжая подобные умножения я могу строить прогноз на любое количество шагов вперед. Именно это свойство я и буду использовать для построения торговой стратегии.

Для описания состояния рынка я буду использовать осциллятор Радемахера. На основе исторических данных я найду максимальное и минимальное значения этого индикатора. Я буду различать N состояний осциллятора. Тогда величину каждого состояния можно найти по формуле:

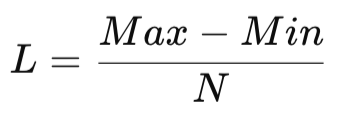
Теперь я могу рассчитать индекс состояния, в котором находится индикатор:

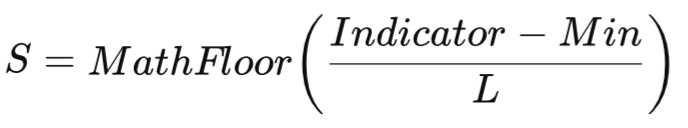
После этого мне нужно создать матрицу размером N*N в которую я буду записывать переходы индикатора из одного состояния в другое. Например, сейчас индикатор находится в состоянии I, а следующее его состояние будет J. Тогда элемент матрицы с этими индексами я увеличу на 1. С помощью этой матрицы я создам матрицу вероятности переходов. Для этого я найду сумму всех элементов в одной строке, а потом разделю каждый элемент этой строки на эту сумму.

Зная значения вероятностей, я могу делать прогноз изменения состояния индикатора на любое количество шагов вперед. На этом прогнозе я и буду строить стратегию. Ее правила будут такими:

• если прогноз показывает, что состояние индикатора будет увеличиваться, то я открою позицию buy;
• если ожидается снижение состояния, то я открою позицию sell;
• закрытие позиций осуществляется по противоположным сигналам.

Несмотря на простоту этой стратегии, ее результаты выглядят обнадеживающе.

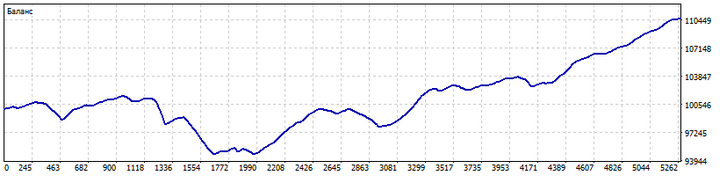
Основная сложность такой стратегии заключается в том, что трейдеру необходимо подбирать не только параметры индикатора, но и параметры цепи Маркова. Результаты зависят от числа состояний. Если состояний немного, то цепь будет слишком обобщающей и плохо различать рыночную обстановку. В этом случае, увеличение числа состояний может положительно сказаться на результатах. С другой стороны, увеличение числа состояний может снизить прогностическую способность цепи.

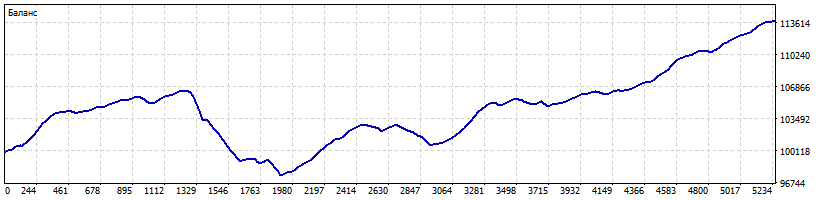
Использование цепей Маркова позволяет использовать более гибкие подходы к сопровождению позиций. Я использовал принудительное закрытие позиций, но вполне возможен и другой вариант. Предположим, что прогноз говорит о том, что рост цены маловероятен или будет небольшим. Тогда, вместо закрытия позиций buy, можно начать сопровождать их трейлинг-стопом. На следующем шаге вероятность роста цены увеличилась — трейлинг-стоп можно отключить.

Заключение

Эта статья показала, что функции Радемахера можно применять для анализа и прогнозирования финансовых временных рядов. Были рассмотрены методы фильтрации шума, выделения трендов и построения торговых стратегий, основанных на этих функциях.

Новый подход к масштабированию периода функций Радемахера открывает новые возможности для адаптации к различным рыночным условиям. Индикатор уровней поддержки и сопротивления, построенный на трендовых функциях, позволяет учитывать не только цены, но и порядок их следования, что может быть полезным при принятии торговых решений.

Прогнозирование на основе CDF и адаптация SMA с использованием функций Радемахера показали перспективные результаты, несмотря на простоту реализации. Использование марковских цепей для прогнозирования состояния рынка на основе осциллятора Радемахера также продемонстрировало обнадеживающие результаты при тестировании торговой стратегии.

Несмотря на некоторые ограничения функций Радемахера, их чувствительность к трендам и возможность гибкой адаптации к рыночной обстановке, делают их ценным инструментом для анализа рынка.

При написании статьи использовались следующие программы.

Название	Тип	Описание
Rademacher Trend	индикатор	Индикатор сглаживает тренд с помощью функций Радемахера с увеличенным периодом. P - максимальный порядок функций (допустимое значение 1 - 10) M - множитель увеличения периода функций (минимальное значение - 1).
Rademacher RS	индикатор	Индикатор показывает уровни функций Радемахера
Trend PDF	скрипт	Скрипт рассчитывает PDF и CDF для функций Радемахера. Картинки сохраняются в папке Files
SMA Forecast	индикатор	Индикатор прогнозирует будущее значение SMA. PeriodSMA - период SMA Percent - точность прогноза
Rademacher Oscillator	индикатор	Индикатор рассчитывает отклонение текущей цены от сглаженного тренда
EA Rademacher Markov	советник	Советник реализует торговую стратегию на основе осциллятора Радемахера и цепей Маркова. P - максимальный порядок функций M - множитель увеличения периода N - количество состояний цепи (не менее 3) Forward - количество шагов прогнозирования (не менее 1) OpenLvl - минимальное количество состояний между прогнозом и текущим, для открытия позиций