Reimaginando Estratégias Clássicas em MQL5 (Parte III): Previsão do FTSE 100

A Inteligência Artificial (IA) oferece um potencial infinito de aplicações na estratégia do investidor moderno. Infelizmente, nenhum investidor individual teria tempo suficiente para analisar cuidadosamente cada estratégia antes de decidir em qual confiar seu capital. Nesta série de artigos, vamos ajudá-lo a navegar pelo vasto universo de possíveis estratégias baseadas em IA, ajudando você a identificar uma abordagem que combine com seu perfil de investidor.

Visão Geral da Estratégia de Negociação

A Bolsa de Valores de Londres (LSE) é uma das mais antigas bolsas do mundo desenvolvido. Foi fundada em 1801 e é a principal bolsa do Reino Unido. É considerada parte do grupo das três grandes, ao lado da Bolsa de Valores de Nova York e da Bolsa de Valores de Tóquio. A Bolsa de Londres é a maior bolsa de valores da Europa e, segundo seu site oficial, o valor de mercado total das empresas listadas atualmente é de aproximadamente 4,4 trilhões de libras esterlinas.

O Financial Times Stock Exchange (FTSE) 100 é um índice derivado da LSE que acompanha as 100 maiores empresas listadas nela. Essas empresas são normalmente chamadas de "blue chips", e são vistas como investimentos relativamente seguros devido à reputação conquistada ao longo do tempo e ao seu histórico comprovado. Podemos aproveitar nosso entendimento de como o índice FTSE 100 é calculado e, potencialmente, criar uma nova estratégia de negociação para prever o preço de fechamento futuro do FTSE 100, considerando tanto o preço de fechamento atual do índice quanto o desempenho de 10 grandes ações que o compõem.

Visão Geral da Metodologia

Construímos nosso Expert Advisor com IA totalmente em MQL5. Isso nos dá flexibilidade, pois nosso modelo pode ser utilizado em diferentes timeframes sem precisar de ajustes constantes. Além disso, podemos ajustar dinamicamente os parâmetros do modelo, como o quanto no futuro desejamos prever. Nosso modelo usou um total de 12 entradas para prever o preço de fechamento futuro do FTSE 100, 20 passos à frente.

Realizamos uma padronização Z para normalizar e escalar cada entrada do modelo, utilizando a média e o desvio padrão de cada coluna. Nosso alvo era o preço de fechamento futuro do índice FTSE100, 20 passos no futuro, e criamos um modelo de Regressão Linear Múltipla para prever esse valor.

Nem todos os modelos de machine learning são criados da mesma forma, especialmente em tarefas de previsão. Vamos considerar as árvores de decisão. Esses algoritmos geralmente funcionam dividindo os dados em grupos e, sempre que o modelo precisa fazer uma previsão, ele retorna simplesmente a média do grupo que mais se encaixa com os dados atuais. Portanto, algoritmos baseados em árvore não fazem extrapolação, ou seja, não têm a capacidade de “olhar para frente” e prever o futuro. Assim, se um modelo baseado em árvore recebesse 5 entradas similares de 5 momentos diferentes, ele poderia prever o mesmo preço de fechamento para todos se fossem suficientemente parecidos, enquanto nosso modelo de regressão linear é capaz de extrapolar, ou seja, consegue prever valores futuros do ativo.

Design Inicial como Script

Vamos inicialmente construir nossa ideia como um simples script em MQL5, para podermos entender como as partes do sistema funcionam em conjunto. Começaremos definindo nossas variáveis globais.

//+------------------------------------------------------------------+
//|                                                        UK100.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+

//1) ADM.LSE  - Admiral
//2) AAL.LSE  - Anglo American
//3) ANTO.LSE - Antofagasta
//4) AHT.LSE  - Ashtead
//5) AZN.LSE  - AstraZeneca
//6) ABF.LSE  - Associated British Foods
//7) AV.LSE   - Aviva
//8) BARC.LSE - Barclays
//9) BP.LSE   - BP
//10) BKG.LSE - Berkeley Group 
//11) UK100   - FTSE 100 Index

//+-------------------------------------------------------------------+
//| Global variables                                                  |
//+-------------------------------------------------------------------+
int fetch = 2000;
int look_ahead = 20;
double mean_values[11],std_values[11];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
vector intercept = vector::Ones(fetch);
matrix target = matrix::Zeros(1,fetch);
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);

A primeira tarefa que realizaremos será buscar e normalizar os dados de entrada. Armazenaremos os dados de entrada em uma matriz e os dados-alvo em outra matriz.

void OnStart()
  {
//--- Fetch the target
target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Fill in the input matrix
for(int i = 0; i < 11; i++)
   {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i);
   }
//--- Add the intercept
input_matrix.Row(intercept,11);

//--- Show the input data
Print("Input data:");
Print(input_matrix);

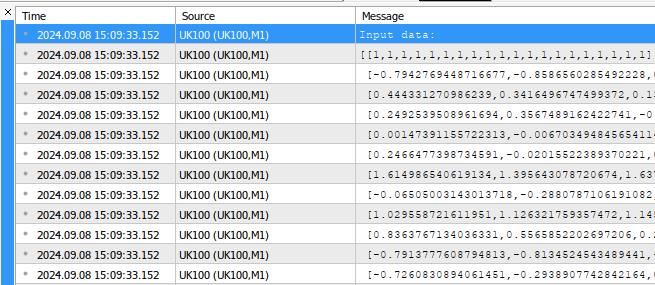
Fig 1: Um exemplo da saída gerada pelo nosso script

Depois de buscar nossos dados de entrada, podemos então calcular os parâmetros do modelo. Felizmente, os coeficientes de um modelo de regressão linear múltipla podem ser calculados por uma fórmula de solução fechada. Veja abaixo um exemplo dos coeficientes do modelo.

//--- Calculating coefficient values
coefficients = target.MatMul(input_matrix.PInv());

//--- Display the coefficient values
Print("UK100 Coefficients:");
Print(coefficients.Transpose());

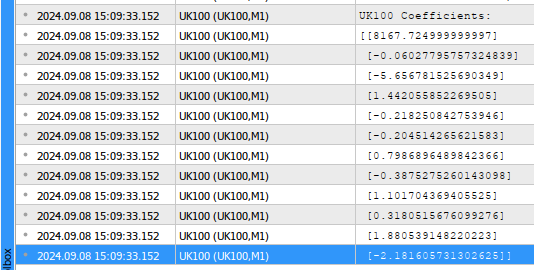
Fig 2: Nossos parâmetros de modelo

Vamos interpretar os resultados juntos. O primeiro valor de coeficiente representa o valor médio do alvo quando todas as entradas do modelo são zero. Esta é a definição matemática do parâmetro de bias. No entanto, em nossa aplicação de trading, faz pouco sentido prático. Tecnicamente, se todas as ações do FTSE 100 estivessem valendo 0 libra esterlina, então o valor médio futuro do índice FTSE 100 também seria 0 libra esterlina. O segundo coeficiente representa a variação marginal no valor futuro do FTSE 100, assumindo que todas as outras ações fecham no mesmo preço. Assim, sempre que as ações da Admiral sobem uma unidade, observamos que o preço de fechamento futuro do índice tende a cair levemente.

Obter uma previsão do nosso modelo é tão simples quanto multiplicar o preço atual de cada ação pelo seu respectivo coeficiente e somar todos esses produtos. Agora que temos uma ideia de como construir nosso modelo, estamos prontos para começar a criar nosso Expert Advisor.

Implementando Nosso Expert Advisor

Vamos começar definindo os inputs que o usuário pode alterar para modificar o comportamento do programa.

//+------------------------------------------------------------------+
//|                                                  FTSE 100 AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int look_ahead = 20;       // How far into the future should we forecast?
input int rsi_period = 20;       // The period of our RSI
input int profit_target = 20;     // After how much profit should we close our positions?
input bool ai_auto_close = true; // Should the AI automatically close positions?

Depois, vamos importar a biblioteca de operações para ajudar a gerenciar nossas posições.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Agora, vamos definir algumas variáveis globais que precisaremos ao longo do nosso Expert Advisor.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
double position_profit = 0;
int fetch = 20;
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);
double mean_values[11],std_values[11],rsi_buffer[1];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
ulong open_ticket;

Agora vamos definir uma função para buscar nossos dados de treinamento. Lembre-se de que nosso objetivo é buscar os dados de treinamento e, em seguida, normalizar e padronizar nossos dados antes de adicioná-los à matriz de entrada.

//+------------------------------------------------------------------+
//| This function will fetch our training data                       |
//+------------------------------------------------------------------+
void fetch_training_data(void)
  {
//--- Fetch the target
   target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Add the intercept
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }
  }

Após obtermos nossos dados de treinamento, também devemos definir uma função para ajustar os coeficientes do nosso modelo.

//+---------------------------------------------------------------------+
//| This function will fit our multiple linear regression model         |
//+---------------------------------------------------------------------+
void model_fit(void)
  {
//--- Calculating coefficient values
   coefficients = target.MatMul(input_matrix.PInv());
  }

Depois que treinamos e ajustamos nosso modelo, finalmente podemos obter previsões a partir dele. Primeiro, buscaremos e normalizaremos os dados atuais do mercado usando nosso modelo para começar. Depois de buscar os dados, aplicamos a fórmula da regressão linear para obter uma previsão do modelo. Por fim, armazenaremos a previsão do modelo como uma flag binária para nos ajudar a acompanhar possíveis reversões.

//+---------------------------------------------------------------------+
//| This function will fetch a prediction from our model                |
//+---------------------------------------------------------------------+
void model_predict(void)
  {
//--- Add the intercept
   intercept = vector::Ones(1);
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Fetch historical data
      vector temp = vector::Zeros(1);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,0,1);
      //--- Normalize and scale the data
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }

//--- Calculate the model forecast
   forecast = (
                 (1 * coefficients[0,0]) +
                 (input_matrix[0,1] * coefficients[0,1]) +
                 (input_matrix[0,2] * coefficients[0,2]) +
                 (input_matrix[0,3] * coefficients[0,3]) +
                 (input_matrix[0,4] * coefficients[0,4]) +
                 (input_matrix[0,5] * coefficients[0,5]) +
                 (input_matrix[0,6] * coefficients[0,6]) +
                 (input_matrix[0,7] * coefficients[0,7]) +
                 (input_matrix[0,8] * coefficients[0,8]) +
                 (input_matrix[0,9] * coefficients[0,9]) +
                 (input_matrix[0,10] * coefficients[0,10]) +
                 (input_matrix[0,11] * coefficients[0,11])
              );
//--- Store the model's state
//--- Whenever the system and model state aren't the same, we may have a potential reversal
   if(forecast > iClose("UK100",PERIOD_CURRENT,0))
     {
      model_state = 1;
     }

   else
      if(forecast < iClose("UK100",PERIOD_CURRENT,0))
        {
         model_state = -1;
        }
  }
//+------------------------------------------------------------------+

Também precisaremos de uma função responsável por buscar os dados atuais do mercado diretamente no nosso terminal.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
//--- Update the bid and ask prices
   bid = SymbolInfoDouble("UK100",SYMBOL_BID);
   ask = SymbolInfoDouble("UK100",SYMBOL_ASK);
//--- Update the RSI readings
   CopyBuffer(rsi_handler,0,1,1,rsi_buffer);
  }

Agora vamos criar funções que irão analisar o sentimento do mercado para ver se está de acordo com o nosso modelo. Sempre que nosso modelo sugerir uma compra, primeiro verificaremos a variação do preço no gráfico semanal ao longo de um ciclo de negócios; se os preços tiverem se valorizado, verificaremos também se nosso indicador RSI sugere um sentimento de alta no mercado. Se for o caso, abriremos uma posição de compra. Caso contrário, não abriremos posição alguma.

//+------------------------------------------------------------------+
//| Check if we have an opportunity to sell                          |
//+------------------------------------------------------------------+
void check_sell(void)
  {
   if(iClose("UK100",PERIOD_W1,0) < iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] < 50)
        {
         Trade.Sell(0.3,"UK100",bid,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = -1;
        }
     }
  }

//+------------------------------------------------------------------+
//| Check if we have an opportunity to buy                           |
//+------------------------------------------------------------------+
void check_buy(void)
  {
   if(iClose("UK100",PERIOD_W1,0) > iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] > 50)
        {
         Trade.Buy(0.3,"UK100",ask,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = 1;
        }
     }
  }

Quando nossa aplicação estiver sendo inicializada, primeiro vamos preparar nosso indicador RSI. A partir daí, validaremos o RSI. Se esse teste for aprovado, prosseguiremos para criar nosso modelo de regressão linear múltipla. Começamos buscando os dados de treinamento e, em seguida, calculando os coeficientes do modelo. Por fim, validaremos as entradas do usuário para garantir que ele definiu uma medida para controlar os níveis de risco.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Prepare the technical indicator
   rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,rsi_period,PRICE_CLOSE);

//--- Validate the indicator handler
   if(rsi_handler == INVALID_HANDLE)
     {
      //--- We failed to load the indicator
      Comment("Failed to load the RSI indicator");
      return(INIT_FAILED);
     }

//--- This function will fetch our training data and scaling factors
   fetch_training_data();

//--- This function will fit our multiple linear regression model
   model_fit();

//--- Ensure the user's inputs are valid
   if((ai_auto_close == false && profit_target == 0))
     {
      Comment("Either set AI auto close true, or define a profit target!")
      return(INIT_FAILED);
     }

//--- Everything went well
   return(INIT_SUCCEEDED);
  }

Sempre que nosso Expert Advisor não estiver em uso, liberaremos os recursos que não estivermos mais utilizando. Em especial, removeremos o indicador RSI e o Expert Advisor do gráfico principal.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we are no longer using
   IndicatorRelease(rsi_handler);
   ExpertRemove();
  }

Por fim, sempre que recebermos preços atualizados, primeiro selecionaremos o símbolo FTSE 100 antes de buscar os dados de mercado e valores dos indicadores técnicos atualizados. A partir daí, poderemos obter uma nova previsão do nosso modelo e tomar uma decisão. Se nosso sistema não possuir posições abertas, verificaremos se o sentimento atual do mercado está alinhado com as previsões do nosso modelo antes de abrir qualquer posição. Se já tivermos posições abertas, testaremos possíveis reversões. Estas podem ser facilmente identificadas por situações em que o estado do nosso modelo e o do sistema não são os mesmos.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Since we are dealing with a lot of different symbols, be sure to select the UK1OO (FTSE100)
//--- Select the symbol
   SymbolSelect("UK100",true);

//--- Update market data
   update_market_data();

//--- Fetch a prediction from our AI model
   model_predict();

//--- Give the user feedback
   Comment("Model forecast: ",forecast,"\nPosition Profit: ",position_profit);



//--- Look for a position
   if(PositionsTotal() == 0)
     {
      //--- We have no open positions
      open_ticket = 0;

      //--- Check if our model's prediction is validated
      if(model_state == 1)
        {
         check_buy();
        }

      else
         if(model_state == -1)
           {
            check_sell();
           }
     }

//--- Do we have a position allready?
   if(PositionsTotal() > 0)
     {

      //--- Should we close our positon manually?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == false))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            if(profit_target < position_profit)
              {
               Trade.PositionClose("UK100");
              }
           }
        }

      //--- Should we close our positon using a hybrid approach?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == true))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            //--- Check if we have passed our profit target or if we are expecting a reversal
            if((profit_target < position_profit) || (model_state != system_state))
              {
               Trade.PositionClose("UK100");
              }
           }
        }


      //--- Are we closing our system just using AI?
      else
         if((system_state != model_state) &&
            (ai_auto_close == true) &&
            (profit_target == 0))
           {
            Trade.PositionClose("UK100");
           }
     }
  }
//+------------------------------------------------------------------+

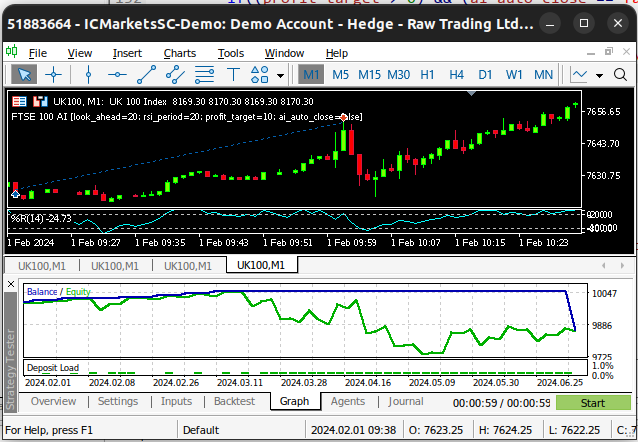
Fig 3: Teste retroativo do nosso Expert Advisor

Otimizando Nosso Expert Advisor

Até agora, nossa aplicação de trading parece instável. Podemos tentar melhorar a estabilidade utilizando ideias estabelecidas pelo economista americano Harry Markowitz. Markowitz é reconhecido por conceituar as bases da Teoria Moderna do Portfólio (MPT) como conhecemos hoje. Em essência, ele percebeu que o desempenho de qualquer ativo individual é insignificante em comparação ao desempenho do portfólio inteiro do investidor.

Fig 4: Foto do laureado com o Nobel Harry Markowitz

Vamos tentar aplicar algumas ideias de Markowitz para, quem sabe, estabilizar o desempenho da nossa aplicação de trading. Começaremos importando as bibliotecas necessárias.

#Import the libraries we need
import pandas            as pd
import numpy             as np
import seaborn           as sns
import MetaTrader5       as mt5
import matplotlib.pyplot as plt
from   scipy.optimize    import  minimize

Precisamos criar uma lista das ações que iremos considerar.

#Create the list of stocks
stocks = ["ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"]

Inicialize o terminal.

#Initialize the terminal
if(!mt5.initialize()):
    print('Failed to load the MT5 Terminal')

True

Agora, precisamos criar um data frame para armazenar os retornos de cada símbolo.

#Create a dataframe to store our returns
amount  = 10000
returns = pd.DataFrame(columns=stocks,index=np.arange(0,amount))

Busque os dados necessários a partir do nosso Terminal MetaTrader 5.

#Fetch the data
for stock in stocks:
     temp = pd.DataFrame(mt5.copy_rates_from_pos(stock,mt5.TIMEFRAME_M1,0,amount))
     returns[[stock]] = temp[['close']]

Para essa tarefa, usaremos os retornos de cada ação em vez do preço de fechamento normal.

#Store the data as returns
returns = returns.pct_change()
returns.dropna(inplace=True)

Por padrão, devemos multiplicar cada entrada por 100 para obter os retornos percentuais reais.

#Let's look at our dataframe
returns = returns * (10.0 ** 2)

Vamos agora observar os dados que temos.

returns

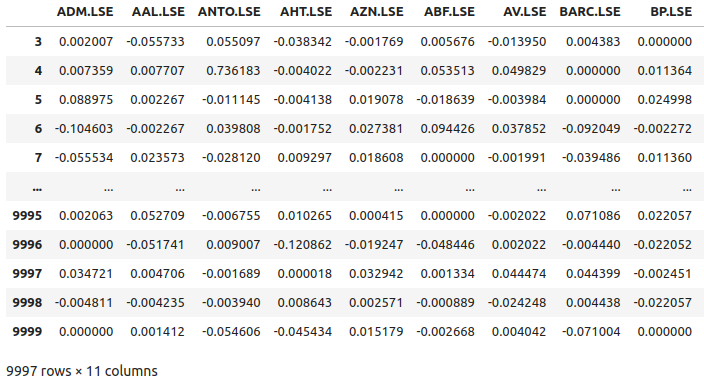
Fig 5: Alguns dos retornos das ações da nossa cesta de ações do FTSE100

Agora vamos plotar os retornos de mercado de cada ação que temos. Podemos ver claramente que certas ações, como Ashtead Group (AHT.LSE), possuem movimentos acentuados e extremos que se desviam do desempenho médio do portfólio das 11 ações que temos. Em essência, o algoritmo de Markowitz nos ajudará a selecionar empiricamente uma menor quantidade dessas ações com maior variância, e uma maior quantidade daquelas com menor variância. A abordagem de Markowitz é analítica e elimina qualquer tentativa de adivinhação da nossa parte.

#Let's visualize our market returns
returns.plot()

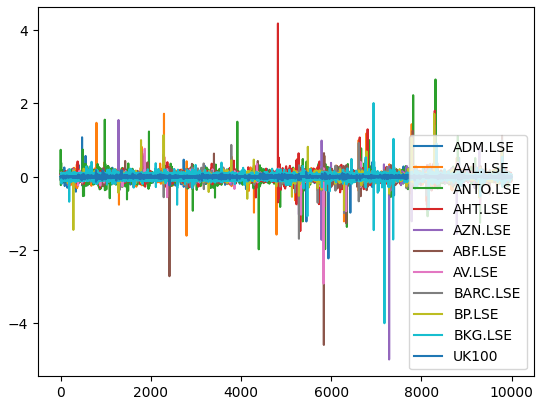
Fig 6: Os retornos de mercado da nossa cesta de ações do FTSE 100

Vamos observar se há algum nível significativo de correlação em nossos dados. Infelizmente, não encontramos níveis de correlação interessantes.

#Let's analyze the correlation coefficients
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(returns.corr(),annot=True,linewidths=.5, ax=ax)

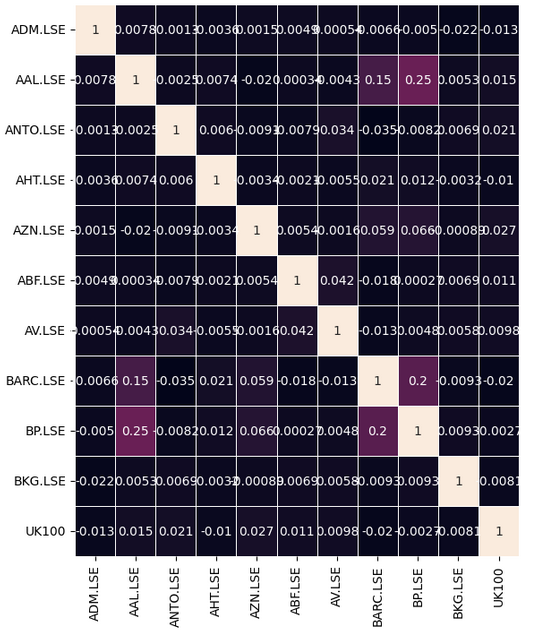
Fig 7: Nosso mapa de calor de correlação do FTSE 100

Alguns relacionamentos não serão fáceis de identificar, e exigirão algumas etapas de pré-processamento para serem revelados. Em vez de simplesmente procurar por correlação direta entre a cesta de ações que temos, também podemos procurar por correlação entre os valores atuais de cada ação e o valor futuro do símbolo UK100. Esta é uma técnica clássica conhecida como correlação lead-lag.

Começaremos deslocando nossa cesta de ações para trás em 20 períodos e avançando o símbolo UK100 em 20 períodos.

# Let's also analyze for lead-lag correlation
look_ahead  = 20
lead_lag    = pd.DataFrame(columns=stocks,index=np.arange(0,returns.shape[0] - look_ahead))
for stock in stocks:
    if stock == 'UK100':
        lead_lag[[stock]] = returns[[stock]].shift(-20)
    else:
        lead_lag[[stock]] = returns[[stock]].shift(20)

# Returns
lead_lag.dropna(inplace=True)

Vamos ver se houve alguma alteração na matriz de correlação. Infelizmente, não obtivemos melhorias com esse procedimento.

#Let's see if there are any stocks that are correlated with the future UK100 returns
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(lead_lag.corr(),annot=True,linewidths=.5, ax=ax)

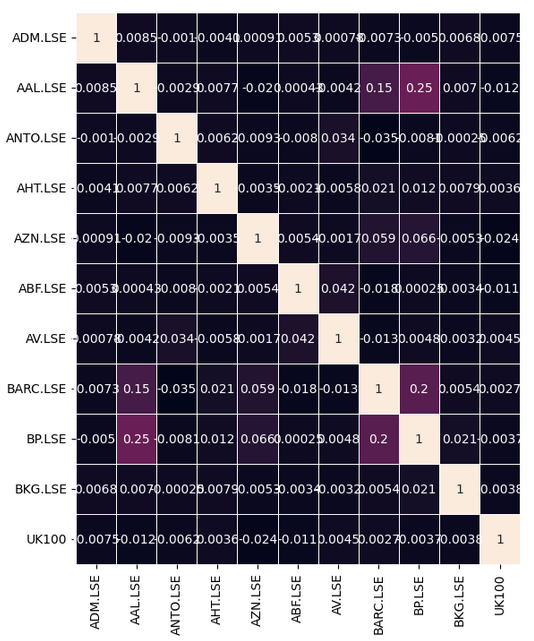
Fig 8: Nosso mapa de calor de correlação lead-lag

Agora vamos tentar minimizar a variância de todo o nosso portfólio. Vamos modelar nosso portfólio de forma que possamos comprar e vender diferentes ações para minimizar o risco. Para atingir nosso objetivo, usaremos a biblioteca de otimização do SciPy. Teremos 11 pesos diferentes para serem otimizados, cada peso representa a alocação de capital para cada ação correspondente. O coeficiente de cada peso indicará se devemos comprar (coeficiente positivo) ou vender (coeficiente negativo) determinada ação. Para ser mais específico, queremos garantir que todos os nossos coeficientes estejam entre -1 e 1, ou seja, no intervalo [-1,1].

Além disso, gostaríamos de usar todo o capital que temos, e não mais do que isso. Por isso, precisamos definir restrições para nosso procedimento de otimização. Especificamente, devemos garantir que a soma dos pesos do portfólio seja igual a 1. Isso significa que alocamos todo o capital disponível. Lembre-se de que alguns coeficientes serão negativos, o que pode dificultar que a soma seja igual a 1. Portanto, precisamos modificar essa restrição para considerar apenas os valores absolutos de cada peso. Em outras palavras, se armazenarmos os 11 pesos em um vetor, queremos garantir que a norma L1 seja igual a 1.

Para começar, inicializaremos nossos pesos com valores aleatórios e calcularemos a covariância da matriz de retornos.

#Let's attempt to minimize the variance of the portfolio
weights = np.array([0,0,0,0,0,0,-1,1,1,0,0])
covariance = returns.cov()

Agora, vamos acompanhar os níveis iniciais de variância.

#Store the initial portfolio variance
initial_portfolio_variance = np.dot(weights.T,np.dot(covariance,weights))
initial_portfolio_variance

0.011959689589562724

Ao otimizar, buscamos as entradas ótimas para uma função que resulta no menor valor de saída possível. Esta função é chamada de função de custo. Nossa função de custo será a variância do portfólio sob os pesos atuais. Felizmente, isso é fácil de calcular com comandos de álgebra linear.

#Cost function
def cost_function(x):
    return(np.dot(x.T,np.dot(covariance,x)))

Agora vamos definir as restrições que especificam que os pesos do portfólio devem somar 1.

#Constraints
def l1_norm(x):
    return(np.sum(np.abs(x))) - 1

constraints = {'type': 'eq', 'fun':l1_norm}

O SciPy espera que forneçamos um valor inicial para a otimização.

#Initial guess
initial_guess = weights

Lembre-se de que queremos que nossos pesos estejam entre -1 e 1, então passamos essas instruções ao SciPy usando uma tupla de limites.

#Add bounds
bounds =   [(-1,1)] * 11

Agora vamos minimizar a variância do nosso portfólio utilizando o algoritmo Sequential Least Squares Programming (SLSQP). O algoritmo SLSQP foi originalmente desenvolvido pelo engenheiro alemão Dieter Kraft nos anos 1980. A rotina original foi implementada em FORTRAN. O artigo científico original de Kraft, detalhando o algoritmo, pode ser encontrado neste link, aqui. SLSQP é um algoritmo quasi-newtoniano, ou seja, ele estima a segunda derivada (matriz Hessiana) da função objetivo para encontrar o ótimo da função.

#Minimize the portfolio variance
result = minimize(cost_function,initial_guess,method="SLSQP",constraints=constraints,bounds=bounds)

Realizamos com sucesso este procedimento de otimização, vamos analisar nossos resultados.

Resultados

 mensagem: Otimização encerrada com sucesso
 success: True
  status: 0
     fun: 0.0004706570068070814
       x: [ 5.845e-02 -1.057e-01  8.800e-03  2.894e-02 -1.461e-01
            3.433e-02 -2.625e-01  6.867e-02  1.653e-01  3.450e-02
            8.675e-02]
     nit: 12
     jac: [ 3.820e-04 -9.886e-04  3.242e-05  4.724e-04 -1.544e-03
            4.151e-04 -1.351e-03  5.850e-04  8.880e-04  4.457e-04
            4.392e-05]
    nfev: 154
    njev: 12

Vamos armazenar os pesos ótimos que nosso solver SciPy encontrou para nós.

#Store the optimal weights
optimal_weights = result.x

Vamos validar que a restrição da norma L1 não foi violada. Observe que, devido à precisão limitada de memória flutuante dos computadores, nossos pesos não somarão exatamente 1.

#Validating the weights add up to one
np.sum(np.abs(optimal_weights))

0.9999999998893961

Armazene a nova variância do portfólio.

#Store the new portfolio variance
otpimal_variance = cost_function(optimal_weights)

Crie um dataframe para que possamos comparar nosso desempenho.

#Portfolio variance
portfolio_var = pd.DataFrame(columns=['Old Var','New Var'],index=[0])

Salve nossos níveis de variância em um dataframe.

portfolio_var.iloc[0,0] = initial_portfolio_variance * (10.0 ** 7)
portfolio_var.iloc[0,1] = otpimal_variance * (10.0 ** 7)

Plote a variância do nosso portfólio. Como podemos ver, nossos níveis de variância caíram significativamente.

portfolio_var.plot.bar()

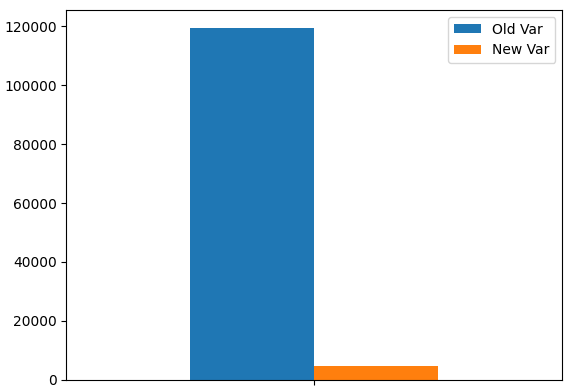
Fig 9: Nossa nova variância do portfólio

Agora vamos obter o número de posições que devemos abrir em cada mercado de acordo com nossos pesos ótimos. Nossos dados sugerem que, sempre que abrirmos 1 posição comprada no símbolo UK100, não devemos abrir posições no Admiral Group (ADM.LSE) e devemos abrir 2 posições vendidas equivalentes em Anglo-American (AAL.LSE).

int_weights = (optimal_weights / optimal_weights[-1]) // 1
int_weights

array([ 0., -2.,  0.,  0., -2.,  0., -4.,  0.,  1.,  0.,  1.])

Atualizando Nosso Expert Advisor

Agora podemos direcionar nossa atenção para a atualização do nosso algoritmo de negociação, para aproveitar nosso novo entendimento do mercado FTSE 100. Primeiro, vamos carregar os pesos ótimos que calculamos usando o SciPy.

int    optimization_weights[11] = {0,-2,0,0,-2,0,-4,0,1,0,1};

Também precisamos de uma configuração para acionar nosso procedimento de otimização, então definiremos um limite de perda. Sempre que a perda de uma negociação aberta for maior que nosso limite de perda, abriremos negociações em outros mercados do FTSE100 para tentar minimizar nossos níveis de risco.

input double  loss_limit = 20;        // After how much loss should we optimize our portfolio?

Agora vamos definir a função que será responsável por chamar o procedimento para minimizar nossos níveis de risco de portfólio. Lembre-se: só executaremos essa rotina se a conta tiver ultrapassado o limite de perda ou estiver em risco de exceder seu limite de patrimônio.

      //--- Should we optimize our portfolio variance using the optimal weights we have calculated
      if((loss_limit > 0))
        {
         //--- Update the position profit
         position_profit = AccountInfoDouble(ACCOUNT_EQUITY) - AccountInfoDouble(ACCOUNT_BALANCE);
         //--- Check if we have passed our profit target or if we are expecting a reversal
         if(((loss_limit * -1) < position_profit))
           {
            minimize_variance();
           }
        }
        

Essa função irá realmente executar a otimização do portfólio, iterando por nossa lista de ações e verificando o número e o tipo de posição que deve ser aberta.

//+------------------------------------------------------------------+
//| This function will minimize the variance of our portfolio        |
//+------------------------------------------------------------------+
void minimize_variance(void)
  {
   risk_minimized = true;

   if(!risk_minimized)
     {
      for(int i = 0; i < 11; i++)
        {
         string current_symbol = list_of_companies[i];

         //--- Add that stock to the portfolio to minimize our variance, buy
         if(optimization_weights[i] > 0)
           {
            for(int i = 0; i < optimization_weights[i]; i++)
              {
               Trade.Buy(0.3,current_symbol,ask,0,0,"FTSE Optimization");
              }
           }
         //--- Add that stock to the portfolio to minimize our variance, sell
         else
            if(optimization_weights[i] < 0)
              {
               for(int i = 0; i < optimization_weights[i]; i--)
                 {
                  Trade.Sell(0.3,current_symbol,bid,0,0,"FTSE Optimization");
                 }
              }
        }
     }
  }

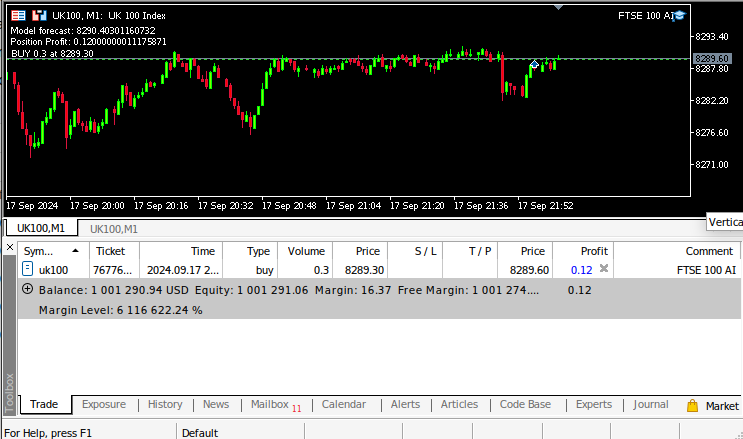
Fig 10: Teste em tempo real do nosso algoritmo

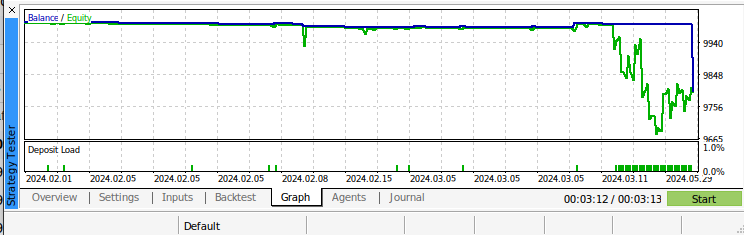
Fig 11: Backtest do nosso algoritmo

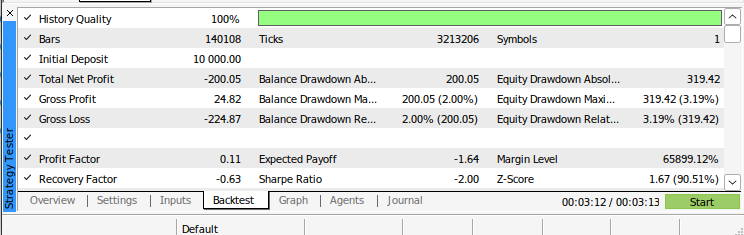
Fig 12: Os resultados do backtest do nosso algoritmo

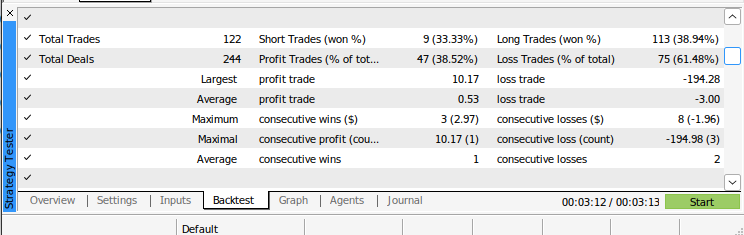
Fig 13: Resultados adicionais do backtest do nosso algoritmo

Conclusão

Neste artigo, demonstramos como você pode construir um conjunto de análise técnica e IA de forma integrada usando Python e MQL5; nossa aplicação é capaz de se ajustar dinamicamente a todos os timeframes disponíveis no terminal MetaTrader 5. Apresentamos os principais princípios fundadores da otimização moderna de portfólio usando algoritmos de otimização contemporâneos. Demonstramos como minimizar o viés humano no processo de seleção de portfólio. Além disso, mostramos como usar dados de mercado para tomar decisões ótimas. Ainda há espaço para melhorias em nosso algoritmo; por exemplo, em artigos futuros, demonstraremos como otimizar 2 critérios simultaneamente, como otimizar níveis de risco considerando a taxa de retorno livre de risco.

No entanto, a maioria dos princípios que apresentamos hoje continuará a mesma mesmo quando estivermos realizando procedimentos de otimização mais sofisticados, só precisaremos ajustar nossas funções de custo, restrições e identificar o algoritmo de otimização apropriado para nossas necessidades.