
O que é uma tendência e qual estrutura o mercado se baseia: Tendência ou Lateral?
Introdução
De acordo com uma das definições de Merriam-Webster, uma tendência é o movimento geral ao longo do tempo de uma mudança estatisticamente detectável e uma curva estatística refletindo essa mudança. Em matemática, as tendências podem ser descritas usando várias equações — linear, logarítmica, polinomial etc. O tipo de tendência real é estabelecido com base na seleção de seu modelo funcional por métodos estatísticos ou pela suavização da série temporal inicial.
Na economia, uma tendência é a direção geral dos indicadores econômicos. Geralmente é considerado no âmbito da análise técnica que implica a direção do movimento dos preços ou os valores do índice. De acordo com Charles Dow, uma tendência de alta (bullish trend) é caracterizada por topos ascendentes em um gráfico, ou seja, topos mais altos do que os anteriores, enquanto uma tendência de baixa (bearish trend) significa fundos descendentes, sendo menores do que os anteriores (veja a Teoria de Dow). Se o gráfico ficar lateralizado, isso significa um movimento lateral. No caso de uma tendência de alta, uma linha de tendência conecta dois ou mais fundos de preços (a linha está localizada abaixo do gráfico como se estivesse apoiando e o empurrando o para cima visualmente). No caso de uma tendência de baixa, uma linha de tendência conecta dois ou mais picos de preços (a linha está localizada acima do gráfico como se estivesse resistindo e empurrando-o para baixo visualmente). As linhas de tendência servem como suporte (para uma tendência de alta) e as linhas de resistência (para uma tendência de baixa).
No entanto, não estamos interessados nos termos, mas na capacidade de lucrar com eles. Os termos acima não revelam como eles podem ser formalizados matematicamente. Todas as definições bem conhecidas parecem vagas e podem ser interpretadas de mais de uma maneira. Por sua vez, a ciência gosta de precisão. Uma definição deve ser clara, compreensível e ter apenas uma interpretação, para que qualquer pessoa que usa o método seja capaz de reproduzir os resultados de outra pessoa que usou o mesmo método antes.
Noções básicas de estratégias de negociação lucrativas
Para avançar para os conceitos de tendência e lateralização, primeiro nós precisamos entender o básico, ou seja, o que precisa ser feito para ganhar dinheiro. Qualquer estratégia de negociação precisa ter um retorno esperado acima de 0. Aqueles familiarizados com a matemática não precisam de mais explicações, mas ainda assim irei fornecê-las. Em palavras simples, o retorno esperado (expectativa de lucro) é o lucro médio. Naturalmente, o lucro médio deve ser maior que 0. Se for igual a 0, nós não obtemos lucro. Se estiver abaixo de 0, nós perdemos dinheiro.
O retorno esperado consiste na probabilidade de um negócio lucrativo, lucro médio e perda média. A equação é simples: a probabilidade de lucro é multiplicada pelo lucro médio. A probabilidade de perda multiplicada pela perda média é subtraída do resultado obtido.
m=(P(tp)*tp)-(P(sl)*sl),
onde
- m — retorno esperado,
- P(tp)— probabilidade de um negócio com lucro,
- P(sl)— probabilidade de um negócio com prejuízo,
- tp — lucro médio de um negócio,
- sl — prejuízo médio de um negócio.
Isso significa que se a probabilidade de um negócio lucrativo for 50% e o tamanho médio de um negócio lucrativo for igual ao tamanho médio de um negócio com prejuízo, o valor esperado é 0, o que significa que não ganhamos nada. Por exemplo, os tamanhos médios de negócios vencedores e perdedores são $10, então m=(50*10)-(50*10)=0. O retorno esperado para a variável aleatória normalmente distribuída é 0 (este é um fato matemático). No meu artigo anterior Discretização da série de preços, componente aleatório e "ruídos", eu considerei que a distribuição de incrementos em mercados reais é muito semelhante à normal e é suspeitamente semelhante ao passeio aleatório (random walk).
Para obter lucro, nós devemos aumentar a probabilidade de um negócio lucrativo ou aumentar o tamanho médio de um negócio lucrativo e reduzir o tamanho médio de um negócio perdedor. Suponha que aumentemos a probabilidade de uma negociação lucrativa em até 60%, enquanto o lucro médio da negociação é igual ao prejuízo médio da negociação = $10. Depois de completar 100 negócios, nós ganharemos m=(60*10)-(40*10)=$200. Se a probabilidade de lucro do negócio permanecer a mesma, nós teremos um lucro estável. Da mesma forma, se aumentarmos o tamanho do lucro médio do negócio, reduzir o tamanho do prejuízo médio do negócio e deixar a probabilidade em 50%, nós também obteremos um lucro estável.
É aqui que muitos traders, especialmente os recém-chegados, geralmente começam a experimentar um viés cognitivo. Eles pensam: "Ok, eu simplesmente deixarei o lucro médio de um negócio ser duas vezes maior do que o prejuízo médio de um negócio e abrirei posições ...digamos, em cruzamentos de Médias Móveis" (o algoritmo de entrada não é importante aqui). Eles inconscientemente querem alcançar o resultado: m=(50*20)-(50*10)=$500, mas na realidade eles só obtêm o retorno esperado m=(33.3*20)-(66.6*10)=0 ou, muito provavelmente, uma perda devido ao spread e comissão. Eu não considerarei spread e comissões neste artigo, uma vez que não são importantes aqui. Alguns outros negociantes podem cair na armadilha oposta: eles podem decidir ter um lucro duas vezes menos do que uma perda, pois, de acordo com suas observações, negócios lucrativos deveriam ser acionados com mais frequência neste caso. Como resultado, eles também obtêm uma perda devido a comissões e spread, uma vez que o retorno real esperado de tal sistema é m=(66.6*10)-(33,3*20)=0. Desta forma, nó podemos aumentar muito o stop loss e reduzir o lucro, trazendo a probabilidade de lucro de 90-99% ou mais, mas todo esse lucro é eventualmente compensado por perdas. Isso também inclui todos os sistemas de martingale que não alteram o retorno esperado, pois ele permanece 0, já que a obtenção de uma perda poderá ocorrer de maneira mais atrasada no tempo.
Isso acontece porque nenhum padrão de lucro foi realmente encontrado. Em vez disso, o trader realiza negociações com base em uma caminhada aleatória. O resultado esperado de um passeio aleatório é 0. Se o retorno esperado for 0, a probabilidade de um negócio com lucro permanece em 50%. As únicas coisas que mudam são as proporções (de agora em diante, vou me referir a isso como "equilíbrio de 50%"). Portanto, nós aumentamos a probabilidade de um negócio com lucro enquanto reduzimos o seu lucro médio, ou aumentamos a probabilidade de um negócio com lucro e reduzimos o seu lucro médio. Nós precisamos quebrar de alguma forma esse "equilíbrio de 50%" e ir além do retorno esperado igual a zero. É importante notar que desenvolver um sistema perdedor é igualmente difícil. Os traders sofrem perdas devido a comissões e depósitos finitos.
De velas à blocos
Como nós negociamos as mudanças de preço que acontecem em pontos (variação de preço mínimo possível) e o lucro depende de quantos pontos o preço passou, nós precisamos nos afastar da forma padrão de representar os preços na forma de velas/barras, uma vez que eles distorcem muito a imagem e dificultam a compreensão do processo. Vamos passar para o método de exibição considerando apenas o movimento do preço em pontos. Neste artigo, eu usarei o meu indicador que constrói blocos depois que o preço move um certo número de pontos. O indicador está anexado abaixo. No entanto, você está livre para usar qualquer outro método. A Figura 1 mostra como os blocos são construídos. Os blocos podem ser de qualquer tamanho, de um ponto ao infinito em incrementos de um ponto. Se o tamanho do bloco for de 10 pontos, o bloco é fechado após o preço ter se movido 10 pontos verticalmente e qualquer bloco é formado. Este bloco é capaz de fechar com um incremento de 10 pontos para cima ou para baixo. O bloco apresenta os preços de abertura, máxima, mínima e fechamento que são semelhantes em funções às velas correspondentes. Considere que um bloco é um passo. Isso será importante mais tarde.
Figura 1
Para avançar para o conceito de tendência, nós precisamos ter algum tipo de amostra. No passeio aleatório, cada passo subsequente não depende do anterior, o processo não tem memória e a probabilidade do passo seguinte mudar de direção é de 50%. Mas a caminhada aleatória é baseada na tendência ou lateralização? Vamos dar uma olhada no gráfico do passeio aleatório na Figura 2.
Figura 2
Se nós quisermos, nós podemos encontrar tendências e áreas laterais na Figura 2, mas na realidade este é um gráfico de passeio aleatório amostrado por velas H1. A probabilidade do próximo passo mover-se para cima ou para baixo aqui é de 50% e não depende da direção do passo anterior. Ao desenvolver o conceito de tendência, eu usarei o passeio aleatório como base, pois, como escrevi anteriormente, o retorno esperado neste caso é 0. Isso decorre do fato de que a probabilidade de cada próximo passo mudar ou manter sua direção aqui é de 50%. A perda média sempre permanece igual ao lucro médio, independentemente do número de passos em que uma posição permanece aberta. A probabilidade de adivinhar a direção também é de 50%. Portanto, eu vou assumir que o gráfico de passeio aleatório não se baseia nem na tendência, nem na lateralização. Ele é aleatório.
Agora nós temos uma amostra com a qual nós podemos comparar uma série de preços, enquanto decidimos se essa série de preços é baseada em tendência ou é lateralizada.
Desenvolvimento do modelo de referência
A Figura 2 mostra o gráfico do passeio aleatório amostrado por velas H1. Tal representação não é muito intuitiva e distorce a percepção do processo. Vamos considerar o seu código-fonte mostrado na Figura 3. Anexei a série em formato CSV abaixo. Você pode baixá-la na plataforma.
Figura 3
A Figura 3 mostra o gráfico do passeio aleatório com passo de 1 ponto e o mesmo gráfico na forma de blocos com tamanho de 1 ponto. Os blocos tornam os passos mais visíveis. Em todos os outros aspectos, os gráficos são idênticos. Uma vez que nós assumimos que o passeio aleatório é uma referência para definir a natureza da tendência de uma série de preços, vamos construir o gráfico de distribuição de densidade de probabilidade do incremento do passeio aleatório para comparar a série de preço real com sua referência. Este problema pode ser resolvido analiticamente, usando a função Gaussiana. No entanto, a solução não é tão visual. Mesmo aqueles familiarizados com a matemática podem não entender completamente o significado de cada forma de distribuição obtida. Por isso, para construir a densidade de probabilidade de referência, eu usarei de regras combinatórias e construirei uma tabela. Seu fragmento é mostrado na Figura 4. A tabela completa do Excel está anexada abaixo.
Figura 4
A tabela nos permite avaliar quanto o passeio aleatório pode ir verticalmente em 40 passos. A taxa qs (na equação da tabela) permite definir o número de amostras para as quais a tabela é construída. No exemplo, a tabela foi construída para 100,000 amostras. A coluna "vertical steps" apresenta o número de passos em que a função vai verticalmente, enquanto a coluna "probability of event %" exibe a frequência desses passos verticais. Por exemplo, o processo tem 40 passos no total e é capaz de subir ou descer 40 passos, nós temos 100,000 amostras (medições). Em média, o processo move 40 passos verticais 0.00000009 vezes em 100,000. 38 passos são feitos 0.0000036 vezes, enquanto 36 passos são feitos 0.00007 vezes em 100,000. Assim, definindo o array de valor na coluna "probability of event %", nós podemos construir o gráfico de distribuição da densidade de probabilidade do incremento exibido na Figura 5.
Figura 5
A tabela nos permite obter a distribuição de densidade de probabilidade do incremento de referência em 40 passos para o processo tendo a mudança de direção e as probabilidades de continuação de cada passo subsequente igual a 50%. Para ter certeza de que tudo está correto, nós podemos medir a distribuição de densidade de probabilidade para o passeio aleatório e compará-la com a referência. As medidas são feitas para o passeio aleatório cujos fragmentos são apresentados nas Figuras 2 e 3. Eu vou medir quantos passos verticais a função deu em 40 passos e 100,000 amostras (medições). Os resultados são exibidos na Figura 6. O eixo Х mostra as amplitudes de -40...0... 40 passos verticais, enquanto o eixo Y especifica o número de eventos para cada número de passos verticais.
Figura 6
A distribuição de referência para 100,000 amostras de 40 passos cada (calculada de acordo com a tabela) é exibida em vermelho, enquanto o histograma branco mostra as 100,000 amostras realmente medidas do passeio aleatório gerado. Como nós podemos ver, a distribuição de referência e o histograma são quase idênticos. Os desvios são insignificantes. Quanto mais amostras nós usarmos, mais precisos os valores medidos corresponderão aos de referência. Agora nós podemos definir o quanto uma distribuição em série difere da de referência. Considerando a distribuição de probabilidade de incremento, eu posso atualmente supor que a série analisada corresponde ao passeio aleatório com a maior precisão possível. Eu explicarei por que isso é necessário mais tarde.
Distribuição incremental no mercado real
Para realizar as medições, vamos usar o gráfico GBPUSD real e transformá-lo em um gráfico de blocos com o tamanho do bloco igual a 0.00022. Como no exemplo acima, calculamos quanto o preço mudou verticalmente em 40 passos usando 100,000 amostras e comparamos com a referência na Figura 7.
Figura 7
Como antes, a distribuição de referência é exibida em vermelho, enquanto a medida é exibida em branco. Agora eu vou precisar da simplificação que apresentei antes (combinatória em vez da função gaussiana). Nós podemos ver que a distribuição dos incrementos de GBPUSD é simétrica em relação a zero. A simetria em relação a zero indica a ausência de inclinação distinta para as tendências de alta ou de baixa. Isso significa que a probabilidade de cada bloco de alta ser seguido pelo bloco de baixa é igual à probabilidade de cada bloco de baixa ser seguido pelo bloco de alta. Em outras palavras, não há inclinação visível para o movimento de preços para cima ou para baixo.
O gráfico de distribuição do GBPUSD sendo menor e mais largo do que a referência é muito mais interessante. Isso indica que, em 40 passos, o preço passa de zero com muito menos frequência do que deveria para a caminhada aleatória e costuma passar verticalmente por muito mais blocos. Isso significa que a probabilidade do próximo passo mudar sua direção é ligeiramente inferior a 50%. O gráfico sugere que a probabilidade de um bloco de alta ser seguido por outro bloco de alta excede 50%, assim como a probabilidade de um bloco de baixa ser seguido por outro bloco de baixa.
Como isso pode ser útil para nós? Vamos lembrar a equação do retorno esperado, que nos permite avaliar o lucro. Toda a questão de obtenção do lucro é que se a probabilidade de uma entrada "correta" fosse superior a 50%, então nós continuaríamos lucrando, desde que a perda média fosse igual ao lucro médio. Para obter lucro, nós precisamos quebrar o "equilíbrio de 50%". Atualmente, eu não avaliei a probabilidade exata de reversão. Ele pode ser calculado usando o gráfico, mas se assumirmos que a probabilidade de continuação neste gráfico é de 55%, enquanto a probabilidade de reversão é de 45% e o lucro médio corresponde à perda média e é igual a 10 passos (tamanho do passo 0.00022*10=0.0022), então o retorno esperado m=(55*0.0022)-(45*0.0022)=0.121-0.099=0.022. Por sua vez, isso significa que após completar 100 negócios, nós continuaremos com o lucro de 0.022. Se nós negociarmos 0.1 lote em GBPUSD, isso significa $220 de lucro.
Sabendo que a probabilidade de continuação da tendência excede 50%, nós podemos usar uma estratégia de continuação da tendência, ou seja, comprar após um bloco de alta. Em outras palavras, se a probabilidade de continuação da tendência exceder 50%, nós usamos uma estratégia de acompanhamento de tendência e obtemos lucro. Por outro lado, se nós sabemos que a probabilidade de uma reversão é maior do que 50% (blocos para cima são mais frequentemente seguidos por blocos para baixo), nós abriremos uma posição de venda toda vez que um bloco para cima for fechado e obteremos lucro usando uma estratégia de contra tendência (lateralização).
Definição de tendência/lateralização
A definição de tendência/lateralização depende diretamente da estratégia que usamos para obter lucro em um determinado mercado. Se, no caso do passeio aleatório, a probabilidade de continuação da tendência for de 50% e o passeio aleatório não se basear na tendência, nem em lateralização, então:
No caso de um movimento de tendência, a probabilidade de continuação da tendência excede a probabilidade de reversão da tendência. Se o preço se mover 10 pontos, ele se moverá mais 10 pontos na mesma direção com a probabilidade de ultrapassar 50%.
No caso de um movimento lateral, a probabilidade de uma reversão da tendência excede a probabilidade de continuação da tendência. Se o preço se mover 10 pontos, ele reverterá e moverá outros 10 pontos na direção oposta com uma probabilidade excedendo os 50%.
Se o preço for exibido como blocos (como eu descrevi acima) de 10 pontos cada, então o movimento da tendência sugere a abertura de Compra após cada bloco de alta subsequente ser fechado e a abertura de Venda após cada bloco de baixa subsequente. Por outro lado, o movimento lateral sugere a abertura de Venda após cada bloco de alta e de Compra após cada bloco de baixa.
Em outras palavras, se o mercado está em tendência, nós simplesmente operamos em sua direção. Se o mercado estiver lateral, negociamos reversões. Se o mercado não estiver em tendência, nem lateralizado, não entre nele.
Não estou dizendo aqui que é impossível ganhar dinheiro no passeio aleatório. Este é um tópico para um estudo separado e rigoroso.
Verificando a afirmação
Afirmações aparentemente lógicas às vezes se revelam falsas. Portanto, vamos verificar as conclusões usando um modelo simples. Para fazer isso, nós criamos 2 processos com probabilidade de reversão de 80% (Figura 8) e 20% (Figura 9).
Figura 8
Figura 9
A Figura 8 mostra que a distribuição da densidade de probabilidade medida é muito mais estreita do que a de referência. O processo retorna a zero com muito mais frequência. A Figura 9 mostra que a distribuição da densidade de probabilidade medida é muito mais ampla do que a de referência. O processo retorna a zero com muito menos frequência. Assim, nós podemos concluir que as operações realizadas anteriormente estão corretas, assim como a lógica. Se a probabilidade de reversão for inferior a 50%, então a distribuição acaba sendo mais ampla do que a de referência, e então essa lógica pode ser usada para analisar o grau de tendência de um determinado instrumento. Aqui, eu vou apresentar o conceito de "tendência", que reflete quantitativamente a inclinação do processo de continuação da tendência.
Estimando o grau de tendência do instrumento
Tendo um valor de referência, nós podemos estimar o grau de tendência de diferentes períodos de um instrumento e de diferentes instrumentos em valores absolutos. Mas primeiro nós precisamos desenvolver um método para comparar os valores absolutos. Eu sugiro dois métodos:
- Por desvio de densidade. Selecionamos uma faixa de amplitudes e contamos quantos eventos caíram nesta faixa para referência. Em seguida, fazemos o mesmo para os valores medidos. Dividimos o valor de referência pelo valor medido para a obtenção de unidades absolutas. Se o valor exceder 1, então a série é de natureza de tendência; se for menor que 1, a série é lateral. Por exemplo, toda a faixa de amplitude é -40...0...40. Não vale a pena contar quantos valores caem no intervalo -40...40, porque 100% dos valores caem aí, então vamos pegar outro valor. De acordo com a teoria da probabilidade "cerca de 68% dos valores da distribuição normal estão localizados a uma distância de não mais de um desvio padrão σ da média; cerca de 95% dos valores estão localizados dentro de dois desvios padrão, enquanto 99,7% podem ser encontrados em não mais do que três desvios padrão". Ou seja, é considerado normal definir quantos eventos se enquadram em um determinado intervalo e comparar isso com a distribuição normal. No entanto, eu não medi o desvio padrão em meu trabalho porque não é necessário. Portanto, eu usarei números absolutos. Eu prefiro o seguinte método:
- Na referência, definimos o percentual da amostra na qual estamos interessados. Por exemplo, nós estamos interessados em 80% das amostras. Isso significa que nós devemos definir a faixa em que esses 80% das amostras se enquadram. Nosso exemplo apresenta 100,000 amostras, o que significa que 80% são 80,000 amostras. Vamos calcular a faixa de amplitude em que essas 80,000 amostras se enquadram. 84.6% das amostras caem na faixa de -8...8, enquanto 73.18% das amostras caem na faixa de -6...6. 84.6% está mais próximo de 80%, então definimos quantas amostras se enquadram na faixa de -8...8 — são 84,614 amostras.
- Agora vamos definir quantas amostras se enquadram na faixa de -8...8 na distribuição construída para a série com probabilidade de reversão de 80%. Em nosso caso, o intervalo apresenta 100,000 amostras. 84,614/100,000=0.8416. Assim, o grau de tendência é 0.8416 para o gráfico da Figura 8.
- Verificamos o grau de tendência do gráfico na Figura 9. O intervalo de -8...8 apresenta 52,034 amostras, portanto, nós obtemos o grau de tendência da série com a probabilidade de reversão de 20% 84,614/52,325 = 1.617.
- Pela amplitude média. Do teorema do limite central, nós podemos concluir que a amplitude vertical média do passeio aleatório é proporcional à potência de 0.5 do número de passos. Anteriormente, eu fiz a tabela para construir a distribuição de referência parcialmente exibida na Figura 4. Além de outras coisas, ele apresenta a célula "bloco médio verticalmente" que calcula o número médio de passos verticais passados pelo passeio aleatório de referência. Este número foi encontrado como a soma da coluna de "frequência da amplitude" para o intervalo de 0 a 40 passos verticais dividido pelo número de amostras (aqui é 100,000). Na tabela, esse é o valor de 5.0148. Isso significa que a caminhada média passa de -5.0148...5.0148 passos verticais para 40 passos em média. Isso é proporcional à potência de 0.437 do número de passos. O desvio da potência de 0.5 decorre do fato de que damos apenas 40 passos, e o teorema do marinheiro bêbado diz que o passeio aleatório deve ser aproximadamente proporcional à potência de 0.5 do número de passos. Usando a tabela, nós obtivemos o valor exato para o número de passos fornecido.
- Se nós medirmos o número médio de passos verticais que foi passado pelo processo com a probabilidade de reversão de 50% e exibido nas Figuras 2 e 3, nós receberemos 5.0363. Vamos definir o grau de tendência da série com a probabilidade de reversão de 50%. Para isso, dividimos o valor de referência pelo valor medido 5.0148/5.0363 = 0.9957. Como podemos ver, o grau de tendência é quase 1, sugerindo que a série está o mais próxima possível do passeio aleatório, e nossa lógica está correta.
- Calculamos o grau de tendência para o processo com 80% de probabilidade de reversão. Para fazer isso, devemos medir sua amplitude média. Ela é igual a 1.6495. A seguir, dividimos o valor medido pelo valor de referência 1.6495/5.0148=0.3289. O valor é muito inferior a 1, o que significa que a série analisada tem baixa tendência.
- Calculamos o grau de tendência para o processo com a probabilidade de reversão de 20%. Para fazer isso, devemos medir sua amplitude média. Ela é igual a 9.95. A seguir, dividimos o valor medido pelo valor de referência 9.95/5.0148=1.98. O valor é quase 2 vezes superior a 1, sugerindo que a série analisada apresenta um alto grau de tendência.
Com essa ferramenta, nós podemos comparar diretamente os graus de tendência em diferentes escalas (tempo gráfico) de um instrumento e avaliar visualmente os seus parâmetros estatísticos. Como exemplo, vamos usar os mesmos 2 processos com probabilidades de reversão de 20% e 80% e avaliar visualmente seus parâmetros estatísticos em escalas diferentes. Anteriormente, eu usei o tamanho do bloco igual a 1 ponto. Agora eu vou criar blocos de tamanho maior, multiplicando cada tamanho de bloco subsequente pela proporção de 1.1. Assim, eu vou obter várias escalas com os tamanhos de bloco de 1; 1.1; 1.21; 1.33 ..... 6.12. A Figura 10 mostra como a tendência muda com o aumento da escala para o processo com probabilidade de reversão de 80%. A Figura 11 mostra o mesmo para o processo com probabilidade de reversão de 20%.
Figura 10
Figura 11
Nas Figuras 10 e 11, a menor escala (1 ponto) está localizada à esquerda, enquanto a maior está localizada à direita no eixo X. O eixo Y apresenta o grau de tendência do instrumento calculado usando o grau de "amplitude média". Na Figura 10, onde o processo de probabilidade de reversão de 80% é inicialmente lateralizado, a primeira coluna do histograma tem uma tendência baixa, mas conforme a escala aumenta, a tendência tende a 1 (o valor de referência do passeio aleatório). Isso sugere que, apesar da probabilidade de reversão na menor escala ser alta, o mesmo não é verdade para escalas maiores onde o processo perde "memória" e se transforma em um passeio aleatório. A Figura 11 mostra uma imagem semelhante. Se inicialmente o processo tem um alto grau de tendência de 2.053, ele é reduzido e tende ao valor de referência do passeio aleatório em escalas maiores.
As Figuras 10 e 11 demonstram que o processo tem "memória" apenas na menor escala e se torna mais e mais parecido com o passeio aleatório à medida que a escala aumenta. Esta conclusão é corroborada pela criação da série. Ao gerar esses dois processos, apenas a direção do passo anterior foi considerada. Os passos restantes não foram levados em consideração, pois o efeito "memória" rapidamente se dissipa com o aumento da escala.
Construindo a dependência do grau de tendência no número de passos
Os mercados reais são diferentes das séries geradas sinteticamente. A detecção de padrões requer mais ferramentas de análise. Portanto, ele seria útil não apenas analisar o grau de tendência em um número fixo de passos, mas também avaliar como a tendência do mercado muda com um aumento no número de passos. Como as tabelas de referência podem ser construídas para um número diferente de passos, nós podemos visualizar simultaneamente não apenas como a ferramenta se comporta com o aumento do tamanho do passo, mas também como ela se comporta quando o número de passos aumenta. A Figura 12 mostra a dinâmica do grau de tendência do GBPUSD para 10,000 amostras com o tamanho do bloco de 0.00314, para o número de passos de 10 a 100. A coluna mais à esquerda do histograma foi construída para 10 passos, enquanto a coluna mais à direita foi construída para 100 passos. Em cada coluna do histograma, o número de passos é aumentado para 2.
Figura 12
De acordo com a Figura 12, na escala atual, a tendência do GBPUSD excede o valor 1 e flutua na faixa de 1.133-1.166 dependendo do número de passos para as quais a análise é realizada. A Figura 13 mostra como o grau de tendência muda com o aumento da escala. O gráfico foi construído para 10,000 amostras de 40 passos cada, para tamanhos de passo de 0.00021 a 0.00495. A coluna mais à esquerda do histograma foi construída para o tamanho de bloco de 0.00021, enquanto cada coluna do histograma subsequente excede a anterior em 1.1 vezes.
Figura 13
A Figura 13 mostra como o grau de tendência diminui com o aumento da escala. Embora ela seja igual a 1.425 para a menor escala, ela já tende a 1 e seu maior valor é igual a 1.062. Enquanto a escala aumenta, o comportamento do GBPUSD tem mais semelhança com o comportamento de uma série sintética com 20% de probabilidade.
Essa abordagem nos permite avaliar dinamicamente a velocidade de mudança do grau de tendência do instrumento de negociação. A animação abaixo mostra a dinâmica da distribuição de densidade de probabilidade do incremento para ações AMD em relação à distribuição de referência. São utilizados como base as velas de período M1. A animação é construída para 40 passo, 1000 amostras. O tamanho do bloco muda dinamicamente dependendo da volatilidade média atual.
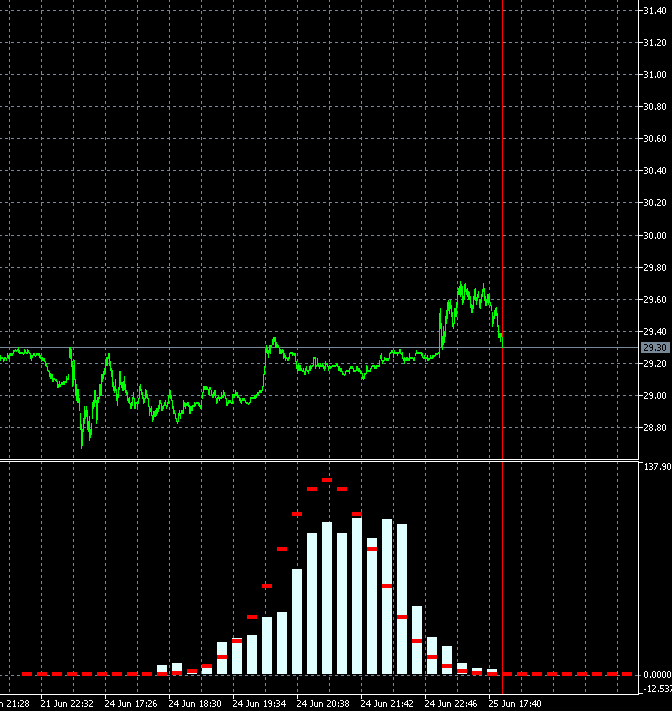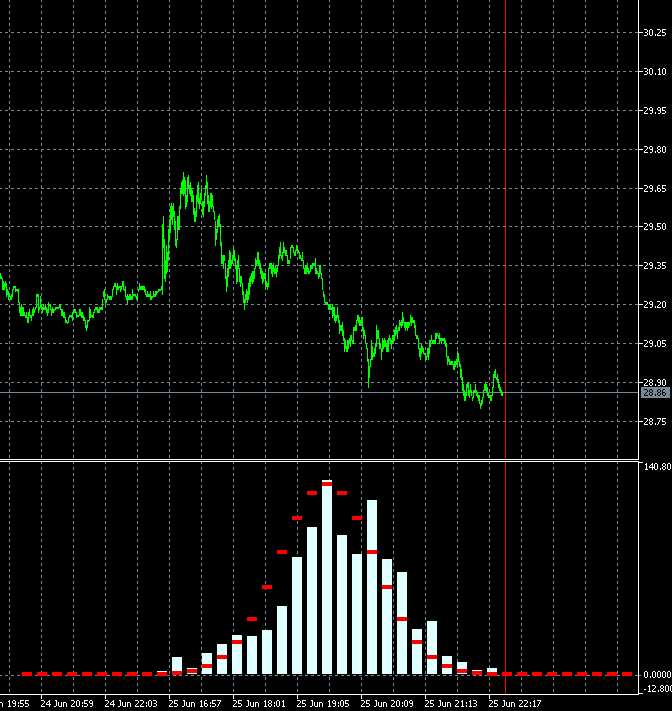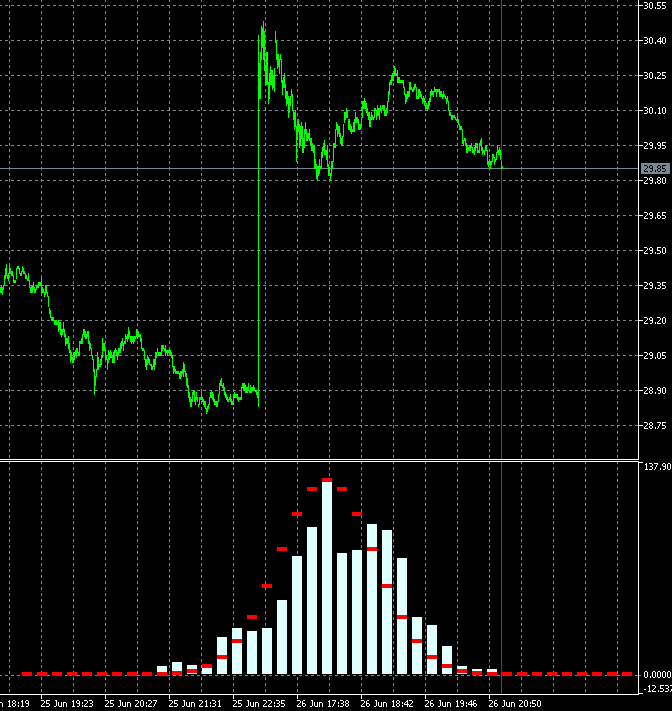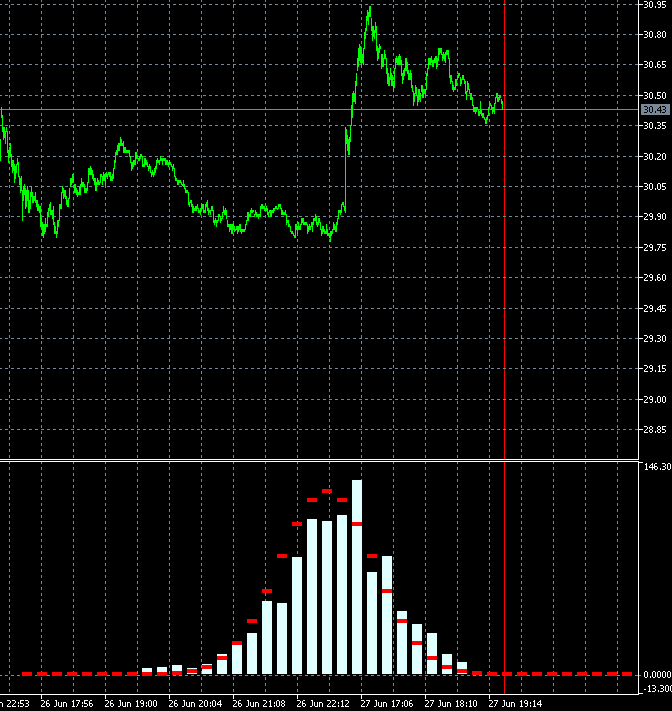
Ao contrário do GBPUSD, a distribuição da densidade de probabilidade do incremento de ações da AMD não é simétrica a zero. O componente de tendência de alta está claramente presente. Isso significa que a probabilidade de continuação da tendência é ligeiramente maior quando um passo ascendente é seguido por um passo ascendente em comparação com o caso quando um passo descendente é seguido por um passo descendente. Isso significa que é mais razoável abrir negociações de Compra em tal instrumento. Nesse caso, é possível permanecer no lucro mesmo ao entrar no mercado em pontos aleatórios.
A estrutura do mercado se baseia em tendência ou lateralização?
Considerando tudo o que foi dito acima, nós podemos fazer uma pergunta, se nos mercados predominam a tendência, lateralização ou o movimento aleatório. Responder à pergunta nos permitirá definir qual estratégia e análise aplicar. Eu analisei mais de 30 pares de moedas, mais de 50 ações do mercado da Rússia e dos EUA, bem como criptomoedas e mercados de commodities. Os mercados de commodities incluíam metais, energia e alimentos. Com base em minha pesquisa, eu posso concluir que:
- Os pares de moedas mais desenvolvidos têm uma tendência fraca que diminui com o aumento da escala e do volume de negociação. Por exemplo, o EURUSD possui menor tendência do que o GBPUSD. A densidade de distribuição de probabilidade no Forex está próxima da distribuição normal.
- O mercado de ações está em maior tendência do que as moedas, mas a tendência ainda é reduzida com o aumento da escala. Ativos que estão se desenvolvendo estão em maior tendência do que os ativos de empresas desenvolvidas. Quanto menos uma empresa estiver inclinada ao desenvolvimento e quanto menor for o seu potencial, menor será a tendência de sua ação. Ativos completamente "desinteressantes" podem exibir um movimento lateral. Quanto maior a liquidez do instrumento, menor o grau de tendência. Analisar a distribuição de tendência no contexto de escala nos permite entender a estrutura do fluxo de capital. Suponha que uma ação esteja em tendência em uma escala menor e lateral em uma escala maior. Isso indica que a empresa não está se desenvolvendo, enquanto o dinheiro é investido apenas por um curto prazo. Em outras palavras, as formas de distribuição mostram se um instrumento é de investimento ou de natureza puramente especulativa. Assim, o gráfico permite avaliar a classificação de crédito de uma empresa, ainda que de forma indireta.
- O mercado de commodities apresenta tendência e instrumentos laterais, dependendo da demanda atual por matérias-primas e nível de produção. Se a demanda cresce enquanto a produção permanece inalterada, o instrumento fica mais na tendência. Da mesma forma, se a demanda cair, o grau de tendência também cresce, desde que o nível do produto permaneça inalterado. Se a oferta e a demanda de commodities estão próximas do equilíbrio, seu movimento se torna mais lateral.
- As criptomoedas estão mais na tendência no estágio de crescente interesse e aumento do volume de negócios. Eles se tornam mais laterais quando o interesse público diminui. Como resultado, o preço de todo o seu histórico tende para o passeio aleatório. Mas assim que uma nova onda começa, o instrumento fica em tendência novamente.
Aqui nós podemos tirar conclusões mais amplas, mas este é um assunto para outro artigo.
Abaixo estão alguns gráficos que descrevem as características dos instrumentos de negociação.
- O BTCUSD torna-se lateral quando a empolgação com a criptomoeda diminui. Curiosamente, a distribuição da densidade de probabilidade para o bitcoin é simétrico em relação a zero, apesar do fato de que visualmente parece que o bitcoin apresenta uma tendência de alta.
- As ações da AMD e AAPL apresentam tendências consistentes, com algumas pequenas quedas. A distribuição de densidade de probabilidade é deslocada para a direita em relação a zero na direção de movimentos de alta. Além disso, é visualmente claro que essas ações têm uma tendência constante de alta.
- O petróleo está em tendência em geral, mesmo em escala crescente.
- No EURUSD, a tendência quase desaparece em grandes escalas. O instrumento fica lateral em algumas escalas. Em geral, ele tende à distribuição da densidade de probabilidade do passeio aleatório mais do que outros.
- Os líderes do mercado russo são semelhantes entre si - tendências estáveis em pequena escala e praticamente nenhuma tendência em grande escala.
Por que um instrumento tem mais tendência em uma escala menor e mais lateral em uma escala maior? No próximo artigo, eu tentarei explicar as razões para tal comportamento. Eu vou desenvolver o algoritmo com base na pesquisa atual e ver se ele é lucrativo.
Conclusão
Os conceitos de tendência e lateralização podem ser definidos de forma clara e completa. Além disso, é possível comparar o grau de tendência de diferentes instrumentos, bem como de um único instrumento em diferentes escalas. Tal análise nos permite avaliar as características e recursos dos instrumentos e construir algoritmos de negociação considerando o comportamento individual de cada instrumento.
Conhecendo as características estatísticas de um instrumento e suas mudanças ao longo do tempo, nós podemos nos livrar dos parâmetros de otimização ao desenvolver um algoritmo de negociação. Em vez disso, nós podemos realizar medições e alterar deliberadamente os parâmetros do algoritmo de negociação, dependendo das características estatísticas de um instrumento negociado.
Abaixo estão os arquivos com o histórico dos gráficos de reversão de probabilidade de 20%, 50% e 80%. Além disso, existe um arquivo em Excel para a construção de uma distribuição de referência, bem como os blocos de construção dos indicadores usados para a análise.
O algoritmo do indicador foi desenvolvido por Maxim Romanov, o código do indicador foi criado por Konstantin Gruzdev.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8184
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
Redes neurais de maneira fácil (Parte 2): Treinamento e teste da rede
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Como obtê-lo.
No momento, de jeito nenhum, não estou distribuindo esse indicador agora. Talvez no futuro eu crie outro indicador e possa compartilhá-lo
As barras do histograma saltam de forma suspeita quando são alteradas em apenas 1 barra: supostamente, 1 barra de 1.000 deve ser removida do final e 1 barra deve ser adicionada no início. Ou seja, a alteração deve ser na proporção de 1/500 para todas as barras do histograma de uma só vez, praticamente 1 ou 2 barras devem mudar.

Pensei que talvez a velocidade estivesse alta e eu não estivesse percebendo a suavidade...
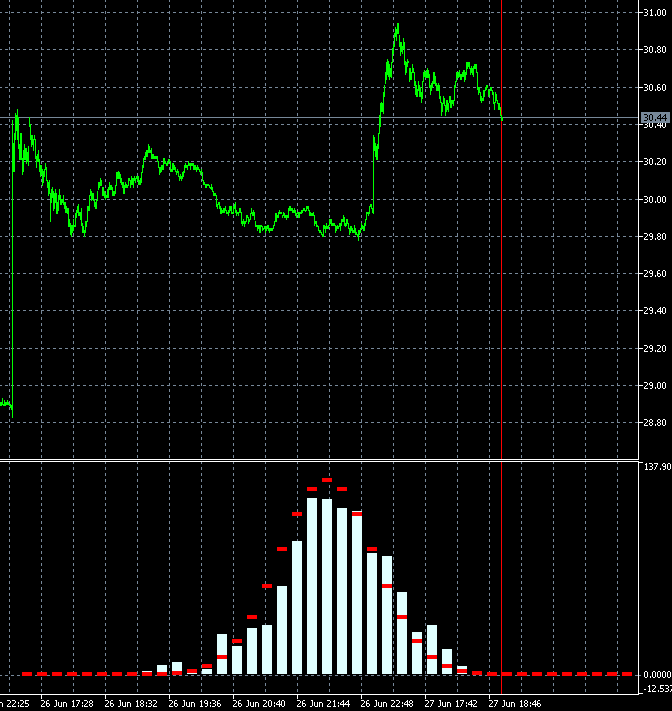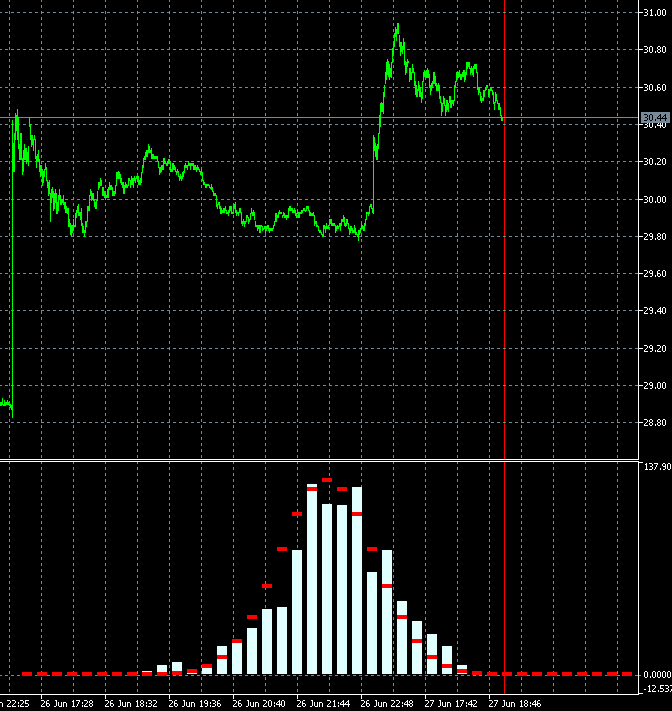
Copiei dois quadros 340 e 341 com barras vizinhas e os tornei mais lentos:
As alterações são muito fortes em todas as barras ao mesmo tempo. Talvez haja um erro em algum ponto do cálculo? 2 barras em 1000 não podem mudar o quadro dessa forma.
Parece que não foram 2 barras que mudaram no cálculo, mas todas as 1000, como se a janela para 1000 (para uma semana, mês...) tivesse se deslocado para o passado, e não para 1 barra.
As barras do histograma saltam de forma suspeita quando são alteradas em apenas 1 barra: supostamente, 1 barra de 1.000 deve ser removida do final e 1 barra deve ser adicionada no início. Ou seja, a alteração deve ser na proporção de 1/500 para todas as barras do histograma ao mesmo tempo, praticamente 1 ou 2 barras devem mudar.
Pensei que talvez a velocidade estivesse alta e eu não percebesse a suavidade...
Copiei dois quadros 340 e 341 com barras vizinhas e os tornei mais lentos:
As alterações são muito fortes em todas as barras ao mesmo tempo. Talvez haja um erro em algum ponto do cálculo? 2 barras em 1000 não podem mudar o quadro dessa forma.
Parece que não foram 2 barras que mudaram no cálculo, mas todas as 1000, como se a janela para 1000 (para uma semana, mês...) tivesse se deslocado para o passado, e não para 1 barra.
Sim, isso pode parecer suspeito, mas há uma peculiaridade na construção dos blocos. Os blocos não são construídos no futuro, mas no passado, a partir da última data. Assim, quando surge uma vela, o preço dos blocos de construção muda e os próprios blocos acabam sendo diferentes. Uma mudança de até 10 pontos pode alterar a configuração dos blocos e, consequentemente, a forma da distribuição.
Por que fiz dessa forma. Há dois motivos
1. O método de construção de blocos é muito sensível ao preço inicial e eu queria ver como a distribuição muda quando se constrói a partir de preços diferentes. Essa abordagem me permitiu ver, de forma dinâmica, como a distribuição muda ao longo do tempo e como a distribuição muda em relação ao preço inicial.
2. Criei um indicador de bloco para um robô grande e lá usei exatamente essa abordagem para evitar a otimização de parâmetros para o histórico. Como as configurações de bloco mudam muito em relação às condições iniciais, um deslocamento de 1 dia para frente/para trás elimina toda a otimização de parâmetros para o histórico. Dessa forma, podemos evitar o ajuste aproximado ao histórico e avaliar a estabilidade dos padrões detectados. Para mim, era importante criar um robô que funcionasse em qualquer instrumento de negociação sem otimizar os parâmetros
Sim, isso pode parecer suspeito. Mas há uma peculiaridade na construção de blocos. Os blocos não são construídos no futuro, mas no passado, a partir da última data. Assim, quando surge uma vela, o preço dos blocos de construção muda e os próprios blocos acabam sendo diferentes. Uma mudança de até 10 pips pode alterar a configuração dos blocos e, consequentemente, a forma da distribuição.
Por que fiz dessa forma. Há dois motivos
1. O próprio método de construção de blocos é muito sensível ao preço inicial e eu queria ver como a distribuição muda ao construir a partir de preços diferentes. Essa abordagem me permitiu ver, de forma dinâmica, como a distribuição muda com o tempo e como a distribuição muda com a alteração do preço inicial.
2. Criei um indicador de bloco para um robô grande e lá usei exatamente essa abordagem para evitar a otimização de parâmetros para o histórico. Como as configurações de bloco mudam muito em relação às condições iniciais, um deslocamento de 1 dia para frente/para trás elimina toda a otimização de parâmetros para o histórico. Dessa forma, podemos evitar o ajuste grosseiro ao histórico e avaliar a estabilidade dos padrões detectados. Para mim, era importante criar um robô que funcionasse em qualquer instrumento de negociação sem otimizar os parâmetros
Entendi o motivo de tais saltos, mas ainda não gosto dele. Esse indicador de histograma está publicado em algum lugar? É interessante vê-lo ao vivo, não em uma imagem.
Pensei no algoritmo de cálculo do MA: 1 removido, 1 adicionado.
Entendi o motivo de tais saltos, mas ainda assim não gostei. Esse indicador de histograma está publicado em algum lugar? É interessante vê-lo ao vivo, não em uma imagem.
Não, eu não publiquei um indicador pronto