
Aplicando a teoria da probabilidade na negociação de gaps
Conteúdo
- Introdução
- Considerações gerais sobre os Expert Advisors
- Estratégia de negociação como tentativa de rejeitar a hipótese do passeio aleatório
- Estratégia de negociação de Gap
- Testando a estratégia e calculando o risco ideal por negócio
- Conclusão
- Arquivos anexados
Introdução
O artigo continua o tópico da aplicação da teoria da probabilidade e estatística matemática na negociação, iniciado nos artigos anteriores do autor. Nós vamos considerar o possível uso dos métodos apropriados para criar e testar estratégias de negociação.
Primeiro, nós veremos como encontrar as oportunidades de negociação como detectar desvios da hipótese do passeio aleatório. Está provado que, se os preços se comportarem como um passeio aleatório de deslocamento de zero (sem tendência direcional), então a negociação com lucro é impossível. Isso fornece uma base para encontrar maneiras de refutar essa hipótese. Se uma maneira de refutar a hipótese for encontrada, nós podemos tentar usá-la para desenvolver uma estratégia de negociação.
Nós também vamos continuar estudando o tópico de risco que começamos nos artigos publicados anteriormente. Mais adiante, nós nos vamos nos referir a eles como primeiro e segundo artigos.
Uma vez que nossa abordagem é baseada na teoria da probabilidade, a compreensão de seus fundamentos é aconselhável, mas não obrigatória. É importante entender a essência dos métodos probabilísticos - quanto mais sistematicamente e frequentemente eles são usados, mais notável e significativo é o resultado obtido (devido à lei dos grandes números). Evidentemente, sua aplicação deve ser suficientemente fundamentada e adequada.
Considerações gerais sobre os Expert Advisors
O desenvolvimento de EAs pode ser dividido em três etapas:
- Gerar uma ideia.
- Verificar a ideia usando todos os tipos de simplificações.
- Adaptar a ideia às realidades do mercado.
O artigo lidará principalmente com a segunda etapa, permitindo que nos concentremos detalhadamente no tópico declarado. Além disso, esta etapa é discutida no fórum com muito menos frequência do que as outras.
Vamos descrever as simplificações implementadas. Nós nos limitaremos aos EAs negociando um único ativo. Nós vamos assumir que o preço do ativo é expresso na moeda da conta. Nós vamos excluir as operações sem negociação (como swap e retirada de fundos da conta) e não consideraremos diferentes tipos de ordens (deixando apenas a compra e venda à mercado). Nós vamos negligenciar o desvio ao executar ordens, enquanto o spread (s) deve ser considerado como um valor fixo. Nós também iremos assumir que o EA gerencia todos os fundos em nossa conta, e não há outros EAs nesta conta.
Com todas essas simplificações, o resultado da operação do EA é definido sem ambigüidade como a função v(t) - volume da posição dependendo do tempo. v(t) positivo corresponde a compra, enquanto que negativo significa venda. Além disso, existe a função p(t) (preço do ativo) e c0 (saldo inicial). A imagem abaixo mostra um possível gráfico da posição v=v(t).
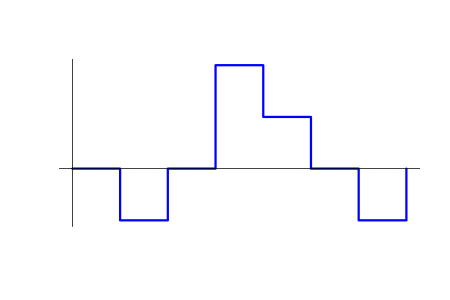
A média aritmética entre os preços de compra e venda.
A v(t) e p(t) são constantes por partes (passo a passo) porque seus valores são múltiplos de algumas etapas de incremento mínimo. Se uma definição matemática mais rigorosa é necessária, então elas podem ser consideradas contínuas da direita e ter um limite nos pontos de gap à esquerda. Nós assumimos que os pontos de gap de v(t) nunca coincidem com a p(t). Em outras palavras, não mais que um valor dos dois pode mudar a qualquer momento - um preço, um volume da posição ou ambos permanecem inalterados. Vale a pena notar que os pontos no tempo, nos quais as alterações de preço ou volume podem ocorrer, também são múltiplos de uma certa etapa mínima.
Com base nesses dados, nós podemos encontrar a função c(t) - o valor dos fundos, dependendo do tempo. Ele é definido como o valor do saldo para a parte da conta gerenciada pelo EA no caso de encerrarmos uma posição no momento t. Como temos um único EA na conta, esse valor coincide com o patrimônio da conta definido na MetaTrader 5.
Definido c(t) que se altera conforme t. Se o volume e o preço não mudarem neste momento, então ele é naturalmente zero. Se o preço muda, o aumento do saldo é igual ao produto do volume pelo incremento de preço. Se o volume muda, duas opções são possíveis - quando o volume da posição absoluta é diminuído, os fundos permanecem os mesmos, quando é aumentado, os fundos são diminuídos em um montante igual ao produto do spread pelo valor absoluto da variação do volume. Em outras palavras, se uma posição for encerrada parcialmente, o patrimônio líquido não se altera, ao passo que o acréscimo à posição leva à uma pequena desvalorização do patrimônio líquido. Portanto, o valor do saldo c(t) no momento t é igual à soma de c0=c(0) e todas as suas alterações que ocorreram a partir do momento zero até t.
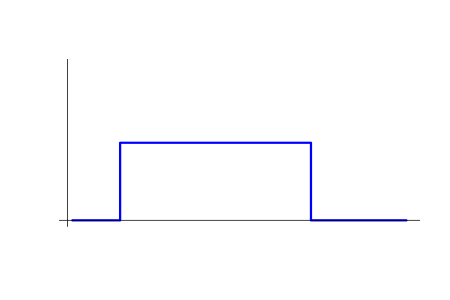
Ao desenvolver nossa teoria de risco (nos dois artigos anteriores), nós usamos o conceito de 'negócio'. Este conceito não coincide exatamente com o que é chamado de 'negócio' na MetaTrader 5 e corresponde mais ao que é chamado de 'negociação' lá. Para ser exato, ele corresponde ao que chamamos de posição simples. Uma posição simples, por nossa definição, é definida pelos momentos de abertura e fechamento. Seu volume e direção permanecem constantes entre esses momentos. Abaixo está um exemplo do gráfico v=v(t) para uma posição simples.
Qualquer posição (uma vez que ele é sempre constante por partes) pode ser imaginada como uma soma de posições simples. Tal representação pode ser feita de um infinito número de maneiras. O gráfico abaixo mostra uma única posição representada de duas maneiras diferentes como uma soma de outras simples. A posição inicial é exibida em azul, enquanto os negócios nos quais ela é dividida são exibidos em verde e vermelho. Ao usar um conceito de negociações na MetaTrader 5, temos ainda outra opção. Cada um desses métodos pode ser bastante razoável.
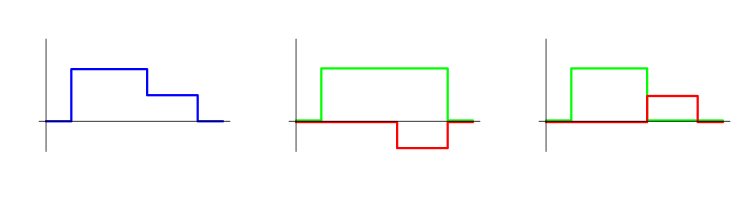
Existem alguns EAs, para os quais tais representações não fazem muito sentido. Por exemplo, pode haver EAs em que uma posição é gradualmente aumentada e gradualmente diminuída posteriormente. Ao mesmo tempo, existem EAs, para os quais tal apresentação é bastante natural. Por exemplo, uma posição pode consistir em uma sequência de posições simples que não se cruzam no tempo. O quadro abaixo contém exemplos de tais posições.
A variação relativa do saldo c1/c0 após cada negócio (posição simples) é expresso em dois valores - rentabilidade a e risco r: c1/c0=1+ra. A rentabilidade é igual à razão entre o aumento do preço durante o negócio e a diferença entre os preços de entrada e o stop loss, enquanto o risco é proporcional ao volume negociado e significa uma parte do saldo que seria perdido em caso da ativação exata do stop loss.
Assim, em vez de considerar as funções pelo tempo v(t), p(t) e c(t), recorremos à análise de seqüências numéricas que caracterizam a sequência de negócios. Isso simplifica muito o estudo adicional. Em particular, evitamos a necessidade de aplicar a teoria de processos aleatórios, limitando-nos a conjuntos finitos de variáveis aleatórias quando procedemos ao modelo probabilístico de incerteza.
A teoria da probabilidade é um método geralmente aceito de modelagem matemática da incerteza no comportamento dos preços dos ativos e nos resultados da negociação. De acordo com esta abordagem, nós devemos considerar as funções v(t), p(t) e c(t) como implementações específicas (trajetórias) de alguns processos aleatórios. Em termos gerais, essa tarefa é praticamente insolúvel. A principal razão é a falta de modelos probabilísticos adequados que descrevam com precisão o comportamento dos preços. Portanto, faz sentido considerar casos especiais em que uma solução é possível. Como mencionado acima, neste artigo, nós vamos considerar os EAs formando posições que podem ser adequadamente representadas como uma sequência de posições simples (negócios).
Vale ressaltar outra questão relacionada aos EAs - parâmetros. Seria útil considerá-los em detalhes para obter alguma formalização (padronização) do processo de desenvolvimento do EA. Vamos dividir os parâmetros em três tipos:
- Parâmetros históricos. Parâmetros que podem mudar durante a operação do EA de um negócio para outro. Estes são valores de indicadores, hora do dia, dados de notícias, fases da lua, etc. Em geral, são funções pelo tempo, assim como preços ou volumes de posição. No caso de simplificação aplicada, nós podemos considerá-las sequências de números conhecidas no momento de realizar um negócio. Os parâmetros de cada negócio específico (direção, volume, stop loss e take profit) são definidos com base nos valores dos parâmetros históricos.
- Parâmetros atuais. Vamos simplesmente chamá-los de parâmetros para brevidade. Eles são definidos quando um EA inicia a negociação e podem ser aplicados somente ao testar e otimizar o EA.
- Meta-parâmetros definem o algoritmo de otimização do EA, por exemplo, parâmetro de critério de otimização personalizado. Suponha que nós queremos otimizar o EA por dois critérios, embora isso possa ser feito apenas por um. Nós formamos um novo critério dos dois originais, tendo sua soma com alguns pesos. Esses pesos são servidos como meta-parâmetros.
Por exemplo, no EA baseado em gap descrito abaixo, o intervalo mínimo é o parâmetro do EA, enquanto o tamanho de cada lacuna específica é um parâmetro histórico. Neste caso, os meta-parâmetros podem incluir o número do critério de otimização (assumimos que os critérios são numerados em alguma ordem, por exemplo, otimização por lucro é #1, enquanto a otimização por rebaixamento é #2, etc.).
Neste artigo, nós usaremos uma simplificação significativa associada aos parâmetros históricos. Quando nós falamos sobre a distribuição de retornos em um negócio, isso geralmente depende desses parâmetros. Nós assumimos que essa dependência é insignificante. A principal razão é que uma tentativa de levar em conta essa dependência, geralmente, complica excessivamente o modelo, o que pode, eventualmente, levar a um ajuste excessivo.
Estratégia de negociação como tentativa de rejeitar a hipótese do passeio aleatório
Nós já mencionamos a ausência de modelos precisos descrevendo o comportamento do preço. No entanto, existem modelos aproximados que podem ser úteis. Por exemplo, há um modelo de comportamento de preço bem conhecido, considerando os preços como um passeio aleatório com desvio zero (ausência de uma tendência direcionada). Este modelo é chamado de hipótese de passeio aleatório. De acordo com essa hipótese, qualquer EA terá um lucro zero, em média, ou uma perda pequena, se considerarmos um spread.
Provar a impossibilidade de ganhar dinheiro em uma caminhada aleatória é bastante difícil porque requer o envolvimento de um aparato matemático complexo da teoria de processos aleatórios (Cálculo de Itô, Tempo de Parada, etc). Em geral, resume-se à afirmação de que, ao negociar em um passeio aleatório sem uma tendência, o capital é um martingale (teoria da probabilidade, não deve ser confundido como o sistema de apostas martingale). Um martingale é um processo aleatório com seu valor médio (expectativa matemática) sem variação com o tempo. No nosso caso, isso significa que a expectativa matemática do valor do capital a qualquer momento é igual ao seu valor inicial.
Assim, nós devemos começar a considerar uma ideia de negociação buscando desvios de preço estatisticamente significativos do passeio aleatório. Para fazer isso, nós usaremos idéias da teoria da probabilidade e estatística matemática, mas primeiro, vamos fazer algumas observações:
- Qualquer solução desse tipo é de natureza probabilística - sempre há alguma probabilidade diferente de zero de que nossas conclusões estejam erradas.
- Se nosso método não detecta desvios, isso não significa sua completa ausência. Talvez, algum outro método poderia detectar.
- Desvios estatisticamente significativos não garantem a obtenção de lucros positivos estatisticamente significativos - a presença de desvios é necessária, mas não é condição suficiente para isso.
Vamos construir um método para a busca por desvios aleatórios. Para fazer isso, nós vamos considerar alguma variável aleatória, para a qual construiremos uma distribuição de probabilidade empírica baseada em uma amostra formada usando preços reais. Além disso, nós construiremos uma distribuição de probabilidade teórica para o mesmo valor, assumindo que o comportamento do preço é um passeio aleatório. Comparando estas distribuições, nós tomaremos uma decisão sobre a rejeição (ou impossibilidade de rejeitar) a hipótese do passeio aleatório.
Vamos construir um exemplo de um valor adequado. Suponha que no momento inicial t0 no tempo, o preço é igual a p0. Vamos dar outro valor de preço p1 diferente de p0. Aguardar até o momento t1 quando o preço atingir o valor p(t1)=p1. Vamos encontrar o preço p2 na qual está mais distante de p1 fora dos preços no intervalo entre t0 e t1. Vamos introduzir o valor K=(p2-p0)/(p0-p1). A condição p1<p0≤p2 ou p2≤p0<p1 está sempre em vigor, portanto K≥0 em todo os momentos. O gráfico que explica essa ideia é fornecido abaixo. A linha azul significa o nível de preço p0, no momento em que ele cruza o gráfico de preços é t0. A linha vermelha significa o nível de preço p1, no momento em que ele toca o gráfico de preços após t0 é t1. A linha verde significa o nível de preço p2 localizado o mais longe de p1 possível.
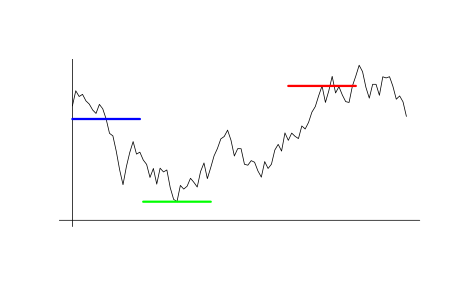
A ideia por trás do valor é simples. Suponha que nós entramos em um negócio em t0. Vamos supor que seja uma venda em p0, enquanto p1, p1>p0 − stop loss. p2 é o preço menos viável para o take profit, enquanto K é o maior lucro viável para um negócio. Na verdade, nós não sabemos o exato valor de K ao realizar um negócio. Dentro da estrutura do modelo probabilístico dessa incerteza, nós podemos apenas falar sobre o conhecimento de seu padrão de distribuição de probabilidade. Suponha que nós conheçamos a função Fk(x) de distribuição de probabilidade, que é definida como a probabilidade em que K<x. Suponha que nós usamos um certo preço pk como um take profit: pk-p0=k(p0-p1). Nesse caso, Fk(k) é igual à probabilidade de que um stop loss seja atingido antes do take profit. Conforme, 1-Fk(k) é igual à probabilidade de que o take profit seja ativado anteriormente. Vamos deixar o spread igual a zero por enquanto. Então, no caso de ativação do stop loss, a rentabilidade é igual a -1, enquanto no caso da ativação do lucro, é igual a k. A expectativa matemática em tal negócio: M=(-1)*Fk(k)+k*(1-Fk(k))=k-(k+1)*Fk(k), que é igual a zero se Fk(k)=k/(k+1).
Se nós sabemos a forma da equação Fk(x), até podemos realizar uma otimização preliminar de um EA. Por exemplo, nós podemos procurar a taxa ótima de take profit/stop loss que maximize a expectativa matemática da lucratividade do negócio. Então, nós podemos encontrar o valor do risco ideal no negócio. Assim, o EA pode ser otimizado antes mesmo de estar pronto. Isso economiza tempo e permite descartar idéias obviamente inadequadas em um estágio inicial.
Se assumirmos que os preços se comportam como um passeio aleatório sem tendência, então a distribuição do valor de K é definido pela função de distribuição Fk(x)=Fk0(x), onde Fk0(x)=0 se x≤0 e Fk0(x)=x/(x+1) se x>0. Para maior certeza, nós podemos supor que o passeio aleatório usado aqui é um processo de Wiener com deslocamento zero (sem tendência). Como nós podemos ver, se a hipótese de passeio aleatório é preenchida e o spread é igual a zero, a expectativa matemática da rentabilidade é igual a zero em qualquer razão de take profit/stop loss. No caso de um spread diferente de zero, ele é negativo.
Em vez de K, nós podemos considerar o valor Q=K/(K+1)=(p2-p0)/(p2-p1), K=Q/(1-Q). Esse valor pode ser representado como a razão de take profit para a soma de stop loss e take profit. É mais conveniente porque leva valores dentro do intervalo [0;1) e tem uma distribuição mais simples do que K (uniforme neste intervalo), no caso de um passeio aleatório.
Mais adiante, nós falaremos principalmente sobre o valor Q. Vamos considerar como sua função de distribuição empírica Fq(x) é construída e aplicada. Suponha que tenhamos uma ideia de negociação, verificamos o histórico de preços. Nós temos um conjunto de n pontos de entrada. O preço de entrada p0,i e o stop loss p1,i, onde i=1,...,n, é definido para cada um deles. Agora nós devemos definir se essa ideia tem algum potencial de lucro. Para cada acordo, devemos encontrar o preço p2,i localizado o mais distante possível do stop loss até o momento de sua ativação. Com base nos preços, nós obtemos a amostra n Qi=(p2,i-p0,i)/(p2,i-p1,i), i=1,...,n. A função de distribuição empírica construída por esta amostra é definida pela equação Fq(x)=m(x)/n onde m(x) é igual ao número de elementos da amostra Qi menores que x. Se os preços se comportam como um passeio aleatório sem uma tendência (processo Wiener com deslocamento zero), a função de distribuição Fq0(x) de valor Q parece simples: Fq0(x)=0 if x≤0, Fq0(x)=x se 0<x≤1, e Fq0(x)=1 se x>1.
Se Fq(x) é significativamente diferente da função de distribuição teórica com um passeio aleatório Fq0(x), nós precisamos verificar o significado dessa diferença em termos de lucratividade. Se a rentabilidade é suficientemente positiva, mesmo que o spread seja levado em consideração, então é hora de escolher a razão apropriada de lucro/stop loss. Isso pode ser feito maximizando a expectativa de lucratividade. Depois disso, nós podemos selecionar um valor ideal para o valor de risco por negócio e passar a testar preliminarmente a ideia. Se o resultado for positivo, faz sentido avançar para a criação de um EA de negociação real. Mais adiante, nós tentaremos mostrar esse algoritmo na prática real.
Surge a questão - como fazer comparações semelhantes com um passeio aleatório para algoritmos de encerramento à mercado mais complexos. A resposta geral é da mesma forma que para o caso considerado acima. A questão principal é que a distribuição de lucratividade em uma passeio aleatório pode ser obtido de forma analítica em raras ocasiões. Mas é sempre possível obter sua aproximação empírica usando o método de simulação de Monte Carlo.
Estratégia de negociação de Gap
Antes de analisar a ideia, devo observar que nossa principal tarefa é demonstrar os métodos de análise, e não estratégias de negociação lucrativas. Muita concentração no lucro nos teria enterrado em detalhes insignificantes que nos distraem do quadro geral.
Os preços dos ativos são discretos e, portanto, sempre mudam rapidamente. Esses saltos podem diferir em tamanho. Quando eles são grandes, eles são chamados de gaps. Não há limites específicos que separem os gaps das alterações de preços usuais. Nós somos livres para estabelecer essa fronteira onde acharmos melhor.
Os gaps são adequadas para demonstrar a teoria descrita na seção anterior. Cada um deles é definido por dois pontos de tempo e preços de ativos dentro deles. Usando a notação de preço anteriormente introduzida, nós assumimos que p0 é o preço posterior, enquanto p1 é o anterior. Entramos em uma negociação assim que o gap ocorrer. O preço p1 pode ser considerado não apenas como um stop loss, mas também como um take profit. Isso significa que nós podemos escolher um sistema de um dos dois tipos - esperando por um rápido fechamento do gap, ou um grande movimento do preço na direção do gap. O fechamento do gap significa que o preço retorna ao nível p1 ou rompe-o.
Uma vez que os gaps em sua forma padrão são relativamente raros para ativos Forex, o autor foi aconselhado a generalizar esse conceito ao discutir o tópico deste artigo com a administração do fórum. Ao definir um gap, você pode abandonar o requisito afirmando que apenas um gap entre dois preços subsequentes é levado em consideração. Obviamente, o número de possíveis gaps neste caso se tornará inimaginavelmente grande e, portanto, vale a pena nos limitarmos às opções razoáveis do ponto de vista de negociação. Por exemplo, o autor foi aconselhado a considerar as diferenças entre o preço de fechamento de uma sessão americana e o preço de abertura da próxima.
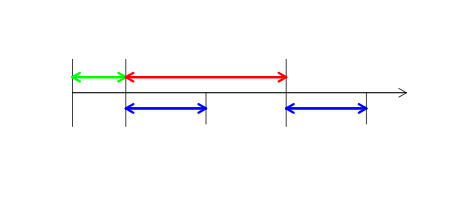
Deixe-me explicar como o conceito de uma sessão é formalizado. É definido pelos três intervalos de tempo: período, duração e deslocamento. As sessões são periódicas e têm um comprimento que não excede o período. Qualquer tick pertence a qualquer sessão ou não pertence a nenhuma delas (o último é possível se seu comprimento for estritamente menor que o período). O deslocamento é um intervalo de tempo entre o ponto zero no tempo e o início da primeira sessão após ele. Ele deve ser menor que o período. Este conceito da sessão é um pouco mais amplo do que o habitual e nos permite considerar, por exemplo, os gaps entre as barras de minutos. Vamos ilustrar no diagrama abaixo. A seta verde representa o período de tempo que define o deslocamento, a vermelha mostra o período, enquanto a azul demonstra a duração da sessão.
Nós usaremos dois EAs ligeiramente diferentes para coletar estatísticas relacionadas aos gaps. O primeiro (gaps_reg_stat.mq5) considera os gaps entre dois pontos subsequentes, enquanto o segundo (gaps_ses_stat.mq5) considera os gaps entre as sessões. Naturalmente, esses EAs não são negociados e são executados apenas no modo de teste. Recomenda-se executar o primeiro deles apenas em ticks reais, enquanto o segundo - em OHLC de barras de minuto. Os códigos do EA são fornecidos abaixo.
// gaps_reg_stat.mq5 #define ND 100 input double gmin=0.1; // tamanho mínimo do gap: USDJPY - 0.1, EURUSD - 0.001 input string fname="gaps\\stat.txt"; // nome do arquivo para estatísticas struct SGap { double p0; double p1; double p2; double p3; double s; void set(double p_1,double p,double sprd); bool brkn(); void change(double p); double gap(); double Q(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p,double sprd); void change(double p); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; bool is0=false; void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; if(is0) { double p=(tick.bid+tick.ask)*0.5, p0=(tick0.bid+tick0.ask)*0.5; gaps.change(p); if(MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid); } else is0=true; tick0=tick; } int OnInit() { gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } void SGap :: set(double p_1,double p,double sprd) { p1=p_1; p0=p2=p3=p; s=sprd; } bool SGap :: brkn() { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1)); } void SGap :: change(double p) { if(brkn()) return; if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p; p3=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { double q=p2-p1; if(q==0.0) return 0.0; return (p2-p0)/q; } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p,double sprd) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].set(p_1,p,sprd); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } void CGaps :: change(double p) { for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; gs[go[i]].change(p); if(gs[go[i]].brkn()) go[i]=-1; } } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c; for(int i=0;i<ngs;++i) { if (gs[i].brkn()) c=1; else c=0; FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s); if(i==ngs-1) break; FileWriteString(f,"\n"); } FileClose(f); } // gaps_ses_stat.mq5 #define ND 100 input double gmin=0.001; // tamanho mínimo do gap: USDJPY - 0.1, EURUSD - 0.001 input uint mperiod=1; // período da sessão em minutos input uint mlength=1; // duração da sessão em minutos input uint mbias=0; // viés da primeira sessão em minutos input string fname="gaps\\stat.txt"; // nome do arquivo para estatísticas struct SGap { double p0; double p1; double p2; double p3; double s; void set(double p_1,double p,double sprd); bool brkn(); void change(double p); double gap(); double Q(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p,double sprd); bool change(double p); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; int ns0=-1; ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60; void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; double p=(tick.bid+tick.ask)*0.5; gaps.change(p); int ns=nsession(tick.time); if(ns>=0) { double p0=(tick0.bid+tick0.ask)*0.5; if(ns0>=0&&ns>ns0&&MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid); ns0=ns; tick0=tick; } } int OnInit() { if(speriod==0||slength==0||speriod<slength||speriod<=sbias) { Print("wrong session format"); return(INIT_FAILED); } gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } int nsession(datetime t) { ulong t0=(ulong)t; if(t0<sbias) return -1; t0-=sbias; if(t0%speriod>slength) return -1; return (int)(t0/speriod); } void SGap :: set(double p_1,double p,double sprd) { p1=p_1; p0=p2=p3=p; s=sprd; } bool SGap :: brkn() { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1)); } void SGap :: change(double p) { if(brkn()) return; if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p; p3=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { double q=p2-p1; if(q==0.0) return 0.0; return (p2-p0)/q; } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p,double sprd) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].set(p_1,p,sprd); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } bool CGaps :: change(double p) { bool chngd=false; for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; gs[go[i]].change(p); if(gs[go[i]].brkn()) {go[i]=-1; chngd=true;} } return chngd; } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c; for(int i=0;i<ngs;++i) { if (gs[i].brkn()) c=1; else c=0; FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s); if(i==ngs-1) break; FileWriteString(f,"\n"); } FileClose(f); }
Os EAs são bem simples, embora faça sentido mencionar o array go[] na classe CGaps onde os índices de gaps, que não foram fechados são armazenados permitindo acelerar o trabalho dos EAs.
Em qualquer caso, os seguintes dados são registrados para cada gap: valor do gap absoluto, valor de Q, dados sobre seu fechamento e valor do spread no momento do gap. Então, a diferença entre o valor da distribuição empírica Q e o uniforme são verificados e a decisão sobre a análise posterior é realizada. Os métodos gráficos e computacionais (cálculo estatístico de Kolmogorov) são usados para verificar a diferença. Por simplicidade, nos restringiremos ao valor-p do teste de Kolmogorov-Smirnov como resultado dos cálculos. Ele leva valores entre zero e um, e quanto menor ele for, menos provável é que a distribuição da amostra coincida com a teórica.
Nós selecionamos o teste de Kolmogorov-Smirnov (uma amostra) para considerações matemáticas. A principal razão é que estamos interessados em distinguir as funções de distribuição na métrica de convergência uniforme, não em nenhuma métrica integral. Este teste não foi encontrado nas bibliotecas MQL5, então eu tive que usar a linguagem R. Vale a pena notar que se houver números correspondentes na amostra, a precisão deste critério é um pouco reduzida (a R dá um aviso apropriado), mas permanece bastante aceitável.
Se uma discrepância significativa entre as distribuições teóricas e empíricas for descoberta, nós deveríamos estudar a possibilidade de extrair lucro disso. Se não houver discrepância significativa, nós descartamos essa ideia ou tentamos melhorá-la.
Como mencionei acima, existem duas maneiras de inserir um negócio no preço p0 quando o gap é formado − na direção do gap ou na direção oposta. Vamos calcular a expectativa de retornos para esses dois casos. Ao fazer isso, vamos considerar um spread considerando-o constante e denotando-o como s. O valor do intervalo absoluto é denotado como g, enquanto que g0 significa seu valor mínimo.
- Entrada na direção do gap. Nesse caso, g+s é um stop loss, enquanto que kg-s é um take profit. Aqui,k é a razão de lucro/prejuízo. Valores de rentabilidade: -1 no caso de uma ativação do stop loss e (kg-s)/(g+s) no caso de uma ativação do take profit. Possibilidades correspondentes: Fq(q) e 1-Fq(q). Vamos expressar k através de q: k=k(q)=q/(1-q). Então, para a expectativa matemática de rentabilidade M, M=Fq(q)*(-1)+(1-Fq(q))*(k(q)g-s)/(g+s). Apenas os valores de q, para o qual M é significativamente positivo para todo g≥g0, são adequados para nós. Nós vamos precisar dos valores de q, em que Fq(q) é significativamente menor do que o valor teórico com o passeio aleatório Fq(q)<Fq0(q) em g=g0.
- Entrada contra-gap. Nesse caso, g-s é um take profit, enquanto kg+s é um stop loss. Aqui, k é a razão de prejuízo/lucro. Valores de rentabilidade: -1 no caso de uma ativação do stop loss e (g-s)/(kg+s) no caso de uma ativação do take profit. Probabilidades correspondentes: 1-Fq(q) e Fq(q). A expressão para k através de q é o mesmo que na passagem anterior: k=k(q)=q/(1-q). Para a expectativa matemática de rentabilidade M, nós obtemos a equação M=(1-Fq(q))*(-1)+*Fq(q)(g-s)/(k(q)g+s). Apenas os valores q, para os quais M é significativamente positivo para todo g≥g0, são adequados para nós. Nós vamos precisar dos valores de q, em que Fq(q) é significativamente maior do que o valor teórico Fq(q)>Fq0(q) em g=g0.
As estatísticas foram coletadas para dois símbolos:
- EURUSD
- USDJPY
Os seguintes tipos de gaps foram considerados para cada um deles:
- Entre ticks consecutivos.
- Entre barras de minuto.
- Entre as sessões de negociação. Para o EURUSD, esta é uma sessão americana (as de Chicago e Nova York combinadas), enquanto o USDJPY é da de Tóquio.
Para cada uma dessas seis opções, as estatísticas foram estudadas para os mais recentes:
- 200 gaps
- 50 gaps
Como resultado, nós temos 12 opções. Os resultados para cada um deles são os seguintes:
- valor-p para a estatística de Kolmogorov
- O valor do spread médio no momento em que o gap é formado
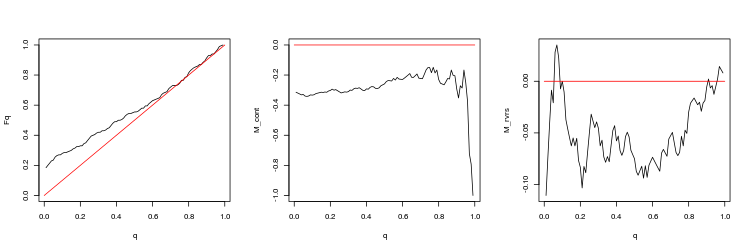
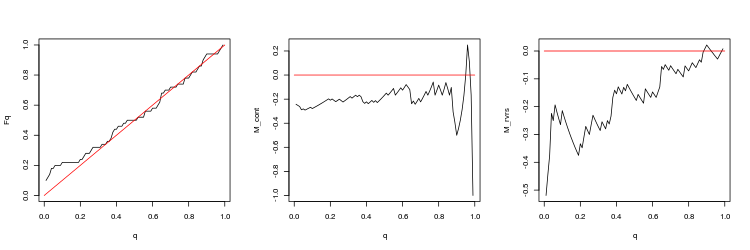
- Gráfico das funções empíricas e teóricas (linha vermelha) do valor da distribuição Q
- O gráfico da expectativa matemática de rentabilidade M_cont para negociação em uma direção do gap, dependendo de q em comparação com a linha teórica (vermelho) M_cont=0. Aqui, q significa a soma da razão de take profit/take profit e stop loss.
- O gráfico da expectativa matemática de rentabilidade M_rvrs para negociação contrária a direção do gap, dependendo de q em comparação com a linha teórica (vermelho) M_rvrs=0. Aqui, q significa a soma da razão stop loss/take profit e stop loss.
Todas as opções de resultados são fornecidas abaixo.
- EURUSD, 200 últimos gaps entre ticks consecutivos. valor-p: 3.471654e-07, spread médio: 0.000695
- EURUSD, 50 últimos gaps entre ticks consecutivos. valor-p: 0.2428457, spread médio: 0.0005724
- EURUSD, 200 últimos gaps entre as barras de minutos. valor-p: 8.675995e-06, spread médio: 0.0004352
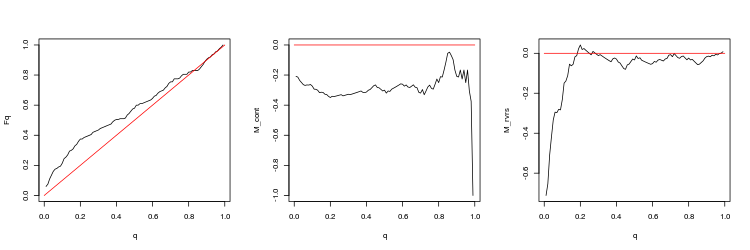
- EURUSD, 50 últimos gaps entre as barras de minutos. valor-p: 0.0125578, spread médio: 0.000404
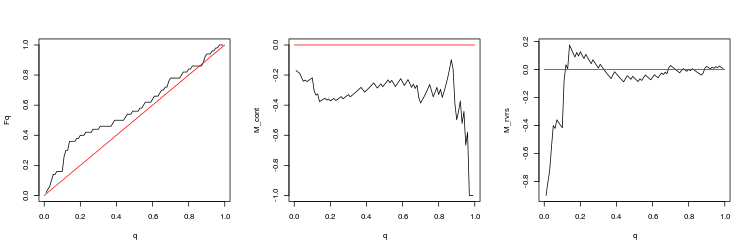
- EURUSD, 200 últimos gaps entre as sessões de negociação. valor-p: 0.6659917, spread médio: 0.0001323
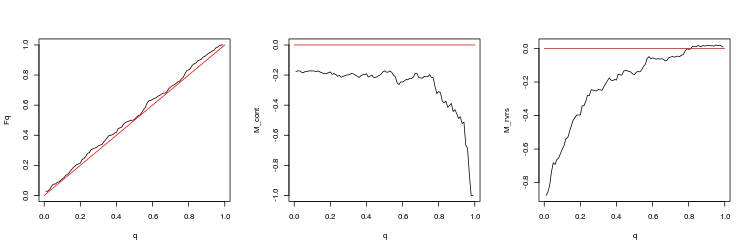
- EURUSD, 50 últimos gaps entre as sessões de negociação. valor-p: 0.08915716, spread médio: 0.0001282
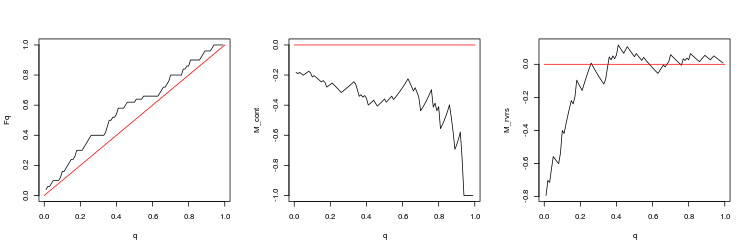
- USDJPY, 200 últimos gaps entre os ticks consecutivos. valor-p: 2.267454e-06, spread médio: 0.09563
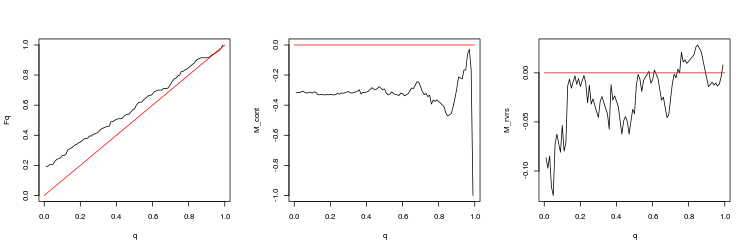
- USDJPY, 50 últimos gaps entre os ticks consecutivos. valor-p: 0.03259067, spread médio: 0.0597
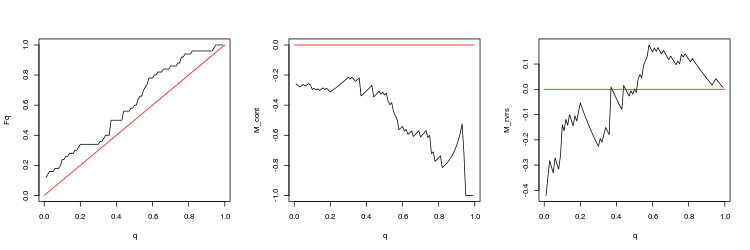
- USDJPY, 200 últimos gaps entre as barras de minutos. valor-p: 0.0003737335, spread médio: 0.05148
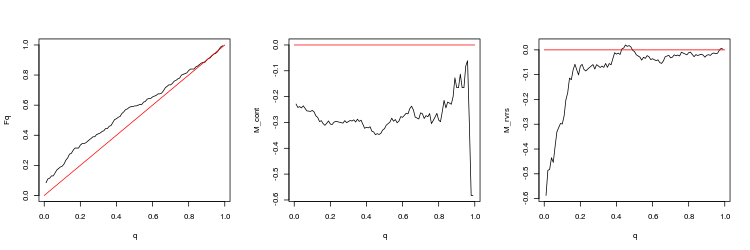
- USDJPY, 50 últimos gaps entre as barras de minutos. valor-p: 0.005747542, spread médio: 0.0474
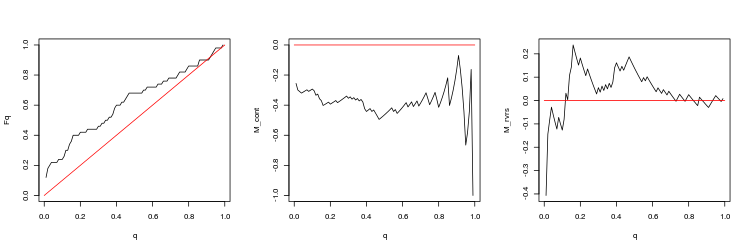
- USDJPY, 200 últimos gaps entre as sessões de negociação. valor-p: 0.07743524, spread médio: 0.02023
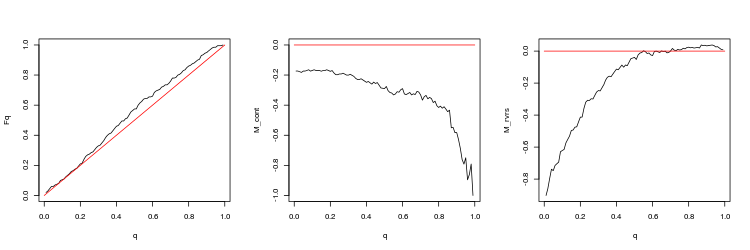
- USDJPY, 50 últimos gaps entre as sessões de negociação. valor-p: 0.009191665, spread médio: 0.0185
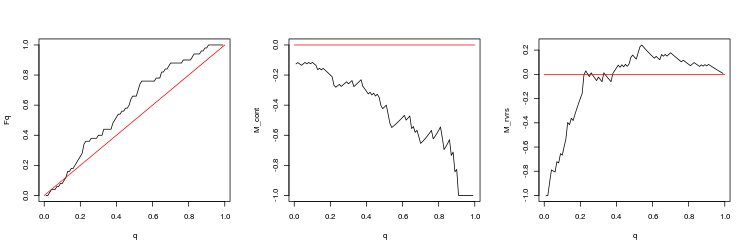
Nós podemos tirar as seguintes conclusões destes resultados:
- Os desvios de um passeio aleatório são bastante significativos.
- Negociar na direção do gap não é promissor. A negociação para o fechamento do gap parece mais preferível, mas o lucro é pequeno (especialmente no EURUSD).
- No momento da formação do gap, os spreads podem crescer várias vezes em comparação com o seu valor médio (verdadeiro para os gaps entre ticks e barras de minuto).
- Os gaps entre as sessões de negociação fornecem um desvio de um passeio aleatório apenas em alguns intervalos de 1-2 meses de duração, enquanto nos intervalos anuais, o desvio é muito pequeno. À primeira vista, isso é determinado pela tendência que prevalece em um determinado momento. Aparentemente, os gaps se aproximam melhor durante os períodos lateralizados e pioram durante as tendências, embora seja necessária uma análise mais detalhada.
- Para uma análise mais aprofundada, nós devemos escolher o intervalo entre as barras de minutos para o USDJPY.
Testando a estratégia e calculando o risco ideal por negócio
A versão do sistema baseada em intervalos entre as barras de minutos do USDJPY parece mais promissora. O aumento significativo do spread que detectamos no momento da formação do gap significa que devemos prestar mais atenção à sua definição. Vamos especificá-lo da seguinte maneira. Nós não vamos considerar o gap para o preço médio, mas para bid e ask. Além disso, nós vamos escolher um deles, para o qual precisamos entrar na operação. Isso significa que nós vamos definir um gap ascendente por bid e um gap descendente — por ask. O mesmo vale para o seu encerramento.
Vamos desenvolver o EA alterando ligeiramente o que nós usamos para coletar estatísticas sobre os gaps entre as sessões. A principal mudança diz respeito à estrutura do gap. Como nós temos uma correspondência definitiva entre gaps e negócios, toda a informação necessária para a negociação (volume de negócios e condição de fechamento) deve ser armazenada nessa estrutura. Duas funções são adicionadas para negociação. Uma delas (pp2v()) calcula o volume para cada negócio individual, enquanto outro (trade()) salva a correspondência entre a soma dos volumes negociados e o volume da posição de negociação. O código do EA (gaps_ses_test.mq5) é fornecido abaixo.
// gaps_ses_test.mq5 #define ND 100 input uint mperiod=1; // período da sessão em minutos input uint mlength=1; // duração da sessão em minutos input uint mbias=0; // viés da primeira sessão em minutos input double g0=0.1; // tamanho mínimo do intervalo: USDJPY - 0.1, EURUSD - 0.001 input double q0=0.4; // q0=sl/(sl+tp) input double r=0.01; // risco no negócio input double s=0.02; // spread aproximado input string fname="gaps\\stat.txt"; // nome do arquivo para estatísticas struct SGap { double p0; double p1; double p2; double v; int brkn(); bool up(); void change(double p); double gap(); double Q(); double a(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p); bool change(double pbid,double pask); double v(); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; int ns0=-1; ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60; double dv=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP); void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; bool chngd=gaps.change(tick.bid,tick.ask); int ns=nsession(tick.time); if(ns>=0) { if(ns0>=0&&ns>ns0) { if(tick0.ask-tick.ask>=g0) {gaps.add(tick0.ask,tick.ask); chngd=true;} else if(tick.bid-tick0.bid>=g0) {gaps.add(tick0.bid,tick.bid); chngd=true;} } ns0=ns; tick0=tick; } if(chngd) trade(gaps.v()); } int OnInit() { gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } int nsession(datetime t) { ulong t0=(ulong)t; if(t0<sbias) return -1; t0-=sbias; if(t0%speriod>slength) return -1; return (int)(t0/speriod); } double pp2v(double psl, double pen) { if(psl==pen) return 0.0; double dc, dir=1.0; double c0=AccountInfoDouble(ACCOUNT_EQUITY); bool ner=true; if (psl<pen) ner=OrderCalcProfit(ORDER_TYPE_BUY,_Symbol,dv,pen+s,psl,dc); else {ner=OrderCalcProfit(ORDER_TYPE_SELL,_Symbol,dv,pen,psl+s,dc); dir=-1.0;} if(!ner) return 0.0; return -dir*r*dv*c0/dc; } void trade(double vt) { double v0=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); if(-v0<vt<v0) vt=v0*MathRound(vt/v0); double vr=0.0; if(PositionSelect(_Symbol)) { vr=PositionGetDouble(POSITION_VOLUME); if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL) vr=-vr; } int vi=(int)((vt-vr)/dv); if(vi==0) return; MqlTradeRequest request={0}; MqlTradeResult result={0}; request.action=TRADE_ACTION_DEAL; request.symbol=_Symbol; if(vi>0) { request.volume=vi*dv; request.type=ORDER_TYPE_BUY; } else { request.volume=-vi*dv; request.type=ORDER_TYPE_SELL; } if(!OrderSend(request,result)) PrintFormat("OrderSend error %d",GetLastError()); } int SGap :: brkn() { if(((p0>p1)&&(p2<=p1))||((p0<p1)&&(p2>=p1))) return 1; if(Q()>=q0) return -1; return 0; } bool SGap :: up() { return p0>p1; } void SGap :: change(double p) { if(brkn()==0) p2=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { if(p2==p1) return 0.0; return (p2-p0)/(p2-p1); } double SGap :: a() { double g=gap(), k0=q0/(1-q0); return (g-s)/(k0*g+s); } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].p0=gs[ngs-1].p2=p; gs[ngs-1].p1=p_1; double ps=p+(p-p_1)*q0/(1-q0); gs[ngs-1].v=pp2v(ps,p); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } bool CGaps :: change(double pbid,double pask) { bool ch=false; for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; if(gs[go[i]].up()) gs[go[i]].change(pbid); else gs[go[i]].change(pask); if(gs[go[i]].brkn()!=0) {go[i]=-1; ch=true;} } return ch; } double CGaps :: v(void) { double v=0; for(int i=0; i<ngo; ++i) if(go[i]>=0) v+=gs[go[i]].v; return v; } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT); int na=0, np=0, bk; double kt=0.0, pk=0.0; for(int i=0;i<ngs;++i) { bk=gs[i].brkn(); if(bk==0) continue; ++na; if(bk>0) ++np; kt+=gs[i].a(); } if(na>0) { kt/=na; pk=((double)np)/na; } FileWriteString(f,"na = "+(string)na+"\n"); FileWriteString(f,"kt = "+(string)kt+"\n"); FileWriteString(f,"pk = "+(string)pk); FileClose(f); }
Vamos testar o EA no ano de 2017 e definir o valor do risco para negociação em 2018 com base em seus resultados. O gráfico de saldo/capital com base nos resultados do teste de 2017 é fornecido abaixo.
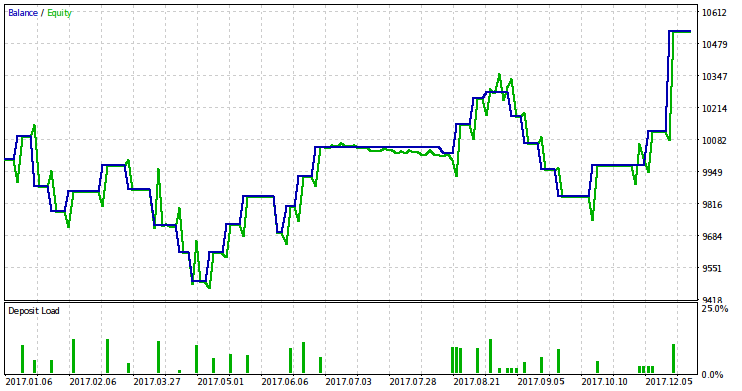
Eu tenho que fazer alguns esclarecimentos antes de proceder ao cálculo de risco. Primeiro, nós precisamos justificar a necessidade de determinar o nível correto de risco. Em segundo lugar, é necessário explicar a vantagem de aplicar nossa teoria para esse propósito.
A negociação especulativa está sempre associada à incerteza. Qualquer sistema de negociação, por sua vez, realiza algumas operações perdedoras. Por esse motivo, o risco não deve ser muito grande. Caso contrário, o rebaixamento será excessivo. Por outro lado, o mercado pode alterar a qualquer momento transformando um sistema lucrativo em um sistema perdedor. Portanto, o "tempo de vida" do sistema é finito e não é conhecido com precisão. Por esse motivo, o risco não deve ser muito pequeno. Caso contrário, você não será capaz de obter todos os lucros possíveis do seu sistema de negociação.
Vamos agora considerar as principais abordagens (diferentes das nossas) para definir o risco acompanhado de características breves:
- Definir o risco por um valor numérico específico com base na opinião de alguns “traders experientes”. A faixa de valor mais popular é 0.5-3% dos fundos. Essa abordagem é bastante adequada, apesar da falta de justificativa. Sua principal desvantagem é a ausência de uma regra para a escolha de um valor de risco específico para um determinado sistema.
- O método "ótimo" de Ralph Vince. Este método é justificado teoricamente, mas geralmente oferece um valor de risco inadequadamente alto que pode causar um rebaixamento muito grande.
- A inclusão do risco aos parâmetros do EA e sua definição durante o teste e otimização. É difícil dizer algo certo sobre a justificativa e a adequação do resultado, pois esses parâmetros dependem muito do dispositivo do EA e de como exatamente a otimização é realizada. Um dos possíveis problemas é a falta de contabilização da incerteza em novos resultados de negociação. O reajuste também é possível, o que pode causar um aumento injustificado no valor de risco (o método anterior é um exemplo claro). O método que nós propomos é uma maneira de otimizar o risco de forma razoável.
Nosso método, ao contrário dos descritos acima, nos permite obter valores de risco adequados e razoáveis. Ele possui parâmetros ajustáveis que podem ser adaptados ao estilo de negociação específico. Vamos descrever a essência de nossa abordagem para o cálculo de risco. Nós assumimos que usamos o sistema de negociação exatamente até que sua lucratividade média dentro do número especificado de negócios caia abaixo do nível mínimo especificado, ou até que o rebaixamento exceda o nível máximo especificado na mesma sequência de negócios. Depois disso, a negociação baseada neste sistema é interrompida (por exemplo, seus parâmetros são re-otimizados). O valor do risco é selecionado de modo que a probabilidade de que o sistema ainda seja lucrativo (e a redução de rebaixamento ou lucratividade seja uma flutuação aleatória natural) não seja maior do que o valor especificado.
O método é descrito em detalhes nos artigos anteriores. No segundo artigo, você pode encontrar um script para calcular o valor de risco ideal. Esse script é aplicável para encerrar os negócios pelos níveis de stop loss e take profit especificados durante a entrada com taxa fixa para todas as operações. Ele é chamado de bn.mq5 no artigo mencionado.
Como resultado de um passe de teste, nosso EA grava os dados que são necessários como parte dos parâmetros para o script de cálculo de risco em um arquivo de texto. Os parâmetros restantes são conhecidos antecipadamente ou selecionados por pesquisa exaustiva. Se o valor de risco proposto pelo script for zero, então nós devemos descartar essa ideia de negociação ou enfraquecer nossos requisitos de rebaixamento/rentabilidade (alterando os parâmetros) ou usar os dados de negócios de um histórico maior. Abaixo está uma parte do script com os valores dos parâmetros a serem definidos.
input uint na=26; // número de negócios na série input double kt=1.162698185452029 // razão take profit/stop loss input double pk=0.5769230769230769 // probabilidade de lucro double G0=0.0; // menor rentabilidade média double D0=0.9; // menor incremento mínimo double dlt=0.17; // nível de significância
Como os resultados dos testes para 2017 não são inspiradores em termos de qualidade de negociação, nossos requisitos são bastante moderados. Nós estabelecemos a condição de que dentro de 26 negócios (na=26), o EA não é deficitário (G0=0.0) e o rebaixamento não excede 10% (D0=0.9). Para obter um valor de risco diferente de zero, nós temos que estabelecer um nível de significância bastante alto (dlt=0.17). Na verdade, é melhor que não seja mais do que um décimo. O fato de termos que torná-lo tão grande indica resultados de negociação ruins. O EA com esses parâmetros não deve ser usado na negociação real neste símbolo. Com os parâmetros especificados, o script fornece o seguinte resultado para o risco: r = 0.014. Abaixo você pode encontrar o resultado do teste do EA para 2018 com este valor de risco.
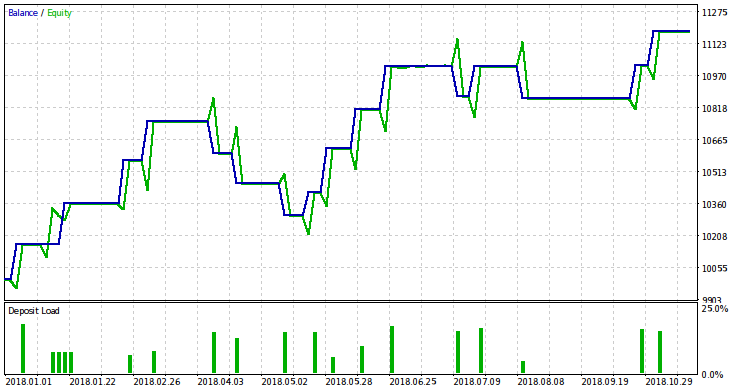
Apesar dos lucros demonstrados pela EA durante o teste, é improvável que eles permaneçam em negociação real. A futilidade de negociar gaps comuns nos símbolos examinados parece óbvia. Esses gaps são muito raros (e se tornam mais raros com o tempo) e pequenos em tamanho. A consideração mais aprofundada da generalização dos gaps - variações de preço entre as sessões - parece mais promissora. Além disso, faz sentido prestar atenção aos ativos onde os gaps comuns são mais comuns.
Conclusão
Métodos probabilísticos são bastante adequados para o desenvolvimento e configuração de EAs. Ao mesmo tempo, eles não são de forma alguma contrários à outros métodos possíveis. Em vez disso, eles muitas vezes tornam possível suplementar ou repensar.
Neste artigo, nós não abordamos o tópico da otimização geral do EA por seus parâmetros, mencionando-o apenas de passagem. Há uma conexão significativa entre essa área e a abordagem probabilística (a teoria das soluções estatísticas). Talvez, eu estudarei essa questão em detalhes mais tarde.
Arquivos anexados
Abaixo, você pode encontrar dois EAs usados para coletar estatísticas e um EA usado para negociação de teste.
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | gaps_reg_stat.mq5 | EA | Coleta estatísticas dos gaps entre ticks consecutivos |
| 2 | gaps_ses_stat.mq5 | EA | Coleta estatísticas de gaps entre as sessões |
| 3 | gaps_ses_test.mq5 | EA | Teste de negociação usando gaps entre as sessões |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/5373
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Reversão: criemos um ponto de entrada e programemos um algoritmo de negociação manual
Reversão: criemos um ponto de entrada e programemos um algoritmo de negociação manual
 Desenvolvimento de um utilitário de navegação e seleção de símbolos em MQL5 e MQL4
Desenvolvimento de um utilitário de navegação e seleção de símbolos em MQL5 e MQL4
 Usando OpenCL para testar padrões de candles
Usando OpenCL para testar padrões de candles
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Há poucas lacunas comuns no Forex, portanto, sua generalização foi estudada além delas.
A questão não está no nome, mas no fato de que os fenômenos são de natureza diferente. Você pode generalizar ou misturá-los).
A diferença em sua natureza não nos impediu de usar o mesmo aparato matemático para eles. Como o tópico principal do artigo é descrever um método matemático, a semelhança desse método é a base para considerar esses fenômenos em conjunto. É semelhante a como, em um livro de problemas escolares, pode haver problemas lado a lado sobre doces e escavadeiras, apesar da diferença essencial nos tipos desses objetos.
A raridade de um fenômeno não significa que ele não seja lucrativo. Pelo contrário, os fenômenos raros são repentinos e grandes, portanto, influenciam mais fortemente o mercado.
Dentro da estrutura do artigo, sua insuficiência significa que é impossível demonstrar a essência do aparato matemático descrito com base apenas nos gaps clássicos.
Nada o impede de demonstrar como deve ser um artigo adequado sobre lacunas. Exceto, é claro, sua incapacidade de escrevê-lo.
Não tenho nenhuma reclamação sobre você ou seu artigo), apenas lhe disse onde estão as possibilidades adicionais. Talvez um pouco agressivo, mas é assim que se faz aqui.)
Também não tenho nenhuma reclamação contra você) No entanto, ainda desejo que você escreva um artigo sobre lacunas, considerando-as de um ângulo diferente e em mais mercados do que é feito aqui) Tenho certeza de que será útil para você e para toda a parte adequada do fórum.