Teoria das probabilidades e estatística matemática com exemplos (Parte I): fundamentos e teoria elementar
2 240
0
Sumário
- Introdução
- Fundamentos da teoria
- Teoria elementar
- 3.1. Probabilidade combinatória
- 3.2. Esquema do princípio de Bernoulli
- Fundamentos de estatística matemática
- Exemplos de aplicação de estatística matemática no âmbito da teoria elementar
- 5.1. Estimativa pontual do parâmetro
- 5.2. Verificação de hipóteses estatísticas
- Fim do artigo
- Arquivos anexados
1.Introdução
Fazer trading é sempre sobre como tomar decisões diante da incerteza. Isso significa que os resultados das decisões tomadas não são muito óbvios no momento em que são tomadas. Por isso, são importantes as abordagens teóricas para a construção de modelos matemáticos que possibilitem descrever tais situações de maneira significativa. Eu gostaria de destacar duas dessas abordagens: teoria das probabilidades e teoria de jogos. Às vezes, elas são combinadas para denotar métodos probabilísticos, como a teoria dos "jogos com a natureza", que mostra bem a existência de dois tipos diferentes de incerteza. A primeira delas, a probabilística, geralmente está associada a fenômenos naturais. A segunda, puramente lúdica, está associada às atividades de outros sujeitos (indivíduos ou suas comunidades). A incerteza do jogo é muito mais difícil de estudar a nível de teoria. Às vezes, essas incertezas são chamadas de "ruins" e "boas". Frequentemente, para compreender melhor a incerteza do jojo é necessário reduzi-la a uma forma probabilística.
No caso do mercado, é óbvio que a incerteza da natureza do jogo é mais importante, já que a atividade das pessoas é o fator determinante. Neste caso, a transição para modelos probabilísticos ocorre, via de regra, porque se considera que existe um grande número de participantes, cada um dos quais individualmente tem pouco efeito sobre as variações de preços. Em parte, isto também acontece com uma abordagem usada na física estatística que levou ao surgimento de um campo de estudo chamado de econofísica.
Na verdade, o porquê de tal transição é muito interessante, não trivial e merece consideração mais detalhada. Espero que algum dia em nosso fórum apareçam artigos dedicados a isso. Neste artigo, vamos nos concentrar em examinar os próprios fundamentos da teoria da probabilidades e da estatística matemática.
2. Fundamentos da teoria
A base da teoria das probabilidades são um sistema formal conhecido como axiomas de Kolmogorov. Não vou me aprofundar em explicar o que é um sistema formal e como entender corretamente a abordagem axiomática matemática, porque todas essas são questões muito complexas trazidas pelo campo da lógica matemática. Em vez disso, vamos nos concentrar no objeto básico da teoria das probabilidades, isto é, no espaço amostral (em inglês, sample space). Ele consiste num conjunto de eventos primários, num conjunto de eventos e nas probabilidades de tais eventos. Vejamos isso de forma um pouco mais detalhada:
1) O espaço amostral compreende os muitos resultados possíveis de um experimento aleatório. Normalmente, ele é denotado pela letra maiúscula grega Ω (omega) e é representado como uma figura. Os eventos primários (em inglês, elementary event ou sample point) são geralmente denotados pela minúscula grega o (ômega) e é representado como um ponto. Eis o exemplo padrão mais simples descrevendo o resultado de um único lançamento de uma moeda: Ω={ω1, ω2}, onde ω1=H e ω2=T indicam cara e coroa (heads e tails), enquanto as chaves são o conjunto dado pela enumeração de seus elementos.
A imagem abaixo mostra um tipo de Ω abstrato em forma de retângulo e vários pontos que são eventos primários pertencendo a ele: ω1, ω2 e ω3.
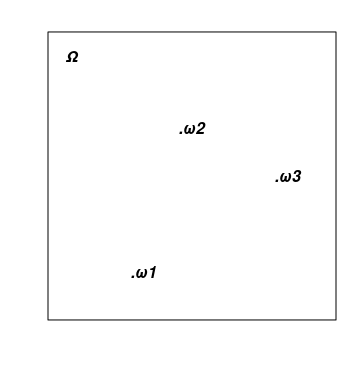
2) Cada um dos eventos, incluídos no conjunto de eventos aleatórios (event), é um conjunto de eventos primários (um subconjunto dos eventos primários Ω). O conjunto de eventos inclui um conjunto vazio ∅={} (evento que nunca vai acontecer) e todo o conjunto Ω (evento que sempre acontece). A união (e interseção) de dois eventos do conjunto também deve pertencer ao conjunto. É comum em matemática chamá-lo de álgebra de conjuntos. Em nosso exemplo de moeda, existem quatro eventos: {}=∅, {H}, {T} e {H,T}=Ω. (Pergunta de autoteste: um evento atômico é um exemplo de um evento aleatório?)
Os eventos aleatórios são geralmente designados em letras latinas maiúsculas: A, B, C, ... e são representados como figuras localizadas dentro da imagem que descreve Ω. A união e a interseção dos eventos são designadas de maneiras diferentes. Às vezes, é usada uma notação semelhante à adição e multiplicação de variáveis numéricas comuns: АВ e А+В, já às vezes são usados os símbolos ∩ e ∪: А∩В e А∪В.
A imagem abaixo mostra Ω como um retângulo e dois eventos - А e В - que se cruzam.
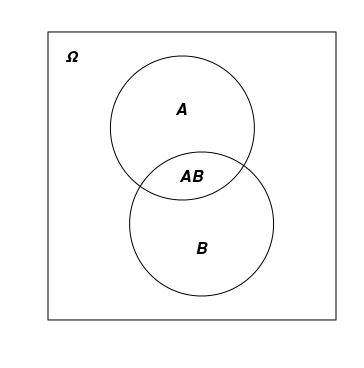
3) A probabilidade é uma função numérica (probability function) P=P(A), que compara, para cada evento aleatório A, um números real no intervalo de 0 a 1. Sendo que P(Ω)=1 e P(∅)=0. Além disso, é cumprida uma regra chamada aditividade: se o evento A for uma união de eventos não sobrepostos B e C, então P(A)=P(B)+P(C). Além do termo "probabilidade", para a função P() são usados os termos "distribuição de probabilidade em Ω" ou simplesmente "distribuição em Ω". É importante não confundir este conceito com o de "função de distribuição de variável aleatória", pois embora estejam relacionados, são diferentes. A primeira é uma função que mapeia um número com um conjunto e a segunda é uma função numérica comum que mapeia um número com um número.
Não é muito claro como representar a distribuição de probabilidade por meio de um gráfico, mas intuitivamente ela pode ser comparada à distribuição de uma unidade de massa sobre o volume Ω. Nesta analogia, o evento é uma parte do volume e a probabilidade é uma fração da massa nesta parte do volume.
Todos os outros conceitos da teoria da probabilidade são derivados deles. Vamos destacar aqui um conceito muito importante de dependência probabilística (independência). Para isso, introduzimos o conceito de probabilidade condicional de um evento А com a condição de que se cumpra o evento B, P(B)>0. Ela é designada como P(A|B) e por definição P(A|B)=P(AB)/P(B) (lembre que AB é intersecção de eventos A e B). O evento A, por definição, é chamado independente do evento B quando sua probabilidade condicionada durante a ocorrência do evento B é igual à sua probabilidade: P(A|B)=P(A). Ao usar uma expressão para probabilidade condicionada, esta definição de independência pode ser reescrita da seguinte forma: P(A)P(B)=P(AB). Se essa igualdade não for satisfeita, diz-se que o evento A depende do evento B.
Intuitivamente, independência significa que o facto de saber a ocorrência de um evento B não muda a incerteza associada ao evento A. Por outro lado, dependência significa que a ocorrência do evento B leva informações sobre o evento A. A expressão precisa desta conceito intuitivo aparece na teoria da informação de Claude Shannon.
É costume destacar a teoria elementar da probabilidade. A diferença entre uma teoria elementar e uma não elementar é que ela considera um conjunto de eventos primários consistindo num número finito de elementos. Logo, o conjunto de eventos aleatórios também acaba sendo finito (pergunta de autoteste: por que isso é verdade?). Essa teoria se desenvolveu muito antes dos axiomas de Kolmogorov e realmente não precisava dela. O resto do artigo se concentrará nesta parte da teoria. A teoria não elementar será discutida no próximo artigo.
3. Teoria elementar
Como o número de resultados elementares é finito, podemos simplesmente definir a probabilidade de eventos contendo exatamente um evento elementar (unit set). Só é preciso ter certeza de que a soma de todas essas probabilidades é igual a um. A probabilidade de qualquer evento será igual à soma de tais probabilidades. Não é necessário que todas essas probabilidades iniciais sejam iguais, mas começaremos apenas com esses modelos, que geralmente são resumidos sob o nome de "probabilidade combinatória".
3.1. Probabilidade combinatória
Assumamos que Ω consiste exatamente em N resultados elementares, então a probabilidade de eventos, que os contêm m vezes, é igual a m/N. Calcular a probabilidade aqui consiste em contar o número de variantes. Via de regra, para isso são usados métodos combinatórios, daí o nome. Eis alguns exemplos:
Exemplo 1. Assumamos que existe um n de vários itens. Quantas maneiras diferentes existem para organizá-los (alinhá-los)? Resposta: n!=1*2*3*....*(n-1)*n maneiras. Cada um desses métodos é chamado de permutação, sendo que cada um deles é um evento elementar. Assim, N=n! e a probabilidade de um evento consistindo em m permutações é m/n! (m/N=m/n!).
Por exemplo, vamos resolver um problema simples: encontremos a probabilidade de que um determinado objeto esteja na primeira posição após um rearranjo aleatório. Se o primeiro lugar for ocupado pelo item escolhido, então os n-1 itens restantes podem ser colocados nos n-1 lugares restantes de (n-1)! maneiras. Assim, m=(n-1)! e, logo, a probabilidade desejada é m/N=m/n!=(n-1)!/n!=1/n.
Exemplo 2. Também há n itens diferentes. Quantos conjuntos diferentes de k (k<=n) itens podemos selecionar a partir deles? Existem duas possíveis respostas, dependendo de se considerarmos dois conjuntos diferentes que diferem apenas na ordem dos itens. Se for assim, a resposta será: n!/(n-k)! conjuntos, caso contrário, será k! vezes menos: n!/((n-k)!*k!). Um conjunto com relação à ordem é chamado de disposição e, independentemente da ordem, é chamado de combinação. Para a fórmula do número de combinações, também conhecida como fórmula do coeficiente binomial, são usadas notações especiais, há duas variações que são mostradas na figura a seguir.
Assim, se a ordem dos elementos do conjunto não é importante no problema a ser resolvido, então, para resolvê-lo, podemos usar combinações como um espaço amostral. Se a ordem for importante, então devem ser usadas as disposições.
Exemplo 3. Consideremos um exemplo importante, nomeadamente um que causa a chamada distribuição hipergeométrica. Agora imaginemos que cada um de nossos n itens são marcados com um de dois rótulos, quer "bom" ou "ruim". Assumamos que b, b⋜n são itens "ruins", enquanto os restantes n-b, "bons". Selecionamos um conjunto de k elementos sem levar em conta a ordem nele (combinação). Qual é a probabilidade de que aconteça o evento em que nosso conjunto contém exatamente x itens "ruins"? O problema é resolvido contando o número de combinações correspondentes. A resposta acaba sendo um tanto complicada e é melhor apontá-la por meio da notação para o número de combinações, conforme mostrado na figura a seguir, onde a probabilidade desejada é denotada por p e é expresso através de x, n, b e k
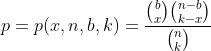
Este exemplo é adequado para entender o conceito de "variável aleatória" (que será discutido em mais detalhes no próximo artigo). É bem provável que aconteça que, para resolver um problema específico relacionado ao cálculo das probabilidades de eventos, baste saber os números x, n, b e k, já as informações completas sobre todo o conjunto inicial de eventos se tornam redundantes. Então, faz sentido simplificar o modelo original descartando informações desnecessárias. Procedemos da seguinte forma:
- Consideramos os números n, b e k como parâmetros fixos.
- Em vez do espaço amostral Ω, vamos construir com base nele um Ωх={0, 1, ..., k} novo consiste em valores possíveis para o número х.
- Para cada evento {х} (consistindo de um evento primário) vamos comparar a probabilidade dada pela fórmula de distribuição hipergeométrica mostrada na figura acima.
O objeto resultante é denominado "variável aleatória discreta". Esta possui uma distribuição hipergeométrica para seus valores possíveis a partir de Ωх.
3.2. Esquema do princípio de Bernoulli
Este é outro modelo bem conhecido do campo da teoria elementar das probabilidades. Normalmente, fala-se em modelar o resultado de vários lançamentos consecutivos de moeda, mas vamos abordar sua construção um pouco mais formalmente.
Assumamos que temos um número inteiro positivo n e um par de números reais não negativos p e q, de tal modo que p+q=1. O espaço amostral Ω consiste em palavras com um comprimento n que permitem apenas dois letras − H e T (H vem de heads, ou seja, cara, já T, de tails, que significa coroa). A probabilidade de um evento consistindo num evento elementar é dada pela fórmula pu({w})=p^nh*q^nt, onde w é uma palavra, já nh e nt, nh+nt=n é a quantidade de letras H e T nela, respectivamente.
É fácil ver que, em contraste com a probabilidade combinatória, as probabilidades iniciais geralmente não são iguais entre si (elas são todas iguais apenas se p=q=0.5).
Por exemplo, consideremos o caso n=2. Neste caso, Ω={HH, HT, TH, TT}. O número de eventos primários aqui é 4, e o número de eventos aleatórios, 16. (Pergunta de autoteste: derive para o esquema de Bernoulli a forma geral das fórmulas para a dependência do número de eventos primários e do número de todos os eventos aleatórios a partir de n)
Consideremos o evento "H vem primeiro"={HH, HT}. Sua probabilidade é pq+p^2=p. O mesmo vale para qualquer lugar, o que permite falar sobre o parâmetro p, como "a probabilidade de obter coroa em cada lance". Agora verifiquemos se o evento é independente А="em segundo lugar está H"={HH, TH} a partir do evento В="em segundo lugar está H"={HH, HT}. Vamos usar a definição de independência − a interseção АВ={HH}, P(A)=p, P(B)=p, P(AB)=p^2 e como P(A)P(B)=p*p=p^2=P(AB), então os eventos são independentes.
Essas afirmações sobre a probabilidade do resultado de cada lance e sua independência acabam sendo verdade para todos n>2.
Observe que poderíamos definir a probabilidade de uma maneira completamente diferente, o que poderia levar tanto à falta de uma probabilidade igual quanto à dependência dos resultados dos lances. A questão aqui é que o esquema de Bernoulli não é o "único modelo correto" que descreve a sequência de eventos, e não devemos nos limitarmos apenas a ele.
Agora calculemos a probabilidade de um evento no esquema de Bernoulli, evento esse que consiste naquelas palavras em que a letra H aparece k vezes, ou menos formalmente, a probabilidade de obter uma moeda com cara é k vezes em n lances. A resposta a essa pergunta é dada pela fórmula da chamada distribuição binomial, mostrada na figura a seguir. Por meio de pb é denotada a probabilidade desejada dependendo de k, n, p e q.
Consideremos outro exemplo que mostra a relação entre a distribuição binomial e a distribuição hipergeométrica considerada acima. É importante por si só e devido às suas aplicações em estatística matemática (teste exato de Fisher) A questão é bastante complexa e significativa do ponto de vista matemático. Vamos escrever todo o raciocínio ponto por ponto.
- Com base no espaço amostral do esquema de Bernoulli Ω construímos um novo, Ω1, que incluirá as palavras cuja letra H pode ser encontrada b vezes.
- Como qualquer evento A de Ω1 é um evento em Ω, sua probabilidade é definica como P(A). Com base nisso, apresentamos a probabilidade P1 em Ω1 de acordo com a fórmula P1(A)=P(A)/Р(Ω1). Na verdade, ao fazer isso, é usada a fórmula de probabilidade condicionada P1(A)=P(A|О1).
- Consideremos agora a probabilidade P1() do evento "sufixo de uma palavra de comprimento k contém exatamente x letras H" a partir de Ω1. Acontece que essa probabilidade é exatamente dada pela fórmula de distribuição hipergeométrica que foi escrita anteriormente. Aqui é notável o fato de que a fórmula não depende do parâmetro p.
4. Fundamentos de estatística matemática
A diferença entre estatística matemática e teoria das probabilidades são geralmente descritas como uma diferença nos tipos de problemas que resolvem. Na teoria das probabilidades, geralmente assume-se que o modelo probabilístico é totalmente conhecido e com base nele é necessário tirar as conclusões. Em estatística matemática, apesar de o conhecimento sobre o modelo ser incompleto, há informações adicionais na forma de dados experimentais que ajudam a refiná-lo. Assim, todas as questões que foram discutidas no capítulo anterior são problemas do campo da teoria das probabilidades.
A definição de estatística matemática que acabamos de dar pode ser considerada clássica. Existe outra abordagem mais moderna para definir a estatística matemática. Ela abrange a teoria da decisão (decision theory). Além disso, a ênfase está na construção de regras de decisão ótimas que sejam ótimas no sentido de minimizar o custo médio de um erro. Aqui acontece uma convergência muito forte com os métodos de aprendizado de máquina. Uma diferença significativa em relação a eles reside no fato de que na estatística matemática o tipo de modelo matemático usado é determinado com bastante clareza (por exemplo, com precisão de um parâmetro desconhecido). Em MO, via de regra, a incerteza se estende ao tipo de modelo.
Voltemos agora a exemplos de problemas em estatística matemática no sentido clássico.
5. Exemplos de aplicação de estatística matemática no âmbito da teoria elementar
Podemos distinguir dois tipos de problemas: estimativa de parâmetros e teste de hipóteses.
Vamos começar com o problema de uma estimativa pontual de um parâmetro. Ele assume a presença de quaisquer variáveis numéricas (não aleatórias, determinísticas) no modelo probabilístico. Seu valor numérico exato é desconhecido, mas é possível calcular seu valor aproximado usando dados obtidos como resultado de um experimento aleatório.
5.1. Estimativa pontual do parâmetro
A abordagem mais geral aqui é usar o método da máxima verossimilhança. Se, como resultado de um experimento aleatório, for realizado algum evento elementar ω, então a função de verossimilhança é a probabilidade de um evento {ω} (consistindo apenas neste evento primário). E ela é chamada de função na medida em que depende do valor do parâmetro do modelo. A estimativa de máxima verossimilhança (abreviada como EMV) é o valor do parâmetro com o qual essa função atinge seu máximo.
De modo geral, podem ser feitas muitas estimativas diferentes do parâmetro, além da EMV, mas, conforme comprovado pelas estatísticas matemáticas, a EMV é o melhor em termos de precisão. Deixaremos a explicação do que se entende aqui por "precisão" para o próximo artigo dedicado a variáveis aleatórias. Em qualquer caso, deve ser lembrado que a estimativa estatística quase sempre será diferente do valor verdadeiro do parâmetro. Por isso, é muito importante distingui-los e não misturá-los. Por exemplo, a probabilidade de um evento no esquema de Bernoulli e sua estimativa na forma de frequência.
Agora abordemos o cálculo da EMV usando exemplos.
Exemplo 1. Estimativa do parâmetro b na distribuição hipergeométrica. Temos um lote de peças n=1000. Depois da verificar k=20 delas, foi encontrada uma peça defeituosa: x=1. Deve-se fazer uma estimativa do número de peças defeituosas em todo o lote.
Abaixo está o script hyperg_be.py, feito em Python, que resolve esse problema enumerando todas as possíveis variações para b. A resposta será uma estimativa be em que o valor de verossimilhança, determinado pela fórmula de distribuição hipergeométrica, é máximo.
from scipy.stats import hypergeom n = 1000 k = 20 x = 1 lhx = 0.0 be = 0 for b in range(x, n - k + x): lh = hypergeom.pmf(x, n, b, k) if lh > lhx: be = b lhx = lh print("be =",be)
Resposta: be = 50, o que era bastante previsível (cada 20º peça)
Exemplo 2. Estimativa do parâmetro n na distribuição hipergeométrica. É necessário estimar a quantidade de peixes num reservatório. Para fazer isso, nele com uma rede foram pescados b=50 peixes, depois, foram marcados e liberados de volta. Depois disso, novamente e da mesma forma, foram pegos k=55 peixes, dos quais x=3 estavam marcados.
Abaixo está o script hyperg_ne.py, feito em Python, que resolve esse problema enumerando todas as possíveis variações para n. A resposta será uma estimativa ne em que o valor da probabilidade é máximo. A pouca precisão é devida a que os valores possíveis para n teoricamente variam de 50+(55-3)=102 ao infinito. Isso pode levar a um loop de iteração sem fim. Mas acontece que até algum valor de n a função de verossimilhança cresce e então começa a diminuir e tende a zero. Assim, a resposta será que o primeiro valor ne em que o valor da função de verossimilhança é maior do que seu valor ne+1.
from scipy.stats import hypergeom b = 50 k = 55 x = 3 lh0 = 0.0 ne = b + k - x - 1 while True: lh = hypergeom.pmf(x, ne+1, b, k) if lh < lh0: break else: lh0 = lh ne += 1 print("ne =",ne)
Resposta: ne = 916, o que é também bastante esperado (ne/b aproximadamente igual a k/x, de onde se descobre que ne é aproximadamente igual a b*k/x).
Todos os exemplos que serão dados abaixo estão relacionados ao esquema de Bernoulli ou suas modificações. A nível de trading, a interpretação tradicional desse modelo consiste em compará-lo com uma versão discretizada do preço de um ativo. Para obter tal visualização são usados, por exemplo, o gráfico renko ou o de pontos e figuras.
Não vamos nos desviar dessa tradição. Em vez de palavras feitas das letras H e T consideremos a sequência de números 1 e -1, que obviamente correspondem a etapas discretas do preço, respectivamente, para cima e para baixo. Em termos gerais, uma etapa do preço pode ser definida como a superação de um novo nível dentro de uma grade de preços. Essas grades de nível são geralmente definidas de forma que a diferença ou a relação entre cada nível e seu vizinho inferior seja a mesma. Vamos usar o segundo método. A desvantagem deste método é que é impossível aplicá-lo com ativos tendo preços negativos, já a vantagem é que não há necessidade de selecionar o tamanho da etapa para cada ativo individualmente. Também há alguma arbitrariedade na escolha de zero, pois usaremos o primeiro preço daqueles que são amostrados.
Abaixo está um script simples que discretiza o preço com uma determinada etapa percentual, para um determinado intervalo. No arquivo Discr.mqh foi colocada apenas a função setmv() na qual acontece a discretização do preço. Para simplificar, apenas os preços de abertura das barras de minutos são considerados como o preço inicial.
// Constructing the array of discrete mv[] movements // at a specified time interval and with a specified percentage step void setmv(int& mv[], datetime t1, datetime t2, double dpr) { int ND = 1000; ArrayResize(mv, 0, ND); // Get price history double price[]; int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price); if(nprice < 2) { Print("not enough price history"); return; } // Construct mv[] int lvl = 0, dlvl, nmv = 0, dmv; double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr); for(int i = 1; i < nprice; ++i) { dlvl = (int)((log(price[i]) - lp0) / lstep - lvl); if(dlvl == 0) continue; lvl += dlvl; dmv = 1; if(dlvl < 0) { dmv = -1; dlvl = -dlvl; } ArrayResize(mv, nmv + dlvl, ND); for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv; nmv += dlvl; } }
O script discret_prices.mq5 exibe o resultado como uma sequência de 1, -1 e como um gráfico de um análogo discreto do preço original.
#include <Discr.mqh> #include <Graphics\Graphic.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[], nmv; setmv(mv, tstart, tstop, dprcnt); nmv = ArraySize(mv); if(nmv < 1) { Print("not enough moves"); return; } // Display mv[] as a sequence of 1 and -1 string res = (string)mv[0]; for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i]; Print(res); // Display the mv[] cumulative sum chart ChartSetInteger(0, CHART_SHOW, false); CGraphic graphic; graphic.Create(0, "G", 0, 0, 0, 750, 350); double x[], y[]; ArrayResize(x, nmv + 1); ArrayResize(y, nmv + 1); x[0] = y[0] = 0.0; for(int i = 1; i <= nmv; ++i) { x[i] = i; y[i] = y[i-1] + mv[i-1]; } ArrayPrint(x); ArrayPrint(y); graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices"); graphic.CurvePlotAll(); graphic.Update(); Sleep(30000); ChartSetInteger(0, CHART_SHOW, true); graphic.Destroy(); }
Todos os exemplos adicionais usarão os resultados da discretização do preço EURUSD em incrementos de 0,5% para o período de 20 de maio a 20 de junho de 2020. O resultado é a seguinte sequência de etapas discretas: 1, -1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, 1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1, -1. Para maior clareza, abaixo também estão gráficos do preço inicial e seu análogo discreto.
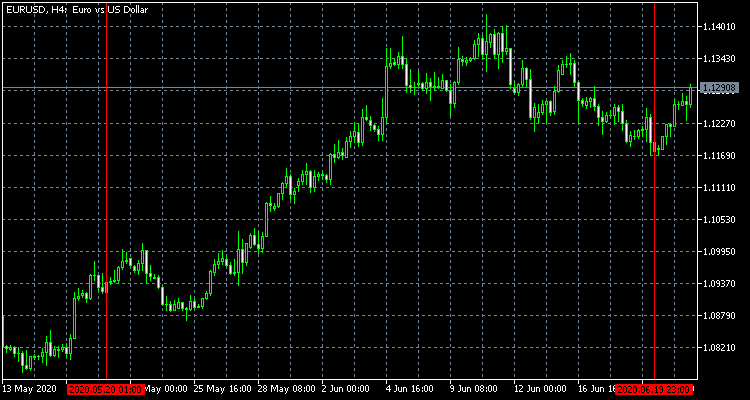
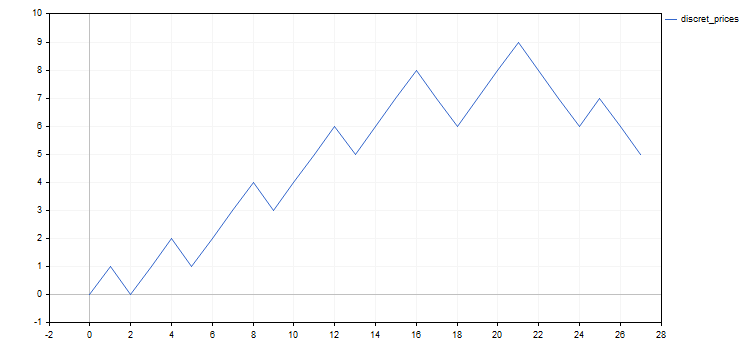
Vale ressaltar que, além de estudar o comportamento do preço discretizado, podem existir outras formas de aplicação do esquema de Bernoulli ou de suas modificações. Vamos apontar dois deles que estão relacionados à negociação.
- Os resultados de uma negociação na qual as transações são executadas com níveis de stop-loss, take-profit e volume fixos. Todos os lucros numa série de transações serão aproximadamente iguais entre si e o mesmo se aplica às perdas. Por isso, a probabilidade de lucro será um parâmetro suficiente para descrever o resultado da negociação. Pode-se, por exemplo, levantar a questão de saber se o valor da probabilidade de se obter lucro na sequência de transações existente é alto o suficiente.
- Seleção de ativos para investimento. Assumamos que no início do período temos uma ampla escolha de como investir. Qualquer um deles, com alguma probabilidade, pode levar a uma perda completa dos fundos investidos. Havendo certa forma de seleção de ativos, pode-se questionar a diferença de probabilidade de falência entre os ativos selecionados em comparação com os rejeitados.
Voltemos aos exemplos.
Exemplo 3. Estimativa do parâmetrop no esquema de Bernoulli. Este é o caso raro em que o problema pode ser resolvido no papel. A função de verossimilhança tem a forma p^nup*(1-p)^ndn. Tomamos a derivada em relação a p e, igualando-a a zero, obtemos um valor bastante esperado para a estimativa р como uma frequência: pe=nup/(nup+ndn)=nup/nmv. É um pouco mais fácil pesquisar o máximo não da função de verossimilhança em si, mas de seu logaritmo. A resposta será a mesma, pois o logaritmo é uma função estritamente crescente e o máximo será alcançado com o mesmo valor do parâmetro. Abaixo está o script p_model.mq5 que calcula esta estimativa.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 1) { Print("not enough moves"); return; } double pe = calcpe(mv); Print("pe=", pe); } //+------------------------------------------------------------------+ // Calculate the probability estimation double calcpe(int& mv[]) { int nmv = ArraySize(mv); if(nmv < 1) return 0.0; int nup = 0; for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup; return ((double)nup) / nmv; }
Resposta: pe = 0.59 (número arredondado)
Exemplo 4. Estimativa de parâmetros no esquema de Bernoulli modificado. Como escrevi acima, o esquema de Bernoulli pode muito bem ser alterado, se necessário, para nossos propósitos de modelagem. Vamos considerar uma possível variante de tal modificação.
Talvez a variação mais fácil é imaginar que a sequência de movimentos seja dividida em duas sequências menores, uma após a outra, e de forma que cada uma delas corresponda ao esquema de Bernoulli com seus próprios parâmetros: n1, p1, n2=n-n1 e p2, onde n é o comprimento da sequência cumulativa.
Assim, precisam ser estimados três parâmetros − n1, p1 e p2. Maximizando o logaritmo da função de verossimilhança em relação a p1 e p2, podemos expressá-los analiticamente por meio de n1. As estimativas para n1 deverão ser encontrados por uma pesquisa simples, substituindo expressões por p1 e p2 na fórmula para o logaritmo de verossimilhança.
Abaixo está o script p1p2_model.mq5 que calcula as estimativas dos parâmetros.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 2) { Print("not enough moves"); return; } double p1e, p2e; int n1e; calc_n1e_p1e_p2e(mv, n1e, p1e, p2e); Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e); } //+------------------------------------------------------------------+ // Calculate the probability estimation void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e) { n1e = 0; p1e = p2e = 0.0; int nmv = ArraySize(mv); if(nmv < 2) return; n1e = 1; double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2; for(int n1 = 2; n1 < nmv; ++n1) { llh = llhx_n1(mv, n1, p1, p2); if(llh > llhx) { llhx = llh; n1e = n1; p1e = p1; p2e = p2; } } } //+------------------------------------------------------------------+ // log-likelihood function maximum depending on n1 double llhx_n1(int& mv[], int n1, double& p1, double& p2) { p1 = p2 = 0.0; int nmv = ArraySize(mv); if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0; int nu1 = 0, nu2 = 0; for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1; for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2; double l = 0.0; if(nu1 > 0) { p1 = ((double)nu1) / n1; l += nu1 * log(p1); } if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1); if(nu2 > 0) { p2 = ((double)nu2) / (nmv - n1); l += nu2 * log(p2); } if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1)); return l; }
Resposta: n1e = 21; p1e = 0.71; p2e = 0.17 (números arredondados). Ele parece bastante óbvio, pois nosso modelo "viu" uma mudança na direção (ou correção) do movimento do preço no final de seu segmento. Isso sugere que a transição para um modelo mais complexo, neste caso, não foi em vão.
Exemplo 5. No exemplo anterior, a probabilidade de um movimento ascendente dependia de seu número (no tempo). Consideraremos outra modificação do esquema de Bernoulli em que essa probabilidade depende de qual o movimento anterior. Vamos construir um modelo que é um exemplo da cadeia de Markov mais simples com dois estados.
Assumamos que a numeração dos movimentos vai de 0 a n. Para movimento zero, a probabilidade de movimento para cima definimos igual a 0,5 já que não há movimento prévio para isso. Para outras posições, a probabilidade de um movimento ascendente será p1 se houve um movimento ascendente na frente dele, e será igual a p2 se houve um movimento descendente. As probabilidades de movimentos descendentes nestes dois casos são iguais, respectivamente, q1=1-p1 e q2=1-p2. Por exemplo, a probabilidade de um evento em que haja exatamente um evento primário "baixo-cima-cima-baixo" será igual a 0.5*p2*p1*q1.
Obtivemos um modelo com dois parâmetros que podem ser estimados usando o EMV. Aqui, novamente, podem-se fazer todos os cálculos no papel, especialmente se maximizar o logaritmo da função de verossimilhança. A resposta, como no caso do esquema de Bernoulli, resume-se às frequências. Vamos denotar por nud o número de vezes que, após o movimento para cima, ocorre um movimento para baixo (u − up, d − down). De maneira semelhante, introduzimos a notação nuu, ndd e ndu. Estimativas para p1 e p2 são denotadas por p1e e p2e. Assim, estas estimativas são encontradas pelas fórmulas p1e=nuu/(nuu+nud) e p2e=ndu/(ndu+ndd).
Abaixo está o script markov_model.mq5 que calcula estas estimativas.
#include <Discr.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input datetime tstart = D'2020.05.20 00:00'; // start of the considered time interval input datetime tstop = D'2020.06.20 00:00'; // end of the considered time interval input double dprcnt = 0.5; // price discretization step in % //+------------------------------------------------------------------+ void OnStart() { int mv[]; setmv(mv, tstart, tstop, dprcnt); if(ArraySize(mv) < 2) { Print("not enough moves"); return; } double p1e, p2e; calcpes(mv, p1e, p2e); Print("p1e=", p1e, " p2e=", p2e); } //+------------------------------------------------------------------+ // Calculate probability estimations void calcpes(int& mv[], double& p1e, double& p2e) { p1e = p2e = 0; int nmv = ArraySize(mv); if(nmv < 2) return; int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd; for(int i = 0; i < nmv - 1; ++i) if(mv[i] > 0) { if(mv[i + 1] > 0) ++nuu; else ++nud; } else { if(mv[i + 1] > 0) ++ndu; else ++ndd; } nu = nuu + nud; nd = ndu + ndd; if(nu > 0) p1e = ((double)nuu) / nu; if(nd > 0) p2e = ((double)ndu) / nd; }
Resposta: p1e = 0.56; p2e = 0.60 (números arredondados). O fato de ambas as probabilidades serem quase iguais indica que não há dependência entre movimentos adjacentes, mas o fato de serem maiores que 0,5 indica a presença de uma tendência ascendente. Também o fato de ambas as estimativas de probabilidade estarem próximas da estimativa de probabilidade para um modelo mais simples (o esquema simples de Bernoulli do terceiro exemplo) sugere que a transição para este modelo complicado acaba por ser desnecessária neste caso particular.
5.2. Verificação de hipóteses estatísticas
Diferentes distribuições de probabilidade podem ser especificadas no mesmo espaço amostral. Uma hipótese é uma declaração que especifica o tipo de distribuição. Deve haver várias hipóteses, pelo menos duas, já que a solução está na preferência de uma hipótese sobre as outras. Uma hipótese é chamada de simples se ela determina exclusivamente o tipo de distribuição.
Mostramos um exemplo para o esquema de Bernoulli: hipótese da igualdade do parâmetro p para um número específico − hipótese simples (exatamente um valor possível do parâmetro que determina exclusivamente a distribuição), e a hipótese de que esse parâmetro é maior do que um determinado número é uma hipótese complexa (infinitos valores possíveis do parâmetro).
Além disso, teremos de escolher entre duas hipóteses. Uma delas é chamada zero, já a outra, alternativa. A escolha de uma hipótese é feita por critério estatístico. Basicamente, é apenas uma função com valores 0 e 1 no espaço dos eventos elementares, onde 0 significa aceitação da hipótese nula, e 1, hipótese alternativa.
Assim, temos a opção de aceitar a hipótese nula ou rejeitá-la. Nesse caso, a hipótese alternativa, respectivamente, ao contrário, é rejeitada ou aceita. Cada uma dessas decisões pode ser certa ou errada. Assim, há quatro resultados possíveis de aceitar a hipótese, dos quais dois são verdadeiros e dois são falsos.
- O erro tipo 1 é a rejeição errônea de hipótese nula.
- O erro de tipo II é a adoção errônea da hipótese nula.
As probabilidades de erros de primeiro e segundo tipo são denotadas por a1 e a2. Naturalmente, gostaríamos de ter essas probabilidades o mais pequenas possível. Infelizmente, isso não é possível. Além disso, ao diminuir a probabilidade de erro de um tipo, naturalmente enfrentamos um aumento na probabilidade de outro tipo de erro. Por esse motivo, geralmente é feito algum tipo de compromisso entre esses erros.
O número 1-a1 é chamado de nível de significância do critério, já o número 1-a2 é sua potência. O poder de um critério, especialmente para uma hipótese complexa, pode ser difícil de calcular. Por isso, eles costumam se contentar apenas com o nível de significância.
Um critério é geralmente construído com base numa função numérica (também definida num espaço amostral), tradicionalmente chamada de "estatística de teste". O conjunto dos seus valores está dividido em duas áreas, uma das quais corresponde à aceitação da hipótese nula e a outra à sua rejeição. A área em que a hipótese nula é rejeitada é chamada de crítica.
Uma observação importante sobre a primeira "hipótese negativa". Com este termo, quero dizer que primeiro precisamos ter certeza de que uma de nossas duas hipóteses seja necessariamente cumprida. A grosso modo, se separarmos os chihuahuas dos cães de outras raças pelo peso, devemos ter certeza de que sempre teremos um cachorro na balança, e não um elefante, rato ou gato. Caso contrário, nosso teste de hipótese não tem sentido. Existem exemplos especialmente frequentes que infringem este princípio em aplicações imprecisas de critérios estatísticos usados em econometria.
A seguir estão exemplos de teste de hipótese para o esquema de Bernoulli.
Exemplo 1. Teste de hipótese nula p=p0 no esquema de Bernoulli. Essa hipótese é simples. Uma hipótese alternativa pode ser uma das duas variações a seguir (em ambos os casos, complexa). As estatísticas do critério em ambos os casos serão kup, isto é, o número de movimentos ascendentes na sequência, mas a área crítica será definida de forma diferente.
- p>p0, área crítica à direita kup⋝kr
- p<p0, região crítica à esquerda kup⋜kl
Valores específicos para kr e kl são encontrados a partir da condição de que a probabilidade de as estatísticas caírem na região crítica não exceda a probabilidade selecionada de um erro tipo I. Gostaria de lembrar que todas essas probabilidades são calculadas sob a condição de que a hipótese nula seja atendida, ou seja, de acordo com a distribuição de Bernoulli com o parâmetro p=p0.
Vamos verificar esta hipótese para p0=0.5 em toda nossa mesma sequência discretizada de preços. Este valor para p0 é ótimo porque se encaixa na hipótese de "passeio aleatório".
Abaixo está o script p0_hypothesis.mq5 que verifica esta hipótese.
#include <Math\Stat\Binomial.mqh> #property script_show_inputs //+------------------------------------------------------------------+ input int nm = 27; // total number of movements in the series input int kup = 16; // number of upward movements input double p0 = 0.5; // checked probability value input double alpha1 = 0.05; // type 1 error probability //+------------------------------------------------------------------+ void OnStart() { int kl, kr, er; kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er); kl=(int)MathQuantileBinomial(alpha1,nm,p0,er); Print("kl=", kl, " kup=", kup, " kr=", kr); Print("kup<=kl = ", kup<=kl); Print("kup>=kr = ", kup>=kr); }
Resposta:
- kl=9; kup=16; kr=18
- kup<=kl = false
- kup>=kr = false
O resultado sugere que a hipótese nula não pode ser rejeitada neste nível de significância em favor de nenhuma das alternativas.
Exemplo 2. Suponhamos que temos duas sequências de comprimento n1 e n2, que são retirados de dois esquemas de Bernoulli com parâmetros p1 e p2. A hipótese nula aqui reside na afirmação de que é atendida a igualdade p1=p2, e as possíveis alternativas são seus diferentes tipos de desigualdade, dos quais também existem dois aqui. O critério estatístico em todos esses casos será k2 −número de movimentos ascendentes na segunda sequência das duas, mas a região crítica será definida de forma diferente.
- p2>p1, área crítica à direita k2⋝kr
- p2<p1, área crítica à esquerda k2⋜kl
Uma diferença significativa em relação ao exemplo anterior é que aqui não estamos falando sobre valores exatos p1 e p2, mas apenas sobre sua proporção. As regiões críticas são definidas da mesma forma que no exemplo anterior, mas a distribuição das estatísticas quando a hipótese nula é satisfeita é hipergeométrica, não binomial. Em estatística matemática, este critério é conhecido como teste exato de Fisher.
Abaixo está o script p1p2_hypothesis.py, escrito em Python, que resolve esse problema para nossa divisão em dois do preço discreto. Por uma questão de interesse, foi feita a análise que saiu no quarto exemplo do parágrafo anterior.
from scipy.stats import hypergeom n1 = 21; n2 = 6 k1 = 15; k2 = 1 alpha1 = 0.05 kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2)) kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2)) print("kl =", kl, " k2 =", k2, " kr =", kr) print("k2<=kl =", k2<=kl) print("k2>=kr =", k2>=kr)
Resposta:
- kl = 2; k2 = 2; kr = 6
- k2<=kl = True
- k2>=kr = False
6. Fim do artigo
O artigo não cobriu áreas importantes da estatística matemática, como estatística descritiva, estimação por intervalo de parâmetros, estimativas assintóticas e a abordagem bayesiana em estatística. O principal motivo para isso não ter sido assim é que primeiro seria necessário esclarecer o conceito de variável aleatória. Mas decidi adiá-lo para o próximo artigo, para que fosse compacto e seu conteúdo, abrangível.
7. Arquivos anexados
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | hyperg_be.py | Script em Python | Calcula a estimativa do parâmetro b da distribuição hipergeométrica. Exemplo 5.1.1 |
| 2 | hyperg_ne.py | Script em Python | Calcula a estimativa do parâmetro n da distribuição hipergeométrica. Exemplo 5.1.2 |
| 3 | Discr.mqh | Arquivo de cabeçalho MQL5 | Arquivo com função setmv() usado em todos os exemplos MQL5 abaixo para discretização do preço |
| 4 | discret_prices.mq5 | Script em MQL5 | Script que realiza a discretização do preço e exibe o resultado como uma sequência 1 e -1 e um gráfico |
| 5 | p_model.mq5 | Script em MQL5 | Calcula a estimativa do parâmetro p no esquema de Bernoulli. Exemplo 5.1.3 |
| 6 | p1p2_model.mq5 | Script em MQL5 | Calcula a estimativa de parâmetros n1, p1 e p2 no modelo a partir de dois esquemas de Bernoulli. Exemplo 5.1.4 |
| 7 | markov_model.mq5 | Script em MQL5 | Calcula a estimativa de parâmetros p1 e p2 da cadeia de Markov. Exemplo 5.1.5 |
| 8 | p0_hypothesis.mq5 | Script em MQL5 | Confirma a hipótese de que o parâmetro do esquema de Bernoulli é igual a um determinado número. Exemplo 5.2.1 |
| 9 | p1p2_hypothesis.py | Script em Python | Teste exato de Fisher. Exemplo 5.2.2 |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8038
Sistema de notificações de voz de eventos e sinais de negociação
Trabalhando com séries temporais na biblioteca DoEasy (Parte 46): buffers de indicador multiperíodos multissímbolos
Usando criptografia com aplicativos externos
Conjunto de ferramentas para negociação manual rápida: trabalhando com ordens abertas e pendentes
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso