MetaTrader 5 / 統計と分析
English Русский 中文 Español Deutsch Português
確率をトレードギャップに適用する

確率をトレードギャップに適用する

MetaTrader 5 — 統計と分析 | 4 2月 2019, 07:15
2 157 0
Aleksey Nikolayev
Aleksey Nikolayev

コンテンツ

イントロダクション

この記事は、著者の以前の記事から始まった、トレードにおける確率と数学的統計を適用するトピックです。 トレード戦略の作成とテストに適切な方法を使用することを検討します。

最初に、ランダムウォーク仮説からの逸脱するようなトレードの可能性を見ていきます。 価格がゼロドリフトランダムウォークのように振る舞うならば、収益性の高いトレードは不可能であることが証明されています。 この仮説を反論する方法を見つけるための基礎を提供します。 仮説を反駁する方法が見つかった場合、トレード戦略を開発するためにそれを使用するかもしれません。

また、以前に公開された記事で発生したリスクのトピックについても引き続き検討します。さらに、１番目 と2 番目の記事を参照します。

アプローチは、確率に基づいているので、その基礎はあった方がいいですが、必須ではありません。 確率方法の本質を理解することが重要です。より体系的かつ頻繁に使用されればされるほど、より顕著かつ有意な結果が得られます (大数の法則による)。 もちろん、そのアプリケーションは十分に立証され、十分であるべきです。

EAに関する一般的な考慮事項

EAの開発は、大まかに3つの段階に分けることができます。

  1. アイデアの生成。
  2. あらゆる種類の簡略化を使ってアイデアをチェック。
  3. 相場の現実にアイデアを適応。

この記事では、主に第2段階について扱い、より徹底的に述べられたトピックに焦点を当てることができます。 また、この段階は、他のものよりもはるかに少ない頻度でフォーラムで考察されています。

実装された簡略化について説明します。 単一の資産をトレードEAに自分自身を閉じ込めます。 資産価格は口座通貨で表されると仮定します。 (スワップと口座から資金を引き出すような) 非トレード操作を除外し、オーダーの異なるタイプを考慮しません (相場価格による売買のみを残します)。 オーダーの実行時にスリッページを無視しますが、スプレッド (s) は固定値とみなされます。 また、EAがアカウント上のすべての資金を管理しており、他のEAが起動されていないと仮定します。

すべての簡略化を使用すると、EAの動作結果は、時間に応じて v(t) 関数-ポジションボリュームとして明確に定義されます。 正のv (t)は買いに対応し、負は売りを意味します。 また、資産価格関数p(t)とc0 (初期資金) があります。 次の図は、可能なv =v (t)ポジションチャートを示します。

サンプルポジション

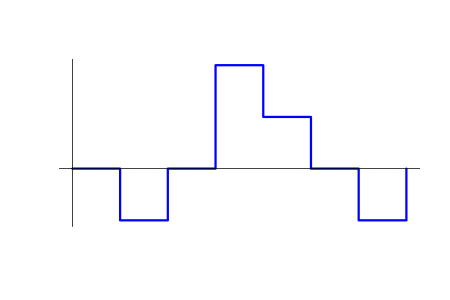
売買価格の算術平均。

v(t) とp (t)は、値が最小増分ステップの倍数であるため、区分定数 (段階的) 関数です。 より厳密な数学的定義が必要な場合は、右側から連続していると見なされ、左側のギャップポイントに制限があります。 v (t)ギャップ点がp (t)のものと一致しないと仮定します。 つまり、価格またはポジションボリュームのいずれか、またはその両方が変更されないままであれば、2つの値のうちの1つだけが任意の時点で変化することはありません。 価格またはボリュームの変更が発生する可能性のある時間内のポイントは、特定の最小ステップの倍数でもあることは注目に値します。

これらのデータに基づいて、 c (t) 関数を見つけることができます-時間に応じて資金の値。 tモーメントでポジションをクローズする場合に、EAによって管理されるアカウントの一部に対する残高として定義されます。 アカウント上には1つのEAのみがあるので、この値は MetaTrader5 で定義されたアカウントエクイティと一致します。

tで c(t) の変更を定義します。 ボリュームと価格は、この時点で変更されていない場合、自然にゼロです。 価格が変更された場合、資金の増加は、価格増分によってボリュームの積と等しくなります。 ボリュームが変更された場合、2つのオプションが可能であり、絶対ポジションボリュームが減少した場合、資金は同じままであり、増加した場合、資金は、ボリューム変化の絶対値によってスプレッドの積に等しい量だけ減少します。 つまり、ポジションが部分的にクローズされた場合、エクイティは変更されず、ポジションに追加するとエクイティのわずかな減少につながります。 したがってc(t) 、 tモーメントでの資金の値は、ゼロモーメントからtに至るまでに発生したすべての変化と、 c0= c (0)の合計です。

リスク理論 (前の2つの記事) を開発するとき、「取引」の概念を使用しました。 この概念は、MetaTrader5 で「取引」と呼ばれるものとは全く一致せず、「トレード」と呼ばれるものに対応します。 正確に言うと、シンプルなポジションと呼ぶものに対応します。 定義によるシンプルなポジションは、オープンとクローズの瞬間によって設定されます。 そのボリュームと方向は、その瞬間の間に一定のままです。 下記は簡単なポジションのサンプル v= v (t)チャートです。

シンプルポジション (取引)

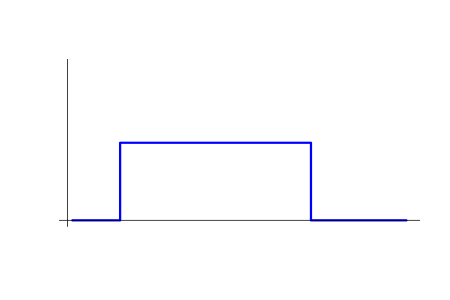
任意のポジション (常に区分的に定数であるため) は、シンプルなポジションの合計として想像することができます。 このような表現は、無限通り行うことができます。 次の図は、シンプルなもの合計として2つの異なる方法で表される単一のポジションを示します。 初期ポジションは青で表示され、分割された取引は緑と赤で表示されます。 MetaTrader5 でトレードの概念を使用する場合、さらに別のオプションが得られます。 方法のそれぞれは、かなり合理的です。

ポジションを取引に分割する2つの方法

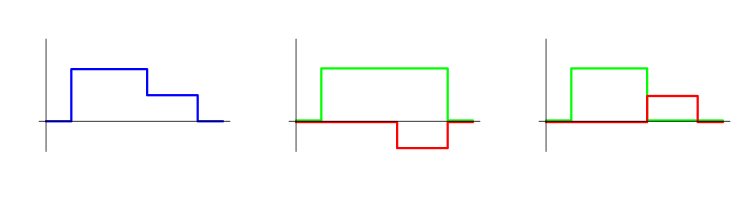
このような表現があまり意味をなさないEAがいくつかあります。 例えば、ポジションを徐々に増加し、その後徐々に減少させるEAがあるかもしれません。 同時に、このようなやり方は自然であるため、この種のEAがあります。 たとえば、あるポジションは、シンプルなポジションのシーケンスで構成される場合があります。 以下のチャートはそのようなポジションの例です。

取引の合計として提示される不適当で適切なポジション

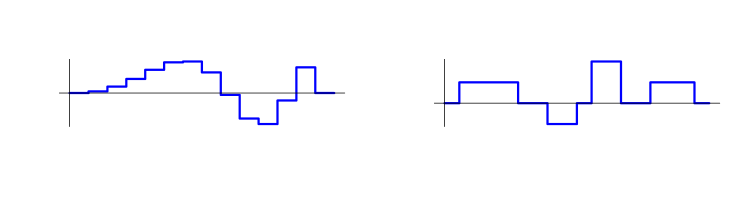
各トレードの後の資金の相対的な変化 (シンプルポジション) は、収益性 aとリスクr /c0= 1 + ra の2 つの値で表されます。 収益性は、インプット価格と ストップロス の差へのトレード中の価格上昇の比率に等しいです。リスクはトレード量に比例していると ストップロス 正確な活性化の場合に失われるであろう資金のシェアを意味します。

したがって、v(t)、 p (t ) およびc (t)時間関数を考慮するのではなく、取引のシーケンスを特徴付ける数値シーケンスを分析することにします。 これは研究を大幅に簡素化します。 特に、不確実性の確率的モデルに進む際に、ランダムな変数の有限集合に自分自身を制限するランダム過程の理論を適用する必要性を避けます。

この確率論は、資産価格とトレード結果における不確実性の数学的モデリングの一般的に受け入れられている方法です。 このアプローチに従って、v(t) とc ( t) 関数がランダムプロセスの特定の実装 (軌道) として機能することを考慮する必要があります。 一般に、このタスクは実質的に未解決です。 主な理由は、価格行動を正確に記述する適切な確率モデルがないことです。 したがって、解決策が可能な場合には、特別のケースを検討することが理にかなっています。 前述のように、この記事では、簡単なポジション (取引) のシーケンスとして適切に表現できるポジションを形成するEAを考えます。

EAに関連する別の問題を言及する価値があります。パラメータです。 EA開発プロセスの形式化 (標準化) を達成するために、詳細に考慮することが有用でしょう。 次の3つのタイプにパラメータを分割してみましょう。

  1. ヒストリカルパラメータ EA操作中に1つの取引から別のトレードに変更される可能性のあるパラメータ。 これらはインジケータ値、時刻、ニュースデータ、ムーンフェイズなどです。 一般的には、価格やポジションボリュームと同様に、時間関数です。 適用されたシンプル化の場合、トレードを行う時点で既知の数字のシーケンスであると考えることができます。 各特定の取引 (方向、ボリューム、SL、TP) のパラメータは、ヒストリーパラメータの値に基づいて定義されます。
  2. 実際のパラメータ。 簡潔にするために、パラメータを呼び出してみましょう。 EAがトレードを開始するときに設定され、EAのテストと最適化を行う場合にのみ適用できます。
  3. メタパラメータは、カスタム最適化基準パラメータなどのEA最適化アルゴリズムを設定します。 EAを2つの基準で最適化しますが、1つによってのみ実行できます。 重みづけで合計を取る2つの新しい基準を形成します。 これらの重みづけは、メタパラメータとして提供されます。

たとえば、以下で説明するギャップベースのEAでは、最小ギャップはEAパラメータであり、各特定ギャップのサイズはヒストリーパラメータです。 この場合、メタパラメータは、最適化基準番号を含みます。 (例えば、利益による最適化は #1、ドローダウンによる最適化は #2 など)、オーダーで基準が番号付けされていると仮定します。

この記事では、ヒストリーパラメータに関連付けられた1つの重要なシンプル化を使用します。 トレードにおけるリターンの分布について話すとき、一般的にパラメータに依存するかもしれません。 この依存関係は重要ではないと仮定します。 主な理由は、この依存を考慮に入れようとすると、通常はモデルが複雑になり、最終的にはオーバーフィッティングにつながる可能性があるということです。

ランダムウォーク仮説を棄却する試みとしてのトレード戦略

すでに価格行動を記述する正確なモデルの欠如を言及しました。 にもかかわらず、有用なおおよそのモデルがあります。 たとえば、価格がゼロドリフトのランダムウォークであることを考慮した、よく知られた価格行動モデルがあります (ディレクテッドトレンドの不在)。 このモデルはランダムウォーク仮説と呼ばれます。 この仮説によれば、EAはスプレッドを考慮すると、平均してゼロの利益を得るか、または少額の損失を持つことになります。

ランダムウォークで資金を稼ぐことの不可能を証明することは、ランダムプロセスの理論の複雑な数学的 (Itô calculus、ストップ時間など) 関与を必要とするので、かなり困難です。 一般的には、トレンドなしでランダムウォークでトレードするとき、資本はマーチンゲール(オッズ理論、賭博システムとしてマーチンゲールと混同されない) という声明に帰着します。 マーチンゲールは、時間とともに変化しない平均値 (数学的期待値) を持つランダムプロセスです。 今回のケースでは、いつでも資本の価値の数学的期待値は、その初期値に等しいことを意味します。

したがって、ランダムウォークからの統計的に有意な価格偏差を検索することから、トレードのアイデアの検討を開始する必要があります。 これを行うには、確率と数学的統計からの考え方を使用しますが、まず、観測を行います。

  • この種の任意のソリューションは、自然界での確率です。結論が間違っている確率があります。
  • この方法は、偏差を検出しない場合、完全な不在を意味するものではありません。 おそらく、人によっては他のメソッドを使うでしょう。
  • 統計的に有意な偏差は、統計的に有意の正の利益の取得を保証するものではありません。偏差が必要ですが、不十分な条件です。

ランダムウォーク偏差を検索する方法を構築してみましょう。 これを行うために、実際の価格を用いて形成されたサンプルに基づいて経験的確率分布を構築するため、ランダム変数を検討します。 また、価格行動がランダムウォークであると仮定して、同じ値の理論的確率分布を構築します。 分布を比較して、ランダムウォーク仮説を棄却する (または拒否できない) ことを決定します。

適切な値の例を構築してみましょう。 t0 の最初の時点で、価格がp0に等しいとします。 p0に等しくない別のp1 価格値を取りましょう。価格がその値(t1) = p1に達すると、 t1 モーメントまで待ちます。 t0 とt1の間の時間間隔で価格のうち最も遠い1からの価格p2 を見つけてみましょう。 値 K を導入してみましょうK=(p2-p0)/(p0-p1).。 p1<p0≤p2 またはp2≤p0<p1の条件は常に有効であり、したがってK≥0は常です。 このアイデアを説明するチャートは、以下に提供あります。 青い線はp0 の価格レベルを意味し、価格チャートを横切る瞬間はt0です。 赤い線はp1 の価格レベルを意味し、t0 の後の価格チャートに触れる瞬間です。 緑色の線は、可能な限りp1 から離れて位置するp2 価格レベルを意味します。

p0、p1、p2 の価格

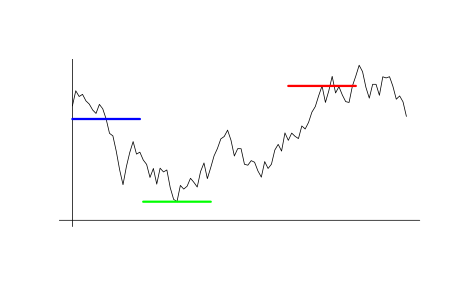
価値の背後にある考え方はシンプルです。 t0でインプットすると仮定します。 p0で売ります。p1, p1>p0はストップロスです。 p2 はTPに対して最も達成可能な価格であり、 Kはトレードに対して最も高い利益を達成することができます。 実際には、トランザクションを実行するときに正確なK値がわかりません。 この不確実性の確率モデルの枠組みの中で、その確率分布パターンを知ることについてのみ話すことができます。 k<>という確率として定義されるFk(x)確率分布関数を仮定します。 TPとして特定のpk 価格を使用すると仮定します: p. 0= k (p 0-p1)。 この場合、 Fk(k)は、SLがTPより早く到達する確率です。 したがって、 1 ~ f.k(k)は、TPが以前にアクティブ化された確率です。 今のところ、スプレッドをゼロにしましょう。 次に、SLアクティベーションの場合、収益性は-1に等しくなりますが、TPアクティベーションの場合はkです。 そのような約定における数学的期待値: M=(-1)*Fk(k)+k*(1-Fk(k))=k-(k+1)*Fk(k), 次の場合ゼロになります。：Fk(k)=k/(k+1).

もし、方程式がFk(x)であれば、EAの予備的な最適化を行うこともできます。 たとえば、トレードの収益性の数学的期待値を最大化する最適なTP/SL比を探すことができます。 その後、トレードにおける最適なリスク値を見つけることができます。 したがって、EAは準備が整う前でも最適化することができます。 時間を節約し、早い段階で明らかに不適当なアイデアを破棄することを可能にします。

価格がトレンドなしでランダムウォークのように振る舞うと仮定した場合、K 値の分布は、x (x) = fk0分布関数によって設定され、ここではfk0は0k0 の場合は x /x + 1となります。 より確実にするために、ここで使用するランダムウォークはゼロドリフト (トレンドなし) を持つウィーナープロセスであると仮定することができます。 ご覧の通り、ランダムウォーク仮説が満たされ、スプレッドがゼロに等しい場合、収益性の数学的期待値は、任意のTP/SL比でゼロです。 ゼロ以外のスプレッドの場合、負の値になります。

K の代わりに、値q = k/k+2 − p1 − p1、 K = q/(1 − q)を考慮することができます。 この値は、SLとTPの合計に対するTPの比率として表すことができます。 [0; 1)間隔内の値を取り、ランダムウォークの場合はKよりもシンプルな分布 (この間隔では一様) を持つため、より便利です。

さらに、主に Q の値についてお話します。 そのエンピリック分布関数のFq(x)がどのように構築され、適用するかを考えてみましょう。 価格のヒストリーを確認するトレードのアイデアがあると仮定します。 n 個のエントリポイントのセットがあります。 インプット価格p0、i および ストップロス p1、i、i は、ここで、i = 1,..., nであり、それぞれについて定義されます。 このアイデアは、利益の可能性があるかどうかを定義する必要があります。 各トレードに、価格p2 を見つける必要があり、そのアクティベートの瞬間まで ストップロス から可能な限り配置します。 その価格に基づいて、 nサンプルのQi= (p2、pn、i)/(p2、i− p1、i)、 i = 1,..., nを得ます。 このサンプルによって構築された経験分布関数は、 m ( x) がxより小さいqi サンプル要素の数に等しいFq( x)/n 方程式によって定義します。 価格がトレンドなしのランダムウォークのように振る舞う場合 (ゼロドリフトのウィーナープロセス)、 Q値のfq0(x)分布関数は単純に見えます。 q0(x) = 1 の場合は x で、x が1の場合は 0 = 。

fq(x)が、ランダムウォークFq0(x)の理論分布関数と大きく異なる場合、収益性の観点からこの差の有意性を確認する必要があります。 スプレッドが考慮されても収益性が十分にプラスであれば、適切な利益/SL比率を選択します。 これは、収益性の期待値を最大化することによって行うことができます。 その後、トレードごとのリスク値に最適な値を選択し、そのアイデアを事前にテストすることができます。 結果が正の場合は、実際のトレードEAの作成に進むことが理にかなっています。 さらに、実際にこのアルゴリズムを示すことを試みます。

問題は、より複雑な相場エグジットアルゴリズムにランダムウォークと同様の比較を行う方法です。 一般的な解答は、上記のケースと同じです。 主な問題は、ランダムウォーク上の確率分布は、まれに分析的な形で得ることができるということです。 しかし、モンテカルロ法を用いて経験的近似を得ることは可能です。

ギャップトレード戦略

アイデアを分析する前に、主なタスクは、収益性の高いトレード戦略ではなく、分析方法を実証することであることに注意してください。 利益に重点を置きすぎると、全体に対してささいな点で気を使い過ぎる結果になるでしょう。

資産価格は離散的であるため、常に飛躍的に変化します。 飛躍はサイズが異なる場合があります。 大きいとき、ギャップと呼ばれます。 通常の価格変更からギャップを区切る特定の境界はありません。 この境界を自由に設定することができます。

ギャップは、前のセクションで概説した理論を実証するのに適しています。 それぞれは、中の2つのタイムポイントと資産価格によって設定されます。 以前に導入された価格チャート記を使用して、p 0 は後の価格であると仮定します。 p1 は以前のものです。 ギャップが発生するとすぐにトレードをインプットします。. 価格p1 はSLとしてだけでなく、TPとしても考慮することができます。 ギャップの迅速な決済に、またはギャップの方向に大きな価格の動きのいずれかを期待して、2つのタイプのいずれかのシステムを選択することができることを意味します。 ギャップの終わりは、価格がp1 レベルに戻るか、ブレイクすることを意味します。

標準的な形式のギャップは、外国為替資産に比較的まれであるので、著者はフォーラムの管理と、この記事のトピックを考察する際に、この概念を一般化するために提供されました。 ギャップを定義する場合、2つのトレーリングの価格の間のギャップのみが考慮されることを示す要件を放棄することができます。 明らかに、この場合の可能なギャップの数は絶する巨大になり、したがって、ビューのトレードの観点から合理的なオプションによって自分自身を制限する価値があります。 例えば、著者は、1つのアメリカのセッションの終値と次の始値の間のギャップを考慮するように提案されました。

セッションの概念がどのように形式化されているかを説明します。 期間、長さ、シフトの3つの時間間隔で設定されます。 セッションは周期的で、期間を超えない長さを持ちます。 任意のティックは、任意のセッションに属しています (後者は、その長さが期間よりも厳密に少ない場合に可能です)。シフトは、時間のゼロ点とその後の最初のセッションの開始との間の時間間隔です。 この期間よりも短くする必要があります。 セッションのこの概念は、通常よりも幾分広く、例えば、分足の間のギャップを考慮することができます。 次の図で説明しましょう。 緑色の矢印は、シフトを定義する時間の長さを表し、赤はピリオドを示し、青はセッション長を示します。

セッション

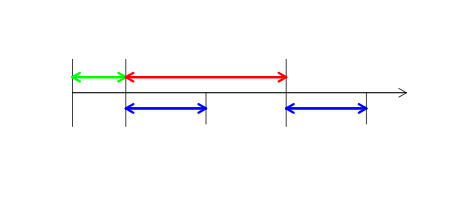
ギャップに関連する統計情報を収集するために、わずかに異なる2つのEAを使用します。 最初の1つ (gaps_reg_stat.mq5) は、2つのトレーリングのティック間のギャップを考慮し、2番目の1つ (gaps_ses_stat.mq5) はセッション間のギャップを考慮します。 もちろん、これらのEAは、テストモードでのみ実行されます。 2番目の1は、分足の OHLC で、実際のティックでのみ、最初のを実行することをお勧めします。 EAコードは以下の通りです。

//gaps_reg_stat.mq5
#define ND 100

input double gmin=0.1;                 //最小ギャップサイズ: USDJPY-0.1、EURUSD-0.001
input string fname="gaps\\stat.txt";   //統計用ファイルの名前

structSGap
  { double p0;
    double p1;
    double p2;
    double p3;
    double s;
    void set(double p_1,double p,double sprd);
    bool brkn();
    void change(double p);
    double gap();
    double Q();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p,double sprd);
    void change(double p);
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
bool is0=false;

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    if(is0)
      { double p=(tick.bid+tick.ask)*0.5, p0=(tick0.bid+tick0.ask)*0.5;
        gaps.change(p);
        if(MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid);
      }
    else is0=true;
    tick0=tick;
  }

int OnInit()
  { gaps.init();
     return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

void SGap :: set(double p_1,double p,double sprd)
  { p1=p_1; p0=p2=p3=p; s=sprd;
  }

bool SGap :: brkn()
  { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1));
  }

void SGap :: change(double p)
  { if(brkn()) return;
    if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p;
    p3=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { double q=p2-p1;
    if(q==0.0) return 0.0;
    return (p2-p0)/q;
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p,double sprd)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].set(p_1,p,sprd);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

void CGaps :: change(double p)
  { for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        gs[go[i]].change(p);
        if(gs[go[i]].brkn()) go[i]=-1;
      }
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c;
    for(int i=0;i<ngs;++i)
      { if (gs[i].brkn()) c=1; else c=0;
        FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s);
        if(i==ngs-1) break;
        FileWriteString(f,"\n");
      }
    FileClose(f);
  }
//gaps_ses_stat.mq5
#define ND 100

input double gmin=0.001;               //最小ギャップサイズ: USDJPY-0.1、EURUSD-0.001
input uint   mperiod=1;                //セッション期間 (分)
input uint   mlength=1;                //セッションの長さ (分)
input uint   mbias=0;                  //最初のセッションバイアス (分)
input string fname="gaps\\stat.txt";   //統計用ファイルの名前

structSGap
  { double p0;
    double p1;
    double p2;
    double p3;
    double s;
    void set(double p_1,double p,double sprd);
    bool brkn();
    void change(double p);
    double gap();
    double Q();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p,double sprd);
    bool change(double p);
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
int ns0=-1;
ulong sbias=mbias*60, speriod=mperiod*60,SLength=mlength*60;

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    double p=(tick.bid+tick.ask)*0.5;
    gaps.change(p);
    int ns=nsession(tick.time);
    if(ns>=0)
      { double p0=(tick0.bid+tick0.ask)*0.5;
        if(ns0>=0&&ns>ns0&&MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid);
        ns0=ns;
        tick0=tick;
      }
  }

int OnInit()
  { if(speriod==0||slength==0||speriod<slength||speriod<=sbias)
      { Print("wrong session format");
        return(INIT_FAILED);
      }
    gaps.init();
    return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

int nsession(datetime t)
  { ulong t0=(ulong)t;
    if(t0<sbias) return -1;
    t0-=sbias;
    if(t0%speriod>slength) return -1;
    return (int)(t0/speriod);
  }

void SGap :: set(double p_1,double p,double sprd)
  { p1=p_1; p0=p2=p3=p; s=sprd;
  }

bool SGap :: brkn()
  { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1));
  }

void SGap :: change(double p)
  { if(brkn()) return;
    if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p;
    p3=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { double q=p2-p1;
    if(q==0.0) return 0.0;
    return (p2-p0)/q;
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p,double sprd)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].set(p_1,p,sprd);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

bool CGaps :: change(double p)
  { bool chngd=false;
    for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        gs[go[i]].change(p);
        if(gs[go[i]].brkn()) {go[i]=-1; chngd=true;}
      }
    return chngd;
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c;
    for(int i=0;i<ngs;++i)
      { if (gs[i].brkn()) c=1; else c=0;
        FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s);
        if(i==ngs-1) break;
        FileWriteString(f,"\n");
      }
    FileClose(f);
  }

このEAはシンプルですが、閉じていないギャップのインデックスが保存されているCGapsクラスの go[] 配列を言及することは意味があります。EAのタスクを高速化することができます。

いずれの場合も、ギャップごとに次のデータが記録されます: 絶対ギャップ値、Q 値、そのクロージャに関するデータ、ギャップの瞬間のスプレッド値。 次に、 Qエンピリック分布値と一様の差をチェックし、さらなる解析の決定を行います。 チャートおよび計算 (コルモゴロフ統計計算) メソッドは、差をチェックするために使用します。 シンプルにするために、計算の結果としてコルモゴロフ-スミルノフ検定のp 値に制限します。 ゼロと1の間の値を取り、小さいほど、サンプルの分布が理論的なものと一致する可能性は低くなります。

数学的な考慮事項について、コルモゴロフ-スミルノフ (1 サンプル) 検定を選択しました。 主な理由は、積分メトリックではなく、一様収束メトリックで分布関数を区別することに関心があるからです。 このテストは MQL5 ライブラリでは見つかりませんでしたので、R 言語を使用しなければなりませんでしました。 サンプルに一致する数値がある場合、この基準の精度は幾分低下します (Rは適切なアラートを示します) が、許容できる範囲です。

理論的と経験的分布の間の有意な不一致が発見された場合、利益を抽出する可能性を検討する必要があります。 重大な不一致がない場合は、このアイデアを破棄するか、改善を試みます。

前述したように、ギャップが形成されている場合、ギャップ方向または反対側のいずれかで、 p0 価格でトランザクションをインプットするには、2つの方法があります。 両方の場合のリターンの期待値を計算してみましょう。 それを行っている間、定数であることを考慮したスプレッドを考慮し、 sとします。 絶対ギャップ値はgと表記され、 g0 は最小値を表します。

  • ギャップ方向へのエントリー。 この場合、g+s は ストップロス であり、 kg-sはTPです。 ここでkは利益/損失率です。 収益性値: -1 ストップロス アクティベーションの場合は、TPアクティベーションの場合はg + s 対応する確率:f q および1 − fq(q)。 q を介してkを表現してみましょう: q /(1-q)。 その後、収益性の数学的期待値については、m = 1 + (1) のq(q) であり、また、g 以上であることが求めています。 Mがすべてのg≥g0に対して有意にポジティブであるq値のみが、適しています。 f q がg = g0でのランダムウォーク<>による理論値よりも有意に低いq値が必要になります。
  • カウンタギャップインプット。 この場合、g-s はTPであり、 kg + sは ストップロス です。 ここでkは損失/利益率です。 収益性の値: -1 ストップロス の活性化の場合には、TPの活性化の場合には ( kg + s) 。 対応する確率: 1 ~f q およびfq(q)。 qを介したkの式は、前の通過と同じです: k = k = q/(1-q)。 収益性数学的期待値mについては、式m = (1 − fq) * (− 1) +q − q g + s) を得られたものです。 Mがすべてのg≥g0に対して有意にポジティブであるq値のみが、適します。 f q ( q) がg = g0での理論値よりも有意に高いq値を必要とすることになります。

2つのシンボルの統計情報が収集されました。

  1. EURUSD
  2. USDJPY

それぞれについて、以下のタイプのギャップが考慮されました。

  1. 連続したティック間。
  2. 分足の間。
  3. トレードセッション間。 EURUSD の場合、アメリカのセッション (シカゴとニューヨークのものが組み合わされたもの) で、USDJPY は東京です。

6つのオプションのそれぞれについて、最新の統計を調査しました。

  1. 200ギャップ
  2. 50ギャップ

その結果、12のオプションがあります。 それぞれの結果は次のとおりです。

  1. p-valueコルモゴロフ統計
  2. ギャップが形成された瞬間の平均拡散値
  3. Q 値分布の経験的および理論的 (赤色線) 関数のチャート
  4. M_contM_cont = 0理論線 (赤) と比較してqに依存してギャップ方向にトレードするための収益性数学的期待値チャート。 ここで、 qはTP/TPと ストップロス の合計比を意味します。
  5. M_rvrs収益性数学的期待値チャートは、 M_rvrs = 0理論線 (赤) と比較してqに依存するチャートとは反対のトレードのものです。 ここで、 qはSL/TPと ストップロス の合計比を意味します。

すべての結果オプションは、以下に提供されます。

  1. EURUSD、200連続したティック間の直近のギャップ。 p 値: 3.471654、平均スプレッド: 0.000695

    EURUSD、200連続ティック間の直近のギャップ


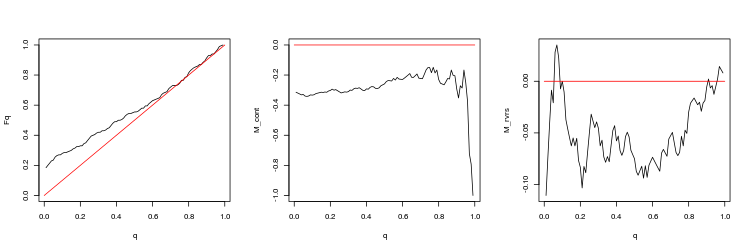
  2. EURUSD、50連続したティック間の直近のギャップ。 p 値: 0.2428457、平均スプレッド: 0.0005724

    EURUSD、50連続ティック間の直近のギャップ

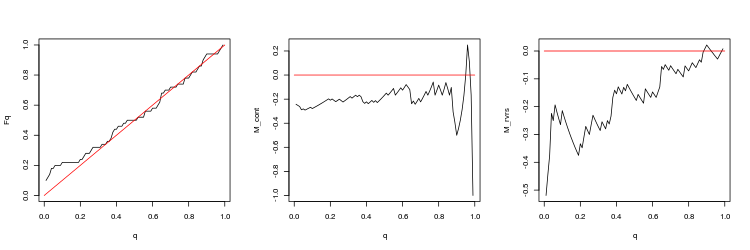
  3. EURUSD, 200 分足の間の直近のギャップ. p 値: 8.675995、平均スプレッド: 0.0004352

    EURUSD、200分足の間の直近のギャップ

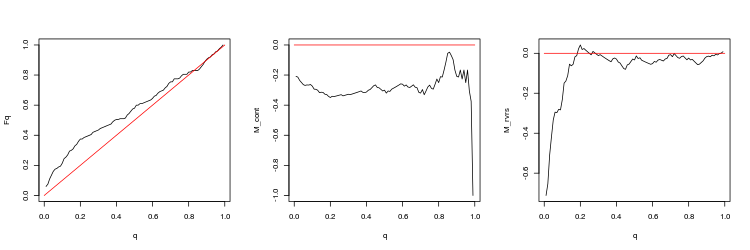
  4. EURUSD, 50 分足の間の直近のギャップ. p 値: 0.0125578、平均スプレッド: 0.000404

    EURUSD、50分足の間の直近のギャップ

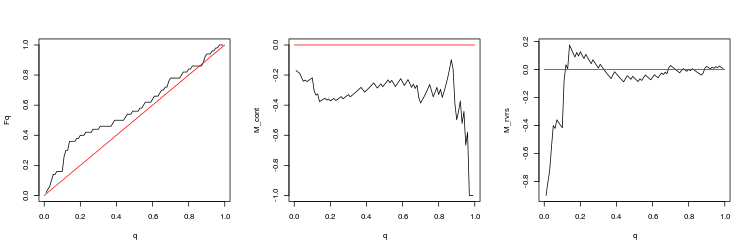
  5. EURUSD, 200 トレードセッション間の直近のギャップ. p 値: 0.6659917、平均スプレッド: 0.0001323

    EURUSD, 200 トレードセッション間の直近のギャップ

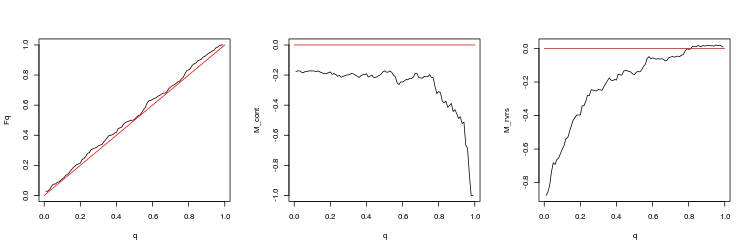
  6. EURUSD, 50 トレードセッション間の直近のギャップ. p 値: 0.08915716、平均スプレッド: 0.0001282

    EURUSD, 50 トレードセッション間の直近のギャップ

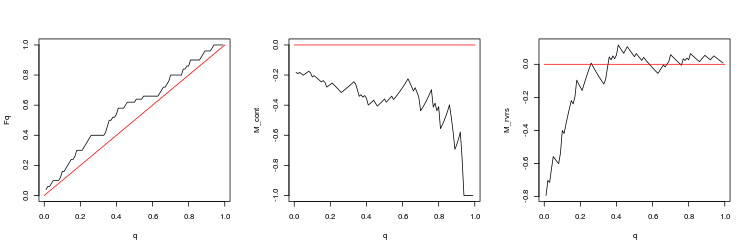
  7. USDJPY、200連続するティック間の直近のギャップ。 p 値: 2.267454、平均スプレッド: 0.09563

    USDJPY、200連続するティック間の直近のギャップ

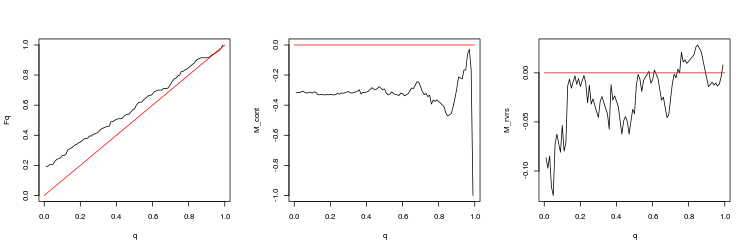
  8. USDJPY、50連続するティック間の直近のギャップ。 p 値: 0.03259067、平均スプレッド: 0.0597

    USDJPY、50連続するティック間の直近のギャップ

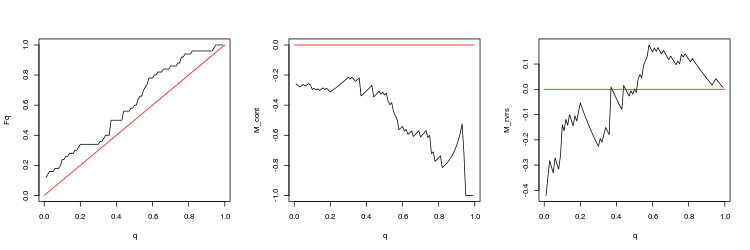
  9. USDJPY、200分足の間の直近のギャップ。 p 値: 0.0003737335、平均スプレッド: 0.05148

    USDJPY、200分足の直近のギャップ

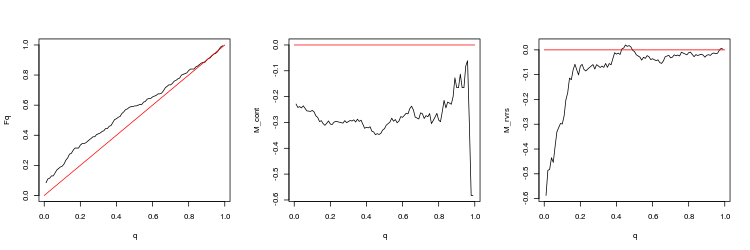
  10. USDJPY、50分足の間の直近のギャップ。 p 値: 0.005747542、平均スプレッド: 0.0474

    USDJPY、50分 の間の最後のギャップ

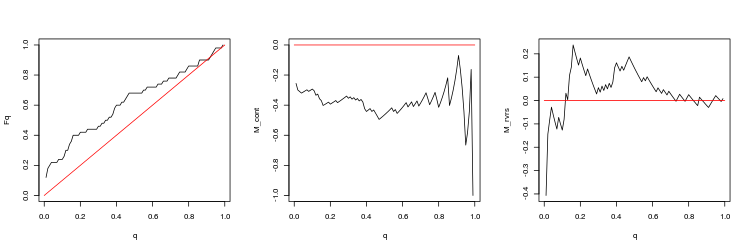
  11. USDJPY、200トレードセッション間の直近のギャップ。 p 値: 0.07743524、平均スプレッド: 0.02023

    USDJPY、200トレードセッション間の直近のギャップ

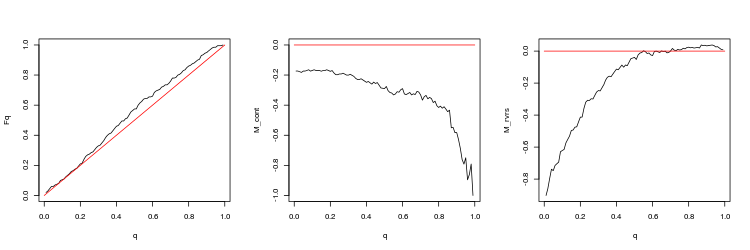
  12. USDJPY、50トレードセッション間の直近のギャップ。 p 値: 0.009191665、平均スプレッド: 0.0185

    USDJPY、50トレードセッション間の直近のギャップ

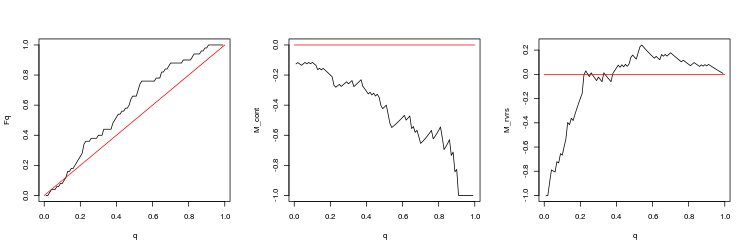
この結果から次の結論を引き出すことができます。

  • ランダムウォークからの逸脱は重要です。
  • ギャップ方向のトレードは unpromising です。 ギャップ終了に向けたトレードがより好ましいように見えますが、利益は小さいです (特に EURUSD ).
  • ギャップ形成時には、スプレッドは平均値と比較して数倍成長します (ティックと分足の間のギャップについては true)。
  • トレードセッション間のギャップは、1-2 ヶ月の一定の間隔でのみランダムウォークからの逸脱します。年間の間隔で偏差は小さいです。 一見, 特定の時間に流行しているトレンドによって決定されます。 明らかに、ギャップは、より詳細な分析が必要です。 
  • さらなる分析に、 USDJPY の分足の間のギャップを選択すべきです。

戦略のテストとトレードごとの最適なリスクの計算

USDJPY 分足の間のギャップに基づくシステムのバージョンは、最も有望に見えます。 ギャップ形成時に検出したスプレッドの著しい急増は、その定義にもっと注意を払うべきであるということを意味します。 次のように指定してみましょう。 平均価格ではなく、BidとAskのためにギャップを考慮します。 また、トレードをインプットする必要があるため、いずれかを選択します。 つまり、ビッドと下向きのギャップによって上向きのギャップを定義します (ask)。 同じことを決済にします。

セッション間のギャップに関する統計情報を収集するために使用したものを少し変更してEAを開発してみましょう。 主な変更はギャップ構造に関するものです。 ギャップと取引の間には明確な対応があるため、トレードに必要な情報全体 (約定量と決済条件) はこの構造に格納されます。 トレードに2つの関数が追加されます。 そのうちの1つ (pp2v()) は個々の取引ごとにボリュームを計算し、もう1つ (トレード()) は取引ボリュームとトレーディングポジションボリュームの合計の間の対応関係を保存します。 EAコード (gaps_ses_test.mq5) を以下に示します。

//gaps_ses_test.mq5
#define ND 100

input uint   mperiod=1;                 //セッション期間 (分)
input uint   mlength=1;                 //セッションの長さ (分)
input uint   mbias=0;                   //最初のセッションバイアス (分)
input double g0=0.1;                    //最小ギャップサイズ: USDJPY-0.1、EURUSD-0.001
input double q0=0.4;                    //(SL+TP)
input double r=0.01;                    //トレードにおけるリスク
input double s=0.02;                    //おおよそのスプレッド
input string fname="gaps\\stat.txt";    //統計用ファイルの名前

structSGap
  { double p0;
    double p1;
    double p2;
    double v;
    int brkn();
    bool up();
    void change(double p);
    double gap();
    double Q();
    double a();
  };

class CGaps
  { SGap gs[];
    int ngs;
    int go[];
    int ngo;
    public:
    void init();
    void add(double p_1,double p);
    bool change(double pbid,double pask);
    double v();
    void gs2f(string fn);
  };

CGaps gaps;
MqlTick tick0;
int ns0=-1;
ulong sbias=mbias*60, speriod=mperiod*60,SLength=mlength*60;
double dv=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP);

void OnTick()
  { MqlTick tick;
    if (!SymbolInfoTick(_Symbol, tick)) return;
    bool chngd=gaps.change(tick.bid,tick.ask);
    int ns=nsession(tick.time);
    if(ns>=0)
      { if(ns0>=0&&ns>ns0)
          { if(tick0.ask-tick.ask>=g0) {gaps.add(tick0.ask,tick.ask); chngd=true;}
              else if(tick.bid-tick0.bid>=g0) {gaps.add(tick0.bid,tick.bid); chngd=true;}
          }
        ns0=ns;
        tick0=tick;
      }
    
    if(chngd) trade(gaps.v());
  }

int OnInit()
  {
     gaps.init();
     return(INIT_SUCCEEDED);
  }
  
void OnDeinit(const int reason)
  { gaps.gs2f(fname);
  }

int nsession(datetime t)
  { ulong t0=(ulong)t;
    if(t0<sbias) return -1;
    t0-=sbias;
    if(t0%speriod>slength) return -1;
    return (int)(t0/speriod);
  }

double pp2v(double psl, double pen)
  { if(psl==pen) return 0.0;
    double dc, dir=1.0;
    double c0=AccountInfoDouble(ACCOUNT_EQUITY);
    bool ner=true;
    if (psl<pen) ner=OrderCalcProfit(ORDER_TYPE_BUY,_Symbol,dv,pen+s,psl,dc);
      else {ner=OrderCalcProfit(ORDER_TYPE_SELL,_Symbol,dv,pen,psl+s,dc); dir=-1.0;}
    if(!ner) return 0.0;
    return -DIr*r*dv*c0/dc;
  }

void trade(double vt)
  { double v0=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
    if(-v0<vt<v0) vt=v0*MathRound(vt/v0);
    double vr=0.0;
    if(PositionSelect(_Symbol))
      { vr=PositionGetDouble(POSITION_VOLUME);
        if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL) vr=-vr;
      }
    int vi=(int)((vt-vr)/dv);
    if(vi==0) return;
    MqlTradeRequest request={0};
    MqlTradeResult  result={0};
    request.action=TRADE_ACTION_DEAL;
    request.symbol=_Symbol; 
    if(vi>0)
      { request.volume=vi*dv;
        request.type=ORDER_TYPE_BUY;
      }
      else
        { request.volume=-vi*dv;
          request.type=ORDER_TYPE_SELL;
        }
    if(!OrderSend(request,result)) PrintFormat("OrderSend error %d",GetLastError());
  }

int SGap :: brkn()
  { if(((p0>p1)&&(p2<=p1))||((p0<p1)&&(p2>=p1))) return 1;
    if(Q()>=q0) return -1;
    return 0;
  }

bool SGap :: up()
  { return p0>p1;
  }

void SGap :: change(double p)
  { if(brkn()==0) p2=p;
  }

double SGap :: gap()
  { return MathAbs(p0-p1);
  }

double SGap :: Q()
  { if(p2==p1) return 0.0;
    return (p2-p0)/(p2-p1);
  }

double SGap :: a()
  { double g=gap(), k0=q0/(1-q0);
    return (g-s)/(k0*g+s);
  }

void CGaps :: init()
  { ngs=ngo=0;
  }

void CGaps :: add(double p_1,double p)
  { ++ngs;
    if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND);
    gs[ngs-1].p0=gs[ngs-1].p2=p;
    gs[ngs-1].p1=p_1;
    double ps=p+(p-p_1)*q0/(1-q0);
    gs[ngs-1].v=pp2v(ps,p);
    int i=0;
    for(; i<ngo; ++i) if(go[i]<0) break;
    if(i==ngo)
      {
        ++ngo;
        if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND);
      }
    go[i]=ngs-1;
  }

bool CGaps :: change(double pbid,double pask)
  { bool ch=false;
    for(int i=0; i<ngo; ++i)
      { if(go[i]<0) continue;
        if(gs[go[i]].up()) gs[go[i]].change(pbid); else gs[go[i]].change(pask);
        if(gs[go[i]].brkn()!=0) {go[i]=-1; ch=true;}
      }
    return ch;
  }

double CGaps :: v(void)
  { double v=0;
    for(int i=0; i<ngo; ++i) if(go[i]>=0) v+=gs[go[i]].v;
    return v;
  }

void CGaps :: gs2f(string fn)
  { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT);
    int na=0, np=0, bk;
    double kt=0.0, pk=0.0;
    for(int i=0;i<ngs;++i)
      { bk=gs[i].brkn();
        if(bk==0) continue;
        ++na; if(bk>0) ++np;
        kt+=gs[i].a();
      }
     if(na>0)
       { kt/=na;
         pk=((double)np)/na;
       }
     FileWriteString(f,"na = "+(string)na+"\n");
     FileWriteString(f,"kt = "+(string)kt+"\n");
     FileWriteString(f,"pk = "+(string)pk);
     FileClose(f);
  }

2017の年にEAをテストし、その結果に基づいて2018でトレードのリスク値を定義してみましょう。 2017のテスト結果に基づくバランス/エクイティグラフは以下の通りです。

2017

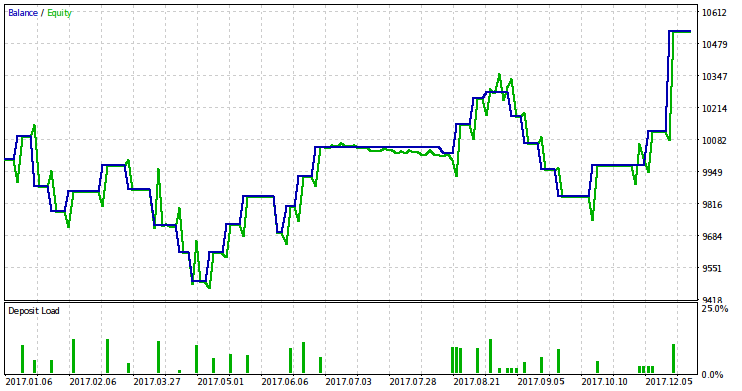
リスクの計算に進む前に明確化をしなければなりません。 まず、適切なレベルのリスクを判断する必要性を正当化する必要があります。 第２に、この目的に理論を適用する利点を説明する必要があります。

投機的トレードは常に不確実性と関連します。 トレードシステムは、時々負けトレードを行います。 このため、リスクは大きすぎてはなりません。 そうでないと、ドローダウンは過剰になります。 一方、相場はいつでも収益性の高いシステムでも負けシステムに変える可能性があります。 したがって、システムの "有効期間" は有限であり、正確には不明です。 このため、リスクは小さすぎてはなりません。 そうしないと、 トレードシステムからすべての可能な利益を得ることができません。.

次に、簡単な特性を伴うリスクの定義について、主に (は異なる) アプローチを考えてみましょう。

  • いくつかの「経験豊富なトレーダー」の意見に基づいて、特定の数値によってリスクを定義します。 最も一般的な値の範囲は、0.5 ~ 3% の資金です。 正当化の欠如それにも関わらず、このアプローチはかなり適切です。 その主な欠点は、特定のシステムの特定のリスク値を選択するためのルールが存在しないことです。
  • ラルフ・ヴィンスの「オプティマル f」メソッド。 この方法は、理論的に正当化されています。通常、大きなドローダウンを引き起こす可能性があるリスクがあります。
  • EAパラメータにリスクを組み込み、テストと最適化の間に定義します。 パラメータは、EAのデバイスや最適化がどのように正確に行われているかに大きく依存するので、結果の正当性と妥当性について確かなことを言うことは困難です。 考えられる問題の1つは、さらなるトレード結果の不確実性を考慮していないことです。 再フィッティングも可能であり、不当なリスク値増加を引き起こす可能性があります (前の方法は明確な例です)。 提案する方法は、リスクを合理的に最適化する方法です。

今回の方法は、上記のものとは異なり、適切かつ合理的なリスク値を取得することができます。 特定のトレードスタイルに合わせて調整することができる調節可能なパラメータがあります。 リスク計算へのアプローチの本質を説明しましょう。 トレードの指定された数の中でその平均収益性が指定された最小レベルを下回るまで、またはドローダウンが約定の同じオーダーで指定された最大レベルを超えるまで、正確にトレードシステムを使用すると仮定します。 その後、このシステムに基づくトレードがストップされます (たとえば、そのパラメータは再最適化されます)。 リスク値は、システムがまだ収益性がある (ドローダウンまたは収益性の低下が自然なランダム変動である) 確率が指定された値以下になるように選択されます。

この方法は、前の記事で詳しく説明されています。 2番目の記事では、最適なリスク値を計算するためのスクリプトを見つけることができます。 このスクリプトは、すべてのトレードに対して固定比率のインプットで指定された ストップロス およびTPレベルによるトレードの決済に適用されます。 これは前述の記事で bn.mq5 と呼ばれています。

テストパスの結果として、EAはリスク計算スクリプトのパラメータの一部として必要なデータをテキストファイルに書き込みます。 残りのパラメータは、事前に知られているか、徹底的な検索によって選択されます。 スクリプトによって提案されたリスク値がゼロであることが判明した場合は、このトレードのアイデアを破棄するか、(パラメータを変更することによって) ドローダウン/収益性の要件を弱めるか、またはより大きなヒストリーからトレードデータを使用する必要があります。 以下は設定するパラメータの値を持つスクリプトの一部です。

input uint na=26;                     //シリーズの取引数
input double kt=1.162698185452029     //TP/SL比
input double pk=0.5769230769230769    //利益確率

double G0=0.0;                        //最低平均収益性
double D0=0.9;                        //最小最低増分
double dlt=0.17;                      //有意水準

2017のテスト結果は、トレード品質を考慮されていないので、要件はやや緩やかです。 EAはロスメイキング (G0 = 0.0) ではなく、ドローダウンは 10% (D0 = 0.9) を超えないという条件を設定しました (na=26)。 ゼロ以外のリスク値を得るためには、有意水準ではなく高い価格率 (dlt = 0.17) を設定する必要があります。 実際には、10分の1以下であれば良いです。 大きなものにしなければならないという事実は貧しいトレード結果になります。 パラメータを持つEAは、このシンボル上の実際のトレードで使用すべきではありません。 指定されたパラメータを使用すると、スクリプトはリスクに対して次の結果を提供します。 r = 0.014。 以下は、このリスク値を持つ2018のEAテスト結果です。

2018

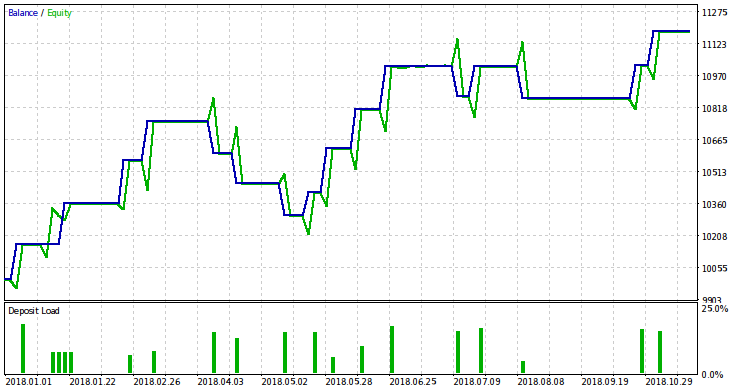
テスト中にEAによって示された利益それにも関わらず、実際のトレードにとどまる可能性は低いです。 調査されたシンボル上の通常のギャップをトレードする無益は明白です。 このようなギャップは稀であり (時間とともに稀になります)、サイズが小さくなります。 トレードセッション間のギャップ汎化−価格変化のより深い考察−より有望であると考えられます。 また、通常のギャップがより一般的な資産に注意を払うことも理にかなっています。

結論

確率メソッドは、EAの開発と設定に適しています。 同時に、他の可能な方法に反している方法ではありません。 代わりに、多くの場合、補うか再考することが可能になります。

この記事では、一般的なEA最適化のトピックについては、そのパラメータが渡すだけで言及していることに触れていません。 この領域と確率アプローチ (統計的解法の理論) との間には、大きなつながりがあります。 おそらく、私も後で詳細にこの質問について勉強します。

添付ファイル

統計を収集するために使用する2つのEAとテストトレードに使用する1つのEAがあります。

 #  名称 タイプ 
  詳細
1 gaps_reg_stat.mq5 EA 連続ティック間のギャップ統計の収集
2
 gaps_ses_stat.mq5 EA セッション間のギャップ統計の収集
3 gaps_ses_test.mq5 EA セッション間のギャップを使用したテストトレード

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/5373

添付されたファイル |
ZIPをダウンロード
gaps_reg_stat.mq5 (2.47 KB)
gaps_ses_stat.mq5 (3.16 KB)
gaps_ses_test.mq5 (4.93 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MetaTrader5でカスタム MOEX シンボルを作成およびテストする方法 MetaTrader5でカスタム MOEX シンボルを作成およびテストする方法
この記事では、MQL5 言語を使用したカスタム交換シンボルの作成について説明します。 特に、人気の Finam ウェブサイトからの為替相場を使用します。 この記事で考えられるもう1つのオプションは、カスタムシンボルの作成に使用するテキストファイルを任意の形式で動作させる方法です。 これにより、任意の財務銘柄とデータソースを操作できるようになります。 カスタムシンボルを作成した後、MetaTrader5 ストラテジーテスターのすべての関数を使用して、交換ツールのトレードアルゴリズムをテストすることができます。
MQL5 と MQL4 でのシンボル選択とナビゲーションユーティリティの開発 MQL5 と MQL4 でのシンボル選択とナビゲーションユーティリティの開発
経験豊富なトレーダーが認識している事実として、トレードにおいて最も時間のかかるものはポジションを開いたり追跡したりするのではなく、シンボルを選択してインプットポイントを探すことというものがあります。 この記事では、ブローカーが提供するトレード商品のインプットポイントの検索を簡素化するEAを開発します。
MQL5 と MQL4 の選択とナビゲーションユーティリティ: 「ホームワーク」タブの追加とグラフィックオブジェクトの保存 MQL5 と MQL4 の選択とナビゲーションユーティリティ: 「ホームワーク」タブの追加とグラフィックオブジェクトの保存
この記事では、必要なシンボルを選択するためのタブを追加することで、以前に作成されたユーティリティの関数を拡張していきます。 また、特定のシンボルチャートで作成したグラフィカルオブジェクトを保存する方法についても説明します。 また、特定のウェブサイトを使用して事前に選択されたシンボルだけで機能する方法を提案します。
ピボット・パターン：『ヘッドアンドショルダー』パターンのテスト ピボット・パターン：『ヘッドアンドショルダー』パターンのテスト
この記事は、前回のピボット・パターン：『ダブルトップ・ダブルボトム』パターンのテストの論理的な続編になります。ここでもう一つのよく知られている『ヘッドアンドショルダー』の反転パターンを検討し、2つのパターンの取引パフォーマンスを比較し、2つのパターンの取引を1つの取引システムに組み合わせてみたいと思います。