
Die Wahrscheinlichkeitstheorie für den Handel von Kurslücken verwenden
Inhalt
- Einführung
- Allgemeine Betrachtungen über den Expert Advisor
- Eine Handelsstrategie als Versuch die Hypothese des Random Walk zurückzuweisen
- Die Handelsstrategie der Kurslücke
- Testen der Strategie und Berechnen des optimalen Risikos je Position
- Schlussfolgerung
- Angehängte Dateien
Einführung
Der Artikel setzt das Thema der Anwendung der Wahrscheinlichkeitstheorie und der mathematischen Statistik im Handel fort, das in den vorherigen Artikeln des Autors begonnen wurde. Wir werden die mögliche Verwendung der geeigneten Methoden zur Erstellung und Erprobung von Handelsstrategien prüfen.
Zuerst werden wir uns mit der Suche nach solchen Handelsmöglichkeiten befassen, wie z.B. der Erkennung von Abweichungen von der Hypothese des Random Walk (zufällige Entwicklung). Es ist bewiesen, dass, wenn sich die Preise wie ein Random Walk mit Null-Drift verhalten (ohne Richtungswechsel), ein profitabler Handel unmöglich ist. Dies bildet die Grundlage, um Wege zu finden, diese Hypothese zu widerlegen. Wenn ein Weg gefunden wird, die Hypothese zu widerlegen, können wir versuchen, dies zu nutzen, um eine Handelsstrategie zu entwickeln.
Wir werden auch das Thema Risiko, das wir in den zuvor veröffentlichten Artikeln begonnen haben, weiter untersuchen. Weiter unten werden wir sie als die ersten und zweiten Artikel bezeichnen.
Da unser Ansatz auf der Wahrscheinlichkeitstheorie basiert, ist das Verständnis der Grundlagen ratsam, aber nicht zwingend erforderlich. Es ist wichtig, die Grundlagen probabilistischer Methoden zu verstehen - je systematischer und häufiger sie eingesetzt werden, desto auffälliger und aussagekräftiger ist das erzielte Ergebnis (aufgrund des Gesetzes der großen Zahlen). Natürlich sollte ihre Anwendung ausreichend begründet und angemessen sein.
Allgemeine Betrachtungen über den Expert Advisor
Die Entwicklung eines EAs kann grob in drei Phasen unterteilt werden:
- Eine Idee entwickeln.
- Überprüfen der Idee durch alle möglichen Vereinfachungen.
- Anpassen der Idee an die Marktgegebenheiten.
Der Artikel wird sich hauptsächlich mit dem zweiten Punkt befassen, so dass wir uns besser auf das genannte Thema konzentrieren können. Außerdem wird diese Phase im Forum viel seltener diskutiert als die anderen.
Lassen Sie uns die implementierten Vereinfachungen beschreiben. Wir werden uns darauf beschränken, dass die EAs einen einzigen Vermögenswert handeln. Wir gehen davon aus, dass der Vermögenspreis in der Kontowährung ausgedrückt wird. Wir werden Nichthandelsbuchungen (wie Swap und Auszahlung von Geldern vom Konto) ausschließen und verschiedene Auftragsarten nicht berücksichtigen (sodass nur Kauf und Verkauf zu Marktpreisen verbleiben). Wir vernachlässigen Schlupf bei der Ausführung der Aufträge, während der Spread (s) als Festwert angesehen wird. Wir werden auch davon ausgehen, dass die EA alle Gelder auf unserem Konto kontrolliert, und es gibt keine anderen EAs, die damit handeln.
Bei all diesen Vereinfachungen ist das EA-Operationsergebnis eindeutig definiert als die Funktion v(t) - ein zeitabhängiges Positionsvolumen. Ein positiver Wert von v(t) entspricht einem Kauf, während ein negativer einem Verkauf. Außerdem gibt es die Funktion p(t) (Vermögenspreis) und c0 (Anfangssaldo). Das folgende Bild zeigt die möglichen v=v(t) Positionsdiagramm.
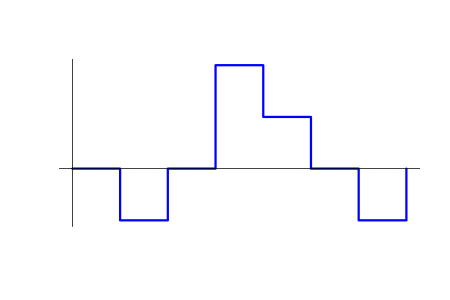
Das arithmetische Mittel zwischen Kauf- und Verkaufspreis.
Die Funktionen v(t) und p(t) sind stückweise konstant (schrittweise), da ihre Werte Vielfache einiger minimaler Schrittweiten sind. Wenn eine strengere mathematische Definition erforderlich ist, dann kann man sie als rechtsseitig kontinuierlich betrachten, mit einer Lücke an der linken Grenze. Wir gehen davon aus, dass die Kurslücken v(t) nie mit denen von p(t) übereinstimmen. Mit anderen Worten, es kann sich nur ein Wert von beiden zu einem Zeitpunkt ändern - entweder ein Preis oder ein Positionsvolumen oder beide bleiben unverändert. Es ist anzumerken, dass die Zeitpunkte, zu denen Preis- oder Mengenänderungen auftreten können, ebenfalls Vielfache einer bestimmten kleinsten Schrittweite sind.
Basierend auf diesen Daten finden wir die Funktion c(t) - den Wert der Geldmittel nach der Zeit. Er ist definiert als der Saldo für den Teil des Kontos, der von der EA verwaltet wird, falls wir eine Position im Moment t schließen würden. Da nur ein einziger EA auf dem Konto läuft, stimmt dieser Wert mit dem in MetaTrader 5 definierten Saldo überein.
Definieren von c(t) bei Änderungen von t. Wenn sich das Volumen und der Preis zu diesem Zeitpunkt nicht ändern, dann ergibt das natürlich Null. Wenn sich der Preis ändert, entspricht die Wertsteigerung dem Produkt von dem Volumen und Preiserhöhung. Wenn sich das Volumen ändert, sind zwei Optionen möglich - wenn das absolute Positionsvolumen verringert wird, bleiben die Geldwerte gleich, wenn es erhöht wird, werden die Geldwerte um einen Betrag verringert, der dem Produkt aus dem Spread und dem absoluten Wert der Volumenänderung entspricht. Mit anderen Worten, wenn eine Position teilweise geschlossen wird, ändert sich der Saldo nicht, während die Addition der Position zu einer leichten Abnahme des Saldos führt. So ist c(t) der Mittelwert im Zeitpunk t gleich der Summe von c0=c(0) und all seinen Änderungen, die vom Zeitpunkt Null bis zu t auftraten.
Bei der Entwicklung unserer Risikotheorie (in den beiden vorangegangenen Artikeln) haben wir das Konzept eines "Deals" verwendet. Dieses Konzept stimmt nicht ganz mit dem überein, was im MetaTrader 5 als "Deal" bezeichnet wird, und entspricht dort einem so genannten "Handel" (Trade). Um genau zu sein, er entspricht einer, wie wir es nennen, einfachen Position. Eine einfache Position wird nach unserer Definition durch die Momente des Öffnens und Schließens festgelegt. Deren Volumen und Richtung bleiben zwischen diesen Momenten konstant. Unten ist ein Beispieldiagramm v=v(t) einer einfachen Position.
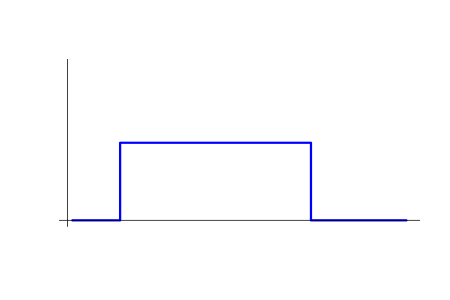
Jede Position (da sie immer stückweise konstant ist) kann als eine Summe von einfachen Positionen betrachtet werden. Eine solche Darstellung kann auf unendlich viele Arten erfolgen. Die folgende Tabelle zeigt eine einzelne Position, die auf zwei verschiedene Arten dargestellt wird, als Summe einfacher Positionen. Die Ausgangsposition ist blau dargestellt, während die Deals, in die sie unterteilt ist, grün und rot dargestellt werden. Wenn wir ein Konzept der Positionen in MetaTrader 5 verwenden, erhalten wir eine weitere Option. Jede dieser Methoden kann sehr sinnvoll sein.
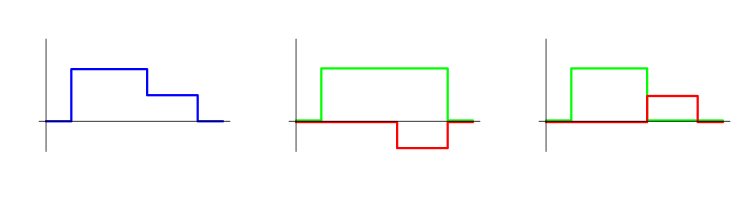
Es gibt einige EAs, für die diese Darstellung keinen Sinn stiftet. Beispielsweise kann es EAs geben, die eine Position schrittweise erhöht und danach schrittweise verringert wird. Gleichzeitig gibt es EAs, für die eine solches Verhalten ganz natürlich ist. Eine Position kann beispielsweise aus einer Folge von einfachen Positionen bestehen, die sich zeitmäßig nicht überlappen. Die folgende Tabelle enthält Beispiele für solche Positionen.
Relative Geldmittelveränderung c1/c0 nach jedem Deal (einfache Position) wird in zwei Werten ausgedrückt - Rentabilität a und Risiko r: c1/c0=1+ra. Die Rentabilität entspricht dem Verhältnis der Preiserhöhung während des Geschäfts zur Differenz zwischen Einstiegspreisen und Stop-Loss, während das Risiko proportional zum Geschäftsvolumen ist und einen Teil der Mittel bedeutet, die bei einer exakten Aktivierung des Stop-Loss verloren gehen würden.
Anstatt also die Zeitfunktionen v(t), p(t) und c(t) zu betrachten, wenden wir uns der Analyse numerischer Sequenzen zu, die die Reihenfolge der Geschäfte charakterisieren. Dies vereinfacht das weitere Studium erheblich. Insbesondere vermeiden wir die Notwendigkeit, die Theorie der Zufallsprozesse anzuwenden, die sich auf endliche Mengen von Zufallsvariablen beschränkt, wenn wir mit dem probabilistischen Modell der Unsicherheit fortfahren.
Die Wahrscheinlichkeitstheorie ist eine allgemein anerkannte Methode zur mathematischen Modellierung der Unsicherheit im Verhalten von Vermögenspreisen und im Handelsergebnis. Gemäß diesem Ansatz sollten wir die Funktionen v(t), p(t) und c(t) als spezifische Implementierungen (Trajektorien) einiger zufälliger Prozesse betrachten. Im Allgemeinen ist diese Aufgabe praktisch unlösbar. Der Hauptgrund ist das Fehlen geeigneter probabilistischer Modelle, die das Preisverhalten genau beschreiben. Daher ist es sinnvoll, Sonderfälle zu berücksichtigen, in denen eine Lösung möglich ist. Wie bereits erwähnt, werden wir in diesem Artikel EAs betrachten, die Positionen bilden, die angemessen als eine Folge von einfachen Positionen (Deals) dargestellt werden können.
Es ist erwähnenswert, ein weiteres Problem im Zusammenhang mit EAs - Parameter. Es wäre sinnvoll, sie im Detail zu betrachten, um eine gewisse Formalisierung (Standardisierung) des EA-Entwicklungsprozesses zu erreichen. Lassen Sie uns die Parameter in drei Typen unterteilen:
- Historische Parameter. Parameter, die sich während des EA-Betriebs von Deal zu Deal ändern können. Dies sind Indikatorwerte, Tageszeit, Nachrichtendaten, Mondphasen, etc. Im Allgemeinen sind es Zeitfunktionen, ebenso wie Preise oder Bestandsvolumina. Im Falle einer angewandten Vereinfachung können wir sie als Zahlenreihen betrachten, die zum Zeitpunkt eines Deals bekannt sind. Die Parameter jedes einzelnen Geschäfts (Richtung, Volumen, Stop-Loss und Take-Profit) werden basierend auf den Werten der historischen Parameter definiert.
- Aktuelle Parameter. Nennen wir sie einfach die Parameter für die Kürze. Sie werden gesetzt, wenn ein EA mit dem Handel beginnt und können nur beim Testen und Optimieren des EAs angewendet werden.
- Metaparameter setzen den EA-Optimierungsalgorithmus, z.B. benutzerdefinierte Parameter für Optimierungskriterien. Angenommen, wir wollen die EA nach zwei Kriterien optimieren, obwohl dies nur mit einem möglich ist. Wir bilden ein neues Kriterium für die beiden Originale, die ihre Summe mit einigen Gewichten nehmen. Diese Gewichte werden als Meta-Parameter verwendet.
So ist beispielsweise bei dem im Folgenden beschriebenen Kurslücken-EA die kleinste Lücke (minimum gap) ein EA-Parameter, während die Größe jeder einzelnen Lücke ein historischer Parameter ist. In diesem Fall können Metaparameter die Nummer des Optimierungskriteriums beinhalten (wir gehen davon aus, dass die Kriterien in einer bestimmten Reihenfolge nummeriert sind, z.B. ist die Optimierung durch Gewinn #1, während die Optimierung durch Absenkung #2, etc. ist).
In diesem Artikel werden wir eine signifikante Vereinfachung im Zusammenhang mit historischen Parametern verwenden. Wenn wir über die Verteilung der Gewinne eines Deals sprechen, kann es im Allgemeinen von diesen Parametern abhängen. Wir gehen davon aus, dass diese Abhängigkeit unbedeutend ist. Der Hauptgrund ist, dass ein Versuch, diese Abhängigkeit zu berücksichtigen, das Modell in der Regel stark verkompliziert, was schließlich zu einer Überpassung führen kann.
Eine Handelsstrategie als Versuch die Hypothese des Random Walk zurückzuweisen
Wir haben bereits erwähnt, dass es keine genauen Modelle gibt, die das Preisverhalten beschreiben. Dennoch gibt es Näherungsmodelle, die nützlich sein können. So gibt es beispielsweise ein bekanntes Preisverhaltensmodell, das die Preise als Random Walk mit Null-Drift (Fehlen eines gerichteten Trends) betrachtet. Dieses Modell wird als Random Walk Hypothese bezeichnet. Gemäß dieser Hypothese erzielt jeder EA im Durchschnitt einen Gewinn von Null oder einen kleinen Verlust, wenn wir einen Spread berücksichtigen.
Der Nachweis der Unmöglichkeit, mit Random Walk Geld zu verdienen, ist ziemlich schwierig, da er die Beteiligung eines komplexen mathematischen Apparats der Theorie der zufälligen Prozesse erfordert (Stochastische Integration, Stoppzeit, etc). Im Allgemeinen läuft es auf die Aussage hinaus, dass beim Handel auf Basis des Random Walk ohne Trend das Kapital ein Martingal ist (Wahrscheinlichkeitstheorie, nicht zu verwechseln mit dem Martingalespiel, ein Wettsystem). Ein Martingal ist ein zufälliger Prozess, bei dem sich sein Mittelwert (mathematische Erwartung) mit der Zeit nicht ändert. In unserem Fall bedeutet dies, dass die mathematische Erwartung des Kapitalwertes zu jedem Zeitpunkt gleich dem Ausgangswert ist.
Daher sollten wir bei der Betrachtung einer Handelsidee zunächst nach statistisch signifikanten Preisabweichungen vom Random Walk suchen. Um dies zu tun, werden wir Ideen aus der Wahrscheinlichkeitstheorie und der mathematischen Statistik verwenden, aber zuerst lassen Sie uns ein paar Beobachtungen machen:
- Jede Lösung dieser Art ist probabilistisch - es gibt immer eine ungleiche Wahrscheinlichkeit, dass unsere Schlussfolgerungen falsch sind.
- Wenn unsere Methode keine Abweichungen erkennt, bedeutet dies nicht, dass sie vollständig fehlen. Vielleicht würde eine andere Methode sie erkennen.
- Statistisch signifikante Abweichungen garantieren nicht den Erhalt statistisch signifikanter positiver Gewinne - das Vorhandensein von Abweichungen ist notwendig, aber keine ausreichende Voraussetzung dafür.
Konstruieren wir eine Methode zur Suche nach Abweichungen vom Random Walk. Um dies zu tun, werden wir einige Zufallsvariablen berücksichtigen, für die wir eine empirische Wahrscheinlichkeitsverteilung basierend auf einer Stichprobe, die aus realen Preisen gebildet wurde, erstellen werden. Außerdem werden wir eine theoretische Wahrscheinlichkeitsverteilung für den gleichen Wert konstruieren, unter der Annahme, dass das Preisverhalten ein Random Walk ist. Wenn wir diese Verteilungen vergleichen, werden wir eine Entscheidung über die Ablehnung (oder Unmöglichkeit der Ablehnung) der Hypothese des Random Walk treffen.
Konstruieren wir ein Beispiel für einen geeigneten Wert. Angenommen, dass beim Anfangszeitpunkt t0 der Preis gleich p0 ist. Nehmen wir noch einen Preiswert p1 ungleich p0. Warten wir auf den Moment t1, wenn der Preis diesen Wert erreicht p(t1)=p1. Finden wir den Preis p2, der der weiteste von p1 ist unter den Preisen im Zeitintervall zwischen t0 und t1. Führen wir den Wert K=(p2-p0)/(p0-p1) ein. Die Bedingung p10≤p2 oder p2≤p0<p1 gilt immer, daher jederzeit K≥0. Die Grafik, die diese Idee erklärt, ist unten aufgeführt. Die blaue Linie bedeutet der Preislevel p0, während im Moment, in dem sie das Preisdiagramm kreuzen, t0 ist. Die rote Linie bedeutet das Preisniveau p1, während der Moment, in dem sie das Preisdiagramm nach t0 berührt, t1 ist. Die grüne Linie bedeutet das Preisniveau p2, das so weit wie möglich von p1 entfernt liegt.
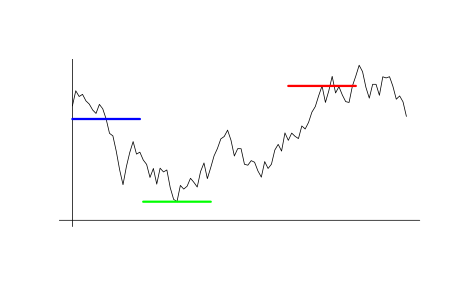
Die Idee hinter dem Wert ist einfach. Angenommen, wir eröffnen einen Deal um t0. Es sei zum Preis von p0 verkauft worden, während p1, p1>p0 - Stop-Loss. p2 ist der am wenigsten erreichbare Preis für einen Take-Profit, während K der höchste erzielbare Gewinn für ein Deal ist. In Wirklichkeit kennen wir den genauen Wert K bei der Durchführung einer Transaktion nicht. Im Rahmen des probabilistischen Modells dieser Unsicherheit können wir nur über die Kenntnis ihres Wahrscheinlichkeitsverteilungsmusters sprechen. Angenommen, wir kennen die Wahrscheinlichkeitsverteilungsfunktion Fk(x), die als die Wahrscheinlichkeit definiert ist, dass K<x. Angenommen, wir verwenden einen bestimmten Preis pk als Take-Profit: pk-p0=k(p0-p1). In diesem Fall ist Fk(k) gleich der Wahrscheinlichkeit, dass ein Stop-Loss früher erreicht wird als ein Take-Profit. Dementsprechend ist 1-Fk(k) gleich der Wahrscheinlichkeit, dass Take-Profit früher aktiviert wird. Der Spread soll vorerst gleich Null sein. Im Falle der Stop-Loss-Aktivierung ist die Rentabilität dann gleich -1, während sie im Falle der Take-Profit-Aktivierung gleich k ist. Die mathematische Erwartung in einem solchen Geschäft: M=(-1)*Fk(k)+k*(1-Fk(k))=k-(k+1)*Fk(k), was gleich Null ist, wenn Fk(k)=k/(k+1).
Wenn wir die Gleichungsform Fk(x) kennen, können wir sogar eine Voroptimierung eines EA durchführen. So können wir beispielsweise nach der optimalen Verhältnis von Take-Profit/Stopp-Loss suchen, die die mathematische Gewinnerwartung des Geschäfts maximiert. Dann können wir den optimalen Risikowert des Deals finden. So kann der EA noch vor der Fertigstellung optimiert werden. Das spart Zeit und ermöglicht es Ihnen, offensichtlich ungeeignete Ideen frühzeitig zu verwerfen.
Wenn wir davon ausgehen, dass sich die Preise wie ein Random Walk ohne Trend verhalten, dann wird die Verteilung des Wertes K durch die Verteilungsfunktion Fk(x)=Fk0(x) eingestellt, wobei Fk0(x)=0 if x≤0 und Fk0(x)=x/(x+1) if x>0. Für mehr Sicherheit können wir davon ausgehen, dass es sich bei dem hier verwendeten Zufallsweg um einen Wiener Prozess mit Nulldrift (kein Trend) handelt. Wie wir sehen können, wenn die Hypothese Random Walk erfüllt ist und der Spread gleich Null ist, ist die mathematische Erwartung der Rentabilität bei jedem Verhältnis von Take-Profit/Stopp-Loss gleich Null. Im Falle eines Spreads ungleich Null ist sie negativ.
Anstelle von K können wir den Wert Q=K/(K+1)=(p2-p0)/(p2-p1), K=Q/(1-Q) berücksichtigen. Dieser Wert kann als Verhältnis von Take-Profit zur Summe von Stop-Loss und Take-Profit dargestellt werden. Es ist bequemer, weil es Werte innerhalb des Intervalls [0;1) nimmt und eine einfachere Verteilung hat als K (gleichmäßig in diesem Intervall) im Falle eines Random Walks.
Im Folgenden werden wir vor allem über den Wert Q sprechen. Betrachten wir, wie seine empirische Verteilungsfunktion Fq(x) konstruiert und angewendet wird. Angenommen, wir haben eine Handelsidee, dann überprüfen wir die Preisentwicklung. Wir haben eine Reihe von Einstiegspunkten n. Der Einstiegspreis p0,i und Stop-Loss p1,i, wobei i=1,...,n für jeden von ihnen definiert ist. Jetzt sollten wir definieren, ob diese Idee ein gewisses Gewinnpotenzial hat. Für jeden Deal sollten wir den Preis p2,i finden, der so weit weg wie möglich vom Stop-Loss bis zum Zeitpunkt seiner Aktivierung liegt. Basierend auf den Preisen erhalten wir die Stichprobe n: Qi=(p2,i-p0,i)/(p2,i-p1,i), i=1,...,n. Die in dieser Stichprobe konstruierte empirische Verteilungsfunktion wird durch die Gleichung Fq(x)=m(x)/n definiert, wobei m(x) gleich ist der Anzahl der Qi Stichprobeelemente kleiner als x. Wenn sich die Preise wie ein Random Walk ohne Trend verhalten (Wiener Prozess mit Nulldrift), sieht die Fq0(x) Verteilungsfunktion des Wertes Q einfach aus: Fq0(x)=0 if x≤0, Fq0(x)=x wenn 0<x≤1, und Fq0(x)=1 if x>1.
Wenn Fq(x) sich signifikant von der theoretischen Verteilungsfunktion mit einem Random Walk Fq0(x) unterscheidet, müssen wir die Bedeutung dieses Unterschieds in Bezug auf die Rentabilität überprüfen. Wenn die Rentabilität auch unter Berücksichtigung der Spreads hinreichend positiv ist, ist es an der Zeit, die richtige Verhältnis von Gewinn/Stopp-Loss zu wählen. Dies kann durch Maximierung der Gewinnerwartung erreicht werden. Danach können wir einen optimalen Wert für den Risikowert pro Deal auswählen und die Idee vorab testen. Wenn das Ergebnis positiv ist, ist es sinnvoll, mit der Erstellung eines tatsächlichen Handels-EAs fortzufahren. Im weiteren Verlauf werden wir versuchen, diesen Algorithmus in der Praxis zu zeigen.
Es stellt sich die Frage, wie man ähnliche Vergleiche mit einem Random Walk für komplexere Algorithmen für das Schließen von Positionen erstellt. Die allgemeine Antwort ist die gleiche wie für den oben genannten Fall. Das Hauptproblem ist, dass die Verteilung der Profitabilität eines Random Walk in recht seltenen Fällen in analytischer Form erreicht werden kann. Aber es ist immer möglich, seine empirische Näherung mit der Monte-Carlo-Simulationsmethode zu erhalten.
Die Handelsstrategie der Kurslücke
Vor der Analyse der Idee, sollte wir bedenken, dass unsere Hauptaufgabe darin besteht, die Analysemethoden und nicht eine profitable Handelsstrategie zu demonstrieren. Eine zu starke Konzentration auf den Gewinn hätte uns unter Kleinigkeiten begraben, die uns vom Gesamtbild ablenken.
Die Anlagepreise sind diskret und ändern sich daher immer wieder sprunghaft. Diese Sprünge können sich in der Größe unterscheiden. Wenn sie groß sind, werden sie als Lücken (gaps) bezeichnet. Es gibt keine bestimmte Grenze, die Lücken von üblichen Preisänderungen trennt. Es steht uns frei, diese Grenze dort zu setzen, wo wir es für richtig halten.
Lücken sind gut geeignet, um die im vorherigen Abschnitt beschriebene Theorie zu demonstrieren. Jeder von ihnen wird durch zwei Zeitpunkte und Vermögenspreise in ihnen festgelegt. Unter Verwendung der zuvor eingeführten Preisnotation gehen wir davon aus, dass p0 ein späterer Preis ist, während p1 ein früherer ist. Wir eröffnen eine Position, sobald eine Lücke entsteht. Der Preis p1 kann nicht nur als Stop-Loss, sondern auch als Take-Profit betrachtet werden. Das bedeutet, dass wir ein System aus zwei Arten wählen können − in der Hoffnung, entweder eine schnelle Schließung der Lücke oder eine große Preisbewegung in Richtung der Lücke zu erreichen. Das Schließen der Lücke bedeutet, dass der Preis zum p1 Niveau zurückkehrt oder es durchbricht.
Da Lücken in ihrer Standardform für Devisenanlagen relativ selten sind, wurde dem Autor vorgeschlagen, dieses Konzept zu verallgemeinern, wenn er das Thema dieses Artikels mit der Forenverwaltung besprach. Bei der Definition einer Lücke können Sie auf die Anforderung verzichten, dass nur eine Lücke zwischen zwei Folgepreisen berücksichtigt wird. Natürlich wird die Zahl der möglichen Lücken in diesem Fall unvorstellbar groß werden, und deshalb lohnt es sich, sich durch die aus Handelssicht vernünftigen Optionen einzuschränken. So wurde dem Autor beispielsweise angeboten, Lücken zwischen dem Schlusskurs einer amerikanischen Sitzung und dem Eröffnungskurs der nächsten zu berücksichtigen.
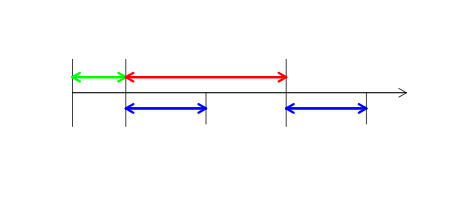
Lassen Sie mich erklären, wie das Konzept einer Sitzung formalisiert ist. Sie wird durch die drei Zeitintervalle bestimmt: Periode, Länge und Verschiebung. Die Sitzungen sind periodisch und haben eine Länge, die den Zeitraum nicht überschreitet. Jeder Tick gehört entweder zu einer Sitzung oder zu keiner von ihnen (letzteres ist möglich, wenn seine Länge strikt kleiner als der Zeitraum ist). Die Verschiebung ist ein Zeitintervall zwischen dem Nullpunkt und dem Beginn der ersten Sitzung danach. Er sollte kleiner als der Zeitraum sein. Dieses Konzept der Sitzung ist etwas breiter als üblich und ermöglicht es uns, beispielsweise Lücken zwischen den Minutenbalken zu berücksichtigen. Lassen Sie es uns in der folgenden Abbildung veranschaulichen. Der grüne Pfeil stellt die Zeitspanne dar, die die Verschiebung definiert, der rote zeigt die Periode, während der blaue die Dauer der Sitzung anzeigt.
Wir werden zwei leicht unterschiedliche EAs verwenden, um Statistiken über Kurslücken zu sammeln. Der erste (gaps_reg_stat.mq5) berücksichtigt Lücken zwischen den beiden nachfolgenden Ticks, während der zweite (gaps_ses_stat.mq5) Lücken zwischen den Sitzungen berücksichtigt. Natürlich handeln diese EAs nicht und laufen nur im Testmodus. Es wird empfohlen, die erste von ihnen nur mit realen Ticks zu testen, den zweite - mit OHLC der Minutenbars. Die EA-Codes sind unten aufgeführt.
// gaps_reg_stat.mq5 #define ND 100 input double gmin=0.1; // Mindestgröße der Lücken: USDJPY - 0.1, EURUSD - 0.001 input string fname="gaps\\stat.txt"; // Dateiname der Statistik struct SGap { double p0; double p1; double p2; double p3; double s; void set(double p_1,double p,double sprd); bool brkn(); void change(double p); double gap(); double Q(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p,double sprd); void change(double p); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; bool is0=false; void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; if(is0) { double p=(tick.bid+tick.ask)*0.5, p0=(tick0.bid+tick0.ask)*0.5; gaps.change(p); if(MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid); } else is0=true; tick0=tick; } int OnInit() { gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } void SGap :: set(double p_1,double p,double sprd) { p1=p_1; p0=p2=p3=p; s=sprd; } bool SGap :: brkn() { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1)); } void SGap :: change(double p) { if(brkn()) return; if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p; p3=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { double q=p2-p1; if(q==0.0) return 0.0; return (p2-p0)/q; } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p,double sprd) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].set(p_1,p,sprd); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } void CGaps :: change(double p) { for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; gs[go[i]].change(p); if(gs[go[i]].brkn()) go[i]=-1; } } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c; for(int i=0;i<ngs;++i) { if (gs[i].brkn()) c=1; else c=0; FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s); if(i==ngs-1) break; FileWriteString(f,"\n"); } FileClose(f); } // gaps_ses_stat.mq5 #define ND 100 input double gmin=0.001; // Mindestgröße der Lücken: USDJPY - 0.1, EURUSD - 0.001 input uint mperiod=1; // Periode der Handelszeit in Minuten input uint mlength=1; // Länge der Handelszeit in Minuten input uint mbias=0; // Bias der ersten Handelszeit in Minuten input string fname="gaps\\stat.txt"; // Dateiname der Statistik struct SGap { double p0; double p1; double p2; double p3; double s; void set(double p_1,double p,double sprd); bool brkn(); void change(double p); double gap(); double Q(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p,double sprd); bool change(double p); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; int ns0=-1; ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60; void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; double p=(tick.bid+tick.ask)*0.5; gaps.change(p); int ns=nsession(tick.time); if(ns>=0) { double p0=(tick0.bid+tick0.ask)*0.5; if(ns0>=0&&ns>ns0&&MathAbs(p-p0)>=gmin) gaps.add(p0,p,tick.ask-tick.bid); ns0=ns; tick0=tick; } } int OnInit() { if(speriod==0||slength==0||speriod<slength||speriod<=sbias) { Print("wrong session format"); return(INIT_FAILED); } gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } int nsession(datetime t) { ulong t0=(ulong)t; if(t0<sbias) return -1; t0-=sbias; if(t0%speriod>slength) return -1; return (int)(t0/speriod); } void SGap :: set(double p_1,double p,double sprd) { p1=p_1; p0=p2=p3=p; s=sprd; } bool SGap :: brkn() { return ((p0>p1)&&(p3<=p1))||((p0<p1)&&(p3>=p1)); } void SGap :: change(double p) { if(brkn()) return; if((p0>p1&&p>p2) || (p0<p1&&p<p2)) p2=p; p3=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { double q=p2-p1; if(q==0.0) return 0.0; return (p2-p0)/q; } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p,double sprd) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].set(p_1,p,sprd); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } bool CGaps :: change(double p) { bool chngd=false; for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; gs[go[i]].change(p); if(gs[go[i]].brkn()) {go[i]=-1; chngd=true;} } return chngd; } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT), c; for(int i=0;i<ngs;++i) { if (gs[i].brkn()) c=1; else c=0; FileWriteString(f,(string)gs[i].gap()+" "+(string)gs[i].Q()+" "+(string)c+" "+(string)gs[i].s); if(i==ngs-1) break; FileWriteString(f,"\n"); } FileClose(f); }
Die EAs sind ziemlich einfach, obwohl es sinnvoll ist, das Array go[] in der Klasse CGaps zu erwähnen, in dem die Indizes der nicht geschlossenen Kurslücken gespeichert sind, was die Arbeit der EAs beschleunigt.
In jedem Fall werden für jede Lücke folgende Daten aufgezeichnet: absoluter Wert der Lücke, Wert Q, Daten über deren Schlusskurs und Spread zum Zeitpunkt der Lücke. Anschließend wird die Differenz zwischen dem empirischen Verteilungswert Q und dem einheitlichen Verteilungswert überprüft und die Entscheidung über die weitere Analyse getroffen. Zur Überprüfung der Differenz werden grafische und rechnerische (statistische Berechnung nach Kolmogorov) Methoden verwendet. Der Einfachheit halber beschränken wir uns auf den p-Wert des Kolmogorov-Smirnov-Tests als Ergebnis von Berechnungen. Es werden Werte zwischen Null und Eins angenommen, und je kleiner sie sind, desto unwahrscheinlicher ist es, dass die Verteilung der Probe mit der theoretischen übereinstimmt.
Wir haben den Kolmogorov-Smirnov-Test (Ein-Stichprobe) aus mathematischen Gründen ausgewählt. Der Hauptgrund ist, dass wir daran interessiert sind, die Verteilungsfunktionen in der einheitlichen Konvergenzmetrik zu unterscheiden und nicht in irgendwelchen integralen Metriken. Dieser Test wurde in den MQL5-Bibliotheken nicht gefunden, also musste ich die Sprache R verwenden. Es ist anzumerken, dass, wenn es übereinstimmende Zahlen in der Stichprobe gibt, die Genauigkeit dieses Kriteriums etwas reduziert ist (R gibt eine entsprechende Warnung ab), aber durchaus akzeptabel bleibt.
Wenn eine signifikante Diskrepanz zwischen den theoretischen und empirischen Verteilungen festgestellt wird, sollten wir die Möglichkeit untersuchen, daraus Gewinne zu ziehen. Wenn es keine signifikante Diskrepanz gibt, dann verwerfen wir diese Idee entweder oder versuchen, sie zu verbessern.
Wie bereits erwähnt, gibt es zwei Möglichkeiten, eine Transaktion zum Preis p0 zu erfassen, wenn eine Lücke gebildet wird − entweder in Richtung der Lücke oder in der entgegengesetzten. Berechnen wir die Erwartung der Ergebnisse für diese beiden Fälle. Während wir das tun, werden wir den Spread betrachten, der als konstant betrachtet und ihn als s bezeichnet ist. Der Absolutwert der Lücke wird als g bezeichnet, während g0 für seinen Minimalwert steht.
- Eröffnung in Richtung der Kurslücke. In diesem Fall ist g+s Stop-Loss, während kg-s der Take-Profit ist. Hier ist k das Verhältnis von Gewinn/Verlust. Profitabilitätswert: -1 bei einer Stop-Loss-Aktivierung und (kg-s)/(g+s) bei einer Take-Profit-Aktivierung. Korrespondierende Wahrscheinlichkeiten: Fq(q) und 1-Fq(q). Berechnen wir k mit q: k=k(q)=q/(1-q). Dann für die mathematische Gewinnerwartung M, M=Fq(q)*(-1)+(1-Fq(q))*(k(q)g-s)/(g+s). Nur die Werte q, für die M signifikant positiv ist für alle g≥g0, sind für uns geeignet. Wir benötigen die Werte q, bei dem Fq(q) signifikant niedriger ist als der theoretische Wert des Random Walk Fq(q)<Fq0(q) bei g=g0.
- Eröffnung gegen die Kurslücke. In diesem Fall ist g-s der Take-Profit und kg+s der Stop-Loss ist. Hier ist k das Verhältnis Verlust/Gewinn. Profitabilitätswerte: -1 bei einer Stop-Loss-Aktivierung und (g-s)/(kg+s) bei einer Take-Profit-Aktivierung. Korrespondierende Wahrscheinlichkeiten: 1-Fq(q) und Fq(q). Die Berechnung von k durch q ist dieselbe wie im vorherigen Abschnitt: k=k(q)=q/(1-q). Für die mathematische Gewinnerwartung M erhalten wir die Gleichung M=(1-Fq(q))*(-1)+*Fq(q)(g-s)/(k(q)g+s). Nur die Werte q, für die M signifikant positiv ist für alle g≥g0, sind für uns geeignet. Wir benötigen die Werte q, wobei Fq(q) signifikant höher ist als der theoretische Wert Fq(q)>Fq0(q) bei g=g0.
Für zwei Symbole wurden Statistiken erhoben:
- EURUSD
- USDJPY
Die folgenden Arten von Lücken wurden für jede von ihnen berücksichtigt:
- Zwischen aufeinanderfolgenden Ticks.
- Zwischen den Minutenbars.
- Zwischen den Handelssitzungen. Für EURUSD wird die amerikanische Handelszeit (die Chicagoer und New Yorker zusammen), während für USDJPY die Tokioer Handelszeit verwendet wird.
Für jede dieser sechs Optionen wurden die Statistiken für die jeweils Letzten untersucht:
- 200 Lücken
- 50 Lücken
Dadurch haben wir 12 Untersuchungen. Die jeweiligen Ergebnisse sind wie folgt:
- p-Wert für Kolmogorov Statistiken
- Der Mittelwert des Spread zum Zeitpunkt der Lückenbildung.
- Grafik der empirischen und theoretischen (rote Linie) Funktionen der Q Werteverteilung
- M_cont Rentabilität mathematisches Erwartungsdiagramm für den Handel in Richtung der Lücke in Abhängigkeit von q im Vergleich zur M_cont=0 theoretische Linie (rot). Hier bedeutet q das Verhältnis Gewinn/Summe von Gewinn und Stop-Loss.
- M_rvrs Diagramm der mathematischen Gewinnerwartung für den Handel entgegen der Richtung der Lücke in Abhängigkeit von q im Vergleich zu M_rvrs=0 theoretische Linie (rot). Hier bedeutet q das Verhältnis Stop-Loss/Summe von Take-Profit und Stop-Loss.
Alle Ergebnisoptionen sind unten aufgeführt.
- EURUSD, 200 letzte Lücken, zwischen aufeinanderfolgenden Ticks. p-Wert: 3.471654e-07, Mittelwert Spread: 0.000695
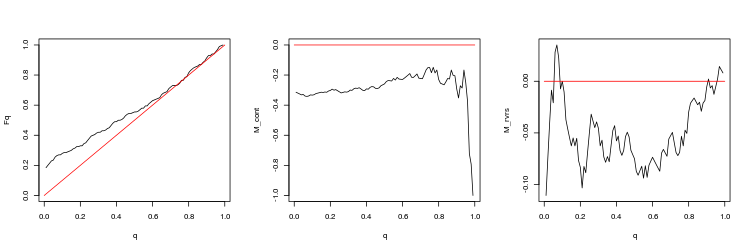
- EURUSD, 50 letzte Lücken, zwischen aufeinanderfolgenden Ticks. p-Wert: 0.2428457, Mittelwert Spread: 0.0005724
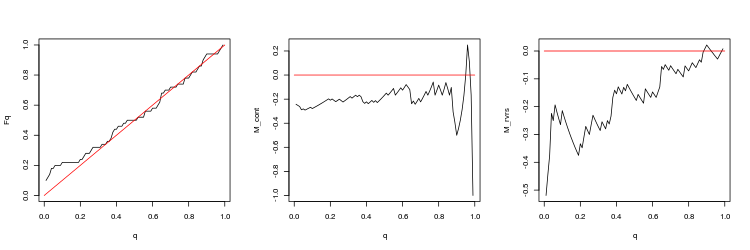
- EURUSD, 200 letzte Lücken, zwischen Minutenbars. p-Wert: 8.675995e-06, Mittelwert Spread: 0.0004352
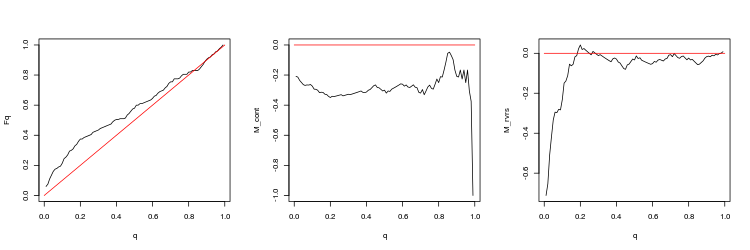
- EURUSD, 50 letzte Lücken, zwischen Minutenbars. p-Wert: 0.0125578, Mittelwert Spread: 0.000404
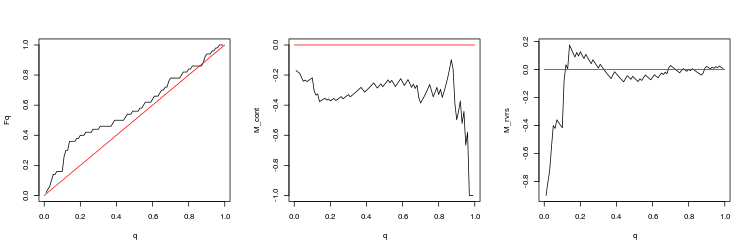
- EURUSD, 200 letzte Lücken, zwischen den Handelssitzungen. p-Wert: 0.6659917, Mittelwert Spread: 0.0001323
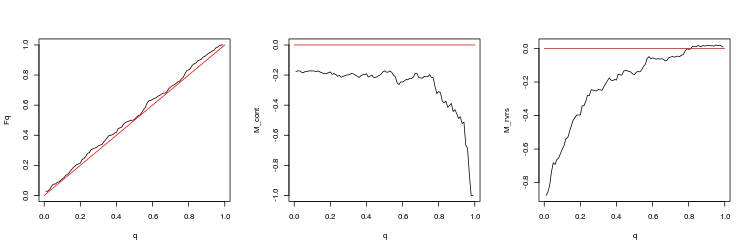
- EURUSD, 50 letzte Lücken, zwischen den Handelssitzungen. p-Wert: 0.08915716, Mittelwert Spread: 0.0001282
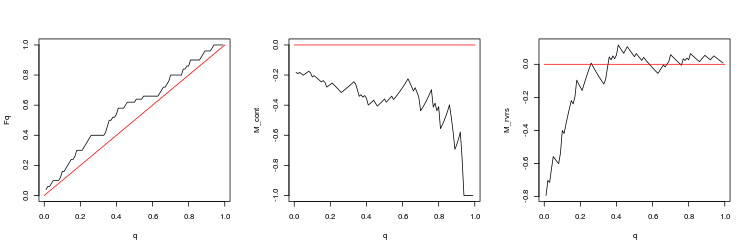
- USDJPY, 200 letzte Lücken, zwischen aufeinanderfolgenden Ticks. p-Wert: 2.267454e-06, Mittelwert Spread: 0.09563
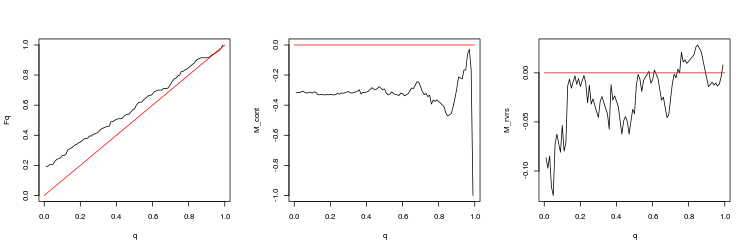
- USDJPY, 50 letzte Lücken, zwischen aufeinanderfolgenden Ticks. p-Wert: 0.03259067, Mittelwert Spread: 0.0597
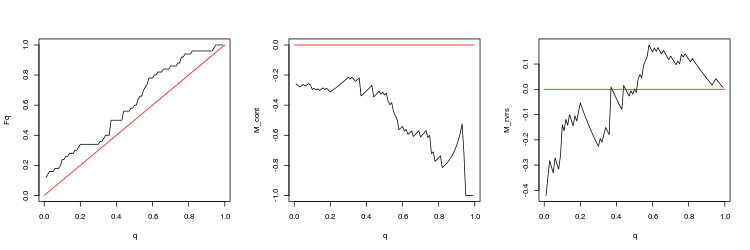
- USDJPY, 200 letzte Lücken, zwischen Minutenbars. p-Wert: 0.0003737335, Mittelwert Spread: 0.05148
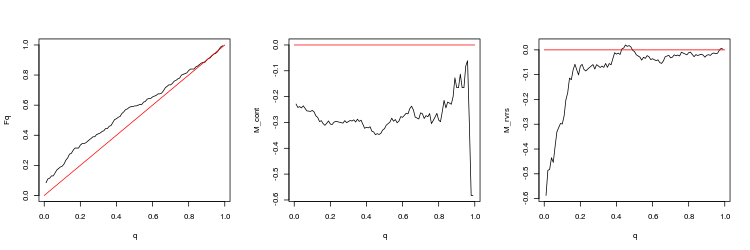
- USDJPY, 50 letzte Lücken, zwischen Minutenbars. p-Wert: 0.005747542, Mittelwert Spread: 0.0474
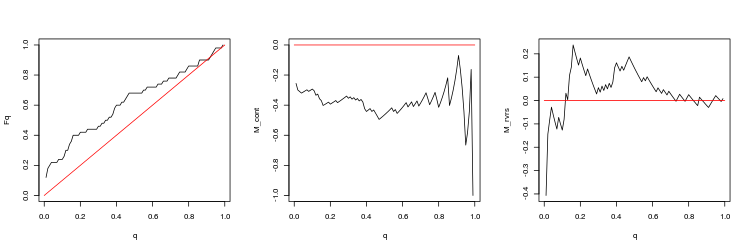
- USDJPY, 200 letzte Lücken, zwischen Handelssitzungen. p-Wert: 0.07743524, Mittelwert Spread: 0.02023
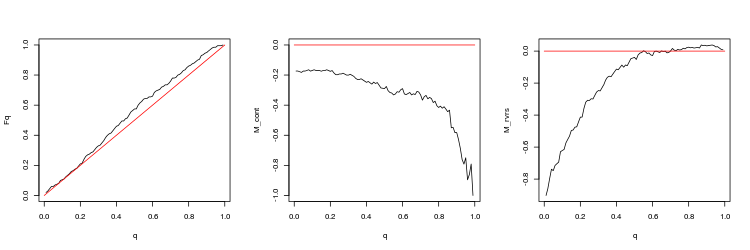
- USDJPY, 50 letzte Lücken, zwischen Handelssitzungen. p-Wert: 0.009191665, Mittelwert Spread: 0.0185
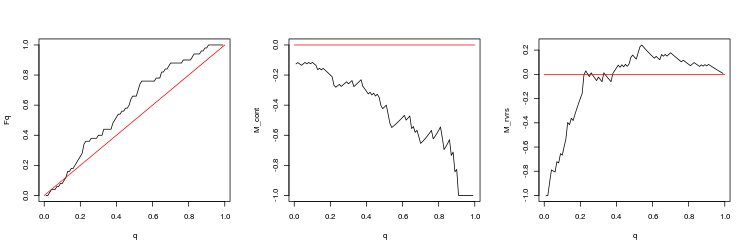
Aus diesen Ergebnissen können wir die folgenden Schlussfolgerungen ziehen:
- Die Abweichungen vom Random Walk sind recht signifikant.
- Der Handel in Richtung der Lücke ist wenig erfolgversprechend. Der Handel in Richtung Lückenschluss erscheint besser, aber der Gewinn ist gering (insbesondere bei EURUSD).
- Zum Zeitpunkt der Bildung der Lücke können die Spreads im Vergleich zu ihrem Mittelwert mehrfach wachsen (gilt für Lücken zwischen Ticks und Minutenbarren).
- Lücken zwischen den Handelssitzungen führen zu einem Unterschied zum Random Walk nur über 1-2 Monaten, während der Unterschied aufs Jahr bezogen sehr gering ist. Auf den ersten Blick wird dies durch den zu einem bestimmten Zeitpunkt vorherrschenden Trend bestimmt. Offensichtlich schließen sich die Lücken in Seitwärtsbewegungen besser und in Trends schlechter, obwohl eine detailliertere Analyse erforderlich ist.
- Für weitere Analysen sollten wir die Lücken zwischen den Minutenbalken für USDJPY wählen.
Testen der Strategie und Berechnen des optimalen Risikos je Position
Die Version des Systems, die auf Lücken zwischen USDJPY-Minutentafeln basiert, sieht vielversprechend aus. Der signifikante Anstieg des Spread, den wir zum Zeitpunkt der Bildung der Lücke festgestellt haben, bedeutet, dass wir ihrer Definition mehr Aufmerksamkeit schenken sollten. Lassen Sie uns das wie folgt beschreiben. Wir werden die Lücke nicht für den Durchschnittspreis, sondern für Angebot und Nachfrage berücksichtigen. Außerdem werden wir denjenigen von ihnen auswählen, für den wir in den Handel eintreten müssen. Das bedeutet, dass wir eine Aufwärtslücke durch Bid-Preis und eine Abwärtslücke durch Ask-Preis definieren werden. Das Gleiche gilt für ihren Lückenschluss.
Lassen Sie uns den EA entwickeln, indem wir den EA leicht ändern, den wir für das Sammeln von Statistiken über Lücken zwischen den Sitzungen verwendet haben. Die wichtigste Änderung betrifft die Struktur der Lücke. Da wir eine eindeutige Übereinstimmung zwischen Lücken und Deals haben, sollen in dieser Struktur alle für den Handel notwendigen Informationen (Geschäftsvolumen und Abschlussbedingung) gespeichert werden. Für den Handel werden zwei Funktionen hinzugefügt. Eine von ihnen (pp2v()) berechnet das Volumen für jeden einzelnen Deal, während die anderer (trade()) die Übereinstimmung zwischen der Summe der Dealvolumina und dem Handelspositionsvolumen speichert. Der EA-Code (gaps_ses_test.mq5) ist unten aufgeführt.
// gaps_ses_test.mq5 #define ND 100 input uint mperiod=1; // Periode der Handelszeit in Minuten input uint mlength=1; // Länge der Handelszeit in Minuten input uint mbias=0; // Bias der ersten Handelszeit in Minuten< input double g0=0.1; // Mindestgröße der Lücken: USDJPY - 0.1, EURUSD - 0.001 input double q0=0.4; // q0=sl/(sl+tp) input double r=0.01; // Risiko je Deal input double s=0.02; // Näherung des Spread input string fname="gaps\\stat.txt"; // Dateiname der Statistik struct SGap { double p0; double p1; double p2; double v; int brkn(); bool up(); void change(double p); double gap(); double Q(); double a(); }; class CGaps { SGap gs[]; int ngs; int go[]; int ngo; public: void init(); void add(double p_1,double p); bool change(double pbid,double pask); double v(); void gs2f(string fn); }; CGaps gaps; MqlTick tick0; int ns0=-1; ulong sbias=mbias*60, speriod=mperiod*60, slength=mlength*60; double dv=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_STEP); void OnTick() { MqlTick tick; if (!SymbolInfoTick(_Symbol, tick)) return; bool chngd=gaps.change(tick.bid,tick.ask); int ns=nsession(tick.time); if(ns>=0) { if(ns0>=0&&ns>ns0) { if(tick0.ask-tick.ask>=g0) {gaps.add(tick0.ask,tick.ask); chngd=true;} else if(tick.bid-tick0.bid>=g0) {gaps.add(tick0.bid,tick.bid); chngd=true;} } ns0=ns; tick0=tick; } if(chngd) trade(gaps.v()); } int OnInit() { gaps.init(); return(INIT_SUCCEEDED); } void OnDeinit(const int reason) { gaps.gs2f(fname); } int nsession(datetime t) { ulong t0=(ulong)t; if(t0<sbias) return -1; t0-=sbias; if(t0%speriod>slength) return -1; return (int)(t0/speriod); } double pp2v(double psl, double pen) { if(psl==pen) return 0.0; double dc, dir=1.0; double c0=AccountInfoDouble(ACCOUNT_EQUITY); bool ner=true; if (psl<pen) ner=OrderCalcProfit(ORDER_TYPE_BUY,_Symbol,dv,pen+s,psl,dc); else {ner=OrderCalcProfit(ORDER_TYPE_SELL,_Symbol,dv,pen,psl+s,dc); dir=-1.0;} if(!ner) return 0.0; return -dir*r*dv*c0/dc; } void trade(double vt) { double v0=SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN); if(-v0<vt<v0) vt=v0*MathRound(vt/v0); double vr=0.0; if(PositionSelect(_Symbol)) { vr=PositionGetDouble(POSITION_VOLUME); if(PositionGetInteger(POSITION_TYPE)==POSITION_TYPE_SELL) vr=-vr; } int vi=(int)((vt-vr)/dv); if(vi==0) return; MqlTradeRequest request={0}; MqlTradeResult result={0}; request.action=TRADE_ACTION_DEAL; request.symbol=_Symbol; if(vi>0) { request.volume=vi*dv; request.type=ORDER_TYPE_BUY; } else { request.volume=-vi*dv; request.type=ORDER_TYPE_SELL; } if(!OrderSend(request,result)) PrintFormat("OrderSend error %d",GetLastError()); } int SGap :: brkn() { if(((p0>p1)&&(p2<=p1))||((p0<p1)&&(p2>=p1))) return 1; if(Q()>=q0) return -1; return 0; } bool SGap :: up() { return p0>p1; } void SGap :: change(double p) { if(brkn()==0) p2=p; } double SGap :: gap() { return MathAbs(p0-p1); } double SGap :: Q() { if(p2==p1) return 0.0; return (p2-p0)/(p2-p1); } double SGap :: a() { double g=gap(), k0=q0/(1-q0); return (g-s)/(k0*g+s); } void CGaps :: init() { ngs=ngo=0; } void CGaps :: add(double p_1,double p) { ++ngs; if(ArraySize(gs)<ngs) ArrayResize(gs,ngs,ND); gs[ngs-1].p0=gs[ngs-1].p2=p; gs[ngs-1].p1=p_1; double ps=p+(p-p_1)*q0/(1-q0); gs[ngs-1].v=pp2v(ps,p); int i=0; for(; i<ngo; ++i) if(go[i]<0) break; if(i==ngo) { ++ngo; if(ArraySize(go)<ngo) ArrayResize(go,ngo,ND); } go[i]=ngs-1; } bool CGaps :: change(double pbid,double pask) { bool ch=false; for(int i=0; i<ngo; ++i) { if(go[i]<0) continue; if(gs[go[i]].up()) gs[go[i]].change(pbid); else gs[go[i]].change(pask); if(gs[go[i]].brkn()!=0) {go[i]=-1; ch=true;} } return ch; } double CGaps :: v(void) { double v=0; for(int i=0; i<ngo; ++i) if(go[i]>=0) v+=gs[go[i]].v; return v; } void CGaps :: gs2f(string fn) { int f=FileOpen(fn, FILE_WRITE|FILE_COMMON|FILE_ANSI|FILE_TXT); int na=0, np=0, bk; double kt=0.0, pk=0.0; for(int i=0;i<ngs;++i) { bk=gs[i].brkn(); if(bk==0) continue; ++na; if(bk>0) ++np; kt+=gs[i].a(); } if(na>0) { kt/=na; pk=((double)np)/na; } FileWriteString(f,"na = "+(string)na+"\n"); FileWriteString(f,"kt = "+(string)kt+"\n"); FileWriteString(f,"pk = "+(string)pk); FileClose(f); }
Lassen Sie uns den EA auf das Jahr 2017 testen und den Risikowert für den Handel im Jahr 2018 basierend auf den Ergebnissen definieren. Die Saldenkurve auf Basis der Testergebnisse von 2017 ist nachfolgend aufgeführt.
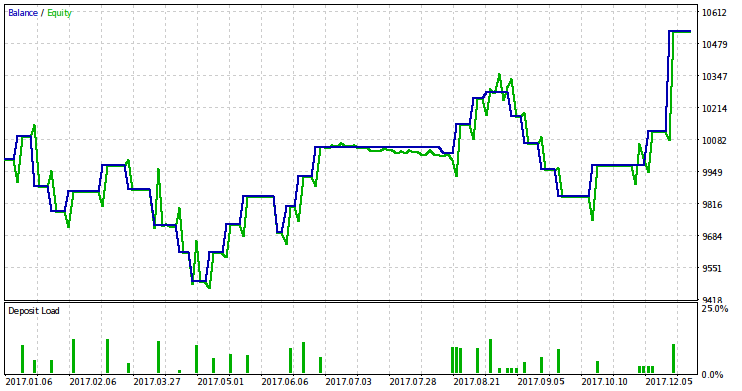
Ich muss einige Klarstellungen vornehmen, bevor ich mit der Risikoberechnung fortfahren kann. Erstens müssen wir die Notwendigkeit rechtfertigen, das richtige Risikoniveau zu bestimmen. Zweitens ist es notwendig, den Vorteil der Anwendung unserer Theorie für diesen Zweck zu erklären.
Spekulativer Handel ist immer mit Unsicherheit verbunden. Jedes Handelssystem führt manchmal dazu, dass Positionen verlieren. Aus diesem Grund sollte das Risiko nicht zu groß sein. Andernfalls ist die Inanspruchnahme zu hoch. Andererseits kann sich der Markt jederzeit ändern, um ein profitables System in ein verlierendes zu verwandeln. Daher ist die "Lebensdauer" des Systems endlich und nicht genau bekannt. Aus diesem Grund sollte das Risiko nicht zu gering sein. Andernfalls können Sie nicht alle möglichen Gewinne mit Ihrem Handelssystem erzielen.
Betrachten wir nun die wichtigsten Ansätze (die sich von unseren unterscheiden) zur Definition des Risikos, zusammen mit einer kurzen Charakteristik:
- Definition des Risikos durch einen bestimmten Zahlenwert, basierend auf der Meinung einiger "erfahrener Händler". Der beliebteste Wertebereich liegt bei 0,5-3% des Saldos. Dieser Ansatz ist trotz mangelnder Rechtfertigung völlig ausreichend. Der größte Nachteil ist das Fehlen einer Regel zur Auswahl eines bestimmten Risikowerts für ein bestimmtes System.
- Ralph Vince Methode des "optimal f". Diese Methode ist theoretisch begründet, bietet aber in der Regel einen unzureichend hohen Risikowert, der zu einem sehr hohen Drawdown führen kann.
- Die Einbeziehung des Risikos in die EA-Parameter und deren Definition während des Tests und der Optimierung. Es ist schwierig, etwas Bestimmtes über die Rechtfertigung und Angemessenheit des Ergebnisses zu sagen, da diese Parameter stark vom Gerät des EA abhängen und davon, wie genau die Optimierung durchgeführt wird. Eines der möglichen Probleme ist die fehlende Berücksichtigung von Unsicherheiten im weiteren Handelsergebnis. Ein Nachjustieren ist ebenfalls möglich, was zu einer ungerechtfertigten Risikosteigerung führen kann (die bisherige Methode ist ein anschauliches Beispiel). Die von uns vorgeschlagene Methode ist eine Möglichkeit, das Risiko sinnvoll zu optimieren.
Unsere Methode ermöglicht es uns, im Gegensatz zu den oben beschriebenen Verfahren angemessene und angemessene Risikowerte zu erhalten. Es verfügt über einstellbare Parameter, die auf den jeweiligen Handelsstil zugeschnitten werden können. Lassen Sie uns die Essenz unseres Ansatzes zur Risikoberechnung beschreiben. Wir gehen davon aus, dass wir das Handelssystem genau so lange nutzen, bis seine durchschnittliche Rentabilität innerhalb der vorgegebenen Anzahl von Geschäften unter das vorgegebene Minimum fällt oder bis die Inanspruchnahme das vorgegebene Maximum in der gleichen Reihenfolge von Geschäften überschreitet. Danach wird der auf diesem System basierende Handel gestoppt (z.B. werden seine Parameter erneut optimiert). Der Risikowert wird so gewählt, dass die Wahrscheinlichkeit, dass das System noch profitabel ist (und der Drawdown oder Gewinnabnahme eine natürliche Zufallsschwankung ist), nicht mehr als der angegebene Wert beträgt.
Das Verfahren ist in den vorangegangenen Artikeln ausführlich beschrieben. Im zweiten Artikel finden Sie ein Skript zur Berechnung des optimalen Risikowertes. Dieses Skript ist anwendbar auf bestehende Deals durch Stop-Loss und Take-Profit, die während der Eröffnung mit einem festen Verhältnis für alle Deals angegeben werden. Es wird im genannten Artikel bn.mq5 genannt.
Als Ergebnis eines Testdurchlaufs schreibt unser EA Daten, die als Teil der Parameter für das Risikokalkulationsskript notwendig sind, in eine Textdatei. Die übrigen Parameter sind entweder im Voraus bekannt oder werden durch eine umfassende Suche ausgewählt. Wenn sich herausstellt, dass der vom Skript vorgeschlagene Risikowert Null ist, dann sollten wir entweder diese Handelsidee verwerfen, unsere Drawdown/Gewinnanforderungen schwächen (durch Änderung der Parameter) oder Daten der Deals aus einer größeren Historie verwenden. Unten ist ein Teil des Skripts mit den Werten der einzustellenden Parameter.
input uint na=26; // Anzahl der Deals in der Serie input double kt=1.162698185452029 // Verhältnis von Take-Profit/Stop-Loss input double pk=0.5769230769230769 // Gewinnprofitabilität double G0=0.0; // kleinster Durchschnitt der Profitabilität double D0=0.9; // kleinstes Inkrement double dlt=0.17; // Signifikanzniveau
Da die Testergebnisse für 2017 in Bezug auf die Handelsqualität nicht inspirierend sind, sind unsere Anforderungen eher moderat. Wir stellen die Bedingung, dass innerhalb von 26 Deals (na=26), das EA nicht verlustbringend ist (G0=0.0) und der Drawdown 10% nicht überschreitet (D0=0.9). Um einen Risikowert ungleich Null zu erhalten, müssen wir das Signifikanzniveau relativ hoch einstellen (dlt=0,17). In der Tat ist es besser, wenn es nicht mehr als ein Zehntel ist. Die Tatsache, dass wir es so groß machen müssen, zeigt ein schlechtes Handelsergebnis. Der EA mit diesen Parametern sollte nicht im realen Handel mit diesem Symbol verwendet werden. Mit den angegebenen Parametern liefert das Skript für das Risiko das folgende Ergebnis: r = 0,014. Nachfolgend finden Sie das EA-Testergebnis für 2018 mit diesem Risikowert.
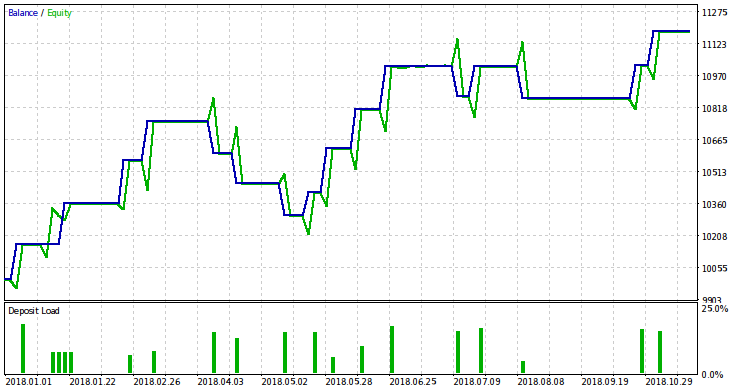
Trotz der Gewinne, die der EA während des Tests gezeigt hat, ist es unwahrscheinlich, dass sie im realen Handel realisierbar sind. Die Sinnlosigkeit des Handels mit gewöhnlichen Lücken auf den untersuchten Symbolen scheint offensichtlich. Solche Lücken sind sehr selten (und werden mit der Zeit immer seltener) und klein. Die eingehendere Betrachtung der Generalisierung der Lücken - Preisänderungen zwischen den Handelssitzungen - erscheint vielversprechender. Außerdem ist es sinnvoll, auf die Vermögenswerte zu achten, bei denen gewöhnliche Lücken häufiger auftreten.
Schlussfolgerung
Probabilistische Methoden eignen sich gut für die Entwicklung und Konfiguration von EAs. Gleichzeitig stehen sie in keiner Weise im Gegensatz zu anderen möglichen Methoden. Stattdessen ermöglichen sie es oft, sie zu ergänzen oder zu überdenken.
In diesem Artikel haben wir das Thema der allgemeinen EA-Optimierung nicht durch seine Parameter angesprochen, die es nur am Rande erwähnen. Es gibt einen signifikanten Zusammenhang zwischen diesem Bereich und dem probabilistischen Ansatz (der Theorie der statistischen Lösungen). Vielleicht werde ich diese Frage später im Detail untersuchen.
Angehängte Dateien
Nachfolgend finden Sie zwei EAs, die die Statistik berechnen und einen EA, der zum Handel verwendet wird.
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | gaps_reg_stat.mq5 | EA | Ermitteln der Statistik der Lücken aufeinanderfolgender Ticks |
| 2 | gaps_ses_stat.mq5 | EA | Ermitteln der Statistik der Lücken zwischen den Handelssitzungen |
| 3 | gaps_ses_test.mq5 | EA | Handelstest mit den Lücken zwischen den Handelssitzungen |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/5373
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wie man nutzerdefinierte MOEX-Symbole in MetaTrader 5 erstellt und testet
Wie man nutzerdefinierte MOEX-Symbole in MetaTrader 5 erstellt und testet
 Entwicklung eines Symbolauswahl- und Navigationsprogramms in MQL5 und MQL4
Entwicklung eines Symbolauswahl- und Navigationsprogramms in MQL5 und MQL4
 Hilfen zur Auswahl und Navigation in MQL5 und MQL4: Tabs für "Hausaufgaben" und das Sichern grafischer Objekte
Hilfen zur Auswahl und Navigation in MQL5 und MQL4: Tabs für "Hausaufgaben" und das Sichern grafischer Objekte
 Verwenden von OpenCL, um Kerzenmuster zu testen
Verwenden von OpenCL, um Kerzenmuster zu testen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Auf dem Forex gibt es nur wenige gewöhnliche Lücken, daher wurde neben ihnen auch ihre Verallgemeinerung untersucht.
Der Punkt liegt nicht in der Bezeichnung, sondern in der Tatsache, dass die Phänomene unterschiedlicher Natur sind. Man kann sie verallgemeinern oder vermischen.)
Die unterschiedliche Natur der Phänomene hat uns nicht daran gehindert, denselben mathematischen Apparat für sie zu verwenden. Da das Hauptthema der Arbeit die Beschreibung einer mathematischen Methode ist, ist die Ähnlichkeit dieser Methode die Grundlage für die gemeinsame Betrachtung dieser Phänomene. Es ist vergleichbar damit, wie in einem Schulaufgabenheft Probleme über Süßigkeiten und Bagger nebeneinander stehen können, obwohl sich die Arten dieser Objekte wesentlich unterscheiden.
Die Seltenheit eines Phänomens bedeutet nicht, dass es unrentabel ist. Ganz im Gegenteil, seltene Phänomene sind plötzlich und groß, so dass sie den Markt stärker beeinflussen.
Im Rahmen dieses Artikels bedeutet ihre Unzulänglichkeit, dass es unmöglich ist, das Wesen des beschriebenen mathematischen Apparats nur auf der Grundlage der klassischen Gaps zu demonstrieren.
Nichts hindert Sie daran zu zeigen, wie ein richtiger Artikel über Lücken aussehen sollte. Außer natürlich Ihrer Unfähigkeit, ihn zu schreiben.
Ich habe keine Beschwerden über Sie oder Ihren Artikel. Ich habe Ihnen nur gesagt, wo die zusätzlichen Möglichkeiten liegen. Vielleicht ein bisschen aggressiv, aber so wird es hier gemacht).
Ich habe auch keine Ansprüche an Sie) Trotzdem wünsche ich mir, dass Sie einen Artikel über Lücken schreiben, der sie aus einem anderen Blickwinkel und auf mehr Märkten betrachtet, als es hier getan wird) Ich bin sicher, dass er sowohl für Sie als auch für den gesamten angemessenen Teil des Forums nützlich sein wird.