Avaliação do risco numa sequência de trades com um ativo. Continuação

Sumário

• Prefácio
• Pressupostos sobre o preço e os sistemas de negociação
• Alocação da rentabilidade. Observações gerais
  
• Stop-loss e take-profit fixos
  
• Trailing-stop fixo
• O que vem agora?
• Estatísticas e gaps
  
• Aprendizado estatístico de máquina
• Estatísticas e otimização do sistemas de negociação
• Arquivos anexados

Prefácio

Continuamos estudando a teoria sobre o cálculo de risco abordada na seção anterior. Ela será condensada em dois exemplos. Também destacaremos brevemente outras possíveis implementações da teoria da probabilidade e estatística matemática.

Pressupostos sobre o preço e os sistemas de negociação

Será que podemos estudar os resultados de negociação de qualquer sistema por meio dos métodos descritos no artigo anterior? Para fazer isso, devemos ter certeza de a sequência de trades ser uma sequência de valores independentes e identicamente distribuídos. Mas, infelizmente, a experiência mostra que isso nem sempre é o caso.

Podem não ser satisfeitas ambas as condições, isto é, a independência e igualdade das distribuições. Em seu livro “The Mathematics of Money Management”, Ralph Vince descreve maneiras de abordar estes problemas. Ele propõe dividir os sistemas em várias partes, para, dessa maneira, ter subsistemas cujas condições são atendidas. Vince dá dois exemplos. O primeiro fala sobre um sistema em que existe uma dependência entre cada trade subsequente. Neste caso, a sequência é dividida em duas partes: trades com números pares e ímpares são tratados como vindos de sistemas diferentes. O segundo exemplo considera um sistema com "pyramiding" - aumento gradual no volume da posição. Cada passo deste aumento é examinado como um sistema separado. Assim, temos um conjunto de sistemas: o primeiro consiste nos primeiros passos, o segundo nos segundos passos, etc.

Como esses "pedaços" de sistemas estão estudados, devemos encontrar a maneira de juntá-los novamente e, assim, torná-los um microportfólio levando em conta as dependências entre eles. Para conseguir isso, precisamos da Teoria moderna do portfólio.

Tudo isso já parece bastante complicado, mas isso não é tudo. Consideremos um sistema em que a saída de cada trade ocorre com base num preço pré-fixado: pstoploss ou ptakeprofit. Com a relação k=|ptakeprofit-penter|/|pstoploss-penter|, ela muda de trade para trade, dependendo do indicador. Em cada trade, a alocação da rentabilidade será muito simples: distribuição discreta, com dois valores -1 e k, tomados com certa probabilidade. Porém, como cada trade tem seu próprio k, cada uma delas terá sua própria distribuição. Assim, caso tentemos dividir o sistema em pedaços, haverá tantos trades quanto pedaços, o que parecerá absurdo. Na prática, ao calcular o risco, estamos propensos a tomar um mesmo valor de k para todos os trades (algum valor médio caraterístico para todos). Assim, para a análise, podemos usar uma versão simplificada do sistema utilizado na negociação real.

Resumimos todas as variações de uso de nossa teoria do risco, para sistemas de negociação do mundo real:

1. Dividimos o sistema de negociação em várias partes.
2. Examinamos a versão simplificada do sistema.
3. Analisamos a sequência de trades, sem verificar se são independentes e ou igualmente distribuídos. Ao fazer isto, podemos ajustar um pouco o valor de risco usando outros métodos de análise.
   

É óbvio que esta abordagem não é universal e nem sempre aplicável a todos os sistemas. Vamos tentar fazer o nosso processo mais sistemático. Para fazer isso, temos de fazer algumas suposições sobre preços e sistemas.

1. A série de preços está perto do passeio aleatório. Não vamos tentar formalizar uma definição matematicamente precisa dessa aproximação. Apenas vamos supor que se realizamos qualquer cálculo sobre o passeio aleatório e nos preços reais, os resultados do passeio aleatório podem ser vistos como uma aproximação de zero dos resultados dos preços reais. Por exemplo, dessa maneria, podemos fazer uma hipótese sobre a distribuição das variáveis ​​aleatórias obtidas a partir de uma série de preços.
   
2. Na entrada do sistema, podem-se enviar as cotações geradas pelo passeio aleatório. Neste caso, os preços aleatórios em média devem ser próximos dos preços reais. Isto significa uma volatilidade semelhante - em intervalos de tempo longos - e uma distribuição (de saltos nos preços de ticks, etc.) parecida.
3. A estrutura da relação entre os trades do sistema é próxima, em ambos os casos (preços reais e passeios aleatórios). A distribuição da rentabilidade em si, portanto, pode variar significativamente. Por exemplo, caso todas as rentabilidades aumentem o mesmo número, as distribuições são alteradas (deslocadas para a direita). Mas, os coeficientes de correlação entre as rentabilidades permanecem os mesmos.
   
4. O sistema é inusitadamente estruturado para que os trades sejam igualmente distribuídos, no passeio aleatório, e possam ser significativamente dependentes uns dos outros, caso os trades se cruzem entre si no tempo (a segunda operação é aberta antes do fechamento da segunda).
   

Descrevamos os detalhes desses pressupostos. O passeio aleatório é uma ampla classe de processos aleatórios. Pode ser discreto ou contínuo. Nos cálculos analíticos, ambos os tipos são usados, e, ao modelar no computador - apenas o primeiro. Entre estes tipos existe um relacionamento: o passeio com um tempo contínuo pode ser obtido a partir de uma passagem discreta extrema, quando o passo tenta se aproximar do zero. Além disso, o passeio pode ser quer simétrico (sem tendência, movimento lateral) quer com um deslocamento positivo/negativo (tendência para cima/baixo). Na maioria das vezes, é considerado o passeio simétrico. Neste caso, a partir de nossos pressupostos sobre os preços, obtemos o seguinte:

• Resultados das operações não podem ser previstos com quaisquer indicadores. Isso simplifica muito a modelagem. Acontece que precisamos estudar apenas a parte do sistema que é responsável pela saída do trade. Não importa quando e como ocorre entrada no trade.
• Lucro em média é zero. Isso não interfere com o fato de podermos obter certo lucro numa só operação. Mas, quanto mais tomamos trades, mais corresponderá o conjunto de resultados a uma distribuição de probabilidade. A forma específica desta distribuição depende do algoritmo de saída do trade, mas a expectância é sempre zero.
  

Estas consequências têm de ser tomadas em consideração durante o teste (e especialmente na otimização) de sistemas reais com base em preços reais. São necessários critérios que indiquem, com suficiente fiabilidade, que o resultado não é obtido num passeio aleatório simétrico. Isto também se aplica não só à distribuição das rentabilidades dos trades, mas também à utilidade dos indicadores técnicos. Além disso, a busca de desvios do passeio aleatório simétrico pode ser útil na procura de ideias para sistemas de negociação. Como exemplo, mais tarde, olharemos para a possibilidade de usar "os gaps são sempre fechados."

Nossos pressupostos colocam restrições nos sistemas de negociação. Em geral, eles exigem simplicidade, uniformidade e transparência nas regras de entrada e saída dos trades. Estas regras não devem aumentar a relação entre os trades, não devem alterar - de operação para operação - arbitrariamente as maneiras de sair do trade (por exemplo, mudar aleatoriamente a relação lucro/stop), os trades em si não devem ser muito frequentes, etc. O desempenho aproximado destas condições pode ser verificado quer especulando ou modelando através do método de Monte Carlo.

Alocação da rentabilidade. Observações gerais

Comecemos comentando de forma geral os tipos de distribuições. Quado se fala sobre o conceito de distribuição de probabilidade, geralmente, são mencionadas tanto as distribuições discretas como as abruptas. No entanto, elas podem ser misturadas, criando mais tipos. Ou seja, são possíveis funções de distribuição apresentadas na forma P(x)=γcPc(x)+γdPd(x), onde γc≥0, γd≥0, γc+γd=1, enquanto Pc(x) e Pd(x) são a distribuição abrupta (possuindo densidade) e a distribuição discreta (em degraus), respectivamente.

Como exemplo, veremos uma maneira simples de sair: stop-loss/take-profit fixados com relação k entre eles, suplementado pela retenção limitada do trade texit. Para simplificar, podemos dizer que o trade com saída no stop-loss/take-profit tem uma distribuição discreta, enquanto a operação com saída no tempo definido tem uma distribuição abrupta (contínua). A distribuição comum será uma mistura das mesmas. Naturalmente, isto complica os raciocínios a seguir. Levantamos uma hipótese simplificadora: vamos supor que texit é grande o suficiente para considerar γc como pequeno. Assumimos que P(x)=Pd(x).

A saída do trade com trailing-stop fixo fará as vezes de γd=0. Também é possível o caso γd≠0 e γс≠0. Por exemplo, essa seria a combinação de ambos os exemplos acima. Neste caso, no período inicial do trade, o stop-loss é fixo, mas, após executada certa condição, ele começa a se mover como um trailing-stop.

Concretizamos nossa teoria de risco para ambos os exemplos discutidos acima. Não será considerada a versão combinada. Abaixo são apresentados scripts para calcular o valor ropt do risco ideal, para cada caso de alocação da rentabilidade. Mas, às vezes, estamos interessados ​​em outras tarefas. Por exemplo, definido o risco, precisamos calcular δ, isto é, o nível de confiança correspondente (ou o valor máximo disponível da rentabilidade média G0, como uma variante). Neste caso, será necessário quer alterar o script quer executar usando diferentes dados de entrada até encontrar o valor desejado para o risco.

Stop-loss e take-profit fixos

Como já mencionado acima, a distribuição será assumida como discreta. A rentabilidade dos trades pode assumir dois valores: -1 e k, com probabilidade P-1 e Pk, respectivamente. Segundo a fórmula, a probabilidade total é P-1+Pk=1. A função de distribuição tem forma de degraus com dois saltos, nos pontos -1 e k, com valores P-1 e Pk. A expectância de nossa distribuição é M=-1*P-1+k*Pk. Introduzimos a notação θ=Pk, de onde P-1=1-θ, M=(1+k)θ-1. Assim, estamos lidando com uma família paramétrica de distribuições, definida pelos parâmetros k>0 e 0≤θ≤1. No caso de um passeio aleatório simétrico, teremos M=0, de onde θ=θ0=1/(1+k).

Suponhamos que temos ai, isto é, a rentabilidade de n trades, cada um dos quais é igual quer a -1 quer a k.

1. Calculamos a estimativa para a expectância M≈Mapr=(a1+a2+...+an)/n=(1+k)nk/n-1, onde nk é a quantidade de trades lucrativos. Se Mapr≤0, não consideramos o sistema de negociação como desfavorável. Nenhum truque aplicado ao gerenciamento de riscos pode fazer com que um sistema desfavorável se torne lucrativo. Se Mapr>0, avançamos para a seguinte etapa.
2. Temos que mostrar que os trades não são o resultado da negociação sobre um passeio aleatório simétrico. Para isto, a estimativa Mapr deve ser significativamente superior a zero (com fiabilidade δ). Tomamos, como a hipótese nula, a afirmação de que M=0. A estatística, para a verificação, será o valor S=n(Mapr+1)/(1+k)=nk, que, ao se cumprir a hipótese nula, tem uma distribuição binomial padrão B(n,θ0). Denotamos sua função de distribuição por P(x). Para aceitar a hipótese alternativa, temos que verificar P(S)>P(nθ0)+δ/2. Se isto for atendido, avançamos para a seguinte etapa. Caso contrário, rejeitamos o sistema de negociação.
3. Verificamos que seja atendida a condição necessária para o valor - escolhido por nos - de rentabilidade média mínima G0. Para fazer isso, G0 não deve ser superior ao quantil δ qδ da distribuição da variável aleatória Λ, introduzida por nos na primeira parte (rentabilidade aritmética média). O valor de Λ coincide com Mapr. Ele é expresso por S. Agora, consideramos o valor de S como uma distribuição binomial com parâmetros n e θapr=nk/n. Se a condição for atendida, passamos para a próxima etapa. Caso contrário, definimos o mínimo de trades n=nmin necessário para ela ser atendida (aumentamos gradualmente n, quando θapr é fixo, até o valor em que a desigualdade exigida é cumprida).
4. Pelo método de Monte Carlo, obtemos a distribuição empírica ρopt. Para fazer isto, modelamos um grande número de conjuntos, de acordo com n rendimentos de trades, para cada um deles. Cada rentabilidade com probabilidade Pk é igual a k, enquanto com probabilidade 1-Pk é igual a -1. Para cada conjunto, definimos o valor ropt,i pelo método examinado na introdução da primeira parte. Seu conjunto define a distribuição empírica da variável aleatória ρopt. Para avaliação do risco ropt, utilizamos o quantil δ amostral desta distribuição.

#include <Math\Stat\Binomial.mqh>
#property script_show_inputs
input uint na=50;        // número de trades em série
input double kt=3;       // relação take-profit/stop-loss
input double pk=0.5;     // probabilidade de lucro

#define NX 300           // número máximo de trades na série (para pesquisa do nmin)
#define NB 10000         // número de amostras geradas para o método de Monte Carlo
#define NR 1000          // número de intervalos de partição para o risco
double G0=0.15;          // menor rendimento médio
double D0=0.9;           // menor aumento mínimo
double dlt=0.05;         // nível de significância

void OnStart()
  {
   if (D0<=0||D0>=1) {Print("D0 deve ser positivo e inferior à unidade"); return;}
   double m=(1+kt)*pk-1;             // valor esperado
   if(m<=0) {Print("expectância deve ser positiva"); return;}
   double s=na*pk;                   // estatística (número médio de trades)
   double s0=na/(1+kt);              // número médio de trades lucrativos com expectância de zero
   int ner;
   double p=MathCumulativeDistributionBinomial(s,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionBinomial(s0,na,1/(1+kt),ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("expectância próxima de zero"); return;}

   double q=MathQuantileBinomial(dlt,na,pk,ner),q0=na*(G0+1)/(kt+1);
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 maior do que o quantil dlt da rentabilidade média aritmética");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileBinomial(dlt,nmin,pk,ner); q0=nmin*(G0+1)/(kt+1);
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin superior a ",NX);
      return;
     }
// método de Monte Carlo
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i) if(MathRandomNonZero()<=pk) a[i]=kt; else a[i]=-1;
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
     ArraySort(ropt);
     uint nr=(uint)(dlt*NB);
     Print("ropt = ",ropt[nr]);
  }

// a função dcalc() aceita a matriz de c1, c2, ... valores de cN e
// retorna o incremento mínimo d. Supomos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

Com os argumentos por padrão, o script calcula o seguinte valor para o risco:

• ropt = 0.011

Isso corresponde a 1,1% do risco, em cada trade, a partir do capital alocado para o sistema.

Trailing-stop fixo

Assumimos que estamos lidando com uma operação do tipo buy (as alterações necessárias para o tipo sell serão óbvias). Denotamos por Δp=penter-pstop a diferença entre o preço de entrada e o stop-loss inicial. O trade será fechado, após o preço atingir o valor pmax-Δp, onde pmax é o preço máximo desde a entrada na transação. Quando a série de preços é modelada por um passeio aleatório, com tempo contínuo e deslocamento linear, a distribuição da rentabilidade pode ser encontrada explicitamente. Isto será a distribuição exponencial deslocada para a esquerda uma unidade. Mais precisamente, a função de distribuição é definida pela fórmula P(x)=1-exp(-θ(x+1)), se x≥-1 e P(x)=0, se x<-1. Quando o deslocamento é positivo (tendência de alta), para o parâmetro θ, é cumprida a desigualdade 0<θ<1, por outro lado, se o deslocamento é negativo (tendência de baixa): θ>1 e o movimento lateral é zero (fase de correção): θ=1. A expectância é dada pela fórmula M=1/θ-1.

Como assumimos que os preços reais são próximos do passeio aleatório, a distribuição de rentabilidade de trades na série também será tratada como se viesse com um certo valor do parâmetro θ. Obtemos uma família monoparamétrica de distribuições contínuas. O valor específico do parâmetro θ, na presença de uma tendência, depende da relação entre a força desta tendência e o trailing-stop. Calculamos esse valor usando os métodos da estatística paramétrica para a distribuição exponencial com base no histórico de transações disponíveis (neste caso, usamos o método da máxima verossimilhança). Além disso, para futuros cálculos, é importante que a soma (e a média aritmética) do número finito de tais valores com o mesmo parâmetro tenha a bem estudada distribuição gama.

Suponhamos que temos ai - rentabilidade de n trades, para cada um dos quais é satisfeito ai>-1 (para isso, ignoramos a derrapagem). Como no capítulo anterior, propomos um plano de ação.

1. Calculamos o valor para a expectância M≈Mapr=(a1+a2+...+an)/n. Se Mapr≤0, consideramos o sistema de negociação como desfavorável. Se Mapr>0, avançamos para a seguinte etapa.
2. Tentamos refutar a hipótese M=0. A estatística, para a verificação, será a magnitude S=Mapr+1, que tem (quando satisfeita a hipótese nula M=0) distribuição gama Γ(n,1/n). Denotamos sua distribuição por P(x), então, para adotar a hipótese alternativa, a desigualdade P(S)≥P(1)+δ/2 deve ser correta. Se for possível refutar a hipótese nula, avançamos para a próxima etapa, caso contrário, rejeitamos o sistema.
3. Verificamos a condição necessária para G0. Primeiro, precisamos obter o valor do parâmetro θ=θapr. Usando o método de máxima verossimilhança, obtemos θapr=1/(1+Mapr). O valor de Λ será distribuído sobre a distribuição gama Γ(n,θapr/n) deslocada uma unidade para esquerda. A condição necessária é satisfeita, se o quantil δ desta distribuição gama não for inferior a G0+1. Se ele for satisfeito, avançamos. Caso contrário, podemos determinar o número mínimo exigido de trades para o cumprimento desta condição. Para fazer isto, aumentamos passo a passo o valor de n e tomamos, como nmin, o valor em que a desigualdade requerida é satisfeita.

4. É o mesmo que no capítulo anterior do artigo. A modificação só tem a ver com a distribuição utilizada para a geração aleatória de rentabilidade. Agora usamos a distribuição exponencial com o parâmetro θ=θapr, deslocado uma unidade para a esquerda. Na biblioteca estatística MQL5, usa-se uma forma ligeiramente diferente de parametrização para a distribuição exponencial - parâmetro μ (expectância), expresso por θ ou através de M sob a forma de μ=1/θ ou μ=M+1.

#include <Math\Stat\Gamma.mqh>
#include <Math\Stat\Exponential.mqh>
#property script_show_inputs
input uint na=50;           // número de trades em série
input double tht=0.65;      // parâmetro de distribuição exponencial 0<tht<1

#define NX 300              // número máximo de trades em série (para pesquisa do nmin)
#define NB 10000            // número de amostras geradas para o método de Monte Carlo
#define NR 1000             // número de intervalos de partição para o risco
double G0=0.15;             // menor rendimento médio
double D0=0.9;              // menor incremento mínimo
double dlt=0.05;            // nível de significância

void OnStart()
  {
   if(D0<=0 || D0>=1) {Print("D0 deve ser positivo e menor que a unidade"); return;}
   double m=1/tht-1;         // valor esperado
   if(m<=0) {Print("expectância deve ser positiva"); return;}

   int ner;   
   double p=MathCumulativeDistributionGamma(m+1,na,1.0/na,ner);
   if(!MathIsValidNumber(p)) {Print("MathIsValidNumber(p) error ",ner); return;}
   double p0=MathCumulativeDistributionGamma(1,na,1.0/na,ner);
   if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;}
   if(p<=p0+dlt/2) {Print("valor esperado perto de zero"); return;}

   double q=MathQuantileGamma(dlt,na,1/tht/na,ner),q0=G0+1;
   if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
   if(q0>q)
     {
      Print("G0 maior do que o quantil dlt da média aritmética da rentabilidade");
      uint nmin=na+1;
      for(;nmin<=NX;++nmin)
        {
         q=MathQuantileGamma(dlt,nmin,1/tht/nmin,ner); q0=G0+1;
         if(!MathIsValidNumber(q)) {Print("MathIsValidNumber(q) error ",ner); return;}
         if(q0<=q) break;
        }
      if(nmin<=NX) Print("nmin = ",nmin);
      else Print("nmin maior do que ",NX);
      return;
     }    

// método de Monte Carlo
   MathSrand(GetTickCount());
   double a[],c[],ropt[NB],A0,A,r,g,d,cn1,cn2,stp=1.0/NR;
   uint ir;
   ArrayResize(a,na);
   ArrayResize(c,na);
   for(uint ib=0; ib<NB;++ib)
     {
      for(uint i=0; i<na;++i)
        {
         a[i]=MathRandomExponential(m+1,ner);
         if(!MathIsValidNumber(a[i])) {Print("Error MathRandomExponential()",ner); return;}
         a[i]-=1.0;
        }
      A=MathMean(a); A0=a[ArrayMinimum(a)];
      if(A<G0) {ropt[ib]=0; continue;}
      if(A0>0) {ropt[ib]=1-stp; continue;}
      cn1=1;
      for(ir=1;ir<NR;++ir)
        {
         r=ir*stp;
         cn2=1; for(uint i=0; i<na;++i) cn2*=1+r*a[i];
         if(cn2<cn1) {ropt[ib]=r-stp; break;}
         cn1=cn2;
         g=(MathPow(cn2,1.0/na)-1)/r;
         if(g<G0) {ropt[ib]=r-stp; break;}
         c[0]=1+r*a[0]; for(uint i=1; i<na;++i) c[i]=c[i-1]*(1+r*a[i]);
         d=dcalc(c);
         if(d<D0) {ropt[ib]=r-stp; break;}
        }
     }
   ArraySort(ropt);
   uint nr=(uint)(dlt*NB);
   Print("ropt = ",ropt[nr]);
  }
// a função dcalc() aceita a matriz de c1, c2, ... valores de cN e
// retorna o incremento mínimo d. Supomos que c0==1
double dcalc(double &c[])
  {
   if(c[0]<=0) return 0;
   double d=c[0], mx=c[0], mn=c[0];
   for(uint i=1; i<na;++i)
     {
      if(c[i]<=0) return 0;
      if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);}
      else {if(c[i]>mx) mx=mn=c[i];}
     }
   return d;
  }
//+------------------------------------------------------------------+

Quando os argumentos são definidos por padrão, obtemos o seguinte valor do risco:

• ropt = 0.015

Isso corresponde a 1,5% do risco, em cada trade, do capital alocado para o sistema.

A sequência a partir de trinta trades, considerada como exemplo na seção anterior, foi obtida precisamente para um sistema com entrada no trailing-stop. Portanto, nosso método pode ser aplicado a ele. Como o método discutido da última vez, ele indica que a sequência não é adequada para o negociar sob as condições definidas (n, δ, G0, D0). Este resultado não mudará, mesmo se removemos a derrapagem, somando a todos os ai um pequeno número positivo tal que para todos i=1,...,n seja cumprida a condição ai>-1.

Nota: O fato de, com os argumentos definidos por padrão, o script retornar o erro número 4 significa que o terminal não passou as atualizações necessárias. Neste caso, parte do script (linhas 21-42) deve ser comentado. Nesta parte, encontram-se os cálculos relacionados com a distribuição gama. Para eles, pode-se usar script em linguagem R, abaixo.

na=50; tht=0.65; dlt=0.05; G0=0.15; nx=300
m=1/tht-1; l1=l2=l3=FALSE
l1 = m > 0
if (l1) l2 = pgamma(m+1,na,scale = 1/na) > pgamma(1,na,scale = 1/na)+dlt/2
if (l2) l3 = G0+1 <= qgamma(dlt,na,scale = 1/tht/na)

if(!l1) cat("m must be greater 0\n")

if(l1 & l3) cat("G0 and na are ok\n") else cat("na too small or G0 too big\n")

if(l1 & l2 & !l3)
{for (nmin in (na+1):(nx+1)) {if(G0+1 <= qgamma(dlt,nmin,scale = 1/tht/nmin)) break()}
 if (nmin<=nx) {cat("nmin =",nmin)} else {cat("nmin >",nx)}
}

O que vem agora?

Obviamente, os métodos acima não podem ser considerados completos e definitivos. Para simplificar o estudo, assumimos a priori que as operações são independentes e identicamente distribuídas. Mas isso requer uma pesquisa mais profunda e pode não dar certo. Pode ser útil que a alocação da rentabilidade pertença ou seja próxima de uma família paramétrica específica. Adicionalmente, essa pertinência/filiação também pode precisar de mais estudo.

Nós nos contentamos com valores pontuais para os parâmetros das distribuições, e não procuramos intervalos de confiança para eles. Porém, após serem definidos, estará em causa a estabilidade da rentabilidade do sistema, durante a oscilação desses parâmetros.

O fato de haver variedade de métodos não significa que eles devam ser usados todos de uma vez. É melhor conhecê-los e saber usá-los, se necessário, do que ser enganado por acaso.

No restante deste artigo, denotamos brevemente outras possíveis direções para a aplicação da teoria das probabilidades.

Estatísticas e gaps

Um gap é um salto grande entre os preços de fechamento e abertura de duas barras consecutivas. Adicionalmente, deve-se verificar que entre essas barras existe uma brecha significativa. Acredita-se que "os gaps são sempre fechados". O fechamento do gap indica que, um tempo após a ruptura, o preço volta para o preço de fechamento da barra, do rompimento anterior. Às vezes, muitos tentam construir seus sistemas de negociação com base nesse padrão. É possível?

Baseados na teoria sobre o passeio aleatório simétrico na linha, nós sabemos que qualquer valor do preço é atingido, após um período suficientemente longo, com uma probabilidade próxima de 1. Isso é, sob essas condições, é quase certo que o "gap sempre é fechado". Mas, como sabemos, quando o passeio aleatório é simétrico, não há hipótese de nenhum sistema rentável. Será que isto quer dizer que o sistema baseado en gaps não tem chance de existir?

Não necessariamente. A maneira como são fechados os gaps também é importante. Quer dizer, também é relevante a forma como se fecha uma população de gaps. E é então que se podem examinar as distribuições de probabilidade empíricas das variáveis ​​aleatórias que lhes estão associadas. Podem se manifestar a diferença entre os preços reais e o modelo do passeio aleatório simétrico. As diferenças podem ser de muitos tipos. Pode se dar que o movimento na direção da brecha seja curto, ou que o tempo antes do fechamento seja inferior ao passeio aleatório, e assim por diante. O que importa é que os métodos da teoria da probabilidade e estatística podem detectar a existência e a relevância destes desvios. Averiguando essas variações, é possível construir um sistema de negociação baseado neles. Adicionalmente, pode-se tentar experimentar a teoria que classifica a disparidade entre os preços.

Consideremos a opção mais simples para encontrar o desvio do passeio aleatório. Ela será um valor que indica o quão forte o preço se move na direção da brecha até o fechamento do gap. Pode-se obter a distribuição empírica deste valor, com base no histórico, e compará-lo com o teórico. Para comparar estas duas distribuições, pode ser usada qualquer adequação de aderência.

Consideremos o modelo de passeio aleatório simétrico com tempo discreto. Suponhamos que tem poucos gaps (como nos preços reais), enquanto, nos trechos entre eles, o passeio se aproxima de ser aleatório com tempo contínuo (processo de Wiener). Introduzimos a notação: g - magnitude do gap, m - movimento máximo na direção do gap antes de ser fechado. Neste caso, a variável aleatória x=m/g terá uma função distribuição próxima da função P(x) - de modo que P(x)=1-1/x, se x≥1 e P(x)=0, se x<1. Imagem para ilustrar os valores que inserimos:

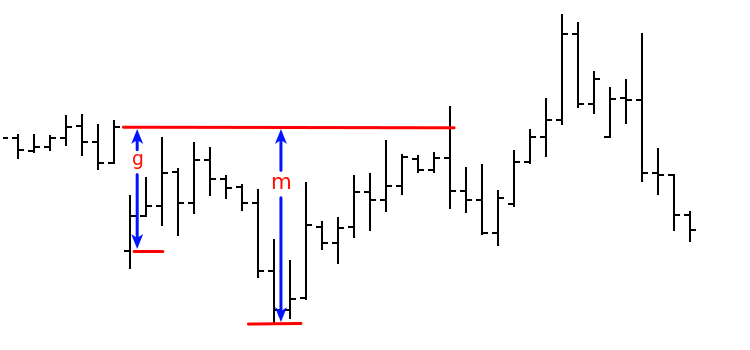
A questão que estamos examinando requer um estudo mais detalhado. Por isso, limitar-nos-emos às seguintes observações:

• O problema na pesquisa dos gaps é a sua raridade. Isto se torna mais evidente, quando se tentam estudar as distribuições relacionadas com eles, dependendo dos parâmetros (no capítulo seguinte, isso será descrito em mais detalhes).
• Para verificar a teoria da classificação de gaps (por exemplo, aqui), será necessário construir um modelo mais complexo que leve em conta não só a disparidade de preços entre a brecha e o fechamento, mas também o anterior e o seguinte. Isto aumentará o número de variáveis ​​aleatórias a serem examinadas. O que, por sua vez, pode criar problemas, devido à pequena quantidade de dados acima mencionada.
  

Aprendizado estatístico de máquina

Estudemos esquematicamente a estrutura do sistema de negociação. Para cada trade, é conhecido o conjunto de parâmetros h, cujos valores permitem definir o volume de transações e o algoritmo (não o preço!) de saída. O valor h deve ser conhecido ao certo no momento da entrada. Podem existir alguns valores de indicadores técnicos, etc. Em termos de aprendizado de máquina, h é um conjunto de atributos.

Por uma questão de precaução, faremos o seguinte esclarecimento. Normalmente, quando as pessoas falam sobre sistemas de negociação, elas não se referem a um sistema específico, mas sim à sua família paramétrica. O objetivo do teste e a optimização consiste em selecionar um sistema particular desta família, ao definir e fixar um valor específico. Para não complicar a exposição (para não confundir h com parâmetros que especificam a escolha do sistema a partir da família), neste capítulo estamos falando de um sistema particular, e não de sua família. No próximo capítulo, falaremos brevemente sobre os problemas da otimização.

Obtemos um algoritmo de entrada/saída fixo no/do trade, ao fixar um valor específico de h. Isso nos dá uma distribuição de probabilidade fixa. Note-se que o mesmo h pode ter diferente rentabilidade. Uma alocação de rentabilidade fixa, ao invés de seu valor específico.

Assim, surge o problema de recuperação da dependência da lei de alocação da rentabilidade a partir dos atributos h. Os dados de origem são o histórico de trades como um conjunto de pares a partir dos valores dos parâmetros e sua respectiva rentabilidade (hi,ai). Estas tarefas são resolvidas por meio do método de aprendizado estatístico de máquina. Adicionalmente, não há diferença fundamental entre estes métodos e os utilizados no aprendizado de máquina para resolução de problemas de recuperação de dependência determinísticas (não aleatórias).

Definimos com um pouco mais de exatidão nosso problema, assumindo que a alocação da rentabilidade pertencente a uma certa família. Definido o conjunto de pares (hi,ai). Alocação de rentabilidade ai pertence à família paramétrica de distribuições dependente do parâmetro θ. Precisamos restaurar a dependência θ (h). Esta dependência não é procurada entre as funções arbitrárias, uma vez que isso não é suficiente para estes dados de origem. Normalmente, ela é procurada entre famílias paramétricas de funções: θ(h)=θ(h,β), onde o parâmetro β é definido pelo conjunto de pares (hi,ai). Uma ampla seleção de famílias de funções determina a enorme variedade disponível de técnicas de aprendizado de máquina. Funções essas que visam procurar dependências, condições ótimas (no que diz respeito a parâmetros) e métodos para buscar valores ideais.

A partir desta variedade, precisamos escolher especialmente aqueles métodos que são significativos do ponto de vista do trader (por exemplo, levam ao aumento no lucro ou à diminuição do rebaixamento). Isso é especialmente importante, ao escolher as condições de otimização para selecionar o parâmetro β. Caso sejam alteradas estas condições, a dependência θ(h,β) obtida pode variar muito.

Vamos supor que, para uma dada família paramétrica das alocações da rentabilidade ai, nós resolvemos o problema da avaliação de risco como feito com os dois casos considerados acima. Assim, como construímos a dependência θ=θ(h) e sabemos como, para cada θ definido, selecionar o valor de risco ropt, conhecemos a dependência ropt=ropt(h). A construção de nosso sistema pode ser considerado concluído.

Estatística e otimização de sistemas de negociação.

Consideremos a seguinte versão simples de otimização. Usando nosso sistema, realizamos N passagens em n trades. Entre elas, escolhemos algumas das melhores εN (com maior rendimento médio), onde 0<ε<<1. De entre estas passagens, usando mopt, encontramos a menor média, assim, saberemos quão bom é o sistema ideal.

Agora, consideraremos um sistema cujos resultados de otimização devem ser tratados com cautela. Embora o exemplo seja artificial, permite ver o problema em si. Vejamos um sistema cuja expectância matemática de rentabilidade e dependência aleatória de parâmetros são nulas.

Este sistema entrará, numa direção aleatória, em pontos fixos no tempo. Um gerador de números aleatórios com igual probabilidade ajudará a selecionar a direção. O valor inicial será uma função de parâmetros, valor esse utilizado para a inicialização do gerador, antes de cada passagem do teste. Assim, para cada conjunto de parâmetros, vamos sempre obter a mesma sequência de operações, mas ao alterar esses parâmetros, estaremos mudando a sequência de forma completamente aleatória - imprevisível. A saída do trade ocorre de acordo com o stop-loss/take-profit fixo com relação constante k. Além disso, assumimos que não existe uma tendência, no trecho do teste.

É óbvio que, como não existe uma tendência, a expectância de rentabilidade deste sistema será próxima de zero (um pouco negativa, se houver spread). Denotamos por n o número de trades em série. A média aritmética da rentabilidade, na série n trades m, será a variável aleatória. Ela é expressa pela variável aleatória nk, isto é, a quantidade de trades lucrativos em série: m=(1+k)nk/n-1. O valor nk tem uma distribuição binomial com parâmetros 1/(1+k) e n.

Quando N é grande o suficiente, o valor mopt estará próximo do quantil (1-ε) de distribuição da magnitude m. Mostramos que, apesar da óbvia inutilidade deste "sistema de negociação" (devido à expectância nula), o valor mopt é suficientemente grande. Definimos: k=3, n=50, ε=0.1 e obtemos mopt=2.52.

É evidente que, ao realizar testes usando sistemas reais bem ponderados, tudo é organizado de forma diferente e muito mais complicado. No entanto, neste caso, podemos e devemos tentar entender se a vantagem de um sistema otimizado é uma coisa do acaso.

Arquivos anexados

№	Nome	Tipo	Descrição
1	bn.mq5	script	cálculo do risco para saída com stop-loss e take-profit fixos
2	exp.mq5	script	cálculo do risco para saída com trailing-stop fixo