
Aplicação do método de Monte Carlo para otimizar estratégias de negociação
Conteúdo
- Teoria geral
- Modelo probabilístico do EA
- Aplicação da teoria
- Robustez de lucro contra a dispersão aleatória
- Robustez do lucro contra o rebaixamento
- Robustez da distribuição de lucros em relação ao preço não estacionário
- Conclusão
- Arquivos anexados
Teoria geral
A ideia para além do Método de Monte Carlo pode ser descrita em termos de analogia — um dos métodos de conhecimento científico. Outros exemplos de analogia são a analogia óptico-mecânica de Hamilton ou organismos semelhantes na biologia.
Se nós temos dois objetos que podem ser descritos pela mesma teoria, então o conhecimento obtido do estudo de um deles é aplicável a outro. Este método é muito útil quando um objeto é muito mais fácil de estudar do que o outro. O objeto mais acessível é considerado um modelo de outro. O método em si é chamado de modelagem. Dependendo do contexto, um modelo é um dos objetos ou uma teoria comum a ambos.
Às vezes, os pesquisadores entendem mal os resultados da modelagem. Quando nós consideramos alguns exemplos explícitos, como a extração de uma cópia reduzida de um avião em um túnel de vento, tudo parece óbvio. No entanto, quando os objetos não estão relacionados e não se assemelham à primeira vista, as conclusões às vezes parecem ser algum tipo de truque ou servem como base para generalizações irracionais mas de longo alcance. A teoria comum para os objetos descreve aproximadamente apenas alguns dos seus aspectos. Quanto menor a precisão necessária da descrição dos objetos, maior o conjunto de objetos que aderem a uma teoria. Por exemplo, a analogia óptico-mecânica de Hamilton é exatamente satisfeita apenas quando o comprimento de uma onda de luz tende a zero. Na realidade, essa analogia é aproximadamente justificada apenas por um comprimento pequeno, mas sempre finito. Como qualquer modelo teórico deve ser simples o suficiente para servir de base para cálculos e conclusões, ele é sempre simplista demais.
Vamos agora esclarecer o conceito do método de Monte Carlo. Esta é uma abordagem para modelar objetos cuja teoria tem uma natureza probabilística (estocástica). O modelo é um programa de computador com um algoritmo construído de acordo com essa teoria. Ele usa geradores de números pseudoaleatórios para simular as variáveis aleatórias necessárias (processos aleatórios) com as distribuições necessárias.
Vale a pena enfatizar (embora não importe para nós aqui) que a natureza de um objeto estudado possa ser tanto probabilística quanto determinística. A presença de uma teoria com natureza probabilística é importante para nós aqui. Por exemplo, o método de Monte Carlo é usado para calcular aproximações de integrais ordinárias. Isso é possível, porque qualquer integral pode ser considerada como uma expectativa matemática de uma variável aleatória.
O primeiro exemplo de uso do método de Monte Carlo, geralmente se considera como uma solução do problema da Agulha de Buffon em que o número de Pi é determinado pelo lançamento aleatório de uma agulha em uma mesa. O nome do método apareceu muito depois, em meados do século XX. Afinal, jogos de azar — por exemplo, uma roleta — são geradores de números aleatórios. Além disso, uma referência deliberada ao jogo sugere as origens da teoria da probabilidade, que começou com os cálculos relacionados aos jogos de dados e cartas.
O algoritmo do programa de modelagem é simples, que é uma das razões para a prevalência do método. O algoritmo apresenta múltiplas variantes geradas aleatoriamente (amostras) de um estado do objeto estudado com a distribuição correspondente à teoria. É calculado um conjunto necessário de características para cada uma delas. Como resultado, nós recebemos uma amostra grande. Embora nós tenhamos apenas um conjunto de características para o objeto estudado, o método de Monte Carlo nos permite obtê-los em grande número e construir suas funções de distribuição, o que nos dá mais dados.
A estrutura geral da modelagem de Monte Carlo descrita acima parece simples. No entanto, ela produz variações múltiplas e algumas vezes complexas ao tentar implementá-la. Mesmo se nós limitarmos nossa aplicação às finanças, nós ainda podemos ver o quão extenso é, por exemplo, este livro. Nós vamos tentar aplicar o método de Monte Carlo para estudar a estabilidade dos Expert Advisors. Para conseguir isso, nós precisamos de um modelo probabilístico descrevendo seu trabalho.
Modelo probabilístico do EA
Antes de iniciar uma negociação real usando um EA, nós geralmente testamos e otimizamos o histórico de cotações. Mas por que nós acreditamos que os resultados de negociação no passado afetam seus resultados no futuro? Naturalmente, nós não esperamos que todas as transações no futuro formem a mesma sequência do passado. Embora nós ainda tenhamos uma suposição sobre sua "similaridade". Vamos formalizar essa ideia intuitiva de "similaridade" usando a teoria da probabilidade. De acordo com essa formalização, nós acreditamos que o resultado de cada negociação é uma certa realização de alguma variável aleatória. A "semelhança" das negociações neste caso é determinada pela proximidade das funções de distribuição correspondentes. Nessa formalização, os negócios anteriores ajudam a esclarecer o tipo de distribuição para os futuros e avaliar seus possíveis resultados.
A formalização probabilística nos permite construir várias teorias. Vamos considerar o mais simples e o mais comumente usado. Nesta teoria, o resultado de cada operação é definido sem ambiguidade por um lucro relativo k=C1/C0, onde C0 e C1 são volumes de capital antes e depois da operação. Mais adiante, o lucro relativo da negociação será simplesmente chamada de lucro, enquanto que a diferença C1-C0 é o lucro absoluto da negociação. Suponha que os lucros de todas as negociações (tanto no passado quanto no futuro) sejam independentes entre si e incluam valores aleatórios distribuídos uniformemente. Sua distribuição é determinada pela função de distribuição F(x). Assim, nossa tarefa é definir o tipo dessa função usando os valores das negociações lucrativas passadas. Este é o problema padrão da estatística matemática — restauração da função de distribuição pela amostra. Qualquer uma de suas soluções sempre fornece respostas aproximadas. Vamos dar uma olhada em alguns desses métodos.
-
A função de distribuição empírica é usado como uma aproximação.
-
Nós tomamos uma distribuição discreta simples, na qual um lucro da negociação leva a um dos dois valores. Isso é uma perda média com uma probabilidade de perda ou um lucro médio com uma probabilidade de lucro.
- Nós construímos não uma aproximação discreta, mas contínua (tendo uma densidade) para a função de distribuição. Para conseguir isso, nós usamos os métodos como a estimativa de densidade kernel.
Mais adiante, nós usaremos a primeira opção - ela é a mais simples e universal. Os traders não estão muito interessados em conhecer a função em si. No entanto, é importante saber quais valores indicam um possível lucro da operação do EA, um nível de risco de seu uso ou a sustentabilidade dos lucros. Estes valores podem ser obtidos conhecendo a função de distribuição.
Vamos especificar o algoritmo de modelagem no nosso caso. O objeto de nosso interesse é um possível resultado da operação do EA no futuro. Ele é inequivocamente definido pela sequência de negociações. Cada negociação é definida pelo valor do lucro. Os lucros são distribuídos de acordo com a distribuição empírica descrita acima. Nós devemos gerar um grande número dessas sequências e calcular as características necessárias para cada uma delas. A geração de cada sequência é simples. Vamos definir a sequência dos lucros de negociação obtidos no histórico como k1, k2, ..., kn. Gerando as sequências com o comprimento de N, nós vamos aleatoriamente (com a probabilidade igual a 1/n) selecionar um dos ki (amostra com retorno) N vezes. Costuma-se supor que N=n, desde que em um N grande, a precisão de aproximação F(x) pela distribuição empírica se deteriora. Esta versão do método de Monte Carlo é às vezes chamada de método de bootstrap.
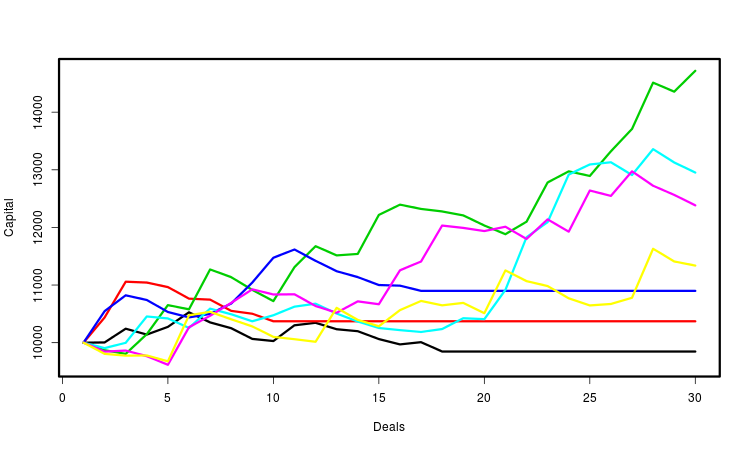
Vamos explicar tudo acima pelo gráfico. Ele mostra várias curvas de capital. Cada um deles é determinado pela sequência gerada de negociações. Eu marquei as curvas com cores diferentes para uma maior conveniência. Na verdade, o número deles é muito maior — várias dezenas de milhares. Para cada um deles, nós calculamos os parâmetros necessários e fazemos conclusões estatísticas com base em sua totalidade. Obviamente, a mais importante dessas características é o lucro final.
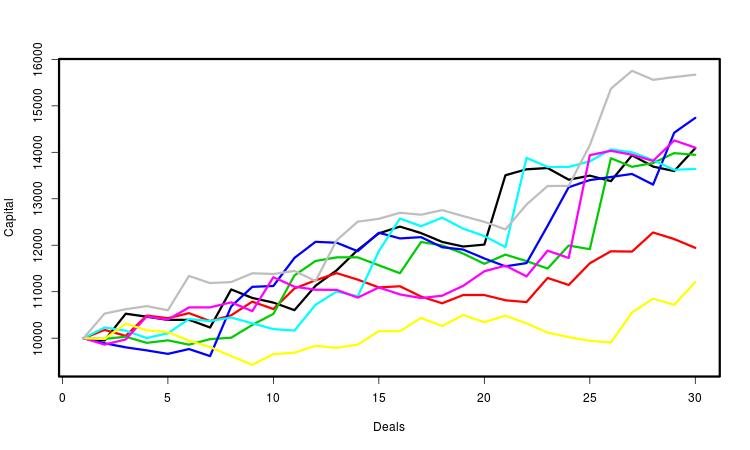
Outras abordagens para a formalização probabilística e a posterior modelagem operacional do EA também são possíveis. Por exemplo, em vez de sequências de negociações, nós podemos simular sequências de preços e estudar os lucros agregados que o EA obteve sobre eles. O princípio de gerar as séries de preços pode ser selecionada dependendo de uma tarefa que você queira resolver. No entanto, esse método requer muito mais recursos de computação. Além disso, a MetaTrader atualmente não fornece formas regulares de usá-lo com um EA aleatório.
Aplicação da teoria
Nossa tarefa é construir critérios de otimização específicos. Cada um deles corresponde a um determinado objetivo. O principal deles é o lucro final obtido como resultado de toda a série de negociações. A otimização por lucro é incorporada ao testador. Como nós estamos interessados no lucro no futuro, nós devemos de alguma forma avaliar o possível grau de desvio dos lucros no presente. Quanto menor o desvio, mais estável é o lucro do sistema. Vamos considerar três abordagens.
- Tendo obtido uma grande amostra de possíveis valores de lucro através do método de Monte Carlo, nós podemos estudar sua distribuição e as quantidades associadas a ela. O valor médio deste lucro é muito importante. A variância também é importante — quanto menor ela for, mais estável é o funcionamento do EA e menor a incerteza em seus resultados futuros. Nosso critério será igual à relação entre o lucro médio e sua dispersão média. Ele é semelhante ao índice de Sharpe.
- Outra característica importante é a redução dos lucros em uma série de negociações. Muito rebaixamento pode levar à perda do saldo, mesmo que o EA seja lucrativo. Por esse motivo, o rebaixamento geralmente é restrito. É útil saber como isso afeta o possível lucro. O critério é definido simplesmente como o lucro médio, mas com a condição de que o término da negociação seja modelado quando o nível permitido de rebaixamento for excedido.
-
Nós construiremos um critério que mede a estabilidade do lucro em termos da persistência da distribuição dos lucros de negociação. Do ponto de vista da teoria da probabilidade, isso significa que a estacionariedade dos lucros de negociação, que, a princípio, é possível no caso do aumento do preços não estacionários. Para fazer isso, nós usaremos uma ideia semelhante ao forward testing. Vamos dividir a amostra inicial das negociações em subamostras iniciais e finais. Para verificar sua homogeneidade, nós podemos aplicar um teste estatístico. Com base neste teste, nós criaremos um critério de otimização.
#include <mcarlo.mqh> Adicione o código para obter e usar nosso parâmetro de otimização no final do EA:
double OnTester() { return optpr(); // parâmetro de otimização }
Os cálculos básicos são feitos nas funções localizadas no arquivo de cabeçalho "mcarlo.mqh". Nós colocamos ele na pasta "MQL5/Include/". A principal função deste arquivo é a optpr(). Quando as condições necessárias são atendidas, ele calcula a variante do critério de otimização especificada pelo parâmetro noptpr, caso contrário, retorna ele zero.
double optpr() { if(noptpr<1||noptpr>NOPTPRMAX) return 0.0; double k[]; if(!setks(k)) return 0.0; if(ArraySize(k)<NDEALSMIN) return 0.0; MathSrand(GetTickCount()); switch(noptpr) { case 1: return mean_sd(k); case 2: return med_intq(k); case 3: return rmnd_abs(k); case 4: return rmnd_rel(k); case 5: return frw_wmw(k); case 6: return frw_wmw_prf(k); } return 0.0; }
A função setks() calcula o array de lucro das negociações com base no histórico de negociação.
bool setks(double &k[]) { if(!HistorySelect(0,TimeCurrent())) return false; uint nhd=HistoryDealsTotal(); int nk=0; ulong hdticket; double capital=TesterStatistics(STAT_INITIAL_DEPOSIT); long hdtype; double hdcommission,hdswap,hdprofit,hdprofit_full; for(uint n=0;n<nhd;++n) { hdticket=HistoryDealGetTicket(n); if(hdticket==0) continue; if(!HistoryDealGetInteger(hdticket,DEAL_TYPE,hdtype)) return false; if(hdtype!=DEAL_TYPE_BUY && hdtype!=DEAL_TYPE_SELL) continue; hdcommission=HistoryDealGetDouble(hdticket,DEAL_COMMISSION); hdswap=HistoryDealGetDouble(hdticket,DEAL_SWAP); hdprofit=HistoryDealGetDouble(hdticket,DEAL_PROFIT); if(hdcommission==0.0 && hdswap==0.0 && hdprofit==0.0) continue; ++nk; ArrayResize(k,nk,NADD); hdprofit_full=hdcommission+hdswap+hdprofit; k[nk-1]=1.0+hdprofit_full/capital; capital+=hdprofit_full; } return true; }
A função sample() gera uma sequência aleatória b[] da sequência original a[].
void sample(double &a[],double &b[]) { int ner; double dnc; int na=ArraySize(a); for(int i=0; i<na;++i) { dnc=MathRandomUniform(0,na,ner); if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc==na) nc=na-1; b[i]=a[nc]; } }
Em seguida, nós consideraremos em detalhes cada um dos três tipos de critérios de otimização mencionados acima. Em todos os casos, nós realizaremos a otimização no mesmo intervalo de tempo - primavera/verão de 2017 para o EURUSD. O período gráfico será sempre de 1 hora e o modo de teste é o "OHLC por 1 minuto". O algoritmo genético pelo critério de otimização personalizado sempre será usado. Como nossa tarefa é demonstrar a teoria em vez de preparar o EA para a negociação real, essa abordagem simplista parece natural.
Robustez de lucro contra a dispersão aleatória
Suponha que nós temos uma amostra dos lucros finais gerados. Nós podemos estudá-lo com a ajuda dos métodos de estatística matemática. A imagem abaixo mostra um histograma com uma mediana selecionada marcada com uma linha pontilhada.
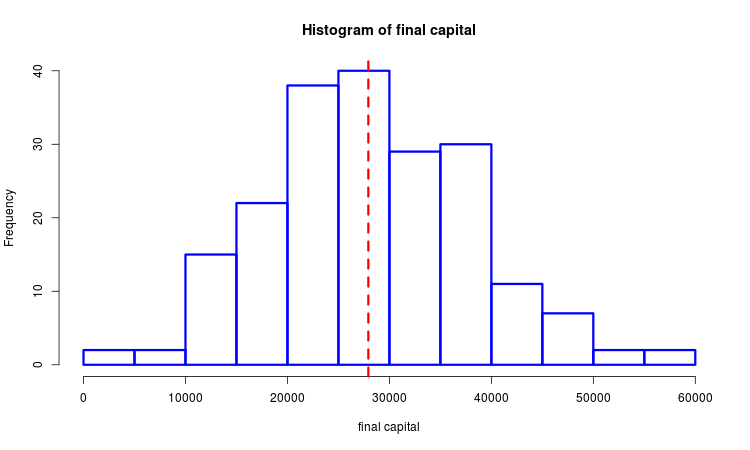
Nós construímos duas versões similares do critério de otimização. Eles são calculados nas funções mean_sd() e med_intq(). A parte comum dessas opções é que elas representam a razão entre a média e a medida de dispersão. A diferença está em como a média e a medida de dispersão são determinadas. No primeiro caso, estas são a média aritmética e o desvio padrão, enquanto que no segundo — a mediana e a amplitude interquartil. Quanto maior o lucro e menor sua dispersão, maiores os valores de ambos. Existe uma semelhança óbvia com o índice de Sharpe, embora aqui nós queremos dizer um lucro em toda a série de negociações, e não em um único negócio. A segunda variante do critério é mais resistente a picos em comparação com a primeira.
double mean_sd(double &k[]) { double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) cn[n]*=km[i]; cn[n]-=1.0; } return MathMean(cn)/MathStandardDeviation(cn); } double med_intq(double &k[]) { double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) cn[n]*=km[i]; cn[n]-=1.0; } ArraySort(cn); return cn[(int)(0.5*NSAMPLES)]/(cn[(int)(0.75*NSAMPLES)]-cn[(int)(0.25*NSAMPLES)]); }
Abaixo estão dois pares de resultados dos testes do EA otimizado por este critério. No primeiro par, há um resultado de otimização para a primeira variante e, para comparação, o resultado com o lucro máximo. Obviamente, o primeiro é preferível, pois dá uma curva de capital mais suave. O lucro final, se desejado, pode ser aumentado se aumentar o volume das negociações.
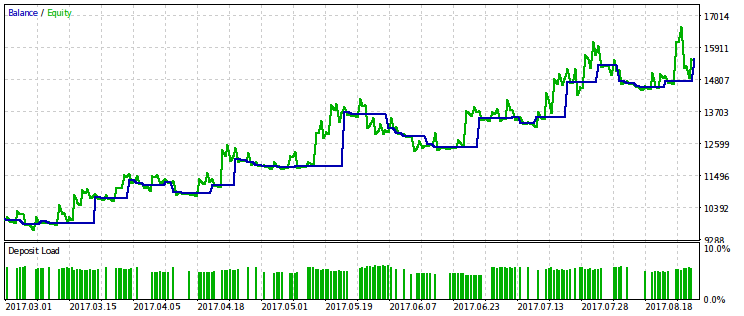
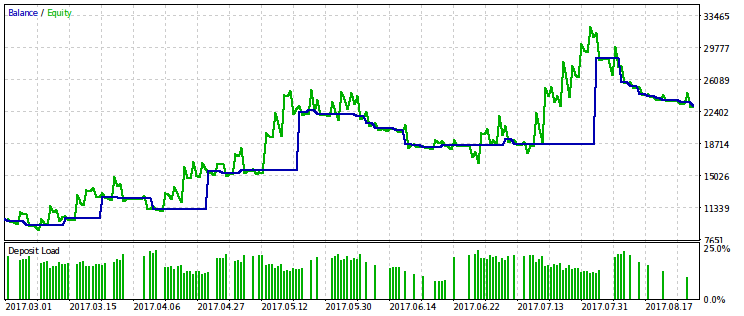
O mesmo par de resultados é fornecido para a segunda variante do critério de otimização. É possível tirar as mesmas conclusões deles.
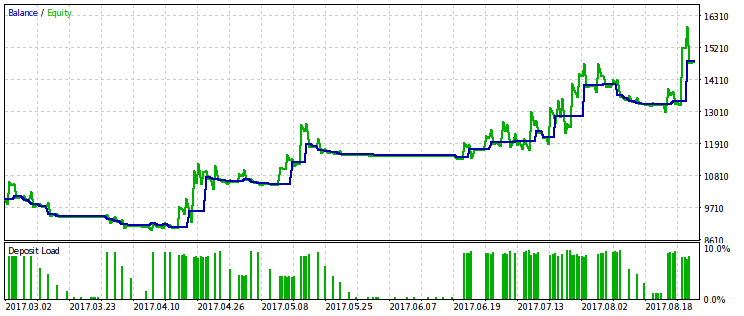
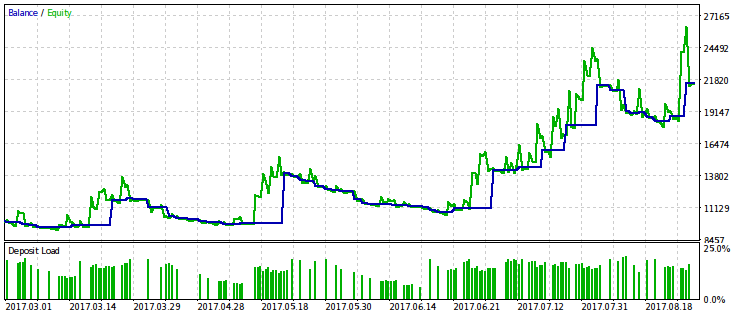
Robustez do lucro contra o rebaixamento
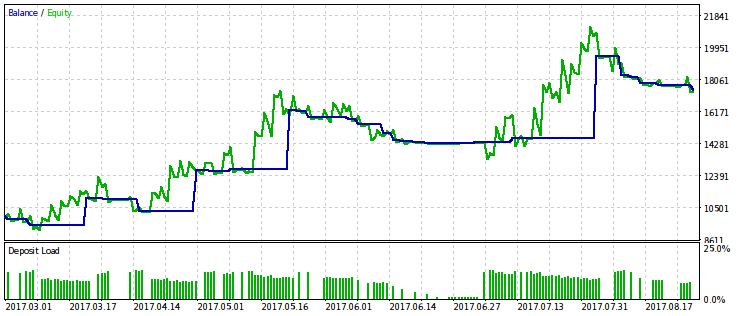
Nós monitoramos a quantidade de rebaixamento em cada sequência gerada de negociações. Se o capital remanescente após a parte inicial da série de negociação compreender uma proporção menor do que o parâmetro rmndmin, as negociações restantes são descartadas. A imagem abaixo mostra que o capital para de mudar e a seção final da linha de capital torna-se horizontal no caso de exceder o nível de rebaixamento relativo.
Nós temos duas opções de cálculo do critério — para rebaixamento absoluto e relativo. No caso do rebaixamento absoluto, a parte do capital é calculada a partir do seu valor inicial, enquanto que no caso de um rebaixamento relativo, o cálculo é feito a partir do valor máximo. As funções que calculam essas variantes de parâmetros são chamadas rmnd_abs() e rmnd_rel(), respectivamente. Em ambos os casos, o valor do critério é a média dos lucros gerados.
double rmnd_abs(double &k[]) { if (rmndmin<=0.0||rmndmin>=1.0) return 0.0; double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) { cn[n]*=km[i]; if(cn[n]<rmndmin) break; } cn[n]-=1.0; } return MathMean(cn); } double rmnd_rel(double &k[]) { if (rmndmin<=0.0||rmndmin>=1.0) return 0.0; double km[],cn[NSAMPLES],x; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); x=cn[n]=1.0; for(int i=0; i<nk;++i) { cn[n]*=km[i]; if(cn[n]>x) x=cn[n]; else if(cn[n]/x<rmndmin) break; } cn[n]-=1.0; } return MathMean(cn); }
Nós podemos realizar a otimização com um parâmetro fixo e adequado de rmndmin ou para procurar o seu valor ideal.
Vamos fornecer os resultados apenas para o critério associado ao rebaixamento relativo, porque sua limitação dá um efeito mais pronunciado. Nós vamos realizar a otimização com várias variantes de valor fixo de rmndmin: 0.95, 0.75 e 0.2.
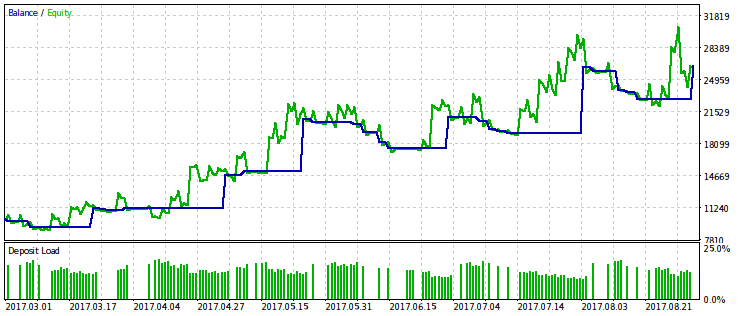
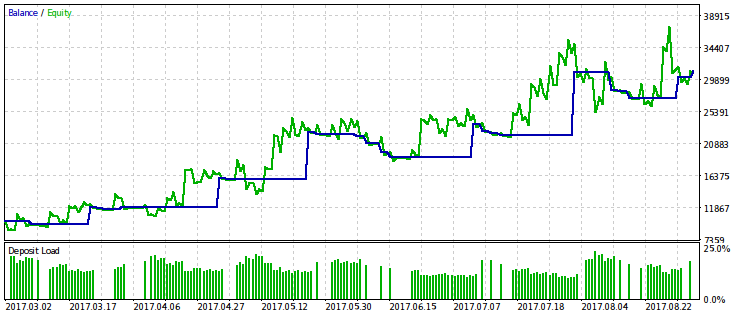
Quanto menor o valor de rmndmin, menos perceptível é o rebaixamento, enquanto que os resultados da otimização são cada vez mais semelhantes àqueles com a maximização do lucro usual. Isso pode ser considerado uma consequência da lei dos grandes números - o princípio da teoria da probabilidade. Nas imagens, este efeito não é imediatamente perceptível, porque eles têm uma escala diferente pelo eixo vertical (devido ao ajuste de todas as imagens para as mesmas dimensões). Além disso, o aumento do rebaixamento devido à diminuição do valor de rmndmin não é imediatamente aparente.
Agora, vamos incluir o parâmetro rmndmin para o número de parâmetros otimizados, e nós continuaremos a otimização pelo mesmo critério.
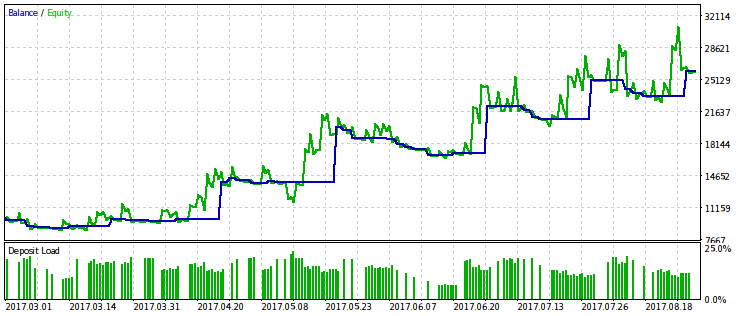
Obtemos o valor ideal rmndmin=0.55. Com esse valor, um rebaixamento pode atingir quase metade da conta, o que é inaceitável. Portanto, dificilmente ele será utilizável em uma negociação real. No entanto, há outro benefício aqui. Nós podemos ver que "esperar" por rebaixamentos ainda maiores, muito provavelmente, não faz o menor sentido. Isso corresponde à segunda metade da regra de negociação: "Deixe seu lucro crescer, corte as perdas".
Robustez da distribuição de lucros em relação ao preço não estacionário
O comportamento do preço pode mudar. Ao mesmo tempo, nós gostaríamos que os resultados do funcionamento do EA fossem estáveis. Do ponto de vista de nosso modelo de probabilidade do EA, isso significa que nós precisamos da estacionariedade do lucro de negociação, mesmo no caso dos incrementos de preço não estacionários.
Nosso critério de otimização compara a parte inicial da sequência de negociação com o final. Quanto mais próximos eles estiverem, maior será seu valor. A proximidade é determinada com base no Critério de Wilcoxon-Mann-Whitney. Vamos explicar sua essência. Suponha que nós temos duas amostras de negociações. O critério determina quanto uma das amostras é deslocada em relação a outra. Quanto menor o deslocamento, maior o valor do critério. Vamos explicar isso pela imagem. Cada amostra é representada pelo histograma correspondente. O maior valor do critério pode ser encontrado na imagem do meio.
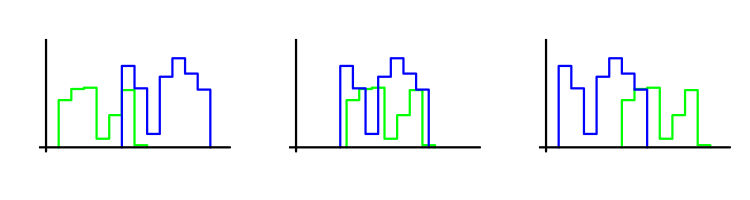
Neste caso, o método de Monte Carlo em si não é usado. No entanto, o grande valor do critério WMW justifica sua aplicação, uma vez que confirma a suposição de que o tipo de distribuição de lucro negociação é preservado.
Nosso arquivo também apresenta outra variante de critério — o produto do critério WMW pelo lucro.
double frw_wmw(double &k[]) { if (fwdsh<=0.0||fwdsh>=1.0) return 0.0; int nk=ArraySize(k), nkf=(int)(fwdsh*nk), nkp=nk-nkf; if(nkf<NDEALSMIN||nkp<NDEALSMIN) return 0.0; double u=0.0; for (int i=0; i<nkp; ++i) for (int j=0; j<nkf; ++j) if(k[i]>k[nkp+j]) ++u; return 1.0-MathAbs(1.0-2.0*u/(nkf*nkp)); } double frw_wmw_prf(double &k[]) { int nk=ArraySize(k); double prf=1.0; for(int n=0; n<nk; ++n) prf*=k[n]; prf-=1.0; if(prf>0.0) prf*=frw_wmw(k); return prf; }
O uso direto do critério WMW é problemático, uma vez que ele pode confundir uma opção deficitária com uma ótima. Seria melhor otimizar as opções do EA por lucro e descartar com um pequeno valor desse parâmetro, mas ainda não está claro como fazer isso. Nós podemos escolher várias das melhores opções do ponto de vista do critério WMW, e depois escolher entre elas a que dá um lucro máximo.
Nós vamos fornecer exemplos de dois dos dez melhores passos. Um deles é lucrativo, enquanto que o outro é com prejuízo.
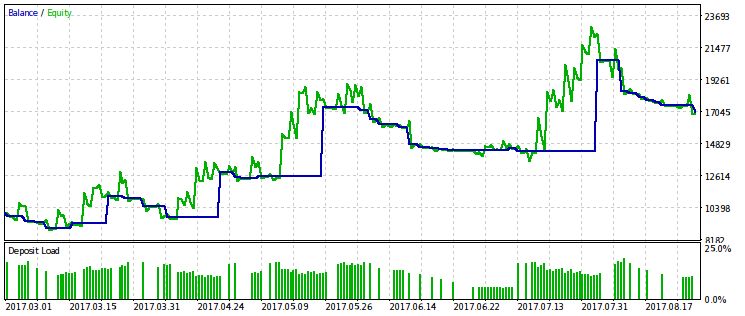
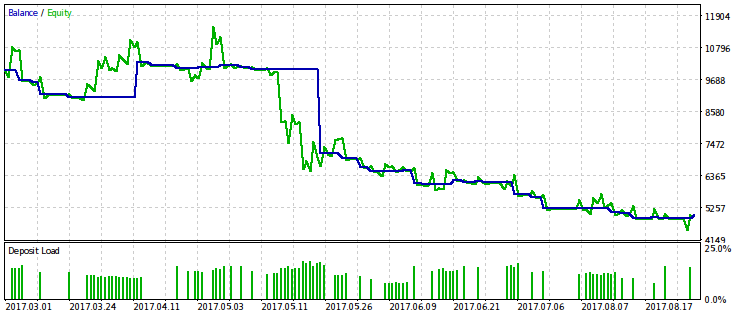
Parece que o critério WMW seria mais útil ao comparar dois EAs diferentes no mesmo intervalo de tempo ou um EA em diferentes intervalos de tempo. Mas ainda não está claro como fazer essa comparação regular.
Nós também daremos um exemplo de otimização por um critério igual ao produto do critério WMW por lucro. Aparentemente, ele é muito semelhante a uma simples otimização por lucro, o que significa que seu uso é excessivo.
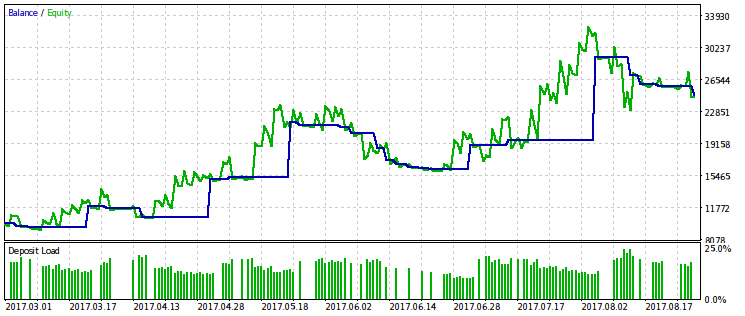
Conclusão
Neste artigo, nós tocamos brevemente alguns aspectos do tópico marcado. Vamos concluir com breves observações.
- Os critérios de otimização construídos no artigo podem ajudar a formalizar ideias intuitivas sobre a sequência mais eficiente das negociações. Isso é útil quando devemos escolher entre um grande número de opções.
- Existem medidas conhecidas para o risco, como o VaR (Value At Risk) ou a probabilidade de ruína. Se você usá-los diretamente como um critério de otimização, o resultado será ruim. Os volumes de negociação e o número de negociações serão subestimados. Portanto, um critério de compromisso é necessário, o que depende das duas variáveis — risco e lucro. A questão é qual versão deste critério nós deveríamos escolher, já que as funções das duas variáveis são infinitas. Por exemplo, o critério pode ser selecionado com base no nível de uma estratégia de negociação "agressividade", que varia muito.
- Diferentes variantes de critérios de otimização que medem a estabilidade podem ser úteis para diferentes classes do EA. Por exemplo, os EAs que seguem as tendências serão diferentes daqueles negociados em um intervalo, enquanto os sistemas com um take profit fixo serão diferentes dos que fecham negócios por um stop móvel. As distribuições de lucro de tais EAs também pertencerão à classes diferentes. Dependendo disso, um ou outro critério será mais apropriado.
- Alguns critérios são úteis para comparar dois EAs diferentes, em vez de comparar o comportamento do mesmo EA em um intervalo de tempo fixo em conjuntos diferentes de parâmetros. Com a ajuda de tais critérios, é possível comparar o trabalho de um único EA em diferentes intervalos de tempo.
- A modelagem de Monte Carlo seria mais completa se fosse possível passar não apenas o histórico de preços existente, mas também suas cópias alteradas aleatoriamente para a entrada do EA. Isso nos permitiria estudar a estabilidade dos EAs mais profundamente, ainda que com o custo de aumentar a quantidade de cálculos.
Arquivos anexados
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Moving Average_mcarlo.mq5 | Script | Moving Average.mq5 padrão modificado |
| 2 | mcarlo.mqh | Arquivo de cabeçalho | Arquivo principal com as funções executando todos os cálculos necessários |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/4347
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Como criar uma Especificação de Requisitos para solicitar um robô de negociação
Como criar uma Especificação de Requisitos para solicitar um robô de negociação
 Redes Neurais Profundas (Parte VI). Ensemble de classificadores de redes neurais: bagging
Redes Neurais Profundas (Parte VI). Ensemble de classificadores de redes neurais: bagging
 O monitoramento da conta de negociação é uma ferramenta essencial do trader
O monitoramento da conta de negociação é uma ferramenta essencial do trader
 Construtor de estratégia visual. Criação de robôs de negociação sem programação
Construtor de estratégia visual. Criação de robôs de negociação sem programação
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Hello. I added the Ontester () method to my EA, and in the backtest a numeric value (4.3222) appears in the OnTester result. How do I interpret this value to improve EA performance?
It is used as a 'Custom max' criterion when optimizing input parameters.
boa ideia, mas só é adequada para posições fixas.
É apenas uma ferramenta aproximada de avaliação de estratégia, com base nas premissas(capítulo 1) da teoria de Ralph Vince.