
Avaliação de risco numa sequência de operações com um ativo
Prefácio
Neste artigo, vamos aproveitar a ideia de Ralph Vince sobre o controle de volumes de posições (neste contexto, será útil lembrar também a fórmula de Kelly). Ela também é conhecida como o melhor f Nesta teoria, f é a fração atribuível ao capital que está em risco em cada transação. De acordo com Vince, f é escolhido segundo as condições de otimização (maximização) do lucro. Existem dois problemas ao usar essa teoria na negociação.
- Rebaixamento de conta grande demais.
- f é conhecido apenas no histórico de transações.
Uma tentativa de resolver esses problemas é apenas um dos objetivos deste artigo. Outro problema, não menos importante, consiste em tentar introduzir a teoria da probabilidade e as estatísticas matemáticas na análise dos sistemas de negociação. Portanto, de vez em quando vamos ligeiramente nos desviar do tópico principal. Abster-me-ei de expor os conceitos básicos: se a necessidade surgir, o leitor pode acessar o livro: "The Mathematics of Technical Analysis: Applying Statistics to Trading Stocks, Options and Futures".
No final deste artigo, são apresentados exemplos. Eles são apenas uma ilustração da teoria considerada no artigo, portanto, eles não são recomendados para serem usados na negociação real.
Introdução: ausência de incerteza
Por uma questão de simplicidade, suponhamos que o preço do ativo expresse seu valor nas unidades do capital, e não o contrário. A etapa mínima do volume da transação é um valor fixo nas unidades do ativo. Esta etapa é igual a um volume mínimo de transação diferente de zero. Usaremos um modelo de transação simples.
Para cada transação, define-se um tipo buy/sell, volume v e preço de entrada, stop-loss e saída: penter, pstop e pexit, respectivamente.
Limitações óbvias:
- volume diferente de zero v≥0
- o preço de saída deve ser inferior ao preço de entrada para compra: pstop<penter
- o preço de saída deve ser superior ao preço de entrada para venda: pstop>penter.
Realizemos as seguintes designações:
- C0 — capital antes de entrar na transação;
- C1 — capital após sair da transação;
- Cs — capital após o stop-loss se desencadear;
- r — parte do capital inicial perdida imediatamente após o stop-loss se desencadear,
ou seja, C0−Cs=rC0.
Para transações do tipo buy: C1=C0+v(pexit−penter) e Cs=C0−v(penter−pstop).
O mesmo vale para transações do tipo sell: C1=C0+v(penter−pexit) e Cs=C0−v(pstop−penter).
Após simples conversões, obtemos C1=C0(1+ra), onde a=(pexit−penter)/(penter−pstop). Estas expressões são válidas para os dois tipos de transações, isto é, buy e sell. Chamemos a magnitude r de risco da transação, e a, sua rentabilidade.
Formulamos o problema do gerenciamento de riscos para nosso modelo. Assumamos que temos n transações com rendimentos ai, onde i=1..n, e é necessário identificar riscos ri. Deve-se ter em conta que ri pode depender apenas das magnitudes conhecidas no momento da entrada numa transação. Os riscos são geralmente considerados iguais entre si ri=r, onde 0≤r<1. r=rmax é o valor que maximiza a magnitude do lucro Cn=C0(1+ra1)(1+ra2)…(1+ran).
Teremos uma abordagem semelhante, mas com algumas diferenças. Levaremos em consideração algumas restrições, nomeadamente, o rebaixamento máximo e o rendimento médio numa série de transações. Realizemos as seguintes designações:
- A0 é o menor de todos os ai,
- A=(a1+a2+…+an)/n é a sua média aritmética.
É sempre verdade que A0≤A e a igualdade só pode ser alcançado se todos ai=A0. Consideremos as restrições sobre r em mais detalhes.
- Cn=Cn(r)>0, o que implica que 1+rA0>0. Se A0≥−1, é verdade para todos 0≤r<1. No caso de A0<−1 —, obtemos 0≤r<−1/A0. Podemos ver que aparece uma restrição adicional sobre r, somente quando há saídas da transação por stop-loss com derrapagem [slippage]. Como resultado, a restrição toma a forma 0≤r<rc, onde rc=1, se A0≥−1, e rc=−1/A0 se A0<−1.
-
Definiremos o rendimento médio g como Cn=C0(1+gr)^n, portanto:
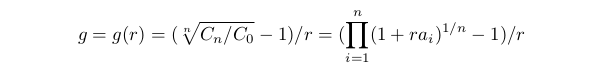
Em outras palavras, g pode ser chamado de rendimento médio da transação numa série em relação ao risco tomado. A função g(r) é definida durante a execução da restrição do ponto anterior. Ela tem uma singularidade removível no ponto r=0: se r→0, então g(r)→A, e nós podemos supor que g(0)=A. Pode ser mostrado que g(r)≡A, apenas se todos ai=A. Se entre ai há diferentes, então g(r) diminui quando r está aumentando. A restrição será na forma g(r)≥G0>0. A constante G0 depende de muitas coisas, isto é, condições de negociação, preferências do trader, etc. No modelo atual, pode-se dizer que se G0>A, o conjunto de r que satisfaz a desigualdade estará vazio. Se G0≤A, nossa restrição se torna 0≤r≤rg, onde rg é a solução da equação g(rg)=G0. Se esta equação não tem solução, então rg=1.
-
Para avaliar o rebaixamento máximo, consideremos seu valor oposto:
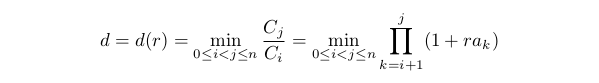
Esse valor pode ser chamado de crescimento mínimo. É conveniente, pois é sempre positivo e finito quando a restrição especificada no primeiro ponto é atendida. É evidente que d(0)=1. Se A0<0, então d(r) diminui quando r está aumentando na área restita pelo primeiro ponto. A restrição será na forma d(r)≥D0, onde 0<D0<1. Quanto maior D0, mais pequeno será o rebaixamento admissível. Reescrevemos nossa restrição como: 0≤r≤rd, onde rd é a solução da equação d(rd)=D0 (se esta equação não tiver solução, então rd=1).
-
Ao entrar na transação, o volume v não pode ter um valor arbitrário. Ele deve ser múltiplo de algum valor Δv>0, o seja, v=kΔvonde o número inteiro k≥0. Então, para transação i:
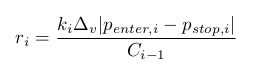
É óbvio que a coincidência de todos os ri é altamente improvável. Assim, verifica-se que o problema mencionado acima não possui uma solução precisa. Por isso, procuraremos uma solução aproximada. Nós nos limitaremos a calcular um valor tão mínimo rv, para que cada ri possa levar pelo menos um valor diferente de zero no intervalo [0,rv]
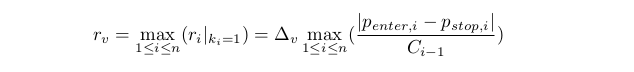
Determinemos também uma estimativa aproximada rvr≥rv. De cumprir a restrição no ponto anterior, segue-se que Ci≥D0C0>0. A partir do qual obtemos (nota: d0 e D0 significam a mesma coisa):
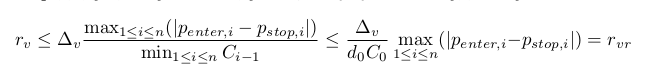
Esta avaliação é conveniente porque tem um relacionamento mais simples com o capital.
Assumimos que o conjunto que satisfaz as três primeiras restrições não está vazio Então, ele aparecerá como o intervalo [0,ra], onde ra=min(rc,rg,rd).
Também assumimos que a quarta restrição é encontrada, o que exige ra≥rv. Consideremos um problema de maximização Cn=Cn(r). Num caso significativo para nós: A>0 e A0<0. Esta função aumenta no intervalo [0,rmax] e diminui na faixa [rmax,rc]. Aqui rmax é o ponto de anulação da primeira derivada dCn(r)/dr=0.
Agora é fácil encontrar ropt, que maximiza Cn(r) no intervalo [0,ra]: ropt=min(ra,rmax). Restam dois casos: 1) A0≤A≤0 e 2) 0≤A0≤A. No primeiro caso, ropt=rmax=0, e no segundo caso, rmax=rс e ropt=ra .
Agora, consideraremos o caso quando o conjunto definido pelas restrições está vazio. Isso só é possível em dois casos: 1) G0>A ou 2) ra<rv. Só temos que assumir que ropt=0.
Agora, encontramos os valores aproximados ri tendo em conta a natureza discreta dos volumes das transações. Seja Ri um conjunto finito não vazio de números no intervalo [0,ra], adequado para o valor do risco ri na transação i. Selecionamos ropt,i , que maximiza Cn(r) em Ri. Se ropt∈Ri, então ropt,i=ropt. Se ropt∉Ri, duas situações são possíveis: 1) todos os pontos Ri se encontram num lado de ropt e 2) os pontos Ri se encontram em ambos lados de ropt. No primeiro caso, como ropt,i tomamos - de Ri - o ponto mais próximo de ropt. No segundo caso, tomamos - de Ri - os dois pontos mais próximos de ropt de cada lado, e como ropt,i tomamos o ponto em que Cn(r) é maior.
Incerteza: exemplo introdutório
Compliquemos um pouco o modelo considerado na introdução. Assumamos que conhecemos n números de ai, mas não conhecemos sua ordem. Desta forma, sua permutação aleatória é permitida. Vejamos o que vai mudar nos resultados obtidos anteriormente. Nos dois primeiros pontos, a permutação aleatória de ai não mudará nada. Não haverá nenhuma alteração no quarto ponto se for usada uma estimativa de ordem de grandeza de rvr.
No terceiro ponto as mudanças são bastante possíveis. Na verdade, é possível fazer uma sequência de maneira que não haja valores positivos entre os negativos, então o rebaixamento será máximo. E, vice-versa, os números positivos e negativos uniformemente misturados reduzirão o rebaixamento. O número total de permutações no caso geral equivale a n!. Este é um número muito grande com n dentro de várias dezenas. Em teoria, podemos resolver o problema definido na introdução para cada j=1..n! permutações da sequência ai e obter um conjunto de números rd,j. Há, no entanto, uma questão persistente, e é que não sabemos qual permutação escolher. Para trabalhar com essa incerteza, precisamos implementar os conceitos e métodos da teoria da probabilidade e estatística matemática.
Consideremos um conjunto de números rd,j como valores da função ρd=ρd(j)=rd,j que depende da permutação. Em termos da teoria das probabilidade, ρd é uma variável aleatória para a qual um conjunto de eventos elementares é igual a um conjunto de n permutações. Vamos tratá-los todos como diferentes, mesmo que alguns ai sejam os mesmos.
Também assumimos que todas as permutações n são igualmente prováveis. Então, a probabilidade de cada um delas será 1/n!, o que define a medida probabilística no conjunto de eventos elementares. Agora, podemos definir - para ρd - a distribuição das probabilidades Pρd(x)=n(x)/n!, onde n(x) é o número de n permutações para as quais rd,j<x. Agora precisamos esclarecer a condição de restrição de rebaixamento. Junto com o mínimo permitido D0, devemos especificar nosso nível de significância aceitável 0<δ<<1. δ indica qual a probabilidade de exceder o rebaixamento acima do limite que consideramos insignificante. Então, podemos definir rd(δ) como quantil δ da distribuição Pρd(x). Para encontrar uma solução aproximada para este problema, geramos aleatoriamente um número suficientemente grande nt, onde 1<<nt<<n!, n permutações. Encontramos para cada um deles o valor rd,j, onde 1≤j≤nt. Então, como avaliação para rd(δ) podemos tomar um quantil δ de amostra da população rd,j.
Embora este modelo seja um pouco artificial, ele tem seus usos. Por exemplo, podemos tomar rd, calculado para a série inicial de negócios e encontrar a probabilidade pd=Pρd(rd). Obviamente, a desigualdade 0≤pd≤1 é válida. pd perto de zero indica um rebaixamento grande causado por negócios desfavoráveis combinados próximos uns dos outros, enquanto um pd próximo a um mostra que os negócios lucrativos e desfavoráveis foram uniformemente misturados. Este é o caminho não só para descobrir uma série de perdas numa sequência de trades (por exemplo, como no método Z-score), mas também seu grau de influência sobre o rebaixamento. Podem ser gerados outros índices dependendo de Pρd() ou de rd.
Incerteza: caso geral
Assumamos que há uma sequência de negócios com rendimentos ai, 1≤i≤n. Também assumiremos que esta sequência é uma implementação de uma sequência independente numa população e variáveis aleatórias λi distribuídas de forma idêntica. Denotamos sua função de distribuição de probabilidade como Pλ(x). Supõe-se que tem as seguintes propriedades:
- expectância Mλ positiva
- restrição para baixo, isto é, exite um número λmin≤−1 para o qual Pλ(x)=0 quando x<λmin e Pλ(x)>0 quando x>λ0.
Estas condições indicam que o rendimento médio é positivo. Embora, sejam possíveis negócios desfavoráveis, sempre existe a possibilidade de não perder todo o capital numa única transação, limitando o risco.
Formulemos nosso problema para determinar a magnitude do risco. Semelhante ao exemplo na parte anterior, devemos, em vez do número ropt , estudar uma variável aleatória ρopt. Em seguida, definindo o nível de significância δ, calculamos ropt=ropt(δ), como quantil δ de distribuição Pρopt(x). Este sistema com este risco pode ser usado até que o rebaixamento e o rendimento médio estejam no intervalo estabelecido. Quando eles excedem os limites do intervalo, este sistema deve ser descartado. A probabilidade de erro não excederá δ.
Eu gostaria de enfatizar a importância de assegurar que δ seja pequeno. Quando δ é grande, não faz sentido o critério obtido. Apenas quando o valor é pequeno, há motivos para se pensar que há dois eventos relacionados entre si: 1) o sistema não funciona devido às mudanças no mercado e 2) o rebaixamento é grande demais ou a rentabilidade é muito baixa. Além do erro que já foi discutido, um tipo diferente de erro pode ser considerado. Quando esse erro está presente, não vemos mudanças no mercado que não afetam o rebaixamento e rentabilidade de nosso sistema. Não é conveniente discutir este erro, pois não afeta o rendimento do sistema.
Em nossa teoria, isso se manifesta no fato de que as mudanças das distribuições Pλ(x) e Pρopt(x) não são importantes para nós. O único que importa é a mudança do quantil δ Pρopt(x). Particularmente, isso significa que não há requisito de sequência estacionária para a sequência de rendimentos. Dizendo isso, precisaremos dela para restaurar a lei de distribuição de rendimento na amostra final ai, 1≤i≤n. Aqui, em vez de um estado estacionário exato, pode ser suficiente exigir uma variabilidade da distribuição não muito forte.
No final, ρopt pode ser expresso através de λi, embora este seja um relacionamento complexo (é expressado por meio de outras variáveis intermediárias aleatórias). Isso exige estudar variáveis aleatórias definidas como funções deλi e construir suas distribuições. Para isso, precisamos conhecer Pλ(x). Listemos três variantes de quais informações sobre esta distribuição podemos ter.
- Existe uma expressão exata para Pλ(x) ou há uma maneira de fazer uma aproximação arbitrariamente aproximada para o sistema de negociação em análise. Geralmente, isso só é possível quando há uma suposição fundada sobre o comportamento dos preços dos ativos. Por exemplo, podemos considerar a hipótese do passeio aleatório como verdadeira. Mas o uso direto desta informação na negociação geralmente é quase impossível. As conclusões tiradas dessa maneira não são realistas e geralmente rejeitam a possibilidade de lucro. Isso pode ser usado de forma diferente. Com essa hipótese, podemos construir a hipótese nula. Então, usando dados empíricos e a qualidade do ajustamento, podemos descartar a hipótese ou admitir que não podemos descartá-la com nossos dados. No nosso caso, tais dados empíricos são a sequência ai, 1≤i≤n.
- Sabe-se que Pλ(x) pertence ou aproximar-se de algumas família paramétrica de distribuições. Isso é possível quando os pressupostos sobre os preços dos ativos do ponto anterior não estão muito longe. Claro, o tipo de família de distribuição é definido também pelo algoritmo do sistema de negociação. Os valores exatos para os parâmetros de distribuição são calculados usando a sequência ai, 1≤i≤n pelos métodos das estatística paramétrica.
- Junto com a sequência ai, 1≤i≤n algumas propriedades comuns de Pλ(x) são conhecidas (ou assumidas). Por exemplo, pode-se especular sobre a existência de expectância finita e variância. Nesse caso, como a aproximação para Pλ(x) usaremos uma função de distribuição de amostra. Vamos construí-la com base na mesma sequência ai, 1≤i≤n. Os métodos que utilizam a função de distribuição de amostra são chamados de bootstrap. Em alguns casos, não é necessário conhecer Pλ(x). Por exemplo, a variável aleatória (λ1+λ2+…+λn)/n, quando n é grande, pode ser tratada como distribuída normalmente (com variância finita λi).
Este artigo terá uma continuação onde serão usados os pressupostos descritos na terceira variante. As duas primeiras variantes serão descritas mais adiante.
Aprenderemos como alterar os cálculos realizados por nós na introdução. Em vez de números absolutos A0 e A lidaremos com variáveis aleatórias expressadas através de λi da mesma maneira: Λ0=min(λ1, λ2, …, λn) e Λ=(λ1+λ2+…+λn)/n.
Vejamos seu comportamento assintótico quando n aumenta indefinidamente. Nesse caso, é sempre verdade que Λ0→λmin. Assumamos que λi tem uma variância finita Dλ, então Λ→Mλ. Conforme mencionado acima, podemos considerar com alta precisão que Λ é normalmente distribuído com expectância Mλ e variância Dλ/n. Se os valores exatos de Mλ e Dλ forem desconhecidos, podem ser usados seus análogos de amostra calculados por ai. As distribuições empíricas para Λ0 e Λ também podem ser construídas usando o bootstrap.
Antes de calcular ropt(δ) pelo método bootstrap, devemos levar em consideração os seguintes pontos sobre como os cálculos realizados na introdução mudarão:
- No primeiro ponto, devido ao comportamento assintótico de Λ0, a avaliação pode ser aproximada para o número rc=−1/λmin. Mas, para a distribuição de amostragem, o valor λmin coincide com А0 e, portanto, tudo neste ponto permanece inalterado.
- É importante certificar-se de que a condição G0≤Λ não é atendida com uma probabilidade não superior a δ. Para fazer isso, o quantil δ de Λ não deve ser inferior a G0. Para um cálculo aproximado deste quantil, usaremos a aproximação normal da distribuição Λ. Como resultado, obteremos nmin, isto é, uma estimativa abaixo do número de negócios necessários para a análise. Também é possível ajustar o método de bootstrap padrão e construir conjuntos de amostras de comprimento de crescimento para encontrar nmin. Do ponto de vista teórico, teremos mais ou menos o mesmo que para a aproximação pela distribuição normal.
- No quarto ponto, o mesmo que antes, teremos uma avaliação mais difícil do rvr.
Definimos nb, isto é, o número de sequências de rendimento, que será gerado. No ciclo de execução do bootstrap, devemos, para cada j=1..nb, iterar as restrições para a magnitude do risco, listadas por nós na introdução. Considerando os pontos acima, basta calcular rg(j), rd(j), rmax(j) e, finalmente, ropt(j). Se o conjunto para r em algum j estiver vazio, então assumimos que ropt(j)=0.
No final do bootstrap, teremos uma matriz de valores ropt[]. Tendo calculado por esta matriz o quantil δ de amostra, ele será tomado como a solução para o problema.Em vez de uma conclusão
Pode-se dizer que tudo escrito acima é apenas o início do tópico. Mencionarei brevemente quais serão os seguintes artigos.
- Para usar o modelo de transações como uma sequência de distribuições independentes, devemos fazer algumas suposições sobre os preços dos ativos e o algoritmo de negociação.
- Esta teoria deve ser feita mais especificamente para alguns métodos particulares para sair das operações, como stop-loss/take-profit fixos e trailing-stop fixo.
- Também é necessário mostrar como essa teoria pode ser usada para construir sistemas de negociação. Consideraremos como a teoria da probabilidade pode ser usada para construir um sistema em gaps. Também tocaremos no tema do uso de aprendizagem de máquina.
Apêndice à introdução
Abaixo está o texto do script r_intro.mq5 e o resultado de seu trabalho em gráficos e resultados numéricos.
#include <Graphics\Graphic.mqh> #define N 30 #define NR 100 #property script_show_inputs input int ngr=0; // número do gráfico exibido na tela double G0=0.25; // menor rendimento médio double D0=0.9; // menor incremento mínimo // capital inicial c0 assumido como igual a 1 void OnStart() { double A0,A,rc,rg,rd,ra,rmax,ropt,r[NR],g[NR],d[NR],cn[NR],a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // rendimentos 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; A=0; for(int i=0; i<N;++i) A+=a[i]; A/=N; rc=1; if(A0<-1) rc=-1/A0; double c[N]; r[0]=0; cn[0]=1; g[0]=A; d[0]=1; for(int i=1; i<NR;++i) { r[i]=i*rc/NR; cn[i]=1; for(int j=0; j<N;++j) cn[i]*=1+r[i]*a[j]; g[i]=(MathPow(cn[i],1.0/N)-1)/r[i]; c[0]=1+r[i]*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+r[i]*a[j]); d[i]=dcalc(c); } int nrg,nrd,nra,nrmax,nropt; double b[NR]; for(int i=0; i<NR;++i) b[i]=MathAbs(g[i]-G0); nrg=ArrayMinimum(b); rg=r[nrg]; for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd=r[nrd]; nra=MathMin(nrg,nrd); ra=r[nra]; nrmax=ArrayMaximum(cn); rmax=r[nrmax]; nropt=MathMin(nra,nrmax); ropt=r[nropt]; Print("rc = ",rc,"\nrg = ",rg,"\nrd = ",rd,"\nra = ",ra,"\nrmax = ",rmax,"\nropt = ",ropt, "\ng(rmax) = ",g[nrmax],", g(ropt) = ",g[nropt], "\nd(rmax) = ",d[nrmax],", d(ropt) = ",d[nropt], "\ncn(rmax) = ",cn[nrmax],", cn(ropt) = ",cn[nropt]); if(ngr<1 || ngr>5) return; ChartSetInteger(0,CHART_SHOW,false); CGraphic graphic; graphic.Create(0,"G",0,0,0,750,350); double x[2],y[2]; switch(ngr) { case 1: graphic.CurveAdd(r,g,CURVE_LINES,"g=g(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=G0; y[1]=G0; graphic.CurveAdd(x,y,CURVE_LINES,"g=G0"); x[0]=rg; x[1]=rg; y[0]=g[0]; y[1]=g[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rg"); break; case 2: graphic.CurveAdd(r,d,CURVE_LINES,"d=d(r)"); x[0]=0; x[1]=r[NR-1]; y[0]=D0; y[1]=D0; graphic.CurveAdd(x,y,CURVE_LINES,"d=D0"); x[0]=rd; x[1]=rd; y[0]=d[0]; y[1]=d[NR-1]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rd"); break; case 3: graphic.CurveAdd(r,cn,CURVE_LINES,"cn=cn(r)"); x[0]=0; x[1]=rmax; y[0]=cn[nrmax]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(rmax)"); x[0]=rmax; x[1]=rmax; y[0]=cn[NR-1]; y[1]=cn[nrmax]; graphic.CurveAdd(x,y,CURVE_LINES,"r=rmax"); x[0]=0; x[1]=ropt; y[0]=cn[nropt]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"cn=cn(ropt)"); x[0]=ropt; x[1]=ropt; y[0]=cn[NR-1]; y[1]=cn[nropt]; graphic.CurveAdd(x,y,CURVE_LINES,"r=ropt"); break; case 4: c[0]=1+ropt*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+ropt*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, ropt"); break; case 5: c[0]=1+rmax*a[0]; for(int j=1; j<N;++j) c[j]=c[j-1]*(1+rmax*a[j]); graphic.CurveAdd(c,CURVE_LINES,"Equity, rmax"); break; } graphic.CurvePlotAll(); graphic.Update(); Sleep(30000); ChartSetInteger(0,CHART_SHOW,true); graphic.Destroy(); } // a função dcalc() aceita a matriz de c1, c2, ... valores de cN e // retorna o incremento mínimo d. Supomos que c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; }
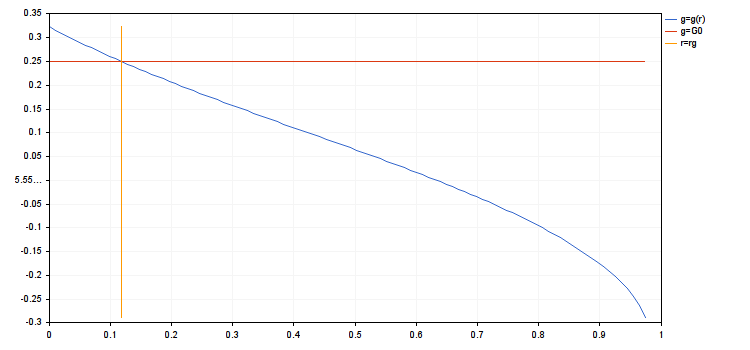
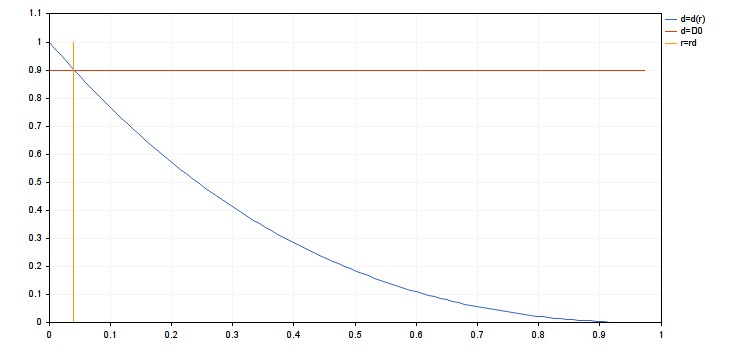
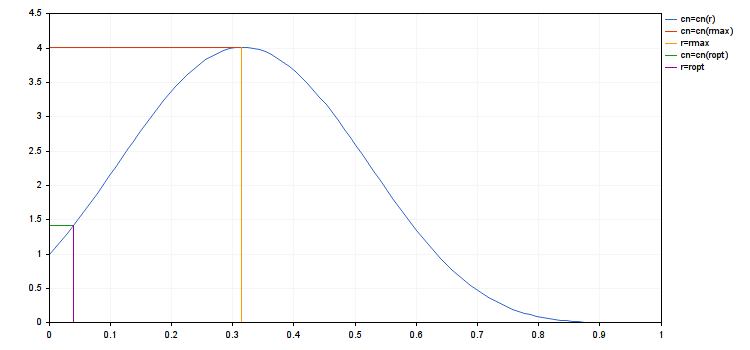
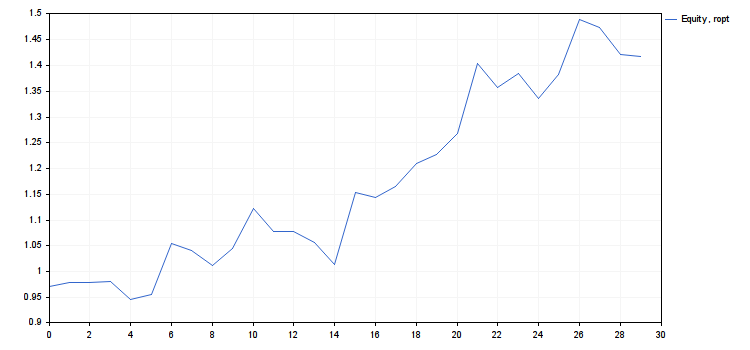
- rc = 0.9839614287119945
- rg = 0.1180753714454393
- rd = 0.03935845714847978
- ra = 0.03935845714847978
- rmax = 0.3148676571878383
- ropt = 0.03935845714847978
- g(rmax) = 0.1507064833125653, g(ropt) = 0.2967587621877231
- d(rmax) = 0.3925358395456308, d(ropt) = 0.9037200051227304
- cn(rmax) = 4.018198063206267, cn(ropt) = 1.416754202013712
- Usar ropt como o valor de risco neste sistema.
- O risco liberado neste rmax−ropt pode ser usado para adicionar novos sistemas (diversificação).
Apêndice ao exemplo introdutório
Abaixo está o texto do script r_exmp.mq5 e os resultados numéricos de seu trabalho.
#include <Math\Stat\Uniform.mqh> #define N 30 // duração da série de operações #define NR 500 // número de segmentos no intervalo [0,rc] #define NT 500 // número de permutações geradas double D0=0.9; // menor incremento mínimo double dlt=0.05; // nível de significância void OnStart() { double A0,rc,r[NR],d[NR],rd[NT],a[N]=//A,rg,ra,rmax,ropt,g[NR],cn[NR], { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969,// rendimento de operação 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; A0=a[ArrayMinimum(a)]; rc=1; if(A0<-1) rc=-1/A0; for(int i=0; i<NR;++i) r[i]=i*rc/NR; double b[NR],c[N]; int nrd; MathSrand(GetTickCount()); for(int j=0; j<NT;++j) { trps(a,N); for(int i=1; i<NR;++i) { c[0]=1+r[i]*a[0]; for(int k=1; k<N;++k) c[k]=c[k-1]*(1+r[i]*a[k]); d[i]=dcalc(c); } for(int i=0; i<NR;++i) b[i]=MathAbs(d[i]-D0); nrd=ArrayMinimum(b); rd[j]=r[nrd]; } double p[1],q[1]; p[0]=dlt; if(!MathQuantile(rd,p,q)) {Print("MathQuantile() error"); return;} PrintFormat("quantil %f de amostra rd[] igual a %f",p[0],q[0]); double rd0=0.03935845714847978; // valor de rd obtido na Introdução double pd0=0; // valor correspondente pd for(int j=0; j<NT;++j) if(rd[j]<rd0) ++pd0; pd0/=NT; PrintFormat("para rd = %f valor pd = %f",rd0,pd0); } // a função dcalc() aceita a matriz de c1, c2, ... valores de cN e // retorna o incremento mínimo d. Supomos que c0==1 double dcalc(double &c[]) { if(c[0]<=0) return 0; double d=c[0], mx=c[0], mn=c[0]; for(int i=1; i<N;++i) { if(c[i]<=0) return 0; if(c[i]<mn) {mn=c[i]; d=MathMin(d,mn/mx);} else {if(c[i]>mx) mx=mn=c[i];} } return d; } // permutação aleatória do primeiro não superior a min(n,ArraySize(b)) // elementos da matriz b[] // em vez de trps() pode ser usada a biblioteca MathSample() void trps(double &b[],int n) { if(n<=1) return; int sz=ArraySize(b); if(sz<=1) return; if(sz<n) n=sz; int ner; double dnc=MathRandomUniform(0,n,ner); if(!MathIsValidNumber(dnc)) {Print("Error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc>=0 && nc<n-1) { double tmp=b[n-1]; b[n-1]=b[nc]; b[nc]=tmp;} trps(b,n-1); }
- quantil 0.05 de amostra rd[] igual a 0.021647
- para rd = 0.039358 o valor de pd = 0.584
A primeira linha de resultados nos diz que devemos reduzir à metade o risco em comparação com o resultado obtido na introdução. Nesse caso, se o rebaixamento exceder o objetivo (10%), isso significará que o sistema provavelmente terá falhas e não deve ser usado para negociação. A probabilidade de erro (o sistema de trabalho é rejeitado) neste caso será δ (0.05 ou 5%). A segunda linha do resultado diz que o rebaixamento na série inicial de negócios é menor do que poderia ser em média. É possível que 30 transações é insuficiente para avaliar o sistema. Portanto, seria útil realizar análises detalhadas de um número maior de operações e ver como isso afeta os resultados.
Apêndice ao caso geral
Abaixo está o script r_cmn.mq5 onde estamos tentando avaliar abaixo do valor nmin e os resultados do trabalho do script:
#include <Math\Stat\Normal.mqh> #include <Math\Stat\Uniform.mqh> #include <Graphics\Graphic.mqh> #define N 30 // comprimento da série de transações #define NB 10000 // o número de amostras geradas para o bootstrap double G0=0.25; // menor rendimento médio double dlt=0.05; // nível de significância void OnStart() { double a[N]= { -0.7615,0.2139,0.0003,0.04576,-0.9081,0.2969, // rendimento de transações 2.6360,-0.3689,-0.6934,0.8549,1.8484,-0.9745, -0.0325,-0.5037,-1.0163,3.4825,-0.1873,0.4850, 0.9643,0.3734,0.8480,2.6887,-0.8462,0.5375, -0.9141,0.9065,1.9506,-0.2472,-0.9218,-0.0775 }; double A=MathMean(a); double S2=MathVariance(a); double Sk=MathSkewness(a); double Md=MathMedian(a); Print("parâmetros de distribuição de amostras:"); PrintFormat("média: %f, variância: %f, assimetria: %f, mediana: %f",A,S2,Sk,Md); PrintFormat("número de transações: %d, magnitude dlt: %f, magnitude G0: %f",N,dlt,G0); // aproximação por distribuição normal Print("aproximação por distribuição normal:"); double q0, p0; int ner; q0=MathQuantileNormal(dlt,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;} Print("quantil dlt: ",q0); p0=MathCumulativeDistributionNormal(G0,A,MathSqrt(S2/N),ner); if(!MathIsValidNumber(p0)) {Print("MathIsValidNumber(p0) error ",ner); return;} Print("nível de significância para G0: ",p0); // bootstrap MathSrand(GetTickCount()); double b[N],s[NB]; p0=0; for(int i=0;i<NB;++i) { sample(a,b); s[i]=MathMean(b); if(s[i]<G0) ++p0; } p0/=NB; double p[1],q[1]; p[0]=dlt; if(!MathQuantile(s,p,q)) {Print("MathQuantile() error"); return;} Print("aproximação por bootstrap"); Print("quantil dlt: ",q[0]); Print("nível de significância para G0: ",p0); // definição de nmin (aproximação por distribuição normal) int nmin; for(nmin=1; nmin<1000;++nmin) { q0=MathQuantileNormal(dlt,A,MathSqrt(S2/nmin),ner); if(!MathIsValidNumber(q0)) {Print("Error ",ner); return;} if(q0>G0) break; } Print("Número mínimo de transações nmin (aproximação por distribuição normal):"); PrintFormat("não inferior a %d, valor do quantil dlt: %f",nmin,q0); } void sample(double &a[],double &b[]) { int ner; double dnc; for(int i=0; i<N;++i) { dnc=MathRandomUniform(0,N,ner); if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc==N) nc=N-1; b[i]=a[nc]; } }
Parâmetros de distribuição de amostra:
- médio: 0.322655
- variância: 1.419552
- assimetria: 0.990362
- mediana: 0.023030
- número de transações: 30
- magnitude dlt: 0.050000
- magnitude G0: 0.250000.
Aproximação pela distribuição normal:
- quantil dlt: -0.03514631247305994;
- nível de significância para G0: 0.3691880511783918.
Aproximação pelo bootstrap:
- quantil dlt: -0.0136361;
- nível de significância para G0: 0.3727.
- número mínimo de transações nmin (aproximação pela distribuição normal): não inferior a 728
- valor do quantil dlt: 0.250022.
Segue imediatamente a partir destes resultados que ropt(δ)=0. Isso significa que nosso critério proíbe a negociação usando este sistema por causa dos dados ou requer um histórico de negociação de maior extensão. Isso é mesmo apesar dos belos gráficos no primeiro apêndice. Além disso, o Bootstrap deu quase os mesmos resultados que a aproximação pela distribuição normal. Naturalmente, surgem questões: em primeiro lugar, por que os resultados são tão ruins? e, em segundo lugar, como podemos melhorar esse sistema? Tentemos respondê-las.
- As razões se encontram nos critérios usados e no próprio sistema. Nosso critério é universal demais. Por um lado, isso é muito bom, pois podemos usá-lo em muitos casos. Por outro lado, não leva em conta não apenas o sistema em questão, mas todos os sistemas que consideramos. Por exemplo, todos os nossos sistemas produzem uma distribuição com um lado esquerdo cortado e alguns deles em teoria podem ter uma expectância infinita. É por isso que, como regra geral, todas as distribuições estão inclinadas para a direta, enquanto sua média converge lentamente com a distribuição normal simétrica. O sistema, em nosso exemplo, tem uma distribuição assimétrica. Isso é indicado pela obliquidade ou pelo viés da expectância para a direita a partir da mediana. Isso é esperado de um sistema que segue a regra "reduzir as perdas e deixar os lucros correr".
- Precisamos de critérios que usem bem as informações sobre um determinado sistema de negociação e sobre uma sequência de preços de ativos. Portanto, é impossível cumprir com nossa tarefa sem suposições sobre preços. Essas suposições não devem distorcer demasiado o cenário real. Isso significa que devemos estar na situação da segunda variante feita de três pontos discutidos no início do capítulo "Caso geral". É por isso que devemos nos concentrar nos métodos paramétricos mais tarde. Do ponto de vista computacional, são mais difíceis e menos universais, mas podem ser mais precisos em cada caso particular.
Até agora, podemos concluir o seguinte. As perdas são causadas não apenas por mudanças inesperadas no comportamento dos preços dos ativos (por exemplo, a mudança da tendência). Isso pode ser causado por ruído ou característica de volatilidade particulares. Os métodos que consideramos são uma das maneiras de tentar separar esses motivos e reduzir sua influência. Se isso não puder ser feito para um sistema de negociação, esse sistema não é recomendado para ser usado.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3650
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Busca automática de divergências e convergência
Busca automática de divergências e convergência
 Expert Advisor Multiplataforma: Stops
Expert Advisor Multiplataforma: Stops
 TradeObjects: Automação de negociação com base em objetos gráficos na MetaTrader
TradeObjects: Automação de negociação com base em objetos gráficos na MetaTrader
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Carregado no script Market Volume Optimizer, usando a teoria apresentada no artigo. Ele determina o volume ideal da transação, com base no histórico de transações.
Exijo a continuação do banquete! :-)
Há uma continuação do artigo. Ou você quer dizer outra coisa? No filme, essa frase é ouvida quando Ivan Vasilyevich claramente precisa terminar o banquete)
Há uma continuação do artigo. Ou você quer dizer outra coisa? No filme, essa frase é ouvida quando Ivan Vasilyevich claramente precisa encerrar o banquete)