Discussão do artigo "Redes Neurais Profundas (Parte V). Otimização Bayesiana de hiperparâmetros de uma DNN"
Experimentei o BayesianOptimisation.
Você tinha o maior conjunto de 9 parâmetros otimizáveis. E você disse que o cálculo leva muito tempo
Tentei otimizar um conjunto de 20 parâmetros com 10 primeiros conjuntos aleatórios. Levei 1,5 hora para calcular as combinações no BayesianOptimisation, sem levar em conta o tempo de cálculo do próprio NS (substituí o NS por uma fórmula matemática simples para o experimento).
E se você quiser otimizar 50 ou 100 parâmetros, provavelmente levará 24 horas para calcular um conjunto. Acho que seria mais rápido gerar dezenas de combinações aleatórias e calculá-las no NS e, em seguida, selecionar as melhores por Precisão.
A discussão do pacote fala sobre esse problema. Há um ano, o autor escreveu que, se encontrar um pacote mais rápido para os cálculos, ele o usará, mas, por enquanto, está como está. Lá, foram fornecidos alguns links para outros pacotes com otimização bayesiana, mas não está claro como aplicá-los em um problema semelhante; nos exemplos, outros problemas são resolvidos.
bigGp - não encontra o conjunto de dados SN2011fe para o exemplo (aparentemente, ele foi baixado da Internet e a página não está disponível). Não pude experimentar o exemplo. E, de acordo com a descrição, algumas matrizes adicionais são necessárias.
laGP - alguma fórmula confusa na função de aptidão e faz centenas de suas chamadas, e centenas de cálculos NS são inaceitáveis em termos de tempo.
kofnGA - pode pesquisar apenas X melhores de N. Por exemplo, 10 de 100. Ou seja, ele não está otimizando um conjunto de todos os 100.
Os algoritmos genéticos também não são adequados, pois geram centenas de chamadas para a função de adequação (cálculos NS).
Em geral, não existe um análogo, e o próprio BayesianOptimisation é muito longo.
Fiz um experimento com o BayesianOptimisation.
Você tinha o maior conjunto de 9 parâmetros otimizáveis. E você disse que levou muito tempo para calcular
Experimentei um conjunto de 20 parâmetros para otimizar com 10 primeiros conjuntos aleatórios. Levei 1,5 hora para calcular as próprias combinações no BayesianOptimisation, sem levar em conta o tempo de cálculo do próprio NS (substituí o NS por uma fórmula matemática simples para o experimento).
E se você quiser otimizar 50 ou 100 parâmetros, provavelmente levará 24 horas para calcular um conjunto. Acho que seria mais rápido gerar dezenas de combinações aleatórias e calculá-las no NS e, em seguida, selecionar as melhores por Precisão.
A discussão do pacote fala sobre esse problema. Há um ano, o autor escreveu que, se encontrar um pacote mais rápido para os cálculos, ele o usará, mas, por enquanto, está como está. Lá, foram fornecidos alguns links para outros pacotes com otimização bayesiana, mas não está claro como aplicá-los a um problema semelhante; nos exemplos, outros problemas são resolvidos.
bigGp - não encontra o conjunto de dados SN2011fe para o exemplo (aparentemente, ele foi baixado da Internet e a página não está disponível). Não pude experimentar o exemplo. E, de acordo com a descrição, algumas matrizes adicionais são necessárias.
laGP - alguma fórmula confusa na função de aptidão e faz centenas de suas chamadas, e centenas de cálculos NS são inaceitáveis em termos de tempo.
kofnGA - pode pesquisar apenas X melhores de N. Por exemplo, 10 de 100. Ou seja, ele não está otimizando um conjunto de todos os 100.
Os algoritmos genéticos também não são adequados, pois também geram centenas de chamadas para a função de adequação (cálculos NS).
Em geral, não existe um análogo, e o próprio BayesianOptimisation é muito longo.
Esse problema existe. Ele está relacionado ao fato de o pacote ser escrito em R puro. Mas as vantagens de usá-lo para mim, pessoalmente, superam os custos de tempo. Há um pacote hyperopt (Python)/ Ainda não tive a chance de experimentá-lo, e ele é antigo.
Mas acho que alguém ainda reescreverá o pacote em C++. É claro que você mesmo pode fazer isso, transferir alguns dos cálculos para a GPU, mas isso levará muito tempo. Somente se eu estiver realmente desesperado.
Por enquanto, usarei o que tenho.
Boa sorte
Também experimentei com exemplos do próprio pacote GPfit.
Aqui está um exemplo de otimização de 1 parâmetro que descreve uma curva com 2 vértices (o GPfit f-ya tem mais vértices, deixei 2):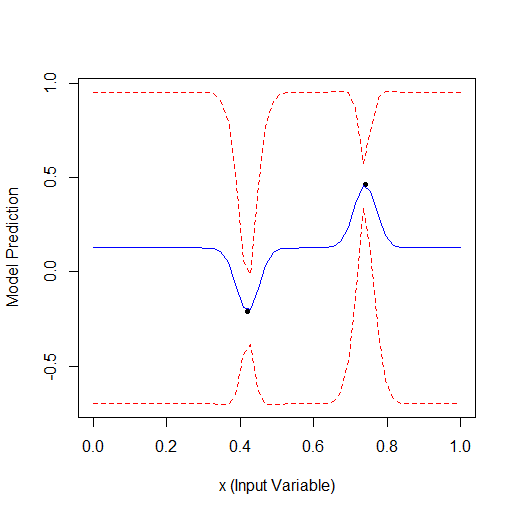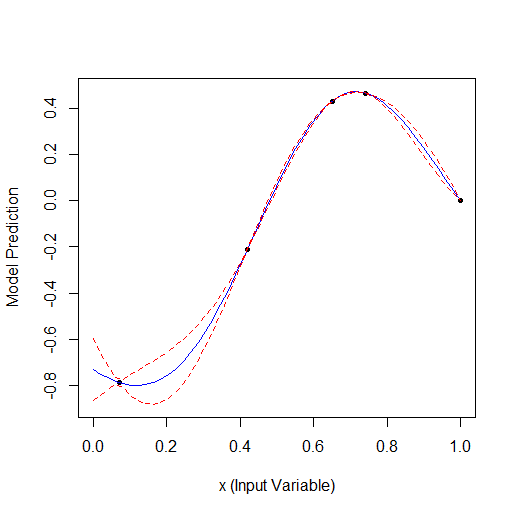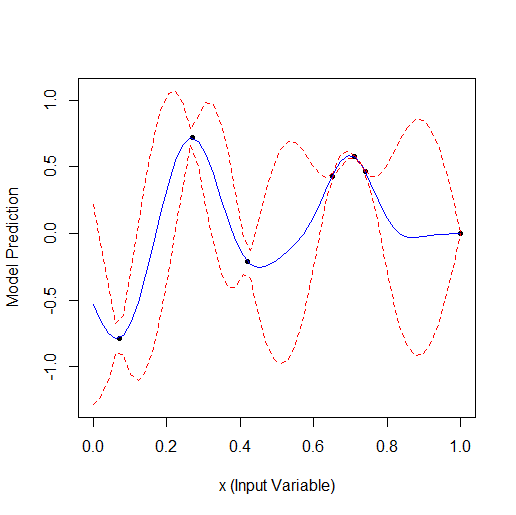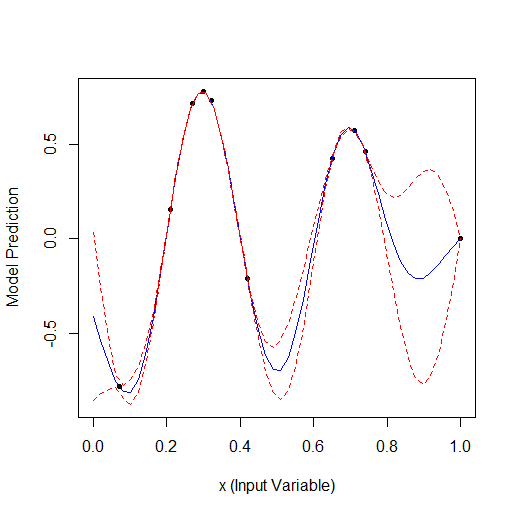
Tomando 2 pontos aleatórios e, em seguida, otimizando. Você pode ver que ele encontra primeiro o vértice pequeno e depois o vértice maior. Total de 9 cálculos - 2 aleatórios e + 7 na otimização.
Outro exemplo em 2D - otimização de 2 parâmetros. O f-y original tem a seguinte aparência: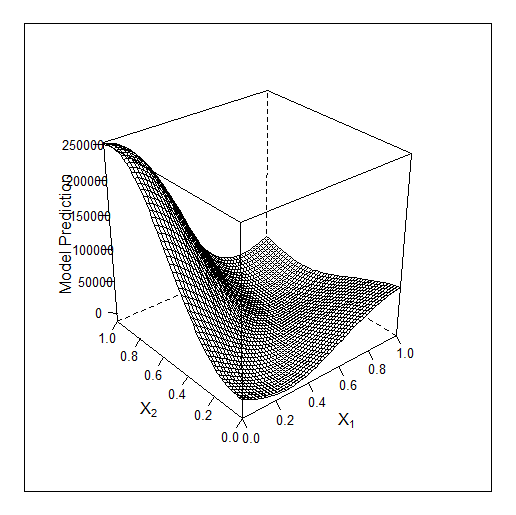
Otimização para 19 pontos:

Total de 2 pontos aleatórios + 17 encontrados pelo otimizador.
Comparando esses dois exemplos, podemos ver que o número de iterações necessárias para encontrar o máximo ao adicionar um parâmetro dobra. Para 1 parâmetro, o máximo foi encontrado para 9 pontos calculados, para 2 parâmetros, para 19.
Ou seja, se você otimizar 10 parâmetros, poderá precisar de 9 * 2^10 = 9000 cálculos.
Embora em 14 pontos o algoritmo quase tenha encontrado o máximo, isso é cerca de 1,5 vezes o número de cálculos. então 9 * 1,5:10 = 518 cálculos. Também é muito, para um tempo de cálculo aceitável.
Os resultados obtidos no artigo para 20 a 30 pontos podem estar longe do máximo real.
Acredito que os algoritmos genéticos, mesmo com esses exemplos simples, precisarão de muito mais pontos para calcular. Portanto, provavelmente não há uma opção melhor.
Também experimentei com exemplos do próprio pacote GPfit.
Aqui está um exemplo de otimização de 1 parâmetro que descreve uma curva com 2 vértices (o GPfit f-ya tem mais vértices, deixei 2):
Tomando 2 pontos aleatórios e, em seguida, otimizando. Você pode ver que ele encontra primeiro o vértice pequeno e depois o vértice maior. Total de 9 cálculos - 2 aleatórios e + 7 na otimização.
Outro exemplo em 2D - otimização de 2 parâmetros. O f-ya original tem a seguinte aparência:
Otimize até 19 pontos:
Total de 2 pontos aleatórios + 17 encontrados pelo otimizador.
Comparando esses dois exemplos, podemos ver que o número de iterações necessárias para encontrar o máximo ao adicionar um parâmetro dobra. Para 1 parâmetro, o máximo foi encontrado para 9 pontos calculados, para 2 parâmetros, para 19.
Ou seja, se você otimizar 10 parâmetros, poderá precisar de 9 * 2^10 = 9000 cálculos.
Embora em 14 pontos o algoritmo quase tenha encontrado o máximo, isso é cerca de 1,5 vezes o número de cálculos. então 9 * 1,5:10 = 518 cálculos. Também é muito, para um tempo de computação aceitável.
1. Os resultados obtidos no artigo para 20 a 30 pontos podem estar longe do máximo real.
Acredito que os algoritmos genéticos, mesmo com esses exemplos simples, precisarão calcular muito mais pontos. Portanto, acho que não há uma opção melhor, afinal.
Bravo.
Sem dúvida.
Há várias palestras no YouTube que explicam como funciona a otimização bayesiana. Se você ainda não viu, sugiro que assista. É muito informativo.
Como você inseriu a animação?
Eu tento usar métodos bayesianos sempre que possível. Os resultados são muito bons.
1. Faço otimização sequencial. Primeiro - inicialização de 10 pontos aleatórios, computação de 10 a 20 pontos, depois - inicialização dos 10 melhores resultados da otimização anterior, computação de 10 a 20 pontos. Normalmente, após a segunda iteração, os resultados não melhoram de forma significativa.
Boa sorte
Várias palestras que explicam como funciona a otimização bayesiana estão postadas no YouTube. Se você ainda não viu, recomendo que assista. Ela é muito informativa.
Dei uma olhada no código e no resultado na forma de imagens (e mostrei a você). O mais importante é o Processo Gaussiano do GPfit. E a otimização é a mais comum - basta usar o otimizador da entrega padrão do R e procurar o máximo na curva/forma que o GPfit encontrou por 2, 3, etc. pontos. E o resultado pode ser visto nas imagens animadas acima. O otimizador está apenas tentando obter os 100 principais pontos aleatórios.
Talvez eu assista a palestras no futuro, quando tiver tempo, mas, por enquanto, usarei o GPfit apenas como uma caixa preta.
Como você inseriu a animação?
Apenas exibi o resultado passo a passo GPfit::plot.GP(GP, surf_check = TRUE), colei no Photoshop e salvei como um GIF animado.
A seguir - inicialização dos 10 melhores resultados da otimização anterior, cálculos de 10 a 20 pontos.
De acordo com meus experimentos, é melhor deixar todos os pontos conhecidos para cálculos futuros, pois se os pontos mais baixos forem removidos, o GPfit poderá pensar que há pontos interessantes e quererá calculá-los, ou seja, haverá repetidas execuções do cálculo NS. E com esses pontos inferiores, o GPfit saberá que não há nada a ser procurado nessas regiões inferiores.
No entanto, se os resultados não melhorarem muito, isso significa que há um platô extenso com pequenas flutuações.
Como instalar e iniciar?
).

- 2016.04.26
- Vladimir Perervenko
- www.mql5.com
Teste futuro dos modelos com parâmetros ideais
Vamos verificar por quanto tempo os parâmetros ideais do DNN produzirão resultados com qualidade aceitável para os testes de valores de cotações "futuros". O teste será realizado no ambiente remanescente após as otimizações e testes anteriores da seguinte forma.
Use uma janela móvel de 1.350 barras, treinar = 1.000, testar = 350 (para validação - as primeiras 250 amostras, para teste - as últimas 100 amostras) com passo 100 para percorrer os dados após as primeiras (4.000 + 100) barras usadas para pré-treinamento. Faça 10 etapas "para frente". Em cada etapa, dois modelos serão treinados e testados:
- um - usando a DNN pré-treinada, ou seja, realizando um ajuste fino em um novo intervalo a cada etapa;
- segundo - treinando adicionalmente o DNN.opt, obtido após a otimização no estágio de ajuste fino, em um novo intervalo.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Execute a primeira parte do teste avançado usando o DNN pré-treinado e os hiperparâmetros ideais, obtidos da variante de treinamento SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
A segunda etapa do teste avançado usandoo Dnn.opt obtido durante a otimização:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Comparar os resultados dos testes, colocando-os em uma tabela:
env$Score3_dnn env$Score3_dnnOpt
| iter | Pontuação3_dnn | Pontuação3_dnnOpt |
|---|---|---|
| Exatidão Precisão Recuperação F1 | Precisão Precisão Recuperação F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 | -1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 | -1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 | -1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 | -1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 | -1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 | -1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 | -1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 | -1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 | -1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
A tabela mostra que as duas primeiras etapas produzem bons resultados. Na verdade, a qualidade é a mesma nas duas primeiras etapas de ambas as variantes e depois cai. Portanto, pode-se presumir que, após a otimização e o teste, a DNN manterá a qualidade da classificação no nível do conjunto de teste em pelo menos 200-250 barras seguintes.
Há muitas outras combinações para treinamento adicional de modelos em testes avançados mencionados noartigo anteriore vários hiperparâmetros ajustáveis.
Olá, qual é a pergunta?
Olá Vladimir,
Não entendi muito bem por que seu NS é treinado em dados de treinamento e sua avaliação é feita em dados de teste (se não me engano, você o usa como validação).
Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3)
Nesse caso, você não obterá um ajuste ao gráfico de teste, ou seja, escolherá o modelo que funcionou melhor no gráfico de teste?
Também devemos levar em conta que o gráfico de teste é bastante pequeno e é possível ajustar uma das regularidades temporais, o que pode parar de funcionar muito rapidamente.
Talvez seja melhor estimar no gráfico de treinamento, ou na soma dos gráficos, ou como no Darch, (com dados de validação enviados) em Err = (ErrLeran * 0,37 + ErrValid * 0,63) - esses coeficientes são padrão, mas podem ser alterados.
Há muitas opções e não está claro qual é a melhor. Seus argumentos a favor do gráfico de teste são interessantes.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Redes Neurais Profundas (Parte V). Otimização Bayesiana de hiperparâmetros de uma DNN foi publicado:
O artigo considera a possibilidade de aplicar a otimização Bayesiana para os hiperparâmetros das redes neurais profundas, obtidas por diversas variantes de treinamento. É realizado a comparação da qualidade de classificação de uma DNN com os hiperparâmetros ótimos em diferentes variantes de treinamento. O nível de eficácia dos hiperparâmetros ótimos da DNN foi verificado nos testes fora da amostra (forward tests). As direções possíveis para melhorar a qualidade da classificação foram determinadas.
Excelente resultado. Observe que usar o valor médio de F1 como critério de otimização produz a mesma qualidade para as duas classes, apesar do desequilíbrio entre elas.
Gráficos do histórico de treinamento:
plot(env$Res3$Dnn.opt, type = "class")Fig. 4. Histórico de treinamento da DNN pela variante SRBM + upperLayer + BP
Autor: Vladimir Perervenko