
Нейросети в трейдинге: Двойная кластеризация временных рядов (Окончание)
Введение
Продолжаем работу над построением подходов, предложенных авторами фреймворка двойной кластеризации многомерных временных рядов DUET, который представляет собой мощный инструмент для прогнозирования финансовых рынков. DUET сочетает временную и канальную кластеризацию, что обеспечивает адаптацию к сложным и изменяющимся паттернам рыночной динамики, устраняя недостатки традиционных методов, склонных к переобучению и ограниченной гибкости.
DUET включает несколько ключевых модулей, каждый из которых выполняет критически важную роль. Первый этап обработки данных — нормализация и устранение выбросов, что повышает устойчивость модели.
Далее идет временная кластеризация, которая разбивает временной ряд на группы с подобной динамикой. Это позволяет учитывать фазовые сдвиги в рыночных процессах, что особенно важно для анализа активов с высокой волатильностью.
Канальная кластеризация используется для выявления наиболее значимых переменных среди множества рыночных факторов. Финансовые данные содержат значительное количество шумов и избыточной информации, что мешает построению точных прогнозов. DUET анализирует корреляции между параметрами и устраняет незначимые компоненты, концентрируя вычислительные ресурсы на ключевых признаках. Частотный анализ сигналов и механизмы выделения латентных признаков делают модель менее восприимчивой к случайным флуктуациям рынка.
Модуль объединения данных синхронизирует информацию, полученную от модулей временной и канальной кластеризации, формируя единое представление об анализируемом состоянии окружающей среды. Этот этап основан на механизме маскированного внимания, который позволяет модели фокусироваться на наиболее релевантных характеристиках, минимизируя влияние нерепрезентативных данных. Благодаря этому, DUET демонстрирует высокую устойчивость к динамическим изменениям и улучшает качество долгосрочных прогнозов.
Завершающий модуль прогнозирования использует агрегированные признаки для вычисления будущих значений временных рядов. В основе этого этапа лежат передовые нейросетевые методы, способные выявлять нелинейные зависимости между рыночными индикаторами. Гибкость архитектуры DUET позволяет динамически адаптироваться к различным условиям, исключая необходимость ручной перенастройки параметров модели.
Авторская визуализация фреймворка DUET представлена ниже.
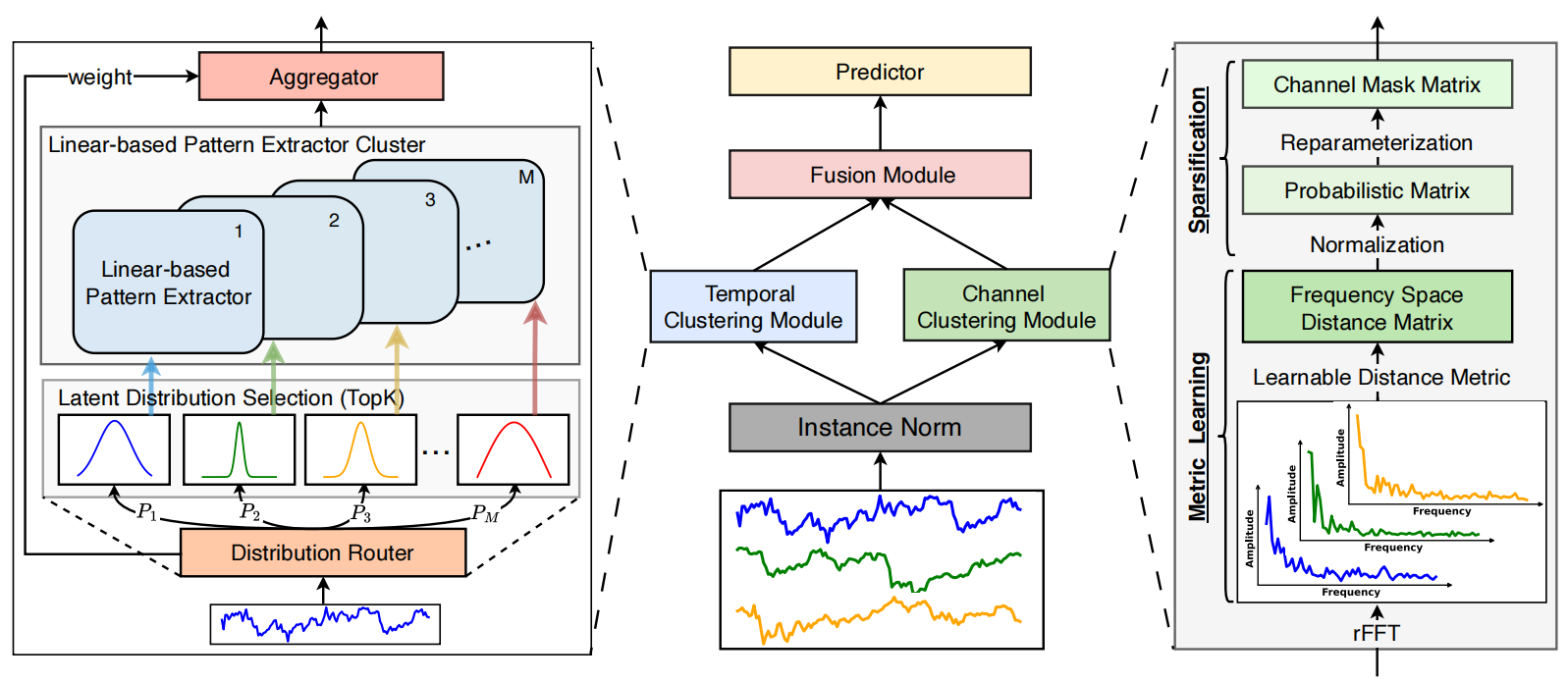
В практической части предыдущей статьи был представлен вариант реализации модуля временной кластеризации. Продолжаем начатую работу и переходим к построению модуля канальной кластеризации.
Channel Clustering Module
Модуль канальной кластеризации решает проблему корректного учета межканальных связей при прогнозировании многомерных временных рядов. Здесь авторы фреймворка DUET используют метрическое обучение, направленное на кластеризацию каналов в частотном пространстве.
Ключевой аспект работы CCM — представление данных в частотном пространстве. Для этого временные ряды разлагаются на частотные компоненты с помощью быстрого преобразования Фурье (FFT). В результате, сигналы анализируются в спектральной области, где взаимосвязи между каналами становятся более явными. Многие скрытые зависимости, незаметные при традиционном анализе, проявляются только после перехода к частотному домену, что делает этот метод особенно ценным для сложных временных рядов.
Оценка взаимосвязей между каналами производится с использованием обучаемой метрики расстояния. В качестве базовой меры используется амплитудное представление частотного спектра сигналов, а само расстояние авторы фреймворка предлагают вычислять на основе модифицированной метрики Махаланобиса. Этот метод учитывает не только попарные расстояния между каналами, но и их корреляции в спектральном пространстве.
После расчета расстояний между каналами формируется матрица отношений, в которой коэффициенты нормализуются в диапазоне [0,1]. Такая нормализация дает возможность выделить наиболее значимые связи, устраняя малозначимые и случайные флуктуации.
Для окончательной фильтрации информации создается бинарная матрица маскирования каналов. Этот процесс основан на вероятностной выборке, где каждому каналу присваивается вероятность полезности в прогнозировании. Такой механизм позволяет учитывать неоднозначность данных и избегать жестких пороговых значений. Таким образом, модель автоматически исключает несущественные каналы, что значительно улучшает интерпретируемость результатов и снижает избыточность информации.
В рамках данной работы мы реализуем немного упрощенный вариант модуля канальной кластеризации. Алгоритм дискретного преобразования Фурье нами был реализован ранее в рамках реализации фреймворка FITS и уже присутствует в нашей библиотеке. Вместо метрики Махаланобиса применяется более простой метод, основанный на векторных расстояниях между амплитудами частотных компонент. Это сохраняет преимущества частотного анализа, снижая вычислительную сложность и упрощая алгоритм.
После преобразования временных рядов в частотную область вычисляются нормы амплитудных спектров каждого канала. Затем определяется их попарное расстояние, формируя матрицу межканальных связей. С целью исключения слабых зависимостей из дальнейшего анализа, применяется нормализация, которая подавляет шум и масштабирует расстояния. Таким образом, сохраняются только значимые корреляции между каналами. На основе этой матрицы строится вероятностная модель связей. Каждый канал получает вес значимости, отражающий его влияние на другие ряды.
Описанный алгоритм мы реализуем в кернеле MaskByDistance на стороне OpenCL-программы. В параметрах кернела передаются указатели на 3 буфера данных. Первые два содержат исходные данные в виде реальной и мнимой части анализируемых сигналов. А третий предназначен для записи результатов работы. В данном случае это будет матрица маскирования каналов.
__kernel void MaskByDistance(__global const float *buf_real, __global const float *buf_imag, __global float *mask, const int dimension ) { const size_t main = get_global_id(0); const size_t slave = get_local_id(1); const int total = (int)get_local_size(1);
В теле кернела сначала идентифицируем текущий поток в двухмерном пространстве задач. Первое измерение указывает на анализируемый канал, а второе — на канал для сопоставления. При этом создаются рабочие группы из потоков второго измерения.
Далее создается массив данных в локальной памяти для обмена данными между потоками одной рабочей группы.
__local float Temp[LOCAL_ARRAY_SIZE]; int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);
И определяем смещения в глобальных буферах данных.
const int shift_main = main * dimension; const int shift_slave = slave * dimension; const int shift_mask = main * total + slave;
После выполнения подготовительной работы, переходим непосредственно к вычислениям и создаем цикл определения расстояния между двумя векторами частотных амплитуд.
//--- calc distance float dist = 0; if(main != slave) { #pragma unroll for(int d = 0; d < dimension; d++) dist += pow(ComplexAbs((float2)(buf_real[shift_main + d], buf_imag[shift_main + d])) - ComplexAbs((float2)(buf_real[shift_slave + d], buf_imag[shift_slave + d])), 2.0f); dist = sqrt(dist); }
Обратите внимание, в нашей матрице потоков существуют диагональные элементы. Думаю вы догадались, что в таком случае алгоритм вычисляет расстояние между двумя копиями одного вектора. Очевидно, что оно равно "0". Поэтому, в таких случаях мы не запускаем цикл определения расстояния, а просто сохраняем нулевое значение в соответствующей переменной.
Далее нам необходимо нормализовать значения. С этой целью реализуем алгоритм поиска максимального расстояния в рамках рабочей группы. Для этого сначала организуем цикл, в рамках которого соберем максимальные элементы отдельных подгрупп потоков в элементах локального массива.
//--- Look Max #pragma unroll for(int i = 0; i < total; i += ls) { if(i <= slave && (i + ls) > slave) Temp[slave % ls] = fmax((i == 0 ? 0 : Temp[slave % ls]), IsNaNOrInf(dist, 0)); barrier(CLK_LOCAL_MEM_FENCE); }
А затем, найдем максимальное значение среди элементов локального массива.
int count = ls; do { count = (count + 1) / 2; if(slave < count && (slave + count) < ls) { if(Temp[slave] < Temp[slave + count]) Temp[slave] = Temp[slave + count]; Temp[slave + count] = 0; } barrier(CLK_LOCAL_MEM_FENCE); } while(count > 1);
После чего, нормализуем расстояние между векторами частотных амплитуд в рамках рабочей группы, разделив на максимальное значение.
//--- Normalize if(Temp[0] > 0) dist /= Temp[0];
Думаю, очевидно, что теперь все нормированные расстояния находятся в диапазоне [0, 1]. При этом "1" получил максимально удаленный канал. Нам же, наоборот, нужно минимизировать влияние такого канала. Поэтому в буфер результатов мы сохраним инверсное значение нормированного расстояния.
//--- result mask[shift_mask] = 1 - IsNaNOrInf(dist, 1); }
И завершаем работу кернела.
Следует отметить важную особенность нашей реализации. В представленном алгоритме отсутствуют обучаемые параметры, так как расстояние между векторами амплитуд частотных спектров является фиксированной величиной, не зависящей от других факторов. Это позволяет нам исключить процесс обратного распространения ошибки, снижая затраты на оптимизацию.
Следующим этапом нашей работы является организация функционала модуля канальной кластеризации на стороне основной программы. Здесь мы создаем новый класс CNeuronChanelMask, структура которого представлена ниже.
class CNeuronChanelMask : public CNeuronBaseOCL { //--- protected: uint iUnits; uint iFFTdimension; CBufferFloat cbFFTReal; CBufferFloat cbFFTImag; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, bool reverse = false); virtual bool Mask(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) { return true; } public: CNeuronChanelMask(void) {}; ~CNeuronChanelMask(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronChanelMask; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
В представленной структуре, среди немного численных внутренних объектов, мы видим лишь 2 буфера хранения вещественной и мнимой части частотных компонент анализируемого сигнала. Более детально с использованием данных буферов познакомимся в процессе построения алгоритмов виртуальных методов нового класса.
Указанные объекты объявлены статично, а значит, мы можем оставить пустыми конструктор и деструктор класса. Инициализация объявленных и унаследованных объектов осуществляется в методе Init.
bool CNeuronChanelMask::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint units_count, ENUM_OPTIMIZATION optimization_type, uint batch) { if(window <= 0) return false; if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * units_count, optimization_type, batch)) return false;
В параметрах метода, как обычно, получаем ряд констант, которые позволяют нам однозначно интерпретировать архитектуру создаваемого объекта:
- window — длина анализируемой последовательности;
- units_count — количество каналов.
Стоит обратить внимание, что на выходе объекта мы ожидаем получить квадратную матрицу маскирования каналов. Размеры результирующей матрицы маскирования равны количеству каналов и не зависят от длины анализируемой последовательности. Однако, данный параметр нам необходим для корректной обработки исходных данных. Поэтому, мы сначала проверяем корректность полученного параметра, а затем вызываем одноименный метод родительского класса, в котором уже реализованы алгоритмы инициализации унаследованных интерфейсов.
После успешного выполнения операций метода родительского класса, мы сохраняем полученные константы.
//--- Save constants
iUnits = units_count;
activation = None;
И здесь хочу напомнить, что реализованный нами ранее алгоритм быстрого разложения Фурье применим только для последовательностей, размер которых является степенью 2. В общем случае — это не проблема, мы всегда можем увеличить размер последовательности, дописав нужное количество "0" в конец вектора. Однако, нам необходимо определить ближайшее верхнее значение.
//--- Calculate FFT dimension int power = int(MathLog(window) / M_LN2); if(MathPow(2, power) != window) power++; iFFTdimension = uint(MathPow(2, power));
И только затем мы инициализируем буфера временного хранения вещественной и мнимой части частотных компонент достаточного размера.
if(!cbFFTReal.BufferInit(iFFTdimension * iUnits, 0) || !cbFFTReal.BufferCreate(OpenCL)) return false; if(!cbFFTImag.BufferInit(iFFTdimension * iUnits, 0) || !cbFFTImag.BufferCreate(OpenCL)) return false; //--- return true; }
На этом мы завершаем работу с методов инициализации и переходим к построению алгоритма прямого прохода в рамках метода CNeuronChanelMask::feedForward. И должен сказать, что здесь все довольно просто и прозаично.
bool CNeuronChanelMask::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false; if(!FFT(NeuronOCL.getOutput(), NULL, GetPointer(cbFFTReal), GetPointer(cbFFTImag), false)) return false; //--- return Mask(); }
В параметрах метода получаем указатель на объект исходных данных, актуальность которого сразу проверяем. После чего, разделяем исходные данные на частотные компоненты и вызываем метод-обертку вышепредставленного кернела. А логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.
Методы постановки кернелов в очередь выполнения построены по уже знакомому вам алгоритму, и мы не будем сейчас останавливаться на их рассмотрении.
Как уже было сказано выше, мы исключаем процессы обратного прохода в данном случае. А соответствующие методы переопределяем заглушками, которые постоянно возвращают значение true. Такой подход позволяет нам беспрепятственно внедрять новый объект в существующую структуру наших моделей.
И на этом мы завершаем работу по построению алгоритмов модуля канальной кластеризации. С полным кодом данного класса и всех его методов вы можете самостоятельно ознакомиться во вложении к статье.
Блок DUET
На данном этапе мы уже построили модули временной и канальной кластеризации. Эти два модуля функционируют параллельно, анализируя многомерные временные ряды в двух представлениях: временном и частотном. Все полученные результаты объединяются в модуле Fusion, который интегрирует информацию о зависимостях каналов, используя механизм маскированного внимания. Это позволяет согласовать прогнозы отдельных каналов с учетом выявленных корреляций. Fusion адаптирует влияние каждого канала с учетом веса межканальной зависимости. В результате, итоговый прогноз становится более устойчивым, а модель — менее подверженной переобучению и случайным шумам.
На практике мы используем модифицированный механизм Self-Attention, в котором коэффициенты зависимости, полученные на основании результатов работы модуля временной кластеризации, умножаются на маску, сгенерированную модулем канальной кластеризации. И только потом осуществляется нормирование весов функцией SoftMax.
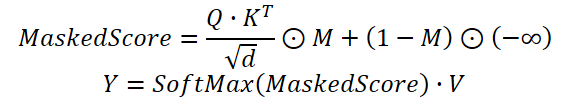
Предложенный алгоритм мы реализуем в рамках объекта CNeuronDUET, который объединит в функционал трех указанных модулей. Структура нового класса представлена ниже.
class CNeuronDUET : public CNeuronTransposeOCL { protected: uint iWindowKey; uint iHeads; //--- CNeuronTransposeOCL cTranspose; CNeuronMoE cExperts; CNeuronConvOCL cQKV; CNeuronBaseOCL cQ; CNeuronBaseOCL cKV; CNeuronChanelMask cMask; CBufferFloat cbScores; CNeuronBaseOCL cMHAttentionOut; CNeuronConvOCL cPooling; CNeuronBaseOCL cResidual; CNeuronMHFeedForward cFeedForward; //--- virtual bool AttentionOut(void); virtual bool AttentionInsideGradients(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); public: CNeuronDUET(void) {}; ~CNeuronDUET(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint units_out, uint experts, uint top_k, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronDUET; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual void TrainMode(bool flag) { bTrain = flag; cExperts.TrainMode(bTrain); } };
Важно отметить, что в данном случае, в качестве родительского класса используется слой транспонирования данных. Это обусловлено структурой исходных данных.
Модель принимает на вход многомерный временной ряд, представленный в виде матрицы, где каждая строка соответствует отдельному временному шагу анализируемой системы. Однако все модули, описанные выше, работают с унитарными временными рядами. Это также справедливо для модуля объединения данных. Чтобы обеспечить корректную обработку информации, исходные данные транспонируются в формат, удобный для анализа. А после завершения операций, результаты преобразуются обратно в исходное представление. Последний процесс мы планируем выполнять средствами родительского класса, что позволяет сохранить согласованность структуры данных и упростить интеграцию модуля.
В представленной выше структуре нового класса можно заметить довольно большое количество внутренних объектов, которые играют важную роль в построении нашего алгоритма. Более детально с их функционалом мы познакомимся в процессе реализации виртуальных методов данного класса. Сейчас мы обращаем внимание, что все объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация всех объектов, в том числе и унаследованных, осуществляется в методе Init.
bool CNeuronDUET::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint units_out, uint experts, uint top_k, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, window, units_out, optimization_type, batch)) return false;
В параметрах метода инициализации получаем ряд констант, позволяющих однозначно интерпретировать архитектуру создаваемого объекта. Структура параметров нам уже знакома. Одни из них использовались при построении выше рассмотренных модулей временной и канальной кластеризации, а другие — в блоках внимания. Стоит лишь обратить внимание на параметр units_out, который позволяет нам указать желаемую длину последовательности на выходе объекта.
В теле метода первым делом вызываем одноименный метод родительского класса, в котором уже реализованы процессы контроля части полученных параметров и инициализации унаследованных интерфейсов.
Затем мы сохраним необходимые параметры во внутренних переменных.
iWindowKey = MathMax(window_key, 1); iHeads = MathMax(heads, 1);
И переходим к инициализации внутренних объектов. Как было сказано выше, перед началом анализа исходные данные необходимо транспонировать. Это функционал выполняет специализированный объект.
int index = 0; if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch)) return false;
Затем, инициализируем модули временной и канальной кластеризации.
index++; if(!cExperts.Init(0, index, OpenCL, units_count, units_out, window, experts, top_k, optimization, iBatch)) return false; index++; if(!cMask.Init(0, index, OpenCL, units_count, window, optimization, iBatch)) return false;
Далее идут объекты модуля объединения данных. По существу, это модифицированный модуль внимания. Здесь мы сначала инициализируем объект генерации сущностей Query, Key и Value. В данном случае мы используем единый сверточный слой параллельной генерации трех сущностей.
index++; if(!cQKV.Init(0, index, OpenCL, units_out, units_out, iHeads * iWindowKey * 3, window, 1, optimization, iBatch)) return false;
Здесь же добавим 2 объекта для разделения сущностей в отдельные тензоры.
index++; if(!cQ.Init(0, index, OpenCL, cQKV.Neurons() / 3, optimization, iBatch)) return false; index++; if(!cKV.Init(0, index, OpenCL, cQ.Neurons() * 2, optimization, iBatch)) return false;
Коэффициенты внимания будем сохранять в буфере данных.
if(!cbScores.BufferInit(cMask.Neurons()*iHeads, 0) || !cbScores.BufferCreate(OpenCL)) return false;
Обратите внимание, что во всех случаях мы указываем размеры объектов с учетом транспонирования матрицы исходных данных.
Далее, инициализируем объект результатов многоголового внимания.
index++; if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch)) return false;
И сверточный слой понижения размерности для объединения результатов работы различных голов внимания.
index++; if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, units_out, window, 1, optimization, iBatch)) return false; cPooling.SetActivationFunction(None);
Добавим объект для записи результатов остаточных связей.
index++; if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch)) return false; cResidual.SetActivationFunction(None);
Далее, согласно авторской архитектуре, идет привычный блок FeedForward. Мы же заменим его многоголовым вариантом, заимствованным из фреймворка StockFormer.
index++; if(!cFeedForward.Init(0, index, OpenCL, units_out, 4 * units_out, window, 1, heads, optimization, iBatch)) return false; //--- return true; }
И завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.
Следующим этапом нашей работы является построение алгоритма прямого прохода в рамках метода CNeuronDUET::feedForward.
bool CNeuronDUET::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTranspose.FeedForward(NeuronOCL)) return false;
В параметрах метода получаем указатель на объект исходных данных, который сразу передаем в одноименный метод внутреннего объекта транспонирования данных. И далее мы уже продолжаем работу с результатами транспонирования.
Сначала мы их передаем в модуль временной кластеризации для получения прогнозных значений унитарных последовательностей.
if(!cExperts.FeedForward(cTranspose.AsObject())) return false;
А затем, результаты транспонирования исходных данных передаются в модуль канальной кластеризации.
if(!cMask.FeedForward(cTranspose.AsObject())) return false;
Далее мы переходим к организации прямого прохода модуля объединения данных. Сначала из результатов работы модуля временной кластеризации мы генерируем сущности блока внимания Query, Key и Value.
if(!cQKV.FeedForward(cExperts.AsObject())) return false;
Результаты операции разделяем на 2 тензора.
if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), iWindowKey, 2 * iWindowKey, cQKV.GetUnits())) return false;
И вызываем метод-обертку маскированного многоголового Self-Attention.
if(!AttentionOut()) return false;
Результаты многоголового внимания проецируем в размерность результатов модуля временной кластеризации.
if(!cPooling.FeedForward(cMHAttentionOut.AsObject())) return false;
К полученным значениям добавляем остаточный связи.
if(!SumAndNormilize(cExperts.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Многоголовый блок FeedForward у нас реализован в виде отдельного модуля с уже существующими остаточными связями. Поэтому нам достаточно лишь вызвать одноименный метод данного объекта, передав ему результаты предыдущих операций в качестве исходных данных.
if(!cFeedForward.FeedForward(cResidual.AsObject())) return false;
Теперь нам остается лишь вернуть результаты выполнения операций в представления исходных данных. Для этого воспользуемся функционалом родительского класса.
return CNeuronTransposeOCL::feedForward(cFeedForward.AsObject());
}
Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.
После завершения работы по организации процессов прямого прохода, мы переходим к выстраиванию алгоритма обратного прохода. Как вы знаете, здесь используется 2 метода:
- распределения градиента ошибки между внутренними объектами и исходными данными в соответствии с их влиянием на итоговый результат — calcInputGradients;
- оптимизации параметров модели с целью минимизации общей ошибки — updateInputWeights.
Все обучаемые параметры нашего блока DUET в представленной реализации содержатся во внутренних объектах, следовательно, процесс их оптимизации сводится к вызову одноименных методов таких объектов. И поэтому, более остро стоит вопрос корректного распределения градиента ошибки между внутренними объектами и исходными данными.
В параметрах метода calcInputGradients мы получаем указатель на объект исходных данных. Это тот же объект, который мы использовали в рамках прямого прохода. Только на этот раз нам предстоит передать в него соответствующие значения градиента ошибки.
bool CNeuronDUET::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Вполне очевидно, что передать данные мы можем только в действительный объект. Поэтому сразу проверяем актуальность полученного указателя. В противном случае, все дальнейшие операции утрачивают смысл.
Как вы знаете, распределение градиента ошибки осуществляется с четким соблюдением информационных потоков прямого прохода, только в обратном направлении. Метод прямого прохода мы завершили вызовом метода родительского класса, следовательно, и операции обратного прохода начинаются с вызова метода родительского класса. Только на этот раз, мы вызываем метод распределения градиента ошибки.
if(!CNeuronTransposeOCL::calcInputGradients(cFeedForward.AsObject())) return false;
Далее проводим градиент ошибки через модуль многоголового FeedForward.
if(!cPooling.calcHiddenGradients(cFeedForward.AsObject())) return false;
И распределяем полученные значения градиента ошибки между головами внимания.
if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject())) return false;
Следующим шагом вызываем метод-обертку распределения ошибки между сущностями Query, Key и Value в рамках механизма маскированного Self-Attention.
if(!AttentionInsideGradients()) return false;
Результаты операций соберем в единый тензор.
if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), iWindowKey, 2 * iWindowKey, iCount)) return false;
При необходимости, скорректируем полученные значения на производную функции активации.
if(cQKV.Activation() != None) if(!DeActivation(cQKV.getOutput(), cQKV.getGradient(), cQKV.getGradient(), cQKV.Activation())) return false;
После чего, передадим градиент на уровень модуля временной кластеризации.
if(!cExperts.calcHiddenGradients(cQKV.AsObject()) || !DeActivation(cExperts.getOutput(), cExperts.getPrevOutput(), cPooling.getGradient(), cExperts.Activation()) || !SumAndNormilize(cExperts.getGradient(), cExperts.getPrevOutput(), cExperts.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Здесь следует обратить внимание, что результаты модуля временной кластеризации использовались и для передачи остаточных связей, следовательно, градиент ошибки необходимо передать и по этому информационному потоку. С этой целью, сначала корректируем градиент ошибки на выходе блока внимания с учетом производной от функции активации модуля временной кластеризации, а затем, суммируем данные двух информационных потоков.
Далее проводим градиент ошибки через модуль временной кластеризации.
if(!cTranspose.calcHiddenGradients(cExperts.AsObject())) return false;
И передаем на уровень исходных данных.
return prevLayer.calcHiddenGradients(cTranspose.AsObject());
}
Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.
Обратите внимание, что в процессе распределения градиента ошибки полностью отсутствует информационный поток модуля канальной кластеризации. Ранее мы уже говорили об отсутствии операций обратного прохода в данном модуле и, на данном этапе, мы просто исключили заведомо излишние операции.
На этом мы завершаем рассмотрение алгоритмов построения нашего видения подходов, предложенных авторами фреймворка DUET. С полным кодом всех представленных объектов и их методов вы можете ознакомиться во вложении к статье.
Архитектура модели
Следующий этап работы включает интеграцию разработанных компонентов в архитектуру обучаемых моделей. С этой целью мы переходим к описанию архитектурного решения моделей.
Как и в предыдущих работах, мы воспользуемся подходами многозадачного обучения и будем обучать одновременно 2 модели: Актера и прогнозирования вероятностей направления предстоящего движения. Архитектура последней полностью заимствована из предыдущих работ, поэтому, в рамках данной статьи, остановимся на рассмотрении архитектуры Актера. Архитектура обеих моделей представлена в методе CreateDescriptions.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
В параметрах метода получаем указатели на 2 динамических объекта для записи описания архитектуры моделей. В теле метода мы сразу проверяем актуальность полученных указателей и, при необходимости, создаем новые экземпляры объектов.
Архитектура модели Актера начинается с полносвязного слоя, который выполняет роль интерфейса исходных данных. Он должен быть достаточного размера, чтобы вместить весь объем анализируемой информации.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Как и предложено авторами фреймворка DUET, далее идет слой пакетной нормализации данных, который предназначен для приведения исходных данных в сопоставимый вид и минимизации влияния выбросов.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
И далее мы используем 2 последовательных блока DUET, созданных нами выше. Однако, подход к сегментации данных был изменен. Вместо традиционной сегментации, в рамках данного эксперимента используется представление данных в многомерном фазовом пространстве. Этот метод, вдохновленный подходами фреймворка Attraos, позволяет более точно учитывать сложные зависимости во временных рядах, улучшая интерпретируемость модели. В первом слое используем шаг 5 минут.
В модуле временной кластеризации инициализируем работу 16 параллельных энкодеров. Для каждого кластера выбираются 4 наиболее подходящих.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDUET; descr.window = BarDescr * 5; // 5 min { int temp[] = {HistoryBars / 5, HistoryBars / 5, 16, 4}; // {Units in (24), Units out (24), Experts, Top K} if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = 256; descr.step = 4; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Во втором блоке DUET мы увеличиваем шаг фазового представления до 15. Однако, сохраняем неизменными остальные параметры.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronDUET; descr.window = BarDescr * 15; // 15 min { int temp[] = {HistoryBars / 15, HistoryBars / 15, 16, 4}; // {Units in (8), Units out (8), Experts, Top K} if(ArrayCopy(descr.units, temp) < (int)temp.Size()) return false; } descr.window_out = 256; descr.step = 4; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Обратите внимание, что в процессе обработки данных мы не изменяем размер тензора. Но следующим сверточным слоем мы уменьшим размер последовательности в 3 раза.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars / 3; descr.window = BarDescr * 3; descr.step = descr.window; int prev_window = descr.window_out = BarDescr; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Далее идет блок принятия решения из 3 полносвязных слоев.
//--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
За которым следует слой пакетной нормализации.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
И на выходе Актера мы добавляем блок риск-менеджмента.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 64; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
С полной архитектурой обеих моделей можно ознакомиться во вложении. Там же представлены программы взаимодействия с окружающей средой и обучения моделей, которые были перенесены без изменения из предыдущих работ.
Тестирование
Мы проделали большую работу по реализации собственного видения подходов, предложенных в фреймворке DUET, средствами MQL5 и имплементации их в обучаемые модели. Теперь наступает ключевой этап — тестирование эффективности реализованных решений на реальных исторических данных.
Для обучения моделей формируется выборка исторических данных валютной пары EURUSD, таймфрейм M1 за весь 2024 год. В процессе сбора данных используются параметры индикаторов, установленные по умолчанию.
Обучение модели проходит в два этапа. Сначала устанавливаем размер пакета равным 1, чтобы на каждой итерации выбирать случайное состояние из обучающей выборки. Это помогает модели адаптироваться к новым условиям. Однако, этого недостаточно для корректной работы блока риск-менеджмента. Поэтому на втором этапе обучения увеличиваем размер пакета до 60, что позволяет учитывать последовательность из 60 состояний окружающей среды и соответствующих действий Актера. Это делает обучение более стабильным и эффективным.
Тестирование обученной модели проводится на исторических данных за Январь-Февраль 2025 года. При этом сохраняются все настройки, что позволяет объективно оценить качество прогнозов. Результаты тестирования представлены ниже.
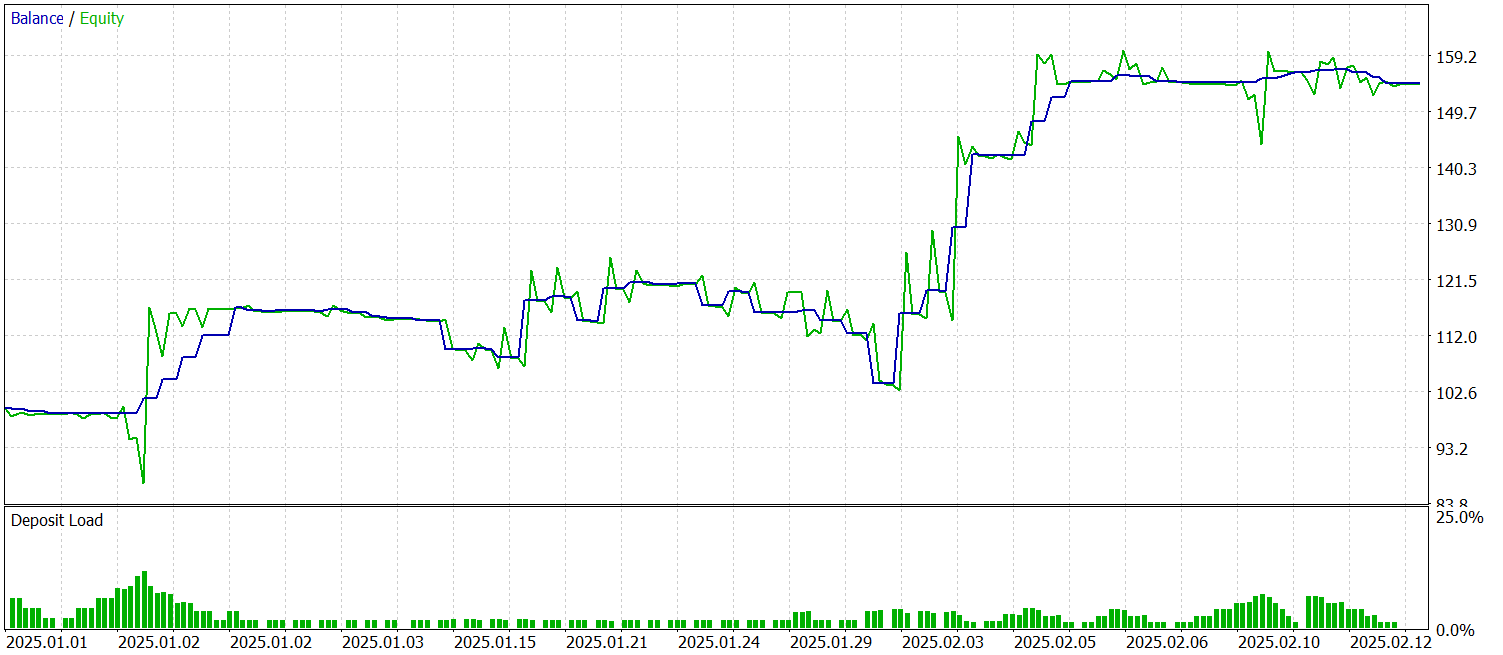

За период тестирования модель совершила 53 торговых операции, более 56% из которых были закрыты с прибылью. Примечательно, что средняя прибыльная операция почти в 2 раза превышает аналогичный показатель убыточных позиций. Все это позволило зафиксировать показатель профит-фактор на уровне 2.44.
Заключение
В данной работе мы познакомились с фреймворком DUET, авторы которого для целей анализа многомерных временных рядов объединили частотный анализ, метрическое обучение и вероятностную фильтрацию. Все это помогло повысить качество прогнозов и сделать модель более устойчивой к шуму.
В практической части мы реализовали свое видение предложенных подходов средствами MQL5 и имплементировали реализованные решения в модель. Провели обучение модели на реальных исторических данных и провели тестирование обученной модели на данных за пределами обучающей выборки. Полученные результаты свидетельствуют о существующем потенциале модели. Однако, перед использованием её в реальных торговых условиях, необходимо обучение модели на более репрезентативной выборке с последующим всесторонним тестированием.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Арбитражный трейдинг Forex: Панель оценки взаимосвязей
Арбитражный трейдинг Forex: Панель оценки взаимосвязей
 Применение теории игр Нэша с фильтрацией НММ в трейдинге
Применение теории игр Нэша с фильтрацией НММ в трейдинге
 Разработка системы репликации (Часть 69): Настройка времени (II)
Разработка системы репликации (Часть 69): Настройка времени (II)
 Возможности Мастера MQL5, которые вам нужно знать (Часть 35): Регрессия опорных векторов
Возможности Мастера MQL5, которые вам нужно знать (Часть 35): Регрессия опорных векторов
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования