Redes neuronales en el trading: Clusterización doble de series temporales (Final)

Introducción

Continuamos nuestro trabajo sobre la construcción de los enfoques propuestos por los autores del framework de clusterización dual de series temporales multivariantes DUET, que supone una potente herramienta para la previsión de los mercados financieros. DUET combina la clusterización temporal y por canales para posibilitar la adaptación a patrones complejos y cambiantes de la dinámica del mercado, subsanando las deficiencias de los métodos tradicionales propensos al sobreentrenamiento y a la flexibilidad limitada.

DUET incluye varios módulos clave, cada uno de los cuales cumple una función esencial. La primera etapa del tratamiento de datos consistirá en la normalización y eliminación de los valores atípicos, lo cual aumenta la solidez del modelo.

A continuación viene la clusterización temporal, que divide las series temporales en grupos con dinámicas similares. Esto nos permite considerar los cambios de fase en los procesos de mercado, lo cual resulta especialmente importante para analizar activos con una gran volatilidad.

La clusterización de canales se usa para identificar las variables más sustanciales entre múltiples factores de mercado. Los datos financieros contienen una cantidad significativa de ruido e información redundante, lo cual impide realizar previsiones precisas. DUET analiza las correlaciones entre parámetros y elimina los componentes insignificantes centrando los recursos informáticos en las características clave. El análisis de frecuencia de las señales y los mecanismos de extracción de características latentes hacen que el modelo resulte menos susceptible a las fluctuaciones aleatorias del mercado.

El módulo de fusión de datos sincroniza la información recibida de los módulos temporal y de clusterización de canales, formando una visión unificada del estado del entorno analizado. Esta etapa se basa en el mecanismo de atención enmascarada, que permite al modelo concentrarse en las características más relevantes, minimizando la influencia de los datos no representativos. Como resultado, DUET muestra una gran solidez frente a los cambios dinámicos y mejora la calidad de los pronósticos a largo plazo.

El módulo de previsión final usa características agregadas para calcular los valores futuros de las series temporales. Esta etapa se basa en métodos avanzados de redes neuronales capaces de identificar relaciones no lineales entre indicadores de mercado. La flexibilidad de la arquitectura DUET le permite adaptarse de forma dinámica a diferentes condiciones, eliminando la necesidad de reconfigurar manualmente los parámetros del modelo.

A continuación le mostramos la visualización del framework DUET realizada por el autor.

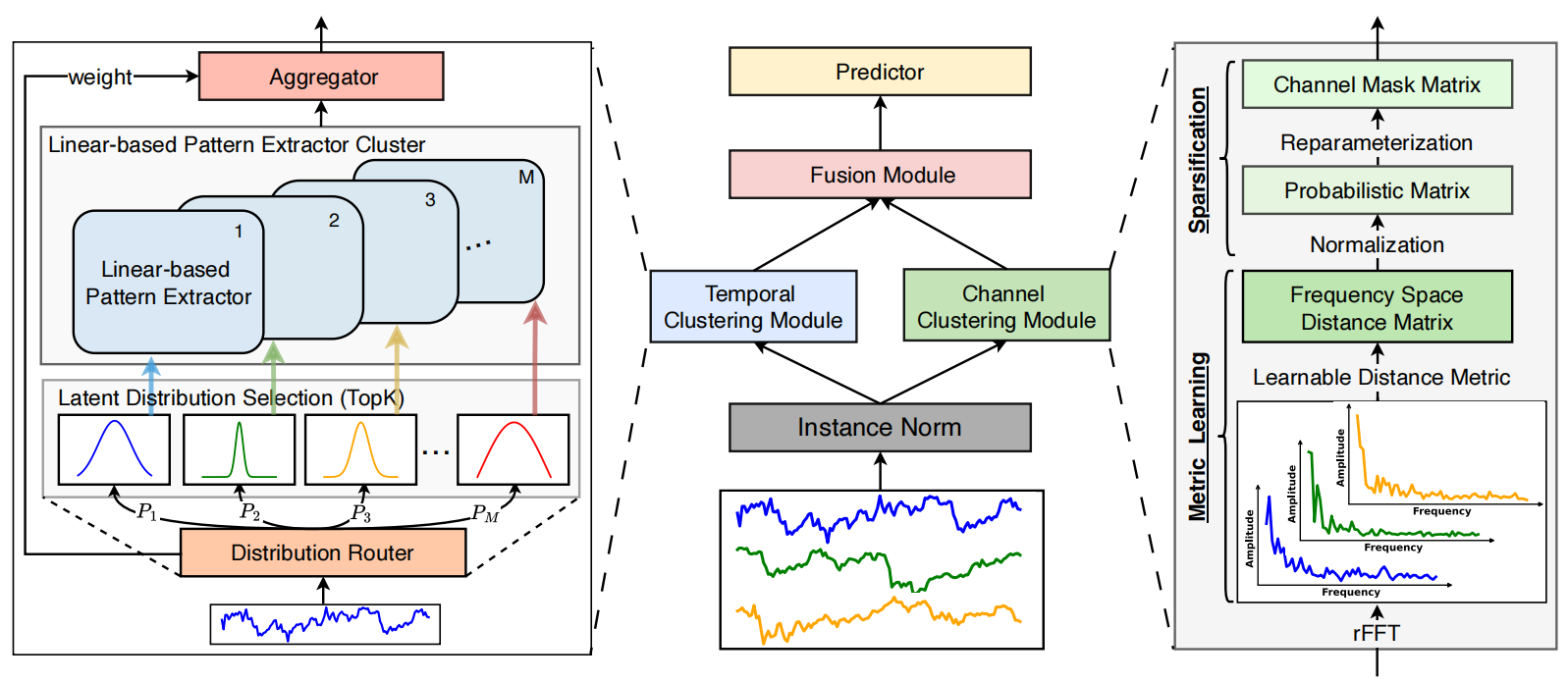
En la parte práctica del artículo anterior, le presentamos una variante de implementación del módulo de clusterización temporal. Hoy continuaremos el trabajo iniciado y construiremos el módulo de clusterización de canales.

Channel Clustering Module

El módulo de clusterización de canales resuelve el problema de la contabilización correcta de los enlaces entre canales al pronosticar series temporales multivariantes. En este caso, los autores del framework DUET usan el aprendizaje métrico para clusterizar canales en el espacio de frecuencias.

Un aspecto clave del CCM es la representación de los datos en el espacio de frecuencias. Para ello, la serie temporal se descompone en componentes de frecuencia usando la transformada rápida de Fourier (FFT). Como resultado, las señales se analizan en el dominio espectral, donde las interconexiones entre canales resultan más evidentes. Muchas dependencias ocultas, imperceptibles en los análisis tradicionales, solo se ponen de manifiesto al pasar al dominio de la frecuencia, lo que hace que este método sea especialmente valioso para las series temporales complejas.

Las interconexiones entre canales se evalúan usando una métrica de distancia entrenada. Como medida básica se usa la representación en la amplitud del espectro de frecuencias de las señales, mientras que los autores del framework proponen calcular la distancia propiamente dicha a partir de una métrica de Mahalanobis modificada. Este método no solo considera las distancias por pares entre canales, sino también sus correlaciones en el espacio espectral.

Tras calcular las distancias entre canales, se forma una matriz de relaciones en la que los coeficientes se normalizan dentro del intervalo [0,1]. Esta normalización permite aislar las relaciones más significativas, eliminando las fluctuaciones aleatorias y poco significativas.

Para el filtrado final de la información, se crea una matriz binaria de enmascaramiento de canales. Este proceso se basa en el muestreo probabilístico, en el que a cada canal se le asigna una probabilidad de utilidad en el pronóstico. Este mecanismo permite considerar la ambigüedad de los datos y evita los umbrales rígidos. Así, el modelo excluye automáticamente los canales irrelevantes, lo cual mejora enormemente la interpretabilidad de los resultados y reduce la redundancia de información.

Como parte de este artículo, vamos a implementar una versión ligeramente simplificada del módulo de clusterización de canales. Ya hemos aplicado anteriormente el algoritmo de la transformada discreta de Fourier como parte de la aplicación del framework de trabajo FITS, y ya se encuentra presente en nuestra biblioteca. En lugar de la métrica de Mahalanobis, se usa un método más sencillo basado en las distancias vectoriales entre las amplitudes de los componentes de frecuencia. Esto conserva las ventajas del análisis de frecuencias, reduciendo la complejidad computacional y simplificando además el algoritmo.

Después de transformar las series temporales en el dominio de la frecuencia, se calculan las normas de los espectros de amplitud de cada canal. Luego se determina su distancia por pares, formando una matriz de conexiones entre canales. Para excluir del análisis posterior las dependencias débiles, se aplica una normalización que suprime el ruido y escala las distancias. Así, solo se conservarán las correlaciones significativas entre canales. A partir de esta matriz, se construye un modelo probabilístico de enlaces. A cada canal se le asigna un peso significativo que refleja su influencia en las demás filas.

El algoritmo descrito lo implementaremos en el kernel MaskByDistance en el lado del programa OpenCL. Los punteros a los 3 búferes de datos se transmiten en los parámetros del kernel. Los dos primeros contienen los datos de origen en forma de partes reales e imaginarias de las señales analizadas. Mientras que el tercero sirve para registrar los resultados del trabajo. En este caso será una matriz de enmascaramiento de canales.

__kernel void MaskByDistance(__global const float *buf_real,
                             __global const float *buf_imag,
                             __global float *mask,
                             const int dimension
                            )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

En el cuerpo del kernel, primero identificamos el flujo actual en el espacio de tareas bidimensional. La primera dimensión indica el canal que hay que analizar, mientras que la segunda indica el canal que hay que comparar. Así se crean grupos de trabajo a partir de los flujos de la segunda dimensión.

Luego se crea un array de datos en la memoria local para el intercambio de datos entre flujos del mismo grupo de trabajo.

__local float Temp[LOCAL_ARRAY_SIZE];
int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

Y determinamos los desplazamientos en los búferes de datos globales.

const int shift_main = main * dimension;
const int shift_slave = slave * dimension;
const int shift_mask = main * total + slave;

Una vez realizado el trabajo preparatorio, podemos pasar directamente a los cálculos y crear un ciclo para determinar la distancia entre dos vectores de amplitud de frecuencia.

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
#pragma unroll
      for(int d = 0; d < dimension; d++)
         dist += pow(ComplexAbs((float2)(buf_real[shift_main + d], buf_imag[shift_main + d])) -
                     ComplexAbs((float2)(buf_real[shift_slave + d], buf_imag[shift_slave + d])), 2.0f);
      dist = sqrt(dist);
     }

Obsérvese que hay elementos diagonales en nuestra matriz de flujo. Creo que habrá adivinado que en este caso el algoritmo calcula la distancia entre dos copias del mismo vector. Obviamente, es igual a "0". Por consiguiente, en estos casos, no ejecutamos un ciclo para determinar la distancia, sino que simplemente almacenamos un valor cero en la variable correspondiente.

A continuación debemos normalizar los valores. Para ello, aplicamos el algoritmo de búsqueda de distancia máxima dentro del grupo de trabajo. Para ello, primero organizamos un ciclo, dentro del cual recopilamos los elementos máximos de subgrupos individuales de flujos en los elementos del array local.

//--- Look Max
#pragma unroll
   for(int i = 0; i < total; i += ls)
     {
      if(i <= slave && (i + ls) > slave)
         Temp[slave % ls] = fmax((i == 0 ? 0 : Temp[slave % ls]), IsNaNOrInf(dist, 0));
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Y luego, encontramos el valor máximo entre los elementos del array local.

int count = ls;
do
  {
   count = (count + 1) / 2;
   if(slave < count && (slave + count) < ls)
     {
      if(Temp[slave] < Temp[slave + count])
         Temp[slave] = Temp[slave + count];
      Temp[slave + count] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);
  }
while(count > 1);

Después normalizamos la distancia entre los vectores de amplitud de frecuencia dentro del grupo de trabajo dividiéndola por el valor máximo.

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];

Creo que resulta obvio que todas las distancias normalizadas están ahora en el intervalo [0, 1]. En este caso, "1" ha recibido el canal más lejano posible. Nosotros, por el contrario, debemos minimizar el impacto de ese canal. Por ello, almacenaremos el valor inverso de la distancia normalizada en el búfer de resultados.

//--- result
   mask[shift_mask] = 1 - IsNaNOrInf(dist, 1);
  }

Y finalizaremos el funcionamiento del kernel.

Debemos destacar una característica importante de nuestra aplicación. En el algoritmo presentado no hay parámetros entrenables, dado que la distancia entre los vectores de amplitud de los espectros de frecuencia es un valor fijo que no depende de otros factores. Esto nos permite eliminar el proceso de propagación inversa del error, reduciendo el coste de la optimización.

La siguiente etapa de nuestro trabajo consiste en organizar la funcionalidad del módulo de clusterización de canales al margen del programa principal. Aquí creamos una nueva clase CNeuronChanelMask, cuya estructura le mostramos a continuación.

class CNeuronChanelMask :  public CNeuronBaseOCL
  {
   //---
protected:
   uint              iUnits;
   uint              iFFTdimension;
   CBufferFloat      cbFFTReal;
   CBufferFloat      cbFFTImag;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im,
                         CBufferFloat *out_re, CBufferFloat *out_im,
                         bool reverse = false);
   virtual bool      Mask(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) { return true; }

public:
                     CNeuronChanelMask(void) {};
                    ~CNeuronChanelMask(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronChanelMask; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

En la estructura presentada, entre los objetos internos ligeramente numéricos, vemos solo 2 búferes para almacenar las partes real e imaginaria de los componentes de frecuencia de la señal analizada. Nos familiarizaremos con mayor detalle con el uso de estos búferes durante la construcción de los algoritmos de los métodos virtuales de la nueva clase.

Los objetos especificados se declaran estáticamente, lo cual significa que podemos dejar vacíos el constructor y el destructor de la clase. La inicialización de los objetos declarados y heredados se realiza en el método Init.

bool CNeuronChanelMask::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                             uint window, uint units_count,
                             ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(window <= 0)
      return false;
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * units_count, optimization_type, batch))
      return false;

En los parámetros del método, como es habitual, obtenemos una serie de constantes que nos permiten interpretar sin ambigüedades la arquitectura del objeto creado:

• window — longitud de la secuencia analizada;
• units_count — número de canales.

Cabe señalar que en la salida del objeto esperamos obtener una matriz cuadrada de enmascaramiento de canales. El tamaño de la matriz de enmascaramiento resultante es igual al número de canales y no depende de la longitud de la secuencia que analizamos. No obstante, necesitamos este parámetro para procesar correctamente los datos de origen. Por ello, primero comprobamos la corrección del parámetro recibido y luego llamamos al método homónimo de la clase padre, que ya implementa algoritmos para la inicialización de interfaces heredadas.

Tras ejecutar con éxito las operaciones del método de la clase padre, guardamos las constantes resultantes.

//--- Save constants
   iUnits = units_count;
   activation = None;

Y aquí me gustaría recordarle que el algoritmo de descomposición rápida de Fourier que implementamos anteriormente solo es aplicable para secuencias cuyo tamaño sea de grado 2. En el caso general esto no es un problema, siempre podemos aumentar el tamaño de la secuencia añadiendo la cantidad correspondiente de números "0" al final del vector. Sin embargo, debemos determinar el valor superior más próximo.

//--- Calculate FFT dimension
   int power = int(MathLog(window) / M_LN2);
   if(MathPow(2, power) != window)
      power++;
   iFFTdimension = uint(MathPow(2, power));

Y solo entonces inicializar los búferes de almacenamiento temporal para las partes real e imaginaria de los componentes de frecuencia de tamaño suficiente.

   if(!cbFFTReal.BufferInit(iFFTdimension * iUnits, 0) ||
      !cbFFTReal.BufferCreate(OpenCL))
      return false;
   if(!cbFFTImag.BufferInit(iFFTdimension * iUnits, 0) ||
      !cbFFTImag.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Con estos damos por completo nuestro trabajo con los métodos de inicialización y podemos proceder a construir el algoritmo de pasada directa dentro del método CNeuronChanelMask::feedForward. Y aquí debo decir que todo resulta bastante sencillo y prosaico.

bool CNeuronChanelMask::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(!FFT(NeuronOCL.getOutput(), NULL, GetPointer(cbFFTReal), GetPointer(cbFFTImag), false))
      return false;
//---
   return Mask();
  }

En los parámetros del método obtenemos el puntero al objeto de datos de origen, cuya relevancia comprobamos de inmediato. Después, dividimos los datos de origen en componentes de frecuencia y llamamos al método-envoltorio del kernel anterior. Luego retornamos el resultado lógico de las operaciones al programa que realiza la llamada y finalizamos el método.

Los métodos para colocar los kernels en la cola de ejecución se basan en el algoritmo que ya conocemos, y no nos detendremos ahora en su consideración.

Como ya hemos dicho, en este caso excluimos los procesos de pasada inversa. Y sobreescribimos los métodos correspondientes con stubs que retornan true todo el tiempo. Este enfoque nos permite incorporar sin problemas un nuevo objeto a la estructura existente de nuestros modelos.

Y con esto podemos concluir nuestro trabajo de construcción de algoritmos para el módulo de clusterización de canales. Podrá leer por sí mismo el código completo de esta clase y todos sus métodos en el archivo adjunto al artículo.

La unidad DUET

En esta fase, ya hemos construido los módulos de clusterización temporal y de canales. Estos dos módulos funcionan en paralelo, analizando las series temporales multivariantes en dos puntos de vista: temporal y frecuencial. Todos los resultados obtenidos se combinan en el módulo Fusion, que integra la información sobre la dependencia del canal mediante un mecanismo de atención enmascarada. Esto permite armonizar las previsiones de los distintos canales considerando las correlaciones detectadas. Fusion adapta el impacto de cada canal teniendo en cuenta el peso de la dependencia entre canales. Como resultado, la predicción final resulta más sólida y el modelo es menos susceptible al sobreentrenamiento y al ruido aleatorio.

En la práctica, usamos un mecanismo de Self-Attention modificado en el que los coeficientes de dependencia derivados de los resultados del módulo de clusterización temporal se multiplican por la máscara generada por el módulo de clusterización de canales. Solo entonces se normalizan los pesos usando la función SoftMax.

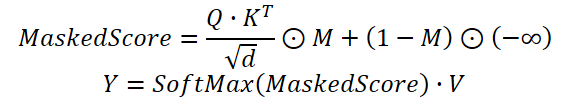
El algoritmo propuesto lo implementamos dentro del objeto CNeuronDUET, que combinará la funcionalidad de los tres módulos mencionados anteriormente. A continuación, le mostramos la estructura de la nueva clase.

class CNeuronDUET :  public CNeuronTransposeOCL
  {
protected:
   uint                       iWindowKey;
   uint                       iHeads;
   //---
   CNeuronTransposeOCL        cTranspose;
   CNeuronMoE                 cExperts;
   CNeuronConvOCL             cQKV;
   CNeuronBaseOCL             cQ;
   CNeuronBaseOCL             cKV;
   CNeuronChanelMask          cMask;
   CBufferFloat               cbScores;
   CNeuronBaseOCL             cMHAttentionOut;
   CNeuronConvOCL             cPooling;
   CNeuronBaseOCL             cResidual;
   CNeuronMHFeedForward       cFeedForward;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionInsideGradients(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronDUET(void) {};
                    ~CNeuronDUET(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint units_out, uint experts, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDUET; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      TrainMode(bool flag)
     {  bTrain = flag; cExperts.TrainMode(bTrain); }
  };

Debemos señalar que, en este caso, la capa de transposición de datos se utiliza como clase padre. Esto se debe a la estructura de los datos de origen.

El modelo toma como entrada una serie temporal multidimensional representada como una matriz en la que cada fila se corresponde con un paso temporal independiente del sistema analizado. No obstante, todos los módulos descritos anteriormente trabajan con series temporales unitarias. Lo mismo ocurre con el módulo de fusión de datos. Para garantizar un procesamiento correcto de la información, los datos de origen se transponen a un formato conveniente para el análisis. Y una vez completadas las operaciones, los resultados se convierten de nuevo a la representación original. Tenemos previsto realizar este último proceso usando la clase padre, lo cual nos permite preservar la coherencia de la estructura de datos y simplificar la integración del módulo.

En la nueva estructura de clases presentada anteriormente, podemos observar un gran número de objetos internos que juegan un papel importante en la construcción de nuestro algoritmo. Conoceremos su funcionalidad con más detalle durante la implementación de los métodos virtuales de esta clase. Ahora debemos observar que todos los objetos se declaran estáticamente, lo que nos permite dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos, incluidos los heredados, se realiza en el método Init.

bool CNeuronDUET::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count,
                       uint heads, uint units_out, uint experts, uint top_k,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, window, units_out, optimization_type, batch))
      return false;

En los parámetros del método de inicialización obtenemos una serie de constantes que nos permiten interpretar sin ambigüedades la arquitectura del objeto creado. Ya conocemos la estructura de los parámetros. Algunos de ellos se han utilizado en la construcción de los módulos de clusterización temporal y de canales comentados anteriormente, mientras que otros se han empleado en las unidades de atención. Solo merece la pena prestar atención al parámetro units_out, que nos permite indicar la longitud deseada de la secuencia a la salida del objeto.

En el cuerpo del método, lo primero que hacemos es llamar al método homónimo de la clase padre, en el que ya están implementados los procesos de control de parte de los parámetros recibidos y de inicialización de las interfaces heredadas.

A continuación, almacenamos los parámetros necesarios en las variables internas.

iWindowKey = MathMax(window_key, 1);
iHeads = MathMax(heads, 1);

Y procedemos a inicializar los objetos internos. Como ya hemos mencionado, debemos transponer los datos de origen antes de iniciar el análisis. Esta función la realiza un objeto especializado.

int index = 0;
if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
   return false;

Luego inicializamos los módulos de clusterización temporal y de canales.

index++;
if(!cExperts.Init(0, index, OpenCL, units_count, units_out, window, experts, top_k, optimization, iBatch))
   return false;
index++;
if(!cMask.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
   return false;

A continuación le mostramos los objetos del módulo de fusión de datos. Se trata esencialmente de un módulo de atención modificado. Aquí primero inicializamos el objeto de generación de las entidades Query, Key y Value. En este caso, usamos una única capa convolucional de generación paralela de tres entidades.

index++;
if(!cQKV.Init(0, index, OpenCL, units_out, units_out, iHeads * iWindowKey * 3, window, 1, optimization, iBatch))
   return false;

Aquí también añadimos 2 objetos para separar las entidades en tensores independientes.

index++;
if(!cQ.Init(0, index, OpenCL, cQKV.Neurons() / 3, optimization, iBatch))
   return false;
index++;
if(!cKV.Init(0, index, OpenCL, cQ.Neurons() * 2, optimization, iBatch))
   return false;

Además almacenamos los coeficientes de atención en el búfer de datos.

if(!cbScores.BufferInit(cMask.Neurons()*iHeads, 0) ||
   !cbScores.BufferCreate(OpenCL))
   return false;

Obsérvese que en todos los casos especificamos los tamaños de los objetos considerando la transposición de la matriz de datos de origen.

A continuación, inicializamos el objeto de resultados de atención multicabeza.

index++;
if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch))
   return false;

Y una capa convolucional de reducción de dimensionalidad para combinar los resultados de diferentes cabezas de atención.

index++;
if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, units_out, window,
                                                                        1, optimization, iBatch))
   return false;
cPooling.SetActivationFunction(None);

Luego añadimos un objeto para registrar los resultados de los enlaces residuales.

index++;
if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch))
   return false;
cResidual.SetActivationFunction(None);

A continuación, según la arquitectura del autor, viene el conocido bloque FeedForward. Sustituiremos este por una variante multicabeza tomada del framework StockFormer.

   index++;
   if(!cFeedForward.Init(0, index, OpenCL, units_out, 4 * units_out, window, 1, heads, optimization, iBatch))
      return false;
//---
   return true;
  }

Y finalizaremos el método retornando el resultado lógico de las operaciones al programa que realiza la llamada.

El siguiente paso en nuestro trabajo consiste en construir un algoritmo de pasada directa dentro del método CNeuronDUET::feedForward.

bool CNeuronDUET::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

En los parámetros del método obtenemos el puntero al objeto de datos de origen, que pasamos inmediatamente al método homónimo del objeto interno de transposición de datos. Y luego seguimos con los resultados de la transposición.

Primero los pasamos al módulo de clusterización temporal para obtener los valores predichos de las secuencias unitarias.

if(!cExperts.FeedForward(cTranspose.AsObject()))
   return false;

A continuación, los resultados de la transposición de los datos de origen se pasan al módulo de clusterización de canales.

if(!cMask.FeedForward(cTranspose.AsObject()))
   return false;

Luego organizamos la pasada directa del módulo de fusión de datos. En primer lugar, generamos las entidades de bloque de atención Query, Key y Value a partir de los resultados del módulo de clusterización temporal.

if(!cQKV.FeedForward(cExperts.AsObject()))
   return false;

Después dividimos los resultados de la operación en 2 tensores.

if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), iWindowKey, 2 * iWindowKey, cQKV.GetUnits()))
   return false;

Y llamamos al método-envoltorio de Self-Attention multicabeza enmascarada.

if(!AttentionOut())
   return false;

Proyectamos los resultados de la atención multicabeza en la dimensionalidad de los resultados del módulo de clusterización temporal.

if(!cPooling.FeedForward(cMHAttentionOut.AsObject()))
   return false;

A los valores obtenidos le añadimos el enlace residual.

if(!SumAndNormilize(cExperts.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1))
   return false;

Nuestro bloque multicabeza FeedForward se implementa como un módulo aparte con enlaces residuales existentes. Por lo tanto, solo debemos llamar al método homónimo de este objeto, transmitiéndole los resultados de las operaciones anteriores como datos de entrada.

if(!cFeedForward.FeedForward(cResidual.AsObject()))
   return false;

Ahora todo lo que debemos hacer es devolver los resultados de las operaciones a las representaciones de datos de origen. Para ello, utilizamos la funcionalidad de la clase padre.

 return CNeuronTransposeOCL::feedForward(cFeedForward.AsObject());
}

Después retornamos el resultado lógico de las operaciones al programa que realiza la llamada y finalizamos el método.

Una vez concluida la organización de los procesos de pasada directa, vamos a construir el algoritmo de pasada inversa. Como sabe, aquí se usan 2 métodos:

• la distribución del gradiente de error entre los objetos internos y los datos de entrada según su influencia en el resultado final, calcInputGradients;
• la optimización de los parámetros del modelo para minimizar el error total, updateInputWeights.

Todos los parámetros entrenados de nuestro bloque DUET en la implementación presentada están contenidos en objetos internos, por consiguiente, su proceso de optimización se reduce a llamar a los métodos homónimos de dichos objetos. Y, por ello resulta más acuciante la cuestión de la correcta distribución del gradiente de error entre los objetos internos y los datos de origen.

En los parámetros del método calcInputGradients, obtenemos el puntero al objeto de datos de origen. Este es el mismo objeto que utilizamos como parte de la pasada directa. Solo que esta vez debemos pasarle los valores de gradiente de error correspondientes.

bool CNeuronDUET::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

Resulta bastante obvio que solo podemos pasar datos a un objeto válido. Por consiguiente, comprobamos inmediatamente la relevancia del puntero recibido. De lo contrario, todas las operaciones posteriores carecerán de sentido.

Como ya sabe, la distribución del gradiente de error se hace con una adhesión explícita a los flujos de información de pasada directa, solo que en la dirección inversa. Ya hemos completado el método de pasada directa llamando al método de la clase padre, por lo tanto las operaciones de pasada inversa también comenzarán llamando al método de la clase padre. Solo que esta vez, llamamos al método de distribución del gradiente de error.

if(!CNeuronTransposeOCL::calcInputGradients(cFeedForward.AsObject()))
   return false;

Luego ejecutamos el gradiente de error a través del módulo FeedForward multicabeza.

if(!cPooling.calcHiddenGradients(cFeedForward.AsObject()))
   return false;

Y distribuimos los valores de gradiente de error obtenidos entre las cabezas de atención.

if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject()))
   return false;

El siguiente paso consiste en llamar al método-envoltorio para distribuir el error entre las entidades Query, Key y Value como parte del mecanismo de Self-Attention enmascarada.

if(!AttentionInsideGradients())
   return false;

Después recopilamos los resultados de las operaciones en un único tensor.

if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), iWindowKey, 2 * iWindowKey, iCount))
   return false;

Si es necesario, corregimos los valores obtenidos mediante la derivada de la función de activación.

if(cQKV.Activation() != None)
   if(!DeActivation(cQKV.getOutput(), cQKV.getGradient(), cQKV.getGradient(), cQKV.Activation()))
      return false;

Después, transmitimos el gradiente al nivel del módulo de clusterización temporal.

if(!cExperts.calcHiddenGradients(cQKV.AsObject()) ||
   !DeActivation(cExperts.getOutput(), cExperts.getPrevOutput(), cPooling.getGradient(), cExperts.Activation()) ||
   !SumAndNormilize(cExperts.getGradient(), cExperts.getPrevOutput(), cExperts.getGradient(), iWindow, false,
                                                                                                   0, 0, 0, 1))
   return false;

Aquí cabe señalar que los resultados del módulo de clusterización temporal también se han utilizado para transmitir los enlaces residuales, por lo que el gradiente de error también debe transmitirse en este flujo de información. Para ello, primero corregimos el gradiente de error a la salida de la unidad de atención considerando la derivada de la función de activación del módulo de clusterización temporal y, a continuación, sumamos los datos de los dos flujos de información.

A continuación, pasamos el gradiente de error por el módulo de clusterización temporal.

   if(!cTranspose.calcHiddenGradients(cExperts.AsObject()))
      return false;

Y lo transmitimos al nivel de datos de origen.

   return prevLayer.calcHiddenGradients(cTranspose.AsObject());
  }

Después retornamos el resultado lógico de las operaciones al programa que realiza la llamada y finalizamos el método.

Obsérvese que el flujo de información del módulo de clusterización de canales está completamente ausente en el proceso de distribución del gradiente de error. Ya hemos hablado antes de la falta de operaciones de pasada directa en este módulo y, en esta fase, nos hemos limitado a eliminar las operaciones obviamente innecesarias.

Con esto concluye nuestro análisis de los algoritmos de construcción de nuestra visión de los enfoques propuestos por los autores del framework DUET. Podrá ver el código completo de todos los objetos presentados y sus métodos en el archivo adjunto al artículo.

Arquitectura del modelo

La siguiente etapa del trabajo consiste en integrar los componentes desarrollados en la arquitectura de los modelos entrenados. Para ello, vamos a describir el diseño arquitectónico de los modelos.

Como en artículos anteriores, aprovecharemos los enfoques de aprendizaje multitarea y entrenaremos 2 modelos simultáneamente: El modelo de Actor y la predicción de las probabilidades de la dirección del próximo movimiento. La arquitectura de este último se toma al completo de trabajos anteriores, por lo que nos centraremos en el análisis de la arquitectura del Actor. La arquitectura de ambos modelos se presenta en el método CreateDescriptions.

bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

En los parámetros del método obtenemos los punteros a 2 objetos dinámicos para registrar la descripción de la arquitectura de los modelos. En el cuerpo del método comprobamos directamente la relevancia de los punteros recibidos y, si es necesario, creamos nuevas instancias de objetos.

La arquitectura del modelo del Actor comienza con una capa totalmente conectada que actúa como interfaz con los datos de origen. Deberá tener el tamaño suficiente para albergar toda la información que se va a analizar.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Al igual como sugieren los autores del framework DUET, a esto le sigue una capa de normalización de datos por lotes, que está diseñada para llevar los datos de origen a una forma comparable y minimizar el impacto de los valores atípicos.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y luego usamos los 2 bloques DUET consecutivos que creamos anteriormente. No obstante, el enfoque de la segmentación de datos ha cambiado. En lugar de la segmentación tradicional, este experimento usa una representación multidimensional del espacio de fases de los datos. Este método, inspirado en los planteamientos del framework Attraos, permite un procesamiento más preciso de las dependencias complejas en las series temporales, mejorando la interpretabilidad del modelo. En la primera capa, usamos un paso de 5 minutos.

En el módulo de clusterización temporal, inicializamos el funcionamiento de 16 codificadores paralelos. Para cada clúster, se seleccionan los 4 más adecuados. 

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDUET;
   descr.window = BarDescr * 5;  // 5 min
     {
      int temp[] = {HistoryBars / 5, HistoryBars / 5, 16, 4}; // {Units in (24), Units out (24), Experts, Top K}
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = 256;
   descr.step = 4;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

En el segundo bloque DUET, aumentamos el paso de representación de fase a 15. No obstante, mantenemos los demás parámetros sin cambios.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDUET;
   descr.window = BarDescr * 15;  // 15 min
     {
      int temp[] = {HistoryBars / 15, HistoryBars / 15, 16, 4}; // {Units in (8), Units out (8), Experts, Top K}
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = 256;
   descr.step = 4;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Tenga en cuenta que no cambiaremos el tamaño del tensor durante el procesamiento de los datos. Pero con la siguiente capa de convolución, reduciremos el tamaño de la secuencia en un factor de 3.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = HistoryBars / 3;
   descr.window = BarDescr * 3;
   descr.step = descr.window;
   int prev_window = descr.window_out = BarDescr;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A continuación viene un bloque de decisión de 3 capas totalmente conectadas.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A esto le sigue una capa de normalización por lotes.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Y en la salida Actor, debemos añadir un bloque de gestión de riesgos.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMacroHFTvsRiskManager;
//--- Windows
     {
      int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = 10;
   descr.window_out = 64;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

La arquitectura completa de ambos modelos figura en el anexo. También se presentan los programas de interacción del entorno y de entrenamiento de modelos, que se han mantenido sin cambios respecto a trabajos anteriores.

Simulación

Hemos trabajado mucho para hacer realidad nuestra propia visión de los enfoques propuestos en el framework DUET usando MQL5 e implementarlos en los modelos entrenados. Ahora viene la fase clave: probar la eficacia de las soluciones aplicadas con datos históricos reales.

Para entrenar los modelos, vamos a formar una muestra de datos históricos del par de divisas EURUSD, marco temporal M1 para todo el año 2024. En el proceso de recogida de datos, se usan los parámetros por defecto del indicador.

El entrenamiento del modelo se realiza en dos fases. En primer lugar, fijamos el tamaño del paquete en 1 para seleccionar un estado aleatorio de la muestra de entrenamiento en cada iteración. Esto ayudará al modelo a adaptarse al nuevo entorno. Sin embargo, esto no resulta suficiente para el correcto funcionamiento de la unidad de gestión de riesgos. Por lo tanto, en la segunda fase de entrenamiento, vamos a aumentar el tamaño de los paquetes a 60, lo cual nos permitirá considerar una secuencia de 60 estados del entorno y las correspondientes acciones del Actor. Esto hace que el aprendizaje sea más estable y eficaz.

El modelo entrenado se pondrá a prueba con los datos históricos de enero-febrero de 2025. Todos los ajustes se guardarán, lo que permite evaluar objetivamente la calidad de las previsiones. Ahora le presentamos los resultados de las pruebas.

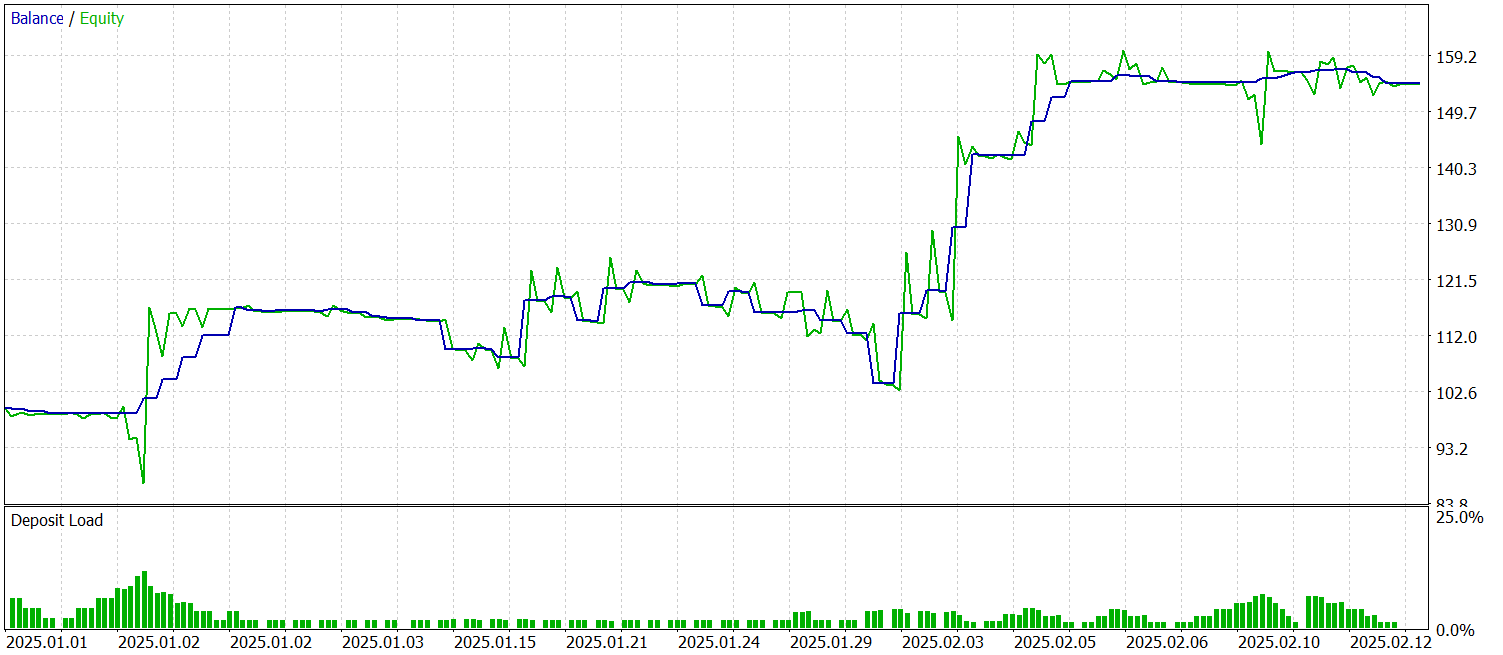
Durante el periodo de prueba, el modelo ha realizado 53 transacciones, más del 56% de las cuales se han cerrado con beneficios. Cabe destacar que la transacción media rentable es casi 2 veces superior al mismo indicador de las posiciones no rentables. Todo ello ha permitido fijar el indicador del factor de beneficio en 2,44.

Conclusión

En este artículo, nos hemos familiarizado con el framework DUET, cuyos autores han combinado el análisis de frecuencias, el aprendizaje métrico y el filtrado probabilístico con el fin de analizar series temporales multivariantes. Todo ello ha contribuido a mejorar la calidad de las predicciones y a hacer el modelo más robusto frente al ruido.  

En la parte práctica, hemos aplicado nuestra visión de los enfoques propuestos utilizando herramientas MQL5 y hemos implementado las soluciones realizadas en el modelo. Además, hemos entrenado el modelo con datos históricos reales y probado el modelo entrenado con datos ajenos a la muestra de entrenamiento. Los resultados indican el potencial del modelo. Sin embargo, antes de usarlo en condiciones comerciales reales, deberemos entrenar el modelo con una muestra más representativa y realizar posteriormente pruebas exhaustivas.

Enlaces

• DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting
• Otros artículos de la serie

Programas usados en el artículo

#	Nombre	Tipo	Descripción
1	Research.mq5	Asesor	Asesor de recopilación de datos
2	ResearchRealORL.mq5	Asesor	Asesor experto para recopilar ejemplos con el método Real-ORL
3	Study.mq5	Asesor	Asesor de entrenamiento de modelos
4	Test.mq5	Asesor	Asesor para la prueba de modelos
5	Trajectory.mqh	Biblioteca de clases	Estructura de descripción del estado del sistema y la arquitectura del modelo
6	NeuroNet.mqh	Biblioteca de clases	Biblioteca de clases para crear una red neuronal
7	NeuroNet.cl	Biblioteca	Biblioteca de código del programa OpenCL