Do básico ao intermediário: Filas, Listas e Árvores (V)

Introdução

No artigo anterior Do básico ao intermediário: Filas, Listas e Árvores (IV), terminamos o que seria o mecanismo básico a fim de criar e manter o que seria uma lista encadeada. Seja ela do tipo simples ou do tipo duplo. Porém apesar de termos viabilizado, o que seria uma implementação de uma lista encadeada, podemos melhorar diversos pontos daquele mesmo modelo de código. Tornando assim as coisas muito mais simples. Pelo menos no que diz respeito a utilização do que foi visto. Ao fazermos tais mudanças, a utilização da lista encadeada passa a ser algo muito mais natural e fácil de entender. Tanto em termos de leitura quando em termos de interpretação do próprio código que estaria sendo implementado. Pelo menos isto ao meu entender.

Porém, toda via e, entretanto, para promover tais melhorias no código, é preciso fazer uso de alguns recursos presentes no MQL5, dos quais ainda não comentei. E como não quero tornar ainda mais complicado, algo que para muitos já é algo bastante confuso e difícil de compreender. Vou deixar para demonstrar como tais mudanças que podem ser promovidas em uma lista encadeada, para serem mostradas em um outro momento, em um futuro não muito distante.

Assim sendo, por hora, vamos nos concentrar naquilo que ainda é o nosso tema principal. Que seria justamente entender os conceitos e diferenças entre fila, lista e árvores. Como já estamos chegando próximo ao que seria o último ponto a ser tratado aqui. Posso começar a falar a respeito de certas coisas interessantes sobre este assunto. Mas para isto, vamos iniciar o que é o tópico principal desta pequena sequência de artigos.

Filas, listas e árvores (V)

Muito bem, chegamos ao nosso quinto artigo, voltado a explicar filas, listas e árvores. Porém antes de entrarmos na questão que será abordada neste artigo. Vamos fazer uma rápida revisão do que já foi visto até aqui.

Começamos vendo o que seria filas e como elas poderiam vir a ser implementadas. Foi demonstrado o tipo de vantagem que elas poderiam nos oferecer, a fim de organizar certos tipos de dados, ou até mesmo eventos em geral. Porém filas tem uma grande desvantagem, que é justamente o fato de não podermos colocar novos elementos, ou remover elementos já existentes, de forma arbitrária. Ou seja, se você desejar remover algo que esteja presente no meio de uma fila, não terá meios de fazer isto. Pelo menos, não de forma rápida e eficiente. Assim como também, não é muito rápido adicionar novos elementos no meio de uma fila.

Por conta desta desvantagem, surgiu a necessidade de se criar um outro tipo de mecanismo. Tal mecanismo, recebeu a denominação de lista. As listas podem ser do tipo simples ou duplamente encadeadas. E o fato de utilizarmos ponteiros a fim de criar uma ligação entre os elementos. Algo que não acontece quando fazermos uso de filas. Permite que venhamos a ter um mecanismo muito eficiente em termos de execução. Isto com o objetivo de adicionar ou remover elementos em uma posição arbitrária, no meio daquilo que agora conhecemos como sendo uma lista. Mas a parte importante de ser lembrada, é justamente o fato de que, uma lista, em boa parte do tempo, pode ser entendida como sendo uma fila melhorada. Podendo inclusive ser utilizada para os mesmos fins dos quais seriam destinados a uma fila. Apesar de precisar de um pouco mais de memória para ser mantida. Isto se comparado com uma fila com o mesmo número de elementos sendo mantidos em memória.

Ok, então se a lista resolve o problema das filas, podendo inclusive as substituir em diversos momentos. Por que das árvores? Onde diabos árvores se encaixariam nesta história toda? Bem, meu caro leitor, árvores são a evolução natural das listas. Tendo um proposito ainda mais nobre. Certo, mas ainda não entendi. Poderia explicar isto melhor, antes de começarmos a ver os códigos? Mas é claro que sim. Acredito que entender o propósito das árvores antes mesmo de ver os códigos, é algo que irá lhe ajudar a entender o próprio código. Para entender árvores, você precisa entender um problema que existe nas listas. E sim, apesar de elas resolverem o problema das filas. As próprias listas têm seus problemas. E por conta disto surgiu a necessidade de ser criar um outro mecanismo, a fim de resolver tal problema. Tal problema se refere justamente a questão de se fazer algum tipo de pesquisa dentro da lista. Não entendi? Como assim?

Para entender isto, você precisa pensar em listas contendo milhares, talvez bilhões de elementos. O que para a maior parte das pessoas pode ser algo impensável. Mas mesmo em lista contendo alguns milhares de elementos, pode ser que venhamos a ter alguns problemas durante a pesquisa. E o problema é justamente o tempo envolvido na própria pesquisa.

Pense o seguinte: Se você admite colocar um dicionário inteiro dentro de uma lista, a fim de criar um corretor de texto. E implementa o sistema de pesquisa de forma a começar na letra A e ir passando palavra por palavra até chegar a última palavra que estaria presente na letra Z. Isto pode parecer bastante prático e viável. Porém, na pratica, não é bem assim. Isto por que, para encontrar certas palavras vai ser bastante demorado. Porém, se você modifica a própria implementação de forma que hora irá começar a pesquisa pela letra A, hora irá começar pela letra Z. Na pior das hipóteses, você irá precisar pesquisar em metade da lista, até encontrar a palavra procurada. O que pode parecer ser algo muito bom. E de fato pode vir a ser isto mesmo. No entanto, podemos melhorar isto ainda mais. Pois se ao invés de começarmos hora pelo início, hora pelo final. Pudermos começar pelo meio da lista. Isto reduziria a pesquisa a um número muito menor de elementos a serem pesquisados. Mesmo em uma lista bastante grande. Que no caso nos daria algo próximo a um quarto da lista a ser pesquisada. Já que dependo da posição selecionada como sendo o meio da lista, poderemos ter mais ou menos elementos de um lado ou de outro.

Acredito que agora você começou a entender o que fez surgir as tais árvores. Em teoria, uma lista não pode ser vista como sendo uma árvore. Porém na prática, uma lista com poucos elementos, cujo elementos estejam distribuídos de uma certa maneira, configura sim o que seria uma árvore. Mesmo que uma árvore desbalanceada.

Agora vem uma questão da qual é muito importante que você entenda, meu caro leitor. Existem diversos tipos de árvores. E cada uma serve para um tipo de proposito particular. Dependendo do objetivo e proposito para qual uma árvore está sendo criada, a mesma pode ser muito diferente do que será visto aqui. Mesmo por que, para explicar todos os tipos, atualmente possíveis, e que podem ser implementados. Seria necessária uma grande quantidade de artigos. E como meu objetivo aqui, é apenas apresentar o conceito para podermos fazer outras coisas no futuro. Deixo a cargo de cada um, procurar pesquisar os demais tipos de árvores. Isto a fim de entender onde cada uma tem maior vantagem em ser utilizada. Aqui irei demonstrar e explicar o que pode ser considerado como sendo um modelo genérico de árvore. Porém como foi dito a pouco, sugiro que você procure estudar este assunto, buscando outros modelos de implementação de árvores. Pois dependendo do problema a ser resolvido, é bem provável que você encontre um modelo, que venha a lhe atender melhor em uma certa questão em particular.

Ok, então vamos começar vendo o que seria a representação, na teoria, de uma árvore muito simples. Esta pode ser visualizada logo abaixo.

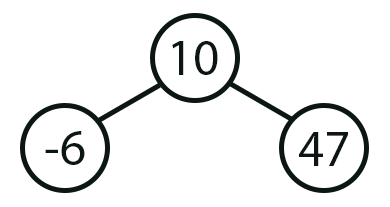
Imagem 01

Mas que coisa estranha. Acho que já vi algo parecido com esta imagem 01. De fato meu caro leitor, esta imagem 01, que trata da representação de uma árvore, isto na teoria, pode ser vista em outras matérias envolvendo programação. Muito provavelmente você já deve ter visto isto, se procurou estudar mecanismos de inteligência artificial. No entanto, normalmente tais mecanismos utilizam um outro conceito ainda mais avançado do que as árvores, que são justamente conhecidos como GRAFOS. Porém, por hora não iremos tratar a respeito de GRAFOS. Já que para falar sobre eles seria preciso entrar em um tipo de abordagem e metodologia, da qual acredito que muitos não estão devidamente preparados para compreender.

No entanto, mesmo sem entrar na questão referente a grafos. Não é nada difícil implementar uma inteligência artificial, usando para isto árvores. Para ser honesto, é perfeitamente possível de se fazer isto. Mas como estamos apenas iniciando o assunto. Vamos dar um passo de cada vez.

Muito bem, existe uma questão da qual é muito importante de ser entendida. E esta está diretamente ligada a esta mesma imagem 01. A questão é a seguinte: Olhando esta imagem 01, e já tendo sido mostrado o que seria uma fila e o que seria uma lista. Você, meu caro leitor, poderia me questiona a respeito de eu estar mencionando que esta imagem 01, seria uma árvore. E você não estaria errado. Muito pelo contrário. Estaria sim demonstrando que conseguiu entender perfeitamente os conceitos referentes a filas e listas. Já que esta mesma imagem 01, poderia ser criada, usando mecanismos, que não estão necessariamente ligados uma implementação de árvore. Ok, então o que você me diria com relação a imagem vista logo abaixo?

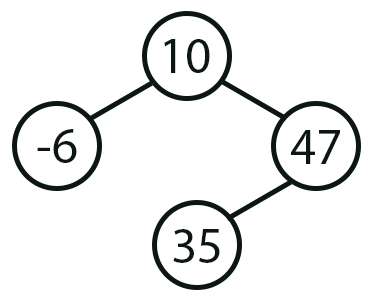
Imagem 02

Agora sim temos uma árvore. Na verdade ainda não meu caro leitor. Da mesma forma que a imagem 01. Aqui na imagem 02, podemos implementar este mesmo tipo de coisa, utilizado um outro tipo de mecanismo. Que não necessariamente precisaria ser uma árvore. Agora preste atenção, o que eu quero mostrar com estas duas imagens, é justamente um problema que muitos iniciantes tem. E acabam não se dando conta. Que é o fato de sempre procurar meios, bem mais complicados, para tentar resolver problemas relativamente simples. O que realmente torna necessário a utilização de uma árvore, em sua implementação é quando algo parecido com a imagem 03, vista logo abaixo, acaba surgindo, durante a fase de modelagem dos dados ou elementos envolvidos na análise.

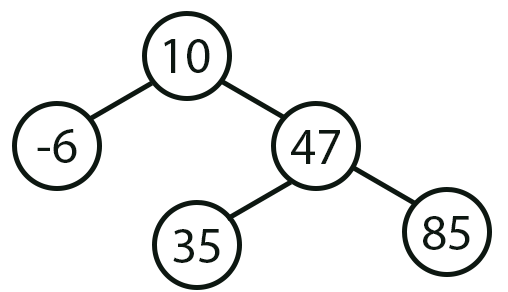
Imagem 03

Agora redobre a sua atenção, pois isto irá lhe ajudar a entender o que iremos implementar. Observe que nas duas primeiras imagens, existia uma única linha ligando cada um dos elementos da imagem. Apesar de existirem árvores construídas daquela maneira. Aquilo pode ser construído, usando mecanismos mais simples. Com seria os mecanismos de fila ou até mesmo o mecanismo de lista. No entanto, nesta imagem 03 temos algo diferente. Isto porque, em um determinado momento, temos uma derivação, que nos possibilita seguir por um outro caminho, mesmo não deixando de manter todos elementos em sua devida localização. E é justamente esta derivação é que faz surgir a tal árvore. Normalmente em implementações simples, como a que iremos ver aqui, temos apenas dois caminhos possíveis. No entanto, existem sistemas, como em casos de se estar utilizando inteligência artificial, podemos ter diversos caminhos, saindo de um único elemento. Mas isto não muda o fato de estarmos lidando com árvores.

Para simplificar o entendimento e também a explicação. Vamos adotar alguns termos aqui. Quando temos um ponto no qual temos algum elemento presente ali, chamaremos este ponto de node, ou nó. Já o caminho que seguimos em direção a um outro elemento, iremos chamar de ramo. E existe um outro termo, que seria o elemento inicial, ou nó inicial de uma árvore. Este elemento recebe uma denominação especial. Então iremos chama-lo de raiz.

Agora, antes de olharmos qualquer código, vamos entender uma outra coisa. Tanto os nodes, quanto os ramos não tem nada de especial neles. Sendo definições muito simples e práticas. Porém, isto não se aplica em relação a raiz. O fato de definimos um ou outro node, como sendo a raiz de uma árvore, muda completamente as características de uma árvore. Muitas das vezes, o simples fato de mudar o node raiz, torna a pesquisa na árvore muito mais eficiente e rápida. Enquanto outras vezes, não estamos interessados na velocidade da pesquisa, mas sim em separar os elementos, em termos de classificação dos mesmos. Daí o fato de que existem implementações de inteligência artificial que fazem uso de árvores. Mas novamente, vamos com calma. Ainda é cedo para se falar a este respeito.

Como o objetivo aqui é a didática e já que fomos apresentados ao que seria o nosso primeiro diagrama de uma árvore. Isto quando olharmos a imagem 03. Podemos começar a implementar algum código, que torna possível criar esta imagem 03. Lembrando que aqui irei mostrar como fazer isto de uma forma o mais genérica possível.

Para começar, uma árvore não é muito diferente do de uma lista duplamente encadeada. Pelo menos não a princípio. Logo você, meu caro leitor, irá conseguir entender isto melhor. Sendo assim, podemos começar com o código visto no artigo anterior, que é replicado logo abaixo.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. //+------------------------------------------------------------------+
004. template <typename T> class stList
005. {
006.     private:
007. //+----------------+
008.         T info;
009.         stList <T>  *prev,
010.                     *start;
011.         uint        counter;
012. //+----------------+
013.     public:
014. //+----------------+
015.         stList(void)
016.             :prev(NULL),
017.             start(NULL),
018.             counter(0)
019.         {}
020. //+----------------+
021.         void Store(T arg, const uint index = 0xFFFFFFFF)
022.         {
023.             stList <T> *loc,
024.                         *ptr1 = start,
025.                         *ptr2 = NULL;
026. 
027.             for (uint c = 0; (ptr1 != NULL) && (c < index); ptr2 = ptr1, ptr1 = (*ptr1).start, c++);
028. 
029.             loc = new stList <T>;
030.             (*loc).info = arg;
031.             (*loc).start = (ptr2 != NULL ? (*ptr2).start : ptr1);
032.             (*loc).prev = (ptr1 != NULL ? (*ptr1).prev : ptr2);
033.             if (ptr2 != NULL) (*ptr2).start = loc; else start = loc;
034.             if (ptr1 != NULL) (*ptr1).prev = loc; else prev = loc;
035. 
036.             counter++;
037.         }
038. //+----------------+
039.         bool Restore(T &arg, const uint index = 0xFFFFFFFF)
040.         {
041.             if ((prev == NULL) || (start == NULL))
042.                 return false;
043. 
044.             stList <T>  *loc = (index < counter ? start : prev),
045.                         *ptr = NULL;
046. 
047.             for (uint c = 0; (loc != NULL) && (c < index) && (index < counter); ptr = loc, loc = (*loc).start, c++);
048.             if (loc == NULL) return false;
049. 
050.             if (index == 0)
051.             {
052.                 start = (*loc).start;
053.                 if (start != NULL) (*start).prev = NULL;
054.             } else if (index >= (counter - 1))
055.             {
056.                 prev = (*loc).prev;
057.                 if (prev != NULL) (*prev).start = NULL;
058.             }
059.             else
060.             {
061.                 (*ptr).start = (*loc).start;
062.                 (*loc).start.prev = ptr;
063.             }
064.             arg = (*loc).info;
065.             delete loc;
066.             counter--;
067. 
068.             return true;
069.         }
070. //+----------------+
071.         bool Exclude(const uint index)
072.         {
073.             T tmp;
074. 
075.             return Restore(tmp, index);
076.         }
077. //+----------------+
078.         void Debug(void)
079.         {
080.             Print("===== DEBUG =====");
081.             for (stList <T> *loc = start; loc != NULL; loc = (*loc).start)
082.                 PrintFormat("0x%06X ->> 0x%06X <<- 0x%06X = [%d]", (*loc).start, loc, (*loc).prev, (*loc).info);
083.             Print("=================");
084.         }
085. //+----------------+
086. };
087. //+------------------------------------------------------------------+
088. void OnStart(void)
089. {
090.     stList <char> list;
091. 
092.     list.Store(10);
093.     list.Store(84);
094.     list.Store(-6);
095.     list.Store(47, 0);
096. 
097.     list.Debug();
098. 
099.     list.Exclude(3);
100.     list.Store(35, 2);
101. 
102.     list.Debug();
103. 
104.     for (char info; list.Restore(info, 0);)
105.         Print(info);
106. };
107. //+------------------------------------------------------------------+

Código 01

Obviamente este código 01, nos permite criar uma lista duplamente encadeada. No entanto, se efetuarmos algumas pequenas mudanças neste mesmo código conseguiremos implementar o que seria a árvore mostrada na imagem 03. Porém, apesar de fazer tais modificações ser algo simples para programadores com experiência. O mesmo não pode ser dito para programadores iniciantes, ou com pouca experiência, como deve ser o caso de muitos de vocês. E por favor, não se sinta mal por ler isto, meu caro leitor. Já que eu mesmo, em algum momento estive na mesma situação em que você se encontra neste momento. Porém, com estudo e um bom tempo praticando, acabei atingindo um bom nível de conhecimento.

Então como sei, que modificar este código 01, que é uma lista duplamente encadeada, para tornar esta lista em uma árvore envolve entender diversas coisas que ainda não foram explicadas aqui, nesta sequência. Vamos fazer algo um pouco diferente. Isto para que a própria didática se mantenha em um patamar o mais elevado, quanto for possível ser feito.

Assim sendo, vamos iniciar com algo bem simples e que funcione. Mesmo que não tenha ainda todas as opções de trabalho, possíveis de serem implementadas em uma árvore. Este código pode ser visto logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. class stTree
05. {
06.     public:
07.         int     info;
08.         stTree  *left,
09.                 *right;
10. };
11. //+------------------------------------------------------------------+
12. stTree *store(stTree *root, stTree *r, int info)
13. {
14.     if (r == NULL)
15.     {
16.         r = new stTree;
17. 
18.         (*r).left = NULL;
19.         (*r).right = NULL;
20.         (*r).info = info;
21.         if (root == NULL) return r;
22.         if (info < (*root).info) (*root).left = r;
23.         else (*root).right = r;
24. 
25.         return r;
26.     }
27.     if (info < (*r).info) return store(r, (*r).left, info);
28.     return store(r, (*r).right, info);
29. }
30. //+------------------------------------------------------------------+
31. void inorder(stTree *root)
32. {
33.     if (root == NULL) return;
34. 
35.     inorder((*root).left);
36.     if (root != NULL) Print((*root).info);
37.     inorder((*root).right);
38. }
39. //+------------------------------------------------------------------+
40. void OnStart(void)
41. {
42.     stTree *root = NULL;
43. 
44.     root = store(root, root, 10);
45.     store(root, root, -6);
46.     store(root, root, 47);
47.     store(root, root, 35);
48.     store(root, root, 85);
49. 
50.     inorder(root);
51. }
52. //+------------------------------------------------------------------+

Código 02

Eu sei, não precisa ficar incomodado com este código 02, meu caro leitor. Eu sei que você deve estar um tanto quanto assustado, com relação a como este código 02 funciona. No entanto, nada do que está sendo feito aqui, é de fato novidade. Talvez apenas esteja um pouco diferente. Mas todas as partes vistas neste código 02, já foram explicadas em outros artigos, nesta mesma sequência. Porém, quando você o executar, irá ver no terminal do MetaTrader 5, algo que é mostrado logo abaixo.

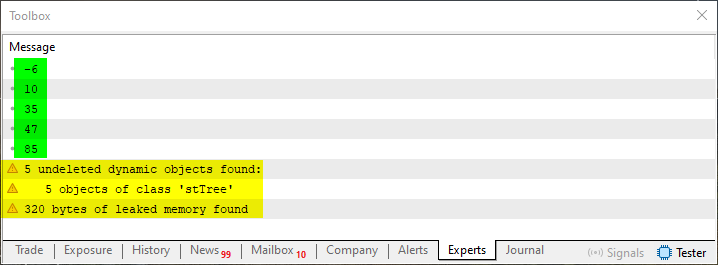
Imagem 04

Nesta imagem 04 estou destacando duas informações. A informação em amarelo, é um alerta que o MetaTrader 5 sobre o fato de que a memória alocada na linha 16, deste código 02, não está sendo devolvida para o sistema. No entanto, por hora, podemos conviver com estes alertas. Visto que eles não afetam de maneira alguma, o resultado do que estamos fazendo. Já esta informação em verde é justamente o que nos interessa de fato. Isto por que, aqui estamos criando o que seria a árvore vista na imagem 03.

Mas espere um pouco aí. Como assim? Na imagem 03 estamos vendo uma árvore, porém nesta região em verde, destacada na imagem 04, me parece ser uma lista de valores. De fato, isto é verdade, meu caro leitor. Porém existe uma forma de provar que aqui não estamos lidando com uma lista e sim com uma árvore. E a forma de provar isto, é justamente a possibilidade de podermos ler os dados em qualquer ordem sem muito trabalho. Mas antes de demonstrar isto, vamos entender rapidamente como este código 02 funciona. Se você observar irá ver que dentro do procedimento OnStart estamos utilizando uma função, cujo objetivo é o de criar a árvore propriamente dita. Assim como temos um procedimento, a fim de visualizar a árvore.

Mas como estas coisas funcionam? Bem, para começar, observe na linha quatro, onde estamos declarando a estrutura a ser utilizada na árvore. Preste atenção, pois apesar de estamos utilizando a palavra class aqui, você deve entender isto como sendo uma struct. Note que temos dois ponteiros, um para ser usado no ramo a direita e outro para o ramo a esquerda. Poderíamos ter muitos outros. Mas vamos nos manter no básico e simples. Ok, tendo definido esta estrutura que ser parece muito com a estrutura vista no código 01, isto dentro da clausula private vista na linha seis do código 01. Podermos começar a implementar a função de criação da árvore. Esta é vista na linha 12 do código 02.

Esta função é recursiva, no artigo Do básico ao intermediário: Recursividade, expliquei o que seria esta tal recursividade. Pois bem a parte recursiva da mesma se encontra justamente nas linhas 27 e 28. Mas a parte que aloca e adiciona novos elementos na árvore está dentro do comando if, visto na linha 14. Basicamente esta parte do código, fará algo muito similar ao que é feito entre as linhas 29 e 34 do código 01. Porém, aqui no código 02, este código entre as linhas 14 e 26 está de fato criando a árvore. Mas preste atenção a um fato aqui. Diferente do que era feito na lista encadeada, onde indicávamos qual o índice a ser usado pelo elemento. Aqui, testamos o elemento com elementos já presentes na árvore. Isto com o objetivo de criar uma árvore já ordenada.

Hum, acho que estou entendendo. Por isto que você disse que ao implementarmos uma árvore, precisaríamos pensar no que estamos tentando fazer. Por isto que quando lemos o conteúdo dá árvore, vemos os dados na ordem correta.

Bem, é mais ou menos isto, meu caro leitor. No entanto, os elementos dentro da árvore não estão necessariamente ordenados. Não da forma como você estaria imaginando. Na verdade, quem faz esta ordenação é justamente o procedimento de leitura, que é mostrado na linha 31. Mas espere um pouco aí. Como assim? Agora definitivamente acabei ficando bastante confuso. Você acabou de dizer que a função da linha 12 está ordenamos os elementos conforme a árvore vai sendo construída. E de fato, observando as linhas 22 e 27, posso notar que os elementos com um valor menor irão ficar nos ramos da esquerda. E elementos com valor maior serão direcionados ao ramo da direita. Imaginei que isto já seria o suficiente para colocar os elementos em ordem dentro da árvore. Mas aí, você vem e diz que quem faz isto é o procedimento de leitura? Isto para mim não faz o mínimo sentido.

Calma meu caro leitor, você logo irá entender. Mas antes note o seguinte: Este procedimento da linha 31, que também é recursivo, irá começar no node raiz, e irá a princípio procurar o elemento mais à esquerda. Até não haver nenhum elemento ali. Isto é feito pela linha 35. Quando esta linha 35 retornar, iremos começar a imprimir os valores daquele node. Logo depois iremos iniciar uma nova procura, só que agora a direita. Isto é feito pela linha 37. No entanto, observe o fato de que ao fazermos isto, iremos retornar novamente a execução da linha 35. E isto fará com que um novo ramo a esquerda seja vistoriado.

A parte que interessa aqui, é justamente esta onde estamos navegando dentro da árvore, buscando os elementos usando um certo caminho. E como durante a fase de criação da árvore, os elementos de menor valor, foram sendo colocados a esquerda dos de maior valor. Acabamos assim criando uma certa ordenação, que para ser visualizada, precisa ser lida de uma determinada maneira.

No entanto, se mudarmos a forma de ler a árvore, podemos ter um resultado completamente diferente. Para demonstrar isto, vamos ver o código logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. class stTree
05. {
06.     public:
07.         int     info;
08.         stTree  *left,
09.                 *right;
10. };
11. //+------------------------------------------------------------------+
12. stTree *store(stTree *root, stTree *r, int info)
13. {
14.     if (r == NULL)
15.     {
16.         r = new stTree;
17. 
18.         (*r).left = NULL;
19.         (*r).right = NULL;
20.         (*r).info = info;
21.         if (root == NULL) return r;
22.         if (info < (*root).info) (*root).left = r;
23.         else (*root).right = r;
24. 
25.         return r;
26.     }
27.     if (info < (*r).info) return store(r, (*r).left, info);
28.     return store(r, (*r).right, info);
29. }
30. //+------------------------------------------------------------------+
31. string inorder(stTree *root)
32. {
33.     static string sz0 = "In Order: ";
34. 
35.     if (root == NULL) return sz0;
36. 
37.     inorder((*root).left);
38.     sz0 += (root != NULL ? StringFormat("%d  ", (*root).info) : "");
39.     inorder((*root).right);
40. 
41.     return sz0;
42. }
43. //+------------------------------------------------------------------+
44. string preorder(stTree *root)
45. {
46.     static string sz0 = "Pre Order: ";
47. 
48.     if (root == NULL) return sz0;
49. 
50.     sz0 += (root != NULL ? StringFormat("%d  ", (*root).info) : "");
51.     preorder((*root).left);
52.     preorder((*root).right);
53. 
54.     return sz0;
55. }
56. //+------------------------------------------------------------------+
57. string postorder(stTree *root)
58. {
59.     static string sz0 = "Post Order: ";
60. 
61.     if (root == NULL) return sz0;
62. 
63.     postorder((*root).left);
64.     postorder((*root).right);
65.     sz0 += (root != NULL ? StringFormat("%d  ", (*root).info) : "");
66. 
67.     return sz0;
68. }
69. //+------------------------------------------------------------------+
70. void OnStart(void)
71. {
72.     stTree *root = NULL;
73. 
74.     root = store(root, root, 10);
75.     store(root, root, -6);
76.     store(root, root, 47);
77.     store(root, root, 35);
78.     store(root, root, 85);
79. 
80.     Print(inorder(root));
81.     Print(preorder(root));
82.     Print(postorder(root));
83. }
84. //+------------------------------------------------------------------+

Código 03

Agora preste muita, mas muita atenção, meu caro leitor. Perceba que o código 03 não mudou frente ao que era o código 02. Porém, adicionamos, duas novas forma de ler a árvore. Isto para que pudéssemos utilizar um caminho diferente a fim de visualizar o conteúdo da mesma. Estas formas podem ser vistas nas linhas 44 e 57. Mas é claro que para facilitar a leitura, já que iremos estar imprimindo muitas informações, mudei um pouco o código a fim de retornar uma string, para ser impressa depois.

Neste caso observe o procedimento OnStart. Ele continua praticamente igual era no código 02. No entanto, quando executamos este código 03, o resultado apresentado é mostrado na imagem logo na sequência.

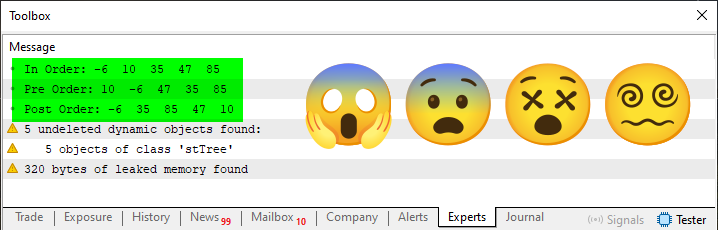
Imagem 05

Novamente, a parte que nos interessa aqui está sendo destacada em verde, nesta imagem 05. Observe o seguinte: Apesar da árvore ter sido construída da mesma maneira, o resultado apresentado irá depender de como estaremos lendo a árvore. Mas também irá depender de como inserirmos os valores na árvore. Mas como assim? Não entendi esta sua colocação. Calma meu caro leitor. Tenha calma, já vamos chegar lá. Primeiro vamos entender esta imagem 05. Observe que nela temos uma linha com os valores na ordem crescente, que é o resultado da execução da linha 80 do código 03. Temos os valores no que seria uma pre ordenação e uma linha onde os valores estariam no que seria uma pós ordenação. Cada uma destas linha nos diz onde começamos a ler a árvore. Porém, e para explicar justamente o fato de que a ordem em que inserirmos os valores, faz com que estas leituras resultem em dados diferentes. Vamos modificar um pequeno detalhe neste código 03. Este detalhe é mostrado no fragmento logo abaixo.

                   .
                   .
                   .
69. //+------------------------------------------------------------------+
70. void OnStart(void)
71. {
72.     stTree *root = NULL;
73. 
74.     root = store(root, root, 10);
75.     store(root, root, -6);
76.     store(root, root, 85);
77.     store(root, root, 35);
78.     store(root, root, 47);
79. 
80.     Print(inorder(root));
81.     Print(preorder(root));
82.     Print(postorder(root));
83. }
84. //+------------------------------------------------------------------+

Fragmento 01

Agora veja o resultado logo abaixo.

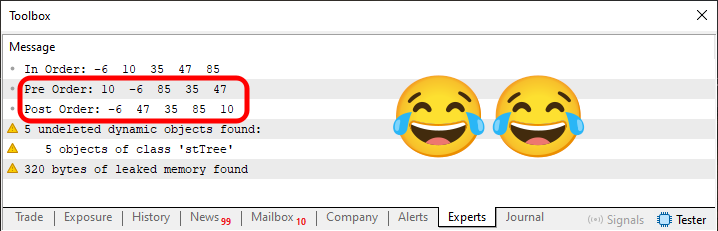
Imagem 06

É de chorar de tanto rir. Note que a mudança no código é muito sutil. Praticamente imperceptível. Porém o resultado é pode ser muito diferente do esperado. Sofri muito quando estava começando a programar e me deparava com este tipo de coisa. Muitos não percebem ou entendem isto. Mas se você comparar a ordem dos elementos vistos na leitura da linha Pre Order, irá perceber que é exatamente a mesma ordem, em que adicionamos os elementos. Doido não é mesmo? Por isto mencionei no início deste artigo, que árvores são coisas que merecem ser estudadas com muita calma e atenção.

Não ache que já entendeu o assunto apenas por conta que sabe como implementar este ou aquele código. Este tipo de mecanismo é muito, mas muito interessante mesmo. Tendo diversas aplicações em diferentes áreas e campos, ligados a análise de dados.

Considerações finais

Neste artigo começamos a trabalhar com a implementação do mecanismo de árvore. Como sei que este mecanismo pode ser extremamente complicado de ser compreendido e assimilado, no começo do aprendizado. Não irei me aprofundar ainda mais nele, neste artigo. Iremos ver isto aos poucos. Mesmo que no final das contas, venhamos a implementar e demonstrar apenas o que seria um mecanismo básico e genérico que permite a criação do que seria uma árvore.

No entanto, quero que você, meu caro leitor, tenha a sua curiosidade despertada. Isto a fim de perceber que existem mecanismos muito simples e rápidos para conseguir um determinado tipo de resultado. E para chegar neste ponto, é necessário que você entenda muito bem, como uma árvore funciona. Isto a fim de conseguir entender, um mecanismo de inteligência artificial que iremos implementar em breve. Algo muito divertido, simples e que funciona de maneira muito surpreendente.

Então procure estudar com calma este artigo, e os demais, a fim de assimilar o máximo do que foi mostrado aqui. Pois no próximo artigo iremos continuar a implementar este mecanismo de árvore genérica.

MQ5	Descrição
Code 01	Árvore Simples
Code 02	Árvore Simples
Code 03	Árvore Simples