Redes neurais no trading: Dupla clusterização de séries temporais (DUET)

Introdução

As séries temporais multivariadas consistem em uma sequência de dados em que cada marca temporal contém várias variáveis interrelacionadas, que caracterizam processos complexos. São amplamente utilizadas em análises econômicas, gestão de riscos e em outras áreas que exigem a previsão de dados multivariados. Ao contrário das séries temporais unidimensionais, as multivariadas permitem considerar as correlações entre variáveis, o que possibilita construir previsões mais precisas.

Nos mercados financeiros, a análise de séries temporais multivariadas é utilizada para prever preços de ativos, avaliar a volatilidade, identificar tendências e desenvolver estratégias de negociação. Na previsão do preço das ações, por exemplo, são considerados fatores como o volume de negociações, as taxas de juros, os indicadores macroeconômicos e as notícias. Todos esses parâmetros estão interligados e, quando analisados conjuntamente, permitem identificar padrões que não seriam detectáveis se cada variável fosse examinada isoladamente.

O principal desafio no processamento de séries temporais multivariadas é desenvolver métodos capazes de identificar dependências temporais e entre canais. No entanto, na prática, surgem dificuldades associadas à variabilidade dos dados. Durante períodos de crises econômicas, as estruturas de correlação entre ativos se modificam, o que dificulta o uso de modelos tradicionais.

Os métodos existentes de processamento de dados podem ser divididos em três categorias. A primeira abordagem consiste na análise independente de cada canal, mas isso ignora as inter-relações entre variáveis. A segunda abordagem combina todos os canais, porém isso pode introduzir informações desnecessárias e reduzir a precisão. A terceira abordagem utiliza a clusterização de variáveis, mas limita a flexibilidade do modelo.

Para resolver esses problemas, os autores do trabalho "DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting" propuseram o método DUET, que combina dois tipos de clusterização: temporal e de canais. A clusterização temporal (TCM) agrupa os dados com base em características semelhantes e permite que os modelos se adaptem às mudanças ao longo do tempo. Na análise de mercados financeiros, isso possibilita considerar diferentes fases dos ciclos econômicos. Já a clusterização de canais (CCM) identifica as variáveis-chave, eliminando o ruído e aumentando a precisão das previsões. Ela revela relações estáveis entre ativos, o que é especialmente importante para a construção de portfólios de investimento diversificados.

Depois disso, os resultados são combinados pelo módulo Fusion Module (FM), que sincroniza as informações sobre os padrões temporais e as dependências entre canais. Essa abordagem permite prever com maior precisão o comportamento de sistemas complexos, como os mercados financeiros. Os experimentos realizados pelos autores do framework demonstraram que o DUET supera os métodos existentes, fornecendo previsões mais precisas. Ele considera padrões temporais heterogêneos e a dinâmica das conexões entre canais, adaptando-se à variabilidade dos dados.

O algoritmo DUET

A arquitetura do framework DUET representa uma abordagem inovadora para a previsão de séries temporais multivariadas, utilizando uma dupla clusterização dos dados brutos nos eixos temporal e de canais. Isso melhora a qualidade do desempenho do modelo e torna seus resultados mais interpretáveis. A abordagem pode ser comparada ao trabalho de um analista experiente que divide um sistema complexo de dados em blocos separados, analisando-os individualmente e, em seguida, em conjunto, para obter uma visão mais detalhada. O framework DUET inclui vários módulos principais, cada um desempenhando um papel especializado no processo de análise de dados:

1. Normalização dos dados brutos (Instance Normalization).
2. Módulo de clusterização temporal (Temporal Clustering Module — TCM).
3. Módulo de clusterização de canais (Channel Clustering Module — CCM).
4. Módulo de fusão de informações (Fusion Module — FM).
5. Módulo de previsão (Prediction Module).

A normalização dos dados brutos permite eliminar valores atípicos e suavizar oscilações abruptas, tornando o modelo mais robusto em relação às diferenças entre os conjuntos de treinamento e de teste. Isso é especialmente importante na análise de dados financeiros, em que o ruído de alta frequência pode mascarar tendências relevantes. A normalização também ajuda a equilibrar as características estatísticas de séries temporais unitárias provenientes de diferentes fontes, reduzindo o impacto de valores anômalos.

Temporal Clustering Module (TCM) analisa as dependências temporais e agrupa as sequências em clusters, de modo semelhante ao que analistas financeiros fazem ao classificar ativos segundo sua volatilidade, liquidez e histórico. A base do funcionamento do TCM é uma arquitetura composta por vários codificadores paralelos (Mixture of Experts — MoE), o que permite selecionar dinamicamente os mais adequados para cada segmento analisado, conforme a clusterização temporal realizada anteriormente. Isso garante uma representação precisa das sequências temporais, já que diferentes grupos de dados podem exigir métodos de processamento específicos. O MoE alterna de forma adaptativa entre os codificadores, permitindo que o modelo trabalhe de maneira eficiente com séries temporais de naturezas distintas, incluindo dados de mercado de alta frequência.

Os codificadores analisam as séries temporais apresentadas sob a forma de características ocultas, que são então decompostas em tendências de longo e curto prazo. Isso permite revelar padrões ocultos que melhoram a previsão das futuras variações de preços nos mercados financeiros.

O Channel Clustering Module (CCM) realiza a clusterização dos canais utilizando as características de frequência dos sinais. Esse módulo avalia as correlações entre os canais, identificando dependências-chave e eliminando componentes redundantes ou insignificantes. De maneira análoga a um analista financeiro que seleciona indicadores macroeconômicos e técnicos relevantes, descartando flutuações aleatórias do mercado, CCM ajuda a destacar os sinais mais informativos.

A análise das distâncias entre os vetores de amplitude das características de frequência dos canais permite determinar sinais correlacionados e eliminar ruídos. Isso é particularmente útil nos mercados financeiros, onde as dependências ocultas entre ativos podem ser exploradas na construção de estratégias de arbitragem ou na identificação de riscos sistemáticos.

O Fusion Module (FM) combina as representações temporais e de canais utilizando um mecanismo de atenção mascarada. Esse processo se assemelha à análise de inter-relações complexas entre diferentes fatores de mercado, quando o analista sintetiza informações de múltiplas fontes para obter uma visão completa. O FM identifica os clusters mais relevantes e filtra os sinais irrelevantes, aumentando a precisão das previsões. O uso do mecanismo de atenção mascarada permite alterar dinamicamente a importância dos diferentes componentes dos dados, tornando o processamento mais adaptativo. Isso é de importância crítica em aplicações financeiras, onde a estrutura de dependências entre ativos pode se modificar sob a influência de eventos macroeconômicos.

Na etapa final, o Prediction Module utiliza as características agregadas para prever os valores futuros das séries temporais. Esse processo pode ser comparado ao trabalho de um investidor profissional, que, com base em dados históricos de mercado, formula previsões fundamentadas sobre futuras variações de preços. O Prediction Module utiliza métodos de redes neurais capazes de capturar dependências não lineares complexas e de se adaptar a possíveis mudanças estruturais nos dados. As previsões finais passam por uma etapa de normalização inversa, o que permite interpretá-las na escala dos dados originais.

Graças à aplicação de métodos avançados de aprendizado de máquina, como o mecanismo de atenção mascarada, a análise das características de frequência e a clusterização de características ocultas, o DUET oferece alta precisão e interpretabilidade nas previsões. Ele ajuda a identificar padrões ocultos em sequências temporais complexas e aplicar o conhecimento obtido para otimizar estratégias de trading, nas quais as abordagens tradicionais se mostram insuficientemente eficazes. Em comparação com os métodos convencionais, que exigem considerável ajuste manual e intervenção de especialistas, o DUET identifica automaticamente as estruturas dos dados e se adapta a elas em tempo real. Isso o torna especialmente útil para a análise de séries temporais de alta frequência e para operar em um ambiente de mercado em constante mudança.

A visualização elaborada pelos autores do framework DUET é apresentada abaixo.

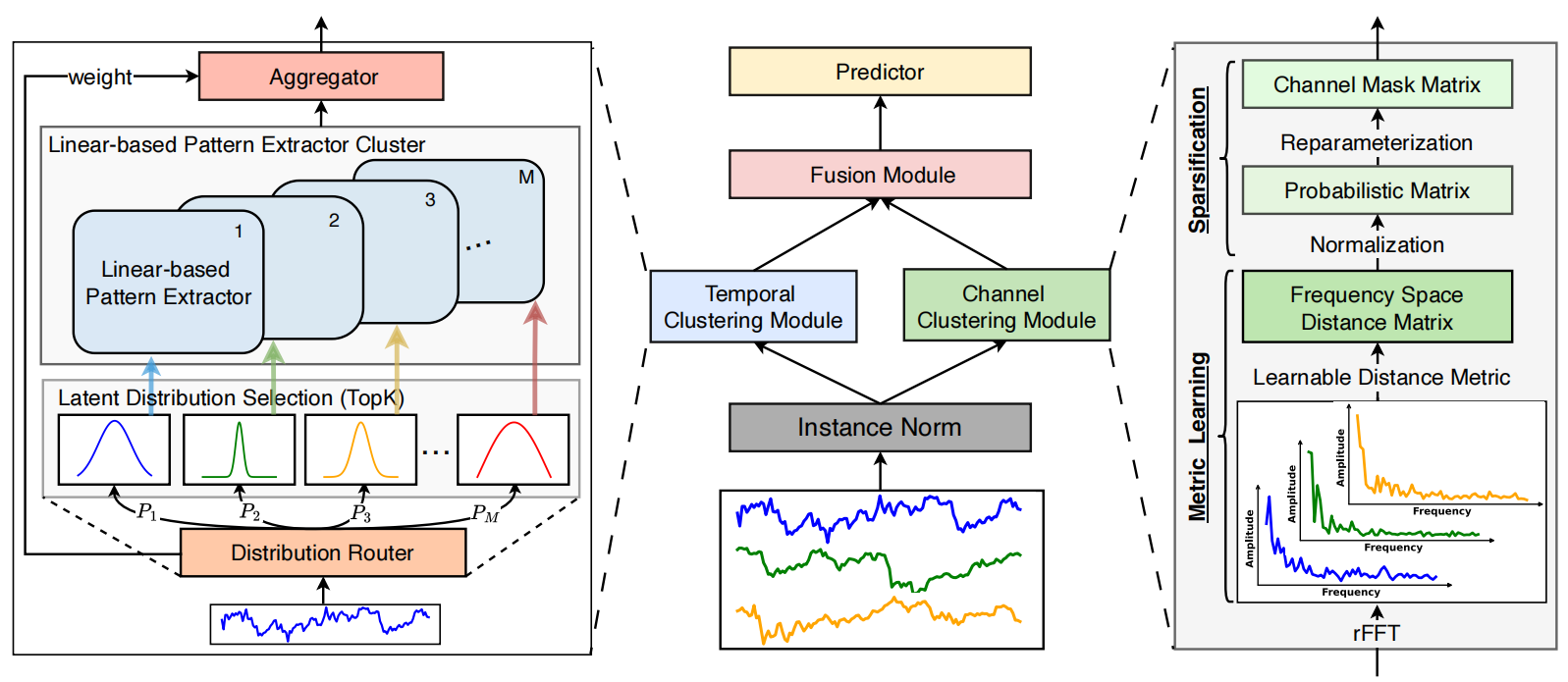
Implementação com os recursos do MQL5

Após a análise detalhada dos aspectos teóricos do framework DUET, passamos à parte prática do trabalho, na qual implementaremos nossa própria visão das abordagens propostas utilizando os recursos do MQL5.

A arquitetura modular do DUET o torna conveniente para um desenvolvimento passo a passo: cada bloco funcional pode ser tratado como um elemento independente do sistema. A divisão em módulos autônomos simplifica o processo de depuração, teste e posterior otimização. E começaremos o trabalho construindo o módulo de clusterização temporal.

Temporal Clustering Module

Como já foi mencionado anteriormente, o módulo de clusterização temporal inclui vários codificadores que operam em paralelo. No âmbito deste trabalho, criaremos uma arquitetura de codificador o mais simples possível, composta por duas camadas totalmente conectadas em sequência, com a introdução de uma não linearidade entre elas por meio de uma função de ativação. No entanto, é importante considerar que cada codificador processa segmentos independentes utilizando seus próprios parâmetros treináveis. Para estruturar esse tipo de operação, utilizaremos camadas convolucionais. Ao alimentar a sequência completa dos dados brutos na entrada, definiremos o tamanho da janela de análise e o passo iguais ao tamanho do segmento. Como resultado, os parâmetros da camada convolucional desempenharão o papel da camada totalmente conectada do codificador, garantindo o processamento paralelo de todos os segmentos da sequência. E, para aumentar o número de codificadores operando em paralelo, basta multiplicar o número de filtros da camada convolucional.

Definimos a organização do trabalho paralelo dos codificadores. No entanto, é importante observar que os autores do framework DUET propõem o uso apenas dos codificadores mais relevantes. Parte-se do pressuposto de que as séries temporais seguem uma distribuição normal latente. Como sabemos, a distribuição normal é caracterizada por um valor médio e uma variância. Para selecionar as k distribuições latentes mais prováveis, os autores do framework utilizam o método "Noisy Gating", que pode ser representado da seguinte forma:

A adição de ruído com distribuição normal (ε) estabiliza o treinamento, enquanto o Softplus mantém a variância positiva.

Em seguida, selecionam-se as k distribuições latentes mais prováveis e calculam-se seus pesos utilizando a função SoftMax. Assim, as séries temporais pertencentes às mesmas k distribuições latentes mais prováveis são processadas por um grupo comum de codificadores. A multiplicação da máscara obtida pelos resultados do trabalho dos codificadores permite gerar um resultado ponderado e eliminar a influência de filtros irrelevantes.

Definida a solução arquitetônica, passamos à implementação. Primeiramente, realizaremos o algoritmo de seleção dos k codificadores mais relevantes. A parametrização dos parâmetros de distribuição dos segmentos individuais será feita utilizando uma camada convolucional. Já o algoritmo de seleção dos k codificadores mais relevantes será implementado no lado do contexto OpenCL. Para isso, criaremos o kernel TopKgates.

__kernel void TopKgates(__global const float *inputs,
                        __global const float *noises,
                        __global float *gates,
                        const uint k)
  {
   size_t idx = get_local_id(0);
   size_t var = get_global_id(1);
   size_t window = get_local_size(0);
   size_t vars = get_global_size(1);

Nos parâmetros do kernel, obtemos ponteiros para 3 buffers de dados (dados brutos, ruído e resultados) e o número de elementos a serem selecionados.

No corpo do kernel, como de costume, identificamos primeiro o fluxo atual dentro do espaço de tarefas. Nesse caso, é utilizado um espaço bidimensional de tarefas, com agrupamento local ao longo da primeira dimensão, que reúne os fluxos pertencentes a um mesmo segmento e corresponde à quantidade de codificadores utilizados pelo modelo.

Em seguida, definimos o deslocamento nos buffers locais de dados.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

E carregamos os dados de entrada correspondentes.

   float logit = IsNaNOrInf(inputs[shift_logit], MIN_VALUE);
   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise != 0)
     {
      noise *= Activation(inputs[shift_std], 3);
      logit += IsNaNOrInf(noise, 0);
     }

Se o ruído não for igual a "0", ajustamos o valor da variável logit levando em consideração a variância e o ruído.

Depois disso, precisamos determinar os k maiores valores de logit dentro de um mesmo grupo de trabalho. Para esse fim, criamos um array na memória local, utilizado para troca de dados entre os fluxos do grupo de trabalho, e declaramos variáveis locais auxiliares.

   __local float temp[LOCAL_ARRAY_SIZE];
//---
   const uint ls = min((uint)window, (uint)LOCAL_ARRAY_SIZE);
   uint bigger = 0;
   float max_logit = logit;

Em seguida, declaramos um laço que percorre os elementos do grupo de trabalho com um passo igual ao tamanho do array local.

//--- Top K
#pragma unroll
   for(int i = 0; i < window; i += ls)
     {
      if(idx >= i && idx < (i + ls))
         temp[idx % ls] = logit;
      barrier(CLK_LOCAL_MEM_FENCE);

No corpo do laço, os elementos da janela atual armazenam seus valores no array local, com a obrigatória sincronização subsequente dos fluxos do grupo de trabalho.

Em seguida, criamos um laço aninhado, dentro do qual, em cada iteração, cada fluxo calcula quantos elementos no array local são maiores que o valor logit do fluxo atual.

      for(int i1 = 0; (i1 < min((int)ls,(int)(window-i)) && bigger <= k); i1++)
        {
         if(temp[i1] > logit)
            bigger++;
         if(temp[i1] > max_logit)
            max_logit = temp[i1];
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Paralelamente, procuramos o valor máximo dentro do grupo local.

Após a execução de todas as iterações do laço interno, sincronizamos novamente o trabalho dos fluxos do grupo e, somente depois disso, passamos para a próxima iteração do laço externo.

É evidente que apenas os k fluxos com os maiores valores de logit não atingem o limite de elementos excedentes. Esses são os valores que salvamos no buffer de resultados.

   if(bigger <= k)
      gates[shift_gate] = logit - max_logit;
   else
      gates[shift_gate] = MIN_VALUE;
  }

Nos demais casos, gravamos no buffer de resultados uma constante de valor mínimo, que, durante a aplicação da função SoftMax, resultará em um coeficiente de influência nulo.

O kernel apresentado acima organiza a propagação para frente do processo de seleção dos k codificadores mais relevantes em cada caso específico. No entanto, para construir um modelo verdadeiramente adaptativo, é necessário implementar o processo de aprendizado da seleção dos codificadores. Claro, dentro do kernel apresentado acima não utilizamos parâmetros treináveis. Contudo, eles são aplicados na geração dos dados brutos usados por nós. Portanto, é indispensável repassar o gradiente do erro ao nível dos dados de entrada. Esse processo é implementado no kernel TopKgatesGrad, cuja estrutura de parâmetros inclui ponteiros para os buffers correspondentes aos gradientes de erro.

__kernel void TopKgatesGrad(__global const float *inputs,
                            __global float *grad_inputs,
                            __global const float *noises,
                            __global const float *gates,
                            __global float *grad_gates)
  {
   size_t idx = get_global_id(0);
   size_t var = get_global_id(1);
   size_t window = get_global_size(0);
   size_t vars = get_global_size(1);

No corpo do kernel, identificamos o fluxo atual de operações dentro do espaço bidimensional de tarefas. A estrutura desse espaço é herdada do kernel da propagação para frente, com a diferença de que agora não agrupamos os fluxos em grupos de trabalho.

Em seguida, determinamos o deslocamento nos buffers globais de dados, de forma análoga ao algoritmo da propagação para frente.

   const int shift_logit = var * 2 * window + idx;
   const int shift_std = shift_logit + window;
   const int shift_gate = var * window + idx;

E, primeiro, carregamos o resultado da propagação direta correspondente ao fluxo atual.

   const float gate = IsNaNOrInf(gates[shift_gate], MIN_VALUE);
   if(gate <= MIN_VALUE)
     {
      grad_inputs[shift_logit] = 0;
      grad_inputs[shift_std] = 0;
      return;
     }

Como é fácil deduzir, se o valor obtido for igual à constante mínima, podemos imediatamente gravar valores nulos no buffer de gradientes dos dados de entrada. Já que esse valor corresponde à exclusão do codificador das operações subsequentes.

Caso contrário, carregamos o valor do gradiente de erro no nível dos resultados e o transferimos diretamente para o elemento correspondente no buffer de gradientes dos dados de entrada (erro logit).

   float grad = IsNaNOrInf(grad_gates[shift_gate], 0);
   grad_inputs[shift_logit] = grad;

No nível do ruído, obviamente, não distribuímos o gradiente de erro. No entanto, ainda precisamos determinar o valor do erro no nível da variância. Como sabemos, durante o processo de propagação para frente, a variância foi multiplicada pelo ruído; portanto, a próxima etapa consiste em extrair o valor do ruído.

   float noise = IsNaNOrInf(noises[shift_gate], 0);
   if(noise == 0)
     {
      grad_inputs[shift_std] = 0;
      return;
     }

É evidente que, quando o ruído é igual a "0", a variância não participa das operações de propagação para frente. Portanto, nesse caso, simplesmente armazenamos um gradiente nulo sem realizar outras operações.

No último caso, ajustamos o valor do gradiente de erro levando em conta o coeficiente de ruído e a derivada da função de ativação.

   grad *= noise;
   grad_inputs[shift_std] = Deactivation(grad, Activation(inputs[shift_std], 3), 3);
  }

O resultado obtido é armazenado no buffer global de dados, e o kernel encerra sua execução.

O código completo dos dois kernels apresentados acima pode ser encontrado no anexo deste artigo.

A próxima etapa do nosso trabalho consiste em organizar esse processo no lado do programa principal. Primeiramente, criaremos o objeto CNeuronTopKGates, no qual construiremos o algoritmo de seleção dos k codificadores mais relevantes. A estrutura desse novo objeto é apresentada abaixo.

class CNeuronTopKGates  :  public CNeuronSoftMaxOCL
  {
protected:
   int               iK;
   CBufferFloat      cbNoise;
   CNeuronConvOCL    cProjection;
   CNeuronBaseOCL    cGates;
   //---
   virtual bool      TopKgates(void);
   virtual bool      TopKgatesGradient(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronTopKGates(void) {};
                    ~CNeuronTopKGates(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint gates, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronTopKGates; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual uint      GetGates(void) const { return cProjection.GetFilters() / 2; }
   virtual uint      GetUnits(void) const { return cProjection.GetUnits(); }
  };

Na estrutura mostrada, observamos que ao conjunto habitual de métodos virtuais sobrescritos são adicionados os métodos TopKgates e TopKgatesGradient. Esses métodos funcionam como interfaces ("wrappers") para os kernels descritos anteriormente, criados no lado do programa OpenCL. O processo de criação deles seguiu o algoritmo que você já conhece, portanto, não entraremos em detalhes sobre ele neste ponto.

Os poucos objetos internos foram declarados de forma estática, o que nos permite deixar o construtor e o destrutor da classe vazios. Já a inicialização de todos os objetos declarados e herdados é realizada no método Init, cujos parâmetros recebem as constantes necessárias para interpretar de forma inequívoca a arquitetura do objeto que está sendo criado.

bool CNeuronTopKGates::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint units_count, uint gates, uint top_k, 
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronSoftMaxOCL::Init(numOutputs, myIndex, open_cl, gates * units_count,
                                                        optimization_type, batch))
      return false;
   SetHeads(units_count);

As operações do método de inicialização começam com a chamada do método homônimo da classe-pai, no qual já estão organizados os controles mínimos necessários e a inicialização dos objetos herdados.

Observe que, neste caso, utilizamos o objeto da função SoftMax como classe-pai. Isso nos permite converter os resultados da seleção dos k codificadores mais relevantes em uma representação probabilística sem a necessidade de criar um objeto interno adicional. Para isso, basta utilizarmos o funcional já presente na classe-pai.

Após a execução bem-sucedida das operações do método da classe-pai, passamos à construção do algoritmo de inicialização dos novos objetos declarados. Aqui, o primeiro passo é inicializar a camada convolucional responsável pela projeção dos parâmetros de distribuição dos dados dos segmentos analisados.

   if(!cProjection.Init(0, 0, OpenCL, window, window, 2 * gates, units_count, 1, optimization, iBatch))
      return false;
   cProjection.SetActivationFunction(None);

Na saída dessa camada, esperamos obter os valores médios e as variâncias correspondentes a cada codificador do modelo. Portanto, o número de filtros da camada convolucional é duas vezes maior que o número de codificadores definidos.

Em seguida, adicionamos o buffer de dados no qual será gerado o ruído.

   if(!cbNoise.BufferInit(Neurons(), 0) ||
      !cbNoise.BufferCreate(OpenCL))
      return false;

Por fim, concluímos as operações do método inicializando a camada totalmente conectada destinada a registrar os resultados do trabalho do kernel de propagação para frente TopKgates.

   if(!cGates.Init(0, 1, OpenCL, Neurons(), optimization, iBatch))
      return false;
   cGates.SetActivationFunction(None);
//---
   return true;
  }

Depois disso, retornamos o resultado lógico da execução das operações ao programa que fez a chamada e encerramos o método.

Observe que, neste caso, não criamos objetos específicos para registrar a distribuição probabilística dos Top K codificadores. A conversão dos valores absolutos de logit para o espaço probabilístico será feita utilizando os recursos da classe-pai. Assim, todos os objetos responsáveis por esse processo já foram criados e inicializados na classe-pai.

A próxima etapa do nosso trabalho é a construção do método de propagação para frente do objeto de seleção dos k codificadores mais relevantes, CNeuronTopKGates::feedForward. Nos parâmetros desse método, como de costume, recebemos um ponteiro para o objeto dos dados de entrada, que é imediatamente transmitido para o método homônimo do objeto responsável pela geração dos indicadores estatísticos da distribuição dos segmentos analisados.

bool CNeuronTopKGates::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cProjection.FeedForward(NeuronOCL))
      return false;

Em seguida, é importante observar que os autores do framework DUET sugerem adicionar o ruído aos valores de logit apenas durante o processo de treinamento. Portanto, verificamos o modo de operação do modelo e, se necessário, geramos o ruído.

   if(bTrain)
     {
      double random[];
      if(!Math::MathRandomNormal(0, 1, Neurons(), random))
         return false;
      if(!cbNoise.AssignArray(random))
         return false;
      if(!cbNoise.BufferWrite())
         return false;
     }
   else
      if(!cbNoise.Fill(0))
         return false;

Caso contrário, o buffer de ruído é preenchido com valores nulos.

Depois disso, chamamos o método-wrapper responsável pela seleção dos k codificadores mais relevantes.

   if(!TopKgates())
      return false;
//---
   return CNeuronSoftMaxOCL::feedForward(cGates.AsObject());
  }

Os resultados obtidos são então transmitidos para o método homônimo da classe-pai, o que permite converter os valores absolutos para o espaço probabilístico.

O resultado lógico da execução das operações é retornado ao programa que fez a chamada, e o método é finalizado.

Como você deve ter percebido, o método de propagação para frente segue um algoritmo linear. Consequentemente, os métodos de propagação reversa seguem o mesmo princípio linear. Por isso, sugiro deixá-los para estudo independente. O código completo deste objeto e de todos os seus métodos pode ser encontrado no anexo do artigo.

Neste ponto, já construímos os algoritmos de seleção dos k codificadores mais relevantes tanto no lado do programa principal quanto no contexto OpenCL. Assim, podemos prosseguir para a construção da arquitetura Mixture of Experts, que será implementada dentro do objeto CNeuronMoE. A estrutura desse novo objeto é apresentada abaixo.

class CNeuronMoE  :  public CNeuronBaseOCL
  {
protected:
   CNeuronTopKGates     cGates;
   CLayer               cExperts;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMoE(void) {};
                    ~CNeuronMoE(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_out, uint units_count,
                          uint experts, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMoE; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      TrainMode(bool flag)
     {  bTrain = flag;  cGates.TrainMode(bTrain); }
  };

Na estrutura mostrada, vemos apenas dois objetos internos. Um deles é o objeto de seleção dos k codificadores mais relevantes, criado anteriormente. O outro é um array dinâmico destinado ao armazenamento dos ponteiros para os objetos correspondentes aos codificadores do modelo. Ambos os objetos são declarados de forma estática, o que nos permite deixar o construtor e o destrutor da classe vazios. Todo o trabalho de inicialização desses objetos é organizado dentro do método Init.

Nos parâmetros do método de inicialização são passadas constantes que fornecem uma representação inequívoca da arquitetura do objeto que está sendo criado. Ao mesmo tempo, é permitida a possibilidade de alterar a dimensionalidade dos dados na saída do objeto.

bool CNeuronMoE::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                      uint window, uint window_out, uint units_count,
                      uint experts, uint top_k,
                      ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window_out * units_count, optimization_type, batch))
      return false;

O algoritmo começa com a chamada do método homônimo da classe-pai, no qual já está organizado o processo de inicialização dos objetos herdados e os pontos de controle dos dados de entrada.

Em seguida, inicializamos o objeto responsável pela seleção dos codificadores mais relevantes.

   int index = 0;
   if(!cGates.Init(0, index, OpenCL, window, units_count, experts, top_k, optimization, iBatch))
      return false;

Depois, passamos à inicialização direta dos objetos dos codificadores. Primeiro, preparamos o array dinâmico e as variáveis locais para o armazenamento temporário dos ponteiros para os objetos.

   cExperts.Clear();
   cExperts.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeRCDOCL *transp = NULL;

Primeiro, criamos a camada convolucional, que atua como a primeira camada dos codificadores. Na entrada desse objeto, planejamos alimentar o tensor dos dados brutos, que será o mesmo para todos os codificadores. O número de filtros dessa camada é igual ao produto entre o tamanho do tensor de saída de um codificador e o número total de codificadores no modelo. Essa abordagem nos permite realizar o cálculo paralelo dos valores para todos os codificadores simultaneamente.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, window_out * experts, units_count, 1, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

Com o objetivo de introduzir uma não linearidade entre as camadas do codificador, utilizamos a função SoftPlus como função de ativação.

Em seguida, precisamos adicionar a segunda camada dos codificadores. E, como você pode imaginar, cada codificador deve possuir seu próprio conjunto de parâmetros. Temos essa possibilidade. Podemos novamente usar uma camada convolucional, bastando apenas especificar o número de codificadores no parâmetro que define a quantidade de sequências independentes a serem analisadas. No entanto, é importante observar que, na saída da primeira camada, obtemos um tensor tridimensional com dimensões { Units, Encoders, Dimension }. Isso não corresponde ao algoritmo de funcionamento da camada convolucional que criamos anteriormente.

Para organizar corretamente o processo, precisamos trocar as duas primeiras dimensões de lugar. Essa tarefa é realizada por uma camada de transposição de dados.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_count, experts, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Agora podemos inicializar a camada convolucional que desempenhará o papel da segunda camada dos nossos codificadores independentes.

   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_out, window_out, window_out, units_count, experts, optimization, iBatch) ||
      !cExperts.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

E, por fim, adicionamos uma camada de transposição reversa de dados.

   transp = new CNeuronTransposeRCDOCL();
   index++;
   if(!transp ||
      !transp.Init(0, index, OpenCL, experts, units_count, window_out, optimization, iBatch) ||
      !cExperts.Add(transp))
     {
      delete transp;
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Com isso, concluímos o algoritmo de inicialização dos objetos internos. Retornamos o resultado lógico da execução das operações ao programa que fez a chamada e encerramos o método.

Após concluir a inicialização do objeto, passamos à construção do algoritmo de propagação para frente dentro do método CNeuronMoE::feedForward.

bool CNeuronMoE::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cGates.FeedForward(NeuronOCL))
      return false;

Nos parâmetros desse método, recebemos um ponteiro para o objeto dos dados de entrada, que é imediatamente passado para o método homônimo do objeto responsável pela seleção dos codificadores mais relevantes.

Em seguida, passamos ao trabalho com os codificadores. Note que, como dados de entrada, eles utilizam o mesmo objeto recebido nos parâmetros do método. Para isso, salvamos previamente o ponteiro obtido em uma variável local.

   CNeuronBaseOCL *prev = NeuronOCL;
   int total = cExperts.Total();
   for(int i = 0; i < total; i++)
     {
      CNeuronBaseOCL *neuron = cExperts[i];
      if(!neuron ||
         !neuron.FeedForward(prev))
         return false;
      prev = neuron;
     }

E organizamos um laço que percorre sequencialmente as camadas dos codificadores, chamando seus respectivos métodos de propagação para frente.

Após a execução de todas as iterações do laço, obtemos o conjunto completo dos resultados do trabalho de todos os codificadores. Vale lembrar que anteriormente já havíamos obtido a máscara probabilística dos codificadores mais relevantes para cada segmento dos dados de entrada. E agora, para obter a soma ponderada de cada segmento dos dados analisados, basta multiplicar o vetor-linha da distribuição probabilística de relevância dos codificadores para o segmento pela matriz dos resultados produzidos por esses codificadores.

   if(!MatMul(cGates.getOutput(), prev.getOutput(), getOutput(),
              1, cGates.GetGates(), Neurons() / cGates.GetUnits(), cGates.GetUnits()))
      return false;
//---
   return true;
  }

Os valores obtidos são armazenados no buffer de resultados do nosso objeto. Em seguida, encerramos a execução do método, retornando previamente o resultado lógico das operações ao programa que o chamou.

Com isso, concluímos a análise dos algoritmos utilizados na construção dos métodos do objeto que compõe o conjunto de codificadores. Os métodos de propagação reversa deste objeto eu recomendo deixar para estudo independente. O código completo deste objeto e de todos os seus métodos, como sempre, está disponível no anexo do artigo.

Hoje trabalhamos intensamente e praticamente atingimos o limite do conteúdo deste artigo. No entanto, nossa jornada ainda não terminou. Faremos uma pequena pausa e continuaremos a implementação da nossa própria visão das abordagens propostas pelos autores do framework DUET no próximo artigo.

Considerações finais

Hoje conhecemos o framework DUET, que combina a clusterização temporal (TCM) e a clusterização de canais (CCM) de séries temporais multivariadas para uma análise e previsão mais precisas. O TCM adapta os modelos às mudanças ao longo do tempo, enquanto o CCM destaca as variáveis-chave, reduzindo o nível de ruído.

Na parte prática do artigo, apresentamos a implementação do módulo de clusterização temporal (TCM). No próximo artigo, continuaremos essa implementação, apresentando nossa própria visão das abordagens propostas pelos autores do framework e levando o trabalho à sua conclusão lógica, realizando o teste do modelo com dados históricos reais.

Referências

• DUET: Dual Clustering Enhanced Multivariate Time Series Forecasting
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca de código do programa OpenCL