
Redes neurais em trading: Pipeline inteligente de previsões (Time-MoE)
Introdução
A previsão de séries temporais continua sendo uma das tarefas-chave sobre as quais se constrói o trading algorítmico moderno. Da precisão do modelo depende não apenas o sucesso da estratégia de negociação, mas também sua capacidade de se adaptar ao caráter constantemente mutável do mercado. A maioria dos modelos foi desenvolvida para uma tarefa específica, perdendo robustez diante de pequenas mudanças no ambiente de mercado. Nos últimos tempos, observa-se um desenvolvimento acelerado dos modelos fundamentais (foundation models). Um desses modelos foi apresentado no trabalho "Time-MoE: Billion-Scale Time Series Foundation Models with Mixture of Experts".
Time-MoE é um Decoder-Only Transformer de nova geração, desenvolvido especificamente para sequências temporais. Sua base está nos princípios de aprendizado esparso, modularidade e previsão em múltiplas escalas. Os autores do framework demonstram como é possível transferir a escalabilidade e a flexibilidade de modelos de grande porte para o domínio das séries temporais, sem sacrificar a eficiência computacional. A arquitetura do modelo apresentada por eles permite suportar comprimentos arbitrários das sequências analisadas e dos horizontes de planejamento. Ao mesmo tempo, o modelo é capaz de processar fluxos de dados em tempo real.
O primeiro elo da arquitetura é a tokenização ponto a ponto da série temporal (Point-Wise Tokenization). Diferentemente das abordagens baseadas em janelas ou agregações, aqui cada passo temporal é convertido em um token separado. Essa característica pode se mostrar útil no trading de alta frequência, em que até mesmo um único tick pode alterar o cenário. No ambiente MQL5, os tokens podem ser formados com base em barras, ticks e indicadores derivados, incluindo volatilidade, volumes e sinais de estratégias personalizadas.
Após a tokenização, os dados passam por uma camada de incorporação com ativação SwiGLU, que representa um híbrido Swish e Gated Linear Unit. Ela permite formar representações mais suaves e estáveis das informações analisadas, o que é especialmente útil na presença de ruído de mercado e tendências instáveis.
O coração do modelo é uma pilha de N blocos repetidos, cada um combinando atenção multihead causal (Causal Multi-Head Self-Attention) e mistura esparsa de especialistas (Sparse MoE). A atenção é estritamente orientada ao passado, o que garante uma cronologia honesta — o modelo não vê o futuro e, portanto, é aplicável em condições reais de mercado. MoE adiciona escalabilidade à arquitetura, pois, em vez de ativar todos os parâmetros do modelo, para cada token é selecionado um número limitado de submodelos especializados, chamados especialistas. Alguns deles aprendem melhor a trabalhar com movimentos impulsivos, outros com fases de consolidação ou mercados laterais. Um mecanismo adaptativo toma a decisão sobre o roteamento dos tokens.
Mas o modelo não se limita apenas ao nível de processamento de dados. Uma das principais características do Time-MoE é a previsão multiescalar (Multiscale Forecasting). Durante o treinamento, o modelo recebe a tarefa de realizar previsões simultaneamente em diferentes horizontes temporais. Isso é implementado por meio de módulos de saída paralelos (cabeças), cada um treinado com seu próprio rótulo-alvo, seja de curto, médio ou longo prazo. Essa arquitetura permite considerar simultaneamente a microdinâmica e o comportamento macro do mercado. E o modelo é capaz de alternar entre eles dependendo do contexto de mercado.
Durante a inferência, entra em ação a seleção dinâmica da cabeça de previsão (Dynamic Head Scheduling). Dependendo da volatilidade, da força da tendência ou do grau de confiança do modelo, diferentes módulos de previsão são ativados. Essa abordagem adaptativa torna Time-MoE especialmente valioso no trading, onde o comportamento do mercado pode mudar instantaneamente.
É importante destacar que Time-MoE é otimizado para treinamento em conjuntos massivos de séries temporais. Pelos autores do framework, o modelo foi treinado no Time-300B, o maior dataset aberto, contendo mais de 300 bilhões de pontos de dados temporais provenientes de nove domínios. Isso permitiu alcançar alta universalidade do modelo, robustez a desvios de distribuição e capacidade de generalização para tarefas desconhecidas. Ao mesmo tempo, Time-MoE escala até 2.4 bilhões de parâmetros, ativando apenas parte deles durante o processo de inferência, o que o torna simultaneamente eficiente e econômico.
Algoritmo Time-MoE
Na base do Time-MoE está a ideia de criar um modelo único e escalável para previsão de séries temporais, capaz de se adaptar a quaisquer condições do ambiente analisado e, ao mesmo tempo, manter uma carga controlável sobre os recursos computacionais. O algoritmo do framework começa com a tokenização ponto a ponto (Point-Wise Tokenization), na qual são fixadas todas as características importantes de cada etapa da série temporal. Essa abordagem garante que nenhum detalhe se perca durante a agregação.
A transformação dos tokens brutos em um espaço latente informativo é realizada por meio da incorporação SwiGLU.
![]()
onde as matrizes W e V são treinadas juntamente com o modelo. A multiplicação elemento a elemento ⨂ reforça as características relevantes, e a combinação da função Swish com o mecanismo de portas (Gated Linear Unit) forma incorporações mais expressivas, capazes de codificar dependências não lineares complexas.
Após a incorporação, os tokens são enviados para uma pilha de N blocos transformadores idênticos. Cada bloco consiste em três etapas:
- Normalização e atenção causal: na entrada são fornecidos vetores ht,l-1, que primeiro passam por normalização e depois são analisados por Self-Attention multihead, limitado por uma máscara que exclui informações sobre valores futuros. O token literalmente volta a cabeça para trás, olhando para todo o histórico já percorrido, mas não pode olhar para frente, como se seguisse uma regra rígida: as decisões presentes se baseiam apenas na experiência passada.
- A repetida normalização permite evitar reação excessiva a anomalias raras.
- Camada esparsa Mixture-of-Experts. Aqui direcionamos cada janela histórica para um grupo de especialistas — Mixture-of-Experts. Um roteador adaptativo decide quais K especialistas, dentre N, devem ser ativados. Um especialista (comum N+1) sempre participa por meio de uma função de ponderação sigmoidal. Os especialistas ativos processam os dados de forma independente e retornam suas previsões. A saída final do bloco é somada ao sinal original.
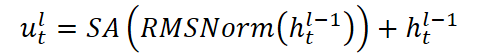
onde SA é o Self-Attention com H cabeças, cada uma das quais analisa as t-1 posições anteriores. Tal construção permite que o modelo acompanhe eventos importantes no histórico, preservando as relações de causa e efeito.
![]()
![]()
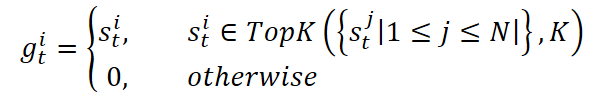
![]()
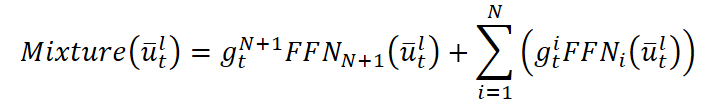
![]()
Essa estrutura garante a seleção dinâmica de especialização: em períodos de alta volatilidade, os tokens são redirecionados para especialistas treinados para reconhecer movimentos impulsivos, enquanto em momentos de tranquilidade são enviados àqueles que melhor compreendem tendências ou mercados laterais. Top-K seleção de especialistas permite limitar o número de sub-redes ativas, mantendo o principal conjunto de parâmetros em estado latente. Isso possibilita escalar o modelo para bilhões de parâmetros com um orçamento de inferência constante.
Quando o token xT passa por todas as N camadas, obtemos um vetor contextual hT,L, que contém todo o histórico e os padrões de mercado. Para Multi-Resolution Forecasting, a partir dele são formadas P previsões para horizontes p1,…,pP por meio de uma única camada FFN.
![]()
Tal arquitetura permite gerar simultaneamente previsões para diferentes intervalos temporais, preservando uma representação latente unificada.
Durante o treinamento, o modelo enfrenta a tarefa de prever simultaneamente vários horizontes temporais: desde as oscilações mais próximas em minutos até tendências atrasadas em dias e semanas. Para cada previsão, os autores do framework utilizam Huber loss, que combina a suavidade do componente quadrático com a robustez da parte linear. Para erros pequenos, Huber loss comporta-se como o MSE clássico, penalizando cuidadosamente pequenos desvios, e para erros grandes passa gradualmente para L1, reduzindo a influência de valores atípicos e prevenindo a explosão de gradientes. Em seguida, o modelo acumula as perdas de todas as cabeças de previsão.
Graças a esse esquema, o modelo aprende simultaneamente a capturar impulsos de curto prazo e a manter tendências de longo prazo, preservando a integridade da previsão em todos os níveis.
No entanto, o uso de especialistas esparsos (MoE) gera o risco de carga desigual: alguns especialistas podem ficar sobrecarregados, enquanto outros permanecem ociosos. Com o objetivo de eliminar esse efeito, foi adicionada uma regularização auxiliar que mede o desequilíbrio. O objetivo final do treinamento passa a ser a soma das partes principal e auxiliar.
O resultado final é um pipeline único e coordenado: desde a tokenização refinada até o roteamento dinâmico entre especialistas, a previsão multinível e o treinamento balanceado.
Visualização autoral do framework Time-MoE apresentada abaixo.
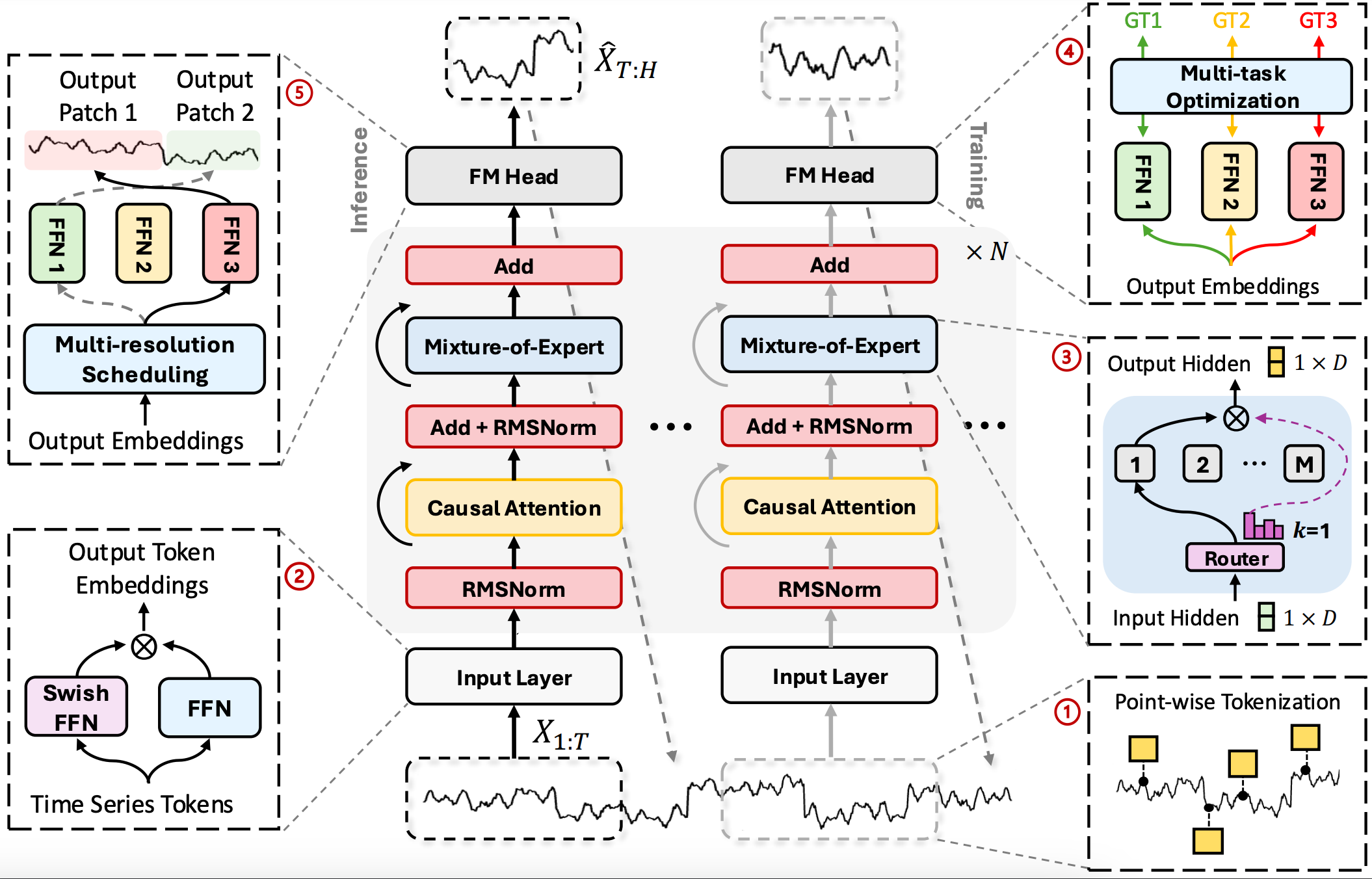
Implementação com MQL5
Depois de termos analisado detalhadamente a teoria e os principais aspectos do framework Time-MoE, é hora de passar para a parte prática do nosso trabalho e dar vida à teoria no código. No entanto, para não tentar abraçar o impossível de uma só vez, dividiremos todo o sistema em blocos lógicos. E, seguindo o fluxo informacional, implementaremos o framework passo a passo por meio do MQL5. Essa abordagem gradual e orientada à prática não apenas facilitará o teste e a depuração de cada bloco, como também permitirá montar, a partir deles, uma implementação viva e responsiva do Time-MoE, pronta para um funcionamento poderoso e eficiente em condições reais de mercado.
De acordo com a ideia original dos autores do Time-MoE, todos os dados brutos passam pelo módulo Point-Wise Tokenization, que pode ser implementado de forma eficiente por meio de uma camada convolucional existente. Essencialmente, um pequeno filtro convolucional 1D é alimentado com cada barra ou tick, e o resultado da convolução nada mais é do que um token atômico com um conjunto de características. Essa abordagem nos oferece duas vantagens importantes: em primeiro lugar, preservamos as informações de cada instante no tempo sem perdas associadas à agregação; em segundo lugar, a convolução já identifica padrões locais.
Em seguida, os dados são enviados para a incorporação SwiGLU, sobre a qual ainda precisaremos trabalhar.
Incorporação SwiGLU
Após a formação dos tokens, eles são enviados para a segunda etapa — o módulo de incorporação SwiGLU, que transforma as características brutas em vetores compactos do espaço latente. SwiGLU realiza sobre eles uma dupla transformação:
- primeiro, o token passa por uma projeção linear e pela função suave e contínua Swish;
- depois, por outra projeção e pela seletiva Gated Linear Unit (GLU).
Na saída, os dois resultados são combinados por multiplicação elemento a elemento.
![]()
Swish confere suavidade à incorporação, permitindo que o modelo não deixe passar sinais sutis, enquanto GLU abre ou fecha componentes individuais do vetor, destacando os padrões realmente importantes.
Em nossa implementação, a camada SwiGLU será representada na forma da classe CNeuronSwiGLUOCL, herdada do objeto base das camadas neurais. Dentro dessa classe, criaremos duas camadas convolucionais especiais, que executam a dupla projeção do vetor analisado e produzem duas versões do sinal. A estrutura do novo objeto é apresentada abaixo.
class CNeuronSwiGLUOCL : public CNeuronBaseOCL { protected: CNeuronConvOCL caProjections[2]; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronSwiGLUOCL(void) {}; ~CNeuronSwiGLUOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronSwiGLUOCL; } //--- methods for working with files virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual void SetOpenCL(COpenCLMy *obj) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; };
Todos os objetos internos da nossa nova classe são declarados como estáticos. Portanto, o construtor e o destrutor permanecem vazios. A inicialização de todas as projeções, dos parâmetros da convolução e da conexão com o contexto OpenCL é atribuída ao método Init. É nos parâmetros dessa função que o usuário define os tamanhos da janela convolucional, o passo de deslocamento, o número de filtros e o ponteiro para o OpenCL. Tudo isso permite realizar a configuração completa da camada antes da utilização prática.
bool CNeuronSwiGLUOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint step, uint window_out, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * window_out * variables, optimization_type, batch)) return false; SetActivationFunction(None);
Dentro do método, delegamos toda a preparação básica para cima, isto é, ao nível da classe pai, onde já estão implementados os pontos de controle e a configuração das interfaces gerais. Para isso, basta chamar o método com o mesmo nome da classe pai. Isso nos permite não duplicar operações de baixo nível e ter segurança quanto à confiabilidade do ambiente de execução.
Aqui também desativamos explicitamente a função de ativação da nossa camada no nível das interfaces, pois todas as não linearidades são criadas pelos objetos internos.
Quando os detalhes de infraestrutura estão resolvidos, começamos o ajuste fino da nossa camada. Aqui vale observar que ambas as camadas convolucionais internas foram projetadas para produzir vetores do mesmo tamanho, isso é criticamente importante. Afinal, somente com dimensões coincidentes conseguiremos multiplicá-las corretamente elemento a elemento. A única diferença entre elas está na aplicação posterior de diferentes funções de ativação.
Por isso, na etapa de preparação, iniciamos a inicialização dessas camadas em um laço, atribuindo automaticamente a cada uma a mesma configuração de janela convolucional, o número de filtros e o passo de deslocamento. Isso evita a duplicação de código e garante que ambas as projeções permaneçam sempre sincronizadas em dimensionalidade.
for(uint i = 0; i < caProjections.Size(); i++) { if(!caProjections[i].Init(0, i, OpenCL, window, step, window_out, units_count, variables, optimization, iBatch)) return false; }
Depois que os tamanhos e os parâmetros básicos foram verificados, configuramos separadamente, para cada camada, sua própria função de ativação, para que nas incorporações finais surja a combinação de características suaves e seletivas. Esse procedimento simplifica a manutenção do código e assegura uma separação clara de papéis dentro da camada SwiGLU.
caProjections[0].SetActivationFunction(GELU); caProjections[1].SetActivationFunction(None); //--- return true; }
Agora podemos concluir o trabalho do método de inicialização da camada SwiGLU, retornando à aplicação chamadora o resultado lógico da execução das operações.
Quando toda a configuração da camada estiver concluída, é hora de ligar o motor e passar os dados analisados pelas nossas duas convoluções de projeção. Começamos a construir o algoritmo de propagação para frente, implementado no método feedForward.
bool CNeuronSwiGLUOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caProjections.Size(); i++) if(!caProjections[i].FeedForward(NeuronOCL)) return false;
Como de costume, nos parâmetros desse método recebemos um ponteiro para o objeto dos dados de entrada. É exatamente ele que devemos passar para ambas as nossas camadas de projeção de dados. Essa operação é realizada em um laço. Essa possibilidade nos é dada pela declaração de um array de objetos.
Justamente por ambas as camadas produzirem tensores da mesma dimensionalidade, podemos multiplicá-los imediatamente elemento a elemento, sem nos preocupar com incompatibilidade de dimensões. Como resultado, obtemos um tensor de saída unificado, em que cada valor é o produto das vozesSwish- e GLU das projeções. Esse procedimento, baseado na passagem cíclica do ponteiro de dados para dentro do array de camadas, garante a compactação do código e permite escalar facilmente a quantidade de "vozes" dentro da camada, apenas alterando o tamanho do array.
if(!ElementMult(caProjections[0].getOutput(), caProjections[1].getOutput(), Output)) return false; //--- return true; }
Salvamos os resultados obtidos no buffer de resultados da interface externa e encerramos o método, retornando o resultado lógico à aplicação chamadora.
Quando a propagação para frente dos dados pela camada SwiGLU foi concluída, chega a hora de acompanhar para onde foi cada gota de erro — organizar a propagação reversa. A essência é espalhar o gradiente a partir do nível dos resultados de volta aos dados de entrada, passando cuidadosamente por ambos os nossos projetores convolucionais. Esse processo é organizado no método calcInputGradients.
bool CNeuronSwiGLUOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
No corpo do método, recebemos um ponteiro para o objeto dos dados de entrada. O mesmo que usamos na propagação para frente. Só que, desta vez, precisamos devolver nele o gradiente do erro, de acordo com a influência dos dados de entrada no resultado final. Naturalmente, para a transferência correta dos dados precisamos de um objeto válido. Por isso, antes de iniciar as operações seguintes, verificamos a validade do ponteiro recebido.
Nas interfaces externas da nossa camada, já temos a diferença entre a previsão atual e o valor desejado. Em seguida, graças à coincidência dos tamanhos dos vetores, isolamos facilmente a parcela do erro que corresponde a cada um dos filtros internos.
if(!ElementMultGrad(caProjections[0].getOutput(), caProjections[0].getGradient(), caProjections[1].getOutput(), caProjections[1].getGradient(), Gradient, caProjections[0].Activation(), caProjections[1].Activation() )) return false;
Esses dois fluxos enviamos aos respectivos neurônios convolucionais. Como ambas as camadas armazenam seus próprios buffers de gradientes, cada uma recebe seu vetor, idêntico em tamanho aos dados de entrada.
Depois disso, cada objeto convolucional interno decomporá de forma independente sua própria parcela de erro. Porém, desta vez, não podemos em um laço transmitir os valores ao nível do objeto dos dados de entrada. O problema é que cada operação subsequente sobrescreverá os dados, removendo os valores anteriormente salvos. No entanto, precisamos acumular os valores de todos os fluxos de informação. Por isso, primeiro transmitimos os gradientes de erro da primeira camada de projeção.
if(!NeuronOCL.calcHiddenGradients(caProjections[0].AsObject())) return false;
Em seguida, salvamos o ponteiro para o buffer de gradientes de erro do objeto dos dados de entrada em uma variável local. Seu lugar é então ocupado por outro buffer de dados livre, do mesmo tamanho.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(NeuronOCL.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(caProjections[1].AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false) ) return false; //--- return true; }
Agora podemos transmitir com segurança os dados pelo segundo fluxo de informação. Depois disso, somamos os valores obtidos das duas camadas de projeção. Esse procedimento garante que cada partícula de erro proveniente de diferentes fluxos de informação seja preservada e corretamente agregada, proporcionando uma atualização de pesos precisa e estável na etapa subsequente de otimização.
Ao final, retornamos os ponteiros dos buffers de dados ao estado original e encerramos o método, retornando à aplicação chamadora o resultado lógico da execução das operações.
O algoritmo de propagação reversa, como de costume, divide-se em duas etapas lógicas. A primeira etapa — a distribuição do gradiente de erro — já foi analisada detalhadamente. Trata-se do passo-chave que permite transmitir corretamente o erro da saída da camada para os dados de entrada, respeitando todas as particularidades do fluxo de informação multicanal.
A segunda etapa — a otimização dos parâmetros, voltada para a redução do erro total, permanece fora do escopo do presente artigo. Não porque não seja importante, mas porque sua implementação está estritamente encapsulada dentro de cada um dos objetos convolucionais. Isso nos oferece uma vantagem importante: a interface da nossa classe não fica sobrecarregada com detalhes excessivos, mantendo a pureza arquitetural e a modularidade.
Todos os passos necessários para a correção dos pesos já estão implementados dentro de cada camada de projeção. Portanto, para executar todo o ciclo de otimização, basta chamar sequencialmente os métodos correspondentes de todos os objetos internos. Graças a essa abordagem, a classe principal permanece compacta, e a lógica de atualização de parâmetros se mantém confiável e testada de forma isolada.
O código-fonte completo da classe CNeuronSwiGLUOCL e de todos os seus métodos, incluindo as funções de propagação para frente e propagação reversa, é apresentado em anexo e pode ser estudado para uma compreensão mais aprofundada de todos os mecanismos internos de funcionamento.
Concluímos a implementação do componente de incorporação SwiGLU e agora podemos avançar com segurança para a próxima etapa, que é a implementação da parte principal do framework Time-MoE — o bloco Transformer modificado. Esse passo abre uma nova página na construção do modelo, pois é justamente no bloco Transformer que ocorre a formação da compreensão de alto nível da sequência: o modelo aprende a capturar dependências de longo prazo, analisar o contexto e prever a provável dinâmica do desenvolvimento dos eventos.
A transferência da série temporal transformada do bloco SwiGLU para o módulo Transformer não é apenas uma transmissão de dados, mas, em essência, uma transferência de conhecimento. As incorporações, compactadas e saturadas com informações sobre padrões locais, agora se tornam material para uma análise profunda. No entanto, a arquitetura do Transformer no Time-MoE difere significativamente da implementação clássica. E a primeira coisa que chama a atenção é a ausência do tradicional bloco FeedForward, que normalmente segue imediatamente o mecanismo de atenção em cada camada.
Em vez do módulo padrão, os autores propuseram utilizar a chamada mistura esparsa de especialistas (Sparse Mixture of Experts, ou simplesmente MoE). Essa decisão arquitetural não apenas adiciona flexibilidade intelectual ao modelo, como também torna seu treinamento mais significativo e dependente do contexto. A ideia principal do MoE é dividir uma camada universal em vários submódulos altamente especializados (especialistas), cada um treinado para processar um tipo específico de dados de entrada. Essa abordagem permite que cada token da sequência de entrada recorra apenas aos especialistas mais adequados para tratar suas características, deixando os demais em estado latente.
O mecanismo adaptativo de seleção de especialistas é realizado por meio de um roteador, um subbloco separado que, com base na representação inicial do token, decide quais especialistas serão ativados. No artigo original, destaca-se um ponto importante: utiliza-se roteamento esparso, no qual cada token é direcionado não a todos os especialistas simultaneamente, mas apenas a alguns, por exemplo, dois dentre dez possíveis. Isso reduz significativamente os custos computacionais, permitindo o uso do MoE mesmo em larga escala, sem carga crítica sobre os recursos.
Essa abordagem oferece ao modelo inúmeras vantagens. Em primeiro lugar, ele aprende a distribuir tarefas entre especialistas: alguns se ajustam a oscilações de preço de curto prazo, outros a movimentos de tendência ou à volatilidade. Em segundo lugar, o modelo ganha a capacidade de generalizar conhecimento: graças à experiência diferenciada entre os especialistas, torna-se possível modelar interações mais complexas do que em uma arquitetura tradicional de nível único.
Assim, o uso do Sparse Mixture of Experts no Transformer do Time-MoE pode ser considerado a inovação central do framework. Não se trata apenas de um experimento arquitetural, mas de uma revisão fundamental da abordagem ao processamento de sequências temporais.
E diante de nós surge a questão: como levar essas ideias arquiteturais para o plano prático? Afinal, não estamos apenas teorizando, mas criando passo a passo um sistema funcional. Se recordarmos as etapas anteriores de nossas pesquisas, já nos deparamos com o conceito de Mixture of Experts (MoE) no desenvolvimento do framework DUET. Naquela ocasião, implementamos um protótipo simples, que ajudou a compreender melhor como funcionam o roteamento e a agregação das decisões dos especialistas. No entanto, aquela implementação dificilmente pode ser chamada de verdadeiramente esparsa. Na prática, tratava-se mais de uma imitação do mecanismo de seleção, na qual todos os especialistas calculavam suas saídas simultaneamente, e depois seus resultados eram apenas multiplicados pelas máscaras correspondentes.
Do ponto de vista matemático, o resultado final parecia plausível: as máscaras permitiam zerar as saídas dos desnecessários especialistas, formando assim uma superposição controlada. Porém, do ponto de vista da eficiência computacional, estávamos, francamente, perdendo. Afinal, cada especialista ainda executava todo o seu volume de trabalho, independentemente de seu resultado ser utilizado ou não. Dessa forma, a complexidade computacional crescia linearmente com o número de especialistas, anulando uma das principais vantagens da arquitetura MoE — sua capacidade de escalar sem crescimento exponencial de custos.
Tal abordagem é aceitável para modelos pequenos, nos quais o número de especialistas e sua dimensionalidade são reduzidos, e as exigências de desempenho não são tão críticas. Contudo, em cenários reais — por exemplo, ao trabalhar com Transformers profundos e amplos, onde MoE é utilizado em cada segunda camada, e o número de especialistas pode chegar a dezenas — tal solução torna-se simplesmente inviável. A carga computacional rapidamente ultrapassa limites razoáveis, especialmente se desejamos utilizar o modelo em condições de tempo real — como no trading algorítmico nos mercados financeiros.
Além disso, com o aumento do número de especialistas, o próprio procedimento de roteamento se torna mais complexo. Se continuarmos utilizando todos simultaneamente, inevitavelmente enfrentaremos sobrecarga de memória de vídeo e perda de eficiência no OpenCL. E aqui torna-se especialmente importante seguir a filosofia da verdadeira esparsidade: que apenas uma pequena parte da rede esteja ativa, mas precisamente aquela necessária aqui e agora. Essa abordagem não apenas economiza recursos, como também torna o próprio modelo mais adaptativo e resistente ao ruído.
Na implementação atual, decidimos não nos limitar à mascaramento formal, mas ir além — construindo um algoritmo realmente esparso, alinhado à filosofia do framework Time-MoE. Sem dúvida, temos diante de nós uma tarefa extensa, que abrange vários níveis da arquitetura. Aqui, o importante não é simplesmente programar mais um módulo, mas estruturar um sistema lógico no qual roteamento, ativação, agregação e otimização de parâmetros funcionem de maneira coordenada, exatamente como concebido no algoritmo original. Por isso, nesta etapa, proponho fazer uma breve pausa.
Demos um passo significativo adiante: implementamos nossa própria SwiGLU incorporação, organizamos o fluxo de informação e preparamos a base arquitetural para conectar o Mixture of Experts. Isso já constitui um fundamento sólido sobre o qual poderemos construir o próximo nível do modelo. Mas, para não dispersar o foco e não sobrecarregar o material, é lógico dedicar a construção do MoE esparso a um artigo separado. Isso nos permitirá não apenas analisar todos os detalhes de forma completa, mas também evitar fragmentação no código e na lógica.
Assim, neste ponto lógico encerramos a parte atual e convidamos você a continuar nossa jornada no próximo artigo — já com o MoE esparso a bordo.
Considerações finais
Neste artigo, conhecemos a arquitetura Time-MoE — um framework progressivo proposto pelos autores do trabalho "Time-MoE: Temporal Mixture of Experts for Long-Term Time Series Forecasting". Esse modelo combina com sucesso as vantagens da abordagem Transformer com a ideia de Sparse Mixture of Experts, permitindo melhorar a qualidade da previsão por meio do roteamento adaptativo dos cálculos. Uma das principais virtudes do Time-MoE é a capacidade de processar de forma eficiente tanto dependências de curto prazo quanto de longo prazo em séries temporais. E a introdução dos módulos SwiGLU torna o modelo mais flexível.
Na parte prática, iniciamos a implementação do nosso próprio entendimento das abordagens propostas por meio do MQL5, transformando passo a passo os conceitos teóricos em código real. No âmbito da etapa atual, foi implementado o bloco SwiGLU de incorporação, construído com base em duas projeções convolucionais com multiplicação elemento a elemento. Dedicamos atenção às questões de propagação para frente e propagação reversa, à correta distribuição do gradiente e ao processamento da informação dentro das camadas convolucionais.
Assim, o fundamento está lançado, e estamos prontos para avançar. Na próxima parte, focaremos na construção de um bloco MoE esparso de fato, que exige uma lógica mais complexa de roteamento e gerenciamento de especialistas. Essa parte será fundamental na arquitetura do Time-MoE, e sua implementação exigirá tanto planejamento cuidadoso quanto soluções de engenharia originais.
Links
- Time-MoE: Billion-Scale Time Series Foundation Models with Mixture of Experts
- Outros artigos da série
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA coletor de exemplos |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA de coleta de exemplos pelo método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA de treinamento offline dos modelos |
| 4 | StudyOnline.mq5 | Expert Advisor | EA de treinamento online dos modelos |
| 5 | Test.mq5 | Expert Advisor | EA para teste do modelo |
| 6 | Trajectory.mqh | Biblioteca de classe | Estrutura de descrição do estado do sistema e arquitetura das redes |
| 7 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para construção da rede neural |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programas OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/18499
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Do básico ao intermediário: Sub Janelas (III)
Do básico ao intermediário: Sub Janelas (III)
 Redes neurais em trading: Framework de previsão cross-domain de séries temporais (Conclusão)
Redes neurais em trading: Framework de previsão cross-domain de séries temporais (Conclusão)
 Rede neural na prática: Grafico da Rectifier
Rede neural na prática: Grafico da Rectifier
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 54): Aprendizado por Reforço com SAC híbrido e Tensores
Técnicas do MQL5 Wizard que você deve conhecer (Parte 54): Aprendizado por Reforço com SAC híbrido e Tensores
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso