MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 49): Verstärkungslernen mit Optimierung der proximalen Politik

Einführung

Wir setzen unsere Serie über den MQL5-Assistenten fort, in der wir in letzter Zeit abwechselnd einfache Muster aus gängigen Indikatoren und Algorithmen des Reinforcement Learning verwenden. Nachdem wir uns im letzten Artikel mit Indikatormustern (Bill Williams' Alligator) beschäftigt haben, kehren wir nun zum Reinforcement Learning zurück, wobei wir uns diesmal mit dem Algorithmus „Proximal Policy Optimization“ (PPO) beschäftigen. Es wird berichtet, dass dieser Algorithmus, der vor 7 Jahren zum ersten Mal veröffentlicht wurde, der bevorzugte Verstärkungs-Lern-Algorithmus für ChatGPT ist. Es gibt also einen gewissen Hype um diesen Ansatz des Reinforcement Learning. Der PPO-Algorithmus zielt darauf ab, die Politik (die Funktion, die die Handlungen des Akteurs definiert) so zu optimieren, dass die Gesamtleistung verbessert wird, indem drastische Änderungen verhindert werden, die den Lernprozess instabil machen könnten.

Er tut dies nicht unabhängig, sondern arbeitet mit anderen Algorithmen des verstärkten Lernens zusammen, von denen wir einige in dieser Serie betrachtet haben und die im Großen und Ganzen in zwei Kategorien fallen. Richtlinienbasierte Algorithmen und wertbasierte Algorithmen. Wir haben uns in dieser Reihe bereits Beispiele für jede dieser Methoden angesehen, und um es noch einmal zusammenzufassen, die richtlinienbasierten Algorithmen, die wir gesehen haben, waren Q-Learning und SARSA. Wir haben nur eine wertbezogene Methode in Betracht gezogen, und zwar die zeitliche Differenz. Worum geht es also bei PPO?

Wie bereits angedeutet, besteht das „Problem“, das PPO löst, darin, zu verhindern, dass sich die Politik bzw. Handelsstrategie bei Aktualisierungen zu sehr verändert. Dahinter steht die These, dass der Agent, wenn er nicht eingreift, um die Häufigkeit und den Umfang der Aktualisierungen zu steuern, möglicherweise vergisst, was er gelernt hat, unberechenbare Entscheidungen trifft oder in der Umgebung schlechtere Leistungen erbringt. PPO stellt somit sicher, dass die Aktualisierungen klein, aber sinnvoll sind. Beim PPO geht man von einer Police aus, die mit ihren Parametern vordefiniert ist. Politiken sind einfach Funktionen, die die Handlungen der Akteure auf der Grundlage von Belohnungen und Umweltzuständen festlegen.

Bei Vorliegen einer Strategie würde die Interaktion des Agenten mit der Umgebung so erfolgen, dass Daten gesammelt werden. Diese „Datenerhebung“ würde ein Gefühl für die Paarung von Zustand, Aktion und Belohnung sowie für die Wahrscheinlichkeiten der verschiedenen Aktionen im Rahmen dieser Politik vermitteln. Nachdem dies festgestellt wurde, geht es nun darum, die Zielfunktion zu definieren. Wie bereits in der Einleitung erwähnt, geht es bei PPO darum, das Ausmaß der Aktualisierungen beim Reinforcement Learning zu dämpfen, und zu diesem Zweck verwenden wir eine Funktion „Clipping“ (Zuschneiden). Diese Funktion wird durch die folgende Gleichung definiert:

wobei:

• r t (θ)=πθ(at∣st)/πθ old (at∣st) das Wahrscheinlichkeitsverhältnis zwischen der neuen Politik (mit Parametern θ) und der alten Politik (mit Parametern θ old ​) ist.
• Â t ist die Vorteilsschätzung zum Zeitpunkt t, die misst, wie viel besser eine Handlung im Vergleich zur durchschnittlichen Handlung in einem bestimmten Zustand ist.
• ϵ ist ein Hyperparameter (häufig 0,1 oder 0,2), der den Begrenzungsbereich steuert und die Schrittgröße der Richtlinienaktualisierung begrenzt.

Die Vorteilsschätzung kann auf verschiedene Weise definiert werden, die in unserer Implementierung verwendete Methode ist jedoch die folgende:

wobei:

• Q(s t ,a t ) ist der Q-Wert (erwartete Rendite) für die Durchführung der Aktion a t ​ im Zustand s t ​.
• V(s t ) ist die Wertfunktion für den Zustand s t ​und stellt die erwartete Rendite dar, wenn wir die Politik von diesem Situation an verfolgen.

Diese Methode der Quantifizierung der Vorteilsfunktion unterstreicht die Abhängigkeit oder den Einsatz von politikbasierten Algorithmen und wertbasierten Algorithmen, auf die wir oben bereits hingewiesen haben. Sobald wir unsere Zielfunktion definiert haben, führen wir Aktualisierungen an unserer Politik durch. Bei der Aktualisierung werden die Parameter der Politik mit dem Ziel angepasst, die beschnittene Zielfunktion zu maximieren. Dadurch wird sichergestellt, dass die Änderungen der Politik schrittweise erfolgen und die jüngsten Daten nicht zu stark angepasst werden. Dieser Prozess wird dann durch eine Interaktion mit der Umwelt unter Verwendung der aktualisierten Strategie wiederholt, indem kontinuierlich Daten gesammelt und die Strategie verfeinert wird.

Warum ist PPO so beliebt? Es ist einfacher zu implementieren als ältere Optimierungsverfahren wie die „Trust Region Policy Optimization“, es bietet stabile Aktualisierungen dank Clipping (dessen Formel wir oben hervorgehoben haben), es ist sehr effizient, da es gut mit modernen neuronalen Netzen arbeiten kann, und es kann große Aufgaben bewältigen. Sie ist auch insofern vielseitig, als sie sowohl im kontinuierlichen als auch im diskreten Raum gute Leistungen erbringen kann. Eine andere Art, die Intuition hinter PPO zu betrachten, wäre, wenn man sich vorstellt, dass man ein Spiel lernt. Wenn Sie Ihre Herangehensweise an das Spiel nach jedem Versuch drastisch ändern, verlieren Sie zwangsläufig die wenigen guten Manöver oder Taktiken, die Sie am Anfang gelernt haben. PPO dient als Mittel, um sicherzustellen, dass Sie beim Erlernen des Spiels nur kleine, schrittweise und bewusste Änderungen vornehmen und radikale Veränderungen vermeiden, die Sie schlechter machen könnten.

In vielerlei Hinsicht ist dies die Debatte zwischen Erkundung und Ausbeutung, die das Verstärkungslernen angehen soll. Und es kann argumentiert werden, dass zu Beginn der meisten Lernprozesse radikale Änderungen des Ansatzes notwendig sind, die mehr Erkundung als Ausbeutung ermöglichen. In diesen Ausgangssituationen wäre das öffentliche Beschaffungswesen natürlich nicht sehr nützlich. Nichtsdestotrotz ist PPO sehr populär, weil man argumentieren kann, dass die Befürworter in den meisten Disziplinen und Lernbereichen eher bei der Feinabstimmung als bei der ursprünglichen Entdeckung angelangt sind. Zu diesem Zweck wird PPO häufig in der Robotik eingesetzt, z. B. um Robotern beizubringen, zu gehen oder Objekte zu manipulieren, oder bei Videospielen, bei denen z. B. die KI trainiert wird, komplexe Spiele wie Schach oder Dota zu spielen.

Die Rolle des PPO beim Reinforcement Learning für Händler

PPO als Strategiealgorithmus, der mit anderen zentralen Algorithmen des Reinforcement Learning zusammenarbeitet, hat nicht viele Alternativen. Die wenigen verfügbaren, die erwähnenswert sind, sind Deep Q-Networks, die wir in einem früheren Artikel hier vorgestellt haben, „Asynchronous Advantage Actor-Critic“, die wir uns noch ansehen müssen, und „Trusted Region Policy Optimization“, die wir oben erwähnt haben. Betrachten wir nun, wie sich PPO von jeder dieser Umsetzungen unterscheidet. Wenn wir mit DQN beginnen, verwendet es Q-Learning, und es kann mit Instabilität aufgrund von großen Policy-Updates zu kämpfen haben, insbesondere in kontinuierlichen Aktionsräumen. Mit kontinuierlichen Aktionsräumen sind RL-Zyklen gemeint, bei denen die Wahl des Akteurs nicht durch zählbare Optionen wie Kaufen-Verkaufen-Halten vorgegeben ist, sondern durch eine Fließkommazahl oder eine Verdopplung in Anwendungsfällen wie der Bestimmung der idealen Positionsgröße für den nächsten Handel festgelegt wird.

PPO ist jedoch wohl stabiler und einfacher zu implementieren, da es kein separates Zielnetz oder gar eine Erfahrungswiederholung benötigt, ein Konzept, das wir in einem späteren Artikel untersuchen werden. Durch eine vereinfachte Trainingspipeline funktioniert PPO direkt sowohl in diskreten als auch in kontinuierlichen Handlungsräumen, während DQN eher für diskrete Räume geeignet ist.

Im Vergleich zu „Asynchronous Advantage Actor-Critic“ (A3C) neigt A3C (ein Politikalgorithmus, den wir in dieser Serie noch besprechen werden) dazu, mehrere RL-Zyklen (oder Agenten) zu verwenden, um eine gemeinsame Politik zu verschiedenen Zeiten zu aktualisieren; etwas, das normalerweise die Komplexität des Modells erhöht, in dem die mehreren RL-Zyklen vorkommen. PPO hingegen ist auf synchrone Updates und Policy-Clipping angewiesen, um einen stabilen Lernprozess ohne allzu aggressive Updates zu gewährleisten, die das Risiko eines Policy-Kollapses mit sich bringen können.

PPO weist im Vergleich zu der „Trust Region Policy Optimization“ (TRPO) auch einige deutliche Unterschiede auf. Dazu gehört vor allem, dass TRPO einen komplexen Optimierungsprozess zur Begrenzung von Änderungen an der Politik einsetzt, ein Prozess, der oft die Lösung eines eingeschränkten Optimierungsproblems erfordert. PPO hingegen vereinfacht dies, wie bereits erwähnt, durch das Clipping, bei dem durch die Einschränkung der Aktualisierungen eine höhere Recheneffizienz bei gleichbleibender Stabilität und Leistung erzielt werden kann.

Es gibt noch einige weitere Merkmale des öffentlichen Postwesens, die es wert sind, dass wir sie hier in der Einleitung erwähnen, bevor wir uns mit dem Hauptteil befassen. Wie bereits oben erwähnt, verwendet PPO einen Clipping-Mechanismus für die Aktualisierung der Richtlinien, um allzu drastische Aktualisierungen zu vermeiden. Die vielleicht nicht beabsichtigte Folge davon ist jedoch, dass ein Gleichgewicht zwischen Ausbeutung und Erkundung hergestellt wird, ein Schlüsselprinzip des Verstärkungslernens. Dies kann für Händler vor allem in Umgebungen mit hoher Volatilität von Vorteil sein, in denen ein übermäßiges Ausnutzen von Gewinnen ein Fehler sein könnte, und stattdessen ist es besser, sein Pulver trocken zu halten, um ein langfristiges Gefühl für die Märkte zu bekommen.

In Fällen, in denen ein gewisses Maß an Erkundung gerechtfertigt ist, kann PPO jedoch die Entropie-Regulierung einsetzen, die den Algorithmus daran hindert, zu viel Vertrauen in eine bestimmte Aktion zu gewinnen, sodass er weniger auf die Begrenzung der Aktualisierungen der Richtlinien setzt. Wir werden die Entropie-Regularisierung in einem späteren Artikel behandeln.

PPO ist auch effizient bei der Bearbeitung großer Aktionsräume. Dies ist darauf zurückzuführen, dass der akteurskritische Rahmen eine bessere Vorhersage der Werte in der Akteursdomäne ermöglicht, selbst wenn diese, wie bereits oben erwähnt, kontinuierlich sind. Darüber hinaus kann die Verringerung der Varianz der Strategieaktualisierungen dank der Verwendung einer Ersatzverlustfunktion zu einem konsistenteren Verhalten bei allen Geschäften führen, selbst in Fällen, in denen das RL in hochvolatilen Umgebungen wie im Devisenhandel operiert.

PPO lässt sich auch gut skalieren, da es nicht auf die Speicherung großer Erfahrungswiedergabepuffer angewiesen ist, die oft ressourcenintensiv sind. Dieser Vorteil könnte sich für Anwendungsfälle wie den Hochfrequenzhandel mit vielen Instrumenten oder sogar komplexe Handelsregelungen eignen.

PPO kann mit begrenzten Daten effizient lernen. Diese im Vergleich zu anderen Anbietern hohe Effizienz bei der Datenerhebung macht das System besonders geeignet für Umgebungen, in denen die Beschaffung von Marktdaten schwierig oder teuer sein kann. Dieses Szenario ist für viele Händler, die ihre Strategien über längere Zeiträume auf Basis realer Ticks testen müssen, von großer Bedeutung. Zwar kann der MetaTrader-Strategietester Tick-Daten generieren, wenn keine echten Ticks verfügbar sind, doch wird es in der Regel vorgezogen, eine Strategie mit echten Tick-Daten des vorgesehenen Handelsmaklers zu testen.

Dieses Volumen von realen Tick-Daten ist bei vielen Brokern nur selten in ausreichendem Maße vorhanden, und selbst in den Fällen, in denen die erforderlichen Jahre für den Testzeitraum verfügbar sind, könnte eine Qualitätsprüfung erhebliche Lücken im Datensatz aufdecken. Dies ist eine Art Spezialproblem für Finanzdaten, denn wenn man es mit anderen Bereichen wie der Entwicklung von Videospielen oder Simulationen vergleicht, ist die Erzeugung großer Datenmengen und das anschließende Training in der Regel unkompliziert. Außerdem hängen Schlüsselsignale oft von seltenen Ereignissen wie Marktzusammenbrüchen oder Booms ab, die nicht häufig genug auftreten, damit die Modelle daraus lernen können.

PPO „umgeht“ diese Probleme, indem es von Natur aus stichprobeneffizient ist, d. h. es kann aus begrenzten Datenmengen lernen. Der Bedarf an großen Datenmengen zur Erstellung angemessener Strategien ist keine Voraussetzung für PPO. Dies ist zum Teil der Vorteilsschätzung zu verdanken, die es ermöglicht, die verfügbaren Marktdaten in kleineren Stücken und weniger Episoden besser zu nutzen. Dies kann bei der Modellierung seltener, aber wichtiger Ereignisse von entscheidender Bedeutung sein, da PPO auch bei Datenknappheit schrittweise aus guten und schlechten Geschäften lernt.

Bei den meisten Handelssystemen kann sich die „Belohnung“, die in der Regel als Gewinn oder Verlust quantifiziert wird, bei jeder Entscheidung erheblich verzögern. Diese Situation bringt insofern Probleme mit sich, als es problematisch wird, eine bestimmte, früher durchgeführte Maßnahme mit einer Gutschrift zu versehen. Wenn man beispielsweise zu einem bestimmten Zeitpunkt eine Kaufposition eingeht, kann sich der Gewinn erst Tage oder sogar Wochen später einstellen, was RL-Algorithmen vor die Herausforderung stellt, zu lernen, welche Handlungen oder Umgebungszustände genau welche Belohnungen auslösen.

Dieses Szenario wird zusätzlich durch Marktrauschen und Zufälligkeiten geschwächt, die vielen Marktpreisen innewohnen und es schwierig machen, zu erkennen, ob ein positives Ergebnis auf eine gute Entscheidung oder eine Ad-hoc-Marktbewegung zurückzuführen ist. Die Vorteilsfunktion, deren Gleichung oben erläutert wurde, hilft PPO dabei, die erwartete Belohnung für eine bestimmte Handlung besser abzuschätzen, indem sie sowohl den Wert (langfristige Gewichtung V(s t )) als auch die Q-Werte der Zustands-Aktions-Paarung (dargestellt als Q(s t , a t )) berücksichtigt, sodass die getroffenen Entscheidungen in Richtung beider Extreme besser ausbalanciert sind.

Einrichten der Signalklasse PPO in MQL5

Um dies in MQL5 zu implementieren, werden wir die Klasse „Cql“ verwenden, die unsere Hauptquelle in allen Artikeln zum Reinforcement Learning war. Wir müssen Änderungen vornehmen, um sie für PPO zu erweitern, und die erste dieser Änderungen ist die Einführung einer Datenstruktur zur Verarbeitung von PPO-Daten. Die Auflistung ist unten zu finden:

//+------------------------------------------------------------------+
//| PPO                                                              |
//+------------------------------------------------------------------+
struct Sppo
{  matrix            policy[];
   matrix            gradient[];
};

In der obigen Datenstruktur befinden sich zwei Arrays, deren Größe an die Anzahl der verfügbaren Aktionen für den Akteur im Verstärkungslernzyklus angepasst wird. Jede der Matrizen für den Gradienten und die Politik ist entsprechend der Anzahl der Zustände mal der Anzahl der Zustände in der typischen quadratischen Form dimensioniert. Das Matrix-Array dient daher als Äquivalent von Q-Map, da es die Gewichte und damit die Wahrscheinlichkeit der Auswahl jeder Aktion in jedem Zustand protokolliert. Wir halten uns an die gleichen einfachen Umgebungsbedingungen, die wir in diesen Serien von steigenden, fallenden und Seitwärtsphasen des Marktes verwendet haben. Zusammenfassend kann man sagen, dass diese 3 Zustände sowohl über einen kurzen als auch über einen längeren Zeithorizont erfasst werden.

Bei der Definition von Zeithorizonten würden sich die meisten Menschen auf Zeitrahmen konzentrieren und z. B. danach suchen, ob der Kurstrend eines bestimmten Wertpapiers auf dem täglichen Zeitrahmen steigt oder fällt, und diesen Prozess dann auf dem einstündlichen Zeitrahmen wiederholen, um zu den beiden Messgrößen zu gelangen. Die von uns gewählte und in diesen Reihen verwendete Definition der Zeithorizonte ist sehr viel einfacher, da wir einfach eine Verzögerung von einer bestimmten Anzahl von Kursbalken verwenden, um das Kurzfristige vom Langfristigen zu trennen.

Dieser nachlaufende Wert ist ein einstellbarer Eingangsparameter, den wir im Code der Signalklasse als „Signal_PPO_RL_Scale“ oder m_scale bezeichnen, und der Prozess des Mappings der beiden Preisaktionstrends wird in der Funktion „getOutput“ erfasst, die später in diesem Artikel erläutert wird. Kehren wir jedoch zu PPO zurück. So bedeutet die Umsetzung dieses Vorhabens durch Änderung der Klasse Cql in erster Linie die Einführung von 2 neuen Funktionen. Die Funktion set-policy und die Funktion get-clipping. Um die nächste Aktion des Akteurs zu bestimmen, rufen wir keine dieser Funktionen auf, sie könnten auch geschützte Funktionen der Klasse Cql sein.

Die Einstellung der Politik wird im Rahmen der Funktionen für setOn und setOff der Politik aufgerufen. Die Liste ist nachstehend aufgeführt:

//+------------------------------------------------------------------+
//| PPO policy update function                                       | 
//+------------------------------------------------------------------+
void Cql::SetPolicy()
{  matrix _policies;
   _policies.Init(THIS.actions, Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _policies.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies[i][GetMarkov(ii, iii)] += Q_PPO.policy[i][ii][iii];
         }
      }
   }
   vector _probabilities;
   _probabilities.Init(Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _probabilities.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies.Row(i).Activation(_probabilities, AF_SOFTMAX);
            double _old = _probabilities[states[1]];
            double _new = _probabilities[states[0]];
            double _advantage = Q_SA[i][ii][iii] - Q_V[ii][iii];
            double _clip = GetClipping(_old, _new, _advantage);
            Q_PPO.gradient[i][ii][iii] = (_new - _old) * _clip;
         }
      }
   }
   for(int i = 0; i < THIS.actions; i++)
   {  for(int ii = 0; ii < int(Q_PPO.policy[i].Rows()); ii++)
      {  for(int iii = 0; iii < int(Q_PPO.policy[i].Cols()); iii++)
         {  Q_PPO.policy[i][ii][iii] += THIS.alpha * Q_PPO.gradient[i][ii][iii];
         }
      }
   }
}

Innerhalb dieser Funktion decken wir im Wesentlichen 3 Schritte zur Aktualisierung der Policenwerte für unsere PPO-Struktur ab, deren Code wir oben geteilt haben. Da es sich hierbei um eine alte Funktion handelt, auf die wir in früheren Artikeln Bezug genommen haben, ist ihre Verwendung hier relevant, da wir ihre Auflistung, wie sie hier angegeben ist, überarbeitet haben:

//+------------------------------------------------------------------+
//| Choose an action using epsilon-greedy approach                   |
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   //printf(__FUNCSIG__+" next state is: %i, with best act as: %i ",_next_state,_best_act);
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   states[1] = states[0];
   states[0] = GetMarkov(_next_row, _next_col);
   td_value = Q_V[_next_row][_next_col];
   td_policies[1][0] = td_policies[0][0];
   td_policies[1][1] = td_policies[0][1];
   td_policies[1][2] = td_policies[0][2];
   td_policies[0][0] = _next_row;
   td_policies[0][1] = td_value;
   td_policies[0][2] = _next_col;
   q_sa_act = 1;
   q_ppo_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[q_sa_act][_next_row][_next_col])
      {  q_sa_act = i;
      }
      if(Q_PPO.policy[i][_next_row][_next_col] > Q_PPO.policy[q_ppo_act][_next_row][_next_col])
      {  q_ppo_act = i;
      }
   }
//update last acts
   acts[1] = acts[0];
   acts[0] = q_ppo_act;
}

Um jedoch auf die Funktion der Mengenpolitik und ihre 3 Schritte zurückzukommen, quantifiziert der erste davon das Gesamtgewicht der Politik für jede Aktion über alle Zustände hinweg. Im Wesentlichen handelt es sich dabei um eine Form der Abflachung der Matrix der Umgebungszustände durch Verwendung einer get-Markov-Funktion, die einen Solo-Index aus zwei Indexwerten (die kurzfristige und langfristige Muster darstellen) zurückgibt. Sobald wir diese kumulativen Gewichte für jede Aktion in der Matrix mit der Bezeichnung „_policies“ haben, können wir die Aktualisierungsgradienten für unsere Politikgewichte berechnen.

Die Gradienten, die in der Gradientenmatrix gespeichert werden, die wir oben in der PPO-Struktur eingeführt haben, aktualisieren unsere Richtliniengewichte, ähnlich wie ein neuronales Netz seine Gewichte aktualisiert. Die Ermittlung der Gradientenwerte ist jedoch, ähnlich wie bei den meisten modernen neuronalen Netzen, ein wenig mühsam. Zunächst müssen wir einen Vektor „_probabilities“ definieren, dessen Größe dem abgeflachten Index der Umgebungszustände entspricht. In diesem Fall sind es 3 x 3, was 9 ergibt. Eine weitere Einführung bzw. Änderung der Cql-Klasse, die wir mit PPO vorgenommen haben, ist die Einführung des 2-großen Status-Arrays. Dieses Array protokolliert oder puffert einfach die letzten beiden Umgebungszustandsindizes, die der Akteur „erlebt“ hat, und der Zweck dieser Protokollierung ist die Unterstützung bei der Aktualisierung der Gradienten.

Mit der Matrix „_policies“, die für jede Aktion und jeden abgeflachten Zustandsindex die kumulative Politikgewichtung enthält, erhalten wir also eine Wahrscheinlichkeitsverteilung über alle Zustände für jede Aktion. Da die Richtliniengewichtung negativ sein kann, müssen wir die Rohwerte auf den Bereich 0 - 1 normalisieren, und eine der einfachsten Möglichkeiten, dies zu erreichen, ist die Verwendung der eingebauten Aktivierungsfunktionen mit SoftMax-Aktivierung. Wir führen diese Aktivierungen reihenweise durch und erhalten dann Wahrscheinlichkeiten für den vorherigen Zustand und den aktuellen Zustand der Umgebung. Der Einfachheit halber werden auch hier die Indizes abgeflacht.

Die andere wichtige Kennzahl, die wir in dieser Phase brauchen, ist der Vorteil. Wie bereits erwähnt, hilft uns dieser Vorteil, unsere Aktualisierungen der Politikgewichte zu normalisieren oder auszubalancieren, um sowohl die kurzfristigen, auf dem Zustand basierenden Gewichte als auch die langfristigen, auf dem Wert basierenden Gewichte zu berücksichtigen, ein Prozess, der die Auswahl von PPO-Aktionen besser macht, wenn es darum geht, kurzfristige Preisaktionen mit langfristigen Belohnungen zu verbinden, wie bereits oben argumentiert wurde. Dieser Vorteil ergibt sich aus der Subtraktion der Q-Wert-Gewichtsmatrix, die wir im Artikel über die zeitliche Differenz eingeführt haben, von der Zustands-Aktionspaar-Matrix, die wir in unserem ersten Artikel über Verstärkungslernen eingeführt haben. Beide werden umbenannt, aber ihre Funktionsweise und Grundsätze bleiben gleich.

Anhand dieses Vorteils können wir dann berechnen, um wie viel wir die Aktualisierungen kürzen müssen. Wie bereits in der Einleitung erwähnt, hebt sich PPO von anderen Algorithmen zur Verwaltung von Richtlinien dadurch ab, dass es seine Aktualisierungen mäßigt, indem es sicherstellt, dass sie nicht zu drastisch ausfallen und für einen langfristigen Erfolg meist inkrementell sind. Die Bestimmung von „_clip“ erfolgt durch die Funktion get-clipping, deren Quelltext unten angegeben ist:

//+------------------------------------------------------------------+
//| Helper function to compute the clipped PPO objective             |
//+------------------------------------------------------------------+
double Cql::GetClipping(double OldProbability, double NewProbability, double Advantage)
{  double _ratio = NewProbability / OldProbability;
   double _clipped_ratio = fmin(fmax(_ratio, 1 - THIS.epsilon), 1 + THIS.epsilon);
   return fmin(_ratio * Advantage, _clipped_ratio * Advantage);
}

Der Code in dieser Funktion ist sehr kurz, und die alte Wahrscheinlichkeit sollte nicht Null sein; andernfalls kann ein Epsilon-Wert zum Nenner hinzugefügt werden, um dies zu überprüfen. Sobald wir den „_clip“ haben, der im Wesentlichen ein normalisierter Bruch ist, multiplizieren wir diesen mit der Differenz zwischen den beiden Wahrscheinlichkeiten. Dabei ist zu beachten, dass der Vorteil und auch das Produkt zwischen dem Clip und der Wahrscheinlichkeitsdifferenz positiv oder negativ sein kann. Dies bedeutet, dass die Aktualisierungsgradienten auch mit Vorzeichen versehen sein können, d. h. negativ oder positiv.

Dies führt zu den eigentlichen Aktualisierungen der Politikgewichte, die, wie oben erwähnt, der Aktualisierung der Gewichte des neuronalen Netzes sehr ähnlich sind, und auch sie können, da sie auf den oben genannten Gradienten basieren, negativ oder positiv sein. Diese Unterzeichnung der Gewichte der PPO-Politik ist der Grund, warum wir die Gewichtssummen jeder Aktion mit SoftMax aktivieren müssen, wenn wir die Wahrscheinlichkeitsverteilungen ausrechnen, die in der zweiten Phase der Festlegung der Politik hervorgehoben werden. Sobald die Gewichte der Richtlinien aktualisiert sind, werden sie wie folgt in der geänderten Aktionsfunktion verwendet, deren aktualisierte Auflistung oben mitgeteilt wurde.

Die Anpassung an die alte Funktion „Aktion“ ist sehr gering, da wir lediglich die Höhe der Gewichtung der Politik überprüfen, wobei die Aktion mit der höchsten Gewichtung gemäß unserem oben beschriebenen PPO-Aktualisierungsschema ausgewählt wird. Angesichts der nächsten Aktion können wir diese nun mit der Funktion getOutput abrufen, die auch, wie bereits oben erwähnt, die Umgebungszustandsmatrizen definiert; die Auflistung hierfür ist unten angegeben. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalPPO::GetOutput(Cql *QL, int RewardSign)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = RewardSign*_in_row[m_scale - 1];
      double _reward_max = RewardSign*_in_row.Max();
      double _reward_min = RewardSign*_in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float, RewardSign);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
   }
}

Sie ist, wie die obige Aktionsfunktion, dem sehr ähnlich, was wir in den Artikeln zum Reinforcement Learning verwendet haben, wobei die Änderungen fast nicht vorhanden zu sein scheinen (abgesehen von einigen wichtigen Auslassungen), da die Schlüsselfunktionen, die wir jetzt mit PPO aufrufen, verborgen sind, nämlich die Funktionen setPolicy und getClipping. Es scheint eindeutig eine verwässerte Version der bisherigen getOutput zu sein. Um das oben Gesagte noch einmal zusammenzufassen: Die „m_scale“ kann hier als unsere Verzögerung betrachtet werden, die die kurzfristigen Markttrends von den langfristigen Trends trennt, während sie einen einzigen Zeitrahmen verwendet. Alternativen, die andere Zeiträume verwenden, können vom Leser erforscht werden, aber in diesem Fall müsste ein alternativer Zeitrahmen als Eingabe hinzugefügt werden. Die wichtigsten Änderungen in der nutzerdefinierten Signalklasse betreffen die Funktionen für Kauf- und Verkaufs-Bedingung, deren Code im Folgenden erläutert wird:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::LongCondition(void)
{  int result = 0;
   GetOutput(RL_BUY, 1);
   if(RL_BUY.q_ppo_act==0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::ShortCondition(void)
{  int result = 0;
   GetOutput(RL_SELL, -1);
   if(RL_SELL.q_ppo_act==2)
   {  result = 100;
   }
   return(result);
}

Die Auflistung ist fast identisch mit derjenigen, die wir bisher verwendet haben, mit dem Hauptunterschied, dass auf die „q_ppo_act“ verwiesen wird, im Gegensatz zu der Aktion, die nur durch den Markov-Entscheidungsprozess ausgewählt wurde.

Strategy Tester Berichte und Analysen

Wir bauen diese nutzerdefinierte Signalklasse mit Hilfe des MQL5-Assistenten in einen Expert Advisor ein. Für Leser, die neu sind, gibt es hier und hier Anleitungen, wie er das umsetzen kann. Wenn wir einige günstige Einstellungen aus der Optimierung von GBP JPY über das Jahr 2022 auf dem 4-Stunden-Zeitrahmen extrahieren, erhalten wir die folgenden Ergebnisse:

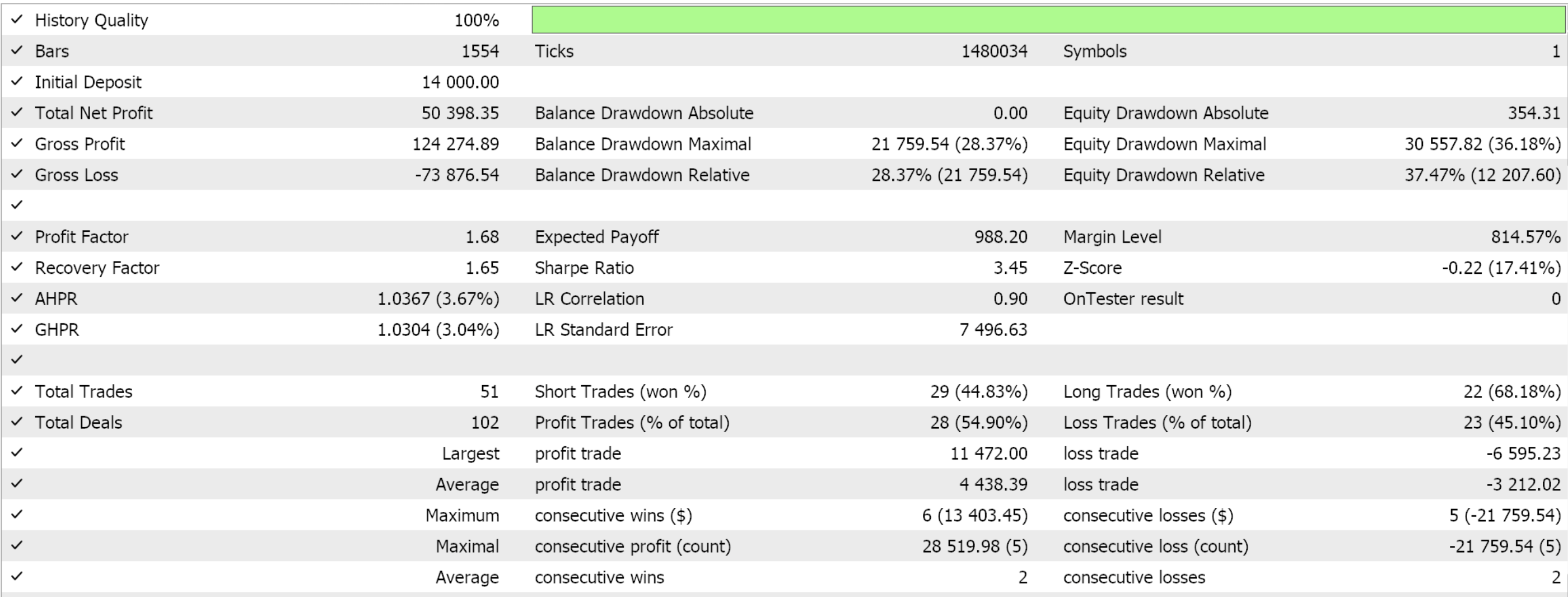
Wie immer sollen die hier vorgestellten Ergebnisse das Potenzial des nutzerdefinierten Signals aufzeigen. Die für diesen Bericht verwendeten Eingabeeinstellungen sind nicht kreuzvalidiert und werden daher nicht gemeinsam genutzt. Der Leser ist eingeladen, sich darauf einzulassen, indem er sie seinen Erwartungen anpasst.

Meine Philosophie ist, dass ein Expert Advisor, egal ob er vollautomatisch oder zur Unterstützung eines manuellen Handelssystems eingesetzt wird, nie mehr als 50 % zum gesamten „Handelssystem“ beitragen darf. Die menschliche Emotion ist immer die andere Hälfte. Selbst wenn Sie also jemandem einen „Gral“ präsentieren, der mit seinen Feinheiten oder seiner Funktionsweise nicht vertraut ist, wird er zwangsläufig ungestüm werden und viele seiner wichtigen Handelsentscheidungen in Frage stellen. Durch die Präsentation eines nutzerdefinierten Signals ohne seine „Gral“-Einstellungen wird der Leser also nicht nur aufgefordert zu verstehen, warum der Expert Advisor in dem kurzen, optimierten Zeitraum, der in den Artikeln vorgestellt wird, günstig abgeschnitten hat, sondern auch zu verstehen, warum er in anderen Testzeiträumen möglicherweise nicht ähnlich abschneidet, und diese beiden Informationen sollten dabei helfen, Einstellungen zu finden, die über größere Zeiträume hinweg funktionieren.

Ich glaube, dass dieser Prozess, bei dem der Händler seine eigenen Einstellungen entwickelt oder verschiedene nutzerdefinierte Signale zu einem funktionsfähigen Expert Advisor kombiniert, der Grund dafür ist, dass sie ihre 50 % ausgleichen.

Schlussfolgerung

Wir haben uns einen anderen Algorithmus des Reinforcement Learning angesehen, die „Proximal Policy Optimization“, eine sehr beliebte und effektive Methode, da sie die Aktualisierung der Richtlinien während der Reinforcement-Learning-Episoden moderiert.

Der PPO-Algorithmus stellt einen bahnbrechenden Ansatz für das Verstärkungslernen dar, der Stabilität und Anpassungsfähigkeit miteinander verbindet, was für reale Anwendungen wie den Handel entscheidend ist. Die maßgeschneiderte Clipping-Strategie berücksichtigt sowohl diskrete als auch kontinuierliche Aktionen und bietet eine skalierbare Effizienz ohne intensive Ressourcenabhängigkeit, was sie für komplexe Systeme, die einer Vielzahl von Marktbedingungen ausgesetzt sind, von unschätzbarem Wert macht.

Datei Name	Beschreibung
Cql.mqh	Verstärkungslernen Quellenklasse
SignalWZ_49.mqh	Nutzerdefinierte Signalklassendatei
wz_49.mqh	Assistent Assemblierter Expert Advisor, dessen Kopfzeile dazu dient, die verwendeten Dateien anzuzeigen