Recursos do Assistente MQL5 que você precisa conhecer (Parte 43): Aprendizado por reforço com SARSA

Introdução

Aprendizado por reforço (reinforcement learning, RL) permite que sistemas de negociação aprendam com base em dados do ambiente ou do mercado e, assim, melhorem suas capacidades de negociação ao longo do tempo. O RL possibilita adaptação a condições de mercado em constante mudança, tornando-o adequado para determinados mercados financeiros e ativos de natureza dinâmica. Os mercados financeiros são imprevisíveis, pois geralmente apresentam um alto grau de incerteza. O RL lida muito bem com a tomada de decisões nesse cenário, ajustando continuamente suas ações com base no feedback recebido (recompensas), o que é extremamente útil para traders que atuam em condições de mercado instáveis.

Essa abordagem pode ser comparada a um Expert Advisor anexado a um gráfico, que realiza sua própria otimização periodicamente com base no histórico recente de preços para ajustar precisamente seus parâmetros. O RL busca realizar algo semelhante. Em nossa série de artigos, abordamos o RL em sentido estrito, como a terceira abordagem de aprendizado de máquina, além do supervisionado e do não supervisionado. No entanto, ainda não o exploramos como um modelo independente que possa ser utilizado para previsão.

É exatamente isso que faremos neste artigo. Não apenas apresentaremos o algoritmo de RL SARSA, mas também buscaremos implementá-lo em uma nova classe personalizada de sinais para Expert Advisors gerados no Wizard, como um modelo de sinal independente. Quando utilizado como modelo de sinal, o RL automatiza o processo de tomada de decisões, reduzindo a necessidade de intervenção humana constante, o que, por sua vez (pelo menos em teoria), pode possibilitar negociações de alta frequência e reação em tempo real aos movimentos do mercado. Além disso, graças ao feedback contínuo do mecanismo de recompensas, modelos de aprendizado por reforço tendem a desenvolver uma melhor gestão de riscos. Isso ocorre por meio da penalização de ações de alto risco com recompensas baixas, e o efeito líquido é que o RL minimiza a exposição a operações voláteis ou potencialmente deficitárias.

O RL também envolve o equilíbrio entre exploração e aproveitamento, ou seja, o equilíbrio entre testar novas estratégias e utilizar aquelas que já se mostraram lucrativas. Isso é possível graças à abordagem "epsilon-greedy" para atualização do Q-map, que representa uma matriz de ações nos possíveis estados do ambiente, a partir dos quais o agente pode escolher sua ação.

Há ainda outros benefícios do RL que podem parecer secundários, mas que merecem ser mencionados, considerando o papel cada vez mais relevante do RL na inteligência artificial.

Ele pode ajudar a otimizar a execução de ordens, aprendendo os melhores momentos e preços para comprar ou vender com base em dados históricos e feedback em tempo real, aumentando assim a lucratividade. Isso pode ser alcançado quando, como no caso abordado neste artigo, ele é utilizado como modelo básico de sinal em conjunto com outro sinal, de forma que sua função se limite a determinar como agir em situações nas quais se utilizam ordens pendentes. Se o Q-map contiver, por exemplo, 3 ações — ordens limitadas, ordens stop e ordens a mercado — é possível ajustar precisamente os pontos de entrada de uma estratégia já consolidada e familiar.

O RL é um modelo não convencional, diferente dos lineares tradicionais, e talvez mais adequado para estudar e implementar estratégias de negociação complexas e não lineares, que supostamente refletem melhor o comportamento real do mercado. Ele também é escalável para lidar simultaneamente com múltiplas classes de ativos ou estratégias, dependendo de como o Q-map e as ações associadas forem definidos, o que o torna uma solução versátil para a gestão de portfólios ou para a negociação algorítmica envolvendo diversos instrumentos financeiros. Por fim, ele é especialmente apropriado para sistemas de tomada de decisão em tempo real, englobando não apenas Expert Advisors totalmente automatizados, mas também sistemas de negociação parcialmente manuais, conforme a estratégia e as configurações vigentes.

Introdução ao SARSA

A sigla SARSA significa State-Action-Reward-State-Action (estado–ação–recompensa–estado–ação). O nome vem da forma como os valores do Q-map são atualizados. Esse método de atualização dos valores de Q difere claramente da abordagem do Q-learning que analisamos no artigo anterior, pois segue a política (on-policy), em contraste com o método fora da política (off-policy) que vimos anteriormente. Na prática, nossa implementação do SARSA para este artigo é idêntica àquela que utilizamos quando apresentamos o Q-learning, com a única diferença no modo de atualização dos valores do Q-map.

O algoritmo SARSA, por ser baseado na política, aprende os valores de Q com base nas ações que já executou seguindo sua política atual, e não com base nas ações que pretende realizar a partir do estado atual do ambiente. Ele atualiza os valores de Q utilizando a ação escolhida pela política que está sendo seguida. Por outro lado, o Q-learning é um algoritmo fora da política, ou seja, atualiza os valores de Q utilizando a melhor ação possível do próximo estado do ambiente, independentemente da ação tomada pela política atual. Ele aprende a política ótima sem depender das ações atuais do agente. Implementamos essa atualização de valores de Q para o SARSA, dentro da política, da seguinte forma:

//+------------------------------------------------------------------+
// Update Q-value using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q-action from Q-Map
   double _action = Q[act[1]][e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _action *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  if(i == act[0])
      {  continue;
      }
      Q[i][e_row[1]][e_col[1]] += THIS.alpha * (Reward + (THIS.gamma * _action) - Q[act[0]][e_row[1]][e_col[1]]);
   }
}

A regra de atualização do SARSA utiliza a ação efetivamente executada no próximo estado (Estado → Ação → Recompensa → Estado → Ação). O processo segue a política epsilon-greedy em relação à exploração e ao aprendizado. Isso é muito parecido com o que foi abordado no Q-learning; no entanto, o que antes não estava tão evidente e agora fica em destaque é como a escolha epsilon-greedy pode levar a resultados bastante inconsistentes, já que o processo de atualização do Q-map é randomizado. De forma geral, quanto menor o valor de epsilon, menores serão os efeitos aleatórios.

Quando se trata do equilíbrio entre exploração e aproveitamento, o SARSA adota uma abordagem mais equilibrada, pois segue a mesma política tanto durante o aprendizado quanto na execução das ações. Em teoria, isso significa que o algoritmo é mais seguro em condições incertas de alguns mercados financeiros. Já o Q-learning tende a ser mais agressivo, pois sempre busca obter o máximo proveito do próximo estado, o que potencialmente o torna mais propenso a tomar decisões de alto risco em condições instáveis.

Assim, o SARSA é mais adequado para cenários em que é fundamental manter o equilíbrio entre exploração e aproveitamento, e o ambiente apresenta riscos ou não é estacionário, e um bom exemplo, nesse caso, seria a negociação de qualquer par envolvendo o JPY. Por outro lado, o Q-learning é mais apropriado quando o ambiente é relativamente estável e a busca pela estratégia ótima é mais importante do que a gestão contínua dos riscos. Um exemplo provável aqui seria o par EURCHF.

Também analisamos outro algoritmo de RL, as redes neurais profundas de Q (Deep-Q-Networks), no artigo mencionado, e ele difere do SARSA em vários aspectos. À primeira vista, a principal diferença é que o SARSA, assim como o Q-learning, utiliza uma Q-tabela para armazenar os valores de estado e ação. Isso limita o SARSA a ambientes com pequenos espaços de estados, já que, em ambientes maiores, manter uma Q-tabela torna-se impraticável. Já o DQN, como vimos no referido artigo, utiliza redes neurais para aproximar os valores de Q para cada par estado–ação, o que o torna mais escalável e eficiente em ambientes com espaços de estados grandes ou contínuos.

No que diz respeito à reprodução de experiências, o SARSA não a utiliza, pois o algoritmo aprende com cada experiência de forma sequencial. Isso pode resultar em um aprendizado menos eficiente, já que o agente aprende apenas com a experiência mais recente. Por sua vez, o DQN pode implementar a reprodução de experiências, em que eventos passados são armazenados em buffer e selecionados aleatoriamente durante o treinamento. Isso pode reduzir significativamente a correlação entre eventos consecutivos, levando, assim, a um aprendizado mais estável.

Outra diferença entre o SARSA e o DQN decorre do uso de redes-alvo. No SARSA, tal conceito não existe, pois ele atualiza os valores de Q diretamente a cada etapa com base na política atual. Já no DQN, como vimos no artigo respectivo, o uso de uma rede-alvo em conjunto com a rede Q principal para estabilizar o aprendizado é obrigatório. No DQN, a rede-alvo é atualizada periodicamente, o que garante atualizações mais estáveis dos valores de Q e evita grandes oscilações no processo de aprendizado.

Escalabilidade e complexidade são outra diferença importante entre DQN e SARSA, pois o SARSA é mais adequado para resolver tarefas pequenas e simples devido às limitações do tamanho da Q-tabela e ao fato de aprender seguindo a política. O DQN, por outro lado, é projetado para lidar com tarefas mais complexas e multidimensionais, como aquelas encontradas em problemas relacionados a imagens ou em ambientes com um grande número de estados. Neste artigo sobre o SARSA, assim como no artigo sobre o Q-learning, limitamos o número de estados do ambiente a nove, por uma questão de simplicidade.

Esses estados são baseados em três condições simplificadas de mercado: tendência de alta, tendência de baixa e movimento lateral irregular. Cada uma dessas condições é aplicada a um período de tempo curto e a um período de tempo longo para criar uma matriz 3 x 3, resultando em 9 estados possíveis. Nos casos em que seja necessário considerar parâmetros adicionais, como dados de notícias econômicas ou os movimentos de preços correlacionados de outros ativos, o espectro contínuo de valores que esses dados podem assumir acaba restringindo a aplicabilidade do SARSA.

Por fim, a taxa de aprendizado representa outra diferença importante entre o SARSA e o DQN. O SARSA pode ser mais lento em ambientes complexos devido ao processo sequencial de atualização e à ausência de generalização por rede neural. O DQN, por sua vez, tende a operar mais rapidamente em ambientes grandes graças à sua capacidade de generalizar estados semelhantes por meio de uma rede neural, especialmente quando essa capacidade é combinada com o aprendizado em lote por meio da reprodução de experiências.

Configuração do ambiente MQL5 para o SARSA

Para implementar nossa classe personalizada de sinais, utilizando como modelo base o RL em vez de um MLP ou outro algoritmo de aprendizado de máquina, é essencial simplificar a classe de sinais apresentada no artigo introdutório para uma versão do RL voltada ao Q-learning. Nesse artigo, o MLP era usado para previsão, enquanto o RL ficava restrito ao processamento da função de perda durante o treinamento. Assim como naquela ocasião, o RL com SARSA utiliza a abordagem epsilon-greedy para definir quando o agente deve selecionar aleatoriamente a melhor ação.

Quando utilizávamos o RL apenas para gerenciar o processo de treinamento do MLP, essas escolhas frequentemente aleatórias eram "aceitáveis", pois o valor de perda resultante do treinamento não era tão sensível ao desempenho geral do MLP. No entanto, agora que o modelo é o próprio RL e não mais um MLP, a escolha de ações aleatórias exerce um impacto desproporcional sobre o desempenho total.

Em aprendizado de máquina, é comum haver um conjunto de treino e um conjunto de teste. Geralmente, o conjunto de dados para treinamento é um pouco maior que o de teste e, seguindo esse protocolo de separação entre treino e teste, o uso do epsilon pode ser construtivo para a performance global do modelo. O Q-map, que é basicamente uma matriz, não é exportado por nenhuma função no código fornecido. Qualquer pessoa interessada em continuar usando esse método para treinamento e teste independentes precisará exportar essa matriz como um arquivo binário ou CSV para seu próprio sistema após o treinamento, antes de carregá-la novamente para uso nos testes.

Implementação da classe personalizada de sinais

Conforme mencionado anteriormente, nossa classe personalizada de sinais é uma simplificação do que foi abordado no artigo sobre o algoritmo Q-learning, e uma das principais mudanças está na função de obtenção de saídas, que foi revisada da seguinte forma:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalSARSA::GetOutput(int &Output, Cql *QL)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.SetOnPolicy(_reward, _in_e);
      Output = QL.transition_act;
   }
}

Para iniciantes, o processo de compilação do código em um Expert Advisor está descrito aqui e aqui. O EA compilado será testado com um valor otimizado de epsilon apenas para demonstrar a facilidade de uso do robô. Na prática, esse valor idealmente deve ser definido com base no conhecimento do próprio usuário sobre a importância relativa e a relevância de diferentes estados do ambiente e das ações correspondentes.

Testes e depuração do sinal baseado em SARSA

Para testar e utilizar melhor o sinal personalizado do SARSA, é necessário realizar algumas alterações na classe de sinais, sendo talvez a mais importante delas a adição de uma função para exportar o array da matriz Q-map. Isso permitirá realizar testes e treinamentos independentes no sentido tradicional. No entanto, essas possibilidades de verificação cruzada já estão incorporadas ao testador de estratégias, já que o teste forward está disponível.

Também é possível ajustar a forma de definição dos estados do ambiente, considerando estados de mercado alternativos, como níveis absolutos de preços, valores de indicadores RSI ou bandas de Bollinger, e associá-los a diferentes períodos gráficos para cada um desses pontos de dados. Depuração começa pela verificação de como essas variáveis de estado são registradas e atualizadas.

A função de recompensa também precisa refletir com precisão os resultados da negociação. Neste artigo, nosso código utiliza o desvio favorável como uma porcentagem da faixa de preços de cada novo candle. Isso ocorre porque treinamos simultaneamente o Q-map e posicionamos decisões de negociação com base em seus coeficientes ponderados de valores Q no momento apropriado. Naturalmente, essa abordagem não é perfeita, já que há a necessidade de buscar conjuntos de dados independentes adequados para testes e treinamento. Entretanto, os critérios de recompensa podem ser definidos para um horizonte mais longo do que o utilizado aqui, considerando, por exemplo, a lucratividade e o desempenho do Expert Advisor ao longo de períodos mais extensos.

Para evitar perseguir cegamente a lucratividade do EA, é aconselhável testar pares específicos de "estado–ação" e garantir que o robô responda adequadamente às condições de mercado, conforme o esperado. Por exemplo, ao verificar os coeficientes ponderados dos valores Q no Q-map, em nossa versão simplificada para este artigo, na primeira coordenada da grade 0 e 0 — que representa condições de mercado de baixa tanto no curto quanto no longo prazo —, o maior peso deveria estar atribuído à ação 0, que representa a venda, e não a um "valor que corresponda à curva" que contradiga o que se espera em mercados de baixa.

Verificar o equilíbrio adequado entre exploração e aproveitamento, implementado por meio da política "epsilon-greedy", também é fundamental, e isso pode ser alcançado otimizando o valor ideal de epsilon. No entanto, essa otimização precisa ser feita em um conjunto de dados de treinamento separado, no qual os Q-maps sejam preservados nas execuções com desempenho mais elevado. Após o treinamento em um conjunto de dados independente, o teste forward poderá confirmar ou refutar o valor de epsilon utilizado.

O aprendizado reverso deve ser realizado em conjuntos de dados de qualidade aceitável. Os relatórios do testador de estratégias refletem a qualidade dos dados utilizados após cada execução de teste, sendo, portanto, um bom indicador da confiabilidade do treinamento. Esse processo de treinamento incluirá a exportação dos Q-maps ao final de cada execução, sempre que os resultados do teste superarem os indicadores de referência anteriores. Os Q-maps exportados serão reutilizados em rodadas subsequentes de aprendizado reverso, de modo que essas execuções adicionais atuem como épocas no treinamento de redes neurais.

Ao final do processo de treinamento, o Q-map que apresentar o desempenho mais satisfatório do Expert Advisor será utilizado em uma execução de teste forward, para verificar se os resultados obtidos no treinamento podem ser reproduzidos com esse Q-map específico em um conjunto de dados de teste ainda "não visto". Os testes forward fazem parte integrante do testador de estratégias. E esta artigo pode servir como guia para iniciantes.

Além da verificação cruzada em conjuntos de dados históricos, o mesmo método pode ser considerado para contas reais antes de uma implantação completa — mantendo um registro de desempenho no qual diferentes Q-maps sejam organizados em uma tabela juntamente com seus respectivos resultados no testador. É possível ir além e implementar um registro detalhado nos testes forward em tempo real para registrar estados de mercado, ações, recompensas e atualizações de valores de Q, o que, pelo menos em teoria, ajudaria a identificar falhas no processo de tomada de decisão e permitiria ajustar parâmetros como a taxa de aprendizado ou o decaimento de ε.

Relatórios do testador de estratégias

As execuções de teste no período diário para o par EURJPY ao longo de 2022, feitas exclusivamente para demonstrar a facilidade de uso do Expert Advisor, produziram os seguintes resultados:

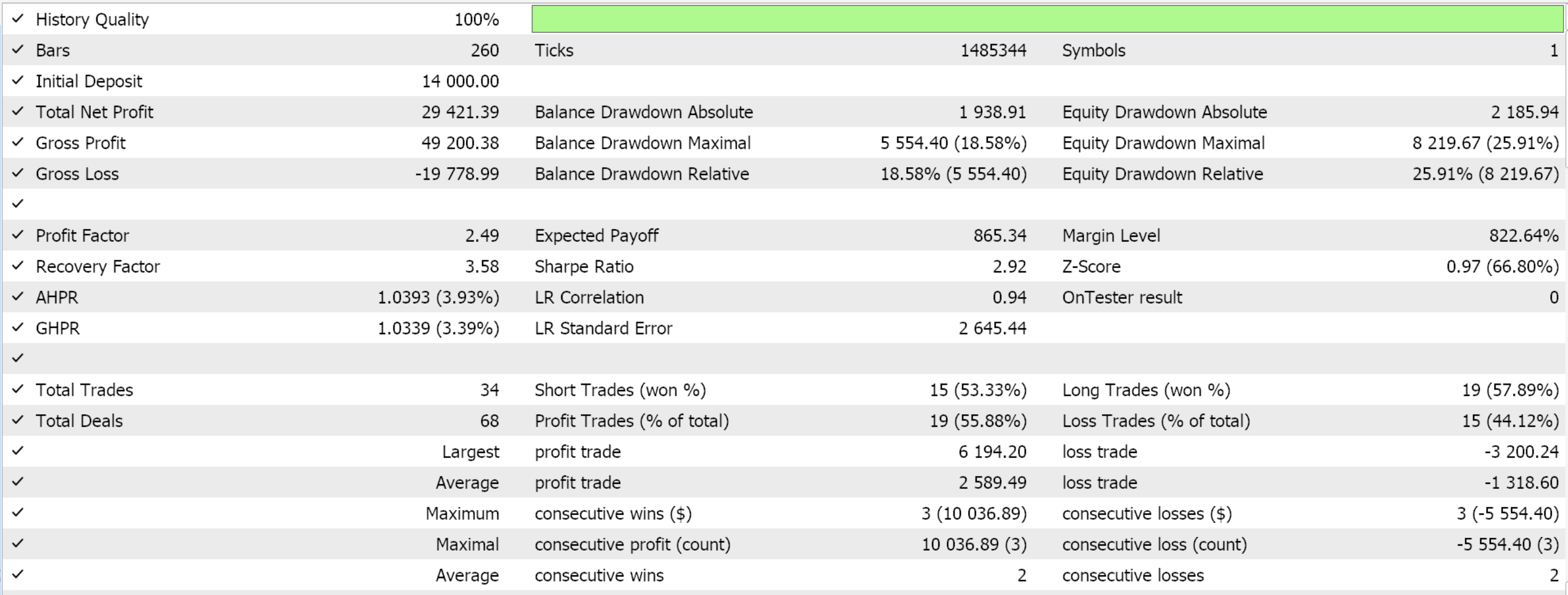
Aplicação prática do SARSA na negociação real

Como o SARSA é um algoritmo baseado na política, ele leva em consideração diretamente as ações dessa política durante o processo de treinamento, o que o torna mais adaptável a dados com ruído. O método de valores do Q-map que utilizamos atualiza todos os valores de Q no mapa proporcionalmente ao seu afastamento em relação à ação atual, conforme mostrado no código da política apresentado anteriormente. Essa atualização ocorre após o ajuste epsilon-greedy executado na função Action, equilibrando a exploração (descoberta de novas estratégias) e o aproveitamento (uso de estratégias já conhecidas), ajudando o modelo a evitar o sobreajuste ao ruído de curto prazo presente nos dados de mercado. A escolha da próxima ação que será utilizada pelo agente é feita por meio de um processo de decisão de Markov, independentemente de ser aplicado ou não um coeficiente de ponderação de Markov ao processo de atualização dos valores de Q, como foi feito anteriormente no artigo sobre Q-learning. O processamento é realizado na função Action, como mostrado a seguir:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//
   int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   transition_act = 0;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q[i][_next_row][_next_col] > Q[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
}

O suavizamento temporal com o auxílio do mecanismo de recompensa contribui para reduzir o ruído de curto prazo, focando na recompensa acumulada ao longo de várias iterações temporais. Isso dá ao algoritmo a capacidade de identificar padrões que vão além do ruído imediato dos dados. Além disso, o ajuste constante da política garante que ela seja baseada tanto no estado atual quanto no estado futuro. Isso pode ajudar a mitigar o impacto de dados com ruído, permitindo que o algoritmo se adapte à medida que novas informações chegam, especialmente quando as condições de mercado mudam rapidamente.

O SARSA é bastante robusto no trabalho com mercados instáveis, devido à sua estrutura interna de seleção de ação de transição, como descrito na função Action, cujo código foi mostrado anteriormente. Dadas as coordenadas do estado atual do ambiente, esses dois valores precisam ser convertidos em um único índice reconhecido pela matriz de Markov da classe QL. Isso é feito por meio da função Get Markov, cujo código é apresentado a seguir:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

De posse desse índice, podemos proceder à leitura da linha correspondente na matriz de Markov (representada por esse índice), identificando a coluna com o maior valor de probabilidade. A matriz de Markov é especialmente adequada para isso, pois não é armazenada em buffer nem mantida de forma persistente, ao contrário da maioria dos indicadores tradicionais. Ela não possui memória, o que a torna facilmente adaptável a condições incertas, como cenários de alta volatilidade. Assim, a partir da linha da matriz de Markov referente ao estado atual do ambiente, identificamos a coluna com a maior probabilidade; seu índice nos dará um número inteiro representando o próximo estado do ambiente. Esse número inteiro precisará ser novamente decomposto em dois valores, semelhantes àqueles que tínhamos no início — o índice da linha e o índice da coluna.

Uma vez obtidos os valores de linha e coluna que representam as coordenadas do próximo estado, podemos então ler da nossa Q-map a ação com o maior valor de Q. O índice dessa ação representa o que chamamos de "ação de transição" (transition action). Trabalhamos aqui com três possíveis ações, a saber: 0 — vender, 1 — não fazer nada e 2 — comprar. Além disso, o ambiente está limitado a três estados em três "períodos gráficos" considerados pelo Q-map.

Na prática, utilizamos apenas um período gráfico. O leitor, naturalmente, pode modificar o código e fazer os ajustes necessários. O parâmetro de entrada m_scale define até que ponto são monitoradas alterações mais amplas no "período gráfico" ao capturar essas mudanças de dois níveis que utilizamos para mapear e definir os estados do ambiente.

O SARSA leva em conta tanto as ações quanto as recompensas dentro da política atual, o que ajuda a estabilizar o processo de aprendizado durante períodos de alta volatilidade no mercado. Isso evita oscilações bruscas nas decisões que poderiam ocorrer devido a mudanças repentinas nas condições de mercado, tornando-o mais adequado para cenários instáveis do que algoritmos fora da política, como o Q-learning. Como mostrado no código da função de política apresentado anteriormente, aqui atualizamos os valores para a ação de índice 1, e não para a de índice 0, como no caso do Q-learning.

Como o SARSA avalia diretamente as ações executadas pela política em vigor, ele tende a adotar uma postura mais cautelosa em condições extremamente instáveis, evitando, assim, estimativas excessivamente otimistas sobre o valor de determinadas ações que poderiam levar a decisões incorretas diante de movimentos inesperados no mercado. Além disso, em mercados instáveis, a exploração epsilon-greedy do SARSA permite que o modelo investigue estratégias mais seguras, em vez de assumir ações de alto risco. Isso reduz a probabilidade de perdas significativas em períodos de fortes oscilações de preços, ao mesmo tempo em que mantém a possibilidade de descobrir novas estratégias lucrativas. Essa exploração de estratégias mais seguras é viabilizada pelo epsilon, que possibilita a escolha aleatória de ações, em vez de limitar-se apenas às ações aparentemente mais vantajosas no momento — que, em um cenário volátil, podem não gerar o resultado esperado. 

A aproximação de longo prazo do SARSA em direção à política ótima depende da interação contínua com o ambiente. Nos mercados financeiros, onde tendências de longo prazo e mudanças estruturais são a norma, a avaliação iterativa da política pelo SARSA garante que os valores de Q tendam a convergir ao longo do tempo, refletindo assim esses padrões de longo prazo. 

Ajustando o SARSA para estratégias mais complexas

A agregação do espaço de estados (State-Space Aggregation) no SARSA pode ser uma forma de particionar espaços de estados complexos, especialmente nos mercados financeiros, onde o espaço de estados (dinâmica de preços, indicadores, condições de mercado, notícias do calendário econômico) pode ser muito grande e contínuo. A agregação do espaço de estados reduz essa complexidade agrupando estados semelhantes em estados "agregados" ou "abstratos". O exemplo mais simples disso são os estados de ambiente que usamos neste artigo, representando apenas 3 variações imediatas e variações de prazo mais longo. No entanto, um uso mais elaborado desse método poderia ser feito ao considerar um ambiente mais multifacetado, como um Q-map cujos eixos contivessem dados sobre rendimento de títulos de 10 anos, taxas básicas de juros, índice de preços ao produtor (PPI), índice de preços ao consumidor (CPI) e taxa de desemprego.

Considerando a natureza das Q-maps, essas informações seriam aplicáveis a cada moeda de um par de moedas negociado. Assim, em vez de lidar com valores individuais para cada um desses indicadores, poderíamos agrupá-los da mesma forma que fizemos neste artigo, determinando apenas se cada indicador aumentou, permaneceu inalterado ou diminuiu. Esses resultados seriam então utilizados para determinar qual índice atribuir a cada ponto da matriz Q-map, exatamente como fizemos na atribuição dos valores de índice no Q-map deste estudo.

Conclusão

Neste artigo, analisamos outro algoritmo de aprendizado por reforço, o SARSA. Vale mencionar que a implementação utilizada no primeiro algoritmo de RL abordado, o Q-learning, assim como no algoritmo subsequente, que tratou das redes neurais profundas de Q, não aplicava corretamente o processo de decisão de Markov na escolha da próxima ação. Em vez disso, as cadeias de Markov eram usadas apenas como um mecanismo de ponderação no processo de atualização. Esse comportamento foi corrigido no artigo atual. O código-fonte completo está incluído.