MQL5 Wizard Techniques you should know (Part 49): Reinforcement Learning with Proximal Policy Optimization

Introduction

We continue our series on the MQL5 wizard, where lately we are alternating between simple patterns from common indicators and reinforcement learning algorithms. Having considered indicator patterns (Bill Williams’ Alligator) in the last article, we now return to reinforcement learning, where this time the algorithm we are looking at is Proximal Policy Optimization (PPO). It is reported that this algorithm, that was first published 7 years ago, is the reinforcement-learning algorithm of choice for ChatGPT. So, clearly there is some hype surrounding this approach to reinforcement learning. The PPO algorithm is intent on optimizing the policy (the function defining the actor’s actions) in a way that improves overall performance by preventing drastic changes that could make the learning process unstable.

It does not do this independently, but works in tandem with other reinforcement learning algorithms, some of which we have looked at in these series, that broadly speaking are in two categories. Policy-based algorithms and value-based algorithms. We have already looked at examples of each of these in the series, and perhaps to recap, the policy-based algorithms we saw were Q-Learning, and SARSA. We have only considered one value-based method, and that is temporal difference. So, what is PPO all about, then?

As alluded to above, the ‘problem’ PPO solves is preventing the policy from changing too much during updates. The thesis behind this is if there is no intervention in managing update frequency and magnitude, the agent might: forget what it learned, make erratic decision, or perform worse in the environment. PPO thus ensures the updates are small but meaningful. PPO works by starting with a policy that is predefined with its parameters. Where policies are simply functions that define actor’s actions based on rewards and environment states.

Given a policy, agent interaction with the environment would be performed so as to collect data. This ‘data collection’ would get a sense of the state-action-reward pairing, as well as the probabilities of the various actions taken under that policy. Having established this, what follows next is defining the objective function. As mentioned in the intro above, PPO is about moderating the magnitude of updates in reinforcement learning, and to this end we use a ‘clipping’ function to achieve this. This function is defined by the following equation:

Where:

• r t (θ)=πθ(at∣st)/πθ old (at∣st) is the probability ratio between the new policy (with parameters θ) and the old policy (with parameters θ old ​).
• Â t  is the advantage estimate at time t, which measures how much better an action is compared to the average action at a given state.
• ϵ is a hyperparameter (often 0.1 or 0.2) that controls the clipping range, limiting the policy update's step size.

The advantage estimate can be defined in a number of ways, however the one we use in our implementation is given below:

Where:

• Q(s t ,a t ) is the Q-value (expected return) for taking action a t ​ in state s t ​.
• V(s t ) is the value function for the state s t ​, representing the expected return if we follow the policy from that state onward.

This method of quantifying the advantage function does emphasize the dependence or the using of policy-based algorithms and value-based algorithms, which we also alluded to above. Once we have defined our objective function, we proceed to perform updates on our policy. The update adjusts the policy parameters with the goal of maximizing the clipped objective function. This ensures the policy changes are gradual and do not overfit recent data. This process then gets repeated by having an interaction with the environment using the updated policy, by continually collecting data and refining the policy.

Why is PPO popular? Well, it is easier to implement when compared to older policy optimizers like trust region policy optimization, it provides stable updates thanks to clipping (whose formula we highlight above), is very efficient in that it can work well with modern neural networks and can handle large-scale tasks. It is also versatile in that it can perform well in both continuous and discrete space. Another way of considering the intuition behind PPO would be if one imagines they are learning to play a game. If you drastically alter your approach to the game after each attempt, continuously, you are bound to lose the few good manoeuvres or tactics you may have picked up early on. PPO serves as a way of ensuring as you learn the game you only make small, gradual and deliberate changes by avoiding radical shifts that could make you worse.

In many ways, this is the exploration/ exploitation debate which reinforcement learning is meant to address. And it can be argued that at the onset of most learning processes radical shifts in the approach, that facilitate more exploration than exploitation, are necessary. In these initial situations, PPO would not be very useful, clearly. Nonetheless, because it can be argued for most disciplines and learning fields, proponents are more at the point of fine-tuning, than initial discovery, PPO is very popular. To this end, PPO is widely used in robotics such as teaching robots to walk or manipulate objects, or video-games where for instance AI is trained to play complex games like chess or Dota.

PPO Role in Reinforcement Learning for Traders

PPO as a policy algorithm that works together with other core reinforcement learning algorithms, does not have a lot of alternatives. The few, available, that are worth mentioning are Deep Q-Networks that we considered in an earlier article here, Asynchronous Advantage Actor-Critic that we are yet to look at, and Trusted Region Policy Optimization that we mentioned above. Let us consider how PPO is distinguished from each of these implementations. If we start with DQN, it uses Q-Learning, and it can struggle with instability due to large policy updates, especially in continuous action spaces. By continuous action spaces what is meant is in RL cycles where the actor’s choice is not predefined by enumerable choices like buy-sell-hold but rather is set by a floating-point number or double in use cases such as determining the ideal position size for the next trade.

PPO, however, is arguably more stable and easier to implement since it does not need a separate target network or even experience replay, a concept we will explore in a future article. By having a simplified training pipeline, PPO works directly in both discrete and continuous action spaces, while DQN is better favoured for discrete spaces.

When compared to Asynchronous Advantage Actor-Critic (A3C), A3C (a policy algorithm we are yet to consider in these series) tends to utilize multiple RL cycles (or agents) in order to update a shared policy at different times; something which usually increases the complexity of the model in which the multiple RL cycles are featured. PPO, on the other hand, depends on synchronous updates and policy-clipping to preserve a stable learning process without overly aggressive updates which can pose a risk of policy collapse.

PPO when compared to Trust Region Policy Optimization (TRPO) also presents a few marked differences. Prime among these is that TRPO uses a complex optimization process to limit policy changes, a process that often necessitates solving a constrained optimization problem. PPO on the other hand simplifies this through clipping, as afore mentioned, where, by constraining the updates, computational efficiencies can be garnered while still achieving similar levels of stability and performance.

There are a few more characteristics of PPO worth sharing here in the introduction, so we’ll run over them before dealing with the main body. PPO, as already emphasized above, uses a clipping mechanism to policy updates with the immediate intended goal of avoiding overly drastic updates. However, the perhaps non-intended consequence of this is providing a balance between exploitation and exploration, a key tenet in reinforcement learning. This can be beneficial for traders specifically in high-volatility environments where over exploiting of rewards could be a fool’s errand, and instead keeping one’s powder dry so as to get a long-term sense of the markets is a more suitable strategy.

However, in cases where some exploration is warranted, PPO can engage entropy-regularization which would prevent the algorithm from becoming too confident in a particular action such that it leans less on clipping the policy updates. We will consider entropy regularization in a future article.

PPO is also efficient at handling or dealing with large action spaces. This is because its actor-critic framework allows it to better forecast actor-domain values even when they are continuous as already mentioned above; but even more than that its reduction in the variance of policy updates, thanks to the use of a surrogate loss function, can lead to more consistent behaviour across trades even in cases where the RL is operating in high volatile environments such as those seen in forex.

PPO also scales well given that it does not rely on storing large experience replay buffers that are often resource heavy. This advantage could arguably make suited for use-cases such as high-frequency trading with many instruments or even complex trade-rule setups.

PPO can be efficient at learning with limited data. This data-sample-efficiency, when compared to its peers, makes it highly effective for environments where obtaining market data can be inhibited or expensive. This is a very poignant scenario for many trades that need to test their strategies over extended history periods on a real-tick basis, for example. While the MetaTrader strategy tester can generate tick data if no real ticks are available, as a rule, it is often preferred to test out on’ strategy on real-tick data of the intended trading broker.

This volume real-tick data is rarely sufficiently available for many brokers and even in cases where the requisite years for the test period are available, a quality-review could reveal significant holes in the data set. This is a sort of special problem for financial data because if one compares in other fields such as video game development or simulations, the generation of large amounts of data and subsequent training is usually straightforward. Furthermore, key-signals often depend on rare events such as market crashes or booms, and these do not appear frequently enough for models to learn from them.

PPO ‘circumvents’ these problems by inherently being sample-efficient, in that it is able to learn from limited volumes of data. The need for large volumes of data to generate decent policies is not a prerequisite for PPO. This in part is thanks to advantage-estimation that allows it to make better use of available market data in smaller chunks and fewer episodes. This can be key when trying to model rare but important events since PPO learns incrementally from both good and bad trades even when facing data scarcity.

For most trading systems the ‘rewards’, which are typically quantified as profit or loss, from any decision can be delayed significantly. This situation does present challenges in that it becomes problematic to assign a credit to a specific action taken earlier. For instance, when entering a long position at a particular time, the payoff might only be realized days or even weeks later; which clearly challenges RL algorithms on learning which actions or environment states accurately precipitate which rewards.

This scenario is further debilitated by market noise and randomness, which is so inherent in a lot of market price action that makes it difficult to discern whether a positive outcome resulted from a good decision or an ad hoc market move. The advantage-function, whose equation has been shared above, helps PPO better estimate the expected reward from a specific action by considering both the value (long-term weighting V(s t )), and also the state-action pairing Q-Values (represented as Q(s t , a t )) such that decisions taken are better balanced towards both extremes.

Setting Up the PPO Signal Class in MQL5

So, to implement this in MQL5, we will be using the ‘Cql’ class that has been our main source through all the reinforcement learning articles. We do need to make changes to it in order to expand it to accommodate PPO and the first of these is the introduction of a data struct to handle PPO data. The listing of this is presented below:

//+------------------------------------------------------------------+
//| PPO                                                              |
//+------------------------------------------------------------------+
struct Sppo
{  matrix            policy[];
   matrix            gradient[];
};

In the data struct above are two arrays that get resized to the number of available actions for the actor in the reinforcement learning cycle. Each of the matrices for both the gradient and policy are sized to the number of states by the number of states, in the typical square fashion. The policy matrix array therefore serves as our Q-Map equivalent in that it logs the weights and therefore likelihood of selection of each action at each state. We are sticking to the same simple environment states that we have been using in these series of bullishness, bearishness, and whipsaw market. To recap, these 3 states are logged on both a short time horizon, and a longer time horizon.

In defining time horizons, most people would gravitate to time frames and for instance look for whether a given security’s price action is bullish or bearish on the daily time frame and then repeating this process on the one-hourly time frame to come up with the two sets of metrics. What we chose, and have been using in these series, to define our time horizons, has been a lot simpler in that we simply use a lag of a set number of price-bars, to separate what is short term from what is long term.

This lagging value is an adjustable input parameter that we label ‘Signal_PPO_RL_Scale’ or m_scale within the signal class code and the process of mapping the two price action trends is captured in the get output function, that will be shared later in this article. For now, though, if we return to PPO the implementation of this in modifying the Cql class primarily involves introducing 2 new functions. The set-policy function and the get-clipping function. In determining the actor’s next action, we call neither of these functions, in fact, they might as well be protected functions in the Cql class.

The setting of policy gets called within the set on policy function and the set-off policy function. Its listing is presented below:

//+------------------------------------------------------------------+
//| PPO policy update function                                       | 
//+------------------------------------------------------------------+
void Cql::SetPolicy()
{  matrix _policies;
   _policies.Init(THIS.actions, Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _policies.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies[i][GetMarkov(ii, iii)] += Q_PPO.policy[i][ii][iii];
         }
      }
   }
   vector _probabilities;
   _probabilities.Init(Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _probabilities.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies.Row(i).Activation(_probabilities, AF_SOFTMAX);
            double _old = _probabilities[states[1]];
            double _new = _probabilities[states[0]];
            double _advantage = Q_SA[i][ii][iii] - Q_V[ii][iii];
            double _clip = GetClipping(_old, _new, _advantage);
            Q_PPO.gradient[i][ii][iii] = (_new - _old) * _clip;
         }
      }
   }
   for(int i = 0; i < THIS.actions; i++)
   {  for(int ii = 0; ii < int(Q_PPO.policy[i].Rows()); ii++)
      {  for(int iii = 0; iii < int(Q_PPO.policy[i].Cols()); iii++)
         {  Q_PPO.policy[i][ii][iii] += THIS.alpha * Q_PPO.gradient[i][ii][iii];
         }
      }
   }
}

Within this function, we essentially cover 3 steps in updating the policy values for our PPO struct, whose code we shared above. These policy values guide the selection of the next action in the action function and this being an old function that we have referred to in previous articles, its use here is relevant because we’ve made more revisions to its listing as is given here:

//+------------------------------------------------------------------+
//| Choose an action using epsilon-greedy approach                   |
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   //printf(__FUNCSIG__+" next state is: %i, with best act as: %i ",_next_state,_best_act);
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   states[1] = states[0];
   states[0] = GetMarkov(_next_row, _next_col);
   td_value = Q_V[_next_row][_next_col];
   td_policies[1][0] = td_policies[0][0];
   td_policies[1][1] = td_policies[0][1];
   td_policies[1][2] = td_policies[0][2];
   td_policies[0][0] = _next_row;
   td_policies[0][1] = td_value;
   td_policies[0][2] = _next_col;
   q_sa_act = 1;
   q_ppo_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[q_sa_act][_next_row][_next_col])
      {  q_sa_act = i;
      }
      if(Q_PPO.policy[i][_next_row][_next_col] > Q_PPO.policy[q_ppo_act][_next_row][_next_col])
      {  q_ppo_act = i;
      }
   }
//update last acts
   acts[1] = acts[0];
   acts[0] = q_ppo_act;
}

Returning to the set policy function though, and its 3 steps, the first of these quantifies the total policy weight for each action across all states. Essentially, it is a form of flattening the environment states’ matrix by using a get-Markov function that returns a solo index from two index values (that represent short-term and long-term patterns). Once we’re armed with these cumulative weights for each action in the matrix we’ve labelled ‘_policies’, we can then proceed to work out the update gradients to our policy weights.

The gradients that get stored in the gradient matrix array that we introduced in the PPO struct above update our policy weights, much like a neural network updates its weights. To get the gradient values though, much like in most modern neural networks, is a bit of a process. First, we need to define a vector ‘_probabilities’ whose size matches the flattened index of the environment states. In this case, this is 3 x 3 which brings it to 9. One other introduction or change to the Cql class that we’ve made with PPO is the introduction of the 2-sized state array. This array simply logs or buffers the last two environment state indices that have been ‘experienced’ by the actor, and the purpose of this logging is to aid in updating the gradients.

So, with the ‘_policies’ matrix where for each action and flattened state index we have the cumulative policy-weight, we get a probability distribution across all states for each action. Now, since the policy weighting can be negative, we need to normalize the raw values to the range 0 – 1, and one of the simplest ways of accomplishing this is by using the inbuilt activation functions with SoftMax activation. We perform these activations on a row basis and once done we get probabilities for the previous state and the current environment state. Again, using flattened indices here for brevity.

The other important metric we need to get at this stage is the advantage. Recall, as mentioned above this advantage helps us normalize or balance our policy weight updates to factor in both the short-term state-action based weights with the long-term value-based weights, a process which makes PPO action-selections better at pairing short-term price action to long-term rewards as already argued above. This advantage is got from subtracting the Q-Value weights matrix we introduced in the temporal difference article from the state-action pair matrix we introduced in our first reinforcement learning article. Both are renamed, but their operation and principles remain the same.

With the advantage, we then work out by how much we need to clip the updates. As mentioned in the introductions above, PPO is set apart from other policy managing algorithms because of how it moderates its updates by ensuring they are not too drastic and are mostly incremental for long-term success. The determining of the ‘_clip’ is done by the get-clipping function, whose source is shared below:

//+------------------------------------------------------------------+
//| Helper function to compute the clipped PPO objective             |
//+------------------------------------------------------------------+
double Cql::GetClipping(double OldProbability, double NewProbability, double Advantage)
{  double _ratio = NewProbability / OldProbability;
   double _clipped_ratio = fmin(fmax(_ratio, 1 - THIS.epsilon), 1 + THIS.epsilon);
   return fmin(_ratio * Advantage, _clipped_ratio * Advantage);
}

The code in this function is very brief, and the old probability should not be zero; otherwise an epsilon value can be added to the denominator to check this. Once we have the ‘_clip’ that in essence is a normalized fraction, we multiply this with the difference between the two probabilities. Noteworthy here is that the advantage and also the product between the clip and the probability difference can be positive or negative. This implies that the update gradients can also be signed, i.e. negative or positive.

This leads to the actual updates of the policy weights, which as mentioned above, is very similar to neural network weight update and they too, being based on the gradients above can be negative or positive. This signing of PPO policy weights is why we need to activate, by SoftMax, each action’s weight sums when working out the probability distributions highlighted in the second phase of setting policy. Once policy weights are updated, they are used as follows in the modified action function whose updated listing was shared above.

The adjustment to the old Action function is very small as we simply check for the magnitude of the policy weight where the action with the highest weight, following our PPO update regimen above, does get selected. Given the next action we can now retrieve this with the get output function which also, as already reiterated above, defines the environment state matrices and the listing for this is given below. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalPPO::GetOutput(Cql *QL, int RewardSign)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = RewardSign*_in_row[m_scale - 1];
      double _reward_max = RewardSign*_in_row.Max();
      double _reward_min = RewardSign*_in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float, RewardSign);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
   }
}

It, like the action function above, is very similar to what we have been using in the reinforcement learning articles with the changes seeming almost none-existent (besides some key omissions) given that the key functions we are calling now with PPO are hidden; namely the set policy function and the get clipping function. It clearly seems like a watered-down version of the get output we have been using. As a recap follow-up from what was mentioned above, the ‘m_scale’ can be seen here as our lag that separates the short-time horizon market trends from the long-term trends while using a single time frame. Alternatives that use different time frames can be explored by the reader, but in that, case an alternative time frame would have to be added as an input. ‘Significant’ changes we have in the custom signal class are in the long and short condition functions, whose code is shared below:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::LongCondition(void)
{  int result = 0;
   GetOutput(RL_BUY, 1);
   if(RL_BUY.q_ppo_act==0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::ShortCondition(void)
{  int result = 0;
   GetOutput(RL_SELL, -1);
   if(RL_SELL.q_ppo_act==2)
   {  result = 100;
   }
   return(result);
}

The listing is almost identical to what we have been using, with the main difference being the reference to the ‘q_ppo_act’ as opposed to the action that was selected purely from the Markov decision process.

Strategy Tester Reports and Analysis

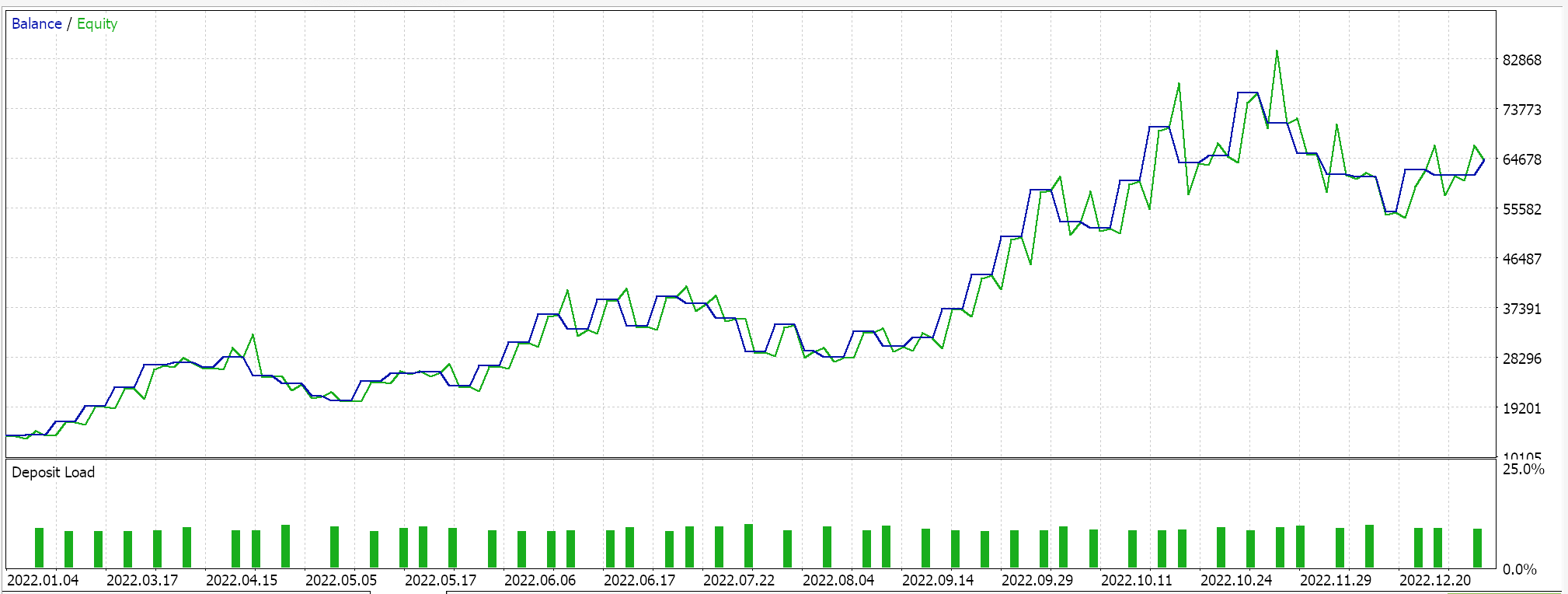
We assemble this custom signal class into an Expert Advisor by using the MQL5 wizard. For readers that are new, there are guides here and here on how to do this. If we extract some favourable settings from optimizing GBP JPY over the year 2022 on the 4-hour time frame, they present us with the following results:

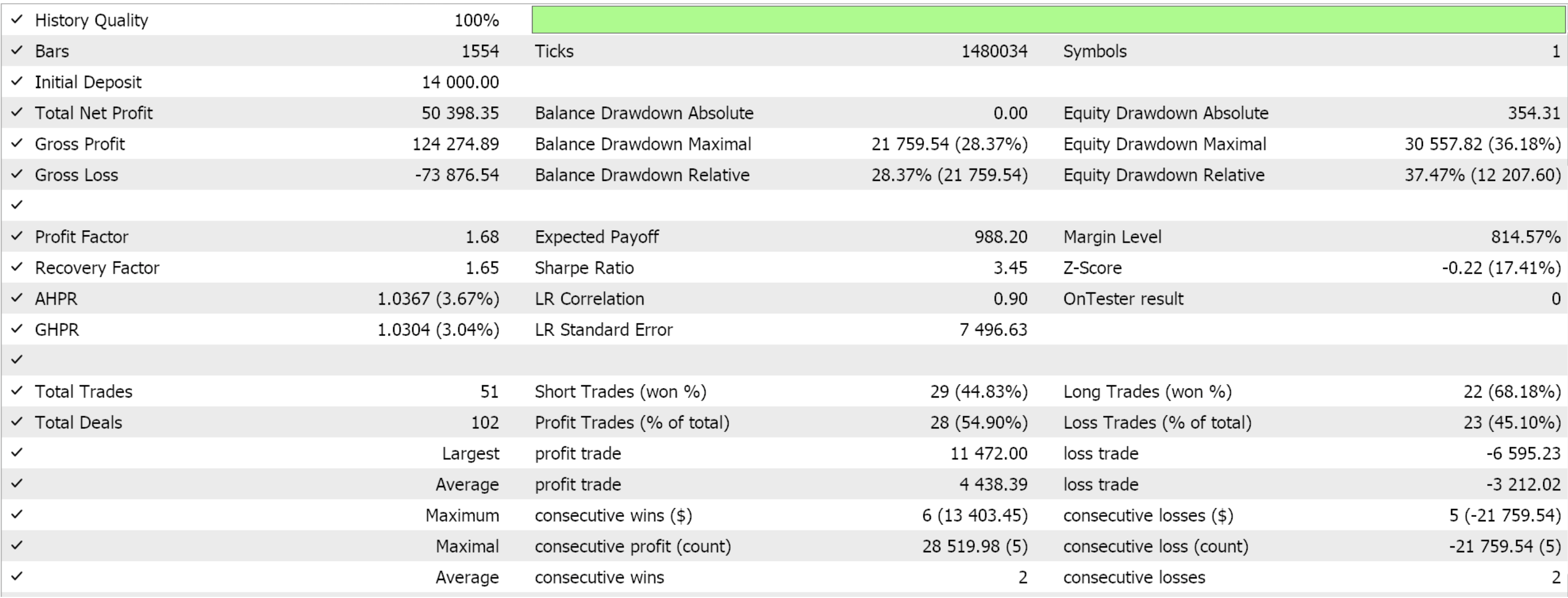
As always, the results presented here are meant to exhibit the custom signal’s potential. The input settings used for this report are not cross-validated and therefore are not shared. The reader is invited to engage in this by customizing it to his expectations.

My philosophy on this is that any Expert Advisor, whether to be used fully automated or to support a manual trading system, can never contribute more than 50% to the entire ‘trade system’. Human emotions are always the other half. So, even if you present a ‘the grail’ to someone who is unfamiliar with its intricacies or how it works, he is bound to become impetuous and second guess many of its key trade decisions. So, by presenting a custom signal without its ‘grail’ settings the reader is invited to not only understand why the Expert Advisor may have performed favourably in the short optimized-period that is presented in the articles, also to understand why it may not perform similarly in different test periods, and these two pieces of information should help begin the process of revealing settings that may work over wider periods.

I believe this process of the trader developing his own settings, or combining different custom signals into a workable Expert Advisor, is how they make up for their 50%.

Conclusion

We have looked at another reinforcement learning algorithm, Proximal Policy Optimization, and it is a very popular, effective method thanks to its moderation of policy updates during reinforcement learning episodes.

The PPO algorithm presents a pioneering approach to reinforcement learning, blending policy stability and adaptability, which are crucial for real-world applications like trading. Its tailored clipping strategy accommodates both discrete and continuous actions and offers scalable efficiency without intensive resource dependency, making it invaluable for complex systems encountering a wide array of market conditions.

File Name	Description
Cql.mqh	Reinforcement Learning Source Class
SignalWZ_49.mqh	Custom Signal Class File
wz_49.mqh	Wizard Assembled Expert Advisor whose header serves to show files used