知っておくべきMQL5ウィザードのテクニック（第49回）：近接方策最適化による強化学習

はじめに

MQL5ウィザードに関する連載を続けます。最近では、一般的なインジケーターの単純なパターンと強化学習アルゴリズムを交互に取り上げています。前回の記事ではインジケーターパターン（ビル・ウィリアムズの「アリゲーター」）について検討しましたが、今度は強化学習に戻ります。ここで取り上げるアルゴリズムは、近接方策最適化(PPO)です。このアルゴリズムは7年前に初めて発表され、ChatGPTが採用している強化学習アルゴリズムとしても知られているため、このアプローチには明らかに注目が集まっていることがわかります。PPOの目的は、学習プロセスが不安定になるような急激な方策の変化を防ぎつつ、全体的なパフォーマンスを向上させることです。具体的には、PPOは方策（Actorが行動を決定する関数）の最適化をおこないますが、その際、急激な変化がないように細心の注意を払います。

これは独立しておこなわれるわけではなく、他の強化学習アルゴリズムと連携して動作します。これらのアルゴリズムのいくつかは本連載で取り上げてきましたが、大まかに言えば方策ベースのアルゴリズムと値ベースのアルゴリズムの2つに分類されます。これまでの連載では、方策ベースのアルゴリズムとしてはQ学習とSARSAを、値ベースのアルゴリズムとしては時間差学習のみを取り上げ、それぞれの例を見てきました。では、PPOは一体何を解決するのでしょうか。

上記で述べたように、PPOが解決しようとする「問題」は、更新時に方策が過度に変更されるのを防ぐことです。この問題の背後にある論理は、更新の頻度や規模を管理しないと、エージェントは学習した内容を忘れたり、行動が不安定になったり、環境内でのパフォーマンスが低下したりする可能性があるということです。したがって、PPOは、更新を小さく、しかし意味のあるものに保つことを保証します。PPOは、あらかじめ定義されたパラメータを持つ方策から始まります。方策とは単に、報酬と環境の状態に基づいてActorがどのような行動を取るかを定義する関数です。

方策が与えられると、エージェントは環境との相互作用を通じてデータを収集します。この「データ収集」によって、状態、行動、報酬の組み合わせと、その方策に基づいて選択された各行動の確率を把握することができます。次に、目的関数を定義します。PPOの目標は強化学習における更新規模を調整することです。このため、PPOは「クリッピング」関数を使用します。この関数は次の式で定義されます。

ここで

• rt(θ)=πθ(at∣st)/πθold(at∣st)は、新しい方策（パラメータθ）と古い方策（パラメータθold）の確率比です。
• Âₜは時刻tにおけるアドバンテージ推定値であり、ある状態において特定の行動が平均的な行動と比べてどれほど優れているかを示します。
• ϵはクリッピング範囲を制御し、方策更新のステップサイズを制限するハイパーパラメータ（多くの場合0.1または0.2）です。

アドバンテージの推定方法にはいくつかの種類がありますが、私たちの実装で使用している方法は以下の通りです。

ここで

• Q(sₜ, aₜ)は、状態sₜにおいて行動aₜを取ったときのQ値 （期待されるリターン）を表します。
• V(sₜ)は状態sₜにおける価値関数であり、その状態から方策に従って行動した場合に得られると期待されるリターンを示します。

アドバンテージ関数をこのように定量化する方法は、上でも触れたように、方策ベースおよび価値ベースのアルゴリズムの利用やそれらへの依存性を強調するものです。目的関数を定義した後は、方策の更新をおこないます。この更新では、クリッピングされた目的関数の最大化を目指して、方策パラメータを調整します。これにより、方策の変化は緩やかになり、最新のデータに過剰に適合することを防ぎます。このプロセスは、更新された方策を用いて環境と再び相互作用し、継続的にデータを収集しながら方策を洗練させていく、というサイクルで繰り返されます。

では、なぜPPOがこれほど人気なのでしょうか。まず、PPOは、従来の方策最適化手法である「信頼領域方策最適化(Trust Region Policy Optimization)」と比べて実装が容易であるという利点があります。さらに、クリッピング（式は前述）により、更新の安定性が向上しています。また、最新のニューラルネットワークと組み合わせても高いパフォーマンスを発揮でき、大規模なタスクにも対応可能であるため、非常に効率的です。加えて、PPOは連続空間と離散空間の両方において高い性能を示すため、応用範囲の広いアルゴリズムです。PPOの直感的な理解としては、ゲームを学習している状況を想像すると分かりやすいかもしれません。試行ごとにアプローチを大幅に変更してしまうと、初期に身につけた有効な操作や戦術を失ってしまう恐れがあります。PPOは、学習の過程で急激な変化を避け、少しずつ計画的かつ段階的に方策を改善していく手法です。

このように、PPOの思想は探索と活用のバランスに深く関係しています。学習初期の段階では、活用よりも探索を重視した大胆なアプローチの変化が必要であるとも言えます。したがって、PPOはこうした初期段階ではあまり効果的ではないかもしれません。それでも、現在の多くの分野では、既に「初期の発見」フェーズを越え、いかに精度を高めるかという「微調整」の段階にあります。この点が、PPOが多くの現場で支持される理由のひとつです。実際、PPOはロボティクスの分野（たとえば、ロボットに歩行や物体操作を学習させるタスク）や、AIがチェスやDotaのような複雑なゲームをプレイできるように訓練されるビデオゲームの分野でも広く利用されています。

トレーダーのための強化学習におけるPPOの役割

PPOは、他の主要な強化学習アルゴリズムと連携して動作する方策ベースの手法であり、その代替手段は多くありません。言及に値するものとしては、以前の記事で取り上げたDeep Q-Network(DQN)、今後取り上げる予定のAsynchronous Advantage Actor-Critic (A3C)、そして上で触れたTrust Region Policy Optimization (TRPO)などが挙げられます。ここでは、それぞれの手法と比較してPPOがどのように際立っているのかを見ていきましょう。まずDQNはQ学習に基づいており、特に連続行動空間においては、大幅な方策の更新によって不安定になることがあります。ここで言う「連続行動空間」とは、強化学習における行動の選択肢が「買う」「売る」「保持する」といった離散的で明示的なものではなく、例えば次の取引での最適なポジションサイズを決定するような、浮動小数点数（もしくは倍精度浮動小数点数）で定義されるケースを指します。

これに対してPPOは、別途ターゲットネットワークや経験再生といった仕組みを必要とせず、より安定性が高く、実装も比較的容易です（これらの概念については今後の記事で詳しく扱います）。訓練パイプラインがシンプルであるため、PPOは離散的な行動空間と連続的な行動空間のどちらにも直接対応できるのに対し、DQNは基本的に離散的な行動空間に適しています。

Asynchronous Advantage Actor-Critic (A3C)と比較すると、A3C（この連載ではまだ取り上げていない方策アルゴリズム）は、複数のエージェントがそれぞれ異なるタイミングで学習をおこない、共有された方策を非同期に更新するという特徴を持っています。この仕組みは学習の多様性を高める一方で、複数の強化学習サイクルを同時に運用する必要があるため、システム全体の構造が複雑になりやすいという課題があります。一方、PPOは同期的に方策を更新し、「方策クリッピング」と呼ばれる手法によって過度な方策の変動を抑えつつ、安定した学習過程を実現します。これにより、過剰に急激な更新による方策崩壊のリスクを効果的に回避することができます。

Trust Region Policy Optimization (TRPO)とPPOを比較すると、いくつかの顕著な違いが浮かび上がります。TRPOでは、方策の更新幅を厳密に制限するために、制約付き最適化問題を解く必要があります。このような複雑な最適化処理により、更新が理論的に安定する一方で、計算コストは高くなりがちです。それに対してPPOは、「クリッピング」というよりシンプルなアプローチを採用することで、更新幅に自然な制約を加えつつ、同様の安定性とパフォーマンスを維持することに成功しています。計算効率が良く、実装も直感的であるため、現場での導入もしやすい点が特徴です。

PPOの特徴の中には、紹介する価値のあるものがいくつかあるので、主要部分に進む前にそれらを簡単に確認しておきましょう。PPOは、前述したように、方策更新にクリッピングメカニズムを使用しており、過度に急激な更新を避けることを即座に目的としています。しかし、これによって意図しない結果として、強化学習における「探索と活用」のバランスを取ることができるようになっています。これは、特に高ボラティリティの環境では、報酬を過度に活用することが愚行となる可能性があり、むしろ市場の長期的な動向を見極めるために冷静に戦略を取る方が適切な戦略である場合に有益です。

ただし、探索が必要な場合には、PPOはエントロピー正則化を用いて、特定の行動に過度に自信を持つことを避け、方策更新のクリッピングに依存しないようにします。エントロピー正規化については、今後の記事で検討します。

PPOはまた、大規模な行動空間を扱うのにも非常に効果的です。これは、前述のように、Actor-Criticフレームワークを用いることによって、連続的な値の予測をより良くおこなうことができるためです。その上で、代理損失関数を使用することにより、方策更新の分散を減らすことができ、外国為替などの非常に不安定な環境でも一貫した動作を実現することができます。

PPOはまた、大きな経験再生バッファを保持する必要がないため、リソースに優れ、スケーラブルです。この特性は、高頻度取引や多くの金融商品を扱う取引、あるいは複雑な取引ルールの設定が必要なユースケースに適しています

PPOは、限られたデータでも効率的に学習できます。このサンプル効率の高さは、市場データが制限されている場合やデータ収集が高コストである場合に非常に効果的です。これは、例えば多くの取引者が、自分の戦略を長期的な履歴データに基づいて実ティックデータでテストする必要があるという非常に重要なシナリオです。MetaTraderストラテジーテスターは、実ティックが利用できない場合にティックデータを生成できますが、原則として、対象の取引ブローカーの実ティックデータで戦略をテストすることが好まれることがよくあります。

このように、実ティックデータは多くのブローカーにとって十分に利用できることがほとんどなく、テスト期間に必要な年数分のデータが利用できる場合でも、品質レビューによってデータセットに重大な欠陥が見つかることがあります。これは金融データに特有の問題であり、他の分野（ビデオゲーム開発やシミュレーションなど）では、大量のデータを生成して訓練をおこなうことが容易であるのに対し、金融市場ではそれが非常に難しいという問題があります。さらに、市場クラッシュや好況といったまれなイベントは、モデルが学習するために必要な頻度で発生するわけではありません。

PPOは、限られた量のデータから学習できるため、本質的にサンプル効率が高く、これらの問題を「回避」します。適切な方策を生成するために大量のデータが必要であることは、PPOの前提条件ではありません。これは、優位推定によって、利用可能な市場データをより小さなチャンクとより少ないエピソードでより有効に活用することができるからです。この特性により、データが限られている状況でも、PPOは良い取引と悪い取引から段階的に学習し、まれで重要なイベントをモデル化する際に非常に有用です。

ほとんどの取引システムでは、通常「報酬」は利益や損失として定量化されますが、その報酬はしばしば決定からかなり遅れることがあります。このような状況は、以前に取った特定の行動に対してクレジットを適切に割り当てることを困難にするため、課題をもたらします。例えば、特定の時点でロングポジションを取ると、その報酬が実現するのは数日後、あるいは数週間後になることもあります。このような遅延は、強化学習(RL)アルゴリズムが、どの行動や環境状態がどの報酬を引き起こすかを正確に学習することを難しくします。

さらに、このシナリオは市場ノイズやランダム性によって悪化します。市場でのプライスアクションには非常に多くのノイズやランダム性が含まれており、良い結果が良い決定によるものか、それとも偶発的な市場の動きによるものかを区別することが困難です。その式を前述したアドバンテージ関数は、PPOが特定の行動から期待される報酬をより適切に推定できるようにします。この推定は、価値（長期的重み付け V(s t)）と状態と行動のペアリングに基づくQ値（Q(s t , a t)）を考慮することで行われ、これにより取られる決定が両極端にバランスの取れたものとなります。

MQL5でのPPOシグナルクラスの設定

MQL5で実装するには、すべての強化学習記事を通じて主な情報源となっているCqlクラスを使用します。PPOに対応するために拡張するには変更を加える必要があり、その最初の変更はPPOデータを処理するためのデータ構造体の導入です。コードを以下に示します。

//+------------------------------------------------------------------+
//| PPO                                                              |
//+------------------------------------------------------------------+
struct Sppo
{  matrix            policy[];
   matrix            gradient[];
};

上記のデータ構造体には、強化学習サイクルにおいてActorが選択できる行動の数に応じてサイズが変更される2つの配列があります。gradientとpolicyの各行列は、典型的な正方行列として、状態数×状態数のサイズで構成されます。方策行列配列は、各状態における各行動の重み、つまり選択される確率を記録する点で、Qマップに相当する役割を果たします。本連載でこれまで使用してきたのと同様に、環境状態は「強気相場」「弱気相場」「もみ合い相場(whipsaw)」というシンプルな3つに限定しています。これら3つの状態は、それぞれ短期的な時間軸と長期的な時間軸の両方で記録されます。

時間軸を定義する方法として、多くの人は時間枠に基づいて、例えば日足チャートでプライスアクションが強気か弱気かを確認し、次に1時間足で同様の分析をおこなって、2種類の評価指標を得る方法を選びます。しかし、本連載で採用しているのはより単純な方法で、一定本数の価格バーの遅延を用いて、短期と長期を区別しています。

この遅延値は、Signal_PPO_RL_Scaleまたはsignalクラス内ではm_scaleとしてラベル付けされた調整可能な入力パラメータです。2つのプライスアクションをマッピングする処理は、この記事の後半で紹介するGetOutput関数内で実装されています。さて、話をPPOに戻すと、この処理をCqlクラスに組み込む際に主に追加されたのは2つの新しい関数、GetPolicy関数とGetClipping関数です。ただし、Actorが次に取る行動を決定する際には、これらの関数は直接呼び出されることはありません。実際、これらの関数はCqlクラス内でprotectedとして定義されていても差し支えないレベルの補助的な役割を持っています。

方策の設定は、SetOnPolicy関数とSetOffPolicy関数内で呼び出されます。そのコードは以下のとおりです。

//+------------------------------------------------------------------+
//| PPO policy update function                                       | 
//+------------------------------------------------------------------+
void Cql::SetPolicy()
{  matrix _policies;
   _policies.Init(THIS.actions, Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _policies.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies[i][GetMarkov(ii, iii)] += Q_PPO.policy[i][ii][iii];
         }
      }
   }
   vector _probabilities;
   _probabilities.Init(Q_PPO.policy[acts[0]].Rows()*Q_PPO.policy[acts[0]].Cols());
   _probabilities.Fill(0.0);
   for(int ii = 0; ii < int(Q_PPO.policy[acts[0]].Rows()); ii++)
   {  for(int iii = 0; iii < int(Q_PPO.policy[acts[0]].Cols()); iii++)
      {  for(int i = 0; i < THIS.actions; i++)
         {  _policies.Row(i).Activation(_probabilities, AF_SOFTMAX);
            double _old = _probabilities[states[1]];
            double _new = _probabilities[states[0]];
            double _advantage = Q_SA[i][ii][iii] - Q_V[ii][iii];
            double _clip = GetClipping(_old, _new, _advantage);
            Q_PPO.gradient[i][ii][iii] = (_new - _old) * _clip;
         }
      }
   }
   for(int i = 0; i < THIS.actions; i++)
   {  for(int ii = 0; ii < int(Q_PPO.policy[i].Rows()); ii++)
      {  for(int iii = 0; iii < int(Q_PPO.policy[i].Cols()); iii++)
         {  Q_PPO.policy[i][ii][iii] += THIS.alpha * Q_PPO.gradient[i][ii][iii];
         }
      }
   }
}

この関数では、基本的に、上でコードを共有したPPO構造体の方策値を更新するための3つの手順をカバーします。これらの方策値は、Action関数の次の行動の選択をガイドします。これは以前の記事で参照した古い関数であるため、ここでの使用は関連性があります。これは、次に示すように、コードにさらに修正を加えたためです。

//+------------------------------------------------------------------+
//| Choose an action using epsilon-greedy approach                   |
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   //printf(__FUNCSIG__+" next state is: %i, with best act as: %i ",_next_state,_best_act);
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   states[1] = states[0];
   states[0] = GetMarkov(_next_row, _next_col);
   td_value = Q_V[_next_row][_next_col];
   td_policies[1][0] = td_policies[0][0];
   td_policies[1][1] = td_policies[0][1];
   td_policies[1][2] = td_policies[0][2];
   td_policies[0][0] = _next_row;
   td_policies[0][1] = td_value;
   td_policies[0][2] = _next_col;
   q_sa_act = 1;
   q_ppo_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[q_sa_act][_next_row][_next_col])
      {  q_sa_act = i;
      }
      if(Q_PPO.policy[i][_next_row][_next_col] > Q_PPO.policy[q_ppo_act][_next_row][_next_col])
      {  q_ppo_act = i;
      }
   }
//update last acts
   acts[1] = acts[0];
   acts[0] = q_ppo_act;
}

ただし、SetPolicy関数とその3つのステップに戻ると、最初のステップでは、すべての状態にわたる各行動の合計方策重みを定量化します。本質的には、これは、2つのインデックス値（短期パターンと長期パターンを表す）から単独のインデックスを返すGetMarkov関数を使用して、環境状態の行列を平坦化する形式です。「_policies」というラベルを付けた行列内の各行動の累積重みを取得したら、方策の重みに対する更新勾配の計算に進むことができます。

上記のPPO構造体で導入した勾配行列配列に格納される勾配は、ニューラルネットワークが重みを更新するのと同じように、方策の重みを更新します。ただし、ほとんどの最新のニューラルネットワークと同様に、勾配値を取得するには、少し手間がかかります。まず、環境状態の平坦化されたインデックスと一致するサイズのベクトル「_probabilities」を定義する必要があります。この場合、3x3なので9になります。PPOでCqlクラスに加えたもう1つの導入または変更は、2サイズの状態配列の導入です。この配列は、Actorが「経験した」最後の2つの環境状態インデックスを単純にログに記録またはバッファリングします。このログ記録の目的は、勾配の更新を支援することです。

したがって、各行動と平坦化された状態インデックスに対して累積方策重みを持つ「_policies」行列を使用すると、各行動のすべての状態にわたる確率分布が得られます。ここで、方策の重み付けは負になる可能性があるため、生の値を0～1の範囲に正規化する必要があります。これを実現する最も簡単な方法の1つは、SoftMax活性化関数を備えた組み込みの活性化関数を使用することです。これらの活性化関数を行ごとに実行し、完了すると、前の状態と現在の環境状態の確率が得られます。ここでも、簡潔にするためにフラット化されたインデックスを使用します。

この段階で取得する必要があるもう1つの重要な指標は、アドバンテージです。思い出してください、上で述べたように、アドバンテージは、短期的な状態行動ベースの重みと長期的な価値ベースの重みの両方を考慮して方策重みの更新を正規化またはバランスさせるのに役立ちます。このプロセスにより、上ですでに説明したように、PPO行動選択は短期的なプライスアクションと長期的な報酬をより適切に組み合わせることができます。アドバンテージは、最初の強化学習の記事で紹介した状態-行動ペア行列から、時間差の記事で紹介したQ値の重み行列を減算することで得られます。どちらも名前は変更されていますが、動作と原理は同じままです。

アドバンテージを利用して、更新をどれだけクリップする必要があるかを計算します。上記の紹介で述べたように、PPOは、更新が極端になりすぎず、長期的な成功のためにほとんどが段階的に行われるように更新を調整する点で、他の方策管理アルゴリズムとは一線を画しています。「_clip」の決定はGetClipping関数によっておこなわれます。そのコードは以下に共有されています。

//+------------------------------------------------------------------+
//| Helper function to compute the clipped PPO objective             |
//+------------------------------------------------------------------+
double Cql::GetClipping(double OldProbability, double NewProbability, double Advantage)
{  double _ratio = NewProbability / OldProbability;
   double _clipped_ratio = fmin(fmax(_ratio, 1 - THIS.epsilon), 1 + THIS.epsilon);
   return fmin(_ratio * Advantage, _clipped_ratio * Advantage);
}

この関数のコードは非常に短く、OldProbabilityはゼロであってはなりません。ゼロの場合は、分母にイプシロン値を追加して修正できます。本質的に正規化された分数である「_clip」を取得したら、これを2つの確率の差と掛け合わせます。ここで注目すべきは、アドバンテージと、クリップと確率差の積は正にも負にもなる可能性があるということです。これは、更新される勾配も符号付き、つまり正または負である可能性があることを意味します。

これが実際の方策の重み更新につながりますが、上記でも述べたように、これはニューラルネットワークの重み更新と非常に似ており、それらも上記の勾配に基づいているため、正または負である可能性があります。このPPO方策の重み付けにおける「符号付け」は、方策設定の第二段階で強調された確率分布を算出する際に、各行動の重みの合計をSoftMaxによって活性化する必要がある理由です。ポリシー重みが更新されると、これらは上記で共有された更新されたAction関数において次のように使用されます。

古いAction関数への調整は非常に小さく、単に方策重みの大きさを確認するだけで、PPO更新規則に従って最も重みの大きい行動が選択されます。次に選ばれる行動を得るために、getOutput関数を使用することができます。この関数は、上記でも繰り返し述べたように、環境状態の行列を定義しており、そのコードは以下に示されています。 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalPPO::GetOutput(Cql *QL, int RewardSign)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = RewardSign*_in_row[m_scale - 1];
      double _reward_max = RewardSign*_in_row.Max();
      double _reward_min = RewardSign*_in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float, RewardSign);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
   }
}

これは、上記のAction関数と同様に、強化学習の記事で使用してきたものと非常によく似ていますが、現在PPOで呼び出している主要な関数、つまりSetPolicy関数とGetClipping関数が非表示になっているため、変更点はほとんどないように見えます（いくつかの重要な省略を除く）。 これは明らかに、これまで使用してきたget出力の簡略版のようです。上で述べたことを要約すると、ここではm_scaleは、単一の時間枠を使用しながら、短期的な市場動向と長期的な動向を分離する遅延として見ることができます。読者は異なる時間枠を使用する代替案を検討できますが、その場合には、代替の時間枠を入力として追加する必要があります。カスタムシグナルクラスでの「重要な」変更は、LongCondition関数とShortCondition関数にあります。そのコードは以下に示されています。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::LongCondition(void)
{  int result = 0;
   GetOutput(RL_BUY, 1);
   if(RL_BUY.q_ppo_act==0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPPO::ShortCondition(void)
{  int result = 0;
   GetOutput(RL_SELL, -1);
   if(RL_SELL.q_ppo_act==2)
   {  result = 100;
   }
   return(result);
}

コードはこれまで使用してきたものとほぼ同じですが、主な違いは、純粋にマルコフ決定プロセスから選択された行動ではなく、q_ppo_actを参照していることです。

ストラテジーテスターのレポートと分析

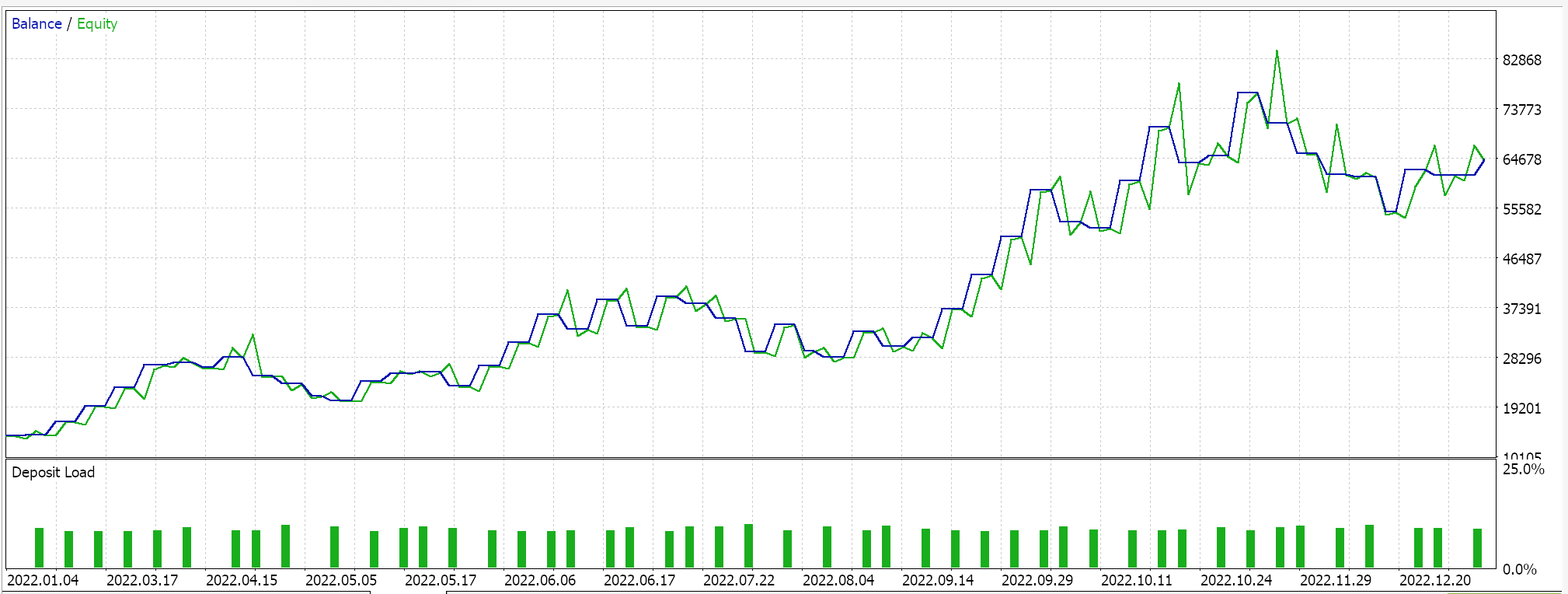
MQL5ウィザードを使用して、このカスタムシグナルクラスからEAを作成します。初めて読む方のために、これをおこなう方法についてのガイドがこちらとこちらにあります。2022年を通じて4時間枠でGBP JPYを最適化した際の好ましい設定を抽出すると、次のような結果が得られます。

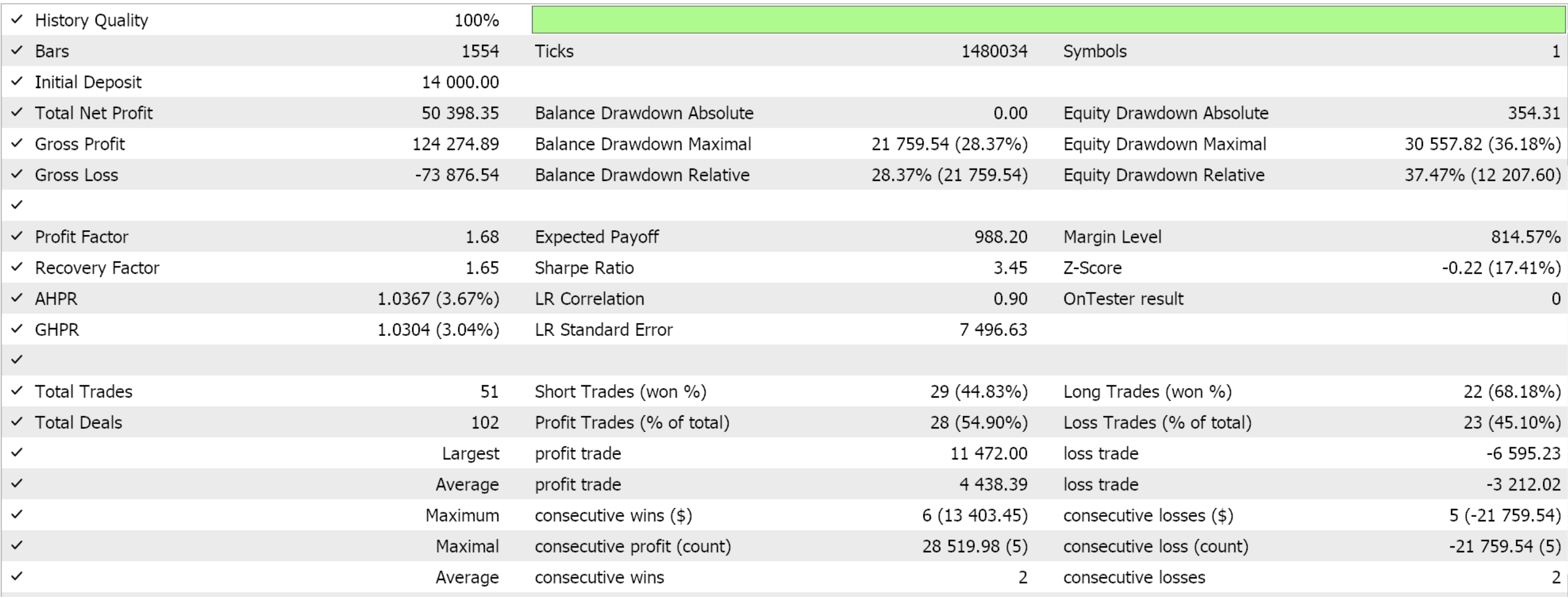
いつものように、ここで提示された結果は、カスタムシグナルの可能性を示すことを目的としています。このレポートに使用される入力設定は交差検証されていないため、共有されません。ご自分の期待に合わせてこれをカスタマイズしてください。

これに関する私の哲学は、完全に自動化されたものであれ、手動取引システムをサポートするものであっても、どんなEAも「取引システム」の全体に対して50%以上の貢献はできないというものです。人間の感情は常にそのもう一方の半分だからです。ですので、「聖杯」のようなものを、その仕組みや働きに不慣れな人に提示しても、その人は必ずや焦って、重要な取引判断の多くを疑い始めてしまうのです。ですから、カスタムシグナルを「聖杯」の設定なしで提示することによって、読者は、EAがこの記事に提示された短期間の最適化された期間内で好ましく動作した理由だけでなく、なぜそれが異なるテスト期間で同じように動作しないかを理解することが求められます。この2つの情報は、より広い期間で機能する設定を明らかにするプロセスを始めるのに役立つはずです。

トレーダーが独自の設定を開発したり、さまざまなカスタムシグナルを組み合わせて実用的なEAを作成するというこのプロセスによって、トレーダーは50%の利益を補うことができると私は考えています。

結論

別の強化学習アルゴリズムである近接方策最適化について検討しました。強化学習エピソード中に方策更新を調整することにより、これは、非常に人気があり効果的な手法です。

PPOアルゴリズムは、取引などの実世界での用途において極めて重要な方策の安定性と適応性を融合した、強化学習への先駆的なアプローチを提供します。そのカスタマイズされたクリッピング戦略は、離散的な行動と連続的な行動の両方に対応し、リソース依存を高めることなくスケーラブルな効率性を提供するため、さまざまな市場条件に直面する複雑なシステムにとって非常に貴重です。

ファイル名	詳細
Cql.mqh	強化学習ソースクラス
SignalWZ_49.mqh	カスタムシグナルクラスファイル
wz_49.mqh	ウィザードで組み立てられたEA。ヘッダーには使用されているファイルが表示されます。