Técnicas do MQL5 Wizard que você precisa conhecer (Parte 36): Q-Learning com Cadeias de Markov

Introdução

As classes de sinal personalizadas para Experts Advisors montados via o assistente podem assumir diversos papéis que valem a pena ser explorados, e continuamos essa jornada examinando como o algoritmo Q-Learning, quando combinado com Cadeias de Markov, pode ajudar a refinar o processo de aprendizado de uma rede de perceptron multicamadas. Q-Learning é um dos vários (aproximadamente 12) algoritmos de aprendizado por reforço, portanto, essencialmente estamos também observando como este assunto pode ser implementado como um sinal personalizado e testado dentro de um Expert Advisor montado pelo Wizard.

Assim, a estrutura deste artigo seguirá do que é o aprendizado por reforço, abordará o algoritmo Q-Learning e seus estágios de ciclo, analisará como as Cadeias de Markov podem ser integradas ao Q-Learning, e então concluirá, como sempre, com relatórios do Strategy Tester. O aprendizado por reforço pode ser utilizado como um gerador de sinais independente, pois seus ciclos ("episódios") são, em essência, uma forma de aprendizado que quantifica resultados como "recompensas" para cada um dos "ambientes" nos quais o "ator" está envolvido. Esses termos entre aspas serão apresentados abaixo. No entanto, não estamos utilizando o aprendizado por reforço como um sinal bruto, mas sim aproveitando suas capacidades para aprimorar o processo de aprendizado suplementando uma rede de múltiplas camadas.

Dado o papel do aprendizado por reforço como o terceiro padrão no treinamento de aprendizado de máquina, além do aprendizado supervisionado e não supervisionado, pensei que poderíamos envolvê-lo mais na função de perda de uma MLP, já que ele atua como uma ponte entre supervisão e ausência de supervisão, usando "CriticRewards" e "environment-states", respectivamente. Ambos os termos citados serão introduzidos na próxima seção. No entanto, isso significa que a maior parte da previsão ainda fica a cargo da MLP e o aprendizado por reforço desempenha mais um papel subordinado. Além disso, o uso de Cadeias de Markov é também complementar ao aprendizado por reforço, já que as seleções do "ator" a partir do "Q-Map" geralmente são suficientes para implementar o algoritmo Q-Learning, mas incluímos aqui para entender se existe, ou não, alguma diferença nos resultados de teste.

Visão Geral do Aprendizado por Reforço

O aprendizado por reforço, que apresentamos acima como o terceiro pilar do treinamento de aprendizado de máquina, é uma maneira de equilibrar Exploração e Exploração (Exploration and Exploitation) durante o processo de treinamento. Isso é possível graças à sua abordagem cíclica de avaliação de cada rodada de treinamento, chamadas de episódios. Esse ciclo pode ser representado no diagrama abaixo:

fonte

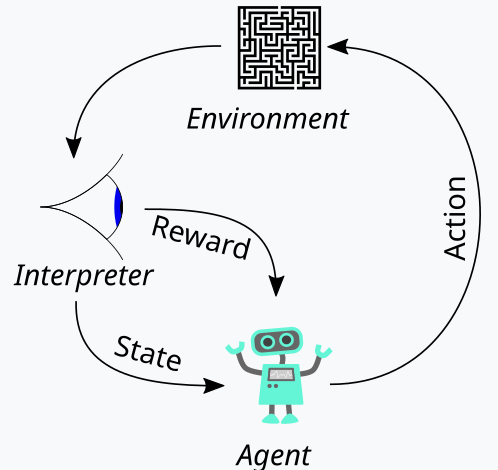
Assim, temos uma sequência de etapas no processo de aprendizado por reforço. No início, existe um "Agente", que atua em nome de uma parte principal — no nosso caso, uma MLP — para selecionar o curso de ação ideal ao se deparar com um mapa Q-Learning atualizado, também chamado de núcleo ou matriz. Esse mapa é um registro de todos os possíveis estados do ambiente, mais uma distribuição de probabilidade sobre as ações possíveis a serem tomadas para cada um dos estados disponíveis.

A melhor forma de ilustrar isso é caminhar pela implementação do ambiente que escolhemos para este artigo. Como traders, buscamos definir os mercados não apenas por suas ações de curto prazo, mas também por suas características de tendência ou de longo prazo. Se focarmos em 3 métricas básicas — alta (bullishness), baixa (bearishness) e lateralidade (flatness) —, cada uma delas pode ter indicadores em uma janela de tempo curta e longa. Assim, nosso "ambiente" se torna um espaço de 9 índices (3 x 3 para curto e longo prazo), onde o índice 0 marca baixa em curto e longo prazo, o índice 4 marca mercado lateral em ambos, e o índice 8 marca alta em ambos os horizontes, etc.

Os ambientes são selecionados com a ajuda de uma função de nome semelhante, cujo código-fonte está abaixo:

//+------------------------------------------------------------------+
// Indexing new Environment data to conform with states
//+------------------------------------------------------------------+
void Cql::Environment(vector &E_Row, vector &E_Col, vector &E)
{  if(E_Row.Size() == E_Col.Size() && E_Col.Size() > 0)
   {  E.Init(E_Row.Size());
      E.Fill(0.0);
      for(int i = 0; i < int(E_Row.Size()); i++)
      {  if(E_Row[i] > 0.0 && E_Col[i] > 0.0)
         {  E[i] = 0.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] == 0.0)
         {  E[i] = 1.0;
         }
         else if(E_Row[i] > 0.0 && E_Col[i] < 0.0)
         {  E[i] = 2.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] > 0.0)
         {  E[i] = 3.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] == 0.0)
         {  E[i] = 4.0;
         }
         else if(E_Row[i] == 0.0 && E_Col[i] < 0.0)
         {  E[i] = 5.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] > 0.0)
         {  E[i] = 6.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] == 0.0)
         {  E[i] = 7.0;
         }
         else if(E_Row[i] < 0.0 && E_Col[i] < 0.0)
         {  E[i] = 8.0;
         }
      }
   }
}

Este código se aplica estritamente ao nosso ambiente de 9 índices e não pode ser usado em matrizes de ambientes de tamanhos diferentes. Ao definir esta matriz de ambiente, utilizamos um parâmetro de entrada extra chamado "escala" (scale). Essa escala ajuda a proporcionalizar o horizonte de longo prazo em relação à janela de curto prazo. O valor padrão é 5, o que significa que em um dos eixos da matriz de ambiente marcamos o estado como alta, baixa ou lateralidade, baseado nas mudanças de preço ao longo de um período que é 5 vezes maior que o período do outro eixo. Digo "plotado" porque esses dois eixos apenas fornecem coordenadas para o estado atual. O índice de 0 a 8 é simplesmente um achatamento da matriz em um array, mas como pode ser visto no código-fonte anexo, a referência contínua a "linha" e "coluna" aponta para as possíveis leituras x e y da matriz que definem o estado atual.

O mapa de Q-Learning reproduz esse array de estados do ambiente adicionando pesos para as possíveis ações a serem tomadas em cada estado. No nosso caso, estamos considerando 3 possíveis ações: comprar, vender ou não fazer nada. Cada estado no mapa de Q-Learning possui um array de tamanho 3 que registra qual ação é mais adequada. Quanto maior o valor do score, mais adequada é a ação. Outra entidade importante no ciclo é o observador, que chamaremos de "crítico" (critic). É o crítico o responsável por determinar as "recompensas" para as ações do ator. E o que são as recompensas? Isso depende do uso do aprendizado por reforço, mas no nosso caso, considerando as 3 ações possíveis, usamos o lucro bruto (tick value) da variação do preço como recompensa.

Assim, se a variação do preço for negativa e nossa última ação foi vender, a magnitude dessa variação é a recompensa. O mesmo vale se a variação for positiva após uma ação de compra. Se a última ação tiver sido comprar e houver uma variação negativa, o valor negativo atua como uma penalidade, assim como variações após vendas são multiplicadas por -1, fazendo qualquer produto negativo agir como penalidade para ações naquele estado (que é a combinação de ações de preço de curto e longo prazo do mercado).  

Este valor de recompensa precisa ser normalizado, e é por isso que usamos a função CriticReward que o mantém no intervalo de 0,0 a 1,0. Todos os valores negativos ficam entre 0,0 e 0,5, enquanto os positivos são normalizados para 0,5 a 1,0. O código-fonte que realiza isso é apresentado abaixo:

//+------------------------------------------------------------------+
// Normalize reward via off-policy
//+------------------------------------------------------------------+
double Cql::CriticReward(double MaxProfit, double MaxLoss, double Float)
{  double _reward = 0.0;
   if(MaxProfit >= Float && Float >= MaxLoss && MaxLoss < MaxProfit)
   {  _reward = (Float - MaxLoss) / (MaxProfit - MaxLoss);
   }
   return(_reward);
}

A atualização do valor de recompensa sempre ocorre durante o processo de treinamento, e não apenas no início. Isso implica que precisamos constantemente passar parâmetros que atualizem os valores de recompensa-máxima, recompensa-mínima e recompensa-normalizada para a função de retropropagação, para que sejam incorporados ao processo. Para fazer isso, começamos modificando a struct de aprendizado, usada para armazenar variáveis de aprendizado que são chamadas a cada execução de retropropagação. O uso de uma struct torna o código facilmente modificável, já que basta adicionar novas variáveis à lista existente, evitando erros. Isso é claramente menos propenso a erros e contrasta fortemente com a necessidade de modificar a lista de parâmetros de entrada em uma função que requer as variáveis ​​nesta estrutura. Certamente seria difícil de manejar então. A estrutura de aprendizado modificada agora se parece com o seguinte:

//+------------------------------------------------------------------+
//| Learning Struct                                                  |
//+------------------------------------------------------------------+
struct Slearning
{  Elearning         type;
   int               epochs;
   double            rate;
   double            initial_rate;
   double            prior_rate;
   double            min_rate;
   double            decay_rate_a;
   double            decay_rate_b;
   int               decay_epoch_steps;
   double            polynomial_power;
   double            ql_reward_max;
   double            ql_reward_min;
   double            ql_reward_float;
   vector            ql_e;

                     Slearning()
   {  type = LEARNING_FIXED;
      rate = 0.005;
      prior_rate = 0.1;
      epochs = 50;
      initial_rate = 0.1;
      min_rate = __EPSILON;
      decay_rate_a = 0.25;
      decay_rate_b = 0.75;
      decay_epoch_steps = 10;
      polynomial_power = 1.0;
      ql_reward_max = 0.0;
      ql_reward_min = 0.0;
      ql_reward_float = 0.0;
      ql_e.Init(1);
      ql_e.Fill(0.0);
   };
                    ~Slearning() {};
};

Além disso, precisamos fazer algumas mudanças na função de retropropagação no momento de chamar a função de perda. Isso porque introduzimos uma nova enumeração subordinada para funções de perda, listada a seguir:

//+------------------------------------------------------------------+
//| Custom Loss-Function Enumerator                                  |
//+------------------------------------------------------------------+
enum Eloss
{  LOSS_TYPICAL = -1,
   LOSS_SVR = 1,
   LOSS_QL = 2
};

Uma das enumerações é ‘LOSS_SVR’, que mede a perda usando regressão por vetores de suporte (Support Vector Regression), abordagem que discutimos no último artigo. As outras são ‘LOSS_TYPICAL’, que usa as funções de perda padrão do MQL5, e ‘LOSS_QL’, onde QL significa Q-Learning e onde o aprendizado por reforço com Q-Learning orienta o processo de aprendizado fornecendo um vetor-alvo com o qual as previsões da MLP são comparadas. As cláusulas if dentro da função de retropropagação verificam isso da seguinte forma:

//+------------------------------------------------------------------+
//| BACKWARD PROPAGATION OF THE MULTI-LAYER-PERCEPTRON.              |
//+------------------------------------------------------------------+
//|                                                                  |
//| -Extra Validation check of MLP architecture settings is performed|
//|  at run-time.                                                    |
//|  Chcecking of 'validation' parameter should ideally be performed |
//|  at class instance initialisation.                               |
//|                                                                  |
//| -Run-time Validation of learning rate, decay rates and epoch     |
//|  index is performed as these are optimisable inputs.             |
//+------------------------------------------------------------------+
void Cmlp::Backward(Slearning &Learning, int EpochIndex = 1)
{  

   ...

   if(THIS.loss_custom == LOSS_SVR)
   {  _last_loss = SVR_Loss();
   }
   else if(THIS.loss_custom == LOSS_QL)
   {  double _reward = QL.CriticReward(Learning.ql_reward_max, Learning.ql_reward_min, Learning.ql_reward_float);
      if(QL.act == 0)
      {  _reward *= -1.0;
      }
      else if(QL.act == 1)
      {  _reward = -1.0 * fabs(_reward);
      }
      QL.CriticState(_reward, Learning.ql_e);
      _last_loss = output.LossGradient(QL.Q_Loss(), THIS.loss_typical);
   }
   

...

}

A adição desta função de perda personalizada não necessariamente nega a necessidade das antigas funções de perda que eram usadas com base nas enumerações internas do MQL5. Renomeamos a perda típica para "typical_loss", e se a entrada "custom_loss" for "LOSS_TYPICAL", este valor deve ser fornecido.

Após a normalização do valor de recompensa, ele é usado para atualizar o mapa de Q-Learning na função CriticState. A atualização dos valores Q é regida pela fórmula:

onde:

• Q(s,a): O valor Q para realizar a ação a no estado s. Isso representa a recompensa futura esperada para esse par estado-ação.
• α: A taxa de aprendizado, um valor entre 0 e 1, que controla o quanto a nova informação substitui a informação antiga. Um α menor significa que o agente aprende mais lentamente, enquanto um α maior o torna mais responsivo às experiências recentes.
• r: A recompensa mais recente recebida após realizar a ação a no estado s.
• γ: O fator de desconto, um valor entre 0 e 1, que desconta as recompensas futuras. Um γ maior faz com que o agente valorize mais as recompensas de longo prazo, enquanto um γ menor faz com que ele foque mais nas recompensas imediatas.
• max a′ Q(s′,a′): O valor Q máximo para o próximo estado s′ considerando todas as ações possíveis a′. Isso representa a estimativa do agente para a melhor recompensa futura possível a partir do próximo estado s′.

E a atualização real do mapa de Q-Learning pode ser implementada em MQL5 da seguinte forma:

//+------------------------------------------------------------------+
// Update Q-value using off-policy (Q-learning formula)
//+------------------------------------------------------------------+
void Cql::CriticState(double Reward, vector &E)
{  int _e_row_new = 0, _e_col_new = 0;
   SetMarkov(int(E[E.Size() - 1]), _e_row_new, _e_col_new);
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   e_row[0] = _e_row_new;
   e_col[0] = _e_col_new;
   int _new_best_q = Action();
   double _weighting = Q[e_row[0]][e_col[0]][_new_best_q];
   if(THIS.use_markov)
   {  LetMarkov(e_row[1], e_col[1], E);
      int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _weighting *= markov[_old_index][_new_index];
   }
   Q[e_row[1]][e_col[1]][act] += THIS.alpha * (Reward + (THIS.gamma * _weighting) - Q[e_row[1]][e_col[1]][act]);
}

Ao atualizar o mapa, aplica-se a regra de atualização off-policy, onde a melhor ação do próximo estado é utilizada para atualizar a ação anterior. Isso contrasta com a atualização on-policy, onde a ação atual é utilizada no próximo estado para fazer a mesma atualização. Isso ocorre porque, para qualquer estado definido por uma coordenada de linha e uma coordenada de coluna dentro da matriz do ambiente, existe um conjunto padrão de ações possíveis que o agente pode executar. E com atualizações off-policy, que é o que o Q-Learning utiliza, escolhe-se a melhor ação ponderada; entretanto, com algoritmos que utilizam atualizações on-policy, a ação atual é mantida durante a atualização. A seleção da melhor ação é realizada através da função ‘Action’, cujo código é fornecido abaixo:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy
//+------------------------------------------------------------------+
int Cql::Action()
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q[e_row[0]][e_col[0]][0];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q[e_row[0]][e_col[0]][i] > _best_value)
         {  _best_value = Q[e_row[0]][e_col[0]][i];
            _best_act = i;
         }
      }
   }
   //update last action
   act = _best_act;
   return(_best_act);
}

O aprendizado por reforço é um pouco semelhante ao aprendizado supervisionado no sentido de que existe uma métrica de recompensa que é utilizada para ajustar e refinar o peso das ações em cada estado do ambiente. Por outro lado, também é como o aprendizado não supervisionado devido ao uso de uma matriz de ambiente cujos valores de coordenadas (os dois valores para o índice de linha e o índice de coluna) servem como entradas para o MLP que o utiliza. O MLP, portanto, funciona como um classificador que tenta determinar a distribuição de probabilidade correta para as três ações aplicáveis quando apresentado com as coordenadas do estado do ambiente como entradas. O treinamento então ocorre como em qualquer classificador MLP, mas desta vez o objetivo é minimizar a diferença entre a distribuição de probabilidade projetada pelo MLP e a distribuição de probabilidade no núcleo do Q-Learning nas coordenadas do mapa de Q-Learning fornecidas como entrada para o MLP.

O papel das Transições de Markov

As cadeias de Markov são modelos probabilísticos estocásticos que utilizam matrizes de transição para mapear as probabilidades de transição de um estado para outro ao serem alimentadas com uma sequência temporal desses estados. Esses modelos probabilísticos são inerentemente sem memória, já que a probabilidade de transição para o próximo estado depende apenas do estado atual e não do histórico de estados anteriores. Essas transições podem ser usadas para atribuir importância aos diversos estados definidos dentro da matriz do ambiente.

Agora, a matriz do ambiente, no nosso caso de uso para o sinal personalizado, considera apenas três estados de mercado: tendência de alta, tendência de baixa e estabilidade, em um horizonte curto e um período de tempo longo, formando assim uma matriz 3 x 3, o que implica nove estados possíveis. Como temos nove estados possíveis, isso significa que nossa matriz de transição de Markov será uma matriz 9 x 9 para mapear as transições de um estado do ambiente para outro. Isso, portanto, exige a capacidade de converter o par de índices da matriz do ambiente em um único índice que possa ser usado na matriz de transição de Markov. Na prática, acabamos precisando de duas funções: uma para converter o par de índices de linha e coluna do ambiente em um único índice para a matriz de Markov, e outra para reconstruir os índices de linha e coluna da matriz do ambiente ao receber um índice da matriz de transição de Markov. Essas duas funções são chamadas de GetMarkov e SetMarkov respectivamente, e seus códigos-fonte são fornecidos abaixo:

//+------------------------------------------------------------------+
// Getting markov index from environment row & col
//+------------------------------------------------------------------+
int Cql::GetMarkov(int Row, int Col)
{  return(Row + (THIS.environments * Col));
}

E:

//+------------------------------------------------------------------+
// Getting environment row & col from markov index
//+------------------------------------------------------------------+
void Cql::SetMarkov(int Index, int &Row, int &Col)
{  Col = int(floor(Index / THIS.environments));
   Row = int(fmod(Index, THIS.environments));
}

Precisamos obter o índice equivalente de Markov das duas coordenadas do estado do ambiente no início da realização dos cálculos de Markov, já que estaremos realizando a transição a partir desse estado. Uma vez obtido esse índice, recuperamos as probabilidades de transição para outros estados ao longo dessa coluna na matriz de transição, pois cada uma delas serve como um peso. Como esperado, todas somam um e, como o ator já selecionou o próximo estado a partir do Mapa-Q, usamos sua probabilidade como numerador sobre um denominador de um, o que significa que apenas sua probabilidade é usada como peso para incrementar o novo valor no Mapa-Q durante o processo de aprendizado. O código-fonte que implementa isso já foi compartilhado acima na função de estado do crítico.

Esse processo de aprendizado essencialmente desconta o incremento de aprendizado na proporção de sua probabilidade na matriz de transição de Markov.

Além disso, realizamos os cálculos da matriz de transição sempre que um novo candle (barra) é registrado e a série temporal de preços é atualizada. O código para realizar esses cálculos é fornecido abaixo:

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Sendo uma matriz de transição sem memória, nosso código acima sempre começa com uma matriz recém-declarada e a variável de classe que armazena as probabilidades também é preenchida com valores zero para cancelar qualquer histórico anterior. A abordagem para calcular as transições é direta, pois contamos a sequência de cada estado no primeiro loop, e seguimos com outro loop que divide as contagens acumuladas que obtivemos para cada transição pelo número total de estados de onde as transições são feitas.

Implementando a classe de sinal personalizada

Como já mencionado, estamos utilizando um MLP que é um classificador para lidar com a previsão principal, com o aprendizado por reforço servindo apenas como uma função de perda subordinada. O aprendizado por reforço também pode ser otimizado ou treinado para gerar sinais de trade utilizáveis maximizando as recompensas do crítico, mas esse não é o objetivo aqui; seu papel é secundário ao do perceptron multicamadas (MLP), sendo usado para quantificar a função objetivo, como em aprendizado supervisionado e não supervisionado.

Assim como em artigos anteriores em que utilizamos MLPs, estamos utilizando as variações de preço como origem para a entrada de dados. Lembre-se: a matriz de ambiente usada neste artigo é uma matriz 3 x 3 que serve como uma grade de possíveis estados do mercado quando analisados em um curto e em um longo horizonte de tempo. Cada um dos eixos para o curto e longo prazo possui métricas ou leituras que variam de alta, neutra a baixa, constituindo assim a grade 3 x 3. E semelhante a essa matriz está a matriz ou mapa de Q-Learning, que também possui essa grade 3 x 3, com a adição de um array de possíveis ações abertas ao ator, que mantêm a pontuação da adequação de cada ação para cada estado. É esse array de adequação que serve como rótulo ou alvo de treinamento para nosso MLP.

As entradas para o MLP, no entanto, não serão as variações de preço brutas como nos artigos recentes com MLP, mas sim as coordenadas do estado do ambiente para a variação de preço mais recente ou atual no curto e no longo prazo. O uso do termo ‘timeframe’ aqui é puramente para ilustrar as diferentes escalas ou horizontes de tempo sobre os quais as variações de preço são medidas. Não temos dois timeframes separados como entrada para a classe de sinal; em vez disso, temos um único parâmetro inteiro de entrada denominado ‘m_scale’, que é um múltiplo de quanto o ‘longo prazo’ é maior em comparação ao curto. Como o curto prazo usa variações entre candles individuais, o ‘longo prazo’ obtém suas leituras de variação sobre um período equivalente a esse parâmetro de escala. Esse processamento é realizado na função get output da seguinte forma:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalQLM::GetOutput(int &Output)
{  m_learning.rate = m_learning_rate;
   for(int i = m_epochs; i >= 1; i--)
   {  MLP.LearningType(m_learning, i);
      for(int ii = m_train_set; ii >= 0; ii--)
      {  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
         if
         (
            _in_row.Init(m_scale) &&
            _in_row.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_row.Size() == m_scale
            &&
            _in_row_old.Init(m_scale) &&
            _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, ii + 1 + 1, m_scale) &&
            _in_row_old.Size() == m_scale
            &&
            _in_col.Init(m_scale) &&
            _in_col.CopyRates(m_symbol.Name(), m_period, 8, ii + 1, m_scale) &&
            _in_col.Size() == m_scale
            &&
            _in_col_old.Init(m_scale) &&
            _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale + ii + 1, m_scale) &&
            _in_col_old.Size() == m_scale
         )
         {  _in_row -= _in_row_old;
            _in_col -= _in_col_old;
            vector _in_e;
            _in_e.Init(m_scale);
            MLP.QL.Environment(_in_row, _in_col, _in_e);
            int _row = 0, _col = 0;
            MLP.QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
            _in.Init(__MLP_INPUTS);
            _in[0] = _row;
            _in[1] = _col;
            MLP.Set(_in);
            MLP.Forward();
            if(ii > 0)
            {  vector _target, _target_data;
               if
               (
                  _target_data.Init(2) &&
                  _target_data.CopyRates(m_symbol.Name(), m_period, 8, ii, 2) &&
                  _target_data.Size() == 2
               )
               {  _target.Init(__MLP_OUTPUTS);
                  _target.Fill(0.0);
                  double _type = _target_data[0] - _in_row[1];
                  int _index = (_type < 0.0 ? 0 : (_type > 0.0 ? 2 : 1));
                  _target[_index] = 1.0;
                  MLP.Get(_target);
                  m_learning.ql_e = _in_e;
                  m_learning.ql_reward_float = _in_row[m_scale - 1];
                  m_learning.ql_reward_max = _in_row.Max();
                  m_learning.ql_reward_min = _in_row.Min();
                  if(i == m_epochs && ii == m_train_set)
                  {  MLP.QL.Action();
                  }
                  MLP.Backward(m_learning, i);
               }
            }
            Output = (MLP.output.Max()==MLP.output[0]?0:(MLP.output.Max()==MLP.output[1]?1:2));
         }
      }
   }
}

Assim, como podemos ver no código-fonte acima, precisamos de 4 vetores para obter as leituras de coordenadas para as entradas do nosso MLP. Uma vez determinadas, com a ajuda da função Environment que converte as duas variações de preço em um único índice de Markov, e da função SetMarkov que fornece essas duas coordenadas a partir do índice de Markov, preenchemos o vetor ‘in’ que é nossa entrada. O classificador MLP tem uma arquitetura muito básica de 2-8-3, representando 2 entradas, uma camada oculta de tamanho 8 e 3 saídas que correspondem às três possíveis ações abertas ao ator. A saída do MLP é essencialmente um mapa de probabilidades que dá valores para vender (índice 0), não fazer nada (índice 1) e comprar (índice 2).

O processo de treinamento do aprendizado por reforço mede o quão distantes essas saídas estão dos vetores similares associados a cada estado do ambiente.  

Resultados do Strategy Tester

Como sempre, realizamos otimizações e testes com dados de ticks reais apenas para fins de demonstração de como um Expert Advisor montado via o assistente do MQL5 com esta classe de sinal poderia executar suas funções básicas. Guias sobre como utilizar o código anexado com o assistente do MQL5 podem ser encontrados aqui e aqui. Muito do trabalho diligente para tornar o Expert Advisor montado ou o sistema de trade pronto para conta real não é tratado nestes artigos e é deixado para o leitor. Realizamos testes no par GBPJPY para o ano de 2023 no timeframe diário. Introduzimos as Cadeias de Markov como uma alternativa para ponderar os valores do mapa de Q-Learning, e portanto executamos dois testes: um sem ponderação de Markov e outro com ponderação. Aqui estão os resultados:

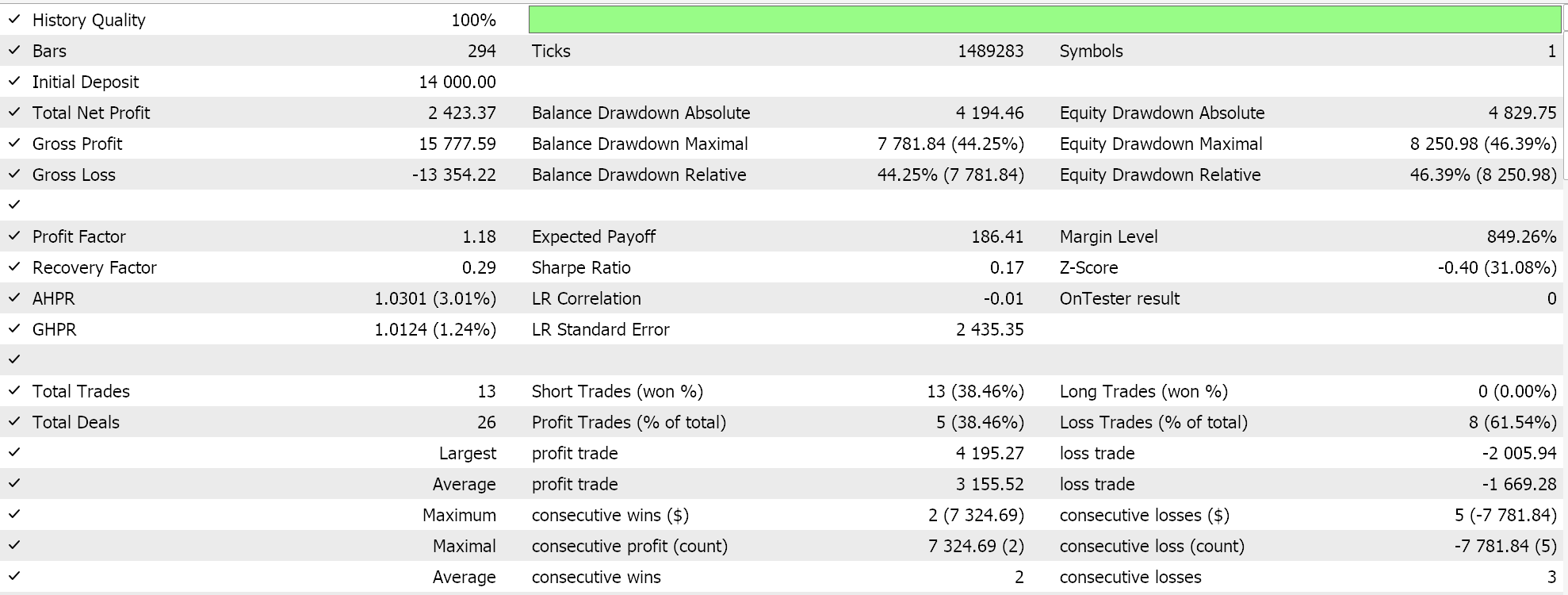
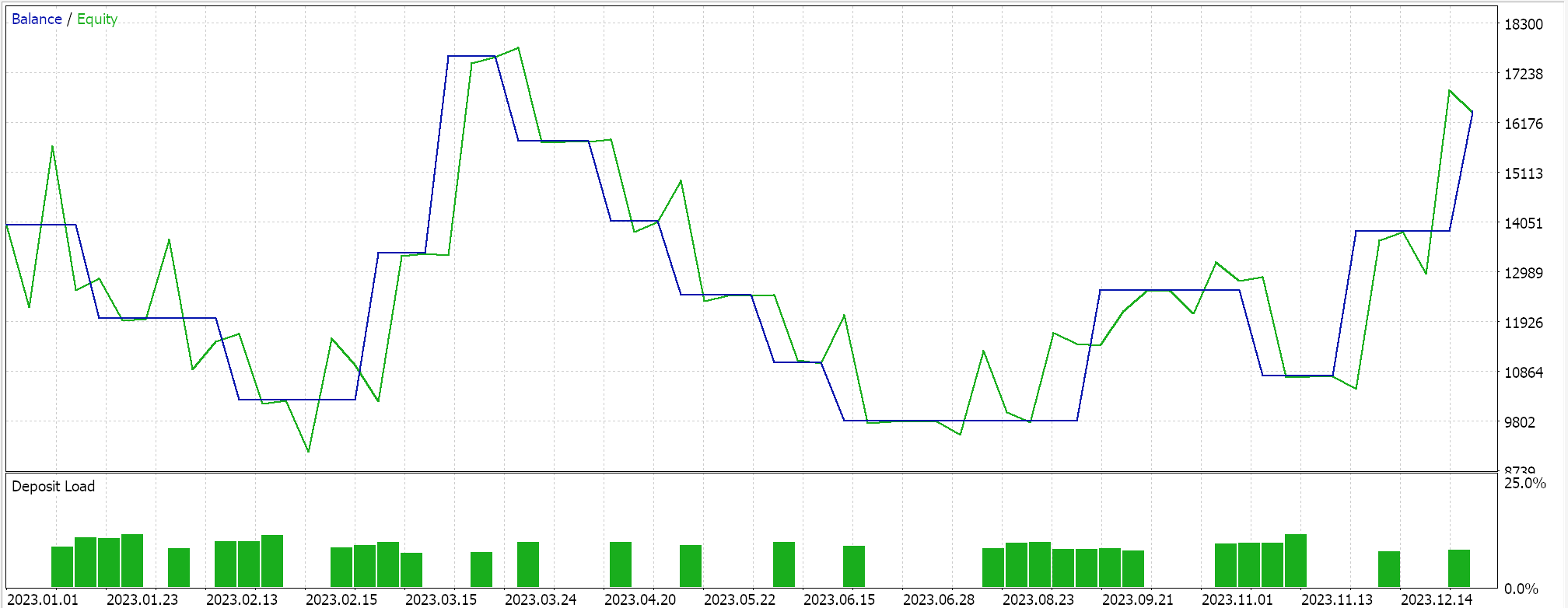
  E então os resultados sem a ponderação de Markov são:

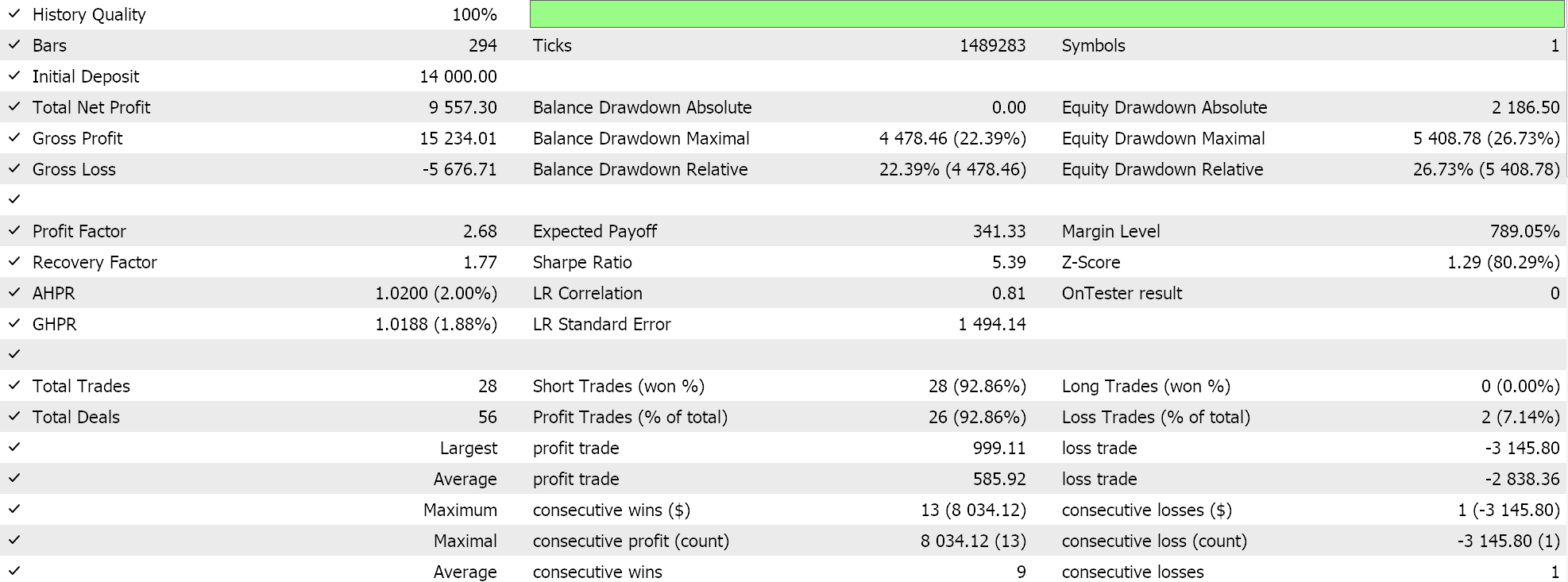
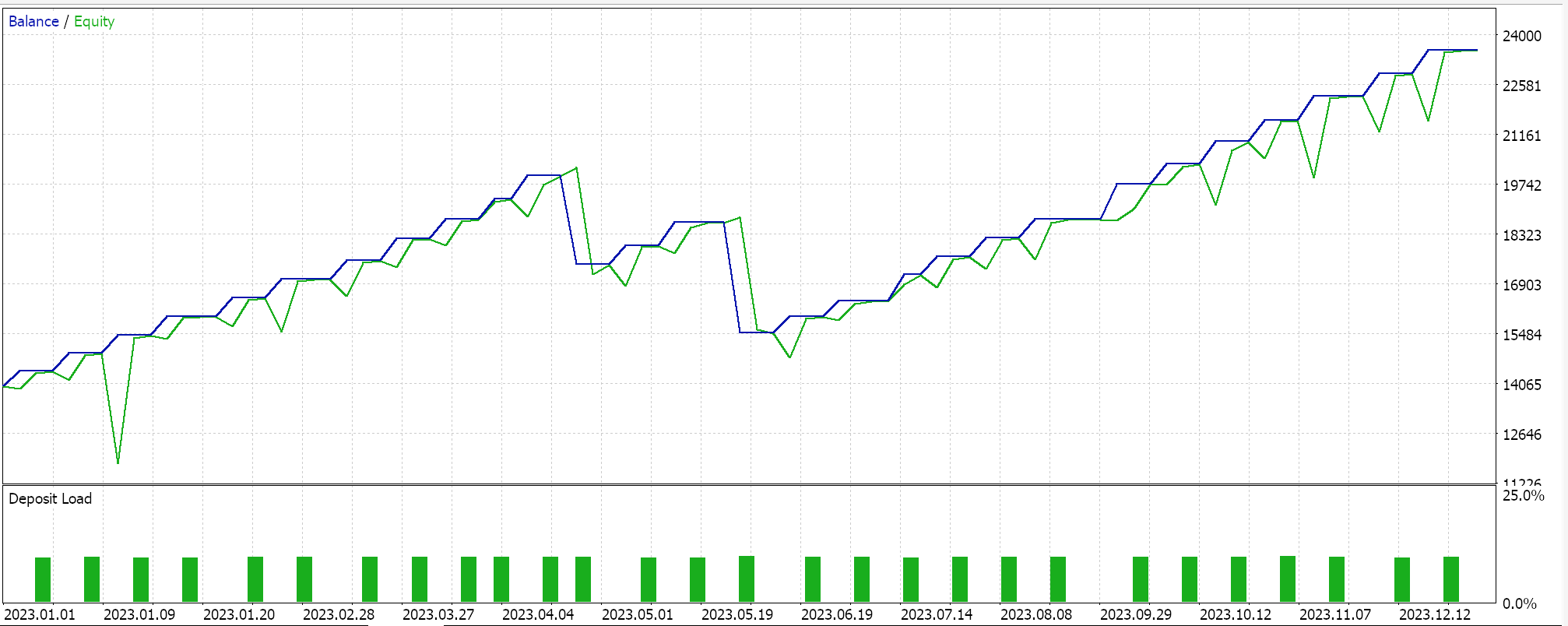
Esses resultados de teste não foram obtidos com as melhores configurações de otimização, nem foram realizados testes walk-forward com essas configurações; portanto, não são um endosso ao uso suplementar das Cadeias de Markov com Q-Learning, embora argumentos sólidos e um regime de teste mais abrangente possam defender seu uso.

Conclusão

Neste artigo, destacamos o que mais poderia ser possível com o assistente do MQL5 introduzindo o aprendizado por reforço, uma alternativa no treinamento de machine learning além dos métodos estabelecidos de aprendizado supervisionado e não supervisionado. Buscamos usar isso no treinamento de um classificador MLP, fazendo com que ele informe e oriente o processo de treinamento em vez de ser apenas o gerador bruto de sinais, o que também seria possível. Ao fazer isso, enquanto focávamos no algoritmo de Q-Learning, exploramos as Cadeias de Markov, uma matriz de transição de probabilidades que pode atuar como um peso no processo de treinamento do aprendizado por reforço, e apresentamos execuções de teste de um Expert Advisor de trading em dois cenários: quando treinado sem as cadeias de Markov, e quando treinado com elas.

Este artigo foi, acredito, um pouco mais complexo em comparação aos anteriores, visto que estamos referenciando duas classes no nosso sinal personalizado e muitos parâmetros sensíveis de entrada foram usados com seus valores padrão, sem grandes ajustes, e muitos novos termos precisaram ser introduzidos para quem não está familiarizado com o assunto. Entretanto, é apenas o começo da nossa abordagem a esse assunto amplo e profundo, o aprendizado por reforço, e espero que em artigos futuros, quando revisitarmos esse tema, ele não pareça tão assustador.