Seleção de características passo a passo em MQL5

Introdução

A seleção de características passo a passo tradicional é uma técnica usada para identificar um subconjunto ótimo de variáveis a partir de um conjunto maior de características candidatas para uma tarefa de aprendizado de máquina. Esse processo começa avaliando cada característica candidata individualmente para selecionar a variável mais promissora a ser incluída no modelo final. Subsequentemente, candidatos adicionais são testados quanto à sua contribuição em combinação com aqueles já escolhidos, continuando até que um nível-alvo de desempenho preditivo ou de classificação seja atingido.

Neste artigo, examinamos as limitações da seleção de características passo a passo convencional, como seu potencial de sobreajuste e seus desafios em capturar interações entre características. Em seguida, introduzimos um algoritmo aprimorado projetado para abordar essas questões, implementado em MQL5, que fornece integração flexível com vários métodos de aprendizado supervisionado.

Essa abordagem aprimorada foi desenvolvida por Timothy Masters e descrita em seu livro Modern Data Mining Algorithms in C++ and CUDA C. Finalmente, mostramos a aplicação prática do algoritmo, usando-o para selecionar variáveis ótimas em uma tarefa de regressão de exemplo, ilustrando sua eficácia.

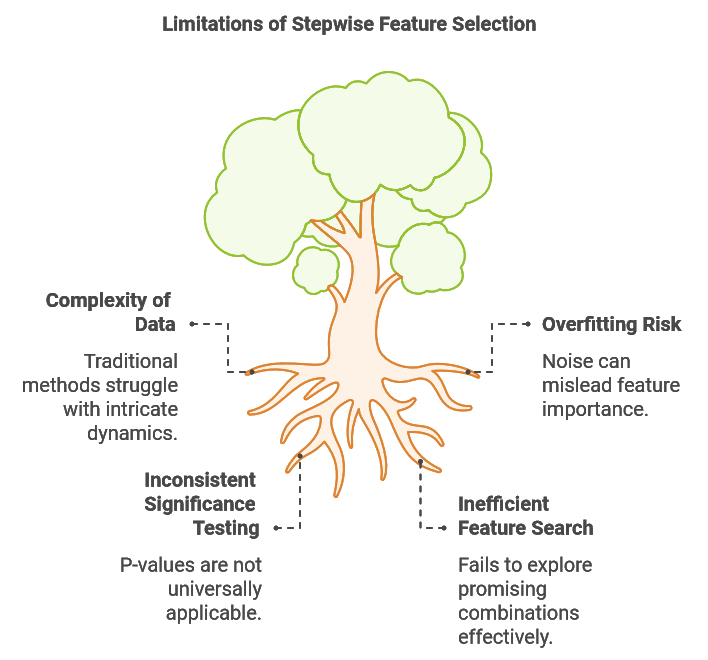
Limitações da Seleção de Características Passo a Passo

Conjuntos de dados usados em tarefas de aprendizado de máquina são frequentemente inerentemente complexos, às vezes apresentando relações não lineares, padrões variáveis no tempo e inúmeros fatores interconectados. Essa complexidade impõe desafios significativos à seleção de características, já que métodos tradicionais como a seleção passo a passo podem ter dificuldade em capturar essas dinâmicas intrincadas. Uma limitação importante da seleção passo a passo é sua incapacidade de avaliar o impacto de diferentes combinações de características. Frequentemente, uma característica que parece não informativa isoladamente ou quando combinada com certas outras variáveis pode se tornar altamente preditiva quando combinada com características complementares específicas.

Considere a tarefa de construir um modelo preditivo para taxas de câmbio. Nesse cenário, poderíamos reunir vários indicadores técnicos e fundamentais. Alguns indicadores fundamentais podem parecer oferecer pouco valor preditivo individualmente ou quando combinados com dados técnicos não complementares. No entanto, combinar indicadores como os resultados de eleições iminentes com a tendência atual do mercado pode gerar uma previsão mais robusta do que confiar apenas nas tendências de mercado. Além disso, compreender o clima econômico geral e antecipar como a liderança entrante pode responder às condições macroeconômicas poderia aumentar significativamente a precisão preditiva do modelo. Esses desafios destacam a necessidade de um método de seleção passo a passo aprimorado que possa testar combinações promissoras de características sem recorrer a uma busca exaustiva computacionalmente proibitiva.

Um segundo desafio da seleção passo a passo é sua suscetibilidade ao sobreajuste devido a ruído. Cada vez que uma nova variável é adicionada, o algoritmo corre o risco de confundir flutuações aleatórias com informações valiosas, levando-o a aprender padrões que não se generalizam. Por exemplo, adicionar múltiplos indicadores técnicos pode aumentar o desempenho em amostras se o modelo começar a se ajustar ao ruído de mercado em vez de a tendências significativas, comprometendo assim sua robustez em dados fora da amostra. Esse problema frequentemente surge quando o desempenho do modelo é avaliado apenas pelo ajuste em amostras, resultando na inclusão de mais variáveis do que o necessário e, em última instância, degradando o desempenho fora da amostra.

A significância estatística da seleção de características é frequentemente avaliada usando valores de p (p-values). Na seleção passo a passo tradicional baseada em regressão, os valores de p avaliam a probabilidade de que o coeficiente de uma característica seja zero, refletindo seu poder preditivo. Intervalos de confiança fornecem ainda uma faixa para o verdadeiro coeficiente da população, considerando a incerteza de amostragem. Um valor de p baixo indica forte evidência contra a hipótese nula (de que o coeficiente é zero), apoiando a significância da característica. Esses valores de p são derivados de testes de hipótese, onde a hipótese nula assume um coeficiente zero e a hipótese alternativa assume um coeficiente diferente de zero. Para obter o valor de p, calculamos um escore t com base na estimativa do coeficiente e seu erro padrão.

No entanto, essa abordagem é específica para modelos de regressão. Para outras técnicas de aprendizado de máquina, obter valores de p comparáveis exigiria um teste de hipótese personalizado, adicionando complexidade à aplicação prática do algoritmo. Idealmente, uma técnica mais universalmente aplicável forneceria uma medida relevante de significância, produzindo um valor de p ou métrica equivalente consistente em diferentes tipos de métodos de aprendizado de máquina.

Considerando as limitações da seleção de características passo a passo convencional, o algoritmo modificado apresentado aqui oferece três melhorias principais em relação ao método tradicional. A primeira melhoria aborda o desafio de buscar de forma eficiente subconjuntos promissores de características. Ao manter múltiplos subconjuntos de alto potencial e avaliar novos candidatos em combinação com esses subconjuntos, o algoritmo modificado alcança um equilíbrio entre exploração abrangente e eficiência computacional. Essa abordagem permite descobrir relações sinérgicas entre características que a seleção passo a passo tradicional pode deixar passar.

Para reduzir o risco de sobreajuste, o algoritmo usa o desempenho em validação cruzada como base para avaliar os conjuntos de características. Esse método rigoroso de avaliação minimiza as chances de confundir ruído aleatório com informação preditiva significativa e fornece um mecanismo direto para interromper automaticamente a inclusão de características adicionais quando retornos decrescentes são detectados.

Além disso, para cada nova característica adicionada, o algoritmo calcula duas probabilidades:

• Probabilidade de ocorrência ao acaso: essa probabilidade mede a chance de que o desempenho observado do conjunto atual de características possa ser atribuído ao acaso, assumindo que todas as características selecionadas sejam irrelevantes.
• Probabilidade de melhoria espúria: essa probabilidade avalia a chance de que o ganho de desempenho da última adição de característica se deva ao acaso e não a um valor preditivo genuíno.
  

Essas probabilidades oferecem insights sobre a significância estatística do processo de seleção de características, ajudando a distinguir poder preditivo genuíno de ruído estatístico. Notavelmente, essas probabilidades calculadas são independentes de modelo, permitindo que o algoritmo se integre perfeitamente com uma ampla variedade de modelos de aprendizado de máquina. Nas próximas seções, examinaremos partes-chave do código que implementam esse algoritmo. Os trechos de código fornecidos são extraídos da classe CStepwisebase, definida em stepwise.mqh. Essa classe é abstrata, exigindo que os usuários criem uma classe derivada que implemente certos membros virtuais, possibilitando a integração de qualquer tipo de modelo.

O Procedimento Passo a Passo

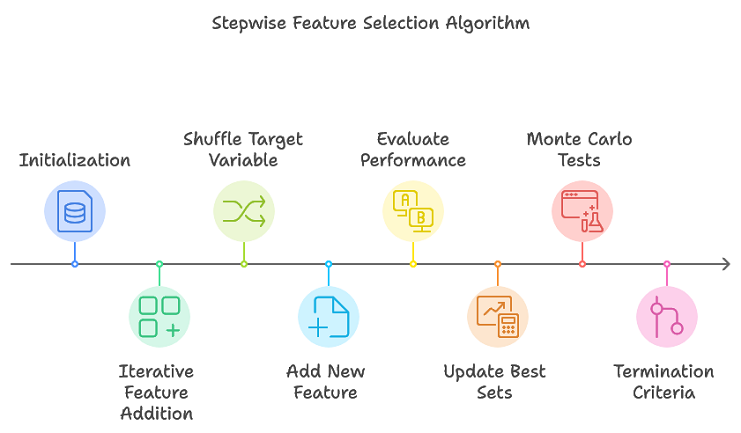
O algoritmo proposto aprimora a seleção passo a passo tradicional acompanhando múltiplos subconjuntos promissores de características, evitando a necessidade de uma busca exaustiva. Essa abordagem reduz eficientemente os subconjuntos de características prováveis de formar o conjunto ótimo final. Uma visão geral do procedimento é a seguinte:

1. Inicialização: Estruturas de dados usadas ao longo do processo para armazenar informações sobre os testes de conjuntos de características são inicializadas.
2. Adição iterativa de características: Para cada iteração, realizar múltiplas replicações de permutação. Embaralhar a variável alvo para criar uma nova permutação. Adicionar uma nova característica ao conjunto atual de características. Avaliar o desempenho do conjunto atualizado de características usando validação cruzada. Atualizar os conjuntos de características de melhor desempenho e suas métricas correspondentes. 
   
3. Critérios de término: o algoritmo é encerrado quando o número máximo de características (conforme definido por max_num_predictors) é atingido ou quando a melhoria de desempenho fica abaixo de um limite predefinido.

   

As etapas principais são implementadas em stepwiseSearch(), com o processo regido por vários hiperparâmetros que controlam diferentes aspectos da busca. Esses hiperparâmetros são:

• num_kept: O número de subconjuntos de características candidatos com melhor desempenho, com base no critério, a serem mantidos em cada iteração. Esses candidatos são considerados prováveis de formar o conjunto ótimo de características,
• num_folds: O número de partições usadas na validação cruzada. Embora valores maiores melhorem a precisão das estimativas de desempenho, também aumentam o custo computacional,
• min_num_predictors: O número mínimo de preditores que o conjunto final de características pode conter, permitindo que os usuários definam um limite inferior para a complexidade do modelo,
• max_num_predictors: O número máximo de preditores permitidos no conjunto final de características, fornecendo um limite superior para a complexidade do modelo,
• num_replications: O número de iterações para o teste de permutação de Monte Carlo, que ajuda a avaliar a significância estatística do desempenho das características,
• verbose_output: Determina se os resultados de cada etapa do processo de seleção de características são exibidos na aba Experts do MetaTrader 5.
  

Esses parâmetros fornecem flexibilidade, permitindo que os usuários ajustem o processo de seleção de características para atender às suas necessidades. Eles podem ser especificados invocando setParams().

//+------------------------------------------------------------------+
//|   set the stepwise selection parameters                          |
//+------------------------------------------------------------------+
void              setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output)
  {
   m_keptvars = num_kept>0?num_kept:1;
   m_folds = num_folds>0?num_folds:ULONG_MAX;
   m_min_num_preds = min_num_predictors;
   m_max_num_preds = max_num_predictors;
   m_reps = num_replications>0?num_replications:1;
   m_verbose = verbose_output;
   return;
  }

O método stepwiseSearch() começa inicializando estruturas de dados internas para acompanhar os diversos testes de conjuntos de características. Em seguida, entra em um laço principal que continua até que o número máximo de preditores seja atingido. Durante cada iteração do laço, a variável alvo é embaralhada aleatoriamente por múltiplas repetições, e uma nova variável é adicionada ao modelo chamando addFeature(). O algoritmo armazena as características do modelo com melhor desempenho e, se a adição de uma nova variável resultar em degradação do desempenho, ele pode encerrar antecipadamente. Se o desempenho continuar melhorando, o processo persiste até que o número máximo de preditores seja alcançado. Por fim, os índices das variáveis selecionadas são salvos no array m_var_indices.

//+------------------------------------------------------------------+
//|  coordinates main stepwise search operation                      |
//+------------------------------------------------------------------+
int               stepwiseSearch(void)
  {
   int done = 1;
   int btrials;
   m_trial_length = m_max_num_preds*m_vars*m_keptvars;

   reset();

   if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars))
     {
      Print(__FUNCTION__," data structure resizing error ", GetLastError());
      return done;
     }

   if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0  ||
      ArrayResize(m_already_tried,int(m_trial_length))<0 ||
      ArrayResize(m_trial_vars,int(m_max_num_preds))<0 ||
      ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0)
     {
      Print(__FUNCTION__,"  error resizing array ", GetLastError());
      return done;
     }


   ArrayInitialize(m_all_best_trials,-1);
   ArrayInitialize(m_already_tried,-1);
   ArrayInitialize(m_trial_vars,-1);
   ArrayInitialize(m_prior_best_trials,-1);

   vector target;
   int n_so_far =0;
   int rval, rem, j,n_this_rep = 0;
   int mcpt_mod_count, mcpt_change_count;
   mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1;
   double temp,prior_crit;
   double original_crit, original_change, new_crit;
   original_crit = original_change = new_crit = -DBL_MIN;

   if(m_verbose)
     {
      if(m_reps>1)
         Print("Criterion  || New pval  || Diff pval  || Column Indices");
      else
         Print("Criterion  || Column Indices");
     }
   while(true)
     {

      target = m_target;

      for(ulong rep=0; rep<m_reps; rep++)
        {


         if(rep)
           {
            rval = 17*int(rep) + 11;
            unif(rval);
            unif(rval);
            rem = int(m_samples);
            while(rem>1)
              {
               j = (int)(unif(rval))*rem;
               if(j>=rem)
                  j = rem-1;
               temp = target[--rem];
               target[rem] = target[j];
               target[j] = temp;
              }
           }

         btrials = int(rep*m_max_num_preds*m_keptvars);
         if(n_so_far == 0)
            prior_crit = -1.e60;
         else
            prior_crit = m_all_best_crits[rep][0];
         n_this_rep = n_so_far;

         done = addFeature(target,n_this_rep,btrials,rep);

         if(done || n_this_rep!=(n_so_far+1))
           {
            Print(__FUNCTION__, " internal error ");
            return 1;
           }

         if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep)
           {
            for(ulong i = 0 ; i<m_keptvars; i++)
              {
               m_all_best_crits[rep][i] = m_prior_best_crits[i];
               if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0)
                 {
                  Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
                  return 1;
                 }
              }
            if(m_verbose)
               Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation");
            return 0;
           }

         if(prior_crit < 0.0)
            prior_crit = 0.0;

         new_crit = m_all_best_crits[rep][0];

         if(new_crit<0.0)
            new_crit = 0.0;

         if(rep == 0)
           {
            original_crit = new_crit;
            original_change = new_crit - prior_crit;
            mcpt_mod_count = mcpt_change_count = 1;
           }
         else
           {
            if(new_crit >= original_crit)
               ++mcpt_mod_count;
            if(new_crit - prior_crit >= original_change)
               ++mcpt_change_count;
           }

        }

      if(n_so_far == 0)
         mcpt_change_count = mcpt_mod_count;

      if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0)
        {
         Print(__FUNCTION__, " container resize error ", GetLastError());
         return 1;
        }

      string msg;
      if(m_reps>1)
        {
         double mod_pval = (double) mcpt_mod_count / (double) m_reps;
         double change_pval = (double) mcpt_change_count / (double) m_reps;

         if(m_verbose)
            msg = StringFormat("%10.8lf %10.8lf %10.8lf  ", original_crit,mod_pval,change_pval);

         m_decision_matrix[n_so_far][0] = original_crit;
         m_decision_matrix[n_so_far][1] = mod_pval;
         m_decision_matrix[n_so_far][2] = change_pval;
        }
      else
        {
         msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL;
         m_decision_matrix[n_so_far][0] = original_crit;
        }
      if(m_verbose)
        {
         for(int i = 0; i<n_this_rep; i++)
           {
            msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i]));
           }
        }
      if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0)
        {
         Print(__FUNCTION__, " array copy error ", GetLastError());
         return 1;
        }

      if(m_verbose)
         Print(msg);

      ++n_so_far;
      if(n_so_far == int(m_max_num_preds))
        {
         if(m_verbose)
            Print(" Stepwise selection successfully completed ");
         break;
        }
     }

   return 0;

  }

Calculando o Critério com Validação Cruzada

Confiar em um único conjunto de treinamento para seleção de características frequentemente gera resultados subótimos devido ao risco de sobreajuste. Para mitigar esse risco, é utilizada a validação cruzada. A validação cruzada envolve dividir o conjunto de dados em múltiplos conjuntos de treinamento e validação, permitindo uma avaliação mais abrangente do desempenho do modelo e da importância das características. Ao treinar e testar iterativamente em diferentes subconjuntos de dados, a validação cruzada reduz o sobreajuste e melhora a capacidade de generalização.

Embora a validação cruzada seja altamente eficaz, ela apresenta um trade-off entre eficiência computacional e confiabilidade estatística. Um número maior de partições geralmente fornece uma estimativa mais precisa do desempenho do modelo, mas aumenta as demandas computacionais. O número ideal de partições depende tanto das características do conjunto de dados quanto dos recursos computacionais disponíveis. Na prática, determinar o número apropriado de partições requer consideração cuidadosa do tamanho do conjunto de dados e do nível desejado de confiança estatística. Ao compreender tanto os princípios quanto as limitações da validação cruzada, os profissionais podem aplicar essa técnica para aumentar a confiabilidade e a robustez de seus processos de seleção de características e construção de modelos.

O procedimento de validação cruzada é implementado pelo método crossEval().

//+------------------------------------------------------------------+
//|  evaluates a predictor set using cross validation                |
//+------------------------------------------------------------------+
int               crossEval(ulong num_vars,vector &target,double &criterion)
  {
   ulong ifold, n_remaining, test_start, test_stop ;
   double error, evalresult ;

   n_remaining = m_samples;
   test_start = 0;

   error = 0.0;

   for(ifold = 0; ifold<m_folds; ifold++)
     {
      test_stop = test_start + (n_remaining/(m_folds-ifold));
      if(!fitModel(num_vars,test_start,test_stop,target))
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " fit() failed ");
         return 1;
        }
      evalresult = evalModel(num_vars,test_start,test_stop,target);
      if(evalresult==EMPTY_VALUE)
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " evalModel() failed ");
         return 1;
        }
      error+=evalresult;
      n_remaining -= test_stop - test_start;
      test_start = test_stop;
     }

   criterion = 1.0 - error/double(m_samples);
   return 0;
  }

Essa função recebe como entrada o número de preditores a serem avaliados, um vetor de valores alvo embaralhados e uma referência a uma variável que retornará o valor de um critério — usado como uma das variáveis de decisão para identificar o subconjunto de características mais adequado. A função retorna 0 em caso de execução bem-sucedida. Ela opera ajustando primeiro um modelo e, em seguida, avaliando seu desempenho em todas as partições dos dados da amostra.

O método fitModel() é responsável por treinar um modelo em um subconjunto de características candidato. Ele recebe as seguintes entradas:

• num_preds: O número de preditores,
• row_start: O índice da primeira amostra,
• row_stop: O índice imediatamente após a última amostra a ser excluída do conjunto de treinamento, e,
• targets: O vetor de valores alvo embaralhados.
  

Essa função retorna um valor booleano indicando se o modelo foi treinado com sucesso.

A função evalModel() tem as mesmas entradas que fitModel(), mas, desta vez, a partição de linhas especificada representa as amostras usadas para avaliar o modelo treinado. Essa função retorna um valor que fornece uma indicação do desempenho do modelo. Tanto fitModel() quanto evalModel() são membros virtuais, exigindo implementação em uma classe derivada para integrar o tipo específico de modelo em uso.

//+------------------------------------------------------------------+
//| fit a model                                                      |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;}
//+------------------------------------------------------------------+
//| evaluate a model                                                 |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}

Encontrando a Primeira Característica

O método addFirstFeature() é invocado por addFeature() para identificar o primeiro preditor em um determinado conjunto.

//+------------------------------------------------------------------+
//|     finds the first predictor in the set                         |
//+------------------------------------------------------------------+
int               addFirstFeature(vector &targ, int bindex,ulong rep_index)
  {
   double crit;

   for(ulong i = 0; i<m_keptvars; i++)
     {
      m_all_best_crits[rep_index][i] = -1.e60;
      m_all_best_trials[bindex+i] = -1;
     }

   for(int i = 0; i<int(m_vars); i++)
     {
      m_trial_vars[0] = i;
      if(crossEval(1,targ,crit))
        {
         Print(__FUNCTION__, " xval error ");
         return 1;
        }
      ulong j;
      for(j = 0; j<m_keptvars; j++)
        {
         if(crit > m_all_best_crits[rep_index][j])
            break;
        }
      if(j<m_keptvars)
        {
         for(long k = long(m_keptvars-2); k>=long(j); k--)
           {
            m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k];
            m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k];
           }
         m_all_best_trials[bindex+j] = i;
         m_all_best_crits[rep_index][j] = crit;
        }
     }

   return 0;
  }

Ele itera sobre cada variável, avaliando seu desempenho usando validação cruzada. O desempenho é avaliado com base em um critério definido em uma classe derivada, que, por sua vez, informa a técnica de aprendizado que determina o modelo.

Durante essa avaliação, o método mantém uma lista das variáveis de melhor desempenho juntamente com seus valores de critério correspondentes. À medida que cada variável é avaliada, seu desempenho é comparado ao das variáveis atualmente melhores. Se uma nova variável superar uma das variáveis de melhor desempenho existentes, ela é inserida na lista, fazendo com que as variáveis de menor desempenho sejam deslocadas para baixo.

Esse processo continua até que todas as variáveis tenham sido avaliadas, culminando na identificação do primeiro preditor. Para chamadas subsequentes a addFeature(), uma nova variável é introduzida invocando addNewFeature(), garantindo uma abordagem sistemática para adição de características.

Adicionando ao Conjunto de Características

O método addNewFeature() identifica o próximo preditor a ser incluído no conjunto de características do modelo.

//+------------------------------------------------------------------+
//|  looks for next predictor to include                             |
//+------------------------------------------------------------------+
int               addNewFeature(vector& target,int &ind, int bindex,ulong rep_index)
  {
   int i, j, k, ivar, ir ;
   int npred, n_already_tried,nbest, rootvars;
   nbest  = -1;
   double crit;

   ind = npred = ind+1;

   for(i = 0; i<int(m_keptvars); i++)
     {
      m_prior_best_crits[i] = m_all_best_crits[rep_index][i];
      if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0)
        {
         Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
         return 1;
        }
      m_all_best_crits[rep_index][i] = -1.e60;
     }
   n_already_tried = 0;
   for(ir = 0; ir<int(m_keptvars); ir++)
     {
      if(m_prior_best_crits[ir] < -1.e59)
         break;
     }
   nbest = ir;

   for(ir = 0; ir<nbest; ir++)
     {
      rootvars = ir*(npred-1);
      for(ivar=0; ivar<int(m_vars); ivar++)
        {
         for(i = 0; i<npred-1; i++)
           {
            if(m_prior_best_trials[rootvars+i] == ivar)
               break;
           }
         if(i < npred-1)
            continue;
         k = 0;

         for(i = 0; i<int(m_vars); i++)
           {
            for(j=0; j<npred-1; j++)
              {
               if(m_prior_best_trials[rootvars+j] == i)
                 {
                  m_trial_vars[k++] = i;
                  break;
                 }
              }
            if(ivar == i)
               m_trial_vars[k++] = i;
           }
         for(i = 0; i<n_already_tried; i++)
           {
            for(j = 0; j<npred; j++)
              {
               if(m_trial_vars[j] != m_already_tried[i*npred+j])
                  break;
              }
            if(j == npred)
               break;
           }
         if(i < n_already_tried)
            continue;

         for(i =0; i<npred; i++)
            m_already_tried[n_already_tried*npred+i]=m_trial_vars[i];
         ++n_already_tried;

         if(crossEval(ulong(npred),target,crit))
           {
            Print(__FUNCTION__, " xval error ");
            return 1;
           }

         for(i = 0; i< int(m_keptvars); i++)
           {
            if(crit > m_all_best_crits[rep_index][i])
               break;
           }

         if(i<int(m_keptvars))
           {
            for(j = int(m_keptvars-2); j>=i; j--)
              {
               m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j];
               if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0)
                 {
                  Print(__FUNCTION__, " array copy error ", GetLastError());
                  return 1;
                 }
              }
            m_all_best_crits[rep_index][i] = crit;
            if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0)
              {
               Print(__FUNCTION__, " array copy error ", GetLastError());
               return 1;
              }
           }
        }
     }
   return 0;
  }

Ele se baseia no conjunto existente de preditores, examinando todas as combinações possíveis dos melhores preditores atuais com variáveis adicionais. Para cada combinação, o método realiza validação cruzada para avaliar seu desempenho, que é medido usando um critério especificado. Tendo examinado os elementos centrais do código de seleção de características passo a passo, agora exploraremos como esses trechos se integram para formar a implementação completa.

A Classe CStepwisebase

A classe CStepwisebase serve como uma implementação fundamental para a seleção de características passo a passo, projetada para selecionar características preditivas iterativamente a partir de um conjunto de candidatas. Esse processo de seleção adiciona variáveis de forma sistemática com base em suas contribuições para o desempenho de um modelo preditivo. Como uma classe abstrata, ela permite a integração de qualquer tipo de técnica de aprendizado e seu critério correspondente dentro de uma classe derivada, implementando os métodos fitModel() e evalModel(). Um exemplo dessa implementação será fornecido na próxima seção.

O método stepwiseSelection() atua como o principal ponto de entrada acessível publicamente, iniciando o processo ao preparar os dados e executar stepwiseSearch().

//+------------------------------------------------------------------+
//|  main method to execute stepwise feature selection               |
//+------------------------------------------------------------------+
bool              stepwiseSelection(matrix& predictors, vector& targets)
  {

   if(targets.Size()!=predictors.Rows() || !targets.Size())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_data = stdmat(predictors);

   m_target = (targets-targets.Mean())/(targets.Std()+1e-10);

   m_vars = predictors.Cols();
   m_samples = predictors.Rows();

   if(m_keptvars>m_vars || m_keptvars<1)
      m_keptvars = m_vars;

   if(m_folds<1)
      m_folds = 1;

   if(m_folds>m_samples)
      m_folds = m_samples;

   if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds)
      m_min_num_preds = m_vars;

   if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds)
      m_max_num_preds = m_vars;

   if(m_reps<1)
      m_reps = 1;

   if(m_verbose)
     {
      Print(" STEPWISE SELECTION PARAMETERS ");
      Print(" Number of retained candidate variables for each iteration ", m_keptvars);
      Print(" Number of folds in cross validation procedure ", m_folds);
      Print(" Final minimum number of selected predictors ", m_min_num_preds);
      Print(" Final maximum number of selected predictors ", m_max_num_preds);
      Print(" Number of replications for MCP test ", m_reps);
     }

   return (stepwiseSearch()==0);
  }

Para configurar previamente os parâmetros do processo de seleção de características, o método setParams() está disponível. A saída do processo de seleção de características pode ser exibida na aba Experts do MetaTrader 5 definindo o último parâmetro de setParams() como true. Além disso, os resultados do procedimento de seleção podem ser recuperados usando os seguintes métodos:

•  Chamar getCriticalVals() retorna uma matriz com um número variável de colunas, dependendo de um teste de permutação de Monte Carlo (MCP) ter sido especificado como parte da busca passo a passo. Isso é obtido definindo num_replications em setParams() para qualquer valor maior que 1. Nesse caso, getCriticalVals() retorna uma matriz com três colunas, onde cada linha contém valores quantificando a adição de uma característica extra. O número de linhas nessa matriz corresponde ao número de iterações pelo laço mais externo do algoritmo passo a passo. Os três valores em cada linha consistem no critério, um p-value indicando a probabilidade de que o desempenho observado seja atribuível ao acaso (assumindo que as características selecionadas sejam irrelevantes) e outro p-value refletindo a probabilidade de que a melhoria de desempenho resultante da adição de característica nessa iteração se deva ao acaso.
  

  //+------------------------------------------------------------------+
  //| get all crit values and corresponding p-values                   |
  //+------------------------------------------------------------------+
  matrix            getCriticalVals(void)
    {
     return m_decision_matrix;
    }

• Quando nenhum teste MCP é especificado, a função retorna uma única coluna contendo os respectivos valores do critério para cada iteração da execução do algoritmo. O número dos melhores subconjuntos de características encontrados pode ser consultado usando getNumFeatureSets(), enquanto os próprios subconjuntos podem ser recuperados chamando getFeatureSetAt(), que aceita um índice correspondente à iteração desejada e uma referência a um array onde os índices das colunas que representam o subconjunto de características serão copiados.
  

  //+------------------------------------------------------------------+
  //|  get the selected features at a specific iteration of the process|
  //|  iterations denoted as zero based indices                        |
  //|  eg, first selected feature located at iteration index 0         |
  //+------------------------------------------------------------------+
  bool              getFeatureSetAt(ulong iteration_index,ulong &selectedvars[])
    {
     if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0)
        return true;
     else
       {
        Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
        return false;
       }
    }
  //+---------------------------------------------------------------------+
  //| get maximum number of iterations cycled through in selection process|
  //+---------------------------------------------------------------------+
  ulong             getNumFeatureSets(void)
    {
     return m_decision_matrix.Rows();
    }

Isto conclui nossa discussão sobre a classe base. Na próxima seção, exploraremos como aplicar esse código integrando um modelo e executando testes.

Um Exemplo Usando um Modelo de Regressão Linear-Quadrática

Para ilustrar o algoritmo aprimorado de seleção passo a passo, demonstraremos sua aplicação na avaliação de um conjunto de dados de preditores candidatos para ajustar um modelo de regressão linear-quadrática. Essa implementação é fornecida no script do MetaTrader 5, StepWiseFeatureSelection_Demo.mq5. Neste script, delinearemos o processo de seleção das características mais preditivas por meio do método aprimorado de seleção passo a passo, mostrando como o algoritmo identifica preditores ótimos para o modelo de regressão linear-quadrática. A demonstração prática incluirá a preparação do conjunto de dados, a configuração dos parâmetros do modelo e a execução do processo de seleção de características dentro do ambiente do MetaTrader 5.

A regressão linear-quadrática é uma extensão da regressão linear que incorpora termos lineares e quadráticos (ao quadrado) da(s) variável(is) preditora(s). Essa abordagem permite que o modelo capture relações não lineares ajustando uma curva aos dados em vez de uma linha reta. A forma geral de uma equação de regressão linear-quadrática para uma única variável preditora X é dada pela fórmula geral abaixo.

Onde:

• y é a variável dependente,
  
• x é a variável independente,
  
• β0, β1 e β2 são coeficientes a serem estimados,
  
• x ao quadrado é o termo quadrático, que permite ao modelo levar em conta a curvatura,
  
• ϵ é o termo de erro.
  

Nessa equação, o termo βx modela a relação linear, enquanto β(x ao quadrado) captura a curvatura, tornando o modelo útil para dados que exibem uma tendência parabólica ou curva. O coeficiente β0 representa o intercepto, β1 controla a inclinação da parte linear e β2 afeta a curvatura, determinando se a parábola se abre para cima (β2>0) ou para baixo (β2<0).

Na prática, a regressão linear-quadrática é aplicada em situações em que a relação entre as variáveis dependente e independente não é estritamente linear. A implementação da regressão linear-quadrática em nosso script é viabilizada aproveitando a classe Ordinary Least Squares (OLS) definida em OLS.mqh.

Em seguida, percorreremos como esse modelo de regressão é integrado ao processo de seleção passo a passo, permitindo a identificação de preditores ótimos em nosso conjunto de dados.

O script StepWiseFeatureSelection_Demo.mq5 implementa de forma eficaz o algoritmo aprimorado de seleção passo a passo de características, adaptado para modelos de regressão linear-quadrática. A seguir está um detalhamento dos componentes e funcionalidades do script. A classe CStepwise herda de CStepwisebase, fornecendo uma implementação concreta dos métodos abstratos definidos na classe base. Esse design permite a integração da lógica específica do modelo para regressão linear-quadrática. A lógica central para ajustar e avaliar o modelo linear-quadrático é encapsulada dentro da classe CStepwise. Isso inclui os ajustes necessários para acomodar tanto os termos lineares quanto os quadráticos das variáveis preditoras.

O método fitModel() é responsável por construir a matriz de projeto (design matrix) com base nas amostras de treinamento. Ele exclui a faixa de dados especificada destinada à validação durante a validação cruzada. Uma instância da classe OLS é criada (denotada como m_ols), a qual gerencia as operações de regressão por mínimos quadrados ordinários.

//+------------------------------------------------------------------+
//|    fit the OLS model                                             |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   ulong ntrain = m_samples - (row_stop - row_start);

   vector dependent(ntrain);
   matrix independent(ntrain,nvars+1);
   ntrain = 0;

   for(ulong sample=0; sample<m_samples; sample++)
     {
      if(sample>=row_start && sample<row_stop)
         continue;
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            independent[ntrain][var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }
      independent[ntrain][nvars] = 1.0;
      dependent[ntrain++] = targets[sample];
     }

   return m_ols.Fit(dependent,independent);
  }

Em evalModel(), o método avalia o desempenho do modelo linear-quadrático treinado usando os dados que foram deixados de fora durante a fase de treinamento. O critério para avaliar o desempenho do modelo é especificado aqui e, neste caso, é a soma dos erros quadráticos (SSE). Esse critério mede quão bem as previsões do modelo se alinham com os resultados reais.

//+------------------------------------------------------------------+
//|      evaluate the model                                          |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   if(m_ols.Loglikelihood()==EMPTY_VALUE)
     {
      Print(__FUNCTION__, " OLS error ");
      return EMPTY_VALUE;
     }

   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   double prediction;
   vector row(nvars);
   double error = 0.0;
   for(ulong sample=row_start; sample<row_stop; sample++)
     {
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            row[var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }

      prediction = m_ols.Predict(row);
      if(prediction == EMPTY_VALUE)
        {
         Print(__FUNCTION__, " OLS predict() error ");
         return EMPTY_VALUE;
        }
      error+=pow(prediction-targets[sample],2.0);
     }

   return error;
  }

Após a definição da classe derivada CStepwise, o script gera uma matriz aleatória 100 por 10, denotada como mat, com valores variando entre 0 e 1. Essa matriz serve como o conjunto de dados contendo as variáveis preditoras.

//---
   MathSrand(120);
//---
   matrix mat(100,10);
//---
   mat.Random(0.0,1.0);
//---

Um vetor alvo é criado somando colunas específicas. A variável alvo é definida como a soma dos valores das colunas 0, 5, 4 e 6 da matriz. Isso define a variável dependente (ou saída) que o modelo busca prever com base nas variáveis independentes (as colunas restantes).

//---
   vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6);
//---

Uma instância da classe CStepwise é criada, referida como stepwise. Essa instância gerenciará o processo de seleção passo a passo de características adaptado para o modelo de regressão linear-quadrática. O método setParams() é invocado na instância stepwise para configurar os parâmetros do processo de seleção passo a passo.

//---
   CStepwise stepwise;
   stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true);
   if(!stepwise.stepwiseSelection(mat,target))
      return;

Os parâmetros, que podem ser ajustados pelo usuário, incluem:

input ulong NumKeptVars = 1;
input ulong NumFolds = 10;
input ulong MinNumVars = 3;
input ulong MaxNumVars = 5;
input long NumReplications = 1;

• NumKeptVars: Especifica o número desejado de características a manter em cada iteração do processo de seleção.

• NumFolds: Determina o número de partições (folds) a serem usadas para validação cruzada, facilitando uma avaliação robusta do desempenho do modelo.

• MinNumVars: Define o número mínimo de características que o conjunto final selecionado pode conter, garantindo que o modelo permaneça adequadamente equipado para previsão.

• MaxNumVars: Estabelece o número máximo de características permitido no conjunto final, prevenindo sobreajuste ao controlar a complexidade do modelo.

• NumReplications: Indica o número de iterações para o teste de permutação de Monte Carlo, aumentando a confiabilidade dos testes de significância realizados durante a seleção de características.

Uma vez que o método stepwiseSelection() é invocado, o processo de seleção passo a passo tem início. Esse método orquestra todo o algoritmo de seleção, implementando as estratégias discutidas anteriormente para identificar os preditores mais relevantes para o modelo de regressão linear-quadrática. A saída gerada pelo script StepWiseFeatureSelection_Demo.mq5 pode fornecer insights valiosos sobre como diferentes hiperparâmetros influenciam o processo de seleção de características. Vamos nos aprofundar nos vários aspectos da saída e como eles se relacionam com os parâmetros de entrada especificados.

Os componentes-chave da saída do algoritmo são:

1. Selected Feature Sets: A saída principal é o conjunto de características selecionadas pelo algoritmo após a execução da seleção passo a passo. Cada conjunto de características representa uma combinação de preditores considerados mais relevantes com base em sua contribuição para o desempenho do modelo.
2. Performance Metrics: Para cada iteração do processo de seleção, o script normalmente exibirá métricas de desempenho, como:
   
   •  Criterion Value: A soma dos erros quadráticos ou outro critério escolhido, fornecendo uma medida quantificável do ajuste do modelo.
   •  P-Values: Se o teste de permutação de Monte Carlo for empregado, a saída incluirá p-values indicando a probabilidade de que as melhorias de desempenho observadas se devam ao acaso.

Na execução inicial do script StepWiseFeatureSelection_Demo.mq5 com parâmetros padrão, preparamos o terreno para observar como o processo de seleção passo a passo funciona em um cenário restrito. Segue um detalhamento do que esperar da saída, a lógica por trás dessas expectativas e como os resultados se alinham com nossas observações.

Como nenhum teste MCP é especificado, a saída realmente será apenas uma única coluna com os valores do critério correspondentes a cada iteração. Isso refletirá o desempenho do modelo à medida que os preditores são adicionados. Espera-se que os valores do critério aumentem a cada iteração. Isso indica que o desempenho do modelo está melhorando à medida que preditores relevantes são adicionados. O algoritmo seleciona estrategicamente características que aumentam a precisão preditiva, impulsionando assim o critério para cima. Eventualmente, à medida que os preditores relevantes são identificados, o critério atingirá um valor ótimo (neste caso, 1). Isso sugere que o modelo incorporou com sucesso os preditores mais informativos e está desempenhando o melhor possível, dadas as restrições do modelo.

MM      0       20:20:28.754    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 
QM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
KG      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
QH      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
FI      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
FM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
PM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 1
KR      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || Column Indices
ED      0       21:05:21.067    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 6
NO      0       21:05:21.089    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 4 6
RG      0       21:05:21.122    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 4 5 6
HH      0       21:05:21.170    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0 4 5 6
GL      0       21:05:21.240    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

No log de saída, cada iteração exibirá o valor atual do critério após a avaliação dos preditores selecionados. A tendência de aumento fornecerá uma visão clara de como cada adição de característica contribui para o desempenho do modelo. A saída também deve indicar o motivo da finalização, que provavelmente mencionará que características adicionais não levaram a uma melhora no desempenho, confirmando o processo de tomada de decisão do algoritmo em tempo real. Isso é possibilitado pelo parâmetro que especifica o número mínimo de preditores permitidos em um conjunto de características.

Em uma execução subsequente do script StepWiseFeatureSelection_Demo.mq5, introduzimos um teste de permutação de Monte Carlo (MCP) com 100 permutações, mantendo os valores padrão para os demais parâmetros. Esse ajuste enriquece significativamente a saída, fornecendo percepções mais profundas sobre o processo de seleção de características.

Com o teste MCP ativado, a saída agora consistirá em várias colunas. Cada linha corresponderá a uma iteração, exibindo o valor do critério, a probabilidade de ocorrência ao acaso e a probabilidade de melhoria espúria. Um valor de p baixo (tipicamente ≤ 0,05) indica que o desempenho observado provavelmente não se deve ao acaso, apoiando a inclusão da característica correspondente.

Os dois valores de p apresentados guiarão os usuários na avaliação da confiabilidade dos preditores selecionados.

RI      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
LK      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
RD      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
EM      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
EQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
OQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
PI      0       21:10:57.101    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
RD      0       21:10:58.851    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 0.01000000 0.01000000   6
EI      0       21:11:01.243    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 0.01000000 0.01000000   4 6
KM      0       21:11:04.482    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 0.01000000 0.01000000   4 5 6
FP      0       21:11:09.151    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
CI      0       21:11:09.214    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

Essa execução, enriquecida pela inclusão de um teste de permutação de Monte Carlo, fornece uma saída mais rica e informativa. As múltiplas colunas permitem que os usuários tomem decisões mais informadas sobre o conjunto ótimo de características, baseando-se tanto nos critérios de desempenho quanto na significância estatística. Como resultado, os usuários podem identificar com confiança quais preditores devem ser mantidos no modelo final, guiados por altos valores de critério e baixos valores de p.

LL      0       07:22:46.657    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
GH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
ID      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 5
FH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 10
JO      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 10
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
LG      0       07:22:47.303    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26726680 0.01000000 0.01000000   6
LJ      0       07:22:48.153    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.56836766 0.01000000 0.01000000   4 6
FH      0       07:22:49.518    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.74542884 0.01000000 0.01000000   4 5 6
NM      0       07:22:51.488    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
KQ      0       07:22:54.163    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.71000000   0 1 4 5 6
JF      0       07:22:57.793    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.85000000   0 1 2 4 5 6
DD      0       07:23:02.436    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.94000000   0 1 2 3 4 5 6
MK      0       07:23:08.007    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7
DH      0       07:23:13.842    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8
HO      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8 9
PL      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 

Na execução final do script StepWiseFeatureSelection_Demo.mq5, o foco está em expandir o escopo do processo de seleção de características, aumentando o parâmetro MinNumVars para permitir um mínimo de 10 preditores. Permitir mais preditores no subconjunto final possibilitará que o algoritmo avalie combinações maiores de características, potencialmente revelando interações ou relações não lineares que um subconjunto menor poderia perder. Embora aumentar o número mínimo de preditores permita uma busca mais extensa, é importante observar que isso também levará a um tempo de execução maior do algoritmo. A complexidade adicional de avaliar conjuntos maiores de características exige mais recursos computacionais e tempo.

As verificações internas do algoritmo garantem que, se MinNumVars ou MaxNumVars forem definidos com valores que excedam o número total de preditores candidatos (neste caso, 10), eles serão automaticamente ajustados para corresponder ao número disponível de preditores no conjunto de dados. Essa proteção evita erros de configuração que poderiam levar a problemas de execução ou a um comportamento inadequado da seleção de características. Ao modificar o parâmetro MinNumVars, os usuários podem personalizar o processo de seleção passo a passo para explorar uma gama mais ampla de características, potencialmente levando à descoberta de conjuntos de preditores mais informativos. Essa flexibilidade aumenta a usabilidade do algoritmo, permitindo que os profissionais adaptem o processo de seleção às características específicas de seus conjuntos de dados e objetivos de análise.

O tempo de execução do algoritmo depende dos hiperparâmetros selecionados. O teste de permutação de Monte Carlo pode desacelerar significativamente o processo, especialmente à medida que o número de permutações aumenta. Cada permutação exige uma avaliação completa do modelo, o que aumenta o número total de cálculos realizados. Assim, embora mais permutações possam aumentar a robustez dos resultados de significância estatística, elas também exigem mais tempo de processamento.

Fora do teste MCP, o próximo parâmetro que pode impactar o tempo de execução do algoritmo é o número de partições especificadas para validação cruzada. A validação cruzada envolve particionar o conjunto de dados em vários subconjuntos e treinar e testar repetidamente o modelo nesses diferentes subconjuntos. À medida que o número de partições aumenta, o algoritmo deve realizar mais iterações de treinamento e avaliação. Isso é particularmente demorado em conjuntos de dados maiores, já que cada partição requer um ajuste e avaliação completos do modelo.

Por fim, deve-se ter cuidado ao selecionar o número mínimo e máximo de preditores permitidos no modelo final. Com mais preditores sendo considerados para inclusão, o algoritmo precisa avaliar mais combinações durante o processo de seleção de características, levando a um aumento no número de ciclos de busca necessários para descobrir os subconjuntos ótimos. Dadas as compensações envolvidas nesses parâmetros, é importante que os profissionais selecionem os hiperparâmetros de forma criteriosa com base em seu caso de uso específico.

Conclusão

Neste artigo, exploramos um algoritmo aprimorado de seleção de características passo a passo, projetado para otimizar a identificação de características preditivas a partir de um conjunto maior de variáveis. Amparado por validação cruzada e testes opcionais de permutação de Monte Carlo, o algoritmo fornece uma estrutura que aborda as limitações dos métodos passo a passo tradicionais, permitindo a seleção de subconjuntos de características que maximizam o desempenho preditivo ao mesmo tempo que minimizam o risco de sobreajuste.

Examinamos a importância do ajuste de hiperparâmetros no equilíbrio entre eficiência computacional e confiabilidade estatística, destacando como parâmetros como o número de partições para validação cruzada, o número de permutações para testes de significância e as restrições sobre o número mínimo e máximo de preditores podem impactar significativamente o tempo de execução do algoritmo.

A demonstração prática usando o script StepWiseFeatureSelection_Demo.mq5 ilustrou como o algoritmo pode ser aplicado de forma eficaz a conjuntos de dados reais, gerando percepções sobre a significância dos subconjuntos de características selecionados. Em conclusão, o método proposto não apenas aprimora o processo de seleção de características, mas também pode capacitar os profissionais a tomar decisões informadas sobre a construção de modelos. Todo o código referenciado no texto está anexado nos arquivos abaixo.

Arquivo	Descrição
MQL5/include/np.mqh	Contém a definição de funções utilitárias para manipulação de matrizes e vetores.
MQL5/include/OLS.mqh	Arquivo de cabeçalho para a classe OLS, que implementa regressão por mínimos quadrados ordinários (Ordinary Least Squares).
MQL5/include/stepwise.mqh	Arquivo de cabeçalho para a classe CStepwisebase, que implementa um método aprimorado de seleção de características passo a passo.
MQL5/scripts/StepWiseFeatureSelection_Demo.mq5	Um script que aplica a classe CStepwisebase para realizar seleção passo a passo de características em um conjunto arbitrário de dados.