Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 29): Taxas de aprendizado e perceptrons multicamadas

Introdução

Estamos finalizando nossa revisão sobre diferentes formatos de taxa de aprendizado aplicados ao desempenho do EA, analisando a taxa de aprendizado adaptativa e a taxa de aprendizado de ciclo único. O formato deste artigo seguirá a abordagem usada no artigo anterior: os relatórios de teste serão organizados em seções separadas para cada formato, em vez de serem colocados no final do artigo.

Antes de entrarmos no assunto, gostaria de mencionar outros aspectos importantes do aprendizado de máquina que podem impactar significativamente a eficácia do modelo. Um desses aspectos é a normalização em lote dos dados de entrada. Já abordei esse tema em artigos anteriores, explicando sua importância. No entanto, em nosso próximo artigo, aprofundaremos essa questão. Por enquanto, ao projetar o regime e o formato da rede, a normalização em lote é considerada juntamente com os algoritmos de ativação que a rede ou modelo utilizará. Até agora, usamos a ativação soft plus, que tende a produzir resultados não normalizados. Diferentemente das ativações TANH ou Sigmoid, que geram resultados nos intervalos de -1,0 a +1,0 e de 0,0 a 1,0, respectivamente, a soft plus pode frequentemente produzir valores que falham na verificação da validade dos números reais, tornando o processo de aprendizado e previsão inválido.

Portanto, como preparação para o próximo artigo, estamos fazendo algumas mudanças não apenas nos algoritmos de ativação utilizados em nossas redes, mas também no símbolo Forex testado. Adotaremos o algoritmo de ativação Sigmoid para todas as ativações de camada. Além disso, o par de teste Forex terá seus dados de entrada (que, neste caso, ainda são preços brutos, pois não estamos aplicando normalização em lote) no intervalo de 0,0 a 1,0. Poucos pares de moedas apresentaram preços dentro desse intervalo durante nosso período de teste (2023), mas o par NZDUSD está dentro desse intervalo, então iremos utilizá-lo.

Isso torna inviável a comparação dos resultados de desempenho com os apresentados no artigo anterior, pois a base foi alterada. No entanto, com essa nova rede, algoritmo de ativação e par de moedas, os formatos de taxa de aprendizado analisados no artigo anterior ainda podem ser testados pelo leitor para que ele próprio possa obter uma comparação mais significativa ao buscar seu próprio método de taxa de aprendizado. Além disso, os resultados dos testes apresentados aqui — assim como, frequentemente, neste tipo de artigo — não são obtidos nas melhores condições, o que já era esperado. Eles são apresentados apenas para fins informativos, cabendo ao leitor ajustar com precisão os dados de entrada do EA para alcançar o melhor resultado, utilizando não apenas dados históricos de alta qualidade, mas também, idealmente, realizando um teste em conta demo após o período de teste da estratégia.

Assim, o artigo demonstra apenas o seu potencial. A taxa de aprendizado é um parâmetro extremamente sensível ao desempenho, como ficou evidente nas variações dos resultados dos testes apresentados no artigo anterior. A taxa de aprendizado adaptável foi desenvolvida para solucionar o problema do excesso de parâmetros necessários para definir a taxa ideal para o modelo. É importante ressaltar que a taxa de aprendizado, por si só, é apenas um meio para se alcançar os pesos e vieses ideais da rede. Por isso, ao utilizar esses métodos, é recomendável evitar o uso de parâmetros adicionais, como o grau do polinômio discutido no artigo anterior ou o limite mínimo da taxa de aprendizado. Para minimizar a parametrização, o aprendizado adaptável gera uma taxa de aprendizado para cada parâmetro da camada com base no seu gradiente de aprendizado. Como resultado, praticamente todos os parâmetros possuem sua própria taxa de aprendizado, embora os dados de entrada necessários sejam mínimos. Existem quatro formatos amplamente utilizados de taxas de aprendizado ajustáveis: gradiente adaptativo, valor médio quadrático adaptativo, valor médio exponencial adaptativo e delta adaptativa. Vamos analisar cada um deles separadamente.

Gradiente adaptativo

Esse é provavelmente o formato mais simples entre as taxas de aprendizado adaptáveis. No entanto, ele ainda mantém uma taxa ajustável para cada parâmetro em todas as camadas, apesar de haver apenas um sinal de entrada: a taxa de aprendizado inicial. A implementação da taxa de aprendizado baseada em parâmetros exige configurações que se estendem à nossa classe pai Expert, além da classe de sinal personalizada, conforme discutido no artigo anterior sobre taxas de aprendizado. Isso ocorre porque os gradientes de aprendizado, que servem como dados de entrada para definir a taxa de aprendizado, estão acessíveis apenas a partir da interface da classe da rede pai. Podemos modificar a classe e torná-la acessível, mas, considerando a necessidade de configuração adicional (em que potencialmente cada peso e viés da camada pode ter sua própria taxa de aprendizado), a chamada da propagação reversa pode se tornar menos eficiente. Ao calcular cada taxa de aprendizado individualmente durante o treinamento, a rede se ajusta para operar quase com a mesma eficiência que ao utilizar uma única taxa para todos os parâmetros. Isso acontece porque a taxa de aprendizado calculada é aplicada imediatamente ao parâmetro específico, em vez de primeiro criar uma estrutura especial para armazenar as novas taxas de aprendizado de todos os parâmetros, executar um processo iterativo para calcular cada taxa de aprendizado separadamente e, por fim, aplicá-las individualmente. No segundo caso, o código não se tornaria necessariamente mais complexo, mas exigiria cálculos mais intensivos. No entanto, antes de qualquer coisa, fazemos modificações na classe de rede pai, introduzindo dois parâmetros de vetor: adaptive_gradients e adaptive_deltas, conforme mostrado na nova interface da classe abaixo:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
enum ENUM_ADAPTIVE
{  ADAPTIVE_NONE = -1,
   ADAPTIVE_GRAD = 0,
   ADAPTIVE_RMS = 1,
   ADAPTIVE_ME = 2,
   ADAPTIVE_DELTA = 3,
};
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmlp
{
protected:
   matrix            weights[];
   vector            biases[];
   
   vector            adaptive_gradients[];
   vector            adaptive_deltas[];
   
....

   bool              validated;
   
   void              AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   void              AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs);
   
public:
   
...

   void              Forward();
   void              Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9);

....

   void              ~Cmlp(void) { };
};

Após as declarações necessárias na interface da classe, precisamos fazer mudanças significativas na função de propagação reversa Backward. A principal alteração envolve a adição de parâmetros de entrada e a verificação do tipo apropriado de taxa de aprendizado. Apenas dois parâmetros são adicionados à função Backward – AdaptiveType e DecayRate. AdaptiveType representa um dos quatro tipos de taxa de aprendizado adaptável. Nossa rede ainda permite a opção de não utilizar taxas de aprendizado adaptáveis, por isso o valor padrão desse parâmetro é ADAPTIVE_NONE. Além disso, os três próximos formatos de taxa de aprendizado adaptável, que discutiremos a seguir, exigem uma taxa de decaimento. Assim, o terceiro e último parâmetro de entrada da nossa função de propagação reversa será esse valor. Como os dois parâmetros anteriores têm valores padrão atribuídos, esse também recebe um valor padrão.

Nesta função, as principais mudanças ocorrem em dois "pontos de aprendizado": onde atualizamos os pesos e vieses da saída e na parte escalável, onde atualizamos os pesos e os vieses ocultos de cada camada oculta, caso existam. Essas partes são separadas porque a inclusão de camadas ocultas é opcional, não sendo obrigatória na construção da rede. A rede é escalável porque atualiza todas as camadas ocultas simultaneamente, independentemente de sua quantidade. Assim, as mudanças feitas na propagação reversa da rede anterior visam verificar se o aprendizado adaptável está sendo utilizado em cada um desses pontos. Existem quatro tipos de taxa de aprendizado adaptável, todos apresentados abaixo para uma visão completa. Nosso primeiro ponto é apresentado da seguinte forma:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   vector _output_error = target - output;
   vector _output_gradients;
   _output_gradients.Init(output.Size());
   for (int i = 0; i < int(output.Size()); i++)
   {  _output_gradients[i] = _output_error[i] * ActivationDerivative(output[i]);
   }
// Update output layer weights and biases
   if(AdaptiveType == ADAPTIVE_NONE)
   {  for (int i = 0; i < int(output.Size()); i++)
      {  for (int j = 0; j < int(weights[hidden_layers].Cols()); j++)
         {  weights[hidden_layers][i][j] += LearningRate * _output_gradients[i] * hidden_outputs[hidden_layers - 1][j];
         }
         biases[hidden_layers][i] += LearningRate * _output_gradients[i];
      }
   }
// Adaptive updates
   else if(AdaptiveType != ADAPTIVE_NONE)
   {  if(AdaptiveType == ADAPTIVE_GRAD)
      {  AdaptiveGradientUpdate(LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_RMS)
      {  AdaptiveRMSUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_ME)
      {  AdaptiveMEUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
      else if(AdaptiveType == ADAPTIVE_DELTA)
      {  AdaptiveDeltaUpdate(DecayRate, LearningRate, hidden_layers, _output_gradients, hidden_outputs[hidden_layers - 1]);
      }
   }
// Calculate hidden layer gradients
   
...

}

Da mesma forma, as mudanças na atualização dos pesos ocultos e vieses ocultos são as seguintes:

//+------------------------------------------------------------------+
//| Backward pass through the neural network to update weights       |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Cmlp::Backward(double LearningRate = 0.1, ENUM_ADAPTIVE AdaptiveType = ADAPTIVE_NONE, double DecayRate = 0.9)
{  if(!validated)
   {  printf(__FUNCSIG__ + " invalid network settings! ");
      return;
   }
// Calculate output layer gradients
   
...

// Calculate hidden layer gradients
   vector _hidden_gradients[];
   ArrayResize(_hidden_gradients, hidden_layers);
   for(int h = hidden_layers - 1; h >= 0;  h--)
   {  vector _hidden_target;
      _hidden_target.Init(hidden_outputs[h].Size());
      _hidden_target.Fill(0.0);
      _hidden_gradients[h].Init(hidden_outputs[h].Size());
      if(h == hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(target.Size()); i++)
            {  if(weights[h + 1][i][j] != 0.0)
               {  _sum += (target[i] / weights[h + 1][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      else if(h < hidden_layers - 1)
      {  for(int j = 0; j < int(hidden_outputs[h].Size()); j++)
         {  double _sum = 0.0;
            for(int i = 0; i < int(hidden_outputs[h + 1].Size()); i++)
            {  if(weights[h][i][j] != 0.0)
               {  _sum += (hidden_outputs[h + 1][i] / weights[h][i][j]);
               }
            }
            _hidden_target[j] = ActivationDerivative(_sum - biases[h][j]);
         }
      }
      vector _hidden_error = _hidden_target - hidden_outputs[h];
      for (int i = 0; i < int(_hidden_target.Size()); i++)
      {  _hidden_gradients[h][i] = _hidden_error[i] * ActivationDerivative(hidden_outputs[h][i]);
      }
   }
// Adaptive updates
   if(AdaptiveType != ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  vector _outputs = inputs;
         if(h > 0)
         {  _outputs = hidden_outputs[h - 1];
         }
         if(AdaptiveType == ADAPTIVE_GRAD)
         {  AdaptiveGradientUpdate(LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_RMS)
         {  AdaptiveRMSUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_ME)
         {  AdaptiveMEUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
         else if(AdaptiveType == ADAPTIVE_DELTA)
         {  AdaptiveDeltaUpdate(DecayRate, LearningRate, h, _hidden_gradients[h], _outputs);
         }
      }
   }
// Update hidden layer weights and biases
   else if(AdaptiveType == ADAPTIVE_NONE)
   {  for(int h = hidden_layers - 1; h >= 0;  h--)
      {  for (int i = 0; i < int(weights[h].Rows()); i++)
         {  for (int j = 0; j < int(weights[h].Cols()); j++)
            {  if(h == 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * inputs[j];
               }
               else if(h > 0)
               {  weights[h][i][j] += LearningRate * _hidden_gradients[h][i] * hidden_outputs[h - 1][j];
               }
            }
            biases[h][i] += LearningRate * _hidden_gradients[h][i];
         }
      }
   }
}

Todas as funções mencionadas acima nessas modificações serão detalhadas nas respectivas seções. A implementação da função de atualização do gradiente adaptativo é a seguinte:

//+------------------------------------------------------------------+
// Adaptive Gradient Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveGradientUpdate(double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (Gradients[i] * Gradients[i]);
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

O vetor de matriz de gradientes adaptáveis adicionado acumula os quadrados dos valores dos gradientes para cada parâmetro em cada camada. Esses valores quadráticos, específicos para cada parâmetro, então reduzem a taxa de aprendizado em diferentes graus, dependendo do parâmetro envolvido e da sua trajetória de gradiente ao longo de todo o processo de aprendizado. A soma dos quadrados dos gradientes atua como denominador da taxa de aprendizado, de modo que, quanto maiores forem os gradientes, menor será a taxa de aprendizado.

Realizamos vários testes com taxas de aprendizado baseadas em gradientes adaptáveis, e aqui estão alguns dos nossos resultados:

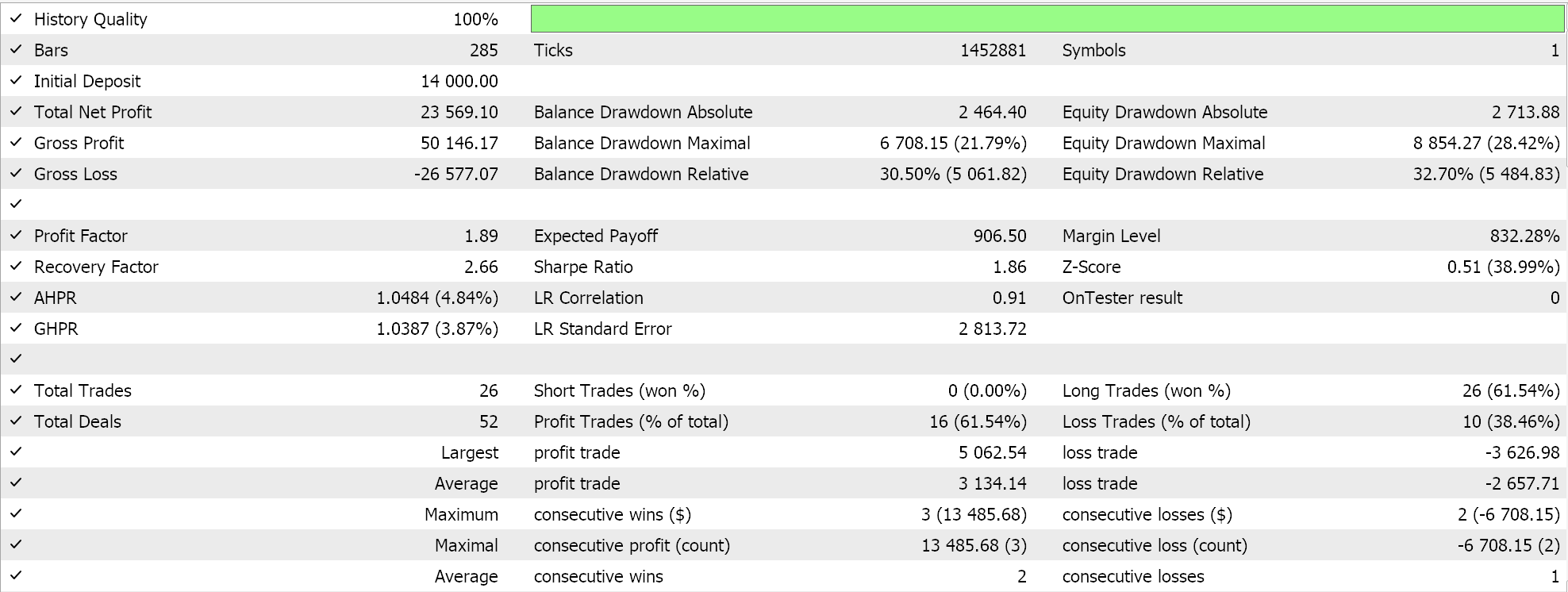
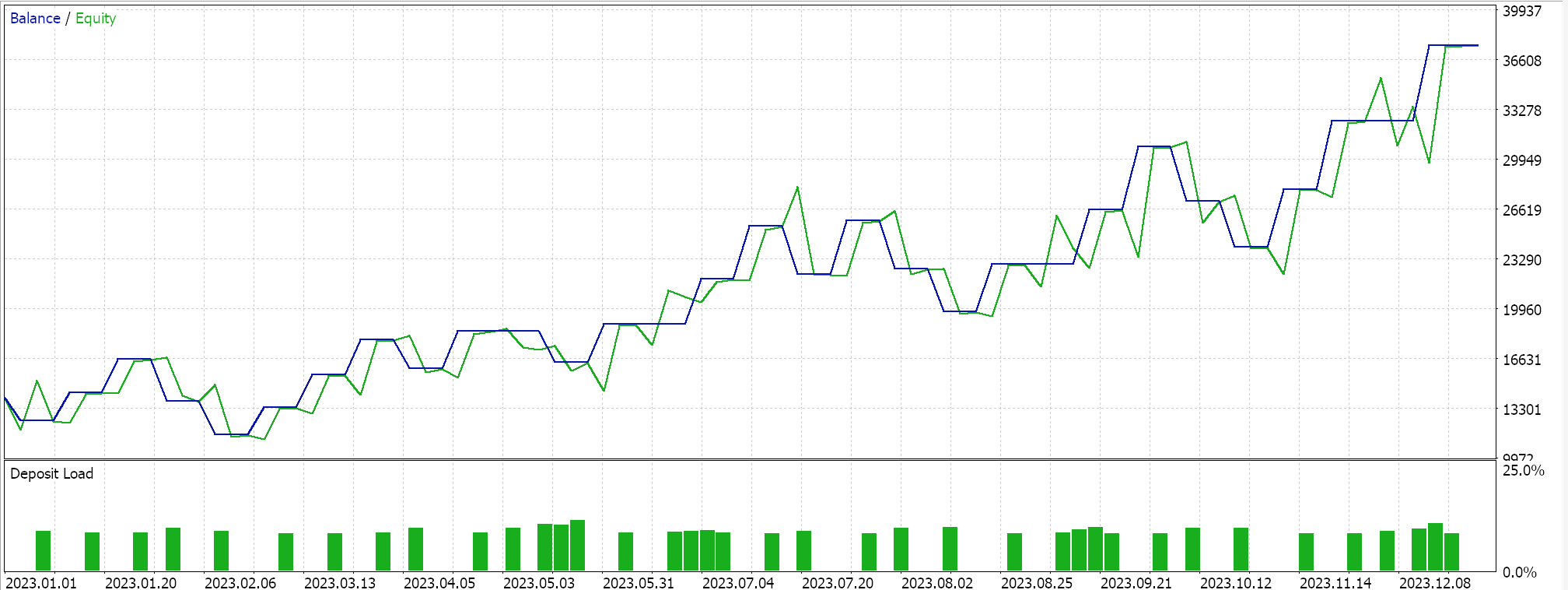
Esses testes foram realizados no ano de 2023, no timeframe diário, para o par de moedas NZDUSD. A escolha do NZDUSD é necessária para a normalização em lote, um tema que abordarei com mais detalhes no próximo artigo. No momento, como mencionado anteriormente, utilizamos a ativação Sigmoid, que mantém sua saída dentro do intervalo de 0,0 a 1,0. Isso se encaixa bem nos propósitos dos testes ao analisar as taxas de aprendizado ideais. Como cada parâmetro tem sua própria taxa de aprendizado, os pesos e vieses são atualizados usando a função de atualização do gradiente adaptativo, cujo código já foi apresentado acima.

Como nossos dados de entrada, que representam preços brutos, estão no intervalo de 0,0 a 1,0, e utilizamos a ativação Sigmoid, as saídas da rede também devem estar dentro desse intervalo. Como lidamos com preços brutos e utilizamos dados históricos de preços para alimentar e treinar nossa rede, podemos esperar que a rede preveja o próximo preço de fechamento. Fazemos tudo isso sem normalização em lote, o que é bastante arriscado, pois, mesmo que o sinal de saída esteja no intervalo desejado de 0,0 a 1,0, ele pode facilmente ficar acima do preço ask atual (ou abaixo do bid), gerando sinais constantes de compra ou venda. Isso já é evidente em nossos "resultados ideais" dos testes apresentados acima. De fato, realizei execuções em que tanto posições longas quanto curtas foram abertas, mas a ausência de normalização em lote continua sendo um fator preocupante. Para gerar valores de sinais ou condições a partir das funções de compra e venda dentro da classe de sinais personalizada, precisamos normalizar o preço previsto para que ele fique dentro de um intervalo inteiro de 0 a 100.

Como sempre, há várias formas de alcançar esse objetivo. No entanto, no nosso caso, basta compararmos o preço previsto com um conjunto de preços de entrada para obtermos um valor percentual double. Em seguida, convertê-lo para um número inteiro no intervalo de 0 a 100 nos fornece a condição de saída. Essa normalização é aplicada apenas nas funções de condição para operações longas e curtas, caso o preço previsto pela rede esteja acima ou abaixo do preço bid, respectivamente. Abaixo, apresentamos o código-fonte correspondente:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::LongCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output > m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalCMLP::ShortCondition(void)
{  int result = 0;
   double _mlp_output = 0.0;
   GetOutput(_mlp_output);
   m_symbol.Refresh();
   m_symbol.RefreshRates();
   if(_mlp_output < m_symbol.Bid())
   {  vector _scale;
      _scale.CopyRates(m_symbol.Name(), m_period, 8, 0, __MLP_INPUTS);
      result = int(round(100.0 * (fmin(_mlp_output, _scale.Max()) - _scale.Min()) / fmax(m_symbol.Point(), _scale.Max() - _scale.Min())));
   }
//printf(__FUNCSIG__ + " output is: %.5f, change is: %.5f, and result is: %i", _mlp_output, m_symbol.Bid()-_mlp_output, result);return(0);
   return(result);
}

A utilização desse código, incluído ao final do artigo, é feita montando o EA através do Assistente MQL5. Os guias necessários podem ser encontrados aqui e aqui.

Valor médio quadrático adaptativo

Esse formato de taxa de aprendizado introduz um parâmetro adicional para controlar a rápida redução da taxa, que geralmente ocorre quando se depara com grandes gradientes, pois eles se acumulam ao longo do processo. Esse parâmetro é a taxa de decaimento, já introduzida anteriormente como um dos novos parâmetros de entrada adicionais na função modificada de propagação reversa. No entanto, no artigo anterior, utilizamos a taxa de decaimento na taxa de aprendizado com decaimento por etapas, decaimento exponencial e decaimento inverso ao tempo, todos com propósitos semelhantes. Na nossa classe de sinais personalizados, há um parâmetro de entrada específico chamado "taxa de decaimento" (decay rate), que serve para todas essas finalidades, já que, em qualquer sessão de treinamento, apenas um formato de taxa de aprendizado pode ser escolhido. Dessa forma, a taxa de decaimento será ajustada de acordo com o tipo de taxa de aprendizado selecionado.

No entanto, dando continuidade ao tema das taxas de aprendizado adaptáveis, a propagação da média quadrática da raiz (RMS-prop) limita o acúmulo de gradientes históricos, o que pode se tornar um problema para os gradientes adaptáveis, pois eles reduzem drasticamente a velocidade do aprendizado, a ponto de, na prática, interrompê-lo. Isso ocorre devido à relação inversa entre os gradientes históricos e a taxa de aprendizado, como mencionado anteriormente. A inovação do RMS-prop está na desaceleração eficiente da queda da taxa de aprendizado por meio do fator de decaimento. Isso é alcançado da seguinte maneira:

//+------------------------------------------------------------------+
// Adaptive RMS Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveRMSUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] += (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (MathSqrt(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Outro problema dos gradientes adaptáveis é que, ao trabalhar com dados não estacionários, a distribuição subjacente e as características dos dados mudam com o tempo. Dessa forma, mesmo ao utilizar um conjunto de treinamento fixo, os gradientes acumulados podem se tornar obsoletos e perder relevância, resultando em taxas de aprendizado não ideais. O RMS-prop assegura que os gradientes mais recentes tenham maior influência na taxa de aprendizado. Isso torna o processo de aprendizado mais adaptável e potencialmente mais útil em cenários particularmente relevantes para traders, como a previsão de séries temporais.

Além disso, em casos em que o treinamento ocorre em conjuntos de dados esparsos — como fora da nossa principal aplicação no mercado financeiro, incluindo processamento de linguagem natural ou sistemas de recomendação —, os gradientes adaptáveis podem reduzir excessivamente os gradientes ao lidar com características raramente utilizadas ou pontos de dados pouco frequentes. Dessa forma, o RMS-prop equilibra melhor o processo de aprendizado, mantendo a taxa de aprendizado relativamente alta por períodos mais longos, o que permite que essas redes (que podem ser úteis para traders em certas situações) ajustem seus pesos e vieses de maneira mais otimizada.

Por fim, os gradientes adaptáveis são altamente suscetíveis a dados ruidosos, pois estão positivamente correlacionados com o ruído. Assim, em situações em que os dados de treinamento não são devidamente filtrados para identificar esses valores atípicos, a rápida redução da taxa de aprendizado pode fazer com que a rede aprenda mais com o ruído do que com os dados principais ou ideais. O efeito suavizante do RMS-prop, por meio do coeficiente de decaimento, permite que a taxa de aprendizado "sobreviva" a picos extremos e continue influenciando efetivamente os pesos e vieses da rede quando os dados principais ou ideais aparecerem no conjunto de treinamento.

Realizamos várias execuções de teste com o aprendizado adaptativo RMS-prop. Abaixo está um exemplo dos resultados obtidos em nossos testes:

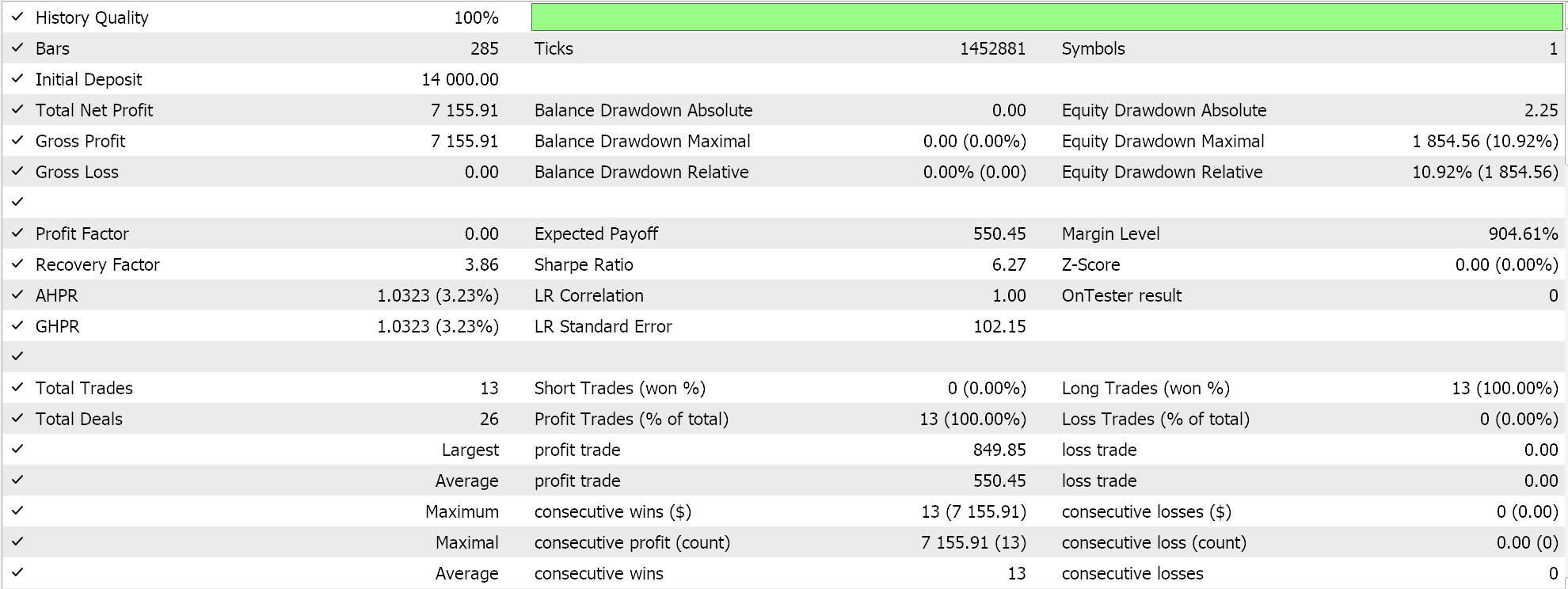
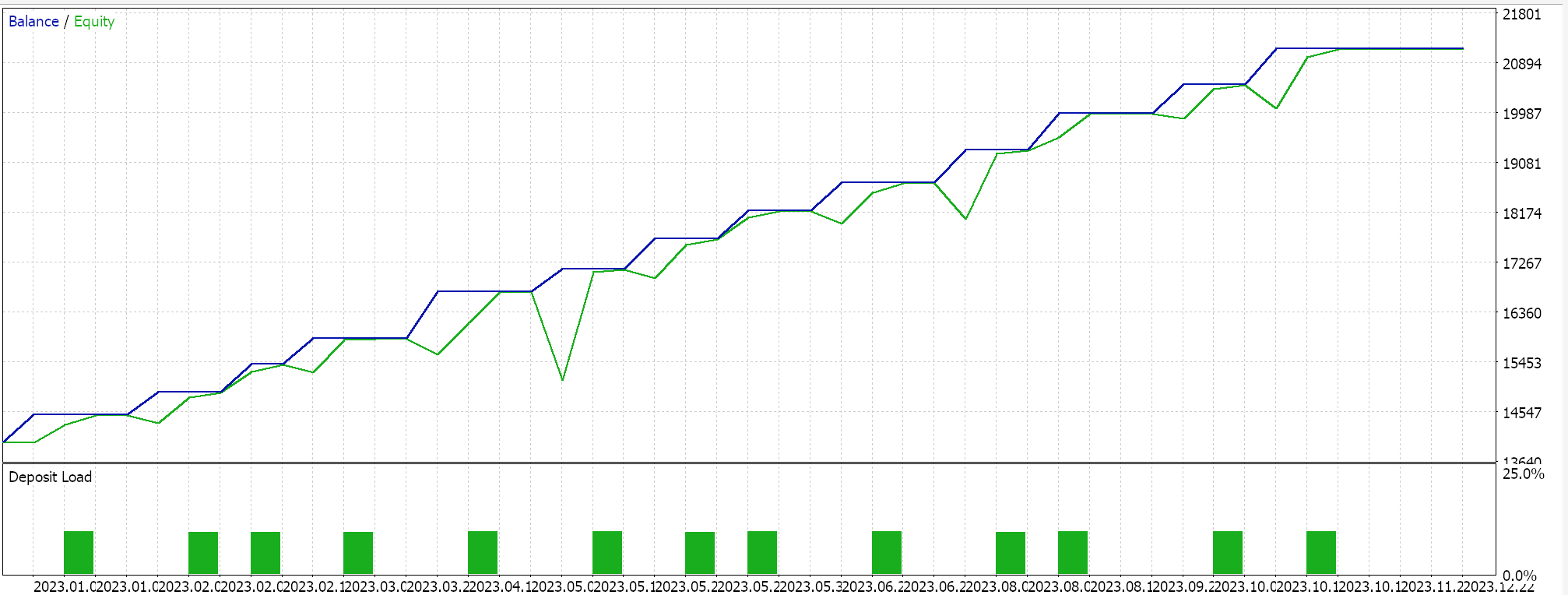
Como os dados de entrada da nossa rede não são normalizados em lote, de acordo com a função de ativação escolhida (Sigmoid em vez de Softmax), nossos resultados de teste estão distorcidos, levando apenas à abertura de posições longas, pois o preço previsto na saída sempre foi maior que o preço bid atual. Pode haver maneiras de normalizar o preço de saída para equilibrar a distribuição entre posições longas e curtas, o que nosso método não leva em consideração. No entanto, prefiro que comecemos com a normalização adequada dos dados de entrada em lote antes de considerarmos tais abordagens. Como mencionado anteriormente, esse tópico será explorado na próxima parte do artigo.

Estimativa adaptativa de momentos (ou média exponencial)

A Estimativa Adaptativa de Momentos (Adaptive Moment Estimation, ADAM) é outra variante das taxas de aprendizado adaptáveis, projetada para tornar abordagens como o RMS-prop ainda mais suaves, considerando tanto a média do gradiente quanto a variância do gradiente (momentum). No MQL5, isso é implementado da seguinte forma:

//+------------------------------------------------------------------+
// Adaptive Mean Exponential(ME) Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveMEUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _learning_rate = LearningRate / (fabs(adaptive_gradients[LayerIndex][i]) + __NON_ZERO);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_learning_rate * Gradients[i] * Outputs[j]);
      }
      //
      biases[LayerIndex][i] -= _learning_rate * Gradients[i];
   }
}

Como visto acima, as taxas de aprendizado RMS-prop representam um avanço em relação às taxas baseadas apenas nos gradientes, pois reduzem a velocidade de queda da taxa de aprendizado, o que pode trazer diversas vantagens, algumas já discutidas anteriormente. O ADAM segue essa mesma linha, especialmente quando aplicado a conjuntos de dados de alta dimensionalidade. À medida que os conjuntos de dados aumentam, cresce também o número de parâmetros no vetor de gradiente. Em cenários como reconhecimento de imagens e voz, considerar o momentum além da média do gradiente permite ajustar a taxa de aprendizado de forma mais eficiente em relação ao conjunto de dados, em comparação ao uso apenas da média. Dependendo da arquitetura da rede, esse tipo de cenário de alta dimensionalidade também pode ocorrer na previsão de séries temporais financeiras.

A convergência relativamente instável e lenta ao utilizar apenas a média quadrática dos gradientes torna o RMS-prop menos confiável para dados ruidosos em comparação com o ADAM. A combinação da média quadrática com a variância proporciona um processo de convergência mais suave, confiável, estável e rápido. Gradientes esparsos em sistemas de processamento de linguagem natural e recomendações são tratados de forma mais eficaz pelo RMS-prop do que pelos gradientes adaptativos convencionais. No entanto, o ADAM apresenta um desempenho ainda melhor nesses casos, pois incorpora o momentum à taxa de aprendizado. Além disso, em cenários nos quais os parâmetros mudam frequentemente — como quando uma nova rede é inicializada com pesos e vieses aleatórios —, a dependência do RMS-prop na história recente dos gradientes pode resultar em atualizações excessivamente conservadoras. Já o ADAM, ao levar em conta o momentum, permite uma adaptação mais ágil nessas situações.

Por fim, ao lidar com objetivos não estacionários, em que a função alvo muda ao longo do tempo, o RMS-prop, apesar de utilizar a média dos gradientes, pode não se adaptar tão bem quanto o ADAM. Consideremos, por exemplo, uma situação em que sua rede foi modelada para prever preços de imóveis e processa dados de entrada, como o tamanho da casa, o número de quartos e a localização. A função alvo usada em nossa rede de perceptron multicamadas (MLP network) durante a propagação reversa é simplesmente a diferença vetorial entre o valor real e a previsão. No entanto, essa função-alvo pode assumir diferentes formas, como o erro quadrático médio (MSE), cuja fórmula, nesta situação, seria a seguinte:

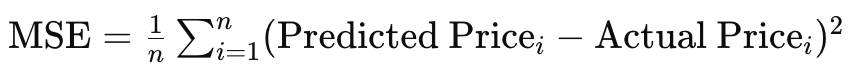
onde:

• n - número de imóveis na amostra de dados
• MSE - erro quadrático médio

Essa será a função de erro utilizada na propagação reversa, cujo valor diminuirá ao longo do tempo à medida que a rede aprende, atualizando seus pesos e vieses correspondentemente. Valores menores de MSE indicam um melhor desempenho da rede. Agora, suponha que o mercado imobiliário analisado passe por uma mudança significativa, alterando drasticamente a relação entre as características da rede (dados de entrada) e os preços previstos. Um exemplo seria a construção de uma estação de metrô próxima à região dos imóveis estudados. Isso certamente modificaria o modelo de precificação dos imóveis naquela área, tornando a função-alvo menos útil para se adaptar a essas mudanças. Revisar a rede adicionando características mais relevantes (novas variáveis de entrada) poderia levar a um resultado mais otimizado, pois os pesos e vieses seriam atualizados. O ADAM lida melhor com essa transição ao reavaliar e atualizar o modelo da rede, pois o processo de atualização dos pesos leva em consideração o momentum.

Os resultados dos testes utilizando ADAM nos fornecem o seguinte relatório:

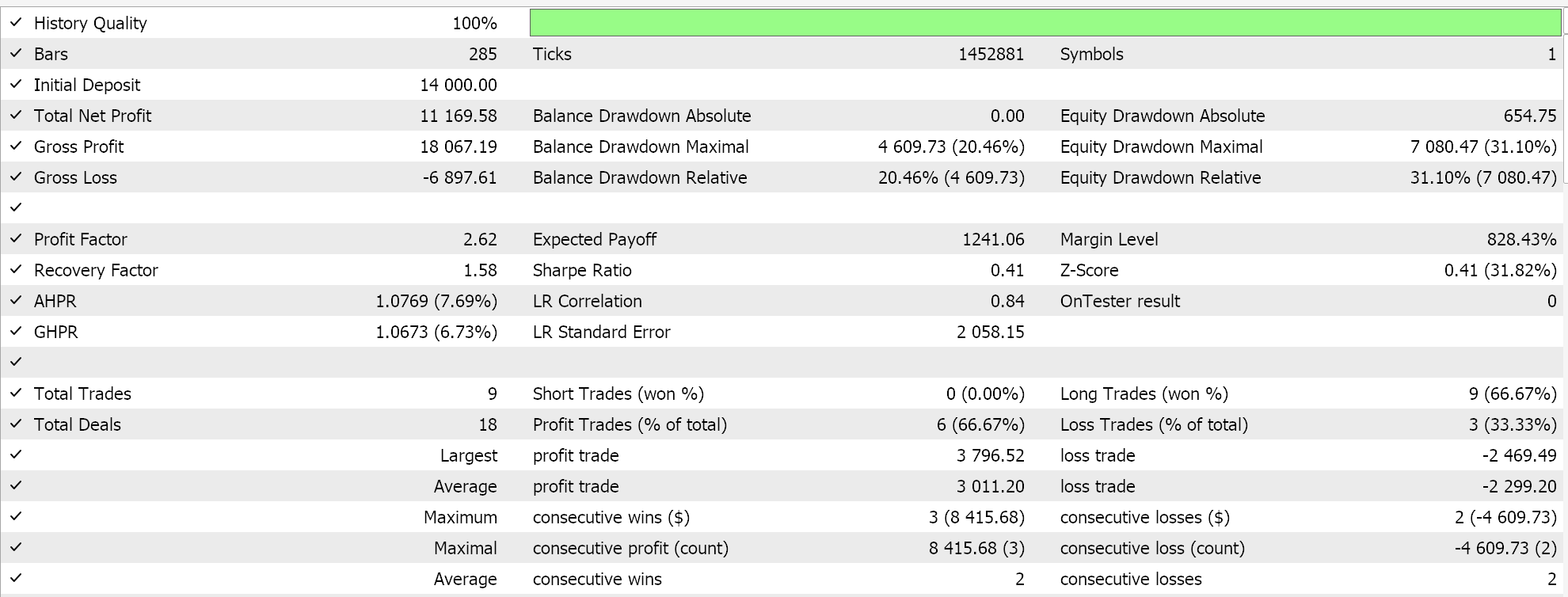
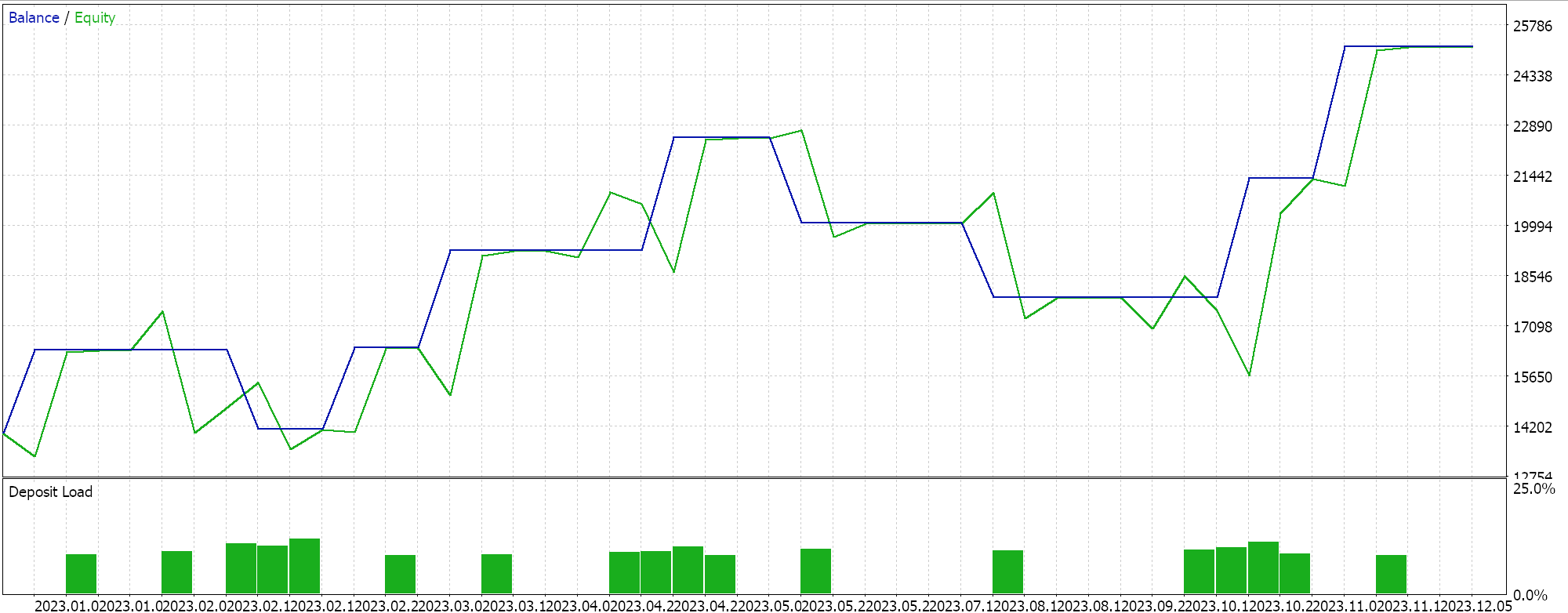
Essas não são as melhores nem as configurações ideais, mas servem apenas para demonstrar como a taxa de aprendizado ADAM é aplicada em uma rede MLP. No artigo anterior, utilizamos um par de redes GAN, enquanto aqui estamos empregando algo mais simples, mas ainda intuitivo: um perceptron multicamadas com apenas três camadas, configuradas como 5-8-1.

Delta adaptativa

Nossa última taxa de aprendizado adaptável é o ADADELTA, que, embora não exija novos parâmetros de entrada, facilita o ajuste ideal da taxa de aprendizado durante o treinamento. Sua fórmula é relativamente complexa, mas, em essência, além de considerar o acúmulo decrescente dos gradientes, também leva em conta o acúmulo decrescente dos pesos. No MQL5, isso é implementado da seguinte maneira:

//+------------------------------------------------------------------+
// Adaptive Delta Update function
//+------------------------------------------------------------------+
void Cmlp::AdaptiveDeltaUpdate(double DecayRate, double LearningRate, int LayerIndex, vector &Gradients, vector &Outputs)
{  for (int i = 0; i < int(weights[LayerIndex].Rows()); i++)
   {  adaptive_gradients[LayerIndex][i] = (DecayRate * adaptive_gradients[LayerIndex][i]) + ((1.0 - DecayRate)*(Gradients[i] * Gradients[i]));
      double _delta = (MathSqrt(adaptive_deltas[LayerIndex][i] + __NON_ZERO) / MathSqrt(adaptive_gradients[LayerIndex][i] + __NON_ZERO)) * Gradients[i];
      adaptive_deltas[LayerIndex][i] = (DecayRate * adaptive_deltas[LayerIndex][i]) + ((1.0 - DecayRate) * _delta * _delta);
      for (int j = 0; j < int(weights[LayerIndex].Cols()); j++)
      {  weights[LayerIndex][i][j] -= (_delta * Outputs[j]);
      }
      // Bias update with AdaDelta
      biases[LayerIndex][i] -= _delta;
   }
}

A maioria das vantagens da desaceleração mais controlada da taxa de aprendizado, mencionadas anteriormente para RMS-prop e ADAM, também se aplicam ao ADADELTA. Aqui, vale destacar um benefício adicional: o uso do buffer de deltas adaptáveis introduzido pelo ADADELTA na avaliação da taxa de aprendizado.

O ADAM usa médias móveis do quadrado da média do gradiente e da variância para ajustar dinamicamente as taxas de aprendizado de cada parâmetro. Embora essa abordagem represente uma melhoria significativa em relação ao RMS-prop, há casos em que a ênfase excessiva nos gradientes históricos pode resultar na ultrapassagem de mínimos, causando instabilidade no aprendizado, especialmente quando há ruído nos dados. A inclusão do buffer de atualizações quadráticas, chamado de "deltas adaptáveis", ajuda a equilibrar melhor as atualizações da taxa de aprendizado, pois se baseia tanto na magnitude dos gradientes recentes quanto na eficácia das últimas atualizações delta.

Ao monitorar as atualizações quadráticas, o ADADELTA ajusta dinamicamente o tamanho dos passos, considerando a eficiência recente dessas atualizações. Isso beneficia o processo de aprendizado, evitando que ele se torne excessivamente conservador, o que pode ocorrer quando os gradientes diminuem significativamente. Além disso, o acúmulo adicional das atualizações de peso fornece um mecanismo de normalização, utilizando a escala das últimas modificações. Assim, a capacidade do otimizador de se adaptar a variações no gradiente do modelo é aprimorada, o que é crucial em cenários nos quais os conjuntos de dados possuem distribuições não estacionárias ou gradientes altamente voláteis.

Outras inovações do ADADELTA incluem a redução da sensibilidade aos hiperparâmetros e a prevenção da diminuição excessiva da taxa de aprendizado. Os testes com ADADELTA em símbolos, períodos de teste e timeframes similares aos mencionados anteriormente apresentam resultados lucrativos diferentes. Abaixo está um dos relatórios:

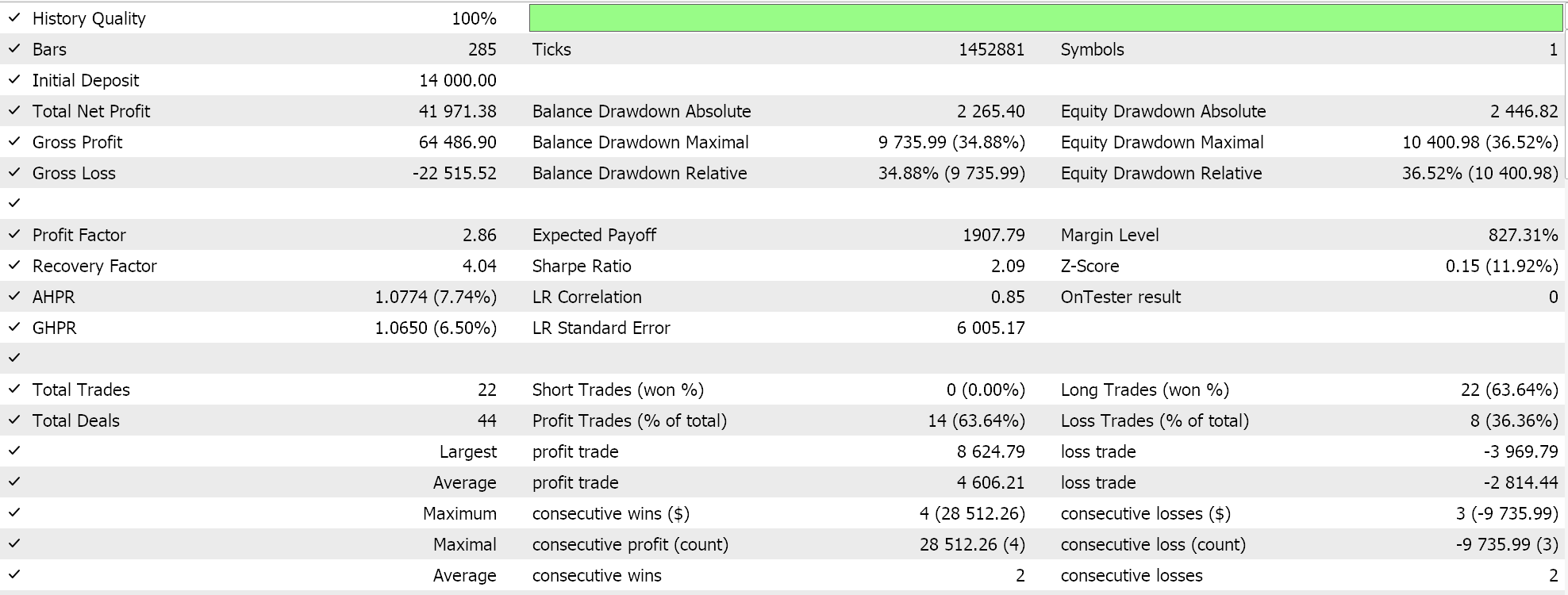
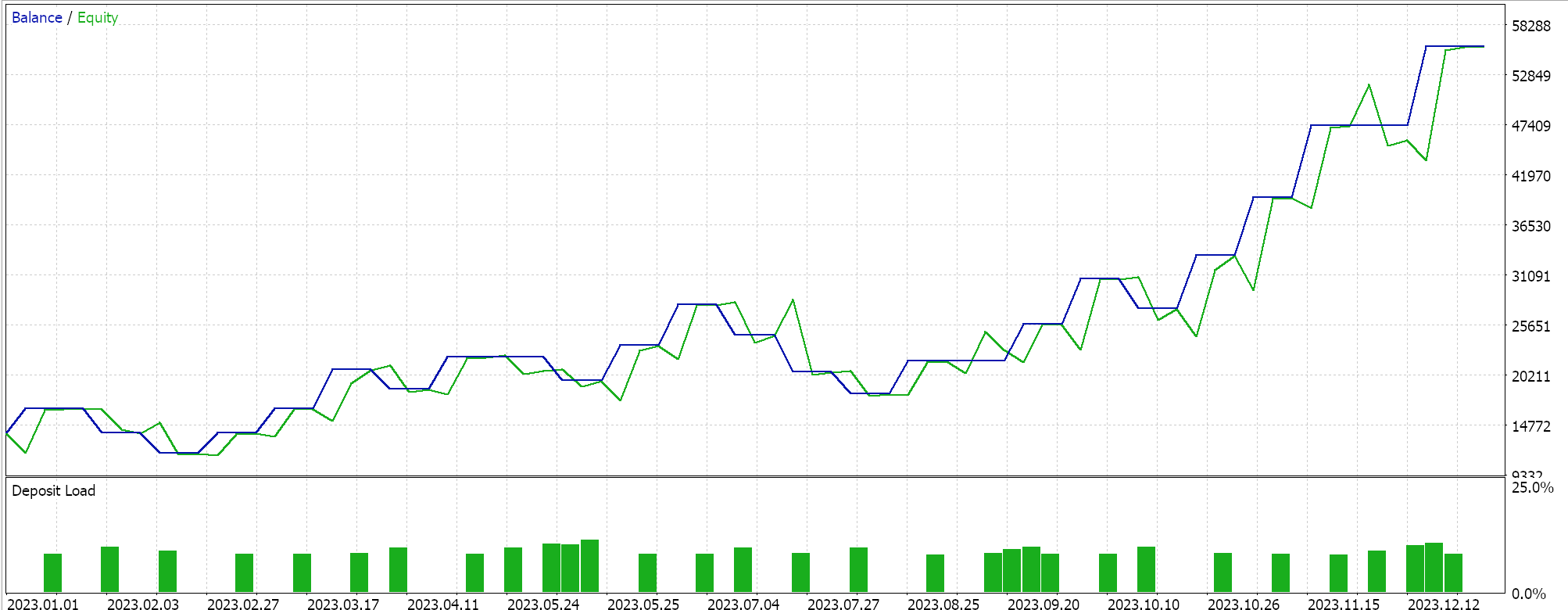
Um ciclo

Essa abordagem de ajuste da taxa de aprendizado não é tão complexa quanto os métodos adaptáveis e se assemelha mais ao formato de Cosine Annealing, que analisamos no artigo anterior. No entanto, é um pouco mais simples, pois a taxa de aprendizado inicialmente aumenta e, em seguida, diminui até o final da sessão de treinamento. Isso é implementado da seguinte forma:

      else if(m_learning_type == LEARNING_ONE_CYCLE)
      {  double _cycle_position = (double)((m_epochs - i) % (2 * m_epochs)) / (2.0 * m_epochs);
         if (_cycle_position <= 0.5)
         {  _learning_rate = m_min_learning_rate + (2.0 * _cycle_position * (m_learning_rate - m_min_learning_rate));
         }
         else
         {  _learning_rate = m_learning_rate - (2.0 * (_cycle_position - 0.5) * (m_learning_rate - m_min_learning_rate));
         }
      }

Assim, diferentemente dos métodos relativamente complexos analisados neste artigo, a taxa de aprendizado em um ciclo único inicialmente aumenta durante a chamada fase de aquecimento, atinge um pico e, em seguida, diminui na fase de resfriamento, que é a parte final do processo de treinamento. Com exceção do Cosine Annealing, a maioria das abordagens para taxa de aprendizado tende a começar com um valor alto e reduzi-lo gradativamente à medida que mais dados são processados.

A taxa de aprendizado em um ciclo único segue uma lógica oposta: ela começa no valor mínimo. Os valores mínimo e máximo da taxa de aprendizado são parâmetros de entrada predefinidos, enquanto o caminho ou a velocidade de variação da taxa de aprendizado dependem do número de épocas ou da duração da sessão de treinamento. Realizamos testes com essa abordagem, e um dos relatórios está apresentado abaixo:

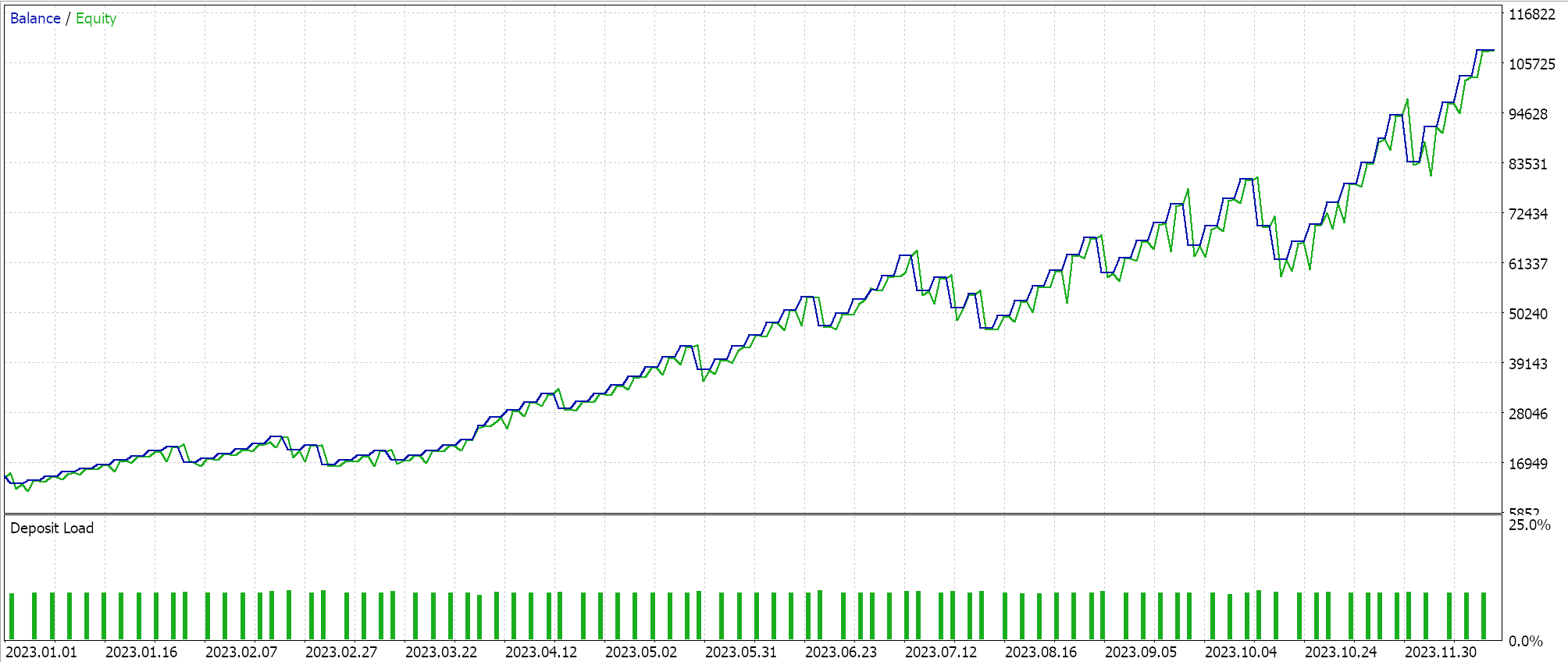
Os resultados acima indicam que, apesar da ausência de uma normalização em lote adequada, conseguimos finalmente abrir algumas posições curtas apenas ajustando a taxa de aprendizado. Isso ocorre ao prever preços brutos de símbolos (sem normalização em lote) e normalizar as condições de compra e venda da mesma forma que fizemos ao testar a taxa de aprendizado adaptável. Isso reforça a ideia de que a abordagem adotada para configurar e ajustar a taxa de aprendizado tem um impacto significativo no desempenho da rede neural.

Considerações finais

Em resumo, a taxa de aprendizado é um dos aspectos mais importantes e sensíveis dos algoritmos de aprendizado de máquina. Analisamos diferentes formas de implementação, focando nas inovações progressivas de cada abordagem, já que a maioria dos métodos foi projetada para aprimorar técnicas anteriores. Esse processo contínuo de aprimoramento das taxas de aprendizado certamente precisa de mais avanços. No entanto, métodos mais simples, como a taxa de aprendizado em um ciclo único, não devem ser subestimados, pois podem ser extremamente eficazes, como evidenciado por alguns dos resultados apresentados em nossos testes.