知っておくべきMQL5ウィザードのテクニック（第47回）：時間差分を用いた強化学習

はじめに

強化学習における時間差分(TD)学習の導入は、TDがモンテカルロ法やQ学習、SARSAといった他のアルゴリズムとどのように異なるのかを理解するための第一歩となります。本記事では、TD学習の特徴や仕組みを解き明かし、特にそのユニークな性質（エピソードが完了するのを待たずに、部分的な情報をもとに値の推定を段階的に更新できる点）に焦点を当てます。この特性により、TD学習は、環境が変動しやすく、学習方策を素早く更新する必要がある状況で特に有効なツールとなります。

前回の強化学習の記事では、モンテカルロ法について説明しました。この手法では、各エピソードの終了後に報酬情報を蓄積し、最終的に単一の更新をおこないます。 一方で、時間差分学習(TD)は、以前こちらとこちらで取り上げたQ学習やSARSAと同様に、部分的かつ未完のエピソードから逐次学習をおこなうアプローチです。

以下は、TD、Q学習、SARSAの主な違いを表にまとめたものです。

また、復習として、SARSAのようなオンポリシー型の更新を伴う状態-行動ペアの更新式は次のようになります。

	時間差分学習	Q学習	SARSA
価値の種類	状態価値V(s)	行動価値Q(s,a)	行動価値Q(s,a)
学習アプローチ	将来の状態価値の推定	オフポリシー	オンポリシー
方策タイプ	特定の方策に依存しない	最適な方策を学習する	現在の行動方策を学ぶ
ターゲットの更新	次の状態価値V(s′)	最大Q(s′,a′)	実際のQ(s′,a′)
探検	多くの場合、別の方策が必要	エージェントが最適なものを探すと仮定	より保守的
行動	次の状態の値に向かって移動	貪欲、最適なパスを優先	実際の探査経路に従う

これまでに説明した専門用語をまとめると、「オンポリシー（方策内）更新」 とは、更新される状態-行動ペアが現在のペアであり、それが必ずしも最適なペアやQ値が最も高いペアとは限らないことを意味します。一方、Q値が最も高い状態-行動ペアを更新する場合、それは「オフポリシー（方策外）」のアプローチとなります。MQL5では、これらの更新を次のように実行します。

//+------------------------------------------------------------------+
// Update using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q_SA-action from Q_SA-Map
   double _sa = Q_SA[transition_act][e_row[1]][e_col[1]];
   double _v = Q_V[e_row[1]][e_col[1]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[1]][e_col[1]]);
   }
   Q_V[e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[1]][e_col[1]]);
}

//+------------------------------------------------------------------+
// Update using Off-policy
//+------------------------------------------------------------------+
void Cql::SetOffPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 0 represents highest valued Q_SA-action from Q_SA-Map
//as determined from Action() function above.
   double _sa = Q_SA[transition_act][e_row[0]][e_col[0]];
   double _v = Q_V[e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[0]][e_col[0]]);
   }
   Q_V[e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[0]][e_col[0]]);
}

修正・改良した関数には、新たに「Q_V」オブジェクトを追加し、環境状態へのマッピングを明確にするために行列表現を採用しました。ただし、環境状態の座標は単一のインデックス整数としてマッピングできるため、ベクトルとして扱うことも可能です。従来のQマップは「Q_SA」と名前変更しました。これは、新しいオブジェクトが行動に依存しないQマップの値を追跡する（これがTDの主な特徴）ことを強調するためです。一方、旧Qマップを「Q_SA」とすることで、関数が呼び出されるたびに更新される状態-行動ペアの値であることを明確にしました。上記のMQL5の実装は、以下のTDの基本式（オンポリシー・オフポリシーの両方に対応）に基づいています。

ここで

• V (s)：現在の状態価値s
• V (s′)：次の状態価値s′
• α：学習率（現在の値をどれだけ調整するかを制御）
• r：行動を取った後に受け取る報酬
• γ：割引率（将来の報酬の重要性を決定）
• この式は、受け取った報酬と次の状態V (s′)の推定値に基づいて、状態V (s)の価値推定値を更新します。

また、復習として、SARSAのようなオンポリシー型の更新を伴う状態-行動ペアの更新式は次のようになります。

ここで

• Q (s, a)：現在の状態-行動ペアのQ値(s, a)
• Q (s′, a′)：次の状態-行動ペア（s′、a′）のQ値。ここでa′は、次の状態s′で現在の方策によって選択される行動
• α：学習率
• r：行動を起こした後に受け取る報酬
• γ：割引率

同様に、オフポリシー更新の計算式は次のようになります。

ここで

• Q (s, a)：現在の状態-行動ペアのQ値(s, a)
• max a′ ​Q (s′, a′)：すべての可能な行動a′における次の状態s′の最大Q値(s′で最善の行動が実行されるものと仮定)
• α：学習率
• r：行動を起こした後に受け取る報酬
• γ：割引率

最後の2つの式から、行動ごとの更新が次の行動選択に影響を与えることは明らかです。しかし、TDの更新ではすべての行動の値を統合し、それぞれの環境状態に割り当てるだけなので、このプロセスが次の行動にどのような影響を与えるかは明確ではありません。

そのため、TDを使用する場合には、追加のモデル（本ケースでは方策ニューラルネットワーク）を導入し、Actorの次の行動選択をガイドする必要があります。このモデルにはさまざまな形式が考えられますが、本記事ではシンプルな3層MLP（3-9-3構造）を採用します。このMLP（多層パーセプトロン）の出力層は確率分布を生成し、買い・売り・保有の3つの選択肢に対して確率を割り当てます。したがって、回帰モデルではなく分類モデルとなります。このクラスの宣言コードは、以下のようにカスタムシグナルクラスのインターフェイスで指定します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalTD   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   
public:
   void                          CSignalTD(void);
   void                          ~CSignalTD(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   int               GetOutput(Cql *QL, CNeuralNetwork &PN);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   CNeuralNetwork    POLICY_NETWORK_BUY,POLICY_NETWORK_SELL;
};

本カスタムシグナルクラスの完全なソースコードは、本記事の末尾に添付されており、MQL5ウィザードを用いてEAを生成するために使用できます。MQL5ウィザードの使用が初めての方は、ガイドをこちらとこちらでご参照ください。添付のソースコードを活用すれば、層の数やサイズを自由に変更し、MLPの設計をカスタマイズすることが可能です。本設計では、入力層（3ノード）はx軸環境座標、遷移値（Q_V行列の読み取り値）、y軸環境座標次の3つの値を入力として受け取るようになっています。ここでの遷移値は、オン・オフ両方の方策設定で更新されるQ_V行列から取得されます（詳細は前述のソースコードをご参照ください）。この遷移値の選択処理は、以下のように改良されたAction関数内で実行されます。

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   transition_value = Q_V[_next_row][_next_col];
   policy_history[1][0] = policy_history[0][0];
   policy_history[1][1] = policy_history[0][1];
   policy_history[1][2] = policy_history[0][2];
   policy_history[0][0] = _next_row;
   policy_history[0][1] = transition_value;
   policy_history[0][2] = _next_col;
   transition_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
   //if(transition_act!=1)printf(__FUNCSIG__+ " act is : %i ",transition_act);
}

したがって、本方策ネットワーク(MLP)における基本的な前提は、次に選択される行動は、現在の環境状態とそのQ値のみを基に決定される点にあります。これは、これまでのアプローチとは異なります。従来はマルコフ決定過程(MDP)を用いて、本記事内でQ_SAに改名したQマップ（添付コード）から適切な行動を選択していました。また、これまでメモリレスなMDPを採用し、最近の環境状態のシーケンスをバッファとして保持することで、意思決定に活用してきました。この環境シーケンスは、以下に再掲するletMarkov関数によって、次の環境状態の予測を提供します。

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

MDPによって次の状態を決定するプロセスは、TDでも同様におこなわれます。しかし、ここでの違いは、予測された次の状態座標のみを使って、次の行動を決定することはできないという点です。以前、Q_SA を使用していたときは、Actorが何をすべきかを知るために、次の状態座標に重み付けして最も高い確率の行動を読み取ることが重要でした。しかし、新たに導入したQ_Vは提供された状態座標の値を返すだけであり、Actorの次の行動を決定するための直接的な情報を持ちません。しかし、強化学習ループにおいて、次の行動の決定は極めて重要です。

そこで、新たに方策ネットワーク(MLP)を導入します。このMLPは3-9-3の構造で、9ユニットの隠れ層を1つ持ち、3つの入力（2つの環境座標とそのQ値）を受け取ります。そして、出力として3つの確率値のベクトルを生成し、それぞれ「買い」「売り」「保有」に対応します。このベクトル内で最も高いスコアを持つ行動が推奨されます。

TDのマクロ的な利点と目的

TDはモンテカルロ法よりも頻繁にQ値を更新します。変化の激しい金融市場において、このメリットは特に重要です。しかし、SARSAやQ学習と比べた場合の優位性は何でしょうか。いくつかの日常的な例を挙げて、この疑問に答えてみましょう。

定義上、TDとSARSA/Q学習の主な違いは、TDが「状態の価値」のみを学習・更新する、価値ベースの学習に重点を置いている一方、SARSAやQ学習は、状態と行動のペアを基に学習・更新をおこなう点です。

シナリオA

倉庫内に、多数の製品の在庫レベルを純粋に追跡する在庫管理システムがあるとします。このシステムの目的は、在庫レベルを管理し、製品の在庫不足や過剰在庫を防ぐことのみです。

この状況では、TDは状態-行動のペアではなく、状態の価値に重点を置くため、SARSAやQ学習よりも有利になります。 この場合、システムは特定の行動（各SKUの注文など）をすべて評価するのではなく、各状態の価値（例：全体の在庫レベル）を予測するだけで十分かもしれません。したがって、方策ネットワーク(MLP)を使わずに、TD学習は各製品のすべての発注パターンを計算することなく、状態（在庫レベル）の価値関数を更新できます。

さらに、在庫管理では、明確な報酬フィードバックを伴う突然の変化よりも、在庫が徐々に変化するケースが多くなります。TD学習は逐次的なフィードバックを扱うため、すべての状態-行動の結果を正確に把握するよりも、全体的な状態を捉えることが重要なスムーズな変化を伴う環境に適しています。最後に、より複雑な在庫管理（各在庫レベルに応じた適切な行動を決定する必要がある）など、状態-行動の組み合わせが膨大になる環境では、Q学習やSARSAも適用可能ですが、その分計算コストが増大します。一方、TDは計算コストが少ないため、このような問題には直面しません。

 

シナリオB

居住者の快適さを維持しつつ、エネルギー消費を最小限に抑えるために、暖房・換気・空調(HVAC)の設定を調整するスマートビルディングシステムを考えてみましょう。このシステムの目的は、短期的な利益と長期的な目標のバランスを取りながら、エネルギーコストを削減し、建物内の温度や空気の質を最適に保つことにあります。

この場合も、エネルギー消費レベルや居住者の快適性は、その数値に直接結びつく特定の行動を持たない絶対的な指標であるため、TDはSARSAやQ学習よりも適しています。このケースでは、短期報酬と長期報酬のバランスをとるために、2つの強化学習サイクルを同時に学習させ、それぞれを並行して予測することができます。また、TDの逐次更新はサイクルごとにおこなわれるため（モンテカルロのようにエピソード単位ではなく）、温度や占有率、空気の質などの環境条件が徐々に変化するこのスマートビルディングシステムに最適です。そのため、TDはシームレスな調整メカニズムを提供できます。

最後に、前述のように、SARSAやQ学習では、環境状態の過不足を修正するために特定の行動を決定する必要があるため、それに伴い追加の計算コストやメモリ使用量が発生します。  

 

シナリオC

交通流の予測と制御システムは、複数の交差点における渋滞を最小限に抑えることを目的としており、交通流の予測とそれに基づくシグナル機の調整をおこないます。これが、TDの3番目の使用例となります。この場合、TDはSARSAやQ学習と比較して有利です。なぜなら、主な関心は個々のシグナル機の動作を最適化することではなく、全体的な交通状態（例えば、混雑レベル）の理解と予測だからです。 TD学習を使用することで、システムは特定のシグナル変更の影響を学ぶのではなく、交通状態の全体的な「価値」を学習することができます。

交通は本質的に動的であり、日中を通して継続的に変化するため、TDの逐次更新方式が非常に適しています。モンテカルロ法のようにエピソードの完了を待ってから更新をおこなうのではなく、TDは随時更新が可能で、非常に適応性の高いアルゴリズムです。この場合、TDによる計算およびメモリの過負荷の軽減も重要な利点となります。特に、比較的小さな都市でも交通の交差点がどれほど相互に影響を及ぼし、絡み合っているかを考慮すると、TDの効果は大きくなります。交通流予測システムの実装において、計算およびメモリのコストは大きな要因となり、TDはその問題を解決するために大いに役立ちます。

シナリオD

製造業における予知保全は、これまで取り上げた強化学習の他のアルゴリズムと比較して、TDが最適なアルゴリズムであることを示す最終的な使用例です。 例えば、製造工場が機械のメンテナンス時期を予測し、ダウンタイムを回避することを目的とするケースを考えてみましょう。そして、スマートビルディングシステムと同様に、このシステムでは短期的な利益（メンテナンスコストの節約のために点検を遅らせること）と長期的な利益（故障の防止）とのバランスを取る必要があります。TD学習は、SARSAやQ学習のように特定の行動（修理や交換）を追跡するのではなく、部分的なフィードバックを元に、時間の経過とともに機械の全体的な健全性値を更新できるため、非常に適しています。

機械の劣化は徐々に進行するため、TDはこのようなケースにおいてより適切なアルゴリズムです。TDは、追加のリスクを避けるために長期間待機するのではなく、逐次的にセンサーデータを基に機械の健康状態を継続的に更新できます。また、複数の機械がある工場環境では、TD学習は各機械の状態や健全性に焦点を当て、各機械の状態と行動のペアを保存・更新する必要がないため、機械の数が増減しても効率的にスケーラブルです。

これらは金融取引や市場以外のいくつかのケースなので、これをカスタムシグナルクラスとして具体的にどのように適用できるかを考えてみましょう。

TDアルゴリズムを使用したカスタムシグナルクラスの構造化

TDを実装するために構築するカスタムシグナルクラスは、2つの追加クラスに依存します。強化学習のアルゴリズムなので、そのクラスの1つがCQLクラスです。このクラスはこれまでのすべての記事ですでに使用または参照されていますが、そのインターフェイスは以下で再度共有されます。

//+------------------------------------------------------------------+
//| Q_SA-Learning Class Interface.                                      |
//+------------------------------------------------------------------+
class Cql
{
protected:
   matrix            markov;
   void              LetMarkov(int OldRow, int OldCol, vector &E);

   vector            acts;
   matrix            environment;
   matrix            Q_SA[];
   matrix            Q_V;

public:
   void              Action(vector &E);
   void              Environment(vector &E_Row, vector &E_Col, vector &E);

   void              SetOffPolicy(double Reward, vector &E);
   void              SetOnPolicy(double Reward, vector &E);

   double            GetReward(double MaxProfit, double MaxLoss, double Float);
   vector            SetTarget(vector &Rewards, vector &TargetOutput);

   void              SetMarkov(int Index, int &Row, int &Col);
   int               GetMarkov(int Row, int Col);


   Sql               THIS;

   int               act[2];

   int               e_row[2];
   int               e_col[2];

   int               transition_act;
   double            transition_value;
   
   matrix            policy_history;

   vector            Q_Loss()
   {  vector _loss;
      _loss.Init(THIS.actions);
      _loss.Fill(0.0);
      for(int i = 0; i < THIS.actions; i++)
      {  _loss[i] = Q_SA[e_row[0]][e_col[0]][i];
      }
      return(_loss);
   }


   void              Cql(Sql &RL)
   {  //
      if(RL.actions > 0 && RL.environments > 0)
      {  policy_history.Init(2,2+1);
         policy_history.Fill(0.0);
         acts.Init(RL.actions);
         ArrayResize(Q_SA, RL.actions);
         for(int i = 0; i < RL.actions; i++)
         {  acts[i] = i + 1;
            Q_SA[i].Init(RL.environments, RL.environments);
         }
         Q_V.Init(RL.environments, RL.environments);
         environment.Init(RL.environments, RL.environments);
         for(int i = 0; i < RL.environments; i++)
         {  for(int ii = 0; ii < RL.environments; ii++)
            {  environment[i][ii] = ii + (i * RL.environments) + 1;
            }
         }
         markov.Init(RL.environments * RL.environments, RL.environments * RL.environments);
         markov.Fill(0.0);
         THIS = RL;
         ArrayFill(e_row, 0, 2, 0);
         ArrayFill(e_col, 0, 2, 0);
         ArrayFill(act, 0, 2, 1);
         transition_act = 1;
      }
   };
   void              ~Cql(void) {};
};

これはメインの強化学習クラスであり、オンとオフの方策更新を定義するクラスのいくつかはすでに上記で共有されています。また、このクラスは、カスタムシグナルクラスの強化学習を実装するには十分な場合が多いですが、TDの場合、取引の決定を下すために環境値を使用したり、環境値にのみ依存したりするのではなく、これまでと同様に適切な行動の予測を継続することを選択しているため、これらの予測をおこなうモデルが必要になります。

そのため、このモデルをニューラルネットワークまたはMLPとして定義するために、追加のクラスであるCNeuralNetworkクラスが使用されます。同様に、そのクラスインターフェイスは以下のように共有されます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CNeuralNetwork
{
protected:
   
   matrix               TransposeToCol(vector &V);
   matrix               TransposeToRow(vector &V);
   
public:
   CLayer               *layers[];
   double               m_learning_rate;
   ENUM_LOSS_FUNCTION   m_loss;
   void                 AddDenseLayer(ulong Neurons, ENUM_ACTIVATION_FUNCTION AF = AF_RELU, ulong LastNeurons = 0)
   {  ArrayResize(layers, layers.Size() + 1);
      layers[layers.Size() - 1] = new CLayer(Neurons, AF);
      if(LastNeurons  != 0)
      {  layers[layers.Size() - 1].AddWeights(LastNeurons);
      }
      else if(layers.Size() - 1 > 0)
      {  layers[layers.Size() - 1].AddWeights(layers[layers.Size() - 2].activations.Size());
      }
   };
   void                 Init(double LearningRate, ENUM_LOSS_FUNCTION LF)
   {  m_loss = LF;
      m_learning_rate = LearningRate;
   };
   
   vector               Forward(vector& Data);
   void                 Backward(vector& LabelAnswer);
   
   void                 CNeuralNetwork(){};
   void                 ~CNeuralNetwork()
   {  if(layers.Size() > 0)
      {  for(int i = 0; i < int(layers.Size()); i++)
         {  delete layers[i];
         }
      }
   };
};

同様の機能を実行していた前回のCMLPクラスから、いくつか注目すべき変更を加えました。全体的に効率性に重点が置かれました。私たちの目的にはある程度の結果をもたらすことができたものの、これはまだベータ版です。主にバックプロパゲーション(Backward)関数における効率性の変更（現在進行中）に加えて、レイヤークラスを導入し、ネットワークの構築方法も変更しました。カスタムシグナルクラスの初期化は次のようになります。 

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CSignalTD::CSignalTD(void) :    m_scale(5),
   m_use_markov(true),
   m_policy(true)

{
//--- initialization of protected data
   m_used_series = USE_SERIES_OPEN + USE_SERIES_HIGH + USE_SERIES_LOW + USE_SERIES_CLOSE + USE_SERIES_SPREAD + USE_SERIES_TIME;
   //
   RL.actions  = 3;//buy, sell, do nothing
   RL.environments = 3;//bullish, bearish, flat
   RL.use_markov = m_use_markov;
   RL.epsilon = m_epsilon;
   QL_BUY = new Cql(RL);
   QL_SELL = new Cql(RL);
   //
   POLICY_NETWORK_BUY.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_BUY.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_BUY.Init(0.0004,LOSS_BCE);
   //
   POLICY_NETWORK_SELL.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_SELL.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_SELL.Init(0.0004,LOSS_BCE);
}

買い側と売り側でそれぞれ強化学習を処理する2つのCQLクラスに加えて、買い側と売り側でそれぞれ行動予測をおこなう2つの方策ネットワークも用意されました。GetOutput関数はこれまでの記事とほぼ同じように実行されますが、主な変更点は、ニューラルネットワーククラスのインスタンスが方策ネットワークとしての入力の1つであることです。新しいコードは次のとおりです。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CSignalTD::GetOutput(Cql *QL, CNeuralNetwork &PN)
{  int _td_act = 1;
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_row.Size() == m_scale+1
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale+1) &&
      _in_row_old.Size() == m_scale+1
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_col.Size() == m_scale+1
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale+1) &&
      _in_col_old.Size() == m_scale+1
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      _in_row.Resize(m_scale);
      _in_col.Resize(m_scale);
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
      PN.Forward(QL.policy_history.Row(1));
      vector _label;
      _label.Init(3);
      _label.Fill(0.0);
      if(_in_row[m_scale-1] > 0.0)
      {  _label[0] = 1.0;
      }
      else if(_in_row[m_scale-1] < 0.0)
      {  _label[2] = 1.0;
      }
      else if(_in_row[m_scale-1] == 0.0)
      {  _label[1] = 1.0;
      }
      PN.Backward(_label);
      vector _td_output = PN.Forward(QL.policy_history.Row(0));
      if(_td_output[0] >= _td_output[1] && _td_output[0] >= _td_output[2])
      {  _td_act = 0;
      }
      else if(_td_output[2] >= _td_output[0] && _td_output[2] >= _td_output[1])
      {  _td_act = 2;
      }
   }
   return(_td_act);
}

方策ネットワークを入力の1つとして使用することで、予測前にデータのバッチではなく最新の単一バーデータのみで訓練するため、オンライン学習または増分学習を実行できるようになりました。バックプロパゲーション実行とフォワードフィード実行は1回のみである必要がありますが、バックワードまたはバックプロパゲーション実行をおこなう前に、現在の価格バー情報をニューラルネットワークに読み込む必要があるため、この情報を読み込むために、その前に前のバー情報を含む単一のフォワード実行をおこないます。Forward関数も変更され、フォワードフィードパスから出力分類ベクトルが返されます。サイズは3で、それぞれのインデックスの各値は、インデックス順序0、1、2に従う場合に、売却、保有、または購入の可能性の「確率」または閾値を提供します。

したがって、上で述べたことを要約すると、私たちは3つの状態と3つの行動というシンプルな強化学習環境と行動設定を維持しています。モンテカルロを扱った前回の記事と同様に、方策の更新方法は最適化可能です。ただし、ここでは、更新がおこなわれる際に、新たに導入した行列Q_VのQ値のみが更新される点が異なります。これまでのアプローチでは、各行動に対して環境全体のQ値を更新していましたが、その方法と異なり、TDでは特定の行動に対してではなく、環境に対して値を割り当てる形になります。この方法により、次の行動を選択する際、マルコフ決定過程を使って次の状態を決定した後、最も高いQ値を持つ行動を選択するという手法が取られます。

TDでは、環境行列Q_Vは、状態に対する値を持つのみで、特定の行動に対するQ値は持ちません。つまり、次の行動方策を選択または決定するためしたがって、次に取るべき行動を決定するためには、方策ネットワーク（この場合はMLP）を使用して予測をおこない、その入力は現在の環境価値（その状態における適用可能な行動のQ値の合計）および環境状態の座標となります。出力は、3つの可能な行動に対する「確率分布」であり、現在の環境とその価値を考慮した最適な行動を示します。

このカスタムシグナルクラスは、MQL5ウィザードを使用してEAとして組み立てられ、その後、2022年に1時間足のGBPUSD銘柄を使用して簡単な最適化を実施しました。その結果、最適化期間中の一部の設定に基づき、以下の報告が得られました。

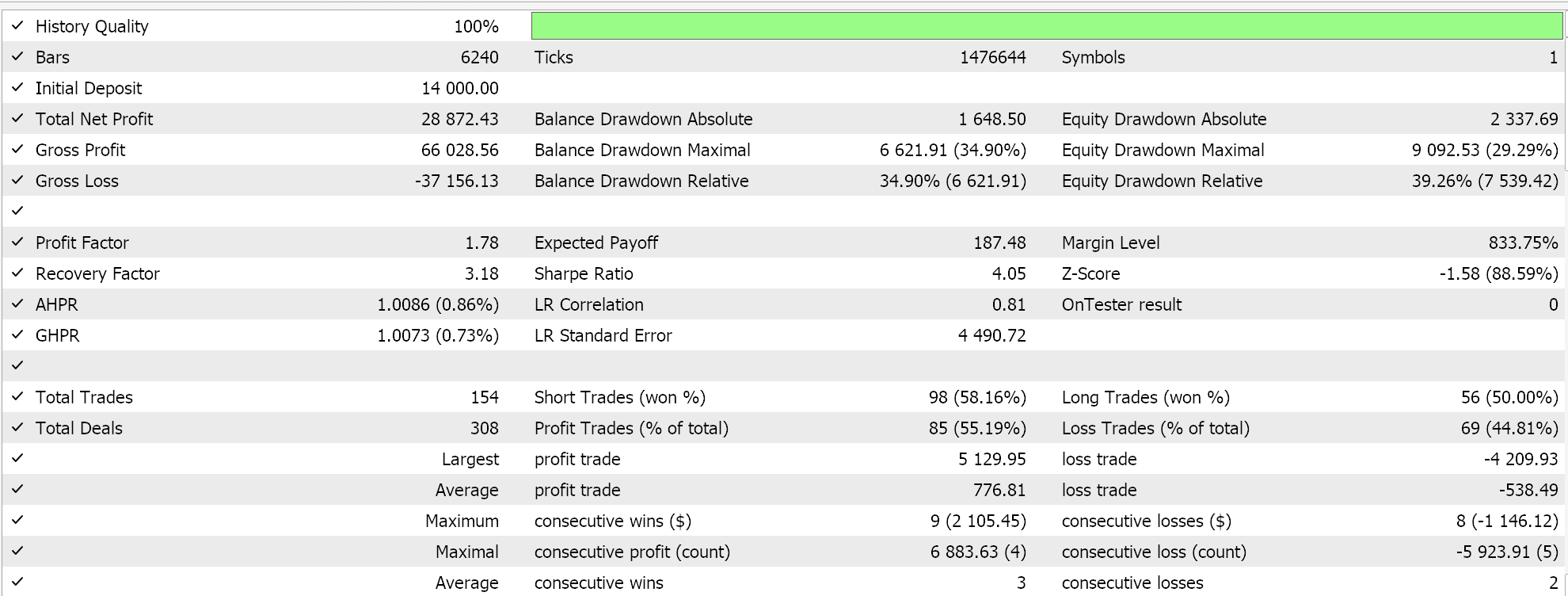
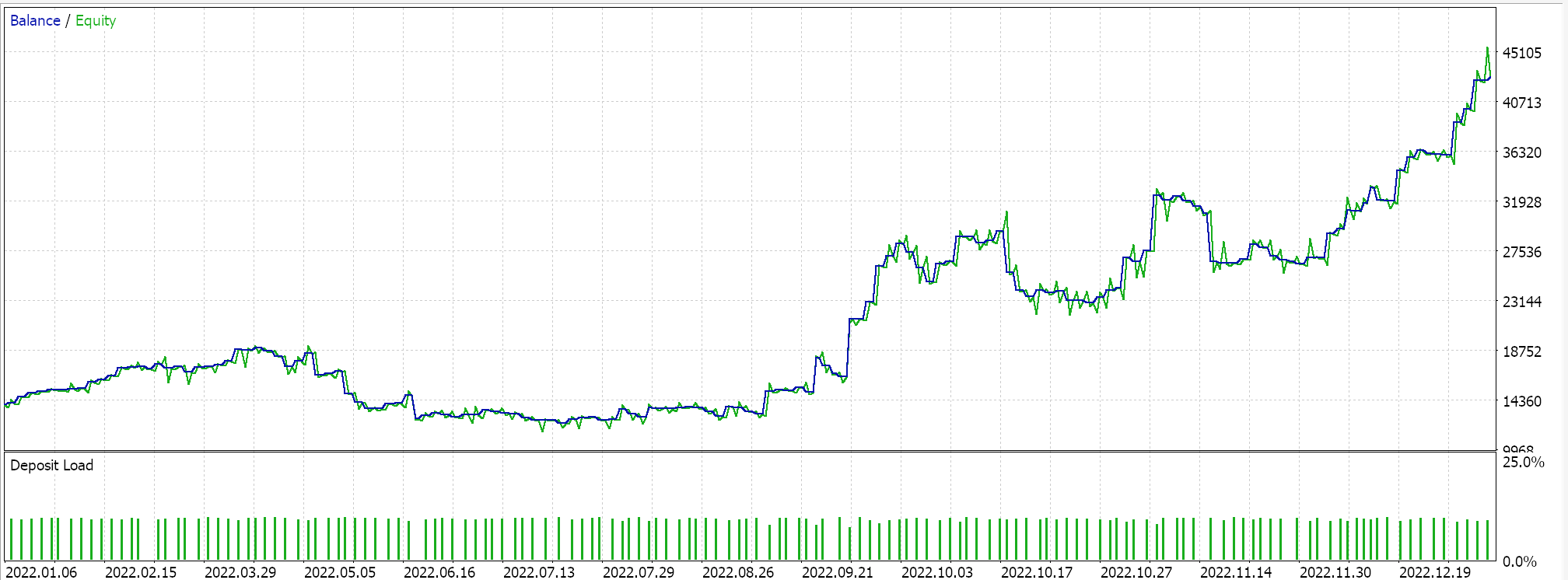
これらの結果は、おそらく私たちのカスタムシグナルクラスの潜在能力を示しているかもしれませんが、それを過小評価することなく、EAの設定をライブ環境に展開する前に交差検証をおこなうことが常に推奨されます。ここでおこなったものよりも長期間にわたる交差検証と追加のテストの注意深さは、読者が適宜検討するべき点として残されます。

TD学習によるシグナルクラスの最適化と調整

上記のテスト実行では、イプシロン、更新プロセスでマルコフ重み付けを使用するかどうか、方策更新を実行するかオフにするかというコアとなるパラメーターを最適化することに主に集中していました。また、ロングおよびショートの条件の始値と終値のしきい値、利益確定レベル、ポイントでのエントリー価格しきい値など、TDに特有ではない一般的なパラメータも考慮しました。

しかし、TDおよび強化学習の文脈においては、無視されたりプリセット値で設定されたパラメータがいくつかあります。これらは、アルファとガンマというパラメータで、それぞれ0.1と0.5の値が割り当てられています。これらのパラメータは方策更新プロセスで重要な役割を果たしており、シグナルクラスの全体的なパフォーマンスに大きな影響を与える可能性があります。さらに、シグナルクラスの実装において見過ごされた重要な部分は、方策ネットワーク自体の調整です。私たちは、3-9-3のネットワークアーキテクチャを使用し、各層の活性化関数や学習率を事前に設定していましたが、これらの値を調整すること（おそらくそれらを同時に調整すること）が、カスタムシグナルクラスのパフォーマンスと結果に大きな影響を与える可能性があります。

結論

この記事では、強化学習の時間差分(TD)アルゴリズムを取り上げ、これまでに議論した他のアルゴリズムとは異なる使用例に焦点を当てました。強化学習全般にとって興味深いが、まだ触れていない側面の1つは、時間の経過に伴う探索の減衰です。この考え方の背後にある論理は、強化学習モデルが学習を重ねるにつれて、新しい領域を探索したり学習を続ける必要が大幅に減少し、その結果として、既存の戦略を活用することがより重要になるというものです。これについては、コードを自分で適応させる際に読者がさらに検討できる点です。

さらに掘り下げるべきもう1つの視点は、イプシロン（探索率）を単に減衰させるのではなく、動的にすることです。先ほど述べた減衰という考え方に関連しますが、強化学習は教師あり学習のような静的データに依存するモデルとは異なり、非常に動的で適応性が高いものです。したがって、TDのフレームワークは変化する環境に積極的に対応できます。過去の記事で動的学習率法について検討したように、イプシロンにも同様のアプローチを適用することで、減衰だけに頼るのではなく、強化学習の本質を保つことができると言えます。