MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 47): Verstärkungslernen mit Temporaler Differenz

Einführung

Die Einführung in das temporale Differenzlernen (TD) beim Reinforcement Learning dient als Einstieg, um zu verstehen, wie sich TD von anderen Algorithmen wie Monte Carlo, Q-Learning und SARSA unterscheidet. Dieser Artikel soll die Komplexität des TD-Lernens entschlüsseln, indem er dessen einzigartige Fähigkeit hervorhebt, Wertschätzungen auf der Grundlage von Teilinformationen aus Episoden schrittweise zu aktualisieren, anstatt wie bei Monte-Carlo-Methoden auf den Abschluss von Episoden zu warten. Diese Unterscheidung macht das TD-Lernen zu einem leistungsstarken Instrument, insbesondere in dynamischen Umgebungen, die eine rasche Aktualisierung der Lernstrategie erfordern.

Im letzten Artikel über Reinforcement-Learning haben wir uns den Monte-Carlo-Algorithmus angesehen, der Informationen über die Belohnung über mehrere Zyklen hinweg sammelt, bevor er eine einzige Aktualisierung für jede Episode durchführt. Beim Temporal Difference Learning (TD) geht es jedoch darum, aus partiellen und unvollständigen Episoden zu lernen, ähnlich wie bei den Algorithmen von Q-Learning und SARSA, die wir bereits hier und hier behandelt haben.

Im Folgenden finden Sie eine tabellarische Zusammenfassung der Hauptunterschiede zwischen TD, Q-Learning und SARSA.

Zusammenfassend lässt sich sagen, dass die Formel für Zustand-Aktions-Paare mit On-Policy-Update, wie z. B. SARSA, wie folgt lautet:

	TD Lernen	Q-Learning	SARSA
Arten von Werten	Zustandswerte V(s)	Aktionswerte Q(s,a)	Aktionswerte Q(s,a)
Ansatz für das Lernen	Schätzungen zukünftiger Zustandswerte	Off-policy	On-policy
Art der Politik	Nicht abhängig von einer bestimmten Politik	Lernt die optimale Politik	Lernt die aktuelle Verhaltenspolitik kennen
Ziel aktualisieren	Nächster Zustandswert V(s′)	Max Q(s′,a′)	Tatsächliches Q(s′,a′)
Erkundung	Erfordert oft eine separate Politik	Angenommen wird, der Agent sucht das Optimum	Eher konservativ
Verhalten	Bewegt sich auf den Wert des nächsten Zustands zu	Gierig; bevorzugt den optimalen Weg	Folgt dem tatsächlichen Erkundungspfad

Um noch einmal auf den Fachjargon zurückzukommen: „On-Policy-Updates“ bedeutet, dass die Zustands-Aktions-Paare (state-action), die aktualisiert wurden, die aktuellen Paare waren und nicht unbedingt die optimalen oder die mit den höchsten Q-Werten. Wenn wir die Zustands-Aktions-Paare mit den höchsten Q-Werten aktualisieren sollen, dann wäre dies ein Off-Policy-Ansatz. Wir führen diese Aktualisierungen in MQL5 wie folgt durch:

//+------------------------------------------------------------------+
// Update using On-policy
//+------------------------------------------------------------------+
void Cql::SetOnPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 1 represents the current Q_SA-action from Q_SA-Map
   double _sa = Q_SA[transition_act][e_row[1]][e_col[1]];
   double _v = Q_V[e_row[1]][e_col[1]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[1]][e_col[1]]);
   }
   Q_V[e_row[1]][e_col[1]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[1]][e_col[1]]);
}

//+------------------------------------------------------------------+
// Update using Off-policy
//+------------------------------------------------------------------+
void Cql::SetOffPolicy(double Reward, vector &E)
{  Action(E);
//where 'act' index 0 represents highest valued Q_SA-action from Q_SA-Map
//as determined from Action() function above.
   double _sa = Q_SA[transition_act][e_row[0]][e_col[0]];
   double _v = Q_V[e_row[0]][e_col[0]];
   if(THIS.use_markov)
   {  int _old_index = GetMarkov(e_row[1], e_col[1]);
      int _new_index = GetMarkov(e_row[0], e_col[0]);
      _sa *= markov[_old_index][_new_index];
      _v *= markov[_old_index][_new_index];
   }
   for (int i = 0; i < THIS.actions; i++)
   {  Q_SA[i][e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _sa)) - Q_SA[i][e_row[0]][e_col[0]]);
   }
   Q_V[e_row[0]][e_col[0]] += THIS.alpha * ((Reward + (THIS.gamma * _v)) - Q_V[e_row[0]][e_col[0]]);
}

In unseren geänderten und überarbeiteten Funktionen sind Aktualisierungen mit der Hinzufügung eines neuen „Q_V“-Objekts enthalten, das wir aus Gründen der Klarheit bei der Zuordnung zu den jeweiligen Umgebungszuständen als Matrix dargestellt haben, aber wir hätten es auch einfach als Vektor haben können, da die Koordinaten der Umgebungszustände in einem einzigen ganzzahligen Index abgebildet werden können. Das alte Q-Map wird in „Q_SA“ umbenannt. Diese neue Benennung steht im Einklang mit dem neuen Objekt, das Q-Map-Werte unabhängig von Aktionen verfolgt, worauf sich TD konzentriert, während die Umbenennung der alten Q-Map in Q_SA die Werte des Zustands-Aktionspaares hervorhebt, die bei jedem Aufruf der Funktion aktualisiert werden. Unsere obigen MQL5-Implementierungen sind von der folgenden Formel für TD abgeleitet (die entweder ein- oder ausgeschaltet sein kann):

wobei:

• V (s) : Wert des aktuellen Zustands s
• V (s′) : Wert des nächsten Zustands s′
• α: Lernrate (steuert, wie stark wir den aktuellen Wert anpassen)
• r: Erhaltene Belohnung nach Durchführung der Maßnahme
• γ: Abzinsungsfaktor (bestimmt die Bedeutung zukünftiger Belohnungen)
• Diese Formel aktualisiert die Wertschätzung eines Zustands V (s) auf der Grundlage der erhaltenen Belohnung und des geschätzten Werts des nächsten Zustands V (s′)

Zusammenfassend lässt sich sagen, dass die Formel für Zustand-Aktions-Paare mit On-Policy-Update, wie z. B. SARSA, wie folgt lautet:

wobei:

• Q (s, a) : Q-Wert des aktuellen Zustands-Aktionspaares (s, a)
• Q (s′, a′) : Q-Wert des nächsten Zustands-Aktionspaares (s′, a′), wobei a′ die von der aktuellen Politik im nächsten Zustand s′ gewählte Aktion ist.
• α: Lernrate
• r: Belohnung nach Durchführung einer Aktion a
• γ: Abschlagsfaktor

Die Formel für Off-Policy-Updates sieht wie folgt aus:

wobei:

• Q (s, a) : Q-Wert des aktuellen Zustands-Aktionspaares (s, a)
• max a′ ​Q (s′, a′) : Maximaler Q-Wert des nächsten Zustands s′ über alle möglichen Aktionen a′ (unter der Annahme, dass die beste Aktion in s′ ausgeführt wird)
• α: Lernrate
• r: Belohnung nach Durchführung einer Aktion a
• γ: Abschlagsfaktor

Aus den letzten beiden Formeln geht hervor, dass die aktionsspezifischen Aktualisierungen einen gewissen Einfluss auf die Auswahl der nächsten Aktion haben. Da bei der TD-Aktualisierung jedoch Werte für alle Aktionen aggregiert und einfach dem jeweiligen Umgebungszustand zugeordnet werden, ist der Einfluss dieses Prozesses auf die auszuwählende Aktion nicht genau definiert.

Deshalb ist bei der Verwendung von TD ein zusätzliches Modell, in unserem Fall ein politisches neuronales Netz, erforderlich, um die Auswahl der nächsten Aktion für den Akteur zu steuern. Dieses Modell kann eine Reihe von Formen annehmen, aber für unsere Zwecke ist es einfach ein 3-Schichten-MLP mit der Größe 3-9-3, wobei die Ausgabeschicht eine Wahrscheinlichkeitsverteilung für jede der möglichen 3 Aktionen liefert, die in unserem Fall immer noch Kaufen, Verkaufen und Halten ist. Dieser MLP ist also ein Klassifikator und kein Regressor. Wir geben den Deklarationscode dieser Klasse in der nutzerdefinierten Signalklassenschnittstelle wie unten gezeigt an:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSignalTD   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   
public:
   void                          CSignalTD(void);
   void                          ~CSignalTD(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   int               GetOutput(Cql *QL, CNeuralNetwork &PN);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   CNeuralNetwork    POLICY_NETWORK_BUY,POLICY_NETWORK_SELL;
};

Der vollständige Quellcode unserer nutzerdefinierten Signalklasse ist am Ende dieses Artikels angehängt und soll über den MQL5-Assistenten verwendet werden, um einen Expert Advisor zu erzeugen. Es gibt hier und hier Anleitungen für Leser, die noch nicht wissen, wie man das macht. Mit dem beigefügten Quellcode kann der Leser leicht Änderungen am MLP-Design vornehmen, indem er nicht nur die Anzahl der Schichten, sondern auch ihre Größe ändert. Nach unserem Entwurf soll die Eingabeschicht 3 als Eingaben die Umgebungskoordinate der x-Achse, den Übergangswert oder den aktuellen Wert der Q_V-Matrix und den Wert der y-Achse der Umgebung erhalten. Der Übergangswert wird der Q_V-Matrix entnommen, die wir in den Einstellungen der Ein- und Ausschaltrichtlinien aktualisieren, wie bereits oben im Quellcode angegeben. Diese Auswahl des Übergangswertes wird in der überarbeiteten Funktion Aktion wie folgt gehandhabt:

//+------------------------------------------------------------------+
// Choose an action using epsilon-greedy approach
//+------------------------------------------------------------------+
void Cql::Action(vector &E)
{  int _best_act = 0;
   if (double((rand() % SHORT_MAX) / SHORT_MAX) < THIS.epsilon)
   {  // Explore: Choose random action
      _best_act = (rand() % THIS.actions);
   }
   else
   {  // Exploit: Choose best action
      double _best_value = Q_SA[0][e_row[0]][e_col[0]];
      for (int i = 1; i < THIS.actions; i++)
      {  if (Q_SA[i][e_row[0]][e_col[0]] > _best_value)
         {  _best_value = Q_SA[i][e_row[0]][e_col[0]];
            _best_act = i;
         }
      }
   }
//update last action
   act[1] = act[0];
   act[0] = _best_act;
//markov decision process
   e_row[1] = e_row[0];
   e_col[1] = e_col[0];
   LetMarkov(e_row[1], e_col[1], E);
   int _next_state = 0;
   for (int i = 0; i < int(markov.Cols()); i++)
   {  if(markov[int(E[0])][i] > markov[int(E[0])][_next_state])
      {  _next_state = i;
      }
   }
   int _next_row = 0, _next_col = 0;
   SetMarkov(_next_state, _next_row, _next_col);
   e_row[0] = _next_row;
   e_col[0] = _next_col;
   transition_value = Q_V[_next_row][_next_col];
   policy_history[1][0] = policy_history[0][0];
   policy_history[1][1] = policy_history[0][1];
   policy_history[1][2] = policy_history[0][2];
   policy_history[0][0] = _next_row;
   policy_history[0][1] = transition_value;
   policy_history[0][2] = _next_col;
   transition_act = 1;
   for (int i = 0; i < THIS.actions; i++)
   {  if(Q_SA[i][_next_row][_next_col] > Q_SA[transition_act][_next_row][_next_col])
      {  transition_act = i;
      }
   }
   //if(transition_act!=1)printf(__FUNCSIG__+ " act is : %i ",transition_act);
}

Die übergeordnete These in unserem Politiknetzwerk (policy network), dem oben erwähnten MLP, ist daher, dass die als nächste auszuwählende geeignete Aktion nur eine Funktion des aktuellen Umgebungszustands und seines Q-Werts ist. Dies unterscheidet sich von dem, was wir bis hierher verwendet haben, wo der Markov-Entscheidungsprozess (MDP) verwendet wurde, um die geeignete Aktion aus der Q-Map auszuwählen, die wir in diesem Artikel (beigefügter Code) in Q_SA umbenannt haben. In allen Fällen haben wir das speicherlose MDP verwendet, indem wir einen Puffer mit den letzten Sequenzen von Umgebungszuständen berechnet haben. Diese Umgebungssequenzen liefern uns dank der Markov-Funktion, auf die wir weiter unten noch einmal eingehen werden, eine Projektion für den nächsten Umgebungszustand.

//+------------------------------------------------------------------+
// Function to update markov matrix
//+------------------------------------------------------------------+
void Cql::LetMarkov(int OldRow, int OldCol, vector &E)  //
{  matrix _transitions;  // Count the transitions
   _transitions.Init(markov.Rows(), markov.Cols());
   _transitions.Fill(0.0);
   vector _states;  // Count the occurrences of each state
   _states.Init(markov.Rows());
   _states.Fill(0.0);
// Count transitions from state i to state ii
   for (int i = 0; i < int(E.Size()) - 1; i++)
   {  int _old_state = int(E[i]);
      int _new_state = int(E[i + 1]);
      _transitions[_old_state][_new_state]++;
      _states[_old_state]++;
   }
// Reset prior values to zero.
   markov.Fill(0.0);
// Compute probabilities by normalizing transition counts
   for (int i = 0; i < int(markov.Rows()); i++)
   {  for (int ii = 0; ii < int(markov.Cols()); ii++)
      {  if (_states[i] > 0)
         {  markov[i][ii] = double(_transitions[i][ii] / _states[i]);
         }
         else
         {  markov[i][ii] = 0.0;  // No transitions from this state
         }
      }
   }
}

Dieser Prozess der Bestimmung der nächsten Zustände dank MDP wird auch mit TD durchgeführt, der Unterschied besteht jedoch darin, dass wir diese projizierten Koordinaten des nächsten Zustands nicht allein zur Bestimmung der nächsten Aktion verwenden können. Früher, als wir Q_SA verwendeten, mussten wir die Aktion mit der höchsten Wahrscheinlichkeitsgewichtung aus den nächsten Zustandskoordinaten ablesen, um zu wissen, was der Akteur tun sollte. Unsere äquivalente Matrix, die Q_V, gibt uns jedoch nur Werte für alle angegebenen Zustandskoordinaten, und dennoch ist die Bestimmung der nächsten Aktion des Akteurs in der Verstärkungslernschleife entscheidend.

Deshalb führen wir ein Politiknetzwerk, ein MLP, ein, das wir für unsere Zwecke einfach als 3-9-3 konzipiert haben, mit einer einzigen versteckten Schicht von 9, die die drei zuvor erwähnten Eingaben der beiden Umgebungskoordinaten und ihren Q-Wert aufnimmt und einen Vektor von 3 ausgibt, der die Wahrscheinlichkeitsverteilung über die drei möglichen Aktionen Kaufen, Verkaufen und Halten erfassen soll, wobei der Wert mit der höchsten Punktzahl im Vektor die empfohlene Aktion ist, wird angenommen.

Makro Nutzen und Zweck von TD

TD aktualisiert seine Q-Werte häufiger als in Monte Carlo, was in den sich schnell verändernden und fließenden Finanzmärkten von großem Vorteil ist. Was unterscheidet es jedoch von SARSA oder Q-Learning in Bezug auf seine Vorteile? Wir versuchen, diese Frage anhand einiger Beispiele aus dem Alltag zu beantworten.

Definitionsgemäß besteht der Hauptunterschied zwischen TD und SARSA/Q-Learning darin, dass TD sich mehr auf wertbasiertes Lernen konzentriert, bei dem nur Zustandswerte geleant und aktualisiert werden, während die beiden anderen Algorithmen sich auf Zustands-Aktions-Paarungen konzentrieren, um ähnliche Aktualisierungen durchzuführen.

Szenario A

Nehmen wir an, in einem Lagerhaus gibt es ein Bestandsverwaltungssystem, das lediglich den Überblick über die Menge der Bestände einer Vielzahl von Produkten behält. Das Ziel dieses Systems wäre lediglich die Verwaltung der Lagerbestände und die Sicherstellung, dass kein Produkt unter- oder überbevorratet ist.

In dieser Situation wäre TD gegenüber SARSA oder Q-Learning im Vorteil, weil es sich auf Zustandswerte und nicht auf Zustands-Aktions-Paare konzentriert. Dies liegt daran, dass das System in diesem Fall möglicherweise nur den „Wert“ jedes Zustands (z. B. den Gesamtbestand) vorhersagen muss, ohne jede spezifische Aktion (z. B. die Bestellung für jede SKU) zu bewerten. In dieser Situation kann das TD-Lernen die Wertfunktion für den Zustand (Lagerbestände) aktualisieren, ohne dass jede mögliche Bestellentscheidung für jedes Produkt berechnet werden muss, ohne dass ein MLP für das Politiknetzwerk erforderlich ist.

Darüber hinaus kann die Bestandsverwaltung allmähliche Veränderungen anstelle von abrupten Zustands-Aktions-Paaren aufweisen, die ein deutliches Belohnungs-Feedback haben. Da das TD-Lernen mit inkrementellem Feedback arbeitet, eignet es sich für Umgebungen mit fließenden Übergängen, in denen die Kenntnis des Gesamtzustands wichtiger ist als die Kenntnis jedes Zustands-Aktionsergebnisses. In Umgebungen mit mehreren Aktionen und großen Zustands-Aktionsräumen, wie z.B. bei der Bestandsverwaltung, die komplexer ist (wo wir jedem Zustand der Bestandsebene eine Aktion zuordnen müssen), sind Q-Learning und SARSA zwar anwendbar, aber zwangsläufig mit Rechenkosten verbunden, die TD aufgrund seiner einfacheren, ganzheitlichen Anwendung nicht verursacht.

 

Szenario B

Ziehen Sie ein intelligentes Gebäudesystem in Betracht, das die Einstellungen für Heizung, Lüftung und Klimatisierung (HVAC) so anpasst, dass der Energieverbrauch minimiert wird und die Bewohner sich wohl fühlen. Das Ziel, einen Ausgleich zwischen kurzfristigen Vorteilen und langfristigen Zielen zu schaffen, zielt auf die Senkung der Energiekosten und die Aufrechterhaltung einer optimalen Gebäudetemperatur bzw. Luftqualität ab.

Auch in diesem Fall wäre TD besser geeignet als SARSA oder Q-Learning, da es sich bei den Energieverbrauchswerten oder dem Nutzerkomfort um absolute Metriken handelt, an die keine von ihren Werten abhängigen Maßnahmen geknüpft sind. In diesem besonderen Fall können zwei Verstärkungslernzyklen trainiert werden, um kurzfristige und langfristige Belohnungen auszugleichen und beide parallel vorherzusagen. Die inkrementellen Aktualisierungen von TD pro Zyklus (und nicht pro Episode wie bei Monte Carlo) machen es auch ideal für dieses intelligente Gebäudesystem, da sich Umgebungsbedingungen wie Temperatur, Belegung und Luftqualität allmählich ändern. Dadurch kann TD einen nahtlosen Anpassungsmechanismus anbieten.

Wie bereits erwähnt, wird das SARSA- oder Q-Learning-Äquivalent zusätzliche Rechen- und Speicheranforderungen mit sich bringen, da spezifische Maßnahmen erforderlich sind, um etwaige Unter- oder Überschreitungen der Umweltzustandswerte zu „beheben“.  

 

Szenario C

Ein System zur Vorhersage und Steuerung des Verkehrsflusses mit dem Ziel, Staus an mehreren Kreuzungen durch die Vorhersage des Verkehrsflusses und die entsprechende Anpassung von Lichtsignalen zu minimieren, ist unser dritter möglicher Anwendungsfall für TD. TD ist auch in dieser Situation im Vergleich zu SARSA oder Q-Learning vorteilhaft, da das Hauptaugenmerk auf dem Verständnis und der Vorhersage des Gesamtverkehrszustands (z. B. Staus) liegt und nicht auf der Optimierung jeder einzelnen Lichtsignalaktion. TD-Lernen ermöglicht es dem System, den gesamten „Wert“ eines Verkehrszustands zu lernen, anstatt die Auswirkungen jeder einzelnen Signaländerung.

Da der Verkehr von Natur aus dynamisch ist und sich im Laufe des Tages ständig ändert, spielt er auch in die schrittweise Aktualisierung von TD hinein. Ein sehr anpassungsfähiger Algorithmus, der im Gegensatz zu Monte Carlo auf den Abschluss einer Episode wartet, bevor er Aktualisierungen vornimmt. Die Verringerung von Rechen- und Speicherüberlastungen für TD gilt auch in diesem Fall, insbesondere wenn man bedenkt, wie verflochten und miteinander verbunden Verkehrsknotenpunkte selbst in einer relativ kleinen Stadt sein können. Rechen- und Speicherkosten wären sicherlich ein großer Faktor bei der Implementierung eines Systems zur Vorhersage des Verkehrsflusses, und TD würde einen großen Beitrag zur Lösung dieses Problems leisten.

Szenario D

Vorausschauende Wartung in der Fertigung, stellt unseren letzten Anwendungsfall für TD als bevorzugten Algorithmus im Vergleich zu anderen Algorithmen des Reinforcement Learning dar, die wir bisher behandelt haben. Nehmen wir einen Fall, in dem ein Produktionsbetrieb vorhersagen will, wann Maschinen gewartet werden müssen, um Ausfallzeiten zu vermeiden. Und genau wie beim intelligenten Gebäudesystem müsste dieses System die kurzfristigen Vorteile (Einsparung von Wartungskosten durch Verzögerung von Kontrollen) mit den langfristigen Vorteilen (Vermeidung von Ausfällen) in Einklang bringen. TD-Lernen wäre hier geeignet, weil es den Gesamtzustandswert der Maschine im Laufe der Zeit auf der Grundlage partieller Rückmeldungen aktualisieren kann, anstatt wie SARSA oder Q-Lernen bestimmte Aktionen (Reparatur oder Austausch) zu verfolgen.

TD wäre auch deshalb ein besserer Algorithmus, weil die Verschlechterung des Zustands der Maschine allmählich eintritt und TD den Zustandswert auf der Grundlage inkrementeller Sensordaten problemlos kontinuierlich aktualisieren kann, anstatt längere Zeiträume abzuwarten, was zusätzliche Risiken mit sich bringen könnte. In einer Anlage mit mehreren Maschinen kann das TD-Lernen auch gut skaliert werden, wenn die Anzahl der Maschinen verringert oder erhöht wird, da es sich auf die Verfolgung des Zustands/der Gesundheit jeder Maschine konzentriert und keine spezifischen Zustands-Aktions-Paare für jede Maschine in der Anlage speichern und aktualisieren muss.

Dies sind nur einige wenige Fälle, die nichts mit dem Finanzhandel und den Märkten zu tun haben. Lassen Sie uns nun überlegen, wie wir dies speziell als nutzerdefinierte Signalklasse anwenden können.

Strukturierung der nutzerdefinierten Signalklasse mithilfe des TD-Algorithmus

Die nutzerdefinierte Signalklasse, die wir zur Implementierung von TD erstellen, stützt sich auf zwei zusätzliche Klassen. Da es sich um einen Algorithmus für Reinforcement Learning handelt, ist eine dieser Klassen die CQL-Klasse. Wir haben diese Klasse bereits in allen vorangegangenen Artikeln verwendet oder auf sie verwiesen; ihre Schnittstelle wird jedoch im Folgenden erneut gemeinsam genutzt:

//+------------------------------------------------------------------+
//| Q_SA-Learning Class Interface.                                      |
//+------------------------------------------------------------------+
class Cql
{
protected:
   matrix            markov;
   void              LetMarkov(int OldRow, int OldCol, vector &E);

   vector            acts;
   matrix            environment;
   matrix            Q_SA[];
   matrix            Q_V;

public:
   void              Action(vector &E);
   void              Environment(vector &E_Row, vector &E_Col, vector &E);

   void              SetOffPolicy(double Reward, vector &E);
   void              SetOnPolicy(double Reward, vector &E);

   double            GetReward(double MaxProfit, double MaxLoss, double Float);
   vector            SetTarget(vector &Rewards, vector &TargetOutput);

   void              SetMarkov(int Index, int &Row, int &Col);
   int               GetMarkov(int Row, int Col);


   Sql               THIS;

   int               act[2];

   int               e_row[2];
   int               e_col[2];

   int               transition_act;
   double            transition_value;
   
   matrix            policy_history;

   vector            Q_Loss()
   {  vector _loss;
      _loss.Init(THIS.actions);
      _loss.Fill(0.0);
      for(int i = 0; i < THIS.actions; i++)
      {  _loss[i] = Q_SA[e_row[0]][e_col[0]][i];
      }
      return(_loss);
   }


   void              Cql(Sql &RL)
   {  //
      if(RL.actions > 0 && RL.environments > 0)
      {  policy_history.Init(2,2+1);
         policy_history.Fill(0.0);
         acts.Init(RL.actions);
         ArrayResize(Q_SA, RL.actions);
         for(int i = 0; i < RL.actions; i++)
         {  acts[i] = i + 1;
            Q_SA[i].Init(RL.environments, RL.environments);
         }
         Q_V.Init(RL.environments, RL.environments);
         environment.Init(RL.environments, RL.environments);
         for(int i = 0; i < RL.environments; i++)
         {  for(int ii = 0; ii < RL.environments; ii++)
            {  environment[i][ii] = ii + (i * RL.environments) + 1;
            }
         }
         markov.Init(RL.environments * RL.environments, RL.environments * RL.environments);
         markov.Fill(0.0);
         THIS = RL;
         ArrayFill(e_row, 0, 2, 0);
         ArrayFill(e_col, 0, 2, 0);
         ArrayFill(act, 0, 2, 1);
         transition_act = 1;
      }
   };
   void              ~Cql(void) {};
};

Dies ist die Hauptklasse des Reinforcement Learning, und einige ihrer Klassen, die Aktualisierungen von Richtlinien ein- und ausschalten, wurden bereits weiter oben beschrieben. Außerdem reicht diese Klasse oft aus, um Reinforcement Learning für eine nutzerdefinierte Signalklasse zu implementieren. Da wir uns bei TD jedoch nicht ausschließlich auf die Umgebungswerte stützen, um Handelsentscheidungen zu treffen, sondern uns dafür entscheiden, mit der Vorhersage geeigneter Maßnahmen fortzufahren, wie wir es in der Vergangenheit getan haben, benötigen wir ein Modell, um diese Prognosen zu erstellen.

Deshalb wird eine zusätzliche Klasse, die Klasse CNeuralNetwork, verwendet, um dieses Modell als neuronales Netz oder MLP zu definieren. Auch die Schnittstelle der Klasse wird im Folgenden gemeinsam genutzt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CNeuralNetwork
{
protected:
   
   matrix               TransposeToCol(vector &V);
   matrix               TransposeToRow(vector &V);
   
public:
   CLayer               *layers[];
   double               m_learning_rate;
   ENUM_LOSS_FUNCTION   m_loss;
   void                 AddDenseLayer(ulong Neurons, ENUM_ACTIVATION_FUNCTION AF = AF_RELU, ulong LastNeurons = 0)
   {  ArrayResize(layers, layers.Size() + 1);
      layers[layers.Size() - 1] = new CLayer(Neurons, AF);
      if(LastNeurons  != 0)
      {  layers[layers.Size() - 1].AddWeights(LastNeurons);
      }
      else if(layers.Size() - 1 > 0)
      {  layers[layers.Size() - 1].AddWeights(layers[layers.Size() - 2].activations.Size());
      }
   };
   void                 Init(double LearningRate, ENUM_LOSS_FUNCTION LF)
   {  m_loss = LF;
      m_learning_rate = LearningRate;
   };
   
   vector               Forward(vector& Data);
   void                 Backward(vector& LabelAnswer);
   
   void                 CNeuralNetwork(){};
   void                 ~CNeuralNetwork()
   {  if(layers.Size() > 0)
      {  for(int i = 0; i < int(layers.Size()); i++)
         {  delete layers[i];
         }
      }
   };
};

Gegenüber dem letzten CMLP-Kurs, der eine ähnliche Funktion erfüllte, haben wir einige deutliche Änderungen vorgenommen. Insgesamt lag der Schwerpunkt auf der Effizienz; es handelt sich jedoch noch um eine Beta-Version, auch wenn sie für unsere Zwecke einige Ergebnisse liefern konnte. Neben den Änderungen an der Effizienz, die vor allem die Backpropagation-Funktion betreffen und noch nicht abgeschlossen sind, haben wir eine neue Schichtklasse eingeführt und auch die Art und Weise geändert, wie das Netz aufgebaut ist. Die Initialisierung der nutzerdefinierten Signalklasse sieht nun wie folgt aus: 

//+------------------------------------------------------------------+
//| Constructor                                                      |
//+------------------------------------------------------------------+
void CSignalTD::CSignalTD(void) :    m_scale(5),
   m_use_markov(true),
   m_policy(true)

{
//--- initialization of protected data
   m_used_series = USE_SERIES_OPEN + USE_SERIES_HIGH + USE_SERIES_LOW + USE_SERIES_CLOSE + USE_SERIES_SPREAD + USE_SERIES_TIME;
   //
   RL.actions  = 3;//buy, sell, do nothing
   RL.environments = 3;//bullish, bearish, flat
   RL.use_markov = m_use_markov;
   RL.epsilon = m_epsilon;
   QL_BUY = new Cql(RL);
   QL_SELL = new Cql(RL);
   //
   POLICY_NETWORK_BUY.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_BUY.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_BUY.Init(0.0004,LOSS_BCE);
   //
   POLICY_NETWORK_SELL.AddDenseLayer(9, AF_SIGMOID, 3);
   POLICY_NETWORK_SELL.AddDenseLayer(3, AF_SOFTMAX);
   POLICY_NETWORK_SELL.Init(0.0004,LOSS_BCE);
}

Neben 2 CQL-Klassen für das Reinforcement Learning auf der Kauf- bzw. Verkaufsseite haben wir jetzt auch 2 Politiknetzwerke, die ebenfalls Handlungsprognosen auf der Kauf- bzw. Verkaufsseite erstellen. Die Get-Output-Funktion läuft immer noch weitgehend so ab wie in früheren Artikeln, wobei die wichtigste Änderung darin besteht, dass eine Instanz der Klasse des neuronalen Netzes einer seiner Inputs als Politiknetzwerk ist. Der neue Code ist wie folgt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CSignalTD::GetOutput(Cql *QL, CNeuralNetwork &PN)
{  int _td_act = 1;
   vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_row.Size() == m_scale+1
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale+1) &&
      _in_row_old.Size() == m_scale+1
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale+1) &&
      _in_col.Size() == m_scale+1
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale+1) &&
      _in_col_old.Size() == m_scale+1
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      _in_row.Resize(m_scale);
      _in_col.Resize(m_scale);
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      double _reward = QL.GetReward(_reward_max, _reward_min, _reward_float);
      if(m_policy)
      {  QL.SetOnPolicy(_reward, _in_e);
      }
      else if(!m_policy)
      {  QL.SetOffPolicy(_reward, _in_e);
      }
      PN.Forward(QL.policy_history.Row(1));
      vector _label;
      _label.Init(3);
      _label.Fill(0.0);
      if(_in_row[m_scale-1] > 0.0)
      {  _label[0] = 1.0;
      }
      else if(_in_row[m_scale-1] < 0.0)
      {  _label[2] = 1.0;
      }
      else if(_in_row[m_scale-1] == 0.0)
      {  _label[1] = 1.0;
      }
      PN.Backward(_label);
      vector _td_output = PN.Forward(QL.policy_history.Row(0));
      if(_td_output[0] >= _td_output[1] && _td_output[0] >= _td_output[2])
      {  _td_act = 0;
      }
      else if(_td_output[2] >= _td_output[0] && _td_output[2] >= _td_output[1])
      {  _td_act = 2;
      }
   }
   return(_td_act);
}

Mit einem Politiknetzwerk als einer seiner Eingaben ist es nun in der Lage, Online- oder inkrementelles Lernen durchzuführen, da wir vor der Vorhersage nicht auf einem Stapel von Daten trainieren, sondern nur auf den letzten einzelnen Taktdaten. Es sollte nur einen Backpropagation-Durchgang und einen Forward-Feed-Durchgang geben, aber da wir die aktuellen Preisbalkeninformationen in unser neuronales Netzwerk laden müssen, bevor wir den Backpropagation-Durchgang durchführen, machen wir einen einzigen Forward-Lauf mit den vorherigen Balkeninformationen davor, um diese Informationen zu laden. Unsere Vorwärtsfunktion wurde auch so geändert, dass sie den Klassifizierungsvektor aus dem Vorwärtsdurchlauf zurückgibt. Er ist dreigeteilt, wobei jeder Wert des jeweiligen Index eine „Wahrscheinlichkeit“ oder einen Schwellenwert für die Wahrscheinlichkeit des Verkaufs, des Haltens oder des Kaufs darstellt, wenn wir der Indexierungsreihenfolge 0, 1 bzw. 2 folgen.

Um das oben Erwähnte zu rekapitulieren, bleiben wir bei der gleichen einfachen Verstärkungslernumgebung und dem gleichen Aktionsaufbau von 3 Zuständen und 3 Aktionen. Die Wahl der Aktualisierungspolitik ist optimierbar, wie im letzten Artikel über Reinforcement Learning, der sich mit Monte Carlo befasste. Wenn hier jedoch Aktualisierungen vorgenommen werden, werden nur die Q-Werte einer neu eingeführten Matrix, der Q_V, aktualisiert. Dies steht im Gegensatz zu dem, was wir in der Vergangenheit getan haben, indem wir die Q-Werte für jede Aktion in einer Umgebungskarte aktualisiert haben. Die Aktualisierung der Werte für jede Aktion war bei der Auswahl der nächsten Aktion konstruktiv, denn sobald der Markov-Entscheidungsprozess verwendet wird, um die Koordinaten des nächsten Umgebungszustands zu bestimmen, ist es nur noch eine Frage des Ablesens der Aktion mit dem höchsten Q-Wert und der Auswahl dieser als nächste Aktion.

Bei TD hat unsere Umgebungsmatrix Q_V keine Aktionen mit Q-Werten, sondern nur Werte, die einer bestimmten Umgebung zugeordnet sind. Das bedeutet, dass für die Auswahl oder Festlegung der nächsten Aktion ein Politik-Netz (in unserem Fall ein MLP) verwendet wird, um diese Vorhersagen zu treffen, und seine Eingaben wären der Wert für die aktuelle Umgebung (der de facto eine Summe aller Q-Werte der anwendbaren Aktionen in diesem Zustand ist) sowie die Koordinaten des Umgebungszustands. Die Ausgabe ist, wie bereits erwähnt, eine „Wahrscheinlichkeitsverteilung“ über die 3 möglichen Aktionen, welche Aktion angesichts der aktuellen Umgebung und ihres Wertes am besten wäre.

Diese nutzerdefinierte Signalklasse wird also mit dem MQL5-Assistenten zu einem Expert Advisor zusammengesetzt, und nach einer kurzen Optimierungsphase für das Jahr 2022 auf dem 1-Stunden-Zeitrahmen, der das Symbol GBP USD verwendet, liefert uns eine der günstigen Einstellungen aus dieser Phase den folgenden Bericht:

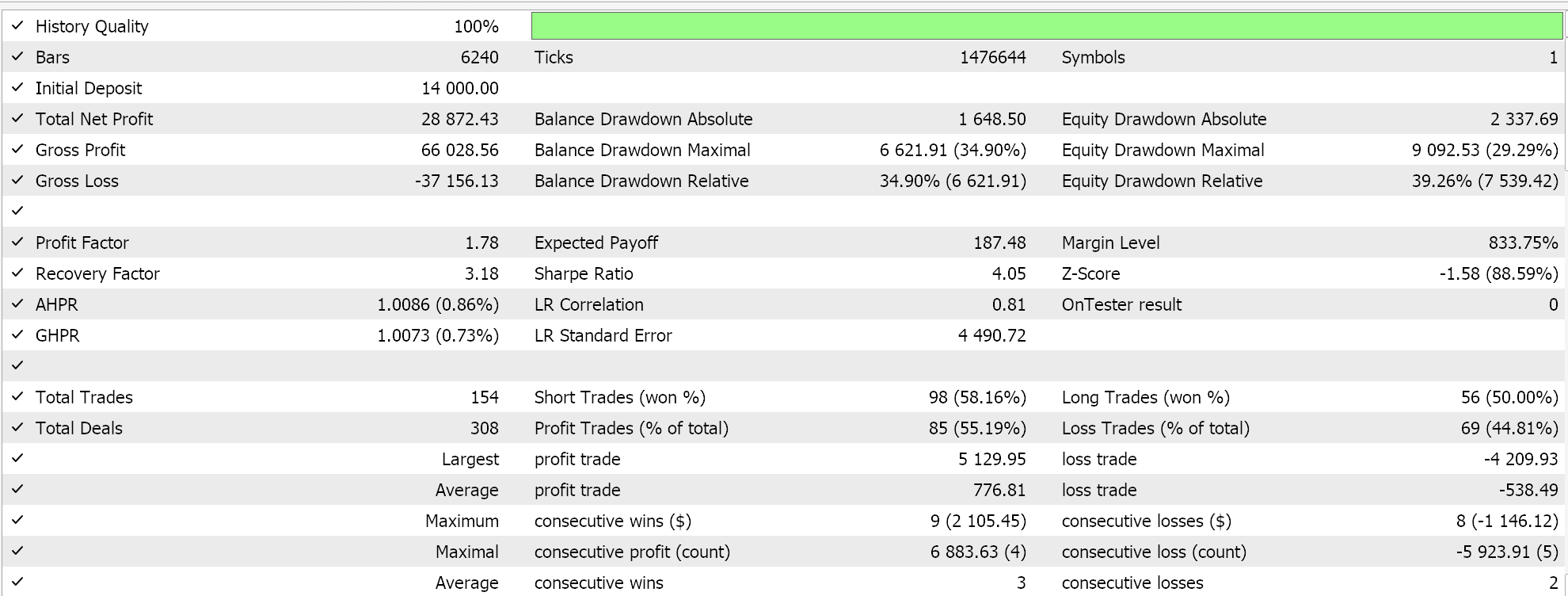
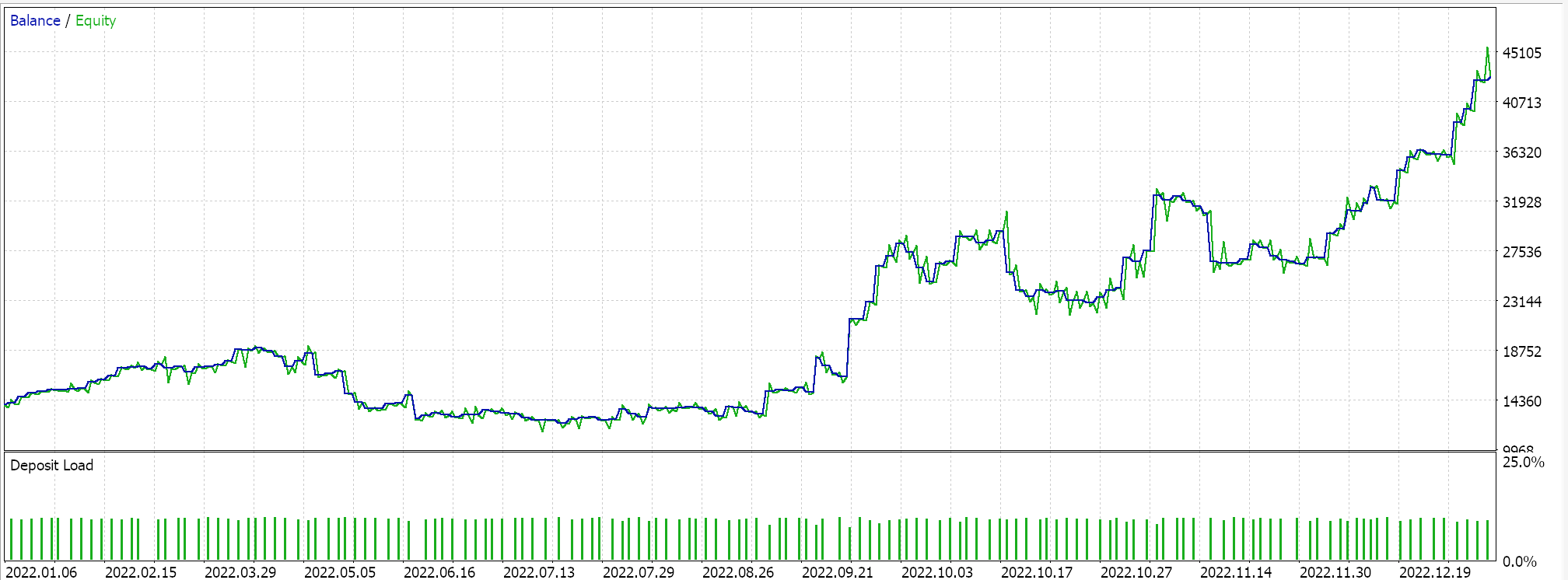
Diese Ergebnisse sprechen vielleicht für das Potenzial unserer nutzerdefinierten Signalklasse, aber ohne sie zu verunglimpfen, ist es immer empfehlenswert, die Einstellungen eines Expert Advisors zu überprüfen, bevor man ihn in einer Live-Umgebung einsetzt. Die Kreuzvalidierung und die zusätzlichen Tests über ein längeres Zeitfenster als das, was wir hier gemacht haben, kann der Leser nach eigenem Gutdünken untersuchen.

Optimieren und Abstimmen der Signalklasse mit TD-Lernen

Bei unseren obigen Testläufen optimierten wir nur für epsilon, ob wir Markov-Gewichtung im Aktualisierungsprozess verwenden und ob wir Aktualisierungen mit oder ohne Richtlinien durchführen. Es gab natürlich weitere typische Nicht-TD-Parameter wie die Schwellenwerte für Eröffnen und Schließen der Kauf- und Verkaufs-Bedingungen, das Take-Profit-Niveau sowie die Einstiegspreisschwelle in Punkten.

Im Rahmen von TD und Reinforcement Learning gibt es jedoch eine ganze Reihe von Parametern, die wir übergangen und mit voreingestellten Werten verwendet haben. Dies sind Alpha und Gamma, denen die Werte 0,1 bzw. 0,5 zugewiesen werden. Diese beiden Parameter sind für die Aktualisierung der Richtlinien von entscheidender Bedeutung und könnten sich sehr positiv auf die Gesamtleistung der Signalklasse auswirken. Die anderen wichtigen Parameter, die wir bei der Implementierung unserer Signalklasse übersehen haben, indem wir ihnen effektiv konstante Werte zugewiesen haben, sind die Einstellungen der Politik-Netze. Wir haben uns für ein 3-9-3-Netz entschieden, bei dem die Aktivierungsfunktionen auf jeder Schicht sowie die Lernrate voreingestellt waren. Jeder dieser Punkte und wahrscheinlich alle, wenn sie gleichzeitig angepasst werden, können große Auswirkungen auf die Ergebnisse und die Leistung der nutzerdefinierten Signalklasse haben.

Schlussfolgerung

Wir haben uns den Temporal Difference-Algorithmus des Reinforcement Learning angesehen und versucht, seine Anwendungsfälle hervorzuheben, die ihn von anderen Algorithmen, die wir bereits behandelt haben, unterscheiden. Ein Aspekt, den wir nicht untersucht haben, der aber für das Verstärkungslernen im Allgemeinen interessant ist, ist das Abklingen der Exploration im Laufe der Zeit. Die These bzw. das Argument, das dahinter steht, ist, dass mit der Zeit, in der ein Reinforcement-Learning-Modell lernt, die Notwendigkeit, neues Terrain zu erkunden oder weiter zu lernen, stark abnimmt; daher wäre die Nutzung wichtiger. Dies ist etwas, das die Leser prüfen können, wenn sie den beigefügten Code für die weitere Verwendung anpassen wollen.

Ein weiterer Aspekt könnte darin bestehen, epsilon variabel zu machen, und zwar nicht nur durch eine Verringerung, wie es der obige Zerfall impliziert. Die These dabei ist, dass Reinforcement Learning sehr dynamisch und anpassungsfähig sein soll, im Gegensatz zu überwachten Lernmodellen, die auf statischen Daten beruhen. Das Reinforcement Learning Framework von TD kann sich daher aktiv mit einer sich verändernden Umgebung auseinandersetzen. In einem früheren Artikel haben wir uns mit Methoden der dynamischen Lernrate befasst, und man könnte argumentieren, dass dasselbe auch für epsilon in Betracht gezogen werden könnte, sodass die Annahme des Abklingens allein nicht als einzige Möglichkeit dient, das Verstärkungslernen an seinen Wurzeln zu halten.