
Gás neural em desenvolvimento: Implementação em MQL5
Introdução
Na década de 90, pesquisadores de redes neurais artificiais chegaram a uma conclusão de que era necessário desenvolver uma nova classe destes mecanismos de computação, cuja função seria a ausência de uma topologia fixa de camadas de rede. Isto significa que o número e disposição dos neurônios artificiais no espaço apresentado não é predeterminado, mas é calculado no processo de aprendizagem de tais modelos, de acordo com as características dos dados de entrada, se ajustando de forma independente a eles.
A razão para o surgimento de tais ideias foi um número de problemas práticos sobre compressão prejudicada e quantização vetorial de parâmetros de entrada, como o reconhecimento de fala e imagem, classificação e reconhecimento de padrões abstratos.
Desde aquela época os mapas auto-organizáveis e a aprendizagem Hebbiana já eram conhecidos (em particular, os algoritmos que produzem tipologização de rede, ou seja, a criação de um conjunto de conexões entre os neurônios, formando um "quadro" de camada), e as abordagens para a aprendizagem competitiva "leve" foram trabalhadas (em tal procedimento a adaptação de carga ocorre não só em um neurônio "vencedor", mas também em seus "vizinhos"), o passo lógico era combinar estes métodos, o que foi feito em 1995 por um cientista alemão, Bernd Fritzke, que criou o algoritmo popular conhecido hoje em dia "gás neural em desenvolvimento"(, GNG).
O método se mostrou bem sucedido, de modo que uma série de suas modificações apareceram, uma delas foi a adaptação para a aprendizagem supervisionada (GNG supervisionado). Como observado pelo autor, o S-GNG mostrou significativamente uma maior eficiência na classificação de dados, supondo que uma rede de funções de base radial, devido à capacidade de otimizar a topologia nas áreas do espaço de entrada são difíceis de classificar. Sem dúvida, o GNG é superior ao grupamento "K-means".
Vale ressaltar que em 2001, Fritzke encerrou sua carreira de cientista da Universidade de Ruhr (Bochum, Alemanha), depois de receber uma oferta de emprego na bolsa de valores alemã (Deutsche Bӧrse). Bem, este fato foi mais um motivo para escolher o seu algoritmo como base para escrever este artigo.
1. Desenvolvimento de gás neural
Assim, GNG é um algoritmo que permite a implementação de grupamento adaptativo de dados de entrada, ou seja, não só divide o espaço em grupamentos, mas também determina sua quantidade necessária com base nas características dos dados.
Começando com apenas dois neurônios, o algoritmo muda consistentemente (principalmente aumenta) o número deles, criando um conjunto de conexões entre os neurônios que melhor correspondem à distribuição dos vetores de entrada, utilizando a abordagem de aprendizagem Hebbiana competitiva. Cada neurônio tem uma variável interna que acumula o chamado "erro local". As conexões entre os nós são caracterizadas por uma variável chamada "idade".
O pseudocódigo GNG parece com isto:
- Inicialização. Crie dois nós com os vetores de cargas, permitidos pela distribuição de vetores de entrada, e valores zero de erros locais; conecte os nós pela definição de sua idade para 0.
- Insira um vetor em uma rede neural
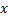 .
. - Encontre dois neurônios
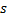 e
e 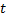 os mais próximos a
os mais próximos a 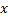 , por exemplo, nós com vetor de carga
, por exemplo, nós com vetor de carga 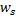 e
e 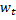 tal qual seja
tal qual seja 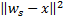 mínimo, e
mínimo, e 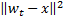 seja o segundo valor mínimo de distância entre todos os nós.
seja o segundo valor mínimo de distância entre todos os nós. -
Atualize o erro local do neurônio vencedor
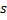 adicionando-lhe a distância quadrada entre os vetores
adicionando-lhe a distância quadrada entre os vetores 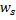 e
e 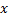 :
: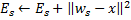
-
Desloque o neurônio vencedor
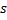 e todos os seus vizinhos topológicos (ou seja, todos os neurônios que têm uma conexão com o vencedor) na direção do vetor de entrada
e todos os seus vizinhos topológicos (ou seja, todos os neurônios que têm uma conexão com o vencedor) na direção do vetor de entrada 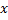 por distâncias iguais aos
por distâncias iguais aos 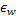 compartilhados e
compartilhados e 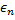 de um completo.
de um completo.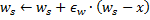
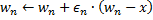
- Aumente a idade de todas as conexões de saída do
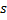 vencedor para 1.
vencedor para 1. - Se os dois melhores neurônios
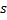 e
e 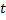 estão conectados, defina a idade de suas conexões para zero. Caso contrário, crie uma conexão entre eles.
estão conectados, defina a idade de suas conexões para zero. Caso contrário, crie uma conexão entre eles. - Remova as conexões com uma idade maior que
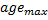 . Se isso resultar em neurônios que não tenham mais arestas incidentes, remova estes neurônios também.
. Se isso resultar em neurônios que não tenham mais arestas incidentes, remova estes neurônios também. -
Se o número de iteração corrente é um múltiplo de
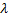 , e o limite de tamanho da rede não tenha atingido, insira um novo neurônio
, e o limite de tamanho da rede não tenha atingido, insira um novo neurônio 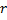 como se segue:
como se segue:- Determine um neurônio
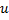 com um erro local grande.
com um erro local grande. - Determine entre os vizinhos de
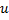 o neurônio
o neurônio 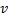 com um erro máximo.
com um erro máximo. - Crie um nó
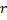 "no meio" entre
"no meio" entre 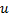 e
e 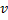 :
:
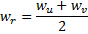
- Substitua a aresta entre
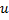 e
e 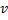 , pelo limite entre
, pelo limite entre 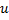 e
e 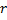 ,
, 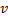 e
e 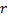 .
. - Diminua os erros dos neurônios
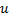 e
e 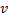 , defina o valor do erro de neurônio
, defina o valor do erro de neurônio 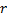 .
.
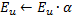
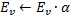
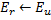
- Determine um neurônio
-
Diminua os erros de todos os neurônios
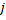 pela fração
pela fração 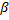 .
.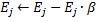
- Se um critério de parada ainda não está completado, continue com o passo 2.
Vamos considerar como o gás neural em desenvolvimento adapta-se às características do espaço de entrada.
Primeiro de tudo, preste atenção ao aumento da variável de erro do vencedor no passo 4. Este procedimento lida com o fato de que os nós que ganham na maioria das vezes, ou seja, aqueles no bairro em que o maior número de sinais de entrada aparece, tem o maior erro e, portanto, essas áreas são as principais candidatas a "compactação" pela adição de novos nós.
O deslocamento de nós, na direção do vetor de entrada, no passo 5, significa que o vencedor tenta "ser o termo médio" da sua posição entre os sinais de entrada localizados em sua vizinhança. Neste caso, o melhor neurônio pouco "puxa" os seus vizinhos na direção do sinal (![]() é escolhido como regra).
é escolhido como regra).
Eu explico a operação de arestas entre os neurônios nos passos 6-8. O significado do envelhecimento e da remoção das ligações velhas é que a topologia da rede deve ser o máximo perto da chamada triangulação Delaunay, ou seja, uma triangulação (subdivisão em triângulos) de neurônios em que, entre outras coisas, o ângulo mínimo de todos os ângulos dos triângulos na triangulação é maximizado (evitando triângulos "finos").
Falando de forma simples, a triangulação de Delaunay corresponde a mais "bela" tipologização de camada, no sentido da entropia máxima. Deve notar-se que a estrutura topológica é necessária, não em uma unidade separada, mas quando é utilizada para determinar a localização dos novos nós quando os mesmos são inseridos no passo 8 - eles são sempre localizados no centro de uma aresta.
O passo p é uma correção das variáveisde erro de todos os neurônios na camada. Isso é para garantir que a rede "se esqueça" dos antigos vetores de entrada e melhor responda aos novos. Assim, obtemos a possibilidade de usar o gás neural em desenvolvimento para a adaptação das redes neurais para o tempo dependente, especialmente a distribuição de deslocamento lento de sinais de entrada. Isso, no entanto, não lhe dá a capacidade de acompanhar as rápidas mudanças nas características das entradas (veja mais detalhes abaixo na seção onde são discutidos os inconvenientes do algoritmo).
Talvez devêssemos considerar separadamente o critério de parada. O algoritmo deixa lugar para a fantasia dos desenvolvedores de sistemas de análise. As opções possíveis são: verificar a eficiência da rede sobre o conjunto de teste, analisar a dinâmica do erro médio de neurônios, limitar a complexidade da rede, etc.
Para fins informativos, trabalharemos com a opção mais fácil - pois o objetivo deste artigo é demonstrar não só o próprio algoritmo, mas as possibilidades de sua implementação por meio de MQL5; continuaremos com a aprendizagem da camada até que nós esgotemos as entradas (naturalmente o seu número está predefinido).
2. Seleção do método para organização de dados
Ao programar o algoritmo vamos, obviamente, ter que lidar com a necessidade de armazenar o que são chamados de "conjuntos". Teremos dois conjuntos - um conjunto de neurônios e um conjunto de arestas entre eles. Embora ambas estruturas evoluirão no decorrer do programa (e estamos planejando tanto a adição quanto a remoção de itens), também deveremos fornecer mecanismos para isso.
Claro, poderíamos tentar usar as matrizes dinâmicas de objetos, mas teríamos de realizar numerosas operações de cópia do movimento de dados o que essencialmente retardaria o programa. Uma opção mais adequada para trabalhar com abstrações de propriedades especificadas é programar gráficos, e suas versões mais simples - uma lista interligada.
Vou lembrar aos nossos leitores o princípio de funcionamento da lista interligada (Fig. 1). Os objetos da classe base contém um ponteiro para o mesmo objeto como um dos membros, o que permite combiná-los em estruturas lineares, independentemente da ordem física de objetos na memória. Além disso, existe a classe "transporte", que encapsula o processo de movimento através da lista, acrescentando, inserindo e excluindo os nós, buscando, comparando e classificando, e, se necessário, outros procedimentos.
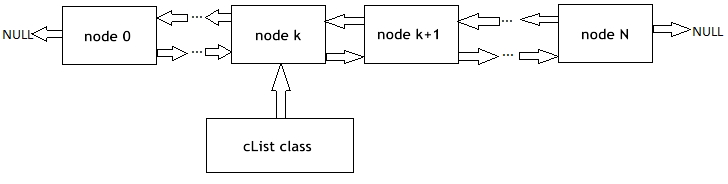
Figura 1. Representação esquemática da organização da lista interligada linear
Especialistas da corporação de software da MetaQuotes já implementaram as listas interligadas dos objetos da classe CObject em uma biblioteca padrão. O código do programa correspondente está localizado no arquivo de cabeçalho List.mqh, que está localizado em MQL5\Include\Arrays do pacote de entrega padrão de MetaTrader 5.
Não reinventaremos a roda e confiaremos na qualificação dos programadores respeitados da MetaQuotes tendo as classes CObject e CList como base de nossas estruturas de dados. Aqui usaremos um dos pilares da abordagem orientada a objeto - o mecanismo herança.
3. Programação do modelo
Primeiro, vamos definir a forma do software do conceito de "neurônio artificial".
Uma das regras de etiqueta ao desenvolver aplicações OOP é começar sempre a programação com as estruturas de dados mais comuns. Mesmo quando você está escrevendo apenas para si mesmo, mas especialmente se for presumido que os códigos estarão disponíveis para outros programadores, você deve ter em mente o fato de que, no futuro, os desenvolvedores podem ter ideias diferentes para o desenvolvimento e modificação da lógica do programa, e você não pode saber de antemão em que lugar serão feitas as alterações.
O princípio do OOP implica que outros desenvolvedores não terão que examinar suas classes, em vez disso, eles deverão ser capazes de herdar as estruturas de dados a partir dos dados disponíveis no lugar certo da hierarquia. Assim, a primeira classe escrita deve ser tão abstrata quanto possível, e os detalhes devem ser adicionados aos níveis mais baixos, quando estiver próximo "à terra do pecado".
Quando aplicado ao nosso problema, isto significa que começamos escrevendo um programa com a definição da classe CCustomNeuron ("algum tipo de neurônio"), que, como todos os neurônios artificiais, terá um certo número de sinapses (cargas de entrada) e valor de saída. Ele será capaz de inicializar (atribuir valores às cargas), calcular o valor do sinal na sua saída e ainda adaptar suas cargas através de um valor especificado.
Dificilmente podemos conseguir mais abstração (levando em conta o fato de que nós herdamos a nossa classe a partir de um CObject maximamente generalizado) - todos os neurônios devem ser capazes de executar as ações especificadas.
Para descrever os dados, crie um arquivo de cabeçalho Neurons.mqh, colocando-o na pasta Include\GNG.
//+------------------------------------------------------------------+ //| a base class to introduce object-neurons | //+------------------------------------------------------------------+ class CCustomNeuron:public CObject { protected: int m_synapses; double m_weights[]; public: double NET; CCustomNeuron(); ~CCustomNeuron(){}; void ZeroInit(int synapses); int Synapses(); void Init(double &weights[]); void Weights(double &weights[]); void AdaptWeights(double &delta[]); virtual void ProcessVector(double &in[]) {return;} virtual int Type() const { return(TYPE_CUSTOM_NEURON);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ void CCustomNeuron::CCustomNeuron() { m_synapses=0; NET=0; } //+------------------------------------------------------------------+ //| returns the dimension of the input vector of a neuron | //| INPUT: no | //| OUTPUT: number of "synapses" of the neuron | //+------------------------------------------------------------------+ int CCustomNeuron::Synapses() { return m_synapses; } //+------------------------------------------------------------------+ //| initializing neuron with a zero vector of weights. | //| INPUT: synapses - number of synapses (input weights) | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::ZeroInit(int synapses) { if(synapses<1) return; m_synapses=synapses; ArrayResize(m_weights,m_synapses); ArrayInitialize(m_weights,0); NET=0; } //+------------------------------------------------------------------+ //| initializing neuron weights with a set vector. | //| INPUT: weights - data vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::Init(double &weights[]) { if(ArraySize(weights)<1) return; m_synapses=ArraySize(weights); ArrayResize(m_weights,m_synapses); ArrayCopy(m_weights,weights); NET=0; } //+------------------------------------------------------------------+ //| obtaining vector of neuron weights. | //| INPUT: no | //| OUTPUT: weights - result | //+------------------------------------------------------------------+ void CCustomNeuron::Weights(double &weights[]) { ArrayResize(weights,m_synapses); ArrayCopy(weights,m_weights); } //+------------------------------------------------------------------+ //| change weights of the neuron by a specified value | //| INPUT: delta - correcting vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::AdaptWeights(double &delta[]) { if(ArraySize(delta)!=m_synapses) return; for(int i=0;i<m_synapses;i++) m_weights[i]+=delta[i]; NET=0; }
As funções definidas na classe são muito simples, por isso não há necessidade de incluir suas descrições detalhadas aqui. Note que definimos a função do processamento dos dados de entrada ProcessVector(double &in[]) (o valor de saída aqui é calculado como de um perceptron comum), com o modificador virtual.
Isto significa que, no caso do método ser redefinido por classes derivadas, o procedimento adequado será escolhido de acordo com a classe do objeto atual, de forma dinâmica no tempo de execução, o que aumenta sua flexibilidade inclusive no sentido de interação com o usuário e reduz os custos de trabalho para a programação.
Apesar do fato de que, aparentemente, não fizemos nada para organizar os neurônios em uma lista interligada, na verdade, isto já aconteceu no momento em que apontamos a nova classe herdada de CObject. Assim, agora os membros privados da nossa classe são m_first_node, m_curr_node e m_last_node, os quais são do tipo "ponteiro em CObject" e ponto, respectivamente, no primeiro, atual e último elemento da lista. Também temos todas as funções necessárias para a navegação através da lista.
Agora é hora de delinear as diferenças de um neurônio da camada de GNG de seus outros colegas, definindo a classe CGNGNeuron:
//+------------------------------------------------------------------+ //| a separate neuron of the GNG network | //+------------------------------------------------------------------+ class CGNGNeuron:public CCustomNeuron { public: int uid; double E; double U; double error; CGNGNeuron(); virtual void ProcessVector(double &in[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGNeuron::CGNGNeuron() { E=0; U=0; error=0; } //+------------------------------------------------------------------+ //| calculating "distance" from the neuron to the input vector | //| INPUT: in - data vector | //| OUTPUT: no | //| REMARK: the current "distance" is placed in the error variable, | //| "local error" is contained in another variable, | //| which is called E | //+------------------------------------------------------------------+ void CGNGNeuron::ProcessVector(double &in[]) { if(ArraySize(in)!=m_synapses) return; error=0; NET=0; for(int i=0;i<m_synapses;i++) { error+=(in[i]-m_weights[i])*(in[i]-m_weights[i]); } }
Então, como você pode ver, estas diferenças estão na presença de campos:
- erro - o quadrado atual da distância do vetor de entrada ao vetor de cargas do neurônio,
- E - uma variável que acumula o erro local e uma ID única,
- uid – é necessário para nos permitir promover a junção de neurônios por meio de conexões em pares (a indexação simples existente na classe CList não é suficiente, porque nós teremos que adicionar e excluir os neurônios, o que levará a uma confusão na numeração).
A função ProcessVector(...) mudou - agora calcula o valor do campo de erro.
Não preste atenção ao campo U no momento, o seu significado será explicado mais tarde na seção de "modificação de algoritmo".
O próximo passo é escrever uma classe que representa uma conexão entre dois neurônios.
//+------------------------------------------------------------------+ //| class defining connection (edge) between two neurons | //+------------------------------------------------------------------+ class CGNGConnection:public CObject { public: int uid1; int uid2; int age; CGNGConnection(); virtual int Type() const { return(TYPE_GNG_CONNECTION);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGConnection::CGNGConnection() { age=0; }
Não há nada difícil aqui - uma aresta tem duas extremidades (neurônios especificados por identificadores uid1 e uid2) e idade inicial igual a zero.
Agora vamos trabalhar com classes de "transporte" de listas interligadas, que conterão as possibilidades necessárias para implementar o algoritmo GNG.
Primeiro de tudo herde uma classe de neurônios a partir da lista CList:
//+------------------------------------------------------------------+ //| linked list of neurons | //+------------------------------------------------------------------+ class CGNGNeuronList:public CList { public: //--- constructor CGNGNeuronList() {MathSrand(TimeLocal());} CGNGNeuron *Append(); void Init(double &v1[],double &v2[]); CGNGNeuron *Find(int uid); void FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner); }; //+------------------------------------------------------------------+ //| adds an "empty" neuron at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new neuron | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGNeuron; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGNeuron; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; while(true) { int rnd=MathRand(); if(!CheckPointer(Find(rnd))) { ((CGNGNeuron *)m_curr_node).uid=rnd; break; } } //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initializing list by way of creating two neurons set | //| by vectors of weights | //| INPUT: v1,v2 - vectors of weights | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGNeuronList::Init(double &v1[],double &v2[]) { Clear(); Append(); ((CGNGNeuron *)m_curr_node).Init(v1); Append(); ((CGNGNeuron *)m_curr_node).Init(v2); } //+------------------------------------------------------------------+ //| search for a neuron by uid | //| INPUT: uid - a unique ID of the neuron | //| OUTPUT: pointer at the neuron if successful, otherwise NULL | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Find(int uid) { if(!GetFirstNode()) return(NULL); do { if(((CGNGNeuron *)m_curr_node).uid==uid) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for two "best" neurons in terms of minimal current error | //| INPUT: no | //| OUTPUT: Winner - neuron "closest" to the input vector | //| SecondWinner - second "closest" neuron | //+------------------------------------------------------------------+ void CGNGNeuronList::FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) { double err_min=0; Winner=NULL; if(!CheckPointer(GetFirstNode())) return; do { if(!CheckPointer(Winner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min= ((CGNGNeuron *)m_curr_node).error; Winner = m_curr_node; } } while(CheckPointer(GetNextNode())); err_min=0; SecondWinner=NULL; GetFirstNode(); do { if(m_curr_node!=Winner) if(!CheckPointer(SecondWinner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min=((CGNGNeuron *)m_curr_node).error; SecondWinner=m_curr_node; } } while(CheckPointer(GetNextNode())); m_curr_node=Winner; }
No construtor da classe, um gerador de números pseudo-aleatórios é inicializado: ele será usado para atribuir os elementos da lista de identificadores únicos.
Vamos esclarecer o significado dos métodos de classe:
- O método Append() é um complemento para a funcionalidade da classe CList. Ao chamá-lo, um nó é anexado no final da lista, ou o primeiro nó é criado, se a lascívia é vazia.
- A função Init(double &v1[],double &v2[]) relaciona sua aparência ao algoritmo GNG. Lembre-se, o desenvolvimento da rede começa com dois neurônios, logo, esta assinatura seria mais conveniente para nós. No corpo da função, ao usar IDs m_curr_node, m_first_node, m_last_nodeé necessário converter explicitamente, em seguida digitar CGNGNeuron*, se quisermos usar a funcionalidade desta classe (as variáveis especificadas foram herdadas de CList, então nominalmente eles apontam para CObject).
- A função Find(int uid), como diz seu nome, procura por um neurônio através de sua ID e retorna um ponteiro ao elemento ou a NULO se não puder encontrá-lo.
- FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) – também parte do algoritmo. Vamos precisar procurar por um vencedor na lista dos neurônios, e o próximo a ele, em termos de proximidade com o vetor de entrada, que é o motivo pelo qual usamos esta função. Note que os parâmetros são passados para essa função por referência, de modo que ainda podemos escrever que há valores retornados (*& significa "referência a um ponteiro" - esta é a sintaxe correta, o &* reverso significa "ponteiro em uma referência", o que é proibido: o compilador irá gerar um erro, neste caso).
A próxima classe é uma lista de conexões entre os neurônios.
//+------------------------------------------------------------------+ //| a linked list of connections between neurons | //+------------------------------------------------------------------+ class CGNGConnectionList:public CList { public: CGNGConnection *Append(); void Init(int uid1,int uid2); CGNGConnection *Find(int uid1,int uid2); CGNGConnection *FindFirstConnection(int uid); CGNGConnection *FindNextConnection(int uid); }; //+------------------------------------------------------------------+ //| adds an "empty" connection at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new binding | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGConnection; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGConnection; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initialize the list by creating one connection | //| INPUT: uid1,uid2 - IDs of neurons for the connection | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGConnectionList::Init(int uid1,int uid2) { Append(); ((CGNGConnection *)m_first_node).uid1 = uid1; ((CGNGConnection *)m_first_node).uid2 = uid2; m_last_node = m_first_node; m_curr_node = m_first_node; m_curr_idx=0; } //+------------------------------------------------------------------+ //| check if there is connection between the set neurons | //| INPUT: uid1,uid2 - IDs of the neurons | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Find(int uid1,int uid2) { if(!CheckPointer(GetFirstNode())) return(NULL); do { if((((CGNGConnection *)m_curr_node).uid1==uid1 && ((CGNGConnection *)m_curr_node).uid2==uid2) ||(((CGNGConnection *)m_curr_node).uid1==uid2 && ((CGNGConnection *)m_curr_node).uid2==uid1)) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the first element of the list | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindFirstConnection(int uid) { if(!CheckPointer(GetFirstNode())) return(NULL); while(true) { if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; if(!CheckPointer(GetNextNode())) return(NULL); } return(m_curr_node); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the list element next to the current one | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindNextConnection(int uid) { if(!CheckPointer(GetCurrentNode())) return(NULL); while(true) { if(!CheckPointer(GetNextNode())) return(NULL); if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; } return(m_curr_node); }
Métodos definidos da classe:
- Append(). A implementação deste método é semelhante ao descrito na classe anterior, exceto o tipo de retorno (infelizmente, não há modelos de classe em MQL5, por isso temos de escrever essas coisas de cada vez).
- Init(int uid1,int uid2) – o algoritmo GNG requer a inicialização de uma conexão no seu início, que é realizado nesta função.
- A função Find(int uid1,int uid2) está clara.
- A diferença entre os métodos FindFirstConnection(int uid) e FindNextConnection(int uid) é que o primeiro é uma procura de uma conexão com um vizinho a partir do início da lista, enquanto que o segundo começa com o nó próximo ao atual (m_curr_node).
Aqui a descrição de estruturas de dados acabada. é hora de começar a programar o nosso próprio algoritmo.
4. A classe do algoritmo
Crie um novo arquivo de cabeçalho GNG.mqh, coloque-o na pasta Include\GNG.
//+------------------------------------------------------------------+ //| GNG.mqh | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #include "Neurons.mqh" //+------------------------------------------------------------------+ //| the main class representing the GNG algorithm | //+------------------------------------------------------------------+ class CGNGAlgorithm { public: //--- linked lists of object-neurons and connection between them CGNGNeuronList *Neurons; CGNGConnectionList *Connections; //--- parameters of the algorithm int input_dimension; int iteration_number; int lambda; int age_max; double alpha; double beta; double eps_w; double eps_n; int max_nodes; CGNGAlgorithm(); ~CGNGAlgorithm(); virtual void Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes); virtual bool ProcessVector(double &in[],bool train=true); virtual bool StoppingCriterion(); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGAlgorithm::CGNGAlgorithm(void) { Neurons=new CGNGNeuronList(); Connections=new CGNGConnectionList(); Neurons.FreeMode(true); Connections.FreeMode(true); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CGNGAlgorithm::~CGNGAlgorithm(void) { delete Neurons; delete Connections; } //+------------------------------------------------------------------+ //| initializes the algorithm using two vectors of input data | //| INPUT: v1,v2 - input vectors | //| __lambda - number of iterations after which a new | //| neuron is inserted | //| __age_max - maximum age of connection | //| __alpha, __beta - used for adapting errors | //| __eps_w, __eps_n - used for adapting weights | //| __max_nodes - limit on the network size | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGAlgorithm::Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes) { iteration_number=0; input_dimension=__input_dimension; lambda=__lambda; age_max=__age_max; alpha= __alpha; beta = __beta; eps_w = __eps_w; eps_n = __eps_n; max_nodes=__max_nodes; Neurons.Init(v1,v2); CGNGNeuron *tmp; tmp=Neurons.GetFirstNode(); int uid1=tmp.uid; tmp=Neurons.GetLastNode(); int uid2=tmp.uid; Connections.Init(uid1,uid2); } //+------------------------------------------------------------------+ //| the main function of the algorithm | //| INPUT: in - vector of input data | //| train - if true, start learning, otherwise | //| only calculate the input values of neurons | //| OUTPUT: true, if stop condition is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::ProcessVector(double &in[],bool train=true) { if(ArraySize(in)!=input_dimension) return(StoppingCriterion()); int i; CGNGNeuron *tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.ProcessVector(in); tmp=Neurons.GetNextNode(); } if(!train) return(false); iteration_number++; //--- Find two neurons closest to in[], i.e. the nodes with weight vectors //--- Ws and Wt, so that ||Ws-in||^2 is minimal and ||Wt-in||^2 - //--- is second minimal value of distance of all the nodes. //--- Under ||*|| we mean Euclidean norm CGNGNeuron *Winner,*SecondWinner; Neurons.FindWinners(Winner,SecondWinner); //--- Update the local error of the winner Winner.E+=Winner.error; //--- Shift the winner and all its topological neighbors (i.e. //--- all neurons connected with the winner) in the direction of the input //--- vector by distances equal to fractions eps_w and eps_n of the full. double delta[],weights[]; Winner.Weights(weights); ArrayResize(delta,input_dimension); for(i=0;i<input_dimension;i++) delta[i]=eps_w*(in[i]-weights[i]); Winner.AdaptWeights(delta); //--- Increment the age of all connections emanating from the winner by 1. CGNGConnection *tmpc=Connections.FindFirstConnection(Winner.uid); while(CheckPointer(tmpc)) { if(tmpc.uid1==Winner.uid) tmp = Neurons.Find(tmpc.uid2); if(tmpc.uid2==Winner.uid) tmp = Neurons.Find(tmpc.uid1); tmp.Weights(weights); for(i=0;i<input_dimension;i++) delta[i]=eps_n*(in[i]-weights[i]); tmp.AdaptWeights(delta); tmpc.age++; tmpc=Connections.FindNextConnection(Winner.uid); } //--- If two best neurons are connected, reset the age of the connection. //--- Otherwise create a connection between them. tmpc=Connections.Find(Winner.uid,SecondWinner.uid); if(tmpc) tmpc.age=0; else { Connections.Append(); tmpc=Connections.GetLastNode(); tmpc.uid1 = Winner.uid; tmpc.uid2 = SecondWinner.uid; tmpc.age=0; } //--- Delete all the connections with an age larger than age_max. //--- If this results in neurons having no connections with other //--- nodes, remove those neurons. tmpc=Connections.GetFirstNode(); while(CheckPointer(tmpc)) { if(tmpc.age>age_max) { Connections.DeleteCurrent(); tmpc=Connections.GetCurrentNode(); } else tmpc=Connections.GetNextNode(); } tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { if(!Connections.FindFirstConnection(tmp.uid)) { Neurons.DeleteCurrent(); tmp=Neurons.GetCurrentNode(); } else tmp=Neurons.GetNextNode(); } //--- If the number of the current iteration is multiple of lambda, and the network //--- hasn't been reached yet, create a new neuron r according to the following rules CGNGNeuron *u,*v; if(iteration_number%lambda==0 && Neurons.Total()<max_nodes) { //--- 1.Find neuron u with the maximum local error. tmp=Neurons.GetFirstNode(); u=tmp; while(CheckPointer(tmp=Neurons.GetNextNode())) { if(tmp.E>u.E) u=tmp; } //--- 2.determin among the neighbors of u the node u with the maximum local error. tmpc=Connections.FindFirstConnection(u.uid); if(tmpc.uid1==u.uid) v=Neurons.Find(tmpc.uid2); else v=Neurons.Find(tmpc.uid1); while(CheckPointer(tmpc=Connections.FindNextConnection(u.uid))) { if(tmpc.uid1==u.uid) tmp=Neurons.Find(tmpc.uid2); else tmp=Neurons.Find(tmpc.uid1); if(tmp.E>v.E) v=tmp; } //--- 3.Create a node r "in the middle" between u and v. double wr[],wu[],wv[]; u.Weights(wu); v.Weights(wv); ArrayResize(wr,input_dimension); for(i=0;i<input_dimension;i++) wr[i]=(wu[i]+wv[i])/2; CGNGNeuron *r=Neurons.Append(); r.Init(wr); //--- 4.Replace the connection between u and v by a connection between u and r, v and r tmpc=Connections.Append(); tmpc.uid1=u.uid; tmpc.uid2=r.uid; tmpc=Connections.Append(); tmpc.uid1=v.uid; tmpc.uid2=r.uid; Connections.Find(u.uid,v.uid); Connections.DeleteCurrent(); //--- 5.Decrease the errors of neurons u and v, set the value of the error of //--- neuron r the same as of u. u.E*=alpha; v.E*=alpha; r.E = u.E; } //--- Decrease the errors of all neurons by the fraction beta tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.E*=(1-beta); tmp=Neurons.GetNextNode(); } //--- Check the stopping criterion return(StoppingCriterion()); } //+------------------------------------------------------------------+ //| Stopping criterion. In this version of file makes no | //| actions, always returns false. | //| INPUT: no | //| OUTPUT: true, if the criterion is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::StoppingCriterion() { return(false); }
A classe CGNGAlgorithm tem dois campos importantes - ponteiros nas listas interligadas de neurônios Neurônios e conexões entre eles Conexões. Eles serão o meio físico da estrutura da nossa rede neural. Os campos restantes são os parâmetros do algoritmo definido a partir do exterior.
Dos métodos de classe auxiliares destaquei Init(...), que passa os parâmetros externos para uma instância do algoritmo e inicializa as estruturas de dados e o critério de parada StoppingCriterion() que, como concordamos antes, não faz nada sempre retornando para falso.
A função ProcessVector(...), que é a principal função do algoritmo que processa o vetor de dados especificado, não contém quaisquer sutilezas: nós organizamos os dados e métodos com que se trabalham com eles para que quando cheguem ao algoritmo, só precisemos ir mecanicamente através de todos os seus passos. A sua localização no código é indicada pelos comentários adequados.
5. Utilização no trabalho
Vamos demonstrar o trabalho do algoritmo em dados reais do terminal MetaTrader 5.
Não estamos visando aqui, a criação de um trabalho de Expert Advisor com base em GNG (isto é um pouco demais para um artigo), queremos apenas ver como gás neural em desenvolvimento está funcionando, o que é chamado de apresentação "ao vivo".
A fim de processar lindamente os dados, crie uma janela vazia em escala ao longo do eixo de preços na faixa de 0-100. Para isso, usamos um indicador "vazio" Dummy.mq5 (que não tem outras funções):
//+------------------------------------------------------------------+ //| Dummy.mq5 | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #property version "1.00" #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_type1 DRAW_LINE #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double DummyBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DummyBuffer,INDICATOR_DATA); IndicatorSetString(INDICATOR_SHORTNAME,"GNG_dummy"); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[]) { //--- an empty buffer ArrayInitialize(DummyBuffer,EMPTY_VALUE); //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
No MetaEditor crie um script chamado GNG.mq5 - ele mostrará a rede na janela do indicador Dummy.
Os parâmetros externos - o número de vetores de dados de aprendizagem e os parâmetros do algoritmo:
//--- the number of input vectors used for learning input int samples=1000; //--- parameters of the algorithm input int lambda=20; input int age_max=15; input double alpha=0.5; input double beta=0.0005; input double eps_w=0.05; input double eps_n=0.0006; input int max_nodes=100;
Declare variáveis globais:
//---global variables CGNGAlgorithm *GNGAlgorithm; int window; int rsi_handle; int input_dimension; int _samples; double RSI_buffer[]; datetime time[];
Comece escrevendo a função OnStart(). Primeiro, vamos encontrar a janela necessária:
void OnStart() { int i,j; int window=ChartWindowFind(0,"GNG_dummy");
Para os dados de entrada, usamos os valores do indicador RSI - ele é conveniente porque seus valores são normalizados no intervalo de 0 a 100, por isso não precisamos realizar o pré-processamento.
Para um vetor de entrada da rede neural assumimos o par (input_dimension=2), que consiste em dois valores de RSI - na barra atual e anterior (cujo nome científico é "imersão de uma série de tempo em um espaço de característica bidimensional"). é mais fácil visualizar vetores bidimensionais de um gráfico plano.
Então, primeiro prepare os dados para inicializar e criar uma instância do objeto do algoritmo:
//--- to have CopyBuffer() work correctly, the number of the vectors //--- must be within the number of bars with a reserve left for the vector length _samples=samples+input_dimension+10; if(_samples>Bars(_Symbol,_Period)) _samples=Bars(_Symbol,_Period); //--- receive input data for the algorithm rsi_handle=iRSI(NULL,0,8,PRICE_CLOSE); CopyBuffer(rsi_handle,0,1,_samples,RSI_buffer); //--- return the user-defined value _samples=_samples-input_dimension-10; //--- remember open time of the first 100 bars CopyTime(_Symbol,_Period,0,100,time); //--- create an instance of the algorithm and set the size of input data GNGAlgorithm=new CGNGAlgorithm; input_dimension=2; //--- data vectors double v[],v1[],v2[]; ArrayResize(v,input_dimension); ArrayResize(v1,input_dimension); ArrayResize(v2,input_dimension); for(i=0;i<input_dimension;i++) { v1[i] = RSI_buffer[i]; v2[i] = RSI_buffer[i+3]; }
Agora inicialize o algoritmo:
//--- initialization
GNGAlgorithm.Init(input_dimension,v1,v2,lambda,age_max,alpha,beta,eps_w,eps_n,max_nodes);
Desenhe uma caixa e rótulos de informação retangulares (para ver visualmente quantas iterações do algoritmo foram processadase quantos neurônios "desenvolveram" na rede):
//-- draw a rectangular box and information labels ObjectCreate(0,"GNG_rect",OBJ_RECTANGLE,window,time[0],0,time[99],100); ObjectSetInteger(0,"GNG_rect",OBJPROP_BACK,true); ObjectSetInteger(0,"GNG_rect",OBJPROP_COLOR,DarkGray); ObjectSetInteger(0,"GNG_rect",OBJPROP_BGCOLOR,DarkGray); ObjectCreate(0,"Label_samples",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_samples",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_YDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: 2"); ObjectCreate(0,"Label_neurons",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_neurons",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_neurons",OBJPROP_YDISTANCE,25); ObjectSetInteger(0,"Label_neurons",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: 2");
No circuito principal, prepare um vetor para a entrada do algoritmo, demonstre-o no gráfico como um ponto azul:
//--- start the main loop of the algorithm with i=2 because 2 were used already for(i=2;i<_samples;i++) { //--- fill out the data vector (for clarity, get samples separated //--- by 3 bars - they are less correlated) for(j=0;j<input_dimension;j++) v[j]=RSI_buffer[i+j*3]; //--- show the vector on the chart ObjectCreate(0,"Sample_"+i,OBJ_ARROW,window,time[v[0]],v[1]); ObjectSetInteger(0,"Sample_"+i,OBJPROP_ARROWCODE,158); ObjectSetInteger(0,"Sample_"+i,OBJPROP_COLOR,Blue); ObjectSetInteger(0,"Sample_"+i,OBJPROP_BACK,true); //--- change the information label ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: "+string(i+1));
Passe o vetor para o algoritmo (apenas uma função - essa é a vantagem da abordagem orientada a objetos!):
//--- pass the input vector to the algorithm for calculation
GNGAlgorithm.ProcessVector(v);
Remova os neurônios antigos do gráfico e desenhe novos (círculos vermelhos) e conexões (linhas pontilhadas amarelas), destaque o vencedor e o segundo melhor neurônio com cores verde-limão e verde:
//--- we need to remove old neurons an connections from the chart to draw new ones then for(j=ObjectsTotal(0)-1;j>=0;j--) { string name=ObjectName(0,j); if(StringFind(name,"Neuron_")>=0) { ObjectDelete(0,name); } else if(StringFind(name,"Connection_")>=0) { ObjectDelete(0,name); } }
double weights[]; CGNGNeuron *tmp,*W1,*W2; CGNGConnection *tmpc; GNGAlgorithm.Neurons.FindWinners(W1,W2); //--- drawing the neurons tmp=GNGAlgorithm.Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.Weights(weights); ObjectCreate(0,"Neuron_"+tmp.uid,OBJ_ARROW,window,time[weights[0]],weights[1]); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_ARROWCODE,159); //--- the winner is colored Lime, second best - Green, others - Red if(tmp==W1) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Lime); else if(tmp==W2) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Green); else ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Red); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_BACK,false); tmp=GNGAlgorithm.Neurons.GetNextNode(); } ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: "+string(GNGAlgorithm.Neurons.Total())); //--- drawing connections tmpc=GNGAlgorithm.Connections.GetFirstNode(); while(CheckPointer(tmpc)) { int x1,x2,y1,y2; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid1); tmp.Weights(weights); x1=weights[0];y1=weights[1]; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid2); tmp.Weights(weights); x2=weights[0];y2=weights[1]; ObjectCreate(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJ_TREND,window,time[x1],y1,time[x2],y2); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_WIDTH,1); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_STYLE,STYLE_DOT); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_COLOR,Yellow); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_BACK,false); tmpc=GNGAlgorithm.Connections.GetNextNode(); } ChartRedraw(); } //--- delete the instance of the algorithm from the memory delete GNGAlgorithm; //--- a pause before clearing the chart while(!IsStopped()); //--- remove all the drawings from the chart ObjectsDeleteAll(0,window); }
Compile o código, inicie o indicador Dummy e depois execute o script GNG no mesmo gráfico. Uma imagem como a seguinte deve aparecer no gráfico:
Você vê, o algoritmo realmente funciona: a rede se adapta progressivamente aos novos dados de entrada tentando cobrir seu espaço de acordo com a densidade de povoamento de pontos azuis.
O vídeo mostra apenas o começo do processo de aprendizagem (apenas 1000 iterações, enquanto que o número real dos vetores necessários para a aprendizagem de GNG pode ser de até dezenas de milhares), porém, isso já nos dá uma compreensão decente e tanto razoável do processo.
6. Problemas conhecidos
Como já mencionado, o principal problema do GNG é a sua incapacidade para acompanhar séries não-estacionárias com características que mudam rapidamente. Tal distribuição do tipo "salto" de sinais de entrada pode lidar com muitos dos neurônios de camada GNG, tendo já ganho uma certa estrutura topológica, repentinamente encontram-se fora do negócio.
Além disso, uma vez que os sinais de entrada não se encontram na região da sua localização, a idade das ligações entre estes neurônios não é aumentada, por conseguinte, a parte "morta" da rede, que "relembra" as características antigas do sinal, não faz um trabalho útil, mas só consome recursos de computação (veja. Fig. 2).
No caso de distribuições de deslocamento lentas, este efeito adverso não é observado: se a velocidade de deslocamento é comparável à "velocidade de movimento" dos neurônios na adaptação de cargas, o GNG é capaz de controlar essas alterações.
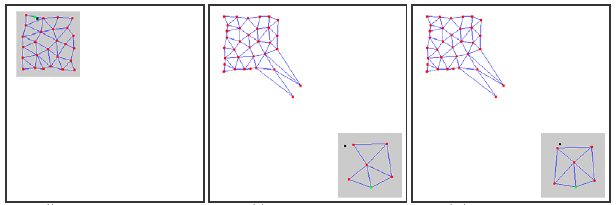
Figura 2. A reação do gás neural em desenvolvimento sobre a distribuição do tipo "salto"
Os nós inativos (mortos) separados também podem aparecer na rede se uma frequência muito alta de inserção de novos neurônios (o parâmetro λ) é dado na entrada do algoritmo.
O seu valor muito baixo conduz ao fato de que a rede começa a controlar as emissões estatisticamente insignificantes da distribuição de sinais de entrada, cuja probabilidade de recorrência é muito pequena. Se um neurônio GNG é inserido neste lugar, é quase certo que permanecerá inativo após isto por um longo tempo.
Além disso, como mostrado por estudos empíricos, o baixo valor de inserção, embora ele contribua para a rápida redução na média de erro da rede no início do processo de aprendizagem, como um resultado da preparação, dá os piores valores deste indicador: tal como dados de grupamento de rede mais brutos.
7. Modificação do algorítimo
O problema da distribuição do tipo "salto" pode ser resolvido através da modificação do algoritmo de uma determinada maneira. A modificação amplamente aceita é a que apresenta o fator chamado da utilidade de neurônios (GNG com fator Utility ou GNG-U). As alterações no pseudocódigo neste caso são mínimas e são como se segue:
- para cada neurônio
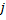 uma variável chamada "fator de utilidade"
uma variável chamada "fator de utilidade" 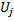 (essa variável U na lista de campos da classe CGNGNeuron) é definida em conformidade;
(essa variável U na lista de campos da classe CGNGNeuron) é definida em conformidade; -
no passo 4, depois de adaptar as cargas do neurônio vencedor, mudamos seu fator de utilidade por um montante igual à diferença entre um erro do segundo melhor neurônio e o vencedor:
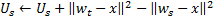
Fisicamente, este aditivo é o montante pelo qual o erro total da rede teria mudado se não houvesse vencedor nele (portanto, o segundo melhor vencedor seria o vencedor), ou seja, na verdade, caracteriza a utilidade do neurônio reduzir o erro global. -
os neurônios são removidos no passo 8 em um princípio diferente: apenas um nó com um valor mínimo de utilidade é removido, e apenas se o valor de erro máximo na camada excede o seu fator de utilidade por mais do que
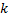 vezes:
vezes: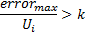
-
ao adicionar um novo nó no passo 9, seu fator de utilidade é calculado como a média aritmética entre as utilidades dos neurônios vizinhos:
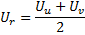
-
no passo 10, o fator de utilidade de todos os neurônios é reduzido da mesma maneira e na mesma ordem que as variáveisde erros:
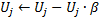
![]() constante, aqui é fundamental à capacidade de rastrear a não estacionaridade: seu valor muito grande leva à retirada de não só realmente a "pequena-utilidade", mas também outros neurônios bastante utilizáveis, já, um valor muito pequeno, leva a remoções raras e consequentemente à taxa reduzida de adaptação.
constante, aqui é fundamental à capacidade de rastrear a não estacionaridade: seu valor muito grande leva à retirada de não só realmente a "pequena-utilidade", mas também outros neurônios bastante utilizáveis, já, um valor muito pequeno, leva a remoções raras e consequentemente à taxa reduzida de adaptação.
No arquivo GNG.mqh o algoritmo GNG-L é descrito como uma classe derivada de CGNGAlgorithm. Os leitores podem acompanhar de forma independente as alterações e tentar usar o algoritmo.
Conclusão
Através da criação de uma rede neural, analisamos as principais características da programação orientada a objetos construídos na linguagem MQL5. Parece um fato bastante óbvio que, na ausência de tais oportunidades (pelas quais sou grato aos desenvolvedores), seria muito mais complicado escrever programas complexos para negociação automatizada.
Tal como para os algoritmos analisados, deve notar-se que, naturalmente, podem ser melhorados. Em particular, o primeiro candidato para a atualização é o número de parâmetros externos. Eles são muito numerosos e isso significa que podem muito bem haver tais modificações, em que os mesmos se tornariam variáveis internas e seriam selecionados com base nas características dos dados de entrada e o estado do algoritmo.
O autor do artigo deseja boa sorte a todos no estudo da neuroinformática e ao uso da mesma na negociação!
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/163
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Assistente MQL5: criar Expert Advisors sem programação
Assistente MQL5: criar Expert Advisors sem programação
 Handler de evento "nova barra"
Handler de evento "nova barra"
 O exemplo simples da criação de um indicador utilizando a lógica Fuzzy
O exemplo simples da criação de um indicador utilizando a lógica Fuzzy
 Simulink: um guia para os desenvolvedores de Expert Advisors
Simulink: um guia para os desenvolvedores de Expert Advisors
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Muito interessante,
Estou ansioso para implementá-la e usá-la em vez de uma rede neuronal fixa.
Artigo interessante!
Mas ele é bastante antigo - o compilador foi alterado e agora o código gera erros e avisos!
Olá
Pergunto se alguém da comunidade conseguiu desenvolver um EA usando GNG?
Pergunto se o resultado é bom?
Obrigado
Olá
Pergunto se alguém da comunidade conseguiu desenvolver um EA usando GNG?
Pergunto se o resultado é bom?
Obrigado
Bem... depois de quê? cinco meses o_O ninguém está disposto, então talvez eu mesmo possa comentar sobre isso.
Na implementação que você viu neste artigo, o NN é uma variante autoadaptável da chamada rede de funções de base radial. Se você comparar um EA baseado no algoritmo GNG com o mesmo tipo de EA baseado em um tipo não adaptável de rede neural de clusterização, provavelmente obterá melhores resultados com o GNG do que sem ele. Portanto, para responder à sua última pergunta, sim, o resultado é bom no sentido que acabei de explicar.
Quanto à primeira pergunta, eu mesmo desenvolvi EAs com um GNG dentro e ele funcionou moderadamente bem. No entanto, para o uso diário, prefiro outros algoritmos que, em geral, não são neurais. Posso confirmar isso lembrando que a RNA sempre apresenta uma "caixa preta", o que significa que você não entende realmente o que está acontecendo lá dentro quando ela processa os dados de entrada. Isso implica que a RNA seria um algoritmo de escolha somente em uma situação em que você tivesse um conjunto de dados completamente desestruturado com dependências intrínsecas absolutamente desconhecidas que você gostaria que a RNA extraísse de alguma forma. Observação: sem qualquer promessa de um resultado preciso. Em qualquer outro caso, ou seja, quando você tem algumas ideias sobre como as dependências em seu conjunto de dados podem ser organizadas, você deve primeiro tentar outras maneiras mais determinísticas de estruturá-lo. Milhares delas.