
Gas neuronal creciente: implementación en MQL5
Introducción
En la década de 1990, los investigadores de redes neuronales artificiales llegaron a la conclusión de que era necesario desarrollar una nueva clase de estos mecanismos de computación cuya característica fuera la ausencia de una topología fija de capas de red. Esto significa que el número y disposición de neuronas artificiales en el espacio no está predeterminado, sino que es calculado en el proceso de aprendizaje de tales modelos de acuerdo con las características de los datos de entrada, ajustándose de forma independiente a ellos.
La razón de la aparición de estas ideas fue la aparición de una serie de problemas prácticos sobre compresión obstaculizada y cuantificación vectorial de los parámetros de entrada, tales como el reconocimiento del habla e imágenes y la clasificación y reconocimiento de patrones abstractos.
Debido a que en aquel entonces los mapas autoorganizados y el aprendizaje Hebbian eran ya conocidos (en particular, los algoritmos que producen la topologización de la red, es decir, un conjunto de conexiones entre neuronas formando un "esquema" de capa) y se había trabajado en los enfoques del aprendizaje competitivo (en tales procedimientos se produce la adaptación no solo de la neurona "ganadora" sino también de sus vecinas) el paso lógico era combinar estos métodos, lo que fue llevado a cabo en 1995 por un científico alemán llamado Bernd Fritzke, quien creó el ahora popular algoritmo "gas neuronal creciente" (GNG).
El método tuvo un gran éxito y ello provocó la aparición de una serie de modificaciones del mismo, una de las cuales fue su adaptación para el aprendizaje supervisado (GNG supervisado). Tal y como afirmó su autor, el GNG supervisado se mostró mucho más eficiente en la clasificación de los datos que, digamos, una red de funciones básicas radiales, debido a su habilidad para optimizar la topología en las áreas de espacio de entrada que son difíciles de clasificar. Sin duda, GNG es superior al agrupamiento "K-means".
Cabe destacar que en 2001, Fritzke terminó su carrera como científico en la Universidad de Ruhr (Bochum, Alemania) después de recibir una oferta de trabajo en la bolsa alemana. Bien, este hecho fue una razón adicional para elegir su algoritmo como base para escribir este artículo.
1. Gas neuronal creciente
Por tanto, GNG es un algoritmo que permite implementar un agrupamiento adaptativo de los datos de entrada, es decir, no solo divide el espacio en conglomerados, sino que también determina el número de clusters necesarios basándose en las características de los datos.
Comenzando solo con dos neuronas, el algoritmo cambia, de forma consistente (en su mayor parte incrementa), el número de estos, mientras crea un conjunto de conexiones entre neuronas que se corresponde mejor con la distribución de vectores de entrada usando el enfoque del aprendizaje de Hebbian competitivo. Cada neurona tiene una variable interna que acumula los llamados "errores locales". Las conexiones entre nodos se caracterizan por una variable llamada "age".
El seudocódigo de GNG es el siguiente:
- Inicialización: crea dos nodos con los vectores de los pesos permitidos por la distribución de los vectores de entrada y los valores cero de los errores locales y conecta los nodos estableciendo su edad a 0.
- Da entrada a un vector a la red neuronal
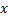 .
. - Encuentra dos neuronas
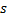 y
y 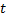 cercanas a
cercanas a 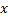 , es decir, nodos con el vector peso
, es decir, nodos con el vector peso 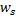 y
y 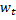 tales que
tales que 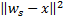 es mínimo, y
es mínimo, y 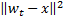 tiene el segundo valor mínimo entre todos los nodos.
tiene el segundo valor mínimo entre todos los nodos. -
Actualiza el error local de la neurona ganadora
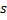 añadiéndola a la distancia al cuadrado entre los vectores
añadiéndola a la distancia al cuadrado entre los vectores 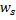 y
y 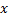 :
: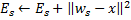
-
Cambia la neurona ganadora
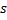 y todas sus vecinas topológicas (es decir, todas las neuronas que tienen una conexión con la ganadora) en la dirección del vector de entrada
y todas sus vecinas topológicas (es decir, todas las neuronas que tienen una conexión con la ganadora) en la dirección del vector de entrada 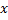 en distancias iguales a los porcentajes
en distancias iguales a los porcentajes 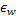 y
y 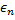 sobre una al completo.
sobre una al completo.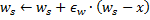
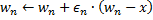
- Incrementa la edad de todas las conexiones que salen de la ganadora
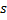 en 1.
en 1. - Si las dos mejores neuronas
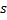 y
y 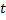 están conectadas, establece la edad de su conexión a cero. En caso contrario crea una conexión entre ellas.
están conectadas, establece la edad de su conexión a cero. En caso contrario crea una conexión entre ellas. - Elimina las conexiones con una edad mayor que
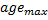 . Si esto da lugar a neuronas que no tengan más extremos, también elimina dichas neuronas.
. Si esto da lugar a neuronas que no tengan más extremos, también elimina dichas neuronas. -
Si el número de la iteración actual es un múltiplo de
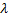 y no se ha alcanzado el tamaño límite de la red, inserta una nueva neurona
y no se ha alcanzado el tamaño límite de la red, inserta una nueva neurona 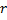 de la siguiente forma:
de la siguiente forma:- Determina una neurona
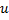 con un mayor error local.
con un mayor error local. - Determina entre las vecinas de
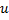 la neurona
la neurona 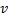 con un error máximo.
con un error máximo. - Crea un nodo
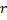 "en el punto medio" entre
"en el punto medio" entre 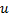 y
y 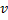 :
:
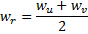
- Sustituye el extremo entre
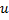 y
y 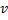 por el extremo entre
por el extremo entre 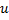 y
y 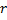 ,
, 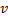 y
y 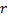 .
. - Disminuye los errores de las neuronas
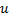 y
y 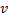 , establece el valor del error de la neurona
, establece el valor del error de la neurona 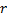 .
.
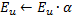
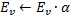
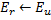
- Determina una neurona
-
Disminuye los errores de todas las neuronas
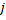 en la fracción
en la fracción 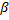 .
.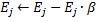
- Si no se cumple con un criterio de parada se continúa con el paso 2.
Vamos a ver cómo el gas neuronal creciente se adapta a las características del espacio de entrada.
En primer lugar, preste atención al incremento de la variable de error de la ganadora en el paso 4. Este procedimiento lleva al hecho de que los nodos que ganan con mayor frecuencia, es decir, los situados en las proximidades de aquellos en los que aparecen un mayor número de señales de entrada, tienen el mayor error y, por tanto, estas áreas son las primeras candidatas a la "compresión", añadiendo nuevos nodos.
El cambio de nodos en la dirección del vector de entrada en el paso 5 significa que la ganadora intenta "promediar" su posición entre las señales de entrada ubicadas en sus proximidades. En este caso, la mejor neurona "tira" de sus vecinas en la dirección de la señal (![]() se elige como regla).
se elige como regla).
En los pasos 6-8 explico la operación con extremos entre neuronas. El significado del envejecimiento y la eliminación de las conexiones antiguas es que la topología de la red debe acercarse al máximo a la llamada triangulación Delaunay, es decir, una triangulación (subdivisión en triángulos) de neuronas en las que, entre otras, el ángulo mínimo de todos los ángulos de los triángulos de la triangulación es máximo (evitando los triángulos "diminutos").
En pocas palabras, la triangulación Delaunay se corresponde con la topologización de la capa más "bonita", en el sentido de máxima entropía. Es preciso señalar que la estructura topológica es necesaria no como una unidad separada, sino cuando se usa para determinar la ubicación de nuevos nodos cuando estos son incluidos en el paso 8 -siempre se ubican en la mitad de un extremo.
El paso p es una corrección de las variables de error de todas las neuronas de la capa. Esto es así para garantizar que la red "olvida" los vectores de entrada antiguos y responde mejor a los nuevos. De esta forma tenemos la posibilidad de usar el gas neuronal creciente para la adaptación de las redes neuronales para las distribuciones de señales de entrada dependientes del tiempo, es decir, de deriva lenta. Esto, sin embargo, no da la posibilidad de seguir los cambios rápidos de las características de las entradas (véanse más detalles a continuación en el apartado donde se tratan las desventajas del algoritmo).
Quizá debamos tratar por separado el criterio de parada. El algoritmo da lugar a la fantasía de los programadores de sistemas de análisis. Las opciones posibles son: verificar la eficiencia de la red en las pruebas establecidas, analizar las dinámicas del error promedio de las neuronas, limitar la complejidad de la red, etc.
Con fines informativos, vamos a trabajar con la opción más sencilla, ya que el propósito de este artículo es demostrar no solo el propio algoritmo, sino las posibilidades de su implementación a través de MQL5. Continuaremos con el aprendizaje de la capa hasta que nos quedemos sin entradas (obviamente, su número está predeterminado).
2. Seleccionar el método para organizar los datos
Al programar el algoritmo, tendremos, obviamente, que hacer frente a la necesidad de almacenar los llamados "conjuntos". Tendremos dos conjuntos: uno de neuronas y uno de extremos entre ellas. Mientras que las dos estructuras evolucionarán durante el transcurso del programa (y hemos pensado que ambas añadirán y eliminarán ítems), debemos también proporcionar los mecanismos para ello.
Por supuesto, podríamos intentar usar matrices dinámicas de objetos, pero tendríamos que realizar muchas operaciones de copia y desplazamiento de datos y esto haría más lento el programa. Una opción más adecuada para trabajar con abstracciones con las propiedades especificadas serían los gráficos de programa y su versión más simple: una lista enlazada.
Recordaré a nuestros lectores el principio de las listas enlazadas (Fig. 1). Los objetos de la clase básica contienen un puntero hacia el mismo objeto, al igual que uno de los miembros, que hace posible combinarlos en estructuras lineales, con independencia del orden físico de los objetos en la memoria. Además, está la clase "carriage" que encapsula el procedimiento de desplazamiento a través de la lista añadiendo, insertando y eliminando nodos, buscando, comparando y clasificando y, si es necesario, realizando otros procedimientos.
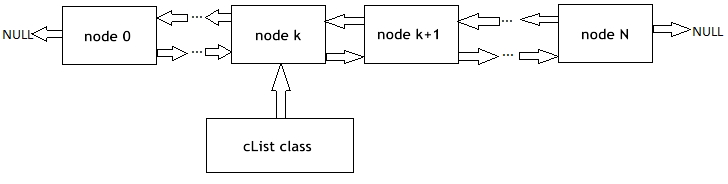
Figura 1. Representación esquemática de la organización de las listas enlazadas lineales
Los especialistas de MetaQuotes Software Corp. ya han implementado las listas enlazadas de los objetos de la clase CObject en una librería estándar. El código del programa correspondiente se encuentra en el archivo de cabecera List.mqh, que está ubicado en MQL5\Include\Arrays, en el paquete estándar de MetaTrader 5.
No vamos a reinventar la rueda y confiaremos en la cualificación de los respectivos programadores de MetaQuotes, tomando las clases CObject y CList como base de nuestras estructuras de datos. Aquí, usaremos uno de los pilares del enfoque orientado a objetos: el mecanismo de herencia.
3. Programar el modelo
Primero definamos el concepto de "neurona artificial" utilizado en informática.
Una de las reglas formales al desarrollar aplicaciones POO (programación orientada a objetos) es que siempre se debe empezar a programar con las estructuras de datos más comunes. Incluso cuando estamos escribiendo solo para nosotros mismos, pero especialmente si se asume que el código estará disponible para otros programadores, debemos tener en cuenta el hecho de que los futuros programadores pueden tener ideas diferentes para el desarrollo y modificación de la lógica del programa, y no podemos saber de antemano en qué parte se harán las enmiendas.
El principio de la POO implica que otros desarrolladores no tendrán que examinar nuestras clases, sino que en lugar de esto deberán poder heredar las estructuras de datos de los datos disponibles en el lugar adecuado de la jerarquía. De esta forma, la primera clase escrita debe ser tan abstracta como sea posible y deben añadirse las más específicas en niveles inferiores cuando estén cerca de "la tierra pecaminosa".
Cuando lo aplicamos a nuestro programa, esto significa que comenzamos a escribir el programa con la definición de la clase CCustomNeuron ("un tipo de neurona") que, como todas las neuronas artificiales, tendrá un número de sinapsis (pesos de entrada) y el valor de salida. Será posible inicializar (asignar valores a los pesos), calcular el valor de la señal a su salida e incluso adaptar sus pesos en un valor especificado.
Es difícil que podamos conseguir una mayor abstracción (teniendo en cuenta que heredamos nuestra clase de un CObject generalizado al máximo). Todas las neuronas deben ser capaces de realizar las acciones especificadas.
Para describir los datos creamos una archivo cabecera Neurons.mqh y lo situamos en la carpeta Include\GNG.
//+------------------------------------------------------------------+ //| a base class to introduce object-neurons | //+------------------------------------------------------------------+ class CCustomNeuron:public CObject { protected: int m_synapses; double m_weights[]; public: double NET; CCustomNeuron(); ~CCustomNeuron(){}; void ZeroInit(int synapses); int Synapses(); void Init(double &weights[]); void Weights(double &weights[]); void AdaptWeights(double &delta[]); virtual void ProcessVector(double &in[]) {return;} virtual int Type() const { return(TYPE_CUSTOM_NEURON);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ void CCustomNeuron::CCustomNeuron() { m_synapses=0; NET=0; } //+------------------------------------------------------------------+ //| returns the dimension of the input vector of a neuron | //| INPUT: no | //| OUTPUT: number of "synapses" of the neuron | //+------------------------------------------------------------------+ int CCustomNeuron::Synapses() { return m_synapses; } //+------------------------------------------------------------------+ //| initializing neuron with a zero vector of weights. | //| INPUT: synapses - number of synapses (input weights) | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::ZeroInit(int synapses) { if(synapses<1) return; m_synapses=synapses; ArrayResize(m_weights,m_synapses); ArrayInitialize(m_weights,0); NET=0; } //+------------------------------------------------------------------+ //| initializing neuron weights with a set vector. | //| INPUT: weights - data vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::Init(double &weights[]) { if(ArraySize(weights)<1) return; m_synapses=ArraySize(weights); ArrayResize(m_weights,m_synapses); ArrayCopy(m_weights,weights); NET=0; } //+------------------------------------------------------------------+ //| obtaining vector of neuron weights. | //| INPUT: no | //| OUTPUT: weights - result | //+------------------------------------------------------------------+ void CCustomNeuron::Weights(double &weights[]) { ArrayResize(weights,m_synapses); ArrayCopy(weights,m_weights); } //+------------------------------------------------------------------+ //| change weights of the neuron by a specified value | //| INPUT: delta - correcting vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::AdaptWeights(double &delta[]) { if(ArraySize(delta)!=m_synapses) return; for(int i=0;i<m_synapses;i++) m_weights[i]+=delta[i]; NET=0; }
Las funciones definidas en la clase son muy simples, luego no necesitamos incluir sus descripciones aquí. Observe que hemos definido la función de procesamiento de datos de entrada ProcessVector(double &in[]) (el valor de salida aquí se calcula como el de un perceptrón ordinario) con el modificador virtual.
Esto significa que en caso de que el método sea redefinido por clases derivadas, se elegirá el procedimiento adecuado dependiendo de la clase objeto actual dinámicamente en la ejecución, lo que incrementa su flexibilidad, incluso la relativa a la interacción, y reduce los costes de mano de obra de la programación.
A pesar del hecho de que aparentemente no hemos hecho nada para organizar las neuronas en una lista enlazada, en realidad esto ya ha ocurrido en el momento en el que hemos señalado que las nuevas clases heredan de CObject. Por tanto, ahora los miembros privados de nuestra clase son m_first_node, m_curr_node y m_last_node, que son del tipo "puntero en CObject" y punto, respectivamente, en el primer, actual y último elemento de la lista. También tenemos todas las funciones necesarias para navegar a través de la lista.
Es el momento de esbozar las diferencias entre una neurona de la capa GNG y otras compañeras mediante la definición de la clase CGNGNeuron:
//+------------------------------------------------------------------+ //| a separate neuron of the GNG network | //+------------------------------------------------------------------+ class CGNGNeuron:public CCustomNeuron { public: int uid; double E; double U; double error; CGNGNeuron(); virtual void ProcessVector(double &in[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGNeuron::CGNGNeuron() { E=0; U=0; error=0; } //+------------------------------------------------------------------+ //| calculating "distance" from the neuron to the input vector | //| INPUT: in - data vector | //| OUTPUT: no | //| REMARK: the current "distance" is placed in the error variable, | //| "local error" is contained in another variable, | //| which is called E | //+------------------------------------------------------------------+ void CGNGNeuron::ProcessVector(double &in[]) { if(ArraySize(in)!=m_synapses) return; error=0; NET=0; for(int i=0;i<m_synapses;i++) { error+=(in[i]-m_weights[i])*(in[i]-m_weights[i]); } }
Por tanto, como puede ver, estas diferencias se dan en presencia de los campos:
- error – el cuadrado actual de la distancia desde el vector de entrada al vector de los pesos de la neurona,
- E – una variable que acumula el error local y un único ID,
- uid – se requiere para permitirnos unir neuronas posteriormente mediante conexión en pares (el indexado simple que existe en la clase CList no es suficiente, ya que tendremos que añadir y eliminar neuronas, lo que llevará a confusión en la numeración).
La función ProcessVector(...) ha cambiado, ahora calcula el valor del campo error.
No preste atención al campo U hasta ahora, su significado será explicado posteriormente en el apartado "modificación del algoritmo".
El siguiente paso es escribir una clase que represente una conexión entre dos neuronas.
//+------------------------------------------------------------------+ //| class defining connection (edge) between two neurons | //+------------------------------------------------------------------+ class CGNGConnection:public CObject { public: int uid1; int uid2; int age; CGNGConnection(); virtual int Type() const { return(TYPE_GNG_CONNECTION);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGConnection::CGNGConnection() { age=0; }
No hay nada difícil aquí, un borde tiene dos extremos (las neuronas especificadas por los identificadores uid1 y uid2) y age, inicialmente iguales a cero.
Ahora trabajaremos con las clases "carriages" de las listas enlazadas, que contendrán las posibilidades requeridas para implementar el algoritmo GNG.
En primer lugar, heredamos una clase de lista de neuronas de CList:
//+------------------------------------------------------------------+ //| linked list of neurons | //+------------------------------------------------------------------+ class CGNGNeuronList:public CList { public: //--- constructor CGNGNeuronList() {MathSrand(TimeLocal());} CGNGNeuron *Append(); void Init(double &v1[],double &v2[]); CGNGNeuron *Find(int uid); void FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner); }; //+------------------------------------------------------------------+ //| adds an "empty" neuron at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new neuron | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGNeuron; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGNeuron; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; while(true) { int rnd=MathRand(); if(!CheckPointer(Find(rnd))) { ((CGNGNeuron *)m_curr_node).uid=rnd; break; } } //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initializing list by way of creating two neurons set | //| by vectors of weights | //| INPUT: v1,v2 - vectors of weights | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGNeuronList::Init(double &v1[],double &v2[]) { Clear(); Append(); ((CGNGNeuron *)m_curr_node).Init(v1); Append(); ((CGNGNeuron *)m_curr_node).Init(v2); } //+------------------------------------------------------------------+ //| search for a neuron by uid | //| INPUT: uid - a unique ID of the neuron | //| OUTPUT: pointer at the neuron if successful, otherwise NULL | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Find(int uid) { if(!GetFirstNode()) return(NULL); do { if(((CGNGNeuron *)m_curr_node).uid==uid) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for two "best" neurons in terms of minimal current error | //| INPUT: no | //| OUTPUT: Winner - neuron "closest" to the input vector | //| SecondWinner - second "closest" neuron | //+------------------------------------------------------------------+ void CGNGNeuronList::FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) { double err_min=0; Winner=NULL; if(!CheckPointer(GetFirstNode())) return; do { if(!CheckPointer(Winner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min= ((CGNGNeuron *)m_curr_node).error; Winner = m_curr_node; } } while(CheckPointer(GetNextNode())); err_min=0; SecondWinner=NULL; GetFirstNode(); do { if(m_curr_node!=Winner) if(!CheckPointer(SecondWinner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min=((CGNGNeuron *)m_curr_node).error; SecondWinner=m_curr_node; } } while(CheckPointer(GetNextNode())); m_curr_node=Winner; }
En la clase constructor se inicializa un generador de números seudoaleatorios que se usará para asignar los elementos de la lista de identificadores únicos.
Vamos a clarificar el significado de los métodos de la clase:
- El método Append() es un elemento adicional de la funcionalidad de la clase CList. Al llamarlo, se anexa un nodo al final de la lista o se crea el primer nodo si está vacío.
- La función Init(double &v1[],double &v2[]) debe su aparición al algoritmo GNG. Recuerde que el crecimiento de la red comienza con dos neuronas, por lo que esta firma nos será más útil. En el cuerpo de la función, al usar los ID m_curr_node, m_first_node y m_last_node, es necesario convertirlos explícitamente al tipo CGNGNeuron* si queremos usar la funcionalidad de su clase (las variables especificadas fueron heredadas de CList, por lo que nominalmente apuntan a CObject).
- La función Find(int uid) como se deduce de su nombre, busca una neurona por su ID y devuelve un puntero en el elemento encontrado o NULL si no puede encontrarlo.
- FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) también parte del algoritmo. Necesitaremos buscar una ganadora en la lista de neuronas y la que esté próxima a ella en términos de cercanía al vector de entrada. Para eso es para lo que usamos esta función. Observe que los parámetros se pasan a esta función por referencia, por lo que posteriormente podremos escribir ahí los valores devueltos (*& significa "referencia a un puntero" -esta es una sintaxis correcta, la inversa &* "puntero a una referencia" está prohibida ya que el compilador generará un error en este caso).
La próxima clase es una lista de conexiones entre neuronas.
//+------------------------------------------------------------------+ //| a linked list of connections between neurons | //+------------------------------------------------------------------+ class CGNGConnectionList:public CList { public: CGNGConnection *Append(); void Init(int uid1,int uid2); CGNGConnection *Find(int uid1,int uid2); CGNGConnection *FindFirstConnection(int uid); CGNGConnection *FindNextConnection(int uid); }; //+------------------------------------------------------------------+ //| adds an "empty" connection at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new binding | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGConnection; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGConnection; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initialize the list by creating one connection | //| INPUT: uid1,uid2 - IDs of neurons for the connection | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGConnectionList::Init(int uid1,int uid2) { Append(); ((CGNGConnection *)m_first_node).uid1 = uid1; ((CGNGConnection *)m_first_node).uid2 = uid2; m_last_node = m_first_node; m_curr_node = m_first_node; m_curr_idx=0; } //+------------------------------------------------------------------+ //| check if there is connection between the set neurons | //| INPUT: uid1,uid2 - IDs of the neurons | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Find(int uid1,int uid2) { if(!CheckPointer(GetFirstNode())) return(NULL); do { if((((CGNGConnection *)m_curr_node).uid1==uid1 && ((CGNGConnection *)m_curr_node).uid2==uid2) ||(((CGNGConnection *)m_curr_node).uid1==uid2 && ((CGNGConnection *)m_curr_node).uid2==uid1)) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the first element of the list | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindFirstConnection(int uid) { if(!CheckPointer(GetFirstNode())) return(NULL); while(true) { if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; if(!CheckPointer(GetNextNode())) return(NULL); } return(m_curr_node); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the list element next to the current one | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindNextConnection(int uid) { if(!CheckPointer(GetCurrentNode())) return(NULL); while(true) { if(!CheckPointer(GetNextNode())) return(NULL); if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; } return(m_curr_node); }
Métodos definidos de la clase:
- Append(). La implementación de este método es similar al descrito en la clase previa, excepto el tipo devuelto (por desgracia no hay plantillas de clases en MQL5, luego tenemos que escribir esto cada vez).
- Init(int uid1,int uid2) – el algoritmo GNG requiere la inicialización de una conexión al inicio que es realizada por esta función.
- La función Find(int uid1,int uid2) está clara.
- La diferencia entre los métodos FindFirstConnection(int uid) y FindNextConnection(int uid) es que el primero busca una conexión con un vecino comenzando desde el principio de la lista, mientras que el segundo comienza con el nodo próximo al actual (m_curr_node).
Aquí finaliza la descripción de las estructuras de datos. Es el momento de empezar a programar nuestro propio algoritmo.
4. La clase del algoritmo
Creamos un nuevo archivo cabecera GNG.mqh y lo situamos en la carpeta Inlude\GNG.
//+------------------------------------------------------------------+ //| GNG.mqh | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #include "Neurons.mqh" //+------------------------------------------------------------------+ //| the main class representing the GNG algorithm | //+------------------------------------------------------------------+ class CGNGAlgorithm { public: //--- linked lists of object-neurons and connection between them CGNGNeuronList *Neurons; CGNGConnectionList *Connections; //--- parameters of the algorithm int input_dimension; int iteration_number; int lambda; int age_max; double alpha; double beta; double eps_w; double eps_n; int max_nodes; CGNGAlgorithm(); ~CGNGAlgorithm(); virtual void Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes); virtual bool ProcessVector(double &in[],bool train=true); virtual bool StoppingCriterion(); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGAlgorithm::CGNGAlgorithm(void) { Neurons=new CGNGNeuronList(); Connections=new CGNGConnectionList(); Neurons.FreeMode(true); Connections.FreeMode(true); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CGNGAlgorithm::~CGNGAlgorithm(void) { delete Neurons; delete Connections; } //+------------------------------------------------------------------+ //| initializes the algorithm using two vectors of input data | //| INPUT: v1,v2 - input vectors | //| __lambda - number of iterations after which a new | //| neuron is inserted | //| __age_max - maximum age of connection | //| __alpha, __beta - used for adapting errors | //| __eps_w, __eps_n - used for adapting weights | //| __max_nodes - limit on the network size | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGAlgorithm::Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes) { iteration_number=0; input_dimension=__input_dimension; lambda=__lambda; age_max=__age_max; alpha= __alpha; beta = __beta; eps_w = __eps_w; eps_n = __eps_n; max_nodes=__max_nodes; Neurons.Init(v1,v2); CGNGNeuron *tmp; tmp=Neurons.GetFirstNode(); int uid1=tmp.uid; tmp=Neurons.GetLastNode(); int uid2=tmp.uid; Connections.Init(uid1,uid2); } //+------------------------------------------------------------------+ //| the main function of the algorithm | //| INPUT: in - vector of input data | //| train - if true, start learning, otherwise | //| only calculate the input values of neurons | //| OUTPUT: true, if stop condition is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::ProcessVector(double &in[],bool train=true) { if(ArraySize(in)!=input_dimension) return(StoppingCriterion()); int i; CGNGNeuron *tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.ProcessVector(in); tmp=Neurons.GetNextNode(); } if(!train) return(false); iteration_number++; //--- Find two neurons closest to in[], i.e. the nodes with weight vectors //--- Ws and Wt, so that ||Ws-in||^2 is minimal and ||Wt-in||^2 - //--- is second minimal value of distance of all the nodes. //--- Under ||*|| we mean Euclidean norm CGNGNeuron *Winner,*SecondWinner; Neurons.FindWinners(Winner,SecondWinner); //--- Update the local error of the winner Winner.E+=Winner.error; //--- Shift the winner and all its topological neighbors (i.e. //--- all neurons connected with the winner) in the direction of the input //--- vector by distances equal to fractions eps_w and eps_n of the full. double delta[],weights[]; Winner.Weights(weights); ArrayResize(delta,input_dimension); for(i=0;i<input_dimension;i++) delta[i]=eps_w*(in[i]-weights[i]); Winner.AdaptWeights(delta); //--- Increment the age of all connections emanating from the winner by 1. CGNGConnection *tmpc=Connections.FindFirstConnection(Winner.uid); while(CheckPointer(tmpc)) { if(tmpc.uid1==Winner.uid) tmp = Neurons.Find(tmpc.uid2); if(tmpc.uid2==Winner.uid) tmp = Neurons.Find(tmpc.uid1); tmp.Weights(weights); for(i=0;i<input_dimension;i++) delta[i]=eps_n*(in[i]-weights[i]); tmp.AdaptWeights(delta); tmpc.age++; tmpc=Connections.FindNextConnection(Winner.uid); } //--- If two best neurons are connected, reset the age of the connection. //--- Otherwise create a connection between them. tmpc=Connections.Find(Winner.uid,SecondWinner.uid); if(tmpc) tmpc.age=0; else { Connections.Append(); tmpc=Connections.GetLastNode(); tmpc.uid1 = Winner.uid; tmpc.uid2 = SecondWinner.uid; tmpc.age=0; } //--- Delete all the connections with an age larger than age_max. //--- If this results in neurons having no connections with other //--- nodes, remove those neurons. tmpc=Connections.GetFirstNode(); while(CheckPointer(tmpc)) { if(tmpc.age>age_max) { Connections.DeleteCurrent(); tmpc=Connections.GetCurrentNode(); } else tmpc=Connections.GetNextNode(); } tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { if(!Connections.FindFirstConnection(tmp.uid)) { Neurons.DeleteCurrent(); tmp=Neurons.GetCurrentNode(); } else tmp=Neurons.GetNextNode(); } //--- If the number of the current iteration is multiple of lambda, and the network //--- hasn't been reached yet, create a new neuron r according to the following rules CGNGNeuron *u,*v; if(iteration_number%lambda==0 && Neurons.Total()<max_nodes) { //--- 1.Find neuron u with the maximum local error. tmp=Neurons.GetFirstNode(); u=tmp; while(CheckPointer(tmp=Neurons.GetNextNode())) { if(tmp.E>u.E) u=tmp; } //--- 2.determin among the neighbors of u the node u with the maximum local error. tmpc=Connections.FindFirstConnection(u.uid); if(tmpc.uid1==u.uid) v=Neurons.Find(tmpc.uid2); else v=Neurons.Find(tmpc.uid1); while(CheckPointer(tmpc=Connections.FindNextConnection(u.uid))) { if(tmpc.uid1==u.uid) tmp=Neurons.Find(tmpc.uid2); else tmp=Neurons.Find(tmpc.uid1); if(tmp.E>v.E) v=tmp; } //--- 3.Create a node r "in the middle" between u and v. double wr[],wu[],wv[]; u.Weights(wu); v.Weights(wv); ArrayResize(wr,input_dimension); for(i=0;i<input_dimension;i++) wr[i]=(wu[i]+wv[i])/2; CGNGNeuron *r=Neurons.Append(); r.Init(wr); //--- 4.Replace the connection between u and v by a connection between u and r, v and r tmpc=Connections.Append(); tmpc.uid1=u.uid; tmpc.uid2=r.uid; tmpc=Connections.Append(); tmpc.uid1=v.uid; tmpc.uid2=r.uid; Connections.Find(u.uid,v.uid); Connections.DeleteCurrent(); //--- 5.Decrease the errors of neurons u and v, set the value of the error of //--- neuron r the same as of u. u.E*=alpha; v.E*=alpha; r.E = u.E; } //--- Decrease the errors of all neurons by the fraction beta tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.E*=(1-beta); tmp=Neurons.GetNextNode(); } //--- Check the stopping criterion return(StoppingCriterion()); } //+------------------------------------------------------------------+ //| Stopping criterion. In this version of file makes no | //| actions, always returns false. | //| INPUT: no | //| OUTPUT: true, if the criterion is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::StoppingCriterion() { return(false); }
La clase CGNGAlgorithm tiene dos campos importantes: los punteros y las listas enlazadas de neuronas Neurons y las conexiones entre ellas Connections. Serán el medio físico de la estructura de nuestra red neuronal. Los campos restantes son los parámetros del algoritmo definido desde el exterior.
De los métodos de clases auxiliares yo destacaría Init(...), que pasa los parámetros externos a una instancia del algoritmo e inicializa las estructuras de datos y el criterio de parada StoppingCriterion() que, como acordamos antes, no hace nada y siempre devuelve false.
La función principal del algoritmo que procesa el vector de datos especificado no contiene nada especial: hemos organizado los datos y métodos para trabajar con ellos de forma que, respecto al algoritmo, solo necesitamos seguir mecánicamente todos los pasos. Su ubicación en el código está indicada por los comentarios apropiados.
5. Su funcionamiento en la práctica
Vamos a ver el funcionamiento del algoritmo con datos reales del terminal de MetaTrader 5.
Aquí no pretendemos crear un asesor experto basado en GNG (esto sería más adecuado para un artículo). Queremos solo ver cómo funciona el gas neuronal creciente en lo que se llama la presentación "en vivo".
Para representar de forma apropiada los datos, vamos a crear una ventana vacía escalada a lo largo del eje de precio en el rango 0-100. Para esta finalidad, usamos un indicador "vacío" Dummy.mq5 (no tiene otra función distinta a esta):
//+------------------------------------------------------------------+ //| Dummy.mq5 | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #property version "1.00" #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_type1 DRAW_LINE #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double DummyBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DummyBuffer,INDICATOR_DATA); IndicatorSetString(INDICATOR_SHORTNAME,"GNG_dummy"); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[]) { //--- an empty buffer ArrayInitialize(DummyBuffer,EMPTY_VALUE); //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
En MetaEditor, creamos un script llamado GNG.mq5 que mostrará la red en la ventana del indicador Dummy.
Parámetros externos, el número de vectores de datos para el aprendizaje y los parámetros del algoritmo:
//--- the number of input vectors used for learning input int samples=1000; //--- parameters of the algorithm input int lambda=20; input int age_max=15; input double alpha=0.5; input double beta=0.0005; input double eps_w=0.05; input double eps_n=0.0006; input int max_nodes=100;
Declaramos variables globales:
//---global variables CGNGAlgorithm *GNGAlgorithm; int window; int rsi_handle; int input_dimension; int _samples; double RSI_buffer[]; datetime time[];
Empezamos escribiendo la función OnStart(). Primero vamos a encontrar la ventana necesaria:
void OnStart() { int i,j; int window=ChartWindowFind(0,"GNG_dummy");
Para los datos de entrada, usamos los valores del indicador RSI. Esto es conveniente ya que sus valores están normalizados en el rango de 0 a 100, por lo que no necesitaremos realizar un preprocesamiento.
Para un vector de entrada de la red neuronal asumimos el par (input_dimension=2) que comprende dos valores RSI, en la barra actual y en la anterior (cuyo nombre científico es "inmersión de una serie de tiempo en un espacio de dos dimensiones"). Es más fácil representar en pantalla vectores de dos dimensiones en un gráfico plano.
Por tanto, primero preparamos los datos para inicializar y creamos una instancia del objeto del algoritmo:
//--- to have CopyBuffer() work correctly, the number of the vectors //--- must be within the number of bars with a reserve left for the vector length _samples=samples+input_dimension+10; if(_samples>Bars(_Symbol,_Period)) _samples=Bars(_Symbol,_Period); //--- receive input data for the algorithm rsi_handle=iRSI(NULL,0,8,PRICE_CLOSE); CopyBuffer(rsi_handle,0,1,_samples,RSI_buffer); //--- return the user-defined value _samples=_samples-input_dimension-10; //--- remember open time of the first 100 bars CopyTime(_Symbol,_Period,0,100,time); //--- create an instance of the algorithm and set the size of input data GNGAlgorithm=new CGNGAlgorithm; input_dimension=2; //--- data vectors double v[],v1[],v2[]; ArrayResize(v,input_dimension); ArrayResize(v1,input_dimension); ArrayResize(v2,input_dimension); for(i=0;i<input_dimension;i++) { v1[i] = RSI_buffer[i]; v2[i] = RSI_buffer[i+3]; }
Ahora inicializamos el algoritmo:
//--- initialization
GNGAlgorithm.Init(input_dimension,v1,v2,lambda,age_max,alpha,beta,eps_w,eps_n,max_nodes);
Dibuja una caja rectangular y etiquetas de información (para ver visualmente cuantas iteraciones del algoritmo fueron procesadas y cuantas neuronas han "crecido" en la red):
//-- draw a rectangular box and information labels ObjectCreate(0,"GNG_rect",OBJ_RECTANGLE,window,time[0],0,time[99],100); ObjectSetInteger(0,"GNG_rect",OBJPROP_BACK,true); ObjectSetInteger(0,"GNG_rect",OBJPROP_COLOR,DarkGray); ObjectSetInteger(0,"GNG_rect",OBJPROP_BGCOLOR,DarkGray); ObjectCreate(0,"Label_samples",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_samples",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_YDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: 2"); ObjectCreate(0,"Label_neurons",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_neurons",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_neurons",OBJPROP_YDISTANCE,25); ObjectSetInteger(0,"Label_neurons",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: 2");
En el bucle principal preparamos un vector para que la entrada del algoritmo lo muestre en el gráfico como un punto azul:
//--- start the main loop of the algorithm with i=2 because 2 were used already for(i=2;i<_samples;i++) { //--- fill out the data vector (for clarity, get samples separated //--- by 3 bars - they are less correlated) for(j=0;j<input_dimension;j++) v[j]=RSI_buffer[i+j*3]; //--- show the vector on the chart ObjectCreate(0,"Sample_"+i,OBJ_ARROW,window,time[v[0]],v[1]); ObjectSetInteger(0,"Sample_"+i,OBJPROP_ARROWCODE,158); ObjectSetInteger(0,"Sample_"+i,OBJPROP_COLOR,Blue); ObjectSetInteger(0,"Sample_"+i,OBJPROP_BACK,true); //--- change the information label ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: "+string(i+1));
Pasa el vector al algoritmo (solo la función -¡esa es la ventaja del enfoque orientado a objeto!)
//--- pass the input vector to the algorithm for calculation
GNGAlgorithm.ProcessVector(v);
Elimina las neuronas antiguas del gráfico y dibuja nuevas neuronas (círculos rojos) y conexiones (líneas discontinuas amarillas), destaca la ganadora y la segunda mejor neurona con los colores lima y verde:
//--- we need to remove old neurons an connections from the chart to draw new ones then for(j=ObjectsTotal(0)-1;j>=0;j--) { string name=ObjectName(0,j); if(StringFind(name,"Neuron_")>=0) { ObjectDelete(0,name); } else if(StringFind(name,"Connection_")>=0) { ObjectDelete(0,name); } }
double weights[]; CGNGNeuron *tmp,*W1,*W2; CGNGConnection *tmpc; GNGAlgorithm.Neurons.FindWinners(W1,W2); //--- drawing the neurons tmp=GNGAlgorithm.Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.Weights(weights); ObjectCreate(0,"Neuron_"+tmp.uid,OBJ_ARROW,window,time[weights[0]],weights[1]); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_ARROWCODE,159); //--- the winner is colored Lime, second best - Green, others - Red if(tmp==W1) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Lime); else if(tmp==W2) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Green); else ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Red); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_BACK,false); tmp=GNGAlgorithm.Neurons.GetNextNode(); } ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: "+string(GNGAlgorithm.Neurons.Total())); //--- drawing connections tmpc=GNGAlgorithm.Connections.GetFirstNode(); while(CheckPointer(tmpc)) { int x1,x2,y1,y2; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid1); tmp.Weights(weights); x1=weights[0];y1=weights[1]; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid2); tmp.Weights(weights); x2=weights[0];y2=weights[1]; ObjectCreate(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJ_TREND,window,time[x1],y1,time[x2],y2); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_WIDTH,1); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_STYLE,STYLE_DOT); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_COLOR,Yellow); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_BACK,false); tmpc=GNGAlgorithm.Connections.GetNextNode(); } ChartRedraw(); } //--- delete the instance of the algorithm from the memory delete GNGAlgorithm; //--- a pause before clearing the chart while(!IsStopped()); //--- remove all the drawings from the chart ObjectsDeleteAll(0,window); }
Compila el código, inicia el indicador Dummy y a continuación ejecuta el script GNG en el mismo gráfico. En el gráfico debe aparecer una imagen similar a la siguiente:
Verá que el algoritmo funciona realmente: la rejilla se adapta gradualmente a los nuevos datos que llegan intentando cubrir su espacio de acuerdo con la densidad de los puntos azules.
El vídeo muestra solo el inicio del proceso de aprendizaje (solo 1.000 iteraciones, mientras que el número real de vectores requeridos para el aprendizaje de GNG puede llegar a ser de hasta decenas de miles). Sin embargo, esto ya nos proporciona una visión bastante decente del proceso.
6. Problemas conocidos
Como ya se ha mencionado, el principal problema del GNG es su incapacidad para hacer un seguimiento de las series no estacionarias con características que cambian rápidamente. Tales distribuciones "cambiantes" de señales de entrada pueden hacer que todas estas neuronas de la capa GNG ganen una cierta estructura topológica y que puedan encontrarse repentinamente sin actividad.
Además, como las señales de entrada no caen en la región de su ubicación, la edad de las conexiones entre estas neuronas no se incrementa y, por tanto, la parte "muerta" de la red que "recuerda" las anteriores características de la señal no realiza un trabajo útil, sino que consume recursos de procesamiento (véase la Fig. 2).
En caso de distribuciones de deriva lenta no se observa este efecto adverso: si la velocidad de deriva es comparable a la "velocidad del movimiento" de las neuronas en la adaptación de los pesos, GNG será capaz de hacer un seguimiento de estos cambios.
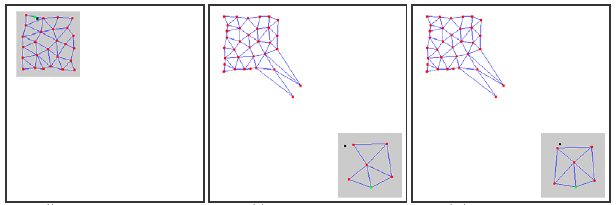
Figura 2. Reacción del gas neuronal creciente en la distribución "cambiante"
Los nodos separados inactivos (muertos) pueden también aparecer en la red si se da una frecuencia muy alta de inserción de nuevas neuronas en la entrada del algoritmo.
Un valor demasiado bajo hace que la red comience a seguir emisiones estadísticamente insignificantes de la distribución de las señales de entrada, cuya probabilidad de recurrencia es muy pequeña. Si una neurona GNG se inserta en este lugar, casi con toda seguridad permanecerá inactiva después por un largo tiempo.
Además, como ha mostrado la investigación empírica, el valor bajo de la inserción, aunque contribuye a la disminución rápida del número promedio de errores de la red al inicio del proceso de aprendizaje, como resultado del entrenamiento proporciona los peores valores de este indicador: dicha red agrupa los datos de forma menos precisa.
7. Modificación del algoritmo
El problema de la distribución "cambiante" puede resolverse modificando el algoritmo de cierta forma. La modificación ampliamente aceptada es la que introduce el llamado factor de utilidad de las neuronas (GNG con factor de utilidad o GNG-U). En este caso, los cambios en el seudocódigo son mínimos y son los siguientes:
- Para cada neurona
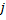 se establece una variable apropiada llamada "factor de utilidad"
se establece una variable apropiada llamada "factor de utilidad"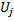 (esa variable U en la lista de campos de la clase CGNGNeuron);
(esa variable U en la lista de campos de la clase CGNGNeuron); -
en el paso 4, después de adaptar los pesos de la neurona ganadora, cambiamos su factor de utilidad por una cantidad igual a la diferencia entre un error de la segunda mejor neurona y la ganadora:
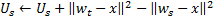
Físicamente, esta adición es la cantidad por la que el error total de la red habría cambiado si no hubiera ganadora en ella (en dicho caso, la segunda mejor ganadora sería la ganadora), es decir, realmente tipifica la utilidad de la neurona para reducir el error total. -
las neuronas se eliminan en el paso 8 según un principio distinto: solo un nodo con un valor de utilidad mínimo es eliminado, y solo si el valor de error máximo en la capa excede su factor de utilidad en más de
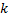 veces:
veces: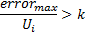
-
al añadir un nuevo nodo en el paso 9 su factor de utilidad se calcula como la media aritmética entre las utilidades de las neuronas vecinas:
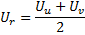
-
en el paso 10 el factor de utilidad de todas las neuronas se disminuye de la misma forma y en el mismo orden que las variables de los errores:
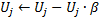
La constante ![]() es aquí crítica para la capacidad de hacer un seguimiento de la ausencia de la característica estacionaria: un valor demasiado grande conduce a la eliminación de no solo la "poca utilidad", sino también de otras neuronas bastante útiles. Un valor demasiado pequeño provoca eliminaciones muy poco frecuentes y, consecuentemente, un ratio de adaptación reducido.
es aquí crítica para la capacidad de hacer un seguimiento de la ausencia de la característica estacionaria: un valor demasiado grande conduce a la eliminación de no solo la "poca utilidad", sino también de otras neuronas bastante útiles. Un valor demasiado pequeño provoca eliminaciones muy poco frecuentes y, consecuentemente, un ratio de adaptación reducido.
En el archivo GNG.mqh, el algoritmo GNG-U se describe como una clase derivada de CGNGAlgorithm. Los lectores pueden hacer un seguimiento de los cambios e intentar usar el algoritmo.
Conclusión
Creando una red neuronal hemos revisado las principales características de la programación orientada a objeto integrada en el lenguaje MQL5. Parece un hecho bastante obvio que en ausencia de tales oportunidades (de las que estoy muy agradecido a los programadores) sería mucho más complicado escribir programas complejos para el trading automatizado.
Por lo que respecta a los algoritmos analizados, debe señalarse que, naturalmente, pueden mejorarse. En particular, el primer candidato para la mejora es el número de parámetros externos. Son muy numerosos y esto significa que pueden realizarse estas modificaciones, para las que estos parámetros se convertirían en variables internas y serían elegidos en base a las características de los datos de entrada y el estado del algoritmo.
¡El autor del artículo desea buena suerte a todos en el estudio de la neuroinformática y su uso en el trading!
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/163
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 MQL5 Wizard: crear asesores expertos sin programar
MQL5 Wizard: crear asesores expertos sin programar
 Interacción entre MetaTrader 5 y MATLAB
Interacción entre MetaTrader 5 y MATLAB
 Ejemplo simple de creación de un indicador usando la lógica difusa
Ejemplo simple de creación de un indicador usando la lógica difusa
 Crear un indicador con opciones de control gráficas
Crear un indicador con opciones de control gráficas
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Muy interesante,
Estoy deseando ponerlo en práctica y utilizarlo en lugar de una red neuronal fija.
¡Interesante artículo!
Pero es bastante viejo - ¡el compilador fue cambiado y ahora el código genera errores y advertencias!
Hola
pregunto si alguien de la comunidad éxito para desarrollar EA utilizando GNG?
pregunto si el resultado es bueno?
Gracias
Hola
pregunto si alguien de la comunidad éxito para desarrollar EA utilizando GNG?
pregunto si el resultado es bueno?
gracias
Bueno.. ¿después de qué? cinco meses o_O nadie se anima, así que quizás pueda comentarlo yo mismo.
En la implementación que has visto en este artículo la NN es una variante autoadaptativa de la llamada red de funciones de base radial. Si compara un EA basado en el algoritmo GNG con el mismo tipo de EA basado en una red neuronal de clusterización de tipo no adaptativo, lo más probable es que obtenga mejores resultados con GNG que sin él. Así que, para responder a su última pregunta, sí, el resultado es bueno en el sentido que acabo de explicar.
Volviendo a la primera, yo mismo he desarrollado EAs con un GNG dentro, y funcionó moderadamente bien, yay. Sin embargo, para el uso diario prefiero otros algoritmos que por regla general no son neuronales. Puedo respaldarlo recordando que ANN siempre presenta una "caja negra", lo que significa que usted no entiende realmente lo que está pasando allí cuando procesa los datos de entrada. Eso implica que la RNA sería un algoritmo de elección sólo en una situación en la que se tuviera un conjunto de datos completamente desestructurados con dependencias intrínsecas absolutamente desconocidas que se quisiera que la RNA extrajera de algún modo. Nota: sin ninguna promesa de obtener un resultado preciso. En cualquier otro caso, es decir, cuando tienes algunas ideas sobre cómo pueden estar organizadas las dependencias en tu conjunto de datos, primero querrías probar otras formas más deterministas "de caja blanca" de estructurarlo. Miles de ellas.