
Growing Neural Gas: Umsetzung in MQL5
Einleitung
In den 1990er Jahren kamen Forscher in Sachen künstlicher neuronaler Netze zu dem Schluss, dass es notwendig sei, eine neue Klasse von Berechnungsmechanismen zu entwickeln, deren Besonderheit im Fehlen einer festgelegten Topologie der Netzwerkschichten besteht. Das heißt, dass Anzahl und Anordnung der künstlichen Neuronen im Raum der Merkmale nicht voreingestellt sind, sondern während des Studiums dieser Modelle in Übereinstimmung mit den Besonderheiten der Eingangsdaten berechnet werden, wobei sie sich selbständig an diese anpassen.
Anlass für das Zustandekommen derartiger Vorstellungen war eine ganze Reihe aktueller praktischer Aufgaben, in denen die Komprimierung und die Vektorquantisierung der Eingangsmerkmale, insbesondere der Sprach- und Bilderkennung sowie der Klassifizierung und Erkennung abstrakter Muster (Patterns), erschwert waren.
Da selbstorganisierende Karten und Hebbsches Lernen (insbesondere Algorithmen, die die Topologisierung des Netzes, das heißt die Erstellung einen Satz von Verbindungen zwischen Neuronen ermöglichen, die ein „Gerüst“ der Ebene bilden) zu jener Zeit bereits bekannt und Ansätze zum „weichen“ kompetitiven Lernen (bei diesen Verfahren erfolgt die Anpassung des Gewichts nicht nur des „Siegerneurons“ sondern auch desjenigen seiner „Nachbarn“) entwickelt worden waren, bestand der logische Schritt in der Vereinigung besagter Methoden, was der deutsche Wissenschaftler Bernd Fritzke 1995 mit der Formulierung des heute weithin bekannten Algorithmus „Growing neural gas“ (GNG) dann auch tat.
Das Verfahren hat sich als recht erfolgreich erwiesen, was zu einer Reihe von Anpassungen an ihm geführt hat, dabei wurde auch eine Fassung zu Ausbildungszwecken unter Anleitung (Supervised-GNG) entwickelt. Wie der Autor selbst feststellt, hat wegen der Fähigkeit zur Abbildung der Topologie in schwer zu klassifizierenden Bereichen des Eingangsraums S-GNG bei der Klassifizierung von Daten eine deutlich größere Effektivität an den Tag gelegt als, sagen wir, Netze auf der Grundlage radialer Basisfunktionen. Auch die Überlegenheit von GNG gegenüber dem K-Means-Clustering ruft kaum Zweifel hervor.
Aus Fritzkes Biografie wird ersichtlich, dass er 2001 seine wissenschaftliche Laufbahn an der Ruhr-Universität (Bochum, Deutschland) aufgab, nachdem er ein Angebot von der Deutschen Börse erhalten hat. Ich will nicht verhehlen, dass dieser Umstand ein weiterer Grund für die Wahl ausgerechnet dieses Algorithmus als Grundlage für diesen Beitrag war.
1. „Growing Neural Gas“
Somit ist GNG ein Algorithmus, der uns das adaptive Clustering der Eingangsdaten ermöglicht, das heißt, nicht nur die Aufteilung des Raums in Cluster, sondern auch die Festlegung der benötigten Clusteranzahl anhand der Besonderheiten der Daten selbst.
Mit insgesamt nur zwei Neuronen beginnend ändert der Algorithmus anschließend ihre Anzahl (zumeist indem er sie herauf setzt), wobei er gleichzeitig mithilfe des Ansatzes des kompetitiven Hebbschen Lernens einen Satz von Verbindungen zwischen Neuronen erstellt, der der Verteilung der Eingangsvektoren am besten entspricht. Jedes Neuron verfügt über eine interne Variable, in der so genannte „lokale Fehler“ gespeichert werden. Die Verbindungen zwischen den Knoten werden durch eine als „Alter“ bezeichnete Variable gekennzeichnet.
Der GNG-Pseudocode sieht so aus:
- Bereitstellung: Anlegen von zwei Knoten mit von der Verteilung der Eingangsvektoren zugelassenen Gewichtsvektoren und dem Wert „0“ bei den lokalen Fehlern; Vernetzen der Knoten mithilfe einer Verbindung, deren Alter auf Null gesetzt wird.
- Anlegen eines Vektors am Eingang zu dem neuronalen Netz
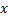 .
. - Auffinden der beiden Neuronen
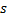 und
und 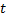 , die am dichtesten bei
, die am dichtesten bei 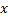 liegen, das heißt der Knoten mit den Gewichtsvektoren
liegen, das heißt der Knoten mit den Gewichtsvektoren 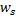 und
und 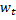 in der Form, dass
in der Form, dass 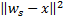 der niedrigste und
der niedrigste und 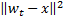 der zweit niedrigste Wert für sämtliche Abstände zwischen allen Knoten ist.
der zweit niedrigste Wert für sämtliche Abstände zwischen allen Knoten ist. -
Aktualisieren des lokalen Fehlers des Gewinnerneurons
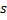 durch Hinzufügen des quadrierten Abstandes zwischen den Vektoren
durch Hinzufügen des quadrierten Abstandes zwischen den Vektoren 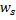 und
und 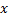 :
: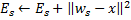
-
Verlagern des Gewinnerneurons
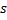 und aller topologischen Nachbarn (das heißt, aller Neuronen, die über eine Verbindung zu dem Gewinner verfügen) in Richtung des Eingangsvektors
und aller topologischen Nachbarn (das heißt, aller Neuronen, die über eine Verbindung zu dem Gewinner verfügen) in Richtung des Eingangsvektors 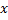 in den Anteilen
in den Anteilen 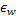 und
und 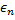 seines vollen Umfangs entsprechenden Abständen.
seines vollen Umfangs entsprechenden Abständen.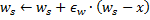
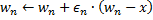
- Heraufsetzen des Alters aller von dem Gewinner
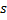 ausgehenden Verbindungen um 1.
ausgehenden Verbindungen um 1. - Bei bestehender Verbindung zwischen den beiden besten Neuronen
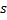 und
und 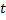 Festlegen des Alters dieser Verbindung auf „0“. Andernfalls Herstellen einer Verbindung zwischen ihnen.
Festlegen des Alters dieser Verbindung auf „0“. Andernfalls Herstellen einer Verbindung zwischen ihnen. - Löschen aller Verbindungen, deren Alter
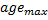 überschreitet. Wenn danach noch Neuronen vorhanden sind, die keine Verbindungen zu anderen Knoten aufweisen, sind auch diese zu löschen.
überschreitet. Wenn danach noch Neuronen vorhanden sind, die keine Verbindungen zu anderen Knoten aufweisen, sind auch diese zu löschen. -
Wenn die Zahl der aktuellen Iteration durch
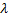 teilbar und die maximale Größe des Netzes noch nicht erreicht ist, Einfügen eines neuen Neurons
teilbar und die maximale Größe des Netzes noch nicht erreicht ist, Einfügen eines neuen Neurons 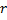 nach folgenden Regeln:
nach folgenden Regeln:- Auffinden des Neurons
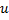 mit dem größten lokalen Fehler.
mit dem größten lokalen Fehler. - Unter den Nachbarn von
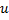 Auffinden des Neurons
Auffinden des Neurons 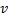 mit dem maximalen Fehler.
mit dem maximalen Fehler. - Anlegen des Knotens
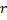 „auf halbem Weg“ zwischen
„auf halbem Weg“ zwischen 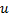 und
und 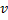 :
:
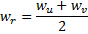
- Austauschen der Verbindung zwischen
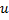 und
und 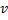 gegen die Verbindung zwischen
gegen die Verbindung zwischen 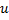 und
und 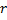 sowie
sowie 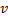 und
und 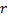 .
. - Herabsetzen des Fehlers der Neuronen
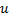 und
und 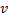 , Festlegen des Wertes für den Fehler des Neurons
, Festlegen des Wertes für den Fehler des Neurons 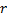 .
.
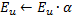
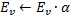
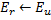
- Auffinden des Neurons
-
Herabsetzen der Fehler aller Neuronen
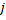 auf den Anteil
auf den Anteil 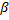 .
.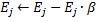
- Weiter zu Schritt 2, wenn das Haltekriterium nicht erfüllt ist.
Wir untersuchen, wie genau die Adaption des GNG an die Besonderheiten des Eingangsraums vor sich gehen wird.
Zunächst einmal richten wir unsere Aufmerksamkeit auf die Heraufsetzung der Variablen für den lokalen Fehler bei dem Gewinnerneuron aus Schritt 4. Dieses Vorgehen führt dazu, dass die Knoten, die am häufigsten gewinnen, das heißt die, in deren nähere Umgebung die größte Anzahl der Eingangssignale fällt, auch die höchsten Fehlercodes aufweisen, was bedeutet, dass eben diese Bereiche zu den Hauptkandidaten für die „Verdichtung“ durch Hinzufügen neuer Knoten werden.
Die Verschiebung der Knoten in Richtung des Eingangsvektors um einen Schritt von 5 besagt, dass der Gewinner versucht, seine Lage zwischen den Eingangssignalen in seiner näheren Umgebung „einzupendeln“. Dabei „zieht“ das beste Neuron auch seine Nachbarn ein wenig in Richtung des Signals (in der Regel wird ![]() gewählt).
gewählt).
Die Arbeit mit Verbindungen zwischen Neuronen wird in den Schritten 6 - 8 erläutert. Ohne uns in Einzelheiten zu verlieren, können wir sagen, dass der Sinn des Alterns sowie des Löschens der alten Verbindungen darin besteht, die Topologie des Netzes im Ganzen möglichst nah an die so genannte Delaunay-Triangulierung anzunähern, das heißt, an die Triangulierung (Aufteilung in Dreiecke) der Mehrzahl der Neuronen, bei der insbesondere der kleinste Winkel der Zerlegungsdreiecke maximiert wird (was die Bildung „schmaler“ Dreiecke verhindert).
Einfach ausgedrückt entspricht die Delaunay-Triangulierung dem „Ideal“ im Sinne des Maximums der Entropie der Topologisierung der Ebene. Es sei festgestellt, dass wir die topologische Struktur nicht um ihrer selbst willen benötigen, ihr Wert besteht in ihrer Verwendung zur Bestimmung der Lage der neuen Knoten bei ihrer Einfügung in Schritt 8, sie liegen stets in der Mitte des einen oder anderen Randes.
Schritt 9 besteht in der Korrektur der Fehlervariablen aller Neuronen der Ebene. Das ist notwendig, damit das Netz die alten Eingangsvektoren „vergisst“ und besser auf die neuen reagiert. So erlangen wir die Möglichkeit, GNG zur Anpassung eines neuronalen Netzes an nicht stationäre, insbesondere langsam wandernde Verteilungen der Eingangssignale zu nutzen. Das verleiht ihr jedoch nicht die Möglichkeit, schnelle Änderungen bei den Merkmalen der Eingänge zu erfassen (ausführlicher befassen wir uns damit weiter unten bei der Behandlung der Unzulänglichkeiten unseres Algorithmus).
Es lohnt sich vielleicht, sich mit dem Haltekriterium gesondert zu befassen. Hier lässt der Algorithmus der Fantasie der Entwickler von Analysesystemen freien Raum. Mögliche Varianten sind die Prüfung der Effektivität des Netzes anhand einer Prüfmenge, die Analyse der Dynamik des durchschnittlichen Fehlers der Neuronen, die Beschränkung der Komplexität des Netzes selbst usw.
Für den Einstieg beschränken wir uns auf die einfachste Variante, da das Ziel dieses Beitrages in der Vorstellung nicht allein des Algorithmus selbst sondern vielmehr auch der Möglichkeit seiner Umsetzung mithilfe von MQL5 besteht; wir werden das Studium der Ebene solange fortsetzen, bis uns schlicht die Eingangssignale ausgehen (deren Anzahl legen wir natürlich im Vorfeld fest).
2. Auswahl des Verfahrens zur Datenorganisation
Bei der Programmierung des Algorithmus stoßen wir offenbar zwangsläufig auf die Notwendigkeit, das, was für gewöhnlich „Mengen“ genannt wird, speichern zu müssen. Wir haben zwei davon, die Menge der Neuronen und die Menge der Verbindungen zwischen ihnen. Da sowohl die Struktur der einen als auch der anderen im Verlauf der Arbeit des Programms ihr Aussehen ändern wird (wobei sowohl die Hinzufügung als auch die Entfernung von Elementen geplant ist), müssen wir Verfahren dazu zur Hand haben.
Wir könnten freilich versuchen, die dynamischen Objektdatenfelder zu verwenden, allerdings müssten dazu eine Vielzahl von Datenkopier- und -verschiebeoperationen ausgeführt werden, wodurch die Arbeit des Programms erheblich verlangsamt würde. Eine geeignetere Alternative für die Arbeit mit Abstraktionen, die über die genannten Eigenschaften verfügen, sind grafische Programmabbildungen und zwar insbesondere in ihrer einfachsten Form als verkettete Liste.
Ich rufe kurz die Funktionsweise einer verketteten Liste in Erinnerung (Abb. 1). Die Objekte der Basisklasse beinhalten als eines ihrer Mitglieder einen Zeiger, der auf eben dieses Objekt verweist, was es ermöglicht, sie in von der physischen Anordnung der Lage der Objekte im Speicher unabhängigen linearen Strukturen zu vereinigen. Darüber hinaus gibt es die Klasse der „Träger“, die Verfahren zur Verschiebung von Knoten innerhalb der Liste sowie zu ihrer Ergänzung, Einfügung und Löschung, zum Suchen, Vergleichen und Sortieren und gegebenenfalls noch weitere Operationen beinhaltet.
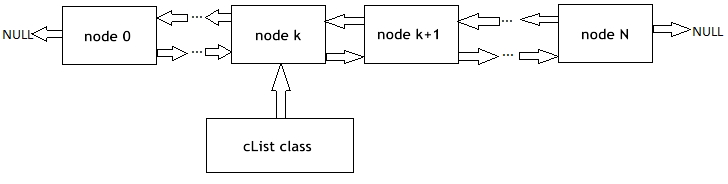
Abbildung 1. Schematische Darstellung des Organisation einfach verketteter Listen
Von den Experten bei MetaQuotes Software Corp. sind die verketteten Listen der Objekte der Klasse CObject bereits in einer Standardbibliothek angelegt worden. Der entsprechende Programmcode befindet sich in der Header-Datei List.mqh, die wiederum in dem im Lieferumfang der MetaTrader 5-Instanz für das Ausgabegerät (Terminal) enthaltenen Ordner MQL5\Include\Arrays zu finden ist.
Wir wollen das Rad nicht neu erfinden und verlassen uns auf die Qualifikation der geschätzten Programmierer von MetaQuotes, wenn wir die Klassen CObject und CList als Grundlage für unsere Datenstrukturen verwenden. Dabei kommt uns eine der Säulen des objektorientierten Ansatzes zu Hilfe, der Mechanismus der Vererbung.
3. Programmieren des Modells
Zunächst befassen wir uns mit der Übersetzung des Begriffs „künstliches Neuron“ in die Form eines Programms.
Eine der Faustregeln bei der Entwicklung objektorientierter Programme (OOP) besteht darin, stets mit den verbreitetsten Datenstrukturen zu beginnen. Selbst wenn man nur für sich schreibt, aber besonders, wenn man davon ausgeht, dass die Codes auch von anderen Programmierern benutzt werden, ist zu bedenken, dass künftige Entwickler durchaus eigene Vorstellungen von der Weiterentwicklung und Modifikation der Programmlogik haben können, wobei man nicht im Voraus wissen kann, an welcher Stelle genau Änderungen vorgenommen werden.
Der Grundsatz der OOP geht davon aus, dass außenstehende Entwickler nicht in Ihren Klassen herumkramen werden, sondern stattdessen die Möglichkeit haben, ihre Datenstrukturen aus den an der benötigten Stelle vorhandenen Hierarchien zu übernehmen, zu „erben“. Somit muss die erste geschriebene Klasse möglichst abstrakt sein, während die Feinheiten auf den unteren Ebenen hinzugefügt werden, je näher wir der „lasterhaften Erde“ kommen.
Bezogen auf unsere Aufgabe bedeutet das Gesagte, dass wir das Schreiben des Programms mit der Festlegung der Klasse CCustomNeuron („irgendein Neuron“) beginnen. Wie alle künstlichen Neuronen wird auch dieses eine gewisse Anzahl an Synapsen (Eingangsgewichten) sowie einen Ausgabewert aufweisen. Es wird in der Lage sein, sich selbst bereitzustellen (den Gewichten Werte zuzuweisen), den Wert des Signals an seinem Ausgang zu berechnen und sogar seine Gewichte an eine vorgegebene Größe anzupassen.
Eine größere Abstraktion (angesichts der Tatsache, dass wir unsere Klasse von der extrem verallgemeinerten Klasse CObject erben) wird kaum zu erzielen sein, die angegebenen Operationen müssen von allen Neuronen ausgeführt werden können.
Zur Beschreibung der Daten erstellen wir die Header-Datei Neurons.mqh, die wir in dem Ordner Include\GNG ablegen.
//+------------------------------------------------------------------+ //| a base class to introduce object-neurons | //+------------------------------------------------------------------+ class CCustomNeuron:public CObject { protected: int m_synapses; double m_weights[]; public: double NET; CCustomNeuron(); ~CCustomNeuron(){}; void ZeroInit(int synapses); int Synapses(); void Init(double &weights[]); void Weights(double &weights[]); void AdaptWeights(double &delta[]); virtual void ProcessVector(double &in[]) {return;} virtual int Type() const { return(TYPE_CUSTOM_NEURON);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ void CCustomNeuron::CCustomNeuron() { m_synapses=0; NET=0; } //+------------------------------------------------------------------+ //| returns the dimension of the input vector of a neuron | //| INPUT: no | //| OUTPUT: number of "synapses" of the neuron | //+------------------------------------------------------------------+ int CCustomNeuron::Synapses() { return m_synapses; } //+------------------------------------------------------------------+ //| initializing neuron with a zero vector of weights. | //| INPUT: synapses - number of synapses (input weights) | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::ZeroInit(int synapses) { if(synapses<1) return; m_synapses=synapses; ArrayResize(m_weights,m_synapses); ArrayInitialize(m_weights,0); NET=0; } //+------------------------------------------------------------------+ //| initializing neuron weights with a set vector. | //| INPUT: weights - data vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::Init(double &weights[]) { if(ArraySize(weights)<1) return; m_synapses=ArraySize(weights); ArrayResize(m_weights,m_synapses); ArrayCopy(m_weights,weights); NET=0; } //+------------------------------------------------------------------+ //| obtaining vector of neuron weights. | //| INPUT: no | //| OUTPUT: weights - result | //+------------------------------------------------------------------+ void CCustomNeuron::Weights(double &weights[]) { ArrayResize(weights,m_synapses); ArrayCopy(weights,m_weights); } //+------------------------------------------------------------------+ //| change weights of the neuron by a specified value | //| INPUT: delta - correcting vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::AdaptWeights(double &delta[]) { if(ArraySize(delta)!=m_synapses) return; for(int i=0;i<m_synapses;i++) m_weights[i]+=delta[i]; NET=0; }
Die in der Klasse definierten Funktionen sind äußerst einfach, deshalb besteht keine Notwendigkeit, ausführlicher auf ihre Beschreibung einzugehen. Es sei lediglich darauf hingewiesen, dass die Funktion zur Verarbeitung des Eingangsvektors ProcessVector(double &in[]) (der Ausgabewert wird hier wie bei einem gewöhnlichen Perzeptron berechnet) von uns mit dem Attribut virtual angelegt worden ist.
Das bedeutet, dass im Fall einer Neufestlegung durch die Erben dieser Methode die Wahl des passenden Verfahrens in Abhängigkeit von der tatsächlichen Objektklasse im Verlauf der Ausführung des Programms dynamisch erfolgt, was ihre Anpassungsfähigkeit auch im Sinn der Interaktion mit dem Anwender erhöht und gleichzeitig den Programmieraufwand verringert.
Ungeachtet dessen, dass wir scheinbar immer noch nichts für die Organisation der Neuronen in einer verketteten Liste getan haben, ist das eigentlich bereits in dem Moment geschehen, in dem wir angegeben haben, dass es sich bei der neuen Klasse um einen Nachkommen der Klasse CObject handelt. So, ab jetzt zählen zu den privaten Elementen unserer Klasse m_first_node, m_curr_node und m_last_node, sie weisen die Art „CObject-Zeiger“ auf und verweisen entsprechend auf das erste, das aktuelle und das letzte Element der Liste. Es sind auch alle für die Navigation innerhalb der Liste erforderlichen Funktionen vorhanden.
Es ist Zeit, die Unterschiede zwischen einem Neuron der GNG-Schicht und seinen „Artgenossen“ zu skizzieren, indem wir die Klasse CGNGNeuron bestimmen:
//+------------------------------------------------------------------+ //| a separate neuron of the GNG network | //+------------------------------------------------------------------+ class CGNGNeuron:public CCustomNeuron { public: int uid; double E; double U; double error; CGNGNeuron(); virtual void ProcessVector(double &in[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGNeuron::CGNGNeuron() { E=0; U=0; error=0; } //+------------------------------------------------------------------+ //| calculating "distance" from the neuron to the input vector | //| INPUT: in - data vector | //| OUTPUT: no | //| REMARK: the current "distance" is placed in the error variable, | //| "local error" is contained in another variable, | //| which is called E | //+------------------------------------------------------------------+ void CGNGNeuron::ProcessVector(double &in[]) { if(ArraySize(in)!=m_synapses) return; error=0; NET=0; for(int i=0;i<m_synapses;i++) { error+=(in[i]-m_weights[i])*(in[i]-m_weights[i]); } }
Also, wie wir sehen, bestehen besagte Unterschiede in dem Vorhandensein der Felder:
- error – das aktuelle Quadrat des Abstandes vom Eingangsvektor zum Vektor der Neuronengewichte;
- E – eine Variable zur Aufnahme des lokalen Fehlers sowie eines eindeutigen Bezeichners;
- uid – ist erforderlich, um später die Neuronen mithilfe von Verbindungen zu Paaren zu vereinigen (die einfache, in der Klasse CList bereits vorhandene Zuordnung von Kennziffern ist unzureichend, da wir Neuronen entfernen und hinzufügen müssen, was zu Ausfällen und Störungen bei der Nummerierung führen kann).
Auch die Funktion ProcessVector(...) wurde verändert, sie berechnet jetzt den Wert des Feldes error.
Das Feld U lassen wir einstweilen außer Acht, ihre Bedeutung wird weiter unten in dem Abschnitt „Anpassung des Algorithmus“ erläutert.
Als Nächstes schreiben wir eine Klasse, die die Verbindung zwischen zwei Neuronen bereitstellt.
//+------------------------------------------------------------------+ //| class defining connection (edge) between two neurons | //+------------------------------------------------------------------+ class CGNGConnection:public CObject { public: int uid1; int uid2; int age; CGNGConnection(); virtual int Type() const { return(TYPE_GNG_CONNECTION);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGConnection::CGNGConnection() { age=0; }
Anscheinend ist da nichts Kompliziertes, die Verbindung hat zwei Enden (die mit den Bezeichnern uid1 und uid2 gekennzeichnet sind) sowie ein Alter (age), das zu Beginn gleich „0“ ist.
Jetzt bearbeiten wir die „Träger“-Klassen der verketteten Listen, in denen die zur Umsetzung des GNG-Algorithmus benötigten Möglichkeiten abgelegt sind.
Zunächst übernehmen („erben“) wir aus CList eine Neuronenlistenklasse:
//+------------------------------------------------------------------+ //| linked list of neurons | //+------------------------------------------------------------------+ class CGNGNeuronList:public CList { public: //--- constructor CGNGNeuronList() {MathSrand(TimeLocal());} CGNGNeuron *Append(); void Init(double &v1[],double &v2[]); CGNGNeuron *Find(int uid); void FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner); }; //+------------------------------------------------------------------+ //| adds an "empty" neuron at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new neuron | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGNeuron; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGNeuron; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; while(true) { int rnd=MathRand(); if(!CheckPointer(Find(rnd))) { ((CGNGNeuron *)m_curr_node).uid=rnd; break; } } //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initializing list by way of creating two neurons set | //| by vectors of weights | //| INPUT: v1,v2 - vectors of weights | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGNeuronList::Init(double &v1[],double &v2[]) { Clear(); Append(); ((CGNGNeuron *)m_curr_node).Init(v1); Append(); ((CGNGNeuron *)m_curr_node).Init(v2); } //+------------------------------------------------------------------+ //| search for a neuron by uid | //| INPUT: uid - a unique ID of the neuron | //| OUTPUT: pointer at the neuron if successful, otherwise NULL | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Find(int uid) { if(!GetFirstNode()) return(NULL); do { if(((CGNGNeuron *)m_curr_node).uid==uid) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for two "best" neurons in terms of minimal current error | //| INPUT: no | //| OUTPUT: Winner - neuron "closest" to the input vector | //| SecondWinner - second "closest" neuron | //+------------------------------------------------------------------+ void CGNGNeuronList::FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) { double err_min=0; Winner=NULL; if(!CheckPointer(GetFirstNode())) return; do { if(!CheckPointer(Winner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min= ((CGNGNeuron *)m_curr_node).error; Winner = m_curr_node; } } while(CheckPointer(GetNextNode())); err_min=0; SecondWinner=NULL; GetFirstNode(); do { if(m_curr_node!=Winner) if(!CheckPointer(SecondWinner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min=((CGNGNeuron *)m_curr_node).error; SecondWinner=m_curr_node; } } while(CheckPointer(GetNextNode())); m_curr_node=Winner; }
In dem Konstruktor der Klasse wird ein Pseudozufallszahlengenerator bereitgestellt: er wird benötigt, um den Elementen der Liste eindeutige Bezeichner zuzuordnen.
Wir erläutern die Bedeutung der Methoden der Klasse:
- Die Methode Append() erweitert den Funktionsumfang der Klasse CList. Wird sie aufgerufen, so erfolgt die Einschreibung des Knotens an das Ende der Liste bzw. die Anlage eines neuen Knotens, wenn die Liste leer ist.
- Die Funktion Init(double &v1[],double &v2[]) verdankt ihre bloße Existenz dem GNG-Algorithmus selbst. Wie wir wissen, beginnt das Wachstum eines Netzes mit zwei Neuronen, weshalb eben diese Signatur die geeignetste für uns ist. Bei Verwendung der Bezeichner m_curr_node, m_first_node und m_last_node müssen diese im Hauptteil der Funktion ausdrücklich in die Art CGNGNeuron* umgewandelt werden, wenn wir den Funktionsumfang dieser Klasse nutzen wollen (wie wir wissen, wurden die angegebenen Variablen aus CList übernommen, deshalb verweisen sie nominell auf das Objekt CObject).
- Die Funktion Find(int uid) führt, wie ihr Name sagt, die Suche nach einem Neuron anhand seines Bezeichners aus, wobei sie entweder den Zeiger für das gefundene Element oder im Fall seines Nichtvorhandenseins „0“ ausgibt.
- FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) ist ebenfalls Teil des Algorithmus. Wir müssen in der Neuronenliste einen Gewinner sowie das ihm hinsichtlich der Nähe zum Eingangsvektor nächst liegende Neuron suchen, eben dazu dient diese Funktion. Wir werden feststellen, dass die Parameter mithilfe von Verweisen an diese Funktion übergeben werden, damit die Aufzeichnung der ausgegebenen Werte (*& steht für „Verweis auf einen Zeiger“ - das ist syntaktisch korrekt; die Umkehrung dieser Eintragung &* bedeutet „Zeiger auf einen Verweis“, was unzulässig ist: in diesem Fall gibt das Kompilierungsprogramm eine Fehlermeldung aus).
Die nächste Klasse ist die Liste der Neuronenverbindungen.
//+------------------------------------------------------------------+ //| a linked list of connections between neurons | //+------------------------------------------------------------------+ class CGNGConnectionList:public CList { public: CGNGConnection *Append(); void Init(int uid1,int uid2); CGNGConnection *Find(int uid1,int uid2); CGNGConnection *FindFirstConnection(int uid); CGNGConnection *FindNextConnection(int uid); }; //+------------------------------------------------------------------+ //| adds an "empty" connection at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new binding | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGConnection; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGConnection; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initialize the list by creating one connection | //| INPUT: uid1,uid2 - IDs of neurons for the connection | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGConnectionList::Init(int uid1,int uid2) { Append(); ((CGNGConnection *)m_first_node).uid1 = uid1; ((CGNGConnection *)m_first_node).uid2 = uid2; m_last_node = m_first_node; m_curr_node = m_first_node; m_curr_idx=0; } //+------------------------------------------------------------------+ //| check if there is connection between the set neurons | //| INPUT: uid1,uid2 - IDs of the neurons | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Find(int uid1,int uid2) { if(!CheckPointer(GetFirstNode())) return(NULL); do { if((((CGNGConnection *)m_curr_node).uid1==uid1 && ((CGNGConnection *)m_curr_node).uid2==uid2) ||(((CGNGConnection *)m_curr_node).uid1==uid2 && ((CGNGConnection *)m_curr_node).uid2==uid1)) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the first element of the list | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindFirstConnection(int uid) { if(!CheckPointer(GetFirstNode())) return(NULL); while(true) { if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; if(!CheckPointer(GetNextNode())) return(NULL); } return(m_curr_node); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the list element next to the current one | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindNextConnection(int uid) { if(!CheckPointer(GetCurrentNode())) return(NULL); while(true) { if(!CheckPointer(GetNextNode())) return(NULL); if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; } return(m_curr_node); }
Festgelegte Methoden der Klasse sind:
- Append(). Die Umsetzung dieser Methode ähnelt der in der vorhergehenden Klasse beschriebenen bis auf die Art des ausgegebenen Wertes (in MQL5 gibt es leider keine Muster oder Templates für die Klassen, weshalb all dies jedes Mal aufs Neue geschrieben werden muss).
- Init(int uid1,int uid2) – der GNG-Algorithmus verlangt an seinem Anfang die Bereitstellung einer Verbindung, das erfolgt in dieser Funktion.
- Die Funktion Find(int uid1,int uid2) ist wieder einmal selbsterklärend.
- Der Unterschied zwischen den Methoden FindFirstConnection(int uid) und FindNextConnection(int uid) besteht darin, das Erstere beginnend mit dem Anfang der Liste nach einer Verbindung zu einem Nachbarn sucht, während die zweite mit dem Knoten anfängt, der dem aktuellen folgt (m_curr_node).
Damit ist die Vorstellung der Datenstrukturen abgeschlossen. Es wird Zeit, mit der Programmierung des Algorithmus selbst zu beginnen.
4. Die Algorithmusklasse
Wir legen die neue Header-Datei GNG.mqh an und legen sie in dem Ordner Include\GNG ab.
//+------------------------------------------------------------------+ //| GNG.mqh | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #include "Neurons.mqh" //+------------------------------------------------------------------+ //| the main class representing the GNG algorithm | //+------------------------------------------------------------------+ class CGNGAlgorithm { public: //--- linked lists of object-neurons and connection between them CGNGNeuronList *Neurons; CGNGConnectionList *Connections; //--- parameters of the algorithm int input_dimension; int iteration_number; int lambda; int age_max; double alpha; double beta; double eps_w; double eps_n; int max_nodes; CGNGAlgorithm(); ~CGNGAlgorithm(); virtual void Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes); virtual bool ProcessVector(double &in[],bool train=true); virtual bool StoppingCriterion(); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGAlgorithm::CGNGAlgorithm(void) { Neurons=new CGNGNeuronList(); Connections=new CGNGConnectionList(); Neurons.FreeMode(true); Connections.FreeMode(true); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CGNGAlgorithm::~CGNGAlgorithm(void) { delete Neurons; delete Connections; } //+------------------------------------------------------------------+ //| initializes the algorithm using two vectors of input data | //| INPUT: v1,v2 - input vectors | //| __lambda - number of iterations after which a new | //| neuron is inserted | //| __age_max - maximum age of connection | //| __alpha, __beta - used for adapting errors | //| __eps_w, __eps_n - used for adapting weights | //| __max_nodes - limit on the network size | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGAlgorithm::Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes) { iteration_number=0; input_dimension=__input_dimension; lambda=__lambda; age_max=__age_max; alpha= __alpha; beta = __beta; eps_w = __eps_w; eps_n = __eps_n; max_nodes=__max_nodes; Neurons.Init(v1,v2); CGNGNeuron *tmp; tmp=Neurons.GetFirstNode(); int uid1=tmp.uid; tmp=Neurons.GetLastNode(); int uid2=tmp.uid; Connections.Init(uid1,uid2); } //+------------------------------------------------------------------+ //| the main function of the algorithm | //| INPUT: in - vector of input data | //| train - if true, start learning, otherwise | //| only calculate the input values of neurons | //| OUTPUT: true, if stop condition is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::ProcessVector(double &in[],bool train=true) { if(ArraySize(in)!=input_dimension) return(StoppingCriterion()); int i; CGNGNeuron *tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.ProcessVector(in); tmp=Neurons.GetNextNode(); } if(!train) return(false); iteration_number++; //--- Find two neurons closest to in[], i.e. the nodes with weight vectors //--- Ws and Wt, so that ||Ws-in||^2 is minimal and ||Wt-in||^2 - //--- is second minimal value of distance of all the nodes. //--- Under ||*|| we mean Euclidean norm CGNGNeuron *Winner,*SecondWinner; Neurons.FindWinners(Winner,SecondWinner); //--- Update the local error of the winner Winner.E+=Winner.error; //--- Shift the winner and all its topological neighbors (i.e. //--- all neurons connected with the winner) in the direction of the input //--- vector by distances equal to fractions eps_w and eps_n of the full. double delta[],weights[]; Winner.Weights(weights); ArrayResize(delta,input_dimension); for(i=0;i<input_dimension;i++) delta[i]=eps_w*(in[i]-weights[i]); Winner.AdaptWeights(delta); //--- Increment the age of all connections emanating from the winner by 1. CGNGConnection *tmpc=Connections.FindFirstConnection(Winner.uid); while(CheckPointer(tmpc)) { if(tmpc.uid1==Winner.uid) tmp = Neurons.Find(tmpc.uid2); if(tmpc.uid2==Winner.uid) tmp = Neurons.Find(tmpc.uid1); tmp.Weights(weights); for(i=0;i<input_dimension;i++) delta[i]=eps_n*(in[i]-weights[i]); tmp.AdaptWeights(delta); tmpc.age++; tmpc=Connections.FindNextConnection(Winner.uid); } //--- If two best neurons are connected, reset the age of the connection. //--- Otherwise create a connection between them. tmpc=Connections.Find(Winner.uid,SecondWinner.uid); if(tmpc) tmpc.age=0; else { Connections.Append(); tmpc=Connections.GetLastNode(); tmpc.uid1 = Winner.uid; tmpc.uid2 = SecondWinner.uid; tmpc.age=0; } //--- Delete all the connections with an age larger than age_max. //--- If this results in neurons having no connections with other //--- nodes, remove those neurons. tmpc=Connections.GetFirstNode(); while(CheckPointer(tmpc)) { if(tmpc.age>age_max) { Connections.DeleteCurrent(); tmpc=Connections.GetCurrentNode(); } else tmpc=Connections.GetNextNode(); } tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { if(!Connections.FindFirstConnection(tmp.uid)) { Neurons.DeleteCurrent(); tmp=Neurons.GetCurrentNode(); } else tmp=Neurons.GetNextNode(); } //--- If the number of the current iteration is multiple of lambda, and the network //--- hasn't been reached yet, create a new neuron r according to the following rules CGNGNeuron *u,*v; if(iteration_number%lambda==0 && Neurons.Total()<max_nodes) { //--- 1.Find neuron u with the maximum local error. tmp=Neurons.GetFirstNode(); u=tmp; while(CheckPointer(tmp=Neurons.GetNextNode())) { if(tmp.E>u.E) u=tmp; } //--- 2.determin among the neighbors of u the node u with the maximum local error. tmpc=Connections.FindFirstConnection(u.uid); if(tmpc.uid1==u.uid) v=Neurons.Find(tmpc.uid2); else v=Neurons.Find(tmpc.uid1); while(CheckPointer(tmpc=Connections.FindNextConnection(u.uid))) { if(tmpc.uid1==u.uid) tmp=Neurons.Find(tmpc.uid2); else tmp=Neurons.Find(tmpc.uid1); if(tmp.E>v.E) v=tmp; } //--- 3.Create a node r "in the middle" between u and v. double wr[],wu[],wv[]; u.Weights(wu); v.Weights(wv); ArrayResize(wr,input_dimension); for(i=0;i<input_dimension;i++) wr[i]=(wu[i]+wv[i])/2; CGNGNeuron *r=Neurons.Append(); r.Init(wr); //--- 4.Replace the connection between u and v by a connection between u and r, v and r tmpc=Connections.Append(); tmpc.uid1=u.uid; tmpc.uid2=r.uid; tmpc=Connections.Append(); tmpc.uid1=v.uid; tmpc.uid2=r.uid; Connections.Find(u.uid,v.uid); Connections.DeleteCurrent(); //--- 5.Decrease the errors of neurons u and v, set the value of the error of //--- neuron r the same as of u. u.E*=alpha; v.E*=alpha; r.E = u.E; } //--- Decrease the errors of all neurons by the fraction beta tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.E*=(1-beta); tmp=Neurons.GetNextNode(); } //--- Check the stopping criterion return(StoppingCriterion()); } //+------------------------------------------------------------------+ //| Stopping criterion. In this version of file makes no | //| actions, always returns false. | //| INPUT: no | //| OUTPUT: true, if the criterion is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::StoppingCriterion() { return(false); }
Die Klasse CGNGAlgorithm enthält zwei wichtige Felder, nämlich die Zeiger für die verketteten Listen mit den Neuronen „Neurons“ und die mit den Verbindungen zwischen ihnen „Connections“. Bei diesen Feldern handelt es sich um den physischen Träger der Struktur unseres neuronalen Netzes. Die übrigen Felder sind die von außen festgelegten Parameter des Algorithmus.
Aus den Hilfsmethoden picken wir uns Init(...) heraus, sie überträgt die externen Parameter an die Instanz des Algorithmus und stellt die Datenstrukturen sowie das Haltekriterium StoppingCriterion() bereit, wobei Letzteres, wie wir es vorher vereinbart haben, nichts anderes ausgibt als false.
Die Funktion ProcessVector(…), die Hauptfunktion des Algorithmus, die die Verarbeitung des vorgegebenen Datenvektors ausführt, birgt im Allgemeinen ebenfalls keinerlei Finessen: wir konnten die Daten und ihre Verarbeitung so organisieren, dass, wenn wir zum eigentlichen Algorithmus kommen, dessen Schritte nur noch mechanisch ausgelesen werden müssen. Ihre Fundorte im Programmcode werden durch entsprechende Kommentare bezeichnet.
5. Praktischer Einsatz
Wir zeigen anhand echter Daten der MetaTrader 5-Anwendung auf dem Ausgabegerät (Terminal) wie der Algorithmus arbeitet.
Wir legen uns darauf fest, dass es hier nicht darum geht, ein funktionierendes Expert-System auf der Grundlage von GNG zu entwickeln (das wäre ein bisschen viel für einen Artikel), wir möchten nur sehen, wie Growing Neural Gas sozusagen „live“ funktioniert.
Um die Daten schön darzustellen, legen wir ein leeres Fenster an, das wir entlang der Kursachse in dem Bereich von 0 bis 100 ausrichten. Dazu verwenden wir den „leeren“ Indikator Dummy.mq5 (andere Funktionen hat er nicht):
//+------------------------------------------------------------------+ //| Dummy.mq5 | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #property version "1.00" #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_type1 DRAW_LINE #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double DummyBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DummyBuffer,INDICATOR_DATA); IndicatorSetString(INDICATOR_SHORTNAME,"GNG_dummy"); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[]) { //--- an empty buffer ArrayInitialize(DummyBuffer,EMPTY_VALUE); //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
In MetaEditor legen wir ein Skript unter der Bezeichnung GNG.mq5 an, es wird das Netz im Fenster des Indikators Dummy abbilden.
Externe Parameter - die Anzahl der Datenvektoren zu Schulungszwecken sowie die eigentlichen Parameter des Algorithmus:
//--- the number of input vectors used for learning input int samples=1000; //--- parameters of the algorithm input int lambda=20; input int age_max=15; input double alpha=0.5; input double beta=0.0005; input double eps_w=0.05; input double eps_n=0.0006; input int max_nodes=100;
Wir deklarieren die globalen Variablen:
//---global variables CGNGAlgorithm *GNGAlgorithm; int window; int rsi_handle; int input_dimension; int _samples; double RSI_buffer[]; datetime time[];
Wir beginnen, die Funktion OnStart() zu schreiben. Zunächst suchen wir das erforderliche Fenster:
void OnStart() { int i,j; int window=ChartWindowFind(0,"GNG_dummy");
Als Eingabedaten verwenden wir die Werte des Indikators RSI, er ist deshalb geeignet, weil seine Werte in dem Bereich zwischen 0 und 100 normiert sind, weshalb wir uns nicht mit der Vorbereitung befassen müssen.
Als Eingangsvektor des neuronalen Netzes betrachten wir ein aus zwei RSI-Werten auf dem aktuellen bzw. dem vorhergehenden Balken (wissenschaftlich wird das als „Immersion einer Zeitreihe in einem zweidimensionalen Merkmalsraum“ bezeichnet) bestehendes Paar (input_dimension=2). Zweidimensionale Vektoren sind in einem Flächendiagramm allemal einfacher darzustellen.
Also, zunächst bereiten wir die Daten zur Bereitstellung auf und legen eine Instanz des Objekts des Algorithmus an:
//--- to have CopyBuffer() work correctly, the number of the vectors //--- must be within the number of bars with a reserve left for the vector length _samples=samples+input_dimension+10; if(_samples>Bars(_Symbol,_Period)) _samples=Bars(_Symbol,_Period); //--- receive input data for the algorithm rsi_handle=iRSI(NULL,0,8,PRICE_CLOSE); CopyBuffer(rsi_handle,0,1,_samples,RSI_buffer); //--- return the user-defined value _samples=_samples-input_dimension-10; //--- remember open time of the first 100 bars CopyTime(_Symbol,_Period,0,100,time); //--- create an instance of the algorithm and set the size of input data GNGAlgorithm=new CGNGAlgorithm; input_dimension=2; //--- data vectors double v[],v1[],v2[]; ArrayResize(v,input_dimension); ArrayResize(v1,input_dimension); ArrayResize(v2,input_dimension); for(i=0;i<input_dimension;i++) { v1[i] = RSI_buffer[i]; v2[i] = RSI_buffer[i+3]; }
Jetzt stellen wir den Algorithmus bereit:
//--- initialization
GNGAlgorithm.Init(input_dimension,v1,v2,lambda,age_max,alpha,beta,eps_w,eps_n,max_nodes);
Wir zeichnen ein rechteckiges Feld und Textsymbole (zur Veranschaulichung wie viele Iterationen von dem Algorithmus abgearbeitet wurden, und wie viele Neuronen im Netz „herangewachsen“ sind):
//-- draw a rectangular box and information labels ObjectCreate(0,"GNG_rect",OBJ_RECTANGLE,window,time[0],0,time[99],100); ObjectSetInteger(0,"GNG_rect",OBJPROP_BACK,true); ObjectSetInteger(0,"GNG_rect",OBJPROP_COLOR,DarkGray); ObjectSetInteger(0,"GNG_rect",OBJPROP_BGCOLOR,DarkGray); ObjectCreate(0,"Label_samples",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_samples",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_YDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: 2"); ObjectCreate(0,"Label_neurons",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_neurons",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_neurons",OBJPROP_YDISTANCE,25); ObjectSetInteger(0,"Label_neurons",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: 2");
Im Hauptarbeitsgang bereiten wir an den Eingang des Algorithmus zu setzenden Vektor vor und bilden ihn im Diagramm als blauen Punkt ab:
//--- start the main loop of the algorithm with i=2 because 2 were used already for(i=2;i<_samples;i++) { //--- fill out the data vector (for clarity, get samples separated //--- by 3 bars - they are less correlated) for(j=0;j<input_dimension;j++) v[j]=RSI_buffer[i+j*3]; //--- show the vector on the chart ObjectCreate(0,"Sample_"+i,OBJ_ARROW,window,time[v[0]],v[1]); ObjectSetInteger(0,"Sample_"+i,OBJPROP_ARROWCODE,158); ObjectSetInteger(0,"Sample_"+i,OBJPROP_COLOR,Blue); ObjectSetInteger(0,"Sample_"+i,OBJPROP_BACK,true); //--- change the information label ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: "+string(i+1));
Wir übergeben den Vektor an den Algorithmus (ja, alles in allem nur eine einzige Funktion, genau das ist der Vorteil des objektorientierten Ansatzes):
//--- pass the input vector to the algorithm for calculation
GNGAlgorithm.ProcessVector(v);
Wir löschen die alten Neuronen aus dem Diagramm und zeichnen neue (rote Kreise) ein sowie die Verbindungen (gelbe gepunktete Linien), zudem heben wir das Gewinnerneuron (hellgrün) und das Zweitplatzierte (grün) hervor:
//--- we need to remove old neurons an connections from the chart to draw new ones then for(j=ObjectsTotal(0)-1;j>=0;j--) { string name=ObjectName(0,j); if(StringFind(name,"Neuron_")>=0) { ObjectDelete(0,name); } else if(StringFind(name,"Connection_")>=0) { ObjectDelete(0,name); } }
double weights[]; CGNGNeuron *tmp,*W1,*W2; CGNGConnection *tmpc; GNGAlgorithm.Neurons.FindWinners(W1,W2); //--- drawing the neurons tmp=GNGAlgorithm.Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.Weights(weights); ObjectCreate(0,"Neuron_"+tmp.uid,OBJ_ARROW,window,time[weights[0]],weights[1]); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_ARROWCODE,159); //--- the winner is colored Lime, second best - Green, others - Red if(tmp==W1) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Lime); else if(tmp==W2) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Green); else ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Red); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_BACK,false); tmp=GNGAlgorithm.Neurons.GetNextNode(); } ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: "+string(GNGAlgorithm.Neurons.Total())); //--- drawing connections tmpc=GNGAlgorithm.Connections.GetFirstNode(); while(CheckPointer(tmpc)) { int x1,x2,y1,y2; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid1); tmp.Weights(weights); x1=weights[0];y1=weights[1]; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid2); tmp.Weights(weights); x2=weights[0];y2=weights[1]; ObjectCreate(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJ_TREND,window,time[x1],y1,time[x2],y2); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_WIDTH,1); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_STYLE,STYLE_DOT); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_COLOR,Yellow); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_BACK,false); tmpc=GNGAlgorithm.Connections.GetNextNode(); } ChartRedraw(); } //--- delete the instance of the algorithm from the memory delete GNGAlgorithm; //--- a pause before clearing the chart while(!IsStopped()); //--- remove all the drawings from the chart ObjectsDeleteAll(0,window); }
Wir stellen unseren Code zusammen, rufen dann zunächst den Dummy-Indikator auf und lassen abschließend das GNG-Skript über dasselbe Diagramm laufen. Auf dem Bildschirm sollte sich in etwa folgendes Bild zeigen:
Wie wir sehen, funktioniert der Algorithmus wirklich: das Gitternetz passt sich schrittweise an die eingehenden neuen Daten an, indem es versucht, ihren Raum entsprechend der Dichte der blauen Punkte abzudecken.
In dem Film wird nur der erste Anfang des Lernvorgangs dargestellt (insgesamt nur etwa 1.000 Iterationen, wogegen die tatsächliche Anzahl der für das GNG-Studium benötigten Vektoren in die Zehntausende gehen kann), das vermittelt jedoch schon eine angemessene Vorstellung von dem Ablauf des Vorgangs.
6. Bekannte Schwierigkeiten
Wie bereits gesagt besteht das Hauptproblem von GNG in der Unfähigkeit, nicht stationäre Reihen mit sich schnell ändernden Merkmalen zu verfolgen. Derartige „springende“ Verteilungen der Eingangssignale können der Grund dafür sein, dass ein beträchtlicher Teil der Neuronen der GNG-Schicht, die bereits eine bestimmte topologische Struktur angenommen hat, sich plötzlich als „arbeitslos“ erweisen.
Dabei erhöht sich, da die eingehenden Signale bereits nicht mehr in den Bereich fallen, an dem sie angesiedelt sind, das Alter der Verbindungen zwischen diesen Neuronen nicht, folglich verrichtet der „tote“ Teil des Netzes, der sich die alten Eigenschaften des Signals „merkt“, keine nützliche Arbeit, sondern vergeudet lediglich Rechnerkapazität (siehe Abbildung 2).
Im Fall langsam wandernder Verteilungen ist dieser nachteilige Effekt nicht zu beobachten: Wenn die Wanderungsgeschwindigkeit mit der „Geschwindigkeit der Verlagerung“ der Neuronen bei der Anpassung der Gewichte vergleichbar ist, erweist sich GNG als geeignet, um diese Veränderungen zu verfolgen.
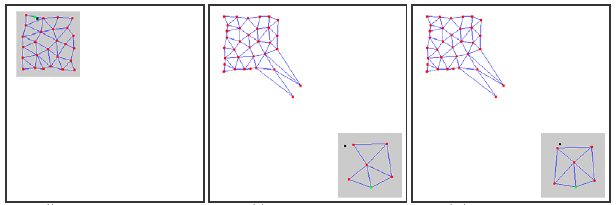
Abbildung 2. Reaktion von Growing Neural Gas auf eine „springende“ Verteilung
Einzelne inaktive („tote“) Knoten können ebenfalls im Netz auftreten, wenn am Eingang des Algorithmus eine zu hohe Frequenz bei der Zufuhr neuer Neuronen (der Parameter λ) angelegt wird.
Ein zu niedriger Wert führt dazu, dass das Netz beginnt, statistisch unerhebliche Aussendungen von Eingangssignalen zu verfolgen, deren Wiederholungswahrscheinlichkeit äußerst gering ist. Wird an dieser Stelle ein GNG-Neuron zugeführt, dürfte es danach mit größter Wahrscheinlichkeit für lange Zeit inaktiv bleiben.
Darüber hinaus wurde in empirischen Studien nachgewiesen, dass ein niedriger Wert des Zufuhrparameters, auch wenn er zu Beginn des Lernvorgangs zu einer schnellen Herabsetzung des mittleren Netzfehlers beiträgt, nach dem „Unterricht“ bei diesem Parameter zu schlechteren Werten führt: ein derartiges Netz „clustert“ die Daten gröber.
7. Anpassung des Algorithmus
Das Problem der „springenden“ Verteilung kann mithilfe bestimmter Anpassungen des Algorithmus behoben werden. Allgemein anerkannt ist eine Anpassung, bei der der so genannte Nutzenfaktor der Neuronen eingeführt wird (GNG with Utility factor oder kurz: GNG-U). Die Änderungen an dem Pseudocode sind dabei minimal und führen zu Folgendem:
- jedem Neuron
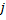 wird die ihm entsprechende als „Nutzenfaktor“ bezeichnete Variable
wird die ihm entsprechende als „Nutzenfaktor“ bezeichnete Variable 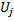 (dieselbe Variable U wie in der Liste der Felder der Klasse CGNGNeuron) beigestellt;
(dieselbe Variable U wie in der Liste der Felder der Klasse CGNGNeuron) beigestellt; -
in Schritt 4 ändern wir nach der Anpassung der Gewichte des Gewinnerneurons dessen Nutzenfaktor auf die dem Unterschied zwischen dem Fehler des zweitbesten Neurons und dem des Gewinners entsprechende Größe:
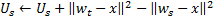
Physisch handelt es sich bei dieser Ergänzung um die Größe, um die sich der summarische Fehler des Netzes ändern würde, wenn das Gewinnerneuron in ihm nicht vorhanden wäre (dann wäre das zweitbeste Neuron der Gewinner), das heißt, in Wirklichkeit bestimmt sie die Nützlichkeit des Neurons für die Herabsetzung des allgemeinen Fehlers. -
das Löschen von Neuronen in Schritt 8 erfolgt nach einem anderen Prinzip: es wird nur der Knoten mit dem niedrigsten Nutzenfaktor gelöscht, und auch nur dann, wenn der höchste Fehlerwert in der betreffenden Schicht diesen Nutzenfaktor um mehr als das
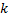 -fache übersteigt:
-fache übersteigt: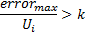
-
bei Hinzufügung eines neuen Knotens in Schritt 9 wird dessen Nutzenfaktor als arithmetisches Mittel der Nutzenfaktoren seiner Nachbarneuronen berechnet:
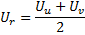
-
in Schritt 10 wird der Nutzenfaktor aller Neuronen nach demselben Prinzip und zu denselben Zielen herabgesetzt wie auch die Fehlervariablen:
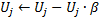
Die Konstante ![]() ist von ausschlaggebender Bedeutung für die Fähigkeit zur Beobachtung von Nichtstationarität: ein zu großer Wert bei ihr führt zur Löschung nicht nur der wirklich „wenig nützlichen“ sondern auch zu der anderer, voll nutzbarer Neuronen, ein zu kleiner Wert dagegen zu selteneren Löschvorgängen und folglich zu einer Verlangsamung der Anpassung.
ist von ausschlaggebender Bedeutung für die Fähigkeit zur Beobachtung von Nichtstationarität: ein zu großer Wert bei ihr führt zur Löschung nicht nur der wirklich „wenig nützlichen“ sondern auch zu der anderer, voll nutzbarer Neuronen, ein zu kleiner Wert dagegen zu selteneren Löschvorgängen und folglich zu einer Verlangsamung der Anpassung.
In der Datei GNG.mqh wird der Algorithmus GNG-U als von CGNGAlgorithm abgeleitete Klasse beschrieben. Die Leser mögen die vorgenommenen Änderungen selbst nachvollziehen und den Algorithmus in der Praxis testen.
Fazit
Am Beispiel der Schaffung eines neuronalen Netzes haben wir die grundlegenden Möglichkeiten der in die Programmiersprache MQL5 integrierten objektorientierten Programmierung kennen gelernt. Der Umstand, dass ohne diese Möglichkeiten (für die wir den Entwicklern größten Dank zollen) das Schreiben komplexer Programme für den automatischen Handel um ein Vielfaches schwerer wäre, dürfte hinreichend deutlich geworden sein.
Was die vorgestellten Algorithmen betrifft, bleibt festzustellen, dass sie selbstverständlich verbessert werden können. Erster Anwärter auf eine Modernisierung ist die Anzahl der externen Parameter. Derer gibt es nicht wenige, was heißt, dass solche Anpassungen durchaus möglich sind, bei denen diese Parameter zu internen Variablen und auf der Grundlage der Eigenschaften der Eingangsdaten sowie des Zustandes des Algorithmus ausgewählt werden.
Der Autor wünscht Ihnen allen viel Erfolg beim Studium der Neuroinformatik und bei ihrem Einsatz im Börsenhandel!
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/163
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Der MQL5-Assistent: Erstellen von Expert-Systemen ohne Programmierung
Der MQL5-Assistent: Erstellen von Expert-Systemen ohne Programmierung
 Die Ereignisverarbeitungsroutine "Neuer Balken"
Die Ereignisverarbeitungsroutine "Neuer Balken"
 Ein einfaches Beispiel zur Erstellung eins Indikators mittels Qualitativaussagenlogik (unscharfer oder fuzzy Logik)
Ein einfaches Beispiel zur Erstellung eins Indikators mittels Qualitativaussagenlogik (unscharfer oder fuzzy Logik)
 Expert Advisors Basierend auf Beliebten Handelssystemen und Alchemie der Handelsroboter Optimierung
Expert Advisors Basierend auf Beliebten Handelssystemen und Alchemie der Handelsroboter Optimierung
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Sehr interessant,
Ich freue mich darauf, es zu implementieren und es anstelle eines festen neuronalen Netzes zu verwenden.
Interessanter Artikel!
Aber er ist ziemlich alt - der Compiler wurde geändert und jetzt erzeugt der Code Fehler und Warnungen!
Hallo
ich frage, ob jemand von der Gemeinschaft Erfolg zu entwickeln EA mit GNG?
Ich frage, ob das Ergebnis gut ist?
danke
Hallo
ich frage, ob jemand von der Gemeinschaft Erfolg zu entwickeln EA mit GNG?
Ich frage, ob das Ergebnis gut ist?
Danke
Nun... nach was? fünf Monaten o_O ist niemand bereit, also kann ich das vielleicht selbst kommentieren.
In der Implementierung, die Sie in diesem Artikel gesehen haben, ist das NN eine selbstanpassende Variante eines so genannten radial-basierten Funktionsnetzes. Wenn Sie einen EA, der auf dem GNG-Algorithmus basiert, mit dem gleichen Typ EA vergleichen, der auf einem nicht-adaptiven Typ eines neuronalen Clusternetzes basiert, werden Sie höchstwahrscheinlich mit GNG bessere Ergebnisse erzielen als ohne GNG. Um also Ihre letzte Frage zu beantworten: Ja, das Ergebnis ist gut in dem Sinne, wie ich es gerade erklärt habe.
Was die erste Frage betrifft, so habe ich selbst EAs mit einem GNG darin entwickelt, und es hat mäßig gut funktioniert, yay. Für den täglichen Gebrauch bevorzuge ich jedoch andere Algorithmen, die in der Regel nicht-neural sind. Ich kann das damit untermauern, dass ANN immer eine "Black Box" darstellen, was bedeutet, dass man nicht wirklich versteht, was da drinnen vor sich geht, wenn es Eingabedaten verarbeitet. Das bedeutet, dass ANN nur dann ein Algorithmus der Wahl wäre, wenn man einen völlig unstrukturierten Datensatz mit absolut unbekannten intrinsischen Abhängigkeiten hätte, die das ANN irgendwie extrahieren soll. Anmerkung: ohne Aussicht auf ein genaues Ergebnis. In jedem anderen Fall, d. h. wenn Sie eine Vorstellung davon haben, wie die Abhängigkeiten in Ihrem Datensatz organisiert sein könnten, sollten Sie zunächst andere, deterministischere "White Box"-Möglichkeiten zur Strukturierung ausprobieren. Es gibt Tausende von ihnen.