
Growing Neural Gas: Implementation in MQL5
Introduction
In 90s researchers of artificial neural networks came to a conclusion that it was necessary to develop a new class of these computing mechanisms, whose feature would be absence of a fixed topology of network layers. This means that the number and arrangement of artificial neurons in the feature space is not pre-specified, but is calculated in the learning process of such models in accordance with the characteristics of input data, independently adjusting to them.
The reason for the emergence of such ideas was a number of practical problems about hampered compression and vector quantization of input parameters, such as speech and image recognition, classification and recognition of abstract patterns.
Since at that time self-organizing maps and Hebbian learning were already known (in particular, algorithms that produce topologization of network, ie create a set of connections between neurons, forming a layer "framework"), and approaches to "soft" competitive learning had been worked out (in such procedures weight adapting of not only the "winner" neuron, but also of its "neighbors" occurs), the logical step was to combine these methods, which was done in 1995 by a German scientist Bernd Fritzke who created the now popular algorithm "Growing neural gas"(,GNG).
The method proved quite successful, so that a series of its modifications appeared; one of them was adaptation for supervised learning (Supervised-GNG). As noted by the author, S-GNG showed significantly greater efficiency in the classification of data than, say, a network of radial basis functions, due to the ability to optimize topology in the input space areas that are hard to classify. No doubt, GNG is superior to "K-means" clustering.
It is noteworthy that in 2001 Fritzke ended his career of a scientist at the Ruhr university (Bochum, Germany) after receiving a job offer at the German stock exchange (Deutsche Bӧrse). Well, this fact was another reason to select his algorithm as a basis for writing this article.
1. Growing Neural Gas
So, GNG is an algorithm that allows to implement adaptive clustering of input data, ie not only divide the space into clusters, but also to determine their required number based on the characteristics of the data.
Starting with only two neurons, the algorithm consistently changes (mostly increases) the number of them, while creating a set of connections between neurons that best corresponds to the distribution of input vectors, using the approach of competitive Hebbian learning. Each neuron has an internal variable that accumulates the so-called "local error". Connections between nodes are characterized by a variable called "age".
GNG pseudocode looks like this:
- Initialization: Create two nodes with the vectors of weights, allowed by the distribution of input vectors, and zero values of local errors; connect nodes by setting its age to 0.
- Input a vector to a neural network
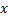 .
. - Find two neurons
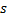 and
and 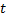 nearest to
nearest to 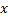 , ie nodes with weight vector
, ie nodes with weight vector 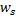 and
and 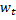 such that
such that 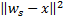 is minimal, and
is minimal, and 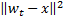 is second minimal value of distance among all nodes.
is second minimal value of distance among all nodes. -
Update the local error of the winner neuron
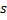 by adding to it the squared distance between the vectors
by adding to it the squared distance between the vectors 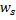 and
and 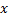 :
: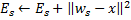
-
Shift the winner neuron
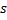 and all of its topological neighbors (ie, all neurons that have a connection to the winner) in the direction of the input vector
and all of its topological neighbors (ie, all neurons that have a connection to the winner) in the direction of the input vector 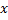 by distances equal to the shares
by distances equal to the shares 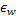 and
and 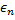 from a full one.
from a full one.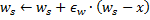
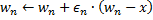
- Increase the age of all connections outgoing from the winner
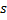 by 1.
by 1. - If the two best neuron
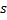 and
and 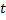 are connected, set the age of their connection to zero. Otherwise create a connection between them.
are connected, set the age of their connection to zero. Otherwise create a connection between them. - Remove connections with an age larger than
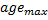 . If this results in neurons having no more emanating edges, remove those neurons as well.
. If this results in neurons having no more emanating edges, remove those neurons as well. -
If the number of the current iteration is a multiple of
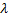 , and the limit size of the network hasn't reached, insert a new neuron
, and the limit size of the network hasn't reached, insert a new neuron 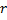 as follows:
as follows:- Determine a neuron
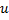 with a largest local error.
with a largest local error. - Determine among the neighbors of
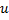 the neuron
the neuron 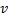 with a maximum error.
with a maximum error. - Create a node
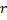 "at the middle" between
"at the middle" between 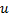 and
and 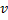 :
:
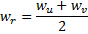
- Replace the edge between
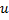 and
and 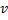 by the edge between
by the edge between 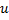 and
and 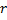 ,
, 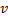 and
and 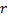 .
. - Decrease the errors of neurons
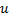 and
and 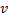 , set the value of the error of neuron
, set the value of the error of neuron 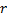 .
.
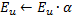
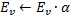
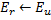
- Determine a neuron
-
Decrease errors of all the neurons
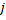 by the fraction
by the fraction 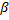 .
.
- If a stopping criterion is not yet fulfilled continue with step 2.
Let's consider how the growing neural gas adapts to the characteristics of the input space.
First of all, pay attention to the increase in the error variable of the winner at step 4. This procedure leads to the fact that nodes that win most often, ie those in the neighborhood of which the largest number of input signals appear, have the largest error, and hence these areas are prime candidates to "compaction" by adding new nodes.
Shift of nodes in the direction of the input vector in step 5 means that the winner tries to "average" its position among input signals located in its neighborhood. In this case, the best neuron little "pulls" its neighbors in the direction of the signal (![]() is chosen as a rule).
is chosen as a rule).
I explain the operation with edges between neurons in steps 6-8. The meaning of aging and removing of old connections is that the topology of the network should be maximally close to the so called Delaunay triangulation, ie a triangulation (subdivision into triangles) of neurons in which, inter alia, the minimal angle of all the angles of the triangles in the triangulation is maximized (avoiding "skinny" triangles).
Simply speaking, the Delaunay triangulation corresponds to the most "beautiful", in the sense of maximum entropy, topologization of the layer. It should be noted that the topological structure is required not in as a separate unit, but when used to determine the location of new nodes when they are inserted in step 8 - they are always located in the middle of an edge.
Step p is a correction of the error variables of all the neurons in the layer. This is to ensure that the network "forgets" the old input vectors and better responds to the new ones. Thus we get the possibility to use the growing neural gas for the adaptation of neural networks for time-dependent, namely, slowly drifting distributions of input signals. This, however, does not give it the ability to track rapid changes in the characteristics of inputs (see more details below in the section where the drawbacks of the algorithm are discussed).
Perhaps we should separately consider the stopping criterion. The algorithm leaves place for the fantasy of the developers of analysis systems. Possible options are: to check the efficiency of the network on the test set, to analyze the dynamics of the average error of neurons, to restrict the complexity of the network, etc.
For informational purposes we will work with the easiest option - because the purpose of this article is to demonstrate not only the algorithm itself, but the possibilities of its implementation by means of MQL5; we'll continue the learning of the layer until we run out of inputs (naturally their number is predefined).
2. Selecting the Method to Organize Data
When programming algorithm we'll obviously have to deal with the need to store what are called "sets". We'll have two sets – a set of neurons and a set of edges between them. While both structure will evolve in the course of the program (and we are planning both to add and remove items), we should also provide mechanisms for this.
Of course, we could try to use dynamic arrays of objects, but we would have to perform numerous data copy-move operations, which would essentially slow down the program. A more suitable option to work with abstractions with the specified properties is program graphs, and their simplest version - a linked list.
I'll remind our readers the working principle of the linked list (Fig. 1). The objects of the base class contain a pointer to the same object as one of the members, which allows to combine them in linear structures, regardless of the physical order of objects in memory. In addition, there is the "carriage" class, which encapsulates procedure of moving through the list, adding, inserting and deleting nodes, searching, comparing and sorting, and, if necessary, other procedures.
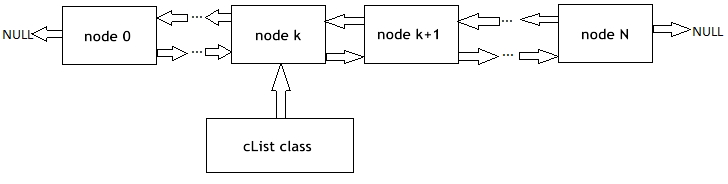
Figure 1. Schematic representation of the organization of linear linked lists
Specialists of MetaQuotes Software Corp. have already implemented linked lists of the objects of the CObject class in a standard library. The corresponding program code is located in the header file List.mqh, which is located in MQL5\Include\Arrays of the standard delivery pack of MetaTrader 5.
We will not reinvent the wheel and trust the qualification of the respected programmers from MetaQuotes, taking classes CObject and CList as the basis of our data structures. Here we'll use one of pillars of the object oriented approach – the mechanism of inheritance.
3. Programming the Model
First let's define the software form of the concept of "artificial neuron".
One of the etiquette rules when developing OOP applications is to always start programming with the most common data structures. Even when you're writing only for yourself, but especially if it is assumed that the codes will be available to other programmers, you should keep in mind the fact that in the future developers can have different ideas for the development and modification of the program logic; and you can't know in advance in what place the amendments will be made.
The principle of the OOP implies that other developers won't have to examine your classes, instead they should be able to inherit data structures from the data available in the right place of hierarchy. Thus, the first written class should be as much abstract as possible, and the specifics should be added at the lower levels, when being closer "to the sinful earth".
When applied to our problem, this means that we start writing a program with the definition of the CCustomNeuron class ("some kind of neuron"), which, like all artificial neurons will have a certain number of synapses (input weights) and the output value. It will be able to initialize (assign values to the weights), calculate the value of the signal at its output, and even adapt its weights by a specified value.
We can hardly achieve more abstraction (taking into account the fact that we inherit our class from a maximally generalized CObject) - all neurons must be able to perform the specified actions.
To describe the data create a header file Neurons.mqh, putting it in the folder Include\GNG.
//+------------------------------------------------------------------+ //| a base class to introduce object-neurons | //+------------------------------------------------------------------+ class CCustomNeuron:public CObject { protected: int m_synapses; double m_weights[]; public: double NET; CCustomNeuron(); ~CCustomNeuron(){}; void ZeroInit(int synapses); int Synapses(); void Init(double &weights[]); void Weights(double &weights[]); void AdaptWeights(double &delta[]); virtual void ProcessVector(double &in[]) {return;} virtual int Type() const { return(TYPE_CUSTOM_NEURON);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ void CCustomNeuron::CCustomNeuron() { m_synapses=0; NET=0; } //+------------------------------------------------------------------+ //| returns the dimension of the input vector of a neuron | //| INPUT: no | //| OUTPUT: number of "synapses" of the neuron | //+------------------------------------------------------------------+ int CCustomNeuron::Synapses() { return m_synapses; } //+------------------------------------------------------------------+ //| initializing neuron with a zero vector of weights. | //| INPUT: synapses - number of synapses (input weights) | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::ZeroInit(int synapses) { if(synapses<1) return; m_synapses=synapses; ArrayResize(m_weights,m_synapses); ArrayInitialize(m_weights,0); NET=0; } //+------------------------------------------------------------------+ //| initializing neuron weights with a set vector. | //| INPUT: weights - data vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::Init(double &weights[]) { if(ArraySize(weights)<1) return; m_synapses=ArraySize(weights); ArrayResize(m_weights,m_synapses); ArrayCopy(m_weights,weights); NET=0; } //+------------------------------------------------------------------+ //| obtaining vector of neuron weights. | //| INPUT: no | //| OUTPUT: weights - result | //+------------------------------------------------------------------+ void CCustomNeuron::Weights(double &weights[]) { ArrayResize(weights,m_synapses); ArrayCopy(weights,m_weights); } //+------------------------------------------------------------------+ //| change weights of the neuron by a specified value | //| INPUT: delta - correcting vector | //| OUTPUT: no | //+------------------------------------------------------------------+ void CCustomNeuron::AdaptWeights(double &delta[]) { if(ArraySize(delta)!=m_synapses) return; for(int i=0;i<m_synapses;i++) m_weights[i]+=delta[i]; NET=0; }
The functions defined in the class are very simple, so no need to include their detailed descriptions here. Note that we defined the function of input data processing ProcessVector(double &in[]) (the output value here is calculated like of an ordinary perceptron) with the virtual modifier.
This means that in case the method is redefined by derived classes, the appropriate procedure will be chosen depending on the actual object class dynamically at runtime, which increases its flexibility, including that in the sense of user interaction, and reduces labor costs for programming.
Despite the fact that seemingly we've done nothing to organize neurons in a linked list, in fact it already happened at the moment when we pointed out that the new class inherits from CObject. So, now private members of our class are m_first_node, m_curr_node and m_last_node, which are of the "pointer at CObject" type and point, respectively, at the first, current and last element of the list. We also have all the functions required for navigating through the list.
Now it's time to outline differences of a neuron of the GNG layer from its other colleagues by defining the CGNGNeuron class:
//+------------------------------------------------------------------+ //| a separate neuron of the GNG network | //+------------------------------------------------------------------+ class CGNGNeuron:public CCustomNeuron { public: int uid; double E; double U; double error; CGNGNeuron(); virtual void ProcessVector(double &in[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGNeuron::CGNGNeuron() { E=0; U=0; error=0; } //+------------------------------------------------------------------+ //| calculating "distance" from the neuron to the input vector | //| INPUT: in - data vector | //| OUTPUT: no | //| REMARK: the current "distance" is placed in the error variable, | //| "local error" is contained in another variable, | //| which is called E | //+------------------------------------------------------------------+ void CGNGNeuron::ProcessVector(double &in[]) { if(ArraySize(in)!=m_synapses) return; error=0; NET=0; for(int i=0;i<m_synapses;i++) { error+=(in[i]-m_weights[i])*(in[i]-m_weights[i]); } }
So, as you can see, these differences are in the presence of fields:
- error – the current square of distance from the input vector to the vector of neuron weights,
- E – a variable that accumulates the local error and a unique ID,
- uid – it is required to enable us further join neurons by connections into pairs (the simple indexing existing in the CList class is not enough, because we'll have to add and delete neurons, which will lead to confusion in numbering).
The ProcessVector(...) function has changed – now it calculates the value of the error field.
Don't pay attention at the U field so far, its meaning will be explained later in the "Algorithm modification" section.
The next step is writing a class that represents a connection between two neurons.
//+------------------------------------------------------------------+ //| class defining connection (edge) between two neurons | //+------------------------------------------------------------------+ class CGNGConnection:public CObject { public: int uid1; int uid2; int age; CGNGConnection(); virtual int Type() const { return(TYPE_GNG_CONNECTION);} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGConnection::CGNGConnection() { age=0; }
There is nothing difficult here – an edge has two ends (neurons specified by identifiers uid1 and uid2) and age initially equal to zero.
Now we'll work with classes "carriages" of linked lists, which will contain possibilities required for implementing the GNG algorithm.
First of all inherit a class of neurons list from CList:
//+------------------------------------------------------------------+ //| linked list of neurons | //+------------------------------------------------------------------+ class CGNGNeuronList:public CList { public: //--- constructor CGNGNeuronList() {MathSrand(TimeLocal());} CGNGNeuron *Append(); void Init(double &v1[],double &v2[]); CGNGNeuron *Find(int uid); void FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner); }; //+------------------------------------------------------------------+ //| adds an "empty" neuron at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new neuron | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGNeuron; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGNeuron; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; while(true) { int rnd=MathRand(); if(!CheckPointer(Find(rnd))) { ((CGNGNeuron *)m_curr_node).uid=rnd; break; } } //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initializing list by way of creating two neurons set | //| by vectors of weights | //| INPUT: v1,v2 - vectors of weights | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGNeuronList::Init(double &v1[],double &v2[]) { Clear(); Append(); ((CGNGNeuron *)m_curr_node).Init(v1); Append(); ((CGNGNeuron *)m_curr_node).Init(v2); } //+------------------------------------------------------------------+ //| search for a neuron by uid | //| INPUT: uid - a unique ID of the neuron | //| OUTPUT: pointer at the neuron if successful, otherwise NULL | //+------------------------------------------------------------------+ CGNGNeuron *CGNGNeuronList::Find(int uid) { if(!GetFirstNode()) return(NULL); do { if(((CGNGNeuron *)m_curr_node).uid==uid) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for two "best" neurons in terms of minimal current error | //| INPUT: no | //| OUTPUT: Winner - neuron "closest" to the input vector | //| SecondWinner - second "closest" neuron | //+------------------------------------------------------------------+ void CGNGNeuronList::FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) { double err_min=0; Winner=NULL; if(!CheckPointer(GetFirstNode())) return; do { if(!CheckPointer(Winner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min= ((CGNGNeuron *)m_curr_node).error; Winner = m_curr_node; } } while(CheckPointer(GetNextNode())); err_min=0; SecondWinner=NULL; GetFirstNode(); do { if(m_curr_node!=Winner) if(!CheckPointer(SecondWinner) || ((CGNGNeuron *)m_curr_node).error<err_min) { err_min=((CGNGNeuron *)m_curr_node).error; SecondWinner=m_curr_node; } } while(CheckPointer(GetNextNode())); m_curr_node=Winner; }
In the class constructor a generator of pseudorandom numbers is initialized: it will be used for assigning the elements of the list unique identifiers.
Let's clarify the meaning of the class methods:
- The Append() method is an addition to the functionality of the CList class. When calling it, a node is appended at the end of the list, or the first node is created if the lust is empty.
- The Init(double &v1[],double &v2[]) function owes its appearance to the GNG algorithm. Remember, the growth of the network begins with two neurons, so this signature would be most convenient to us. In the function body, when using IDs m_curr_node, m_first_node, m_last_node it is necessary to explicitly convert then to type CGNGNeuron*, if we want to use the functionality of this class (the specified variables were inherited from CList, so nominally they point at CObject).
- The Find(int uid) function, as it comes from its name, searches for a neuron by its ID and returns a pointer at the found element or NULL if it can't find it.
- FindWinners(CGNGNeuron *&Winner,CGNGNeuron *&SecondWinner) – also part of the algorithm. We'll need to search for a winner in the list of neurons, and the one next to it in terms of closeness to the input vector, that's what we use this function for. Note that parameters are passed to this function by reference so that further we can write there returned values (*& means "reference to a pointer" - this is a correct syntax, the reverse one &* means "pointer at a reference" which is prohibited: the compiler will generate an error in this case).
The next class is a list of connections between neurons.
//+------------------------------------------------------------------+ //| a linked list of connections between neurons | //+------------------------------------------------------------------+ class CGNGConnectionList:public CList { public: CGNGConnection *Append(); void Init(int uid1,int uid2); CGNGConnection *Find(int uid1,int uid2); CGNGConnection *FindFirstConnection(int uid); CGNGConnection *FindNextConnection(int uid); }; //+------------------------------------------------------------------+ //| adds an "empty" connection at the end of the list | //| INPUT: no | //| OUTPUT: pointer at a new binding | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Append() { if(m_first_node==NULL) { m_first_node= new CGNGConnection; m_last_node = m_first_node; } else { GetLastNode(); m_last_node=new CGNGConnection; m_curr_node.Next(m_last_node); m_last_node.Prev(m_curr_node); } m_curr_node=m_last_node; m_curr_idx=m_data_total++; //--- return(m_curr_node); } //+------------------------------------------------------------------+ //| initialize the list by creating one connection | //| INPUT: uid1,uid2 - IDs of neurons for the connection | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGConnectionList::Init(int uid1,int uid2) { Append(); ((CGNGConnection *)m_first_node).uid1 = uid1; ((CGNGConnection *)m_first_node).uid2 = uid2; m_last_node = m_first_node; m_curr_node = m_first_node; m_curr_idx=0; } //+------------------------------------------------------------------+ //| check if there is connection between the set neurons | //| INPUT: uid1,uid2 - IDs of the neurons | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::Find(int uid1,int uid2) { if(!CheckPointer(GetFirstNode())) return(NULL); do { if((((CGNGConnection *)m_curr_node).uid1==uid1 && ((CGNGConnection *)m_curr_node).uid2==uid2) ||(((CGNGConnection *)m_curr_node).uid1==uid2 && ((CGNGConnection *)m_curr_node).uid2==uid1)) return(m_curr_node); } while(CheckPointer(GetNextNode())); return(NULL); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the first element of the list | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindFirstConnection(int uid) { if(!CheckPointer(GetFirstNode())) return(NULL); while(true) { if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; if(!CheckPointer(GetNextNode())) return(NULL); } return(m_curr_node); } //+------------------------------------------------------------------+ //| search for the first topological neighbor of the set neuron | //| starting with the list element next to the current one | //| INPUT: uid - ID of the neuron | //| OUTPUT: pointer at the connection if there is one, or NULL | //+------------------------------------------------------------------+ CGNGConnection *CGNGConnectionList::FindNextConnection(int uid) { if(!CheckPointer(GetCurrentNode())) return(NULL); while(true) { if(!CheckPointer(GetNextNode())) return(NULL); if(((CGNGConnection *)m_curr_node).uid1==uid || ((CGNGConnection *)m_curr_node).uid2==uid) break; } return(m_curr_node); }
Defined methods of the class:
- Append(). The implementation of this method is similar to that described in the previous class, except the return type (unfortunately, there are no class templates in MQL5, so we have to write these things each time).
- Init(int uid1,int uid2) – the GNG algorithm requires initialization of one connection at its beginning, which is performed in this function.
- The Find(int uid1,int uid2) function is clear.
- The difference between methods FindFirstConnection(int uid) and FindNextConnection(int uid) is that the first one is looking for a connection with a neighbor starting from the beginning of the list, while the second one begins with the node next to the current (m_curr_node).
Here the description of data structures is over. It is time to begin programming our own algorithm.
4. The Class of the Algorithm
Create a new header file GNG.mqh, place it in the folder Include\GNG.
//+------------------------------------------------------------------+ //| GNG.mqh | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #include "Neurons.mqh" //+------------------------------------------------------------------+ //| the main class representing the GNG algorithm | //+------------------------------------------------------------------+ class CGNGAlgorithm { public: //--- linked lists of object-neurons and connection between them CGNGNeuronList *Neurons; CGNGConnectionList *Connections; //--- parameters of the algorithm int input_dimension; int iteration_number; int lambda; int age_max; double alpha; double beta; double eps_w; double eps_n; int max_nodes; CGNGAlgorithm(); ~CGNGAlgorithm(); virtual void Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes); virtual bool ProcessVector(double &in[],bool train=true); virtual bool StoppingCriterion(); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CGNGAlgorithm::CGNGAlgorithm(void) { Neurons=new CGNGNeuronList(); Connections=new CGNGConnectionList(); Neurons.FreeMode(true); Connections.FreeMode(true); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CGNGAlgorithm::~CGNGAlgorithm(void) { delete Neurons; delete Connections; } //+------------------------------------------------------------------+ //| initializes the algorithm using two vectors of input data | //| INPUT: v1,v2 - input vectors | //| __lambda - number of iterations after which a new | //| neuron is inserted | //| __age_max - maximum age of connection | //| __alpha, __beta - used for adapting errors | //| __eps_w, __eps_n - used for adapting weights | //| __max_nodes - limit on the network size | //| OUTPUT: no | //+------------------------------------------------------------------+ void CGNGAlgorithm::Init(int __input_dimension, double &v1[], double &v2[], int __lambda, int __age_max, double __alpha, double __beta, double __eps_w, double __eps_n, int __max_nodes) { iteration_number=0; input_dimension=__input_dimension; lambda=__lambda; age_max=__age_max; alpha= __alpha; beta = __beta; eps_w = __eps_w; eps_n = __eps_n; max_nodes=__max_nodes; Neurons.Init(v1,v2); CGNGNeuron *tmp; tmp=Neurons.GetFirstNode(); int uid1=tmp.uid; tmp=Neurons.GetLastNode(); int uid2=tmp.uid; Connections.Init(uid1,uid2); } //+------------------------------------------------------------------+ //| the main function of the algorithm | //| INPUT: in - vector of input data | //| train - if true, start learning, otherwise | //| only calculate the input values of neurons | //| OUTPUT: true, if stop condition is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::ProcessVector(double &in[],bool train=true) { if(ArraySize(in)!=input_dimension) return(StoppingCriterion()); int i; CGNGNeuron *tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.ProcessVector(in); tmp=Neurons.GetNextNode(); } if(!train) return(false); iteration_number++; //--- Find two neurons closest to in[], i.e. the nodes with weight vectors //--- Ws and Wt, so that ||Ws-in||^2 is minimal and ||Wt-in||^2 - //--- is second minimal value of distance of all the nodes. //--- Under ||*|| we mean Euclidean norm CGNGNeuron *Winner,*SecondWinner; Neurons.FindWinners(Winner,SecondWinner); //--- Update the local error of the winner Winner.E+=Winner.error; //--- Shift the winner and all its topological neighbors (i.e. //--- all neurons connected with the winner) in the direction of the input //--- vector by distances equal to fractions eps_w and eps_n of the full. double delta[],weights[]; Winner.Weights(weights); ArrayResize(delta,input_dimension); for(i=0;i<input_dimension;i++) delta[i]=eps_w*(in[i]-weights[i]); Winner.AdaptWeights(delta); //--- Increment the age of all connections emanating from the winner by 1. CGNGConnection *tmpc=Connections.FindFirstConnection(Winner.uid); while(CheckPointer(tmpc)) { if(tmpc.uid1==Winner.uid) tmp = Neurons.Find(tmpc.uid2); if(tmpc.uid2==Winner.uid) tmp = Neurons.Find(tmpc.uid1); tmp.Weights(weights); for(i=0;i<input_dimension;i++) delta[i]=eps_n*(in[i]-weights[i]); tmp.AdaptWeights(delta); tmpc.age++; tmpc=Connections.FindNextConnection(Winner.uid); } //--- If two best neurons are connected, reset the age of the connection. //--- Otherwise create a connection between them. tmpc=Connections.Find(Winner.uid,SecondWinner.uid); if(tmpc) tmpc.age=0; else { Connections.Append(); tmpc=Connections.GetLastNode(); tmpc.uid1 = Winner.uid; tmpc.uid2 = SecondWinner.uid; tmpc.age=0; } //--- Delete all the connections with an age larger than age_max. //--- If this results in neurons having no connections with other //--- nodes, remove those neurons. tmpc=Connections.GetFirstNode(); while(CheckPointer(tmpc)) { if(tmpc.age>age_max) { Connections.DeleteCurrent(); tmpc=Connections.GetCurrentNode(); } else tmpc=Connections.GetNextNode(); } tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { if(!Connections.FindFirstConnection(tmp.uid)) { Neurons.DeleteCurrent(); tmp=Neurons.GetCurrentNode(); } else tmp=Neurons.GetNextNode(); } //--- If the number of the current iteration is multiple of lambda, and the network //--- hasn't been reached yet, create a new neuron r according to the following rules CGNGNeuron *u,*v; if(iteration_number%lambda==0 && Neurons.Total()<max_nodes) { //--- 1.Find neuron u with the maximum local error. tmp=Neurons.GetFirstNode(); u=tmp; while(CheckPointer(tmp=Neurons.GetNextNode())) { if(tmp.E>u.E) u=tmp; } //--- 2.determin among the neighbors of u the node u with the maximum local error. tmpc=Connections.FindFirstConnection(u.uid); if(tmpc.uid1==u.uid) v=Neurons.Find(tmpc.uid2); else v=Neurons.Find(tmpc.uid1); while(CheckPointer(tmpc=Connections.FindNextConnection(u.uid))) { if(tmpc.uid1==u.uid) tmp=Neurons.Find(tmpc.uid2); else tmp=Neurons.Find(tmpc.uid1); if(tmp.E>v.E) v=tmp; } //--- 3.Create a node r "in the middle" between u and v. double wr[],wu[],wv[]; u.Weights(wu); v.Weights(wv); ArrayResize(wr,input_dimension); for(i=0;i<input_dimension;i++) wr[i]=(wu[i]+wv[i])/2; CGNGNeuron *r=Neurons.Append(); r.Init(wr); //--- 4.Replace the connection between u and v by a connection between u and r, v and r tmpc=Connections.Append(); tmpc.uid1=u.uid; tmpc.uid2=r.uid; tmpc=Connections.Append(); tmpc.uid1=v.uid; tmpc.uid2=r.uid; Connections.Find(u.uid,v.uid); Connections.DeleteCurrent(); //--- 5.Decrease the errors of neurons u and v, set the value of the error of //--- neuron r the same as of u. u.E*=alpha; v.E*=alpha; r.E = u.E; } //--- Decrease the errors of all neurons by the fraction beta tmp=Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.E*=(1-beta); tmp=Neurons.GetNextNode(); } //--- Check the stopping criterion return(StoppingCriterion()); } //+------------------------------------------------------------------+ //| Stopping criterion. In this version of file makes no | //| actions, always returns false. | //| INPUT: no | //| OUTPUT: true, if the criterion is fulfilled, otherwise false | //+------------------------------------------------------------------+ bool CGNGAlgorithm::StoppingCriterion() { return(false); }
The CGNGAlgorithm class has two important fields - pointers at the linked lists of neurons Neurons and connections between them Connections. They will be the physical medium of the structure of our neural network. The remaining fields are the parameters of the algorithm defined from the outside.
Of the auxiliary class methods I'd single out Init(...) which passes the external parameters to an instance of the algorithm and initializes the data structures and the stopping criterion StoppingCriterion() which, as we agreed earlier, does not do anything always returning false.
The ProcessVector(…) function which is the main function of the algorithm that processes the specified data vector, doesn't contain any subtleties: we have organized the data and methods of working with them so that when it comes to the algorithm, we only need to mechanically go through all its steps. Their location in the code is denoted by the appropriate comments.
5. Using in Work
Let's demonstrate the work of the algorithm on real data of the MetaTrader 5 terminal.
Here we are not aimed at creating a working Expert Advisor based on GNG (this is a bit much for one article), we want only to see how the growing neural gas is working, what is called "live" presentation.
In order to beautifully render the data, create an empty window scaled along the price axis in the range of 0-100. For this purpose, we use an "empty" indicator Dummy.mq5 (it has no other functions):
//+------------------------------------------------------------------+ //| Dummy.mq5 | //| Copyright 2010, alsu | //| alsufx@gmail.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2010, alsu" #property link "alsufx@gmail.com" #property version "1.00" #property indicator_separate_window #property indicator_minimum 0 #property indicator_maximum 100 #property indicator_buffers 1 #property indicator_plots 1 //--- plot Label1 #property indicator_type1 DRAW_LINE #property indicator_style1 STYLE_SOLID #property indicator_width1 1 //--- indicator buffers double DummyBuffer[]; //+------------------------------------------------------------------+ //| Custom indicator initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- indicator buffers mapping SetIndexBuffer(0,DummyBuffer,INDICATOR_DATA); IndicatorSetString(INDICATOR_SHORTNAME,"GNG_dummy"); //--- return(0); } //+------------------------------------------------------------------+ //| Custom indicator iteration function | //+------------------------------------------------------------------+ int OnCalculate(const int rates_total, const int prev_calculated, const datetime& time[], const double& open[], const double& high[], const double& low[], const double& close[], const long& tick_volume[], const long& volume[], const int& spread[]) { //--- an empty buffer ArrayInitialize(DummyBuffer,EMPTY_VALUE); //--- return value of prev_calculated for next call return(rates_total); } //+------------------------------------------------------------------+
In the MetaEditor create a script called GNG.mq5 - it will display the network in the window of the Dummy indicator.
External parameters - the number of data vectors for learning and the parameters of the algorithm:
//--- the number of input vectors used for learning input int samples=1000; //--- parameters of the algorithm input int lambda=20; input int age_max=15; input double alpha=0.5; input double beta=0.0005; input double eps_w=0.05; input double eps_n=0.0006; input int max_nodes=100;
Declare global variables:
//---global variables CGNGAlgorithm *GNGAlgorithm; int window; int rsi_handle; int input_dimension; int _samples; double RSI_buffer[]; datetime time[];
Start writing the OnStart() function. First, let's find the necessary window:
void OnStart() { int i,j; int window=ChartWindowFind(0,"GNG_dummy");
For input data we use the values of the RSI indicator - it is convenient because its values are normalized in the range from 0 to 100, so we won't need to conduct preprocessing.
For an input vector of the neural network we assume the pair (input_dimension=2) that consists of two RSI values – on the current and previous bar (whose scientific name is "immersion of a time series in a two-dimensional feature space"). It is easier to display two-dimensional vectors on a flat chart.
So, first prepare the data to initialize and create an instance of the algorithm object:
//--- to have CopyBuffer() work correctly, the number of the vectors //--- must be within the number of bars with a reserve left for the vector length _samples=samples+input_dimension+10; if(_samples>Bars(_Symbol,_Period)) _samples=Bars(_Symbol,_Period); //--- receive input data for the algorithm rsi_handle=iRSI(NULL,0,8,PRICE_CLOSE); CopyBuffer(rsi_handle,0,1,_samples,RSI_buffer); //--- return the user-defined value _samples=_samples-input_dimension-10; //--- remember open time of the first 100 bars CopyTime(_Symbol,_Period,0,100,time); //--- create an instance of the algorithm and set the size of input data GNGAlgorithm=new CGNGAlgorithm; input_dimension=2; //--- data vectors double v[],v1[],v2[]; ArrayResize(v,input_dimension); ArrayResize(v1,input_dimension); ArrayResize(v2,input_dimension); for(i=0;i<input_dimension;i++) { v1[i] = RSI_buffer[i]; v2[i] = RSI_buffer[i+3]; }
Now initialize the algorithm:
//--- initialization
GNGAlgorithm.Init(input_dimension,v1,v2,lambda,age_max,alpha,beta,eps_w,eps_n,max_nodes);
Draw a rectangular box and information labels (to visually see how many iterations of the algorithm were processed and how many neurons have "grown" in the network):
//-- draw a rectangular box and information labels ObjectCreate(0,"GNG_rect",OBJ_RECTANGLE,window,time[0],0,time[99],100); ObjectSetInteger(0,"GNG_rect",OBJPROP_BACK,true); ObjectSetInteger(0,"GNG_rect",OBJPROP_COLOR,DarkGray); ObjectSetInteger(0,"GNG_rect",OBJPROP_BGCOLOR,DarkGray); ObjectCreate(0,"Label_samples",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_samples",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_samples",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_YDISTANCE,10); ObjectSetInteger(0,"Label_samples",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: 2"); ObjectCreate(0,"Label_neurons",OBJ_LABEL,window,0,0); ObjectSetInteger(0,"Label_neurons",OBJPROP_ANCHOR,ANCHOR_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_CORNER,CORNER_RIGHT_UPPER); ObjectSetInteger(0,"Label_neurons",OBJPROP_XDISTANCE,10); ObjectSetInteger(0,"Label_neurons",OBJPROP_YDISTANCE,25); ObjectSetInteger(0,"Label_neurons",OBJPROP_COLOR,Red); ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: 2");
In the main loop, prepare a vector for the input of the algorithm show it on the chart as a blue dot:
//--- start the main loop of the algorithm with i=2 because 2 were used already for(i=2;i<_samples;i++) { //--- fill out the data vector (for clarity, get samples separated //--- by 3 bars - they are less correlated) for(j=0;j<input_dimension;j++) v[j]=RSI_buffer[i+j*3]; //--- show the vector on the chart ObjectCreate(0,"Sample_"+i,OBJ_ARROW,window,time[v[0]],v[1]); ObjectSetInteger(0,"Sample_"+i,OBJPROP_ARROWCODE,158); ObjectSetInteger(0,"Sample_"+i,OBJPROP_COLOR,Blue); ObjectSetInteger(0,"Sample_"+i,OBJPROP_BACK,true); //--- change the information label ObjectSetString(0,"Label_samples",OBJPROP_TEXT,"Total samples: "+string(i+1));
Pass the vector to the algorithm (only one function - that's the advantage of the object-oriented approach!):
//--- pass the input vector to the algorithm for calculation
GNGAlgorithm.ProcessVector(v);
Remove old neurons from the chart and draw new ones (red circles) and connections (yellow dotted lines), highlight the winner and the second best neuron with colors Lime and Green:
//--- we need to remove old neurons an connections from the chart to draw new ones then for(j=ObjectsTotal(0)-1;j>=0;j--) { string name=ObjectName(0,j); if(StringFind(name,"Neuron_")>=0) { ObjectDelete(0,name); } else if(StringFind(name,"Connection_")>=0) { ObjectDelete(0,name); } }
double weights[]; CGNGNeuron *tmp,*W1,*W2; CGNGConnection *tmpc; GNGAlgorithm.Neurons.FindWinners(W1,W2); //--- drawing the neurons tmp=GNGAlgorithm.Neurons.GetFirstNode(); while(CheckPointer(tmp)) { tmp.Weights(weights); ObjectCreate(0,"Neuron_"+tmp.uid,OBJ_ARROW,window,time[weights[0]],weights[1]); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_ARROWCODE,159); //--- the winner is colored Lime, second best - Green, others - Red if(tmp==W1) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Lime); else if(tmp==W2) ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Green); else ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_COLOR,Red); ObjectSetInteger(0,"Neuron_"+tmp.uid,OBJPROP_BACK,false); tmp=GNGAlgorithm.Neurons.GetNextNode(); } ObjectSetString(0,"Label_neurons",OBJPROP_TEXT,"Total neurons: "+string(GNGAlgorithm.Neurons.Total())); //--- drawing connections tmpc=GNGAlgorithm.Connections.GetFirstNode(); while(CheckPointer(tmpc)) { int x1,x2,y1,y2; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid1); tmp.Weights(weights); x1=weights[0];y1=weights[1]; tmp=GNGAlgorithm.Neurons.Find(tmpc.uid2); tmp.Weights(weights); x2=weights[0];y2=weights[1]; ObjectCreate(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJ_TREND,window,time[x1],y1,time[x2],y2); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_WIDTH,1); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_STYLE,STYLE_DOT); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_COLOR,Yellow); ObjectSetInteger(0,"Connection_"+tmpc.uid1+"_"+tmpc.uid2,OBJPROP_BACK,false); tmpc=GNGAlgorithm.Connections.GetNextNode(); } ChartRedraw(); } //--- delete the instance of the algorithm from the memory delete GNGAlgorithm; //--- a pause before clearing the chart while(!IsStopped()); //--- remove all the drawings from the chart ObjectsDeleteAll(0,window); }
Compile the code, start the Dummy indicator and then run the GNG script on the same chart. A picture like the following should appear on the chart:
You see, the algorithm really works: the grid gradually adapts to the new incoming data trying to cover their space in accordance with the stand density of the blue dots.
The video shows only the very beginning of the learning process (only 1000 iterations, while the real number of the required vectors for learning of GNG can be up to tens of thousands); however this already gives us quite a decent understanding of the process.
6. Known Problems
As already mentioned, the main problem of GNG is its inability to track non-stationary series with rapidly changing characteristics. Such "jumping" distributions of input signals can lead to that much of the neurons of the GNG-layer, having already gained a certain topological structure, suddenly find themselves out of business.
Moreover, since the input signals do not fall in the region of their location, age of the connections between these neurons is not increased, therefore, the "dead" part of the network, which "remembers" the old characteristics of the signal, does not do useful work, but only consumes computing resources (see. Fig. 2).
In the case of slowly drifting distributions, this adverse effect is not observed: if the drift velocity is comparable to the "speed of movement" of neurons in the adaptation of weights, GNG is able to track these changes.
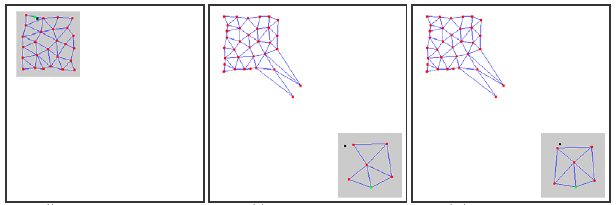
Figure 2. The reaction of the growing neural gas on the "jumping" distribution
Separate inactive (dead) nodes may also appear on the network if a very high frequency of insertion of new neurons (the parameter λ) is given on the input of the algorithm.
Its too low value leads to the fact that the network begins to track statistically insignificant emissions of distribution of input signals, whose probability of recurrence is very small. If a GNG-neuron is inserted in this place, it almost certainly will remain inactive after this for a long time.
In addition, as shown by empirical research, the low value of insertion, although it contributes to the rapid decrease in the average network error at the beginning of the learning process, as a result of training gives the worst values of this indicator: such a network clusters data more crudely.
7. Modification of the Algorithm
The problem of the "jumping" distribution can be solved by modifying the algorithm in a certain way. The widely accepted modification is the one that introduces the so-called factor of the utility of neurons (GNG with Utility factor or GNG-U). Changes in the pseudocode in this case are minimal and are as follows:
- to each neuron
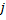 a variable called "factor of utility"
a variable called "factor of utility" 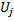 (that variable U in the list of fields of the CGNGNeuron class) is set into conformity;
(that variable U in the list of fields of the CGNGNeuron class) is set into conformity; -
in step 4, after adapting the weights of the neuron-winner, we change its utility factor by an amount equal to the difference between a mistake of the second best neuron and the winner:
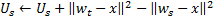
Physically, this additive is the amount by which the total network error would have changed if there were no winner in it (then the second best winner would become the winner), ie actually characterizes the usefulness of the neuron to reduce the overall error. -
neurons are removed in step 8 on a different principle: only a node with a minimum utility value is removed, and only if the maximum error value in the layer exceeds its utility factor by more than
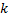 times:
times: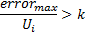
-
when adding a new node in step 9, its utility factor is calculated as the arithmetic mean between the utilities of neighboring neurons:
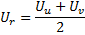
-
in step 10 the utility factor of all the neurons is decreased in the same manner and in the same order as the variables of errors:
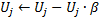
Constant ![]() here is critical to the ability to track non-stationarity: its too large value leads to the removal of not only really "little-utility", but also other quite usable neurons; a too small value leads to rare removals and consequently, to the reduced rate of adaptation.
here is critical to the ability to track non-stationarity: its too large value leads to the removal of not only really "little-utility", but also other quite usable neurons; a too small value leads to rare removals and consequently, to the reduced rate of adaptation.
In the file GNG.mqh the GNG-U algorithm is described as a class derived from CGNGAlgorithm. Readers can independently track the changes and try to use the algorithm.
Conclusion
By creating a neural network, we reviewed the main features of object-oriented programming built in the MQL5 language. It seems a rather obvious fact that in the absence of such opportunities (for which I'm thankful to the developers) it would be much more complicated to write complex programs for automated trading.
As for the analyzed algorithms, it should be noted that, naturally, they can be improved. In particular, the first candidate for upgrade is the number of external parameters. They are quite numerous, and this means there may well be such modifications, in which these parameters would become internal variables and would be selected based on the characteristics of input data and the state of the algorithm.
The author of the article wishes good luck to everyone in studying neuroinformatics and using it in trading!
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/163
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Vladimir Tsyrulnik: The Essense of my program is improvisation! (ATC 2010)
Vladimir Tsyrulnik: The Essense of my program is improvisation! (ATC 2010)
 Interview with Boris Odintsov (ATC 2010)
Interview with Boris Odintsov (ATC 2010)
 Building interactive semi-automatic drag-and-drop Expert Advisor based on predefined risk and R/R ratio
Building interactive semi-automatic drag-and-drop Expert Advisor based on predefined risk and R/R ratio
 Interview with Valery Mazurenko (ATC 2010)
Interview with Valery Mazurenko (ATC 2010)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Very Interesting,
I am looking forward to implement it and use it instead of a fixed neuronal network.
Interesting article!
But it is quite old - the compiler was changed and now the code generates errors and warnings!
Hello
i ask if anyone of the community success to develop EA using GNG?
i ask if the result is good ?
thanks
Hello
i ask if anyone of the community success to develop EA using GNG?
i ask if the result is good ?
thanks
Well.. after what? five months o_O no one is willing, so maybe I can comment on that myself.
In the implementation you've seen in this article the NN is a self-adapting variant of a so called radial-based functions net. If you compare an EA based upon GNG algorithm to the same type of EA based on a non-adaptive type of clusterization neural network you most probably are going to obtain better results with GNG rather than without it. So, to answer your latter question, yes, the result is good in the sense I just explained.
Turning to the former one, I myself have developed EAs with a GNG inside, and it worked moderately well, yay. However, for everyday use I prefer other algorithms which as a rule are non-neural. I can back it up by reminding that ANN always presents a "black box" meaning that you do not really understand what is going on in there when it processes input data. That implies that ANN would be an algorithm of choice only in a situation when you'd have a completely unstructured set of data with absolutely unknown intrinsic dependencies which you would like for the ANN to somehow extract. Note: without any promise for an accurate result. In any other case, i.e. when you have some ideas about how the dependencies in your dataset may be organized, you'd wanna first try other, more deterministic "white box" ways of structuring it. Thousands of them.