Redes neurais em trading: Transformer contrastivo de padrões

Introdução

Ao analisar situações de mercado com a ajuda do aprendizado de máquina, frequentemente focamos em velas individuais e suas características, deixando de lado os padrões de velas, que muitas vezes podem oferecer informações mais relevantes. Os padrões são estruturas estáveis de velas que surgem em condições de mercado semelhantes e podem conter regularidades criticamente importantes.

Anteriormente, conhecemos o framework Molformer, emprestado da área de previsão de propriedades moleculares. Os autores do Molformer combinaram representações de átomos e motivos em uma única sequência, o que permitiu fornecer ao modelo informações sobre a estrutura dos dados analisados. Ao mesmo tempo, isso levou à formulação de uma tarefa bastante complexa: separar as dependências entre nós de diferentes tipos. No entanto, existem métodos alternativos que não apresentam esse problema.

Por exemplo, o framework Atom-Motif Contrastive Transformer (AMCT), apresentado no trabalho "Atom-Motif Contrastive Transformer for Molecular Property Prediction". Para combinar dois níveis de interações e aumentar a capacidade da representação molecular, os autores do AMCT propuseram construir um aprendizado contrastivo átomo-motivo. Considerando que as representações de átomos e motivos da molécula são, na verdade, duas representações diferentes da mesma instância, elas se alinham naturalmente durante o aprendizado. Assim, podem conjuntamente fornecer sinais de autocontrole e, dessa forma, aumentar a confiabilidade da representação molecular aprendida.

Foi identificado que motivos idênticos em diferentes moléculas geralmente possuem propriedades químicas semelhantes. Isso significa que motivos idênticos devem ser representados de maneira alinhada em todas as moléculas. Consequentemente, o uso de perda contrastiva permite maximizar o alinhamento de motivos idênticos em diferentes moléculas e obter uma representação distinta dos motivos.

Além disso, para identificar claramente os motivos cruciais para determinar as propriedades de cada molécula, os autores do método construíram um mecanismo de atenção que considera as propriedades por meio de um módulo de atenção cruzada. Em particular, o módulo de atenção cruzada estabelece a relação entre a incorporação de propriedades moleculares e a representação dos motivos. Como resultado, é possível identificar os motivos-chave com base nos pesos da atenção cruzada.

1. Algoritmo AMCT

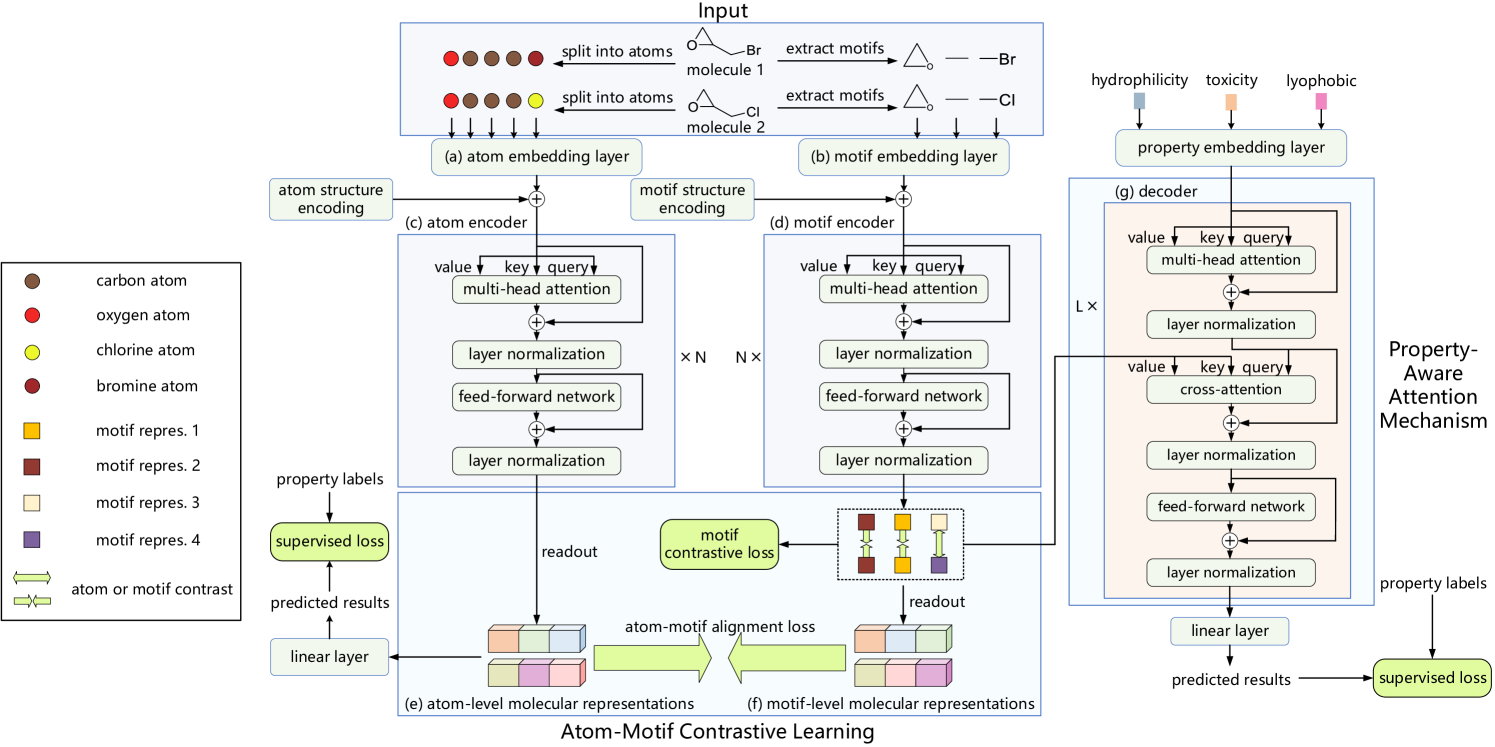
As descrições moleculares inseridas no modelo são inicialmente divididas em um conjunto de átomos e segmentadas em um conjunto de motivos. Em seguida, as sequências resultantes passam por camadas paralelas de codificação de átomos e motivos, que geram as respectivas incorporações. Dois codificadores independentes são utilizados para obter representações moleculares nos níveis de átomos e de motivos. Um decodificador e uma camada totalmente conectada são utilizados para obter os resultados esperados. Durante o treinamento do modelo, são utilizadas perdas de alinhamento átomo-motivo, perdas contrastivas no nível de motivos e perdas na previsão de propriedades.

No processo de codificação dos átomos, primeiro obtemos suas incorporações. Em seguida, usamos o Codificador de átomos para extrair interdependências entre os átomos individuais da molécula. Como resultado, é formada a representação molecular no nível de átomos.

Os autores do AMCT utilizam o grau de centralidade para codificar a informação estrutural entre os átomos, ou seja, as relações de ligação entre eles. Como o grau de centralidade é aplicado a cada átomo, ele é simplesmente adicionado à incorporação do átomo em questão.

Embora as interdependências entre átomos capturam com sucesso os detalhes de baixo nível, ignoram informações estruturais de alto nível entre diferentes átomos, portanto, em alguns casos, não são suficientes para prever propriedades moleculares. Para resolver esse problema, os autores do framework AMCT introduzem uma representação paralela de nível de motivos. No processo de codificação de motivos, primeiro eles são extraídos do conjunto de dados brutos e, em seguida, são geradas suas incorporações. Depois disso, utiliza-se o Codificador de motivos para extrair as interdependências entre os motivos.

Os autores do framework AMCT utilizam o grau de centralidade para codificar a informação estrutural entre os motivos, que é adicionada às respectivas incorporações.

Com o objetivo de explorar a nova informação adicional fornecida pelos motivos, são analisadas as relações de similaridade entre as representações moleculares nos níveis de átomos e de motivos. Como as representações de átomos e motivos de uma mesma molécula são, na verdade, duas representações diferentes de uma mesma entidade, elas naturalmente se alinham para gerar sinais de autocontrole durante o treinamento do modelo. Para alinhar as duas representações, os autores do método utilizam a divergência de Kullback-Leibler.

Como a perda de alinhamento entre átomos e motivos ocorre dentro da molécula e está limitada à coerência entre átomos e motivos de uma mesma molécula, os autores do ACTM buscam realizar contraste intermolecular e investigar a coerência entre diferentes moléculas. Considerando que motivos idênticos em diferentes moléculas apresentam propriedades químicas semelhantes, espera-se que eles tenham representações similares em todas elas. Para atingir esse objetivo, é proposta a perda contrastiva de motivo, que maximiza a coerência da representação de motivos idênticos em diferentes moléculas. Ao mesmo tempo, são afastadas as representações de motivos de classes diferentes.

Um bom processo de decodificação também é importante para obter uma representação confiável. O AMCT propõe uma decodificação com atenção às propriedades. Em particular, primeiro obtemos as incorporações das propriedades, e depois usamos o decodificador para extrair representações moleculares que sejam chave para propriedades específicas. Os resultados previstos são obtidos após uma projeção linear.

O decodificador é projetado para extrair representações moleculares que considerem tais propriedades. Para identificar os motivos cruciais na determinação das propriedades de cada molécula, os autores do AMCT constroem um mecanismo de atenção baseado em propriedades. Nesse mecanismo, é utilizado um módulo de atenção cruzada, que utiliza as incorporações das propriedades como Query e as representações dos motivos como Key-Value. Acredita-se que um motivo com peso elevado na atenção cruzada contribua mais para a propriedade molecular.

A visualização autoral do framework Atom-Motif Contrastive Transformer é apresentada abaixo.

2. Implementação com MQL5

Após considerar os aspectos teóricos do framework Atom-Motif Contrastive Transformer, passamos à parte prática do nosso artigo, onde apresentaremos nossa própria visão dos métodos propostos usando recursos do MQL5.

O framework AMCT é uma estrutura bastante complexa e abrangente. Mas, se observarmos atentamente os blocos utilizados, podemos perceber que grande parte deles já está implementada em nossa biblioteca de uma forma ou de outra. No entanto, ainda temos trabalho a fazer. Por exemplo, a comparação entre representações no nível de átomos e motivos. Espero que você não tenha dúvidas de que, além de simplesmente identificar as divergências, também teremos que distribuir o gradiente de erro entre os dois caminhos com o objetivo de minimizar as diferenças. E aqui existem várias formas possíveis de resolver essa questão.

Nós, é claro, podemos copiar os resultados de um dos caminhos para o buffer de gradientes do outro e, depois, calcular o gradiente do erro usando o método calcOutputGradients, da camada neural básica, que utilizamos para encontrar o erro do funcionamento do modelo. Uma vantagem dessa abordagem é a simplicidade de implementação, já que utilizamos os recursos existentes. No entanto, esse é um método bastante custoso. Durante o treinamento do modelo, será necessário copiar dois buffers de dados (resultados dos dois caminhos) e calcular sequencialmente os gradientes para cada representação.

Por isso, decidimos criar um pequeno kernel no lado do programa OpenCL, que nos permitirá determinar o gradiente de erro para ambos os caminhos ao mesmo tempo e sem cópia excessiva de dados.

__kernel void CalcAlignmentGradient(__global const float *matrix_o1,
                                    __global const float *matrix_o2,
                                    __global float *matrix_g1,
                                    __global float *matrix_g2,
                                    const int activation,
                                    const int add)
  {
   int i = get_global_id(0);

Nos parâmetros do kernel, recebemos ponteiros para 4 buffers de dados. Desses, 2 buffers contêm os resultados dos caminhos de átomos e motivos, no nosso caso velas e padrões. E 2 buffers servem para armazenar os gradientes de erro correspondentes. Além disso, entre os parâmetros do kernel, recebemos um ponteiro para a função de ativação que foi usada em ambos os caminhos.

Observe que aqui restringimos de forma clara a possibilidade de usar funções de ativação diferentes para os caminhos. O motivo é que, para uma comparação correta dos resultados dos dois caminhos, eles devem estar no mesmo subespaço. E é justamente a função de ativação que determina a área de saída da camada. Portanto, usar a mesma função de ativação na saída dos dois caminhos é algo perfeitamente lógico.

Aqui também adicionamos uma flag que indicará a necessidade de adicionar o gradiente de erro aos dados previamente acumulados ou apagar o valor anterior.

Planejamos chamar este kernel em um espaço unidimensional de tarefas. Portanto, o identificador de thread que definimos no corpo do kernel nos indicará o deslocamento necessário nos buffers de dados.

Em seguida, preparamos variáveis locais nas quais armazenaremos os respectivos resultados da propagação para frente dos caminhos e valores nulos para os gradientes de erro.

   const float out1 = matrix_o1[i];
   const float out2 = matrix_o2[i];
   float grad1 = 0;
   float grad2 = 0;

Verificamos a validade dos valores da propagação para frente. E, na presença de valores numéricos válidos, calculamos o desvio, que depois é ajustado pela derivada da função de ativação. Os resultados são armazenados nas variáveis locais preparadas.

   if(!isnan(out1) && !isinf(out1) &&
      !isnan(out2) && !isinf(out2))
     {
      grad1 = Deactivation(out2 - out1, out1, activation);
      grad2 = Deactivation(out1 - out2, out2, activation);
     }

Agora podemos transferir os gradientes de erro para os respectivos buffers globais de dados. Dependendo da flag recebida, ou somamos os valores ao gradiente já acumulado, ou apagamos o valor anterior e gravamos o novo. Depois disso, finalizamos a execução do kernel.

   if(add > 0)
     {
      matrix_g1[i] += grad1;
      matrix_g2[i] += grad2;
     }
   else
     {
      matrix_g1[i] = grad1;
      matrix_g2[i] = grad2;
     }
  }

Vale dizer que esse é nosso único acréscimo ao programa OpenCL. O código completo pode ser consultado no anexo.

Em seguida, iniciaremos o trabalho no lado do programa principal, onde construiremos a arquitetura do framework proposto, o AMCT. Inicialmente, são necessárias duas magistrais: uma para átomos (barras) e outra para motivos (padrões). Os autores do método utilizam, em seu trabalho, um Transformer tradicional como magistral, com a adição de codificação estrutural de átomos e motivos. Eu, no entanto, proponho substituí-lo por um Transformer com codificação relativa (R-MAT), que analisamos em um dos artigos anteriores. Assim, poderíamos encerrar o assunto das magistrais. No entanto, para a magistral de padrões (motivos), precisamos primeiro extraí-los. Por isso, decidi colocá-la em um objeto separado.

2.1 Construção da magistral de padrões

Vamos construir o algoritmo da magistral de padrões na classe CNeuronMotifEncoder, cuja estrutura é apresentada abaixo.

class CNeuronMotifEncoder  :  public CNeuronRMAT
  {
public:
                     CNeuronMotifEncoder(void) {};
                    ~CNeuronMotifEncoder(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void) override   const   {  return defNeuronMotifEncoder; }
  };

Como se pode notar pela estrutura apresentada do novo objeto, usamos a classe CNeuronRMAT como classe pai. Nesta classe, está estruturado o funcionamento de um modelo linear, no qual as camadas neurais estão organizadas em um array dinâmico. Isso nos permite formar facilmente a arquitetura sequencial da nossa magistral de padrões no método Init. Além disso, toda a funcionalidade necessária será herdada da classe pai.

A estrutura dos parâmetros do método de inicialização foi completamente herdada do método correspondente da classe pai.

bool CNeuronMotifEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                               uint window, uint window_key, uint units_count, 
                               uint heads, uint layers, 
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(units_count < 3)
      return false;

No entanto, a extração de padrões impõe uma limitação no comprimento da sequência de dados brutos, o que verificamos imediatamente no corpo do método. Em seguida, preparamos um array dinâmico para registrar os ponteiros para as camadas neurais que vamos criar.

   cLayers.Clear();

Aqui é importante destacar que ainda não chamamos o método da classe pai. Isso significa que todos os objetos herdados ainda não foram inicializados. Por outro lado, nos parâmetros recebidos do programa externo, não há indicação explícita do tamanho do buffer de resultados que será necessário para executar o método da classe pai. E para evitar calcular o tamanho do buffer de resultados neste estágio, inicialmente vamos inicializar as camadas de criação das incorporações dos padrões. O tamanho de um padrão não foi especificado nos parâmetros do método, então vamos torná-lo dependente do tamanho da sequência. Para sequências com mais de 10 elementos, analisaremos padrões com três elementos. Caso contrário, com dois.

   int bars_to_paattern = (units_count > 10 ? 3 : 2);

As incorporações dos padrões serão geradas com a ajuda de uma camada convolucional, que será imediatamente inicializada. E o ponteiro para a camada neural criada será adicionado ao nosso array dinâmico.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   int idx = 0;
   int units = (int)units_count - bars_to_paattern + 1;
   if(!conv ||
      !conv.Init(0, idx, open_cl, bars_to_paattern * window, window, window, units, 1, optimization_type, batch)||
      !cLayers.Add(conv)
     )
      return false;
   conv.SetActivationFunction(SIGMOID);

Observe que estamos construindo incorporações de padrões sobrepostos com um passo de 1 barra. Nesse processo, o tamanho da incorporação de um único padrão é igual à janela de descrição de uma barra. Isso nos permitirá analisar com mais qualidade a sequência bruta em busca de padrões.

No entanto, vamos um pouco além e analisaremos padrões de tamanho ligeiramente maior, compostos por 5 ou 3 barras, dependendo do tamanho da sequência bruta. Nesse caso, concatenamos as incorporações dos padrões de dois níveis para fornecer mais informações sobre a estrutura dos dados brutos ao modelo. Para executar essa funcionalidade, utilizaremos a camada CNeuronMotifs, criada durante o desenvolvimento do framework Molformer. A vantagem dessa camada está na concatenação do tensor dos padrões extraídos com os dados brutos. Por esse mesmo motivo, não podíamos utilizá-la na primeira etapa de extração de padrões. Afinal, precisávamos separar os padrões da representação das barras, que são analisadas na magistral paralela.

   idx++;
   units = units - bars_to_paattern + 1;
   CNeuronMotifs *motifs = new CNeuronMotifs();
   if(!motifs ||
      !motifs.Init(0, idx, open_cl, window, bars_to_paattern, 1, units, optimization_type, batch) ||
      !cLayers.Add(motifs)
     )
      return false;
   motifs.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

As incorporações de padrões geradas são alimentadas na magistral R-MAT. Como você sabe, o tamanho do vetor de resultados da magistral Transformer é igual ao tensor dos dados brutos. Portanto, nesta etapa, podemos chamar o método de inicialização da camada neural base, especificando o tamanho do buffer de resultados com base na dimensão da última camada de extração de padrões.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, motifs.Neurons(), optimization_type, batch))
      return false;
   cLayers.SetOpenCL(OpenCL);

Em seguida, criamos um laço de inicialização das camadas internas do nosso decodificador. A cada iteração do laço, inicializamos sequencialmente uma camada de Self-Attention relativa (CNeuronRelativeSelfAttention) e um bloco convolucional com conexão residual (CResidualConv).

   CNeuronRelativeSelfAttention *attention = NULL;
   CResidualConv *ff = NULL;
   units = int(motifs.Neurons() / window);
   for(uint i = 0; i < layers; i++)
     {
      idx++;
      attention = new CNeuronRelativeSelfAttention();
      if(!attention ||
         !attention.Init(0, idx, OpenCL, window, window_key, units, heads, optimization, iBatch) ||
         !cLayers.Add(attention)
        )
        {
         delete attention;
         return false;
        }
      idx++;
      ff = new CResidualConv();
      if(!ff ||
         !ff.Init(0, idx, OpenCL, window, window, units, optimization, iBatch) ||
         !cLayers.Add(ff)
        )
        {
         delete ff;
         return false;
        }
     }

Exatamente esse mesmo laço foi criado no método de inicialização da classe pai. No entanto, neste caso, não pudemos utilizar o método da classe pai, pois ele teria excluído as camadas de extração de padrões criadas anteriormente.

Agora, resta apenas realizar a substituição dos ponteiros para os buffers de dados, a fim de evitar operações de cópia desnecessárias.

   if(!SetOutput(ff.getOutput()) ||
      !SetGradient(ff.getGradient()))
      return false;
//---
   return true;
  }

Antes de finalizar a execução do método, retornamos o resultado lógico da execução das operações para o programa chamador.

Como já foi dito anteriormente, as funcionalidades de propagação para frente e propagação reversa foram completamente herdadas da classe pai. Portanto, encerramos o trabalho com a classe da magistral de padrões CNeuronMotifEncoder.

2.2 Módulo de Cross-Attention relativo

Acima, utilizamos módulos de Self-Attention relativa para organizar as magistrais de barras e padrões. No entanto, no Decodificador do AMCT, é utilizado um módulo de atenção cruzada. Portanto, para criar uma arquitetura coesa e consistente do framework, precisamos construir um objeto Cross-Attention com codificação relativa. Não nos deteremos agora na descrição teórica dos métodos utilizados. Todos eles foram apresentados no artigo dedicado ao framework R-MAT. Cabe a nós apenas integrar uma segunda fonte de dados brutos, a partir da qual serão formadas as entidades Key e Value. Para executar essa tarefa, criaremos a classe CNeuronRelativeCrossAttention, na qual implementaremos o mecanismo de atenção cruzada com codificação relativa. Como é fácil imaginar, utilizaremos a classe correspondente Self-Attention como classe pai. A estrutura do novo objeto está apresentada abaixo.

class CNeuronRelativeCrossAttention   :  public CNeuronRelativeSelfAttention
  {
protected:
   uint                    iUnitsKV;
   //---
   CLayer                  cKVProjection;
   //---

   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput,
                                                                   CBufferFloat *SecondGradient, 
                                                   ENUM_ACTIVATION SecondActivation = None) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; }
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override;

public:
                     CNeuronRelativeCrossAttention(void) {};
                    ~CNeuronRelativeCrossAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads,
                          uint window_kv, uint units_kv,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronRelativeCrossAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Aqui vemos o já conhecido conjunto de métodos sobrescritos e declaramos um array dinâmico para registrar os ponteiros dos objetos adicionais. Além disso, adicionamos uma variável para registrar o tamanho da sequência da segunda fonte de dados brutos.

A inicialização de todos os objetos herdados e declarados, como sempre, é realizada no método Init.

bool CNeuronRelativeCrossAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                         uint window, uint window_key, uint units_count, 
                                         uint heads, uint window_kv, uint units_kv, 
                                         ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Nos parâmetros desse método, recebemos todas as constantes necessárias para interpretar de forma clara a arquitetura do objeto que está sendo criado. E, no corpo do método, chamamos diretamente o método homônimo da classe base das camadas neurais, no qual é feita a verificação de parte dos parâmetros recebidos e a inicialização das interfaces herdadas.

Optamos por não utilizar o método de inicialização da classe pai direta, já que o tamanho da maior parte dos objetos herdados dessa classe será diferente. E a necessidade de executar operações repetidas não só não reduzirá nosso trabalho, como também aumentará o tempo de execução do programa. Portanto, no corpo deste método, realizaremos adicionalmente a inicialização dos objetos declarados na classe pai.

Após a execução bem-sucedida do método da classe base, armazenamos as constantes de arquitetura do nosso objeto, recebidas do programa externo, em variáveis internas.

   iWindow = window;
   iWindowKey = window_key;
   iUnits = units_count;
   iUnitsKV = units_kv;
   iHeads = heads;

E, em seguida, de acordo com a arquitetura Transformer, inicializamos as camadas convolucionais de geração das entidades Query, Key e Value.

   int idx = 0;
   if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch))
      return false;
   idx++;
   if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch))
      return false;

Observe que para as camadas de formação das entidades Key e Value utilizamos o tamanho da sequência da segunda fonte de dados. Nesse caso, o tamanho do vetor de descrição de um elemento da sequência é tomado a partir da primeira fonte de dados. No entanto, o tamanho do vetor de descrição de um elemento da sequência na segunda fonte pode ser diferente. E, na prática, até agora não tratamos do alinhamento dos tamanhos das sequências brutas, apenas utilizamos janelas diferentes nas camadas de geração das entidades, alinhando apenas o tamanho das respectivas incorporações. Só que, no algoritmo de codificação relativa, é utilizada a distância entre objetos, que só pode ser determinada para objetos que estejam no mesmo subespaço. Portanto, para que a análise seja possível, precisamos de objetos com medidas comparáveis. E para não restringir a área de aplicação do módulo, utilizaremos o mecanismo de projeção treinável de dados. Voltaremos a esse ponto mais adiante, mas por ora, é importante destacar essa observação.

Assim como na implementação do algoritmo de Self-Attention relativa, usaremos como medida de distância entre objetos o produto de duas matrizes dos dados brutos. Mas, primeiro, será necessário transpor uma delas.

   idx++;
   if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch))
      return false;

Em seguida, criamos um objeto para armazenar os resultados da multiplicação matricial.

   idx++;
   if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnitsKV, optimization, iBatch))
      return false;

Depois, estruturamos o processo de geração dos tensores BK e BV. Vale lembrar que, para gerá-los, é utilizado um MLP com uma camada oculta. A camada oculta é compartilhada por todas as cabeças de atenção, enquanto a última camada gera tokens distintos para cada cabeça. Aqui, para cada entidade, criaremos duas camadas convolucionais sequenciais com tangente hiperbólica entre elas para introduzir não linearidade.

   idx++;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) ||
      !cBKey.Add(conv))
      return false;

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) ||
      !cBValue.Add(conv))
      return false;

E adicionamos mais dois MLP para a geração dos vetores de viés global de contexto e de posição. A primeira camada de cada um deles é estática e contém “1”, enquanto a segunda é treinável e gera o tensor necessário. Os ponteiros para os objetos criados são armazenados nos arrays cGlobalContentBias e cGlobalPositionalBias.

   idx++;
   CNeuronBaseOCL *neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;
   idx++;
   CBufferFloat *buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalContentBias.Add(neuron))
      return false;

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;
   idx++;
   buffer = neuron.getOutput();
   buffer.BufferInit(1, 1);
   if(!buffer.BufferWrite())
      return false;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cGlobalPositionalBias.Add(neuron))
      return false;

Com isso, finalizamos a preparação dos objetos de pré-processamento dos dados brutos do nosso módulo de atenção cruzada relativa. E passamos para os objetos de processamento dos resultados da atenção cruzada. Nesta etapa, inicialmente criamos um objeto para armazenar os resultados da atenção multi-cabeça e adicionamos seu ponteiro ao array cMHAttentionPooling.

   idx++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) ||
      !cMHAttentionPooling.Add(neuron)
     )
      return false;

Em seguida, adicionamos o objeto de pooling baseado em dependências. Ele realiza a transição dos resultados da atenção multi-cabeça para a soma ponderada desses resultados. Os coeficientes de influência são determinados individualmente para cada elemento da sequência com base na análise das dependências.

   CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling();
   if(!pooling ||
      !pooling.Init(0, idx, OpenCL, iWindowKey, iUnits, iHeads, optimization, iBatch) ||
      !cMHAttentionPooling.Add(pooling)
     )
      return false;

É importante observar que o tamanho do vetor de descrição de um elemento da sequência na saída da camada de pooling será igual à dimensão interna, que pode ser diferente do comprimento do vetor de descrição de um objeto na sequência bruta. Por isso, adicionamos mais um MLP para escalonar os resultados até o nível dos dados brutos. Nele, utilizamos duas camadas convolucionais com LReLU entre elas para criar a não linearidade.

//---
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(LReLU);
   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) ||
      !cScale.Add(conv)
     )
      return false;
   conv.SetActivationFunction(None);

Depois disso, realizamos a substituição do ponteiro para o buffer de gradientes de erro nas interfaces de troca de dados com outras camadas neurais do nosso modelo.

//---
   if(!SetGradient(conv.getGradient(), true))
      return false;

Agora voltamos à questão das diferenças de dimensionalidade entre as fontes de dados brutos. No nosso módulo de atenção cruzada, a primeira fonte de dados é usada para gerar a entidade Query e serve como base para a formação da magistral. Ela também é usada como conexão residual. Portanto, sua dimensionalidade permanece inalterada. Consequentemente, para alinhar as dimensionalidades das duas fontes de dados brutos, faremos a projeção dos valores da segunda fonte. Para organizar essa projeção treinável de dados, criaremos duas camadas neurais sequenciais, cujos ponteiros serão adicionados ao array cKVProjection. A primeira camada será totalmente conectada. Ela será responsável por armazenar os dados brutos da segunda fonte.

   cKVProjection.Clear();
   cKVProjection.SetOpenCL(OpenCL);
   idx++;
   neuron = new CNeuronBaseOCL;
   if(!neuron ||
      !neuron.Init(0, idx, OpenCL, window_kv * iUnitsKV, optimization, iBatch) ||
      !cKVProjection.Add(neuron)
     )
      return false;

A segunda camada, convolucional, realizará a projeção dos dados para o subespaço necessário.

   idx++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, window_kv, window_kv, iWindow, iUnitsKV, 1, optimization, iBatch) ||
      !cKVProjection.Add(conv)
     )
      return false;

Agora, após a inicialização de todos os objetos necessários para a execução da funcionalidade proposta, retornamos o resultado lógico da execução das operações ao programa chamador e encerramos a execução do método.

//---
   SetOpenCL(OpenCL);
//---
   return true;
  }

Após finalizar a inicialização da nova instância do objeto, passamos à construção dos algoritmos de propagação para frente, que implementaremos no método feedForward. Aqui é importante observar que o algoritmo requer 2 fontes de dados brutos. Por isso, o método herdado da classe pai, que trabalha com apenas um objeto de dados brutos, será sobrescrito com um resultado constante false, sinalizando uma chamada incorreta de método. O algoritmo correto será implementado no método com dois objetos de dados brutos.

bool CNeuronRelativeCrossAttention::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput)
  {
   CNeuronBaseOCL *neuron = cKVProjection[0];
   if(!neuron || !SecondInput)
      return false;
   if(neuron.getOutput() != SecondInput)
      if(!neuron.SetOutput(SecondInput, true))
         return false;

No corpo do método, verificamos a validade do ponteiro para o objeto da segunda fonte de dados brutos. E, se necessário, passamos esse ponteiro para a primeira camada do modelo de projeção de dados, cujos ponteiros estão armazenados no array cKVProjection. Em seguida, definimos um laço para percorrer sequencialmente todas as camadas do modelo de projeção de dados. No corpo do laço, chamamos os métodos de propagação para frente de cada camada, usando como dados de entrada os resultados da camada neural anterior.

   for(int i = 1; i < cKVProjection.Total(); i++)
     {
      neuron = cKVProjection[i];
      if(!neuron ||
         !neuron.FeedForward(cKVProjection[i - 1])
        )
         return false;
     }

Após a projeção bem-sucedida dos dados brutos da segunda fonte, passamos à geração das entidades Query, Key e Value. A Query é gerada a partir dos dados brutos da primeira fonte. E, para Key e Value, utilizamos os resultados da projeção realizada anteriormente dos dados da segunda fonte.

   if(!cQuery.FeedForward(NeuronOCL) ||
      !cKey.FeedForward(neuron) ||
      !cValue.FeedForward(neuron)
     )
      return false;

Em seguida, precisamos calcular os coeficientes de distância entre os objetos. Para isso, primeiro transpomos os dados da primeira fonte. E então multiplicamos os resultados da projeção dos dados brutos da segunda fonte pelos dados transpostos da primeira.

   if(!cTranspose.FeedForward(NeuronOCL) ||
      !MatMul(neuron.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnitsKV, iWindow, iUnits, 1)
     )
      return false;

Com base nos coeficientes estruturais de dados obtidos, formamos os tensores de viés BK e BV. Primeiro, passamos as informações sobre a estrutura dos dados para os métodos de propagação para frente das primeiras camadas dos respectivos modelos.

   if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) ||
      !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject())
     )
      return false;

Depois, criamos laços para percorrer as camadas dos modelos indicados, chamando sequencialmente os métodos de propagação para frente das camadas neurais internas.

   for(int i = 1; i < cBKey.Total(); i++)
      if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1]))
         return false;

   for(int i = 1; i < cBValue.Total(); i++)
      if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1]))
         return false;

Na sequência, geramos as entidades de viés global. Aqui, estruturamos laços análogos aos anteriores.

   for(int i = 1; i < cGlobalContentBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1]))
         return false;
   for(int i = 1; i < cGlobalPositionalBias.Total(); i++)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1]))
         return false;

Com isso, finalizamos as operações de pré-processamento dos dados brutos e passamos os resultados obtidos para o módulo de atenção.

   if(!AttentionOut())
      return false;

Os resultados da atenção cruzada multi-cabeça são processados pelo modelo de pooling.

   for(int i = 1; i < cMHAttentionPooling.Total(); i++)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1]))
         return false;

E escalonados até o tamanho do tensor da primeira fonte de dados brutos. Essa funcionalidade é executada pelo modelo interno de escalonamento.

   if(!((CNeuronBaseOCL*)cScale[0]).FeedForward(cMHAttentionPooling[cMHAttentionPooling.Total() - 1]))
      return false;
   for(int i = 1; i < cScale.Total(); i++)
      if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1]))
         return false;

Agora só resta adicionar as conexões residuais. Os resultados da operação são gravados no buffer da interface de troca de dados com a próxima camada neural do modelo.

   if(!SumAndNormilize(NeuronOCL.getOutput(), ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(),
                                                                      Output, iWindow, true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

Antes de finalizar a execução do método, retornamos ao programa chamador o resultado lógico da execução das operações.

Após construirmos o método de propagação para frente, passamos à implementação dos algoritmos de propagação reversa. Como você sabe, as operações de propagação reversa são divididas em 2 etapas. A distribuição dos gradientes de erro para todos os participantes do processo, conforme sua influência no resultado final, é realizada no método calcInputGradients. E a otimização dos parâmetros do modelo no sentido de reduzir o erro do modelo é feita no método updateInputWeights. O algoritmo deste último não tem nada de especial. Nele, apenas ocorre a chamada sequencial dos métodos de mesmo nome dos objetos internos que contêm parâmetros treináveis. Já o algoritmo do primeiro, propomos analisar com mais atenção.

Nos parâmetros do método de distribuição de gradientes de erro calcInputGradients, recebemos ponteiros para 2 objetos de dados brutos com buffers para o registro dos respectivos gradientes de erro.

bool CNeuronRelativeCrossAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, 
                                                       CBufferFloat *SecondInput, 
                                                       CBufferFloat *SecondGradient, 
                                                       ENUM_ACTIVATION SecondActivation = -1)
  {
   if(!NeuronOCL || !SecondGradient)
      return false;

No corpo do método, verificamos a validade dos ponteiros recebidos. Caso contrário, todas as operações subsequentes perdem o sentido.

Aqui é importante lembrar que, durante as operações de propagação para frente, armazenamos o ponteiro para o buffer da segunda fonte de dados brutos na camada interna. Realizamos operações análogas para o respectivo buffer de gradientes de erro e, em seguida, sincronizamos as funções de ativação.

   CNeuronBaseOCL *neuron = cKVProjection[0];
   if(!neuron)
      return false;
   if(neuron.getGradient() != SecondGradient)
      if(!neuron.SetGradient(SecondGradient))
         return false;
   if(neuron.Activation() != SecondActivation)
      neuron.SetActivationFunction(SecondActivation);

Com isso, concluímos o trabalho preparatório e passamos à distribuição propriamente dita do gradiente de erro para todos os participantes do processo, de acordo com sua influência no resultado final.

Lembro que, durante a inicialização do nosso objeto, substituímos o ponteiro para o buffer de gradientes de erro. Por isso, o trabalho de distribuição dos gradientes de erro começa diretamente com os objetos internos. E aqui vale lembrar que os autores do método AMCT propuseram o aprendizado contrastivo para os motivos. Seguindo essa lógica, adicionaremos o erro de diversificação sobre os resultados do nosso bloco de atenção cruzada.

   if(!DiversityLoss(AsObject(), iUnits, iWindow, true))
      return false;

É importante entender que, ao adicionar o erro de diversificação aos resultados do bloco de atenção cruzada, buscamos maximizar a dispersão, no subespaço, justamente dos resultados que serão repassados às camadas neurais seguintes do modelo. Ao mesmo tempo, ao distribuir o gradiente de erro para baixo pelos objetos do modelo, indiretamente estamos também separando os objetos dos dados brutos analisados, que chegam ao nosso bloco a partir das duas fontes.

Em seguida, aplicamos o gradiente de erro geral ao modelo interno de escalonamento de resultados.

   for(int i = cScale.Total() - 2; i >= 0; i--)
      if(!((CNeuronBaseOCL*)cScale[i]).calcHiddenGradients(cScale[i + 1]))
         return false;
   if(!((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).calcHiddenGradients(cScale[0]))
      return false;

Depois, o distribuímos pelas cabeças de atenção com os meios do modelo de pooling.

   for(int i = cMHAttentionPooling.Total() - 2; i > 0; i--)
      if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).calcHiddenGradients(cMHAttentionPooling[i + 1]))
         return false;

E no método AttentionGradient conduzimos o gradiente de erro até as entidades Query, Key, Value e os tensores de viés, de acordo com sua contribuição para o resultado final.

   if(!AttentionGradient())
      return false;

Na sequência, distribuímos o gradiente de erro pelas modelos internas dos vieses globais treináveis, percorrendo suas camadas neurais em ordem reversa.

   for(int i = cGlobalContentBias.Total() - 2; i > 0; i--)
      if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).calcHiddenGradients(cGlobalContentBias[i + 1]))
         return false;
   for(int i = cGlobalPositionalBias.Total() - 2; i > 0; i--)
      if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).calcHiddenGradients(cGlobalPositionalBias[i + 1]))
         return false;

Da mesma forma, conduzimos o gradiente de erro pelas modelos de geração das entidades de viés com base na estrutura dos objetos BK e BV.

   for(int i = cBKey.Total() - 2; i >= 0; i--)
      if(!((CNeuronBaseOCL*)cBKey[i]).calcHiddenGradients(cBKey[i + 1]))
         return false;
   for(int i = cBValue.Total() - 2; i >= 0; i--)
      if(!((CNeuronBaseOCL*)cBValue[i]).calcHiddenGradients(cBValue[i + 1]))
         return false;

E em seguida até a matriz de estrutura de dados cDistance. Mas aqui existe um detalhe. A matriz de estrutura foi usada para gerar ambas as entidades, então o gradiente de erro precisa ser coletado a partir de dois fluxos de informação. Por isso, primeiro obtemos o gradiente de erro de BK.

   if(!cDistance.calcHiddenGradients(cBKey[0]))
      return false;

Depois, substituímos o ponteiro para o buffer de gradientes de erro desse objeto e obtemos o gradiente de BV. Em seguida, somamos os gradientes de erro das duas modelos e restauramos os ponteiros para os buffers de dados ao estado original.

   CBufferFloat *temp = cDistance.getGradient();
   if(!cDistance.SetGradient(GetPointer(cTemp), false) ||
      !cDistance.calcHiddenGradients(cBValue[0]) ||
      !SumAndNormilize(temp, GetPointer(cTemp), temp, iUnits, false, 0, 0, 0, 1) ||
      !cDistance.SetGradient(temp, false)
     )
      return false;

O gradiente de erro coletado na matriz de estrutura é distribuído entre os objetos dos dados brutos. Só que, nesse caso, a distribuição não é direta, e sim feita por meio da camada de transposição da primeira fonte de dados brutos e do modelo de projeção da segunda fonte.

   neuron = cKVProjection[cKVProjection.Total() - 1];
   if(!neuron ||
      !MatMulGrad(neuron.getOutput(), neuron.getGradient(),
                  cTranspose.getOutput(), cTranspose.getGradient(),
                  temp, iUnitsKV, iWindow, iUnits, 1)
     )
      return false;

Da camada de transposição, transmitimos o gradiente de erro até o nível da primeira fonte de dados brutos. E imediatamente somamos os valores obtidos com o gradiente de erro proveniente do fluxo das conexões residuais. O resultado da operação será registrado no buffer de gradientes da camada de transposição de dados. Ele se ajusta perfeitamente em tamanho, e os valores anteriormente gravados nele podem ser descartados sem problemas.

   if(!NeuronOCL.calcHiddenGradients(cTranspose.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), Gradient, cTranspose.getGradient(), iWindow, false, 0, 0, 0, 1))
      return false;

Em seguida, calculamos o gradiente de erro no nível da primeira fonte de dados brutos, derivado da entidade Query, e o adicionamos aos dados já acumulados. Só que, desta vez, os resultados da soma serão armazenados no buffer de gradientes de erro dos dados brutos.

   if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) ||
      !SumAndNormilize(NeuronOCL.getGradient(), cTranspose.getGradient(), NeuronOCL.getGradient(), 
                                                                       iWindow, false, 0, 0, 0, 1) ||
      !DiversityLoss(NeuronOCL, iUnits, iWindow, true)
     )
      return false;

E a esses resultados, adicionamos também o erro de diversificação.

Com isso, finalizamos a distribuição do gradiente de erro até a primeira fonte de dados brutos e passamos a trabalhar com o segundo fluxo de informações.

Lembro que, anteriormente, já armazenamos no buffer da última camada do modelo interno de projeção da segunda fonte de dados brutos o gradiente de erro proveniente da matriz de estrutura. Agora, precisamos adicionar a ele o gradiente de erro das entidades Key e Value. Para isso, primeiro substituímos o buffer de gradientes de erro no objeto receptor da informação. Em seguida, chamamos sequencialmente o método de distribuição dos gradientes de erro das entidades correspondentes, adicionando os resultados das operações aos valores previamente acumulados.

   temp = neuron.getGradient();
   if(!neuron.SetGradient(GetPointer(cTemp), false) ||
      !neuron.calcHiddenGradients(cKey.AsObject()) ||
      !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) ||
      !neuron.calcHiddenGradients(cValue.AsObject()) ||
      !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) ||
      !neuron.SetGradient(temp, false)
     )
      return false;

Agora, basta realizarmos a retropropagação pelos layers do modelo de projeção, transmitindo os gradientes de erro camada por camada.

   for(int i = cKVProjection.Total() - 2; i >= 0; i--)
     {
      neuron = cKVProjection[i];
      if(!neuron ||
         !neuron.calcHiddenGradients(cKVProjection[i + 1]))
         return false;
     }
//---
   return true;
  }

Vale destacar que, graças à substituição do ponteiro para o buffer de gradientes de erro na primeira camada do modelo pelo objeto recebido do programa externo nos parâmetros do método, eliminamos a necessidade de copiar dados. Assim, ao transferir os gradientes de erro para o nível da primeira camada do modelo, eles são automaticamente registrados no buffer de dados fornecido pela aplicação externa.

Resta apenas retornar o resultado lógico da execução das operações ao programa chamador e finalizar a execução do método.

Com isso, concluímos a análise dos métodos do objeto de atenção cruzada relativa CNeuronRelativeCrossAttention. E o código completo desta classe e de todos os seus métodos está disponível no anexo.

Infelizmente, chegamos ao limite de extensão deste artigo sem concluir nosso trabalho. Portanto, faremos uma breve pausa e continuaremos na próxima parte.

Conclusão

Neste artigo, conhecemos o framework Atom-Motif Contrastive Transformer (AMCT), baseado nos conceitos de elementos atômicos (velas) e motivos (padrões). A ideia central do método está no uso do aprendizado contrastivo do modelo com o objetivo de distinguir padrões informativos dos não informativos em diferentes níveis: desde elementos básicos até estruturas complexas. Isso permite ao modelo não apenas considerar características locais dos movimentos de mercado, mas também captar padrões importantes que podem fornecer informações adicionais para previsões mais precisas do comportamento futuro do mercado. A arquitetura Transformer, sendo a base do método, capta com eficiência dependências de longo prazo e interações complexas entre velas e padrões.

Na parte prática, iniciamos a implementação das abordagens propostas usando recursos do MQL5. No entanto, o volume de trabalho excedeu os limites de um único artigo. Mas continuaremos o trabalho iniciado na próxima publicação. Nela, avaliaremos os resultados práticos que o framework proposto permite alcançar sobre dados históricos reais.

Referências

• Atom-Motif Contrastive Transformer for Molecular Property Prediction
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com código para programa OpenCL