Redes neuronales en el trading: Transformador contrastivo de patrones
Introducción
Al analizar situaciones de mercado usando el aprendizaje automático, a menudo nos centramos en velas individuales y sus características, pasando por alto los patrones de velas, que con frecuencia pueden proporcionar información más significativa. Los patrones son estructuras de velas estables que se producen en condiciones de mercado similares y pueden contener regularidades críticas.
Anteriormente, nos hemos familiarizado con el marco Molformer, tomado del campo de la predicción de propiedades moleculares. Los autores de Molformer combinan la representación de átomos y motivos en una única secuencia para proporcionar al modelo información sobre la estructura de los datos analizados. Al mismo tiempo, esto plantea el difícil problema de separar las dependencias entre nodos de distintos tipos. Sin embargo, existen métodos alternativos exentos de este problema.
Por ejemplo, el marco Atom-Motif Contrastive Transformer (AMCT), presentado en al artículo "Atom-Motif Contrastive Transformer for Molecular Property Prediction". Para combinar los dos niveles de interacción y mejorar la capacidad de representación molecular, los autores del AMCT proponen construir un aprendizaje átomo-motivo contrastado. Como las representaciones de los átomos y los motivos de una molécula son en realidad dos representaciones diferentes de la misma instancia, estas se alinean de forma natural durante el proceso de aprendizaje. De este modo, pueden ofrecer de forma cooperativa señales de autocontrol y aumentar así la fiabilidad de la representación molecular aprendida.
Hemos comprobado que motivos idénticos en moléculas diferentes suelen tener propiedades químicas similares. Esto significa que motivos idénticos deben tener representaciones coherentes en todas las moléculas. Por consiguiente, el uso de la pérdida de contraste maximizará la coincidencia de motivos idénticos en moléculas diferentes y provocará una representación distinguible de los motivos.
Además, para identificar claramente los motivos que son cruciales para determinar las propiedades de cada molécula, los autores del método diseñan adicionalmente un mecanismo de atención que considera las propiedades mediante un módulo de atención cruzada. En particular, el módulo de atención cruzada identifica las dependencias entre las incorporaciones de propiedades moleculares y las representaciones de motivos. Como resultado, pueden identificarse motivos clave basados en pesos de atención cruzada.
1. Algoritmo AMCT
Las descripciones moleculares suministradas a la entrada del modelo se dividen primero en un conjunto de átomos y se segmentan en un conjunto de motivos. Las secuencias resultantes se introducen en capas paralelas de codificación de átomos y motivos que generan las incorporaciones correspondientes. Para obtener las representaciones moleculares a nivel de átomos y motivos, se usan dos codificadores independientes, mientras que el Decodificador y la capa completamente conectada se utilizan para obtener los resultados predichos. El error de alineación átomo-motivo, los errores de contraste a nivel de motivo y los errores de predicción de propiedades se usan durante el entrenamiento del modelo.
En el proceso de codificación de átomos, primero obtenemos sus incorporaciones. Y luego utilizamos el Codificador de átomos para extraer las interdependencias entre los átomos individuales de la molécula. Su resultado constituirá una representación molecular a nivel atómico.
Los autores del AMCT utilizan el grado de centralidad para codificar la información estructural entre átomos, es decir, las relaciones de enlace de los átomos de una molécula. Como el grado de centralidad se aplica a cada átomo, simplemente lo añadiremos a la incorporación del átomo.
Las interdependencias entre átomos captan con éxito los detalles de bajo nivel, pero ignoran la información estructural de alto nivel entre los distintos átomos, por lo que en algunos casos resultarán insuficientes para predecir las propiedades moleculares. Para abordar este problema, los autores del marco AMCT introducen una línea troncal paralela para representar moléculas a nivel de motivo. En el proceso de codificación de motivos, primero los extraeremos del conjunto de datos original y luego generaremos incorporaciones. A continuación, se usará el codificador de motivos para extraer las interdependencias entre estos.
Para codificar la información estructural entre motivos, los autores del marco AMCT utilizan la centralidad de grado, que se añade a las incorporaciones correspondientes.
Para investigar la nueva información adicional que aportan los motivos, se analizarán las relaciones de similitud entre las representaciones moleculares a nivel atómico y de motivo. Como las representaciones de átomos y motivos de una misma molécula son en realidad dos representaciones diferentes de lo mismo, se alinearán de forma natural para generar señales de autocontrol durante el entrenamiento del modelo. Para comparar las dos representaciones, los autores del método utilizan la divergencia Kullback-Leibler.
Dado que el error de alineación de átomos y motivos se produce dentro de una molécula y está limitado por la consistencia entre los átomos y los motivos de la misma molécula, los autores del ACTM intentan efectuar un contraste intermolecular e investigar la consistencia entre distintas moléculas. Dado que motivos idénticos en moléculas diferentes muestran propiedades químicas similares, se espera que tengan representaciones similares para todas las moléculas. Para lograr este objetivo, se propone un error de contraste de motivos que maximiza la coherencia de la representación de motivos idénticos en moléculas diferentes. De este modo, se rechazan las representaciones de motivos pertenecientes a clases diferentes.
Un buen proceso de descodificación también será importante para obtener una representación fiable. El AMCT ofrece descodificación basada en propiedades. En concreto, primero obtendremos incorporaciones de propiedades y luego utilizaremos un descodificador para extraer las representaciones moleculares clave para propiedades individuales. Los resultados proyectados se obtendrán tras una proyección lineal.
El descodificador está diseñado para extraer representaciones moleculares que tengan en cuentan las propiedades. Para identificar los motivos cruciales que determinan las propiedades de cada molécula, los autores del AMCT construyen un mecanismo de atención consciente de las propiedades. Aquí se usará un módulo de atención cruzada que utiliza incorporaciones de propiedades como Query y representaciones de motivos como Key-Value. Se cree que un motivo con un mayor peso de atención cruzada tendrá una mayor contribución a la propiedad molecular.
A continuación le mostramos la visualización del autor del marco Atom-Motif Contrastive Transformer.

2. Implementación con MQL5
Tras considerar los aspectos teóricos del marco Atom-Motif Contrastive Transformer, vamos a pasar a la parte práctica de nuestro artículo, donde presentaremos nuestra propia visión de los enfoques propuestos usando MQL5.
El marco de la AMCT es una estructura bastante compleja y exhaustiva. Pero si se fija bien en los bloques utilizados, notará que la mayoría de ellos ya están implementados en nuestra biblioteca de una forma u otra. Sin embargo, nos queda mucho por hacer. Por ejemplo, la comparación de representaciones a nivel de átomos y motivos. Espero que no tenga ninguna duda de que, además de encontrar simplemente la divergencia, también tendremos que distribuir el gradiente de error en ambas líneas troncales para minimizar la divergencia. Y existen varias opciones para abordar esta cuestión.
Obviamente, podemos copiar los resultados de una línea troncal en el búfer de gradiente de la otra, y entonces encontrar el gradiente de error usando el método básico de la capa neuronal calcOutputGradients que usamos para encontrar el error del rendimiento del modelo. Las ventajas de este planteamiento son, entre otras, su sencillez de aplicación, ya que se utilizan herramientas existentes. No obstante, se trata de un método bastante costoso. Para entrenar el modelo, deberemos copiar dos búferes de datos (los resultados de las dos líneas troncales) y calcular los gradientes de cada representación secuencialmente.
Así que hemos decidido crear un pequeño kernel en el lado del programa OpenCL que nos permitirá determinar el gradiente de error para ambas líneas troncales a la vez y sin un copiado excesivo de datos.
__kernel void CalcAlignmentGradient(__global const float *matrix_o1, __global const float *matrix_o2, __global float *matrix_g1, __global float *matrix_g2, const int activation, const int add) { int i = get_global_id(0);
En los parámetros del kernel, obtendremos los punteros a 4 búferes de datos. De ellos, 2 búferes contendrán los resultados de las líneas troncales de átomos y motivos, en nuestro caso velas y patrones. Y 2 búferes se usarán para registrar los gradientes de error correspondientes. Además, en los parámetros del kernel, obtendremos el puntero a la función de activación que se ha utilizado para ambas líneas troncales.
Nótese que aquí restringimos explícitamente la posibilidad de utilizar una función de activación diferente para las líneas troncales. La cuestión es que, para comparar correctamente los resultados de las dos, deberán estar en el mismo subespacio. Y será precisamente la función de activación la que determine el área de resultados de la capa. Por consiguiente, resulta lógico usar una función de activación en la salida de ambas líneas troncales.
Aquí también añadiremos una bandera para indicar si el gradiente de error debe añadirse a los datos acumulados previamente o si debe eliminarse el valor anterior.
Planeamos llamar este kernel en un espacio de tareas unidimensional. Por ello, el ID de flujo que definamos en el cuerpo del kernel nos indicará el desplazamiento necesario en los búferes de datos.
A continuación, prepararemos las variables locales en las que almacenaremos los resultados correspondientes de la pasada directa de la línea troncal y los valores cero para los gradientes de error.
const float out1 = matrix_o1[i]; const float out2 = matrix_o2[i]; float grad1 = 0; float grad2 = 0;
Luego comprobaremos la validez de los valores de la pasada directa. Y dados los valores numéricos correctos, calcularemos la desviación, que luego corregimos por la derivada de la función de activación. Los resultados se guardarán en las variables locales preparadas.
if(!isnan(out1) && !isinf(out1) &&
!isnan(out2) && !isinf(out2))
{
grad1 = Deactivation(out2 - out1, out1, activation);
grad2 = Deactivation(out1 - out2, out2, activation);
}
Ahora podremos transferir los gradientes de error a los búferes de datos globales correspondientes. Dependiendo de la bandera resultante, añadiremos valores al gradiente acumulado previamente o eliminaremos el valor anterior y escribiremos uno nuevo. Después de lo cual finalizaremos el trabajo del kernel.
if(add > 0) { matrix_g1[i] += grad1; matrix_g2[i] += grad2; } else { matrix_g1[i] = grad1; matrix_g2[i] = grad2; } }
Debemos decir que será nuestra única incorporación al programa OpenCL. Podrá ver su código completo en el archivo adjunto.
A continuación, comenzaremos a trabajar en la parte del programa principal, donde tendremos que construir la arquitectura del marco AMCT propuesto. En primer lugar necesitaremos 2 líneas troncales: átomos (barras) y motivos (patrones). En su artículo, los autores del método utilizan el Transformer vainilla como línea troncal, añadiendo la codificación estructural de átomos y motivos. Yo, en cambio, le sugiero sustituirlo por el Transformer con codificación relativa (R-MAT) del que ya hablamos en un artículo anterior. Y aquí se acabaría el tema de las líneas troncales. Solo necesitaremos preseleccionarlos para la línea troncal de los patrones (motivos). Por consiguiente, hemos decidido poner la línea troncal del patrón en un objeto aparte.
2.1 Construcción de una línea troncal de patrones
Construiremos el algoritmo de la línea troncal del patrón en la clase CNeuronMotifEncoder, cuya estructura se muestra a continuación.
class CNeuronMotifEncoder : public CNeuronRMAT { public: CNeuronMotifEncoder(void) {}; ~CNeuronMotifEncoder(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) override; //--- virtual int Type(void) override const { return defNeuronMotifEncoder; } };
Como podemos ver en la estructura presentada del nuevo objeto, utilizaremos CNeuronRMAT como clase padre. Esta clase organizará el funcionamiento de un modelo lineal cuyas capas neuronales estarán empaquetadas en un array dinámico, lo cual nos permitirá simplemente generar una arquitectura consistente para nuestra línea troncal de patrones en el método Init, mientras que toda la funcionalidad necesaria será heredada de la clase padre.
La estructura de parámetros del método de inicialización se ha heredado completamente del método análogo de la clase padre.
bool CNeuronMotifEncoder::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(units_count < 3) return false;
Sin embargo, la extracción de patrones introducirá una restricción en la longitud de la secuencia de datos de origen que comprobaremos inmediatamente en el cuerpo del método. Después prepararemos un array dinámico para registrar los punteros a las capas neuronales que estamos creando.
cLayers.Clear();
Aquí vale la pena señalar que aún no hemos llamado al método de la clase padre, y esto significa que todos los objetos heredados aún no se han inicializado. Por otro lado, no existe ninguna indicación explícita en los parámetros recibidos del programa externo sobre el tamaño del búfer de resultados que necesitamos para ejecutar el método de la clase padre. Y para no realizar cálculos del tamaño de búfer de resultados en esta etapa, primero inicializaremos las capas de creación de incorporación de patrones. No hemos indicado el tamaño de un patrón en los parámetros del método, por lo que lo haremos depender del tamaño de la secuencia. Para secuencias de más de 10 elementos, analizaremos patrones de tres elementos. Si no, de dos.
int bars_to_paattern = (units_count > 10 ? 3 : 2);
Generaremos incorporaciones de patrones usando una capa de convolución que inicializaremos inmediatamente. Y añadiremos a nuestro array dinámico el puntero a la capa neuronal creada.
CNeuronConvOCL *conv = new CNeuronConvOCL(); int idx = 0; int units = (int)units_count - bars_to_paattern + 1; if(!conv || !conv.Init(0, idx, open_cl, bars_to_paattern * window, window, window, units, 1, optimization_type, batch)|| !cLayers.Add(conv) ) return false; conv.SetActivationFunction(SIGMOID);
Obsérvese que construiremos las incorporaciones de los patrones superpuestos en incrementos de 1 barra. En este caso, el tamaño de la incorporación de un patrón será igual a la ventana de descripción de una barra. Esto nos permitirá analizar mejor la secuencia original en busca de patrones.
Sin embargo, iremos un poco más lejos y analizaremos patrones de un tamaño ligeramente mayor, compuestos por 5 o 3 barras, dependiendo del tamaño de la secuencia original. En este caso, además, concatenaremos las incorporaciones de patrones de los dos niveles para proporcionar al modelo más información sobre la estructura de los datos de origen. Para realizar esta funcionalidad, utilizaremos la capa CNeuronMotifs creada como parte de nuestro artículo en el marco Molformer. Esta capa tiene la ventaja de concatenar el tensor de patrones extraídos con los datos de origen. Por la misma razón, no hemos podido utilizarla en el primer paso de la extracción de patrones. Al fin y al cabo, necesitamos separar los patrones de la representación de las barras analizadas en la línea troncal paralela.
idx++; units = units - bars_to_paattern + 1; CNeuronMotifs *motifs = new CNeuronMotifs(); if(!motifs || !motifs.Init(0, idx, open_cl, window, bars_to_paattern, 1, units, optimization_type, batch) || !cLayers.Add(motifs) ) return false; motifs.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
Los patrones generados se introducirán en la línea troncal de R-MAT. Como ya sabe, el tamaño del vector de resultados de la línea troncal del Transformer es igual al tensor de los datos de origen. Por consiguiente, en esta etapa, podemos llamar al método para inicializar la capa neuronal básica especificando el tamaño del búfer de resultados según el tamaño de la última capa de extracción de patrones.
if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, motifs.Neurons(), optimization_type, batch)) return false; cLayers.SetOpenCL(OpenCL);
Y luego crearemos un ciclo de inicialización de las capas internas de nuestro decodificador. En cada iteración del ciclo, inicializaremos secuencialmente una capa de Self-Attention relativa (CNeuronRelativeSelfAttention) y un bloque convolucional con enlace residual (CResidualConv).
CNeuronRelativeSelfAttention *attention = NULL; CResidualConv *ff = NULL; units = int(motifs.Neurons() / window); for(uint i = 0; i < layers; i++) { idx++; attention = new CNeuronRelativeSelfAttention(); if(!attention || !attention.Init(0, idx, OpenCL, window, window_key, units, heads, optimization, iBatch) || !cLayers.Add(attention) ) { delete attention; return false; } idx++; ff = new CResidualConv(); if(!ff || !ff.Init(0, idx, OpenCL, window, window, units, optimization, iBatch) || !cLayers.Add(ff) ) { delete ff; return false; } }
Crearemos exactamente el mismo ciclo en el método de inicialización de la clase padre. Sin embargo, en este caso, no podríamos usar el método especificado de la clase padre porque borraría las capas de extracción de patrones creadas anteriormente.
Y ahora solo tenemos que intercambiar los punteros a los búferes de datos para eliminar las operaciones de copiado innecesarias.
if(!SetOutput(ff.getOutput()) || !SetGradient(ff.getGradient())) return false; //--- return true; }
Y antes de que el método finalice, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.
Como ya hemos mencionado anteriormente, hemos heredado completamente la funcionalidad de pasada directa e inversa de la clase padre. Por consiguiente, finalizaremos con la clase de línea troncal de patrones CNeuronMotifEncoder.
2.2 Módulo de Cross-Attention relativa
Más arriba, hemos utilizado los módulos de Self-Attention relativa para organizar las líneas troncales de las barras y los patrones. Sin embargo, el Decodificador con AMCT utiliza un módulo de atención cruzada. Por consiguiente, para crear una arquitectura de marco coherente y consistente, tendremos que construir un objeto Cross-Attention con codificación relativa. No nos detendremos ahora en la descripción teórica de los enfoques usados. Todos ellos se presentaron en el artículo dedicado al marco R-MAT. Solo tendremos que integrar una segunda fuente de datos de entrada en la solución previamente implementada, a partir de la cual se generarán las entidades Key y Value. Para llevar a cabo esta tarea, crearemos una clase CNeuronRelativeCrossAttention en la que implementaremos un mecanismo de atención cruzada con codificación relativa. Como podrá adivinar, utilizaremos la clase Self-Attention correspondiente como clase padre. Más abajo resumimos la estructura del nuevo objeto.
class CNeuronRelativeCrossAttention : public CNeuronRelativeSelfAttention { protected: uint iUnitsKV; //--- CLayer cKVProjection; //--- //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = None) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override { return false; } virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) override; public: CNeuronRelativeCrossAttention(void) {}; ~CNeuronRelativeCrossAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_kv, uint units_kv, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronRelativeCrossAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Aquí vemos el conjunto habitual de métodos redefinidos y declararemos un array dinámico para registrar los punteros de objetos adicionales. Además, añadiremos una variable para registrar el tamaño de la secuencia en la segunda fuente de datos de origen.
La inicialización de todos los objetos heredados y declarados se realizará, como siempre, en el método Init.
bool CNeuronRelativeCrossAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint units_count, uint heads, uint window_kv, uint units_kv, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch)) return false;
En los parámetros de este método obtendremos todas las constantes necesarias que nos permiten interpretar inequívocamente la arquitectura del objeto que se está creando. Y en el cuerpo del método llamaremos inmediatamente al método homónimo de la clase básica de capas neuronales, en el que se comprobará una parte de los parámetros recibidos y se inicializarán las interfaces heredadas.
Intencionadamente no utilizaremos el método de inicialización de la clase padre directa, ya que el tamaño de la mayoría de los objetos heredados de ella será diferente. Y la necesidad de realizar operaciones repetidas no solo no reducirá nuestro trabajo, sino que aumentará el tiempo de ejecución del programa. Por consiguiente, en el cuerpo de este método inicializaremos adicionalmente los objetos declarados en la clase padre.
Una vez ejecutado con éxito el método de la clase básica, guardaremos en variables internas las constantes de la arquitectura de nuestro objeto obtenidas del programa externo.
iWindow = window; iWindowKey = window_key; iUnits = units_count; iUnitsKV = units_kv; iHeads = heads;
Y luego, de acuerdo con la arquitectura del Transformer inicializaremos las capas de generación convolucional de entidades Query, Key y Value.
int idx = 0; if(!cQuery.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnits, 1, optimization, iBatch)) return false; idx++; if(!cKey.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch)) return false; idx++; if(!cValue.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch)) return false;
Tenga en cuenta que para las capas de formación de entidades Key y Value, utilizaremos el tamaño de secuencia de la segunda fuente de datos. En este caso, tomaremos el tamaño del vector de descripción de un elemento de la secuencia de la primera fuente de datos. Sin embargo, el tamaño del vector de descripción de un elemento de secuencia en la segunda fuente de datos podría ser diferente. Y, ciertamente, no nos hemos ocupado antes de los problemas de alineación del tamaño de la secuencia fuente, sino que simplemente hemos utilizado diferentes ventanas de capa de generación de entidades, alineando únicamente el tamaño de las incorporaciones correspondientes. Con la salvedad de que el algoritmo de codificación relativa utilizará una distancia entre objetos que solo podrá determinarse para objetos que se encuentren en el mismo subespacio. Por consiguiente, necesitaremos objetos conmensurables para analizar. Y para no limitar el alcance del módulo, utilizaremos el mecanismo de proyección de datos entrenados. Volveremos sobre esta cuestión más adelante: por ahora solo queremos llamar la atención sobre ella.
Al igual que en la implementación del algoritmo de Self-Attention relativa, utilizaremos como medida de la distancia entre objetos el producto de dos matrices de datos de origen. Pero primero tendremos que transponer uno de ellos.
idx++; if(!cTranspose.Init(0, idx, OpenCL, iUnits, iWindow, optimization, iBatch)) return false;
Así que crearemos un objeto para registrar los resultados de la multiplicación de matrices.
idx++; if(!cDistance.Init(0, idx, OpenCL, iUnits * iUnitsKV, optimization, iBatch)) return false;
A continuación, organizaremos el proceso de generación de los tensores BK y BV. Recordemos que para generarlas se utilizará un MLP con una capa oculta. La capa oculta será común a todas las cabezas de atención, mientras que la última capa generará tokens individuales para cada cabeza de atención. Aquí, crearemos dos capas de convolución consecutivas para cada entidad con una tangente hiperbólica entre ellas para crear no linealidad.
idx++; CNeuronConvOCL *conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) || !cBKey.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) || !cBKey.Add(conv)) return false;
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iUnits, iUnits, iWindow, iUnitsKV, 1, optimization, iBatch) || !cBValue.Add(conv)) return false; idx++; conv.SetActivationFunction(TANH); conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindow, iWindow, iWindowKey * iHeads, iUnitsKV, 1, optimization, iBatch) || !cBValue.Add(conv)) return false;
Y añadiremos 2 MLP más de generación de contexto global y vectores de desplazamiento de posición. La primera capa de cada uno será estática y contendrá "1", mientras que la segunda será entrenable y generará el tensor deseado. Almacenaremos los punteros a los objetos creados en los arrays cGlobalContentBias y cGlobalPositionalBias.
idx++; CNeuronBaseOCL *neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false; idx++; CBufferFloat *buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalContentBias.Add(neuron)) return false;
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(iWindowKey * iHeads * iUnits, idx, OpenCL, 1, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false; idx++; buffer = neuron.getOutput(); buffer.BufferInit(1, 1); if(!buffer.BufferWrite()) return false; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cGlobalPositionalBias.Add(neuron)) return false;
Con esto, concluiremos nuestro trabajo de preparación de los objetos de preprocesamiento de los datos de origen de nuestro módulo de atención cruzada relativa, y pasaremos a los objetos de procesamiento de resultados de la atención cruzada. En este paso, primero crearemos un objeto de registro de resultados de atención multicabeza y añadiremos su puntero al array cMHAttentionPooling.
idx++; neuron = new CNeuronBaseOCL(); if(!neuron || !neuron.Init(0, idx, OpenCL, iWindowKey * iHeads * iUnits, optimization, iBatch) || !cMHAttentionPooling.Add(neuron) ) return false;
Y, a continuación, añadiremos un objeto de agrupación basado en la dependencia. Luego realizaremos la transición de los resultados de la atención multicabeza a su suma ponderada. Los coeficientes de influencia se determinarán individualmente para cada elemento de la secuencia basándose en el análisis de dependencia.
CNeuronMHAttentionPooling *pooling = new CNeuronMHAttentionPooling(); if(!pooling || !pooling.Init(0, idx, OpenCL, iWindowKey, iUnits, iHeads, optimization, iBatch) || !cMHAttentionPooling.Add(pooling) ) return false;
Aquí cabe señalar que el tamaño del vector de descripción de un elemento de la secuencia a la salida de la capa de agrupación será igual a la dimensionalidad intrínseca, que puede ser diferente de la longitud del vector de descripción de un objeto de la secuencia original. Así, añadiremos más MLP para escalar los resultados al nivel de los datos de origen. En él, utilizaremos 2 capas de convolución con LReLU entre ellas para crear no linealidad.
//--- idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, iWindowKey, iWindowKey, 4 * iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(LReLU); idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, 1, optimization, iBatch) || !cScale.Add(conv) ) return false; conv.SetActivationFunction(None);
Después, sustituiremos el puntero al búfer del gradiente de error en las interfaces de intercambio de datos con otras capas neuronales de nuestro modelo.
//--- if(!SetGradient(conv.getGradient(), true)) return false;
Volvamos ahora a la cuestión de las diferencias de dimensionalidad en las fuentes de los datos de origen. En nuestro módulo de atención cruzada, la primera fuente de datos se utilizará para formar la entidad Query y será la principal fuente de datos utilizada para formar la línea troncal. También se utiliza como enlaces residuales. Por consiguiente, su dimensionalidad permanecerá inalterada. Por lo tanto, para alinear las dimensionalidades de ambas fuentes de datos de entrada, realizaremos una proyección de los valores de la segunda fuente de datos de entrada. Para organizar la proyección de los datos entrenados, crearemos dos capas neuronales secuenciales cuyos punteros añadiremos al array cKVProjection. La primera capa será una capa completamente conectada. Está diseñada para almacenar los datos de origen de la segunda fuente.
cKVProjection.Clear(); cKVProjection.SetOpenCL(OpenCL); idx++; neuron = new CNeuronBaseOCL; if(!neuron || !neuron.Init(0, idx, OpenCL, window_kv * iUnitsKV, optimization, iBatch) || !cKVProjection.Add(neuron) ) return false;
La segunda capa de convolución realizará la proyección de los datos en el subespacio deseado.
idx++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, idx, OpenCL, window_kv, window_kv, iWindow, iUnitsKV, 1, optimization, iBatch) || !cKVProjection.Add(conv) ) return false;
Ahora, tras inicializar todos los objetos que necesitamos para realizar la funcionalidad especificada, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
//--- SetOpenCL(OpenCL); //--- return true; }
Una vez finalizado el trabajo de inicialización de una nueva instancia de objeto, construiremos los algoritmos de pasada directa, que implementaremos en el método feedForward. Aquí debemos notar inmediatamente que necesitaremos 2 fuentes de datos de entrada para ejecutar el algoritmo. Por consiguiente, sobrescribiremos el método heredado de una clase padre con un único objeto de datos fuente con un resultado constante de false, que señalará una llamada al método no válida. Y construiremos el algoritmo correcto en el método con dos objetos de datos fuente.
bool CNeuronRelativeCrossAttention::feedForward(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput) { CNeuronBaseOCL *neuron = cKVProjection[0]; if(!neuron || !SecondInput) return false; if(neuron.getOutput() != SecondInput) if(!neuron.SetOutput(SecondInput, true)) return false;
En el cuerpo del método comprobaremos si el puntero al objeto de la segunda fuente de datos de origen es correcto. Y, de ser necesario, le transmitiremos el puntero a la primera capa del modelo de proyección de datos cuyos punteros se almacenan en el array cKVProjection. A continuación, organizaremos un ciclo de iteración secuencial de todas las capas del modelo de proyección de datos. En el cuerpo del ciclo, llamaremos a los métodos de pasada directa de cada capa, y utilizaremos los resultados de la capa neuronal anterior como datos de entrada.
for(int i = 1; i < cKVProjection.Total(); i++) { neuron = cKVProjection[i]; if(!neuron || !neuron.FeedForward(cKVProjection[i - 1]) ) return false; }
Una vez proyectados con éxito los datos de origen de la segunda fuente, procederemos a generar las entidades Query, Key y Value. En este caso, Query se generará a partir de los datos de origen de la primera fuente, mientras que para Key y Value utilizaremos los resultados de la proyección anterior de los datos de la segunda fuente.
if(!cQuery.FeedForward(NeuronOCL) || !cKey.FeedForward(neuron) || !cValue.FeedForward(neuron) ) return false;
A continuación deberemos calcular los coeficientes de distancia entre los objetos. Para ello, primero transpondremos los datos de la primera fuente. Y luego multiplicaremos los resultados de la proyección de los datos de origen de la segunda fuente por los datos transpuestos de la primera.
if(!cTranspose.FeedForward(NeuronOCL) || !MatMul(neuron.getOutput(), cTranspose.getOutput(), cDistance.getOutput(), iUnitsKV, iWindow, iUnits, 1) ) return false;
A partir de los coeficientes de estructura de datos obtenidos, formaremos los tensores de desplazamiento BK y BV. Primero transmitiremos la información de la estructura de datos a los métodos de pasada directo de las primeras capas de los modelos correspondientes.
if(!((CNeuronBaseOCL*)cBKey[0]).FeedForward(cDistance.AsObject()) || !((CNeuronBaseOCL*)cBValue[0]).FeedForward(cDistance.AsObject()) ) return false;
Y luego organizaremos los ciclos de enumeración de capas de los modelos especificados con llamadas consecutivas de los métodos de pasada directa de las capas neuronales anidadas.
for(int i = 1; i < cBKey.Total(); i++) if(!((CNeuronBaseOCL*)cBKey[i]).FeedForward(cBKey[i - 1])) return false;
for(int i = 1; i < cBValue.Total(); i++) if(!((CNeuronBaseOCL*)cBValue[i]).FeedForward(cBValue[i - 1])) return false;
A continuación, organizaremos la generación de entidades de desplazamiento global. Aquí organizaremos ciclos similares.
for(int i = 1; i < cGlobalContentBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).FeedForward(cGlobalContentBias[i - 1])) return false; for(int i = 1; i < cGlobalPositionalBias.Total(); i++) if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).FeedForward(cGlobalPositionalBias[i - 1])) return false;
Con esto completaremos las operaciones de preprocesamiento de los datos de origen y transferiremos los resultados del trabajo realizado al módulo de atención.
if(!AttentionOut()) return false;
Luego pasaremos los resultados de la atención cruzada multicabeza por el modelo de agrupación.
for(int i = 1; i < cMHAttentionPooling.Total(); i++) if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).FeedForward(cMHAttentionPooling[i - 1])) return false;
Y escalaremos al tamaño del tensor de la primera fuente de datos originales. Esta función la realizará el modelo de escalado interno.
if(!((CNeuronBaseOCL*)cScale[0]).FeedForward(cMHAttentionPooling[cMHAttentionPooling.Total() - 1])) return false; for(int i = 1; i < cScale.Total(); i++) if(!((CNeuronBaseOCL*)cScale[i]).FeedForward(cScale[i - 1])) return false;
Ahora solo nos quedará añadir los enlaces residuales. Escribiremos los resultados de la operación en el búfer de la interfaz de intercambio de datos con la capa neuronal posterior del modelo.
if(!SumAndNormilize(NeuronOCL.getOutput(), ((CNeuronBaseOCL*)cScale[cScale.Total() - 1]).getOutput(), Output, iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Y antes de que el método finalice, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada.
Tras construir el método de pasada directa, procederemos a implementar los algoritmos de pasada inversa. Como ya sabrá, dividimos las operaciones de pasada inversa en 2 pasos. La distribución de gradientes de error a todos los participantes del proceso según su influencia en el resultado final se realizará en el método calcInputGradients. Y la optimización de los parámetros del modelo para reducir el error del modelo se organizará en el método updateInputWeights. El algoritmo de este último no tiene nada de especial. Simplemente se realizará una llamada secuencial a los métodos homónimos de los objetos anidados que contienen los parámetros a entrenar. Pero le sugiero analizar el algoritmo del primero con más detalle.
En los parámetros del método de distribución de gradientes de error calcInputGradients, obtendremos los punteros a 2 objetos de datos fuente con búferes para escribir los gradientes de error correspondientes.
bool CNeuronRelativeCrossAttention::calcInputGradients(CNeuronBaseOCL *NeuronOCL, CBufferFloat *SecondInput, CBufferFloat *SecondGradient, ENUM_ACTIVATION SecondActivation = -1) { if(!NeuronOCL || !SecondGradient) return false;
En el cuerpo del método, verificaremos la relevancia de los punteros recibidos. De lo contrario, todas las operaciones posteriores carecerán de sentido.
Aquí debemos recordar que, como parte de las operaciones de pasada directa, hemos almacenado un puntero al segundo búfer de datos de origen en la capa interna. Realizaremos operaciones similares para el búfer de gradiente de error correspondiente y sincronizaremos inmediatamente las funciones de activación.
CNeuronBaseOCL *neuron = cKVProjection[0]; if(!neuron) return false; if(neuron.getGradient() != SecondGradient) if(!neuron.SetGradient(SecondGradient)) return false; if(neuron.Activation() != SecondActivation) neuron.SetActivationFunction(SecondActivation);
Con esto completaremos el trabajo preparatorio y procederemos a la distribución directa del gradiente de error a todos los participantes del proceso según su influencia en el resultado final.
Recuerde que al inicializar nuestro objeto, hemos organizado la sustitución del puntero por el búfer del gradiente de error. Por eso, empezaremos directamente el trabajo sobre la distribución de gradientes de error con objetos internos. Y aquí conviene recordar que los autores del método AMCT proponen el aprendizaje contrastivo para los motivos. Siguiendo esta lógica, añadiremos un error de diversificación al nivel de resultados de nuestro bloque de atención cruzada.
if(!DiversityLoss(AsObject(), iUnits, iWindow, true)) return false;
Debemos entender que al añadir el error de diversificación a los resultados del bloque de atención cruzada estamos, obviamente, intentando maximizar la distribución en el subespacio precisamente de los resultados pasados a las capas neuronales posteriores del modelo. Al mismo tiempo, al extender el gradiente de error hacia abajo sobre los objetos modelo, indirectamente separaremos también los objetos de los datos de origen analizados que llegan a nuestro bloque desde ambas fuentes.
A continuación, pasaremos primero el gradiente de error global por un modelo de escalado interno de los resultados.
for(int i = cScale.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cScale[i]).calcHiddenGradients(cScale[i + 1])) return false; if(!((CNeuronBaseOCL*)cMHAttentionPooling[cMHAttentionPooling.Total() - 1]).calcHiddenGradients(cScale[0])) return false;
Luego distribuiremos la atención entre las cabezas mediante el modelo de agrupación.
for(int i = cMHAttentionPooling.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cMHAttentionPooling[i]).calcHiddenGradients(cMHAttentionPooling[i + 1])) return false;
Y en el método AttentionGradient, llevaremos el gradiente de error a las entidades Query, Key, Value y los tensores de desplazamiento, según su impacto en el resultado final.
if(!AttentionGradient()) return false;
Después distribuiremos el gradiente de error sobre los modelos internos de los desplazamientos globales entrenables mediante la iteración inversa de sus capas neuronales.
for(int i = cGlobalContentBias.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cGlobalContentBias[i]).calcHiddenGradients(cGlobalContentBias[i + 1])) return false; for(int i = cGlobalPositionalBias.Total() - 2; i > 0; i--) if(!((CNeuronBaseOCL*)cGlobalPositionalBias[i]).calcHiddenGradients(cGlobalPositionalBias[i + 1])) return false;
Del mismo modo, pasaremos el gradiente de error a través de los modelos de generación de entidades de desplazamientos basados en la estructura de las entidades BK y BV.
for(int i = cBKey.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cBKey[i]).calcHiddenGradients(cBKey[i + 1])) return false; for(int i = cBValue.Total() - 2; i >= 0; i--) if(!((CNeuronBaseOCL*)cBValue[i]).calcHiddenGradients(cBValue[i + 1])) return false;
Y sobre hasta la matriz de la estructura de datos cDistance. Pero aquí habrá un matiz a considerar: utilizaremos la matriz de estructura para generar ambas entidades, así que será necesario recoger el gradiente de error de los dos flujos de información. Por consiguiente, primero obtendremos el gradiente de error de BK.
if(!cDistance.calcHiddenGradients(cBKey[0])) return false;
Y luego sustituiremos el puntero al búfer de gradiente de error de este objeto y tomaremos el gradiente BV. A continuación, sumaremos los gradientes de error de ambos modelos y devolveremos los punteros a los búferes de datos a su estado original.
CBufferFloat *temp = cDistance.getGradient(); if(!cDistance.SetGradient(GetPointer(cTemp), false) || !cDistance.calcHiddenGradients(cBValue[0]) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iUnits, false, 0, 0, 0, 1) || !cDistance.SetGradient(temp, false) ) return false;
Después distribuiremos el gradiente de error recogido en la matriz de estructura entre los objetos de datos de origen. Solo que en este caso no distribuiremos en línea recta, sino a través de la capa de transposición de la primera fuente de datos y el modelo de proyección de la segunda fuente.
neuron = cKVProjection[cKVProjection.Total() - 1]; if(!neuron || !MatMulGrad(neuron.getOutput(), neuron.getGradient(), cTranspose.getOutput(), cTranspose.getGradient(), temp, iUnitsKV, iWindow, iUnits, 1) ) return false;
Desde la capa de transposición, transferiremos el gradiente de error hasta el nivel de la primera fuente de los datos de origen. E inmediatamente sumaremos los valores obtenidos con el gradiente de error del flujo de enlaces residuales. El resultado de la operación se escribirá en el búfer de gradiente de la capa de transposición de datos. Tiene el tamaño perfecto para nosotros, y podremos borrar sin problemas los valores registrados previamente en él.
if(!NeuronOCL.calcHiddenGradients(cTranspose.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), Gradient, cTranspose.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
A continuación, calcularemos el gradiente de error a nivel de la primera fuente de datos, obtenida de la entidad Query, y lo añadiremos a los datos anteriormente acumulados. Solo que esta vez almacenaremos los resultados de la suma en el búfer de gradiente de error de los datos de origen.
if(!NeuronOCL.calcHiddenGradients(cQuery.AsObject()) || !SumAndNormilize(NeuronOCL.getGradient(), cTranspose.getGradient(), NeuronOCL.getGradient(), iWindow, false, 0, 0, 0, 1) || !DiversityLoss(NeuronOCL, iUnits, iWindow, true) ) return false;
Y les añadiremos el error de diversificación.
Con esto completaremos nuestro trabajo sobre la distribución del gradiente de error a la primera fuente de datos de origen y pasaremos a trabajar con el segundo flujo de información.
Recordemos que ya hemos almacenado antes el gradiente de error de la matriz de estructura en el búfer de la última capa del modelo de proyección interna de la segunda fuente de datos. Y ahora tendremos que añadirle el gradiente de error de las entidades Key y Value. Para ello, primero sustituiremos el búfer del gradiente de error en el objeto receptor de información. Y luego implementaremos secuencialmente la llamada del método de distribución del gradiente de error desde las entidades correspondientes con la adición intermedia de los resultados de las operaciones a los valores acumulados previamente.
temp = neuron.getGradient(); if(!neuron.SetGradient(GetPointer(cTemp), false) || !neuron.calcHiddenGradients(cKey.AsObject()) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) || !neuron.calcHiddenGradients(cValue.AsObject()) || !SumAndNormilize(temp, GetPointer(cTemp), temp, iWindow, false, 0, 0, 0, 1) || !neuron.SetGradient(temp, false) ) return false;
Y ahora solo tendremos que realizar la iteración inversa de las capas del modelo de proyección con los sucesivos gradientes de error pasados por el modelo.
for(int i = cKVProjection.Total() - 2; i >= 0; i--) { neuron = cKVProjection[i]; if(!neuron || !neuron.calcHiddenGradients(cKVProjection[i + 1])) return false; } //--- return true; }
Cabe señalar que sustituyendo en los parámetros del método el puntero al búfer del gradiente de error en la primera capa del modelo por el objeto obtenido de un programa externo, hemos eliminado la necesidad de copiar los datos. Así, cuando los gradientes de error pasen al primer nivel de la capa del modelo, se escribirán automáticamente en el búfer de datos proporcionado por el programa externo.
Todo lo que deberemos hacer es devolver el resultado lógico de las operaciones al programa externo y finalizar el método.
Con esto concluye nuestra revisión de los métodos del objeto de atención cruzada relativa CNeuronRelativeCrossAttention. Podrá ver el código completo de esta clase y todos sus métodos en el archivo adjunto.
Lamentablemente, hemos alcanzado el límite de la extensión de este artículo sin completar nuestro trabajo. Así que haremos una breve pausa y continuaremos en el próximo artículo.
Conclusión
En este artículo, nos hemos familiarizado con el marco Atom-Motif Contrastive Transformer (AMCT) basado en los conceptos de elementos (velas) y motivos (patrones) atómicos. La idea principal del método consiste en utilizar el entrenamiento contrastado de modelos para resaltar patrones informativos y no informativos a distintos niveles: desde elementos básicos hasta estructuras complejas. Esto permite al modelo no solo considerar las particularidades locales de los movimientos del mercado, sino también captar patrones importantes que pueden proporcionar información adicional para la previsión cualitativa del comportamiento futuro del mercado. La arquitectura del Transformer, que supone la línea troncal del método, captura eficazmente las dependencias a largo plazo y las relaciones complejas entre velas y patrones.
En la parte práctica, hemos empezado a aplicar los enfoques propuestos utilizando herramientas MQL5. Sin embargo, el volumen de trabajo ha superado el tamaño de un solo artículo, así que continuaremos el trabajo iniciado en el próximo artículo. Y este, evaluaremos los resultados prácticos que el marco propuesto ha logrado con datos históricos reales.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de Modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/16163
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
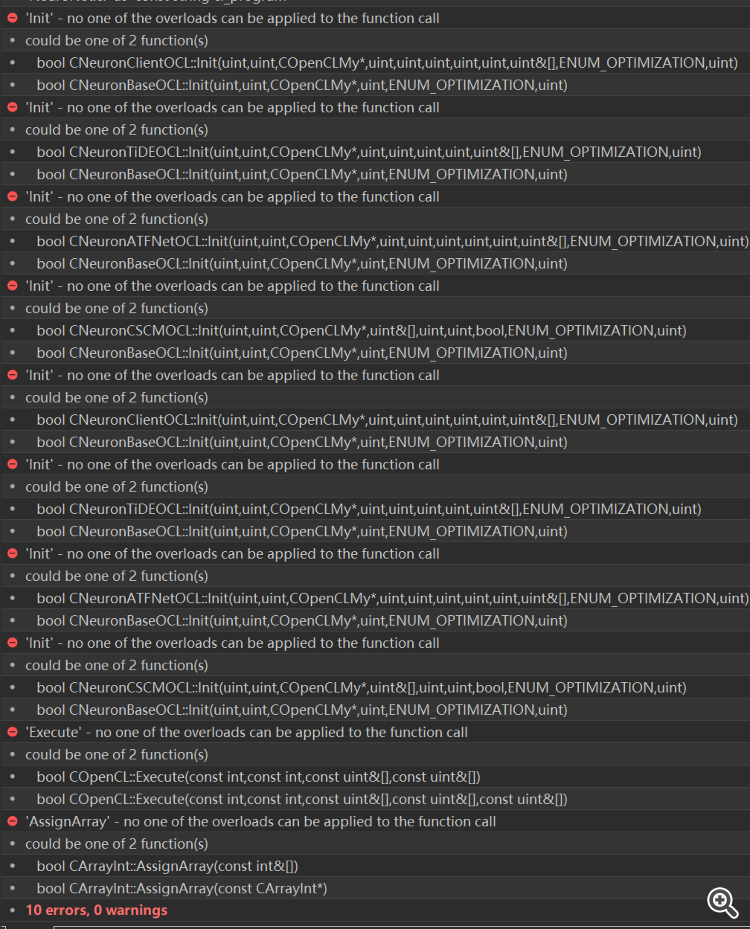
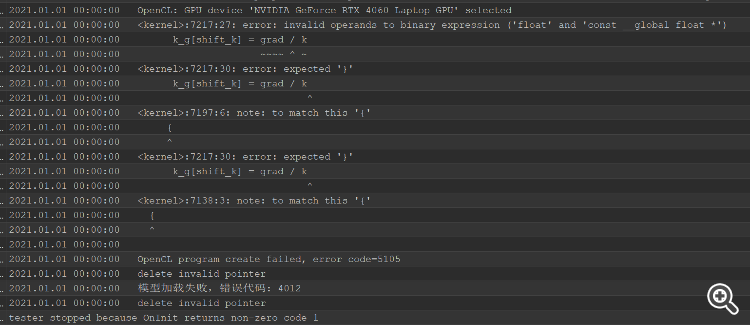 Después de resolver el error de compilación, hay un error probador, toda la cabeza se quema, no puede averiguar dónde resolver el problema
Después de resolver el error de compilación, hay un error probador, toda la cabeza se quema, no puede averiguar dónde resolver el problema
 Ejemplo de optimización estocástica y control óptimo
Ejemplo de optimización estocástica y control óptimo
 Implementación de un algoritmo de trading de negociación rápida utilizando SAR Parabólico (Stop and Reverse, SAR) y Media Móvil Simple (Simple Moving Average, SMA) en MQL5
Implementación de un algoritmo de trading de negociación rápida utilizando SAR Parabólico (Stop and Reverse, SAR) y Media Móvil Simple (Simple Moving Average, SMA) en MQL5
 Creación de un Panel de administración de operaciones en MQL5 (Parte II): Mejorar la capacidad de respuesta y la rapidez de los mensajes
Creación de un Panel de administración de operaciones en MQL5 (Parte II): Mejorar la capacidad de respuesta y la rapidez de los mensajes
 Redes neuronales en el trading: Análisis de la situación del mercado usando el Transformador de patrones
Redes neuronales en el trading: Análisis de la situación del mercado usando el Transformador de patrones
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso