Redes neurais em trading: Análise da situação do mercado usando o transformador de padrões

Introdução

Na última década, o aprendizado profundo (DL) alcançou grandes avanços em diversas áreas, chamando a atenção de pesquisadores dos mercados financeiros. Inspirados pelo sucesso do DL, muitos buscam utilizá-lo para prever tendências de mercado e analisar relações complexas nos dados. Um dos principais aspectos dessa análise é a forma de representar os dados brutos, de modo que as conexões internas e a estrutura dos instrumentos analisados sejam preservadas. A maioria dos modelos existentes trabalha com grafos homogêneos, o que limita sua capacidade de considerar a rica informação semântica associada aos padrões de mercado. De forma análoga às N-gramas no processamento de linguagem natural, padrões de mercado frequentes podem ser usados para identificar relações e prever tendências com mais precisão.

Para resolver essa tarefa, decidimos aplicar algumas abordagens da área de análise de elementos químicos. Assim como os padrões de mercado, os motivos (subgrafos significativos) aparecem frequentemente na estrutura das moléculas, podendo ser usados para revelar propriedades moleculares. Apresento a vocês o framework Molformer, apresentado no trabalho "Molformer: Motif-based Transformer on 3D Heterogeneous Molecular Graphs".

Os autores do Molformer formulam um novo grafo molecular heterogêneo (Heterogeneous Molecular Graph — HMG), que consiste em nós tanto no nível atômico quanto no nível de motivos. Ele oferece uma interface limpa para integrar nós de diferentes níveis e evita a propagação de erros causados por segmentações semânticas incorretas dos átomos. Em relação aos motivos, os autores do método usam estratégias diferentes para diferentes tipos de moléculas. Por um lado, para moléculas pequenas, o vocabulário de motivos é definido com base em grupos funcionais conhecidos na área química. Por outro lado, para proteínas compostas por sequências de aminoácidos, é introduzido um método de análise inteligente de motivos, usando aprendizado por reforço (RL), para detectar as subsequências de aminoácidos mais relevantes.

Para melhor compatibilidade com o HMG foi apresentado o framework Molformer, um modelo geométrico equivariante baseado na arquitetura Transformer. O Molformer se diferencia dos modelos com transformador anteriormente analisados por dois aspectos principais. Primeiro, ele utiliza Self-Attention heterogêneo (HSA) para identificar interações entre nós de diferentes níveis. Segundo, é introduzido o algoritmo de amostragem no ponto mais distante com atenção às dependências (Attentive Farthest Point Sampling — AFPS) para agregar características dos nós e obter uma representação completa da molécula.

O artigo apresenta os resultados de experimentos que confirmam a eficácia da solução proposta para tarefas da indústria química. Propomos avaliar a possibilidade de aplicar essas abordagens à previsão de tendências nos mercados financeiros.

1. Algoritmo Molformer

São padrões estruturais recorrentes que funcionam como blocos de construção de estruturas moleculares complexas. Eles apresentam alta capacidade de expressar características bioquímicas das moléculas como um todo. A comunidade química desenvolveu um conjunto de critérios padrão para identificar motivos com funcionalidades importantes em moléculas pequenas. Em grandes moléculas proteicas, os motivos são áreas locais das estruturas tridimensionais ou sequências de aminoácidos comuns entre proteínas, que influenciam suas funções. Cada motivo geralmente é composto por apenas alguns elementos e pode descrever conexões entre elementos estruturais secundários. Com base nessa característica, os autores do framework Molformer desenvolvem um método heurístico de detecção de motivos proteicos usando RL. Em seu trabalho, eles propõem considerar motivos compostos por quatro aminoácidos, que formam o menor polipeptídeo possível e apresentam propriedades funcionais específicas em proteínas. Neste estágio, o principal objetivo é encontrar o vocabulário mais eficaz 𝓥 dentro de K matrizes quaternárias de aminoácidos. Como o objetivo é encontrar o vocabulário ideal para uma tarefa específica, na prática é possível considerar apenas os quaternários existentes nos conjuntos de dados descendentes, em vez de todos os possíveis.

O vocabulário aprendido é utilizado como modelo para a extração de motivos e a criação do HMG nas tarefas subsequentes. Em seguida, com base nesses HMG, o Molformer é treinado. Sua eficácia é considerada como recompensa r para atualizar os parâmetros θ usando gradientes de política. Como resultado, o Agente pode selecionar o vocabulário ideal de motivos quaternários para a tarefa em questão.

É interessante notar que o processo de mineração de motivos proposto é um jogo de uma única etapa, já que a rede de política πθ gera o vocabulário 𝓥 apenas uma vez em cada iteração. Assim, a trajetória consiste em apenas uma ação, e o resultado do Molformer, baseado no vocabulário escolhido 𝓥, representa uma parte da recompensa total.

Os autores do framework separam motivos e átomos, tratando os motivos como novos nós para formar o HMG. Dessa forma, as representações nos níveis de motivos e átomos são dissociadas, o que facilita a tarefa dos modelos de extrair corretamente os significados semânticos no nível dos motivos.

De forma semelhante às relações entre frases e palavras isoladas na linguagem natural, os motivos em moléculas carregam significados semânticos mais amplos do que os átomos. Por isso, eles têm um papel fundamental na definição das funcionalidades de seus componentes. Os autores do Molformer tratam cada categoria de motivo como um novo tipo de nó e constroem o HMG a partir de dados brutos do modelo, de modo que o HMG inclua nós tanto no nível de motivo quanto no nível atômico. A posição de cada motivo é determinada pela soma ponderada das coordenadas 3D de seus componentes. De forma análoga à segmentação de palavras, os HMG compostos por nós de múltiplos níveis evitam a propagação de erros causados por segmentação semântica inadequada, utilizando informações sobre os átomos para o aprendizado da representação molecular.

O Molformer modifica o Transformer com vários novos componentes, projetados especificamente para 3D HMG. Cada bloco do codificador é composto por HSA, rede FeedForward (FFN) e normalização em dois níveis. Em seguida, aplica-se o AFPS para criar, de forma adaptativa, a representação molecular, que é então alimentada em um preditor totalmente conectado para prever propriedades em uma ampla gama de tarefas subsequentes.

Após a formulação do HMG com N+M nós nos níveis de átomos e motivos, respectivamente, é essencial capacitar o modelo a separar interações entre nós de diferentes ordens. Para isso, os autores do método utilizam a função φ(i,j)→Z, que estabelece relações entre quaisquer dois nós em três tipos: átomo-átomo, átomo-motivo e motivo-motivo. Em seguida, um escalar treinável bφ(i,j) é introduzido para tratar todos os nós de forma adaptativa conforme seus relacionamentos hierárquicos dentro do HMG.

Além disso, os autores do método consideram a possibilidade de utilizar a geometria molecular tridimensional. Como a resistência a transformações globais, como 3D-translações e rotações, é um princípio fundamental no aprendizado de representações moleculares, eles buscam garantir invariância a rotações e translações por meio de uma operação de convolução sobre a matriz de distâncias pareadas 𝑫.

Além disso, o uso de contexto local mostrou-se importante em espaços 3D esparsos. No entanto, observou-se que o Self-Attention é eficaz em capturar padrões globais nos dados, mas negligencia o contexto local. Com base nesse fato, os autores do método impõem uma restrição ao Self-Attention, baseada na distância, para extrair padrões multiescalares tanto do contexto local quanto do global. Para isso, foi desenvolvida uma metodologia multiescalar para capturar detalhes de forma robusta. Em particular, é aplicado um mascaramento de nós que estejam além de uma distância específica τs em cada escala s. Em seguida, as funções extraídas de diferentes escalas são combinadas em uma representação multiescalar e direcionadas ao FFN.

A visualização do framework Molformer, feita pelos autores, é apresentada abaixo.

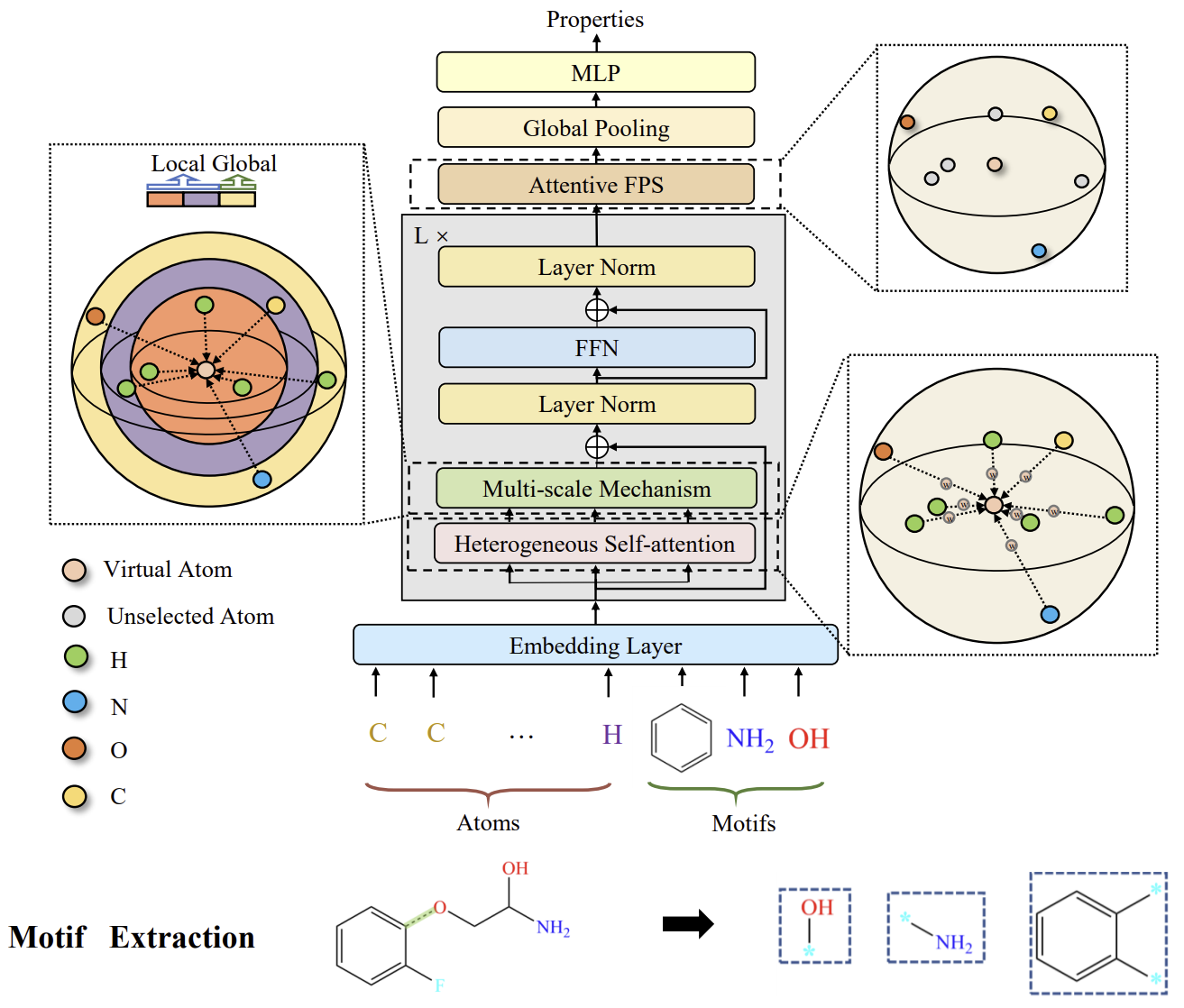
2. Implementação com MQL5

Após a análise dos aspectos teóricos do framework Molformer partimos para a parte prática deste artigo, na qual implementamos nossa visão das abordagens propostas usando MQL5. E aqui, assim como no trabalho anterior, dividiremos todo o processo de implementação do framework em blocos distintos, que executam operações repetitivas.

2.1 Attention pooling

Para começar, destacamos em uma classe separada o algoritmo de pooling baseado em dependências, proposto pelos autores do método R-MAT.

Não se surpreenda por iniciarmos a implementação do framework Molformer com a implementação de uma das abordagens do método R-MAT. Ambos os métodos foram propostos para resolver tarefas semelhantes na indústria química. E, na nossa opinião, eles compartilham alguns pontos em comum que aproveitaremos. Um exemplo é o algoritmo de pooling baseado em dependências.

Os processos desse algoritmo serão organizados na classe CNeuronMHAttentionPooling, cuja estrutura é apresentada a seguir.

class CNeuronMHAttentionPooling  :  public   CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iHeads;
   uint              iUnits;
   CLayer            cNeurons;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMHAttentionPooling(void) {};
                    ~CNeuronMHAttentionPooling(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMHAttentionPooling; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Nesta classe, declaramos três variáveis internas e um array dinâmico, no qual armazenaremos ponteiros para os objetos internos na ordem em que forem chamados. Declaramos o array como estático, o que nos permite deixar o construtor e o destruidor da classe vazios. A inicialização de todos os objetos herdados e dos recém-declarados é feita no método Init, cujos parâmetros recebem constantes que definem de forma única a arquitetura do objeto criado.

bool CNeuronMHAttentionPooling::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                     uint window, uint units_count, uint heads,
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

No corpo do método de inicialização do objeto, primeiro chamamos o método com o mesmo nome da classe pai, no qual já está implementada parte dos controles necessários e o algoritmo de inicialização dos objetos herdados. Em seguida, armazenamos os valores das constantes recebidas do programa externo em variáveis internas.

   iWindow = window;
   iUnits = units_count;
   iHeads = heads;

Preparamos nosso array dinâmico.

   cNeurons.Clear();
   cNeurons.SetOpenCL(OpenCL);

Em seguida, iniciamos a criação da estrutura de objetos aninhados. Aqui, criamos uma MLP de duas camadas, na qual utilizamos a tangente hiperbólica para introduzir não linearidade entre as camadas de neurônios.

   int idx = 0;
   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, iWindow*iHeads, iWindow*iHeads, 4*iWindow, iUnits, 1, optimization, iBatch) ||
      !cNeurons.Add(conv)
     )
      return false;
   idx++;
   conv.SetActivationFunction(TANH);
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, 4*iWindow, 4*iWindow, iHeads, iUnits, 1, optimization, iBatch) ||
      !cNeurons.Add(conv)
     )
      return false;

Os resultados gerados pela MLP criada são normalizados com a função SoftMax aplicada individualmente a cada elemento da sequência.

   idx++;
   conv.SetActivationFunction(None);
   CNeuronSoftMaxOCL *softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, idx, OpenCL, iHeads * iUnits, optimization, iBatch) ||
      !cNeurons.Add(softmax)
     )
      return false;
   softmax.SetHeads(iUnits);
//---
   return true;
  }

E finalizamos a execução do método retornando o resultado lógico da execução das operações ao programa que o chamou.

Vale ressaltar que, neste caso, não há substituição de ponteiros para os buffers de dados. Isso ocorre porque os objetos criados apenas geram dados intermediários. O resultado do objeto criado é obtido multiplicando os resultados normalizados da MLP por um tensor dos dados brutos. São justamente os resultados dessa operação que são armazenados no buffer correspondente, herdado da classe pai. A mesma lógica se aplica ao buffer de gradientes de erro.

Depois de concluído o trabalho com o método de inicialização da classe, passamos à construção do algoritmo de propagação para frente no método feedForward.

bool CNeuronMHAttentionPooling::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *current = NULL;
   CObject *prev = NeuronOCL;

Nos parâmetros do método, recebemos um ponteiro para o objeto com os dados brutos. E no corpo do método criamos duas variáveis locais para armazenar temporariamente os ponteiros para os objetos. E em uma delas, passamos o ponteiro para o objeto de dados brutos.

Em seguida, criamos um laço que itera sobre os objetos internos da MLP, com chamadas sequenciais aos métodos de mesmo nome do modelo interno.

   for(int i = 0; i < cNeurons.Total(); i++)
     {
      current = cNeurons[i];
      if(!current ||
         !current.FeedForward(prev)
        )
         return false;
      prev = current;;
     }

Após todas as iterações do laço, obtivemos os coeficientes de influência das cabeças de atenção no resultado geral de cada elemento da sequência. Como mencionado anteriormente, agora precisamos calcular a média ponderada das cabeças de atenção sobre os dados brutos, multiplicando os coeficientes obtidos pelo tensor dos dados brutos. O produto dos tensores é gravado no buffer de resultados do nosso objeto.

   if(!MatMul(current.getOutput(), NeuronOCL.getOutput(), Output,
                                      1, iHeads, iWindow, iUnits))
      return false;
//---
   return true;
  }

Agora, basta retornarmos o resultado lógico da execução das operações ao programa que o chamou, encerrando assim a execução do método.

Os métodos de propagação reversa desta classe devem ser estudados individualmente. O código completo desta classe e de todos os seus métodos pode ser consultado no anexo.

2.2 Extração de padrões

Na próxima etapa, criaremos o objeto de extração de padrões. Conforme mencionado na parte teórica, as incorporações (ou embeddings, em inglês) dos padrões são adicionadas ao tensor dos dados brutos antes de serem inseridas no modelo. Porém, faremos de maneira um pouco diferente — alimentaremos o modelo com um conjunto de dados comum, e a extração dos padrões e a concatenação de suas incorporações com o tensor dos dados brutos serão feitas dentro do corpo do modelo.

Aqui, vale destacar que cada padrão incorporado aos dados brutos deve ter a mesma dimensionalidade de um elemento da sequência dos dados brutos e estar no mesmo subespaço. A primeira questão é resolvida por meio de decisões de arquitetura. A segunda será tentada a ser resolvida durante o processo de aprendizado das incorporações dos padrões.

Para cumprir essas tarefas, vamos criar uma nova classe chamada CNeuronMotifs. Sua estrutura está apresentada a seguir.

class CNeuronMotifs    :  public CNeuronBaseOCL
  {
protected:
   CNeuronConvOCL    cMotifs;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMotifs(void) {};
                    ~CNeuronMotifs(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint dimension, uint window, uint step, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMotifs; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override;
  };

Nesta classe, declaramos apenas uma camada convolucional interna, responsável por executar o processo de incorporação dos padrões. Porém, chama atenção o fato de que o método de definição da função de ativação foi sobrescrito. É interessante notar que esse método ainda não havia sido sobrescrito em nenhum momento anterior. Neste caso, isso foi feito para sincronizar a função de ativação da camada interna com a do objeto.

void CNeuronMotifs::SetActivationFunction(ENUM_ACTIVATION value)
  {
   CNeuronBaseOCL::SetActivationFunction(value);
   cMotifs.SetActivationFunction(activation);
  }

A inicialização da camada convolucional declarada, assim como de todos os objetos herdados, é realizada no método Init. Nos parâmetros desse método, recebemos constantes que nos permitem definir de forma única a arquitetura do objeto a ser criado.

bool CNeuronMotifs::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                         uint dimension, uint window, uint step, uint units_count,
                         ENUM_OPTIMIZATION optimization_type, uint batch
                        )
  {
   uint inputs = (units_count * step + (window - step)) * dimension;
   uint motifs = units_count * dimension;

No entanto, diferentemente dos métodos semelhantes apresentados anteriormente, neste caso não temos dados suficientes para chamar o método com o mesmo nome da classe pai. Isso se deve principalmente ao tamanho do buffer de resultados. Como mencionado acima, esperamos receber na saída um tensor concatenado dos dados brutos e das incorporações dos padrões. Portanto, primeiro determinaremos os tamanhos dos tensores dos dados brutos e das incorporações com base nos dados disponíveis, e só então chamaremos o método de inicialização da classe pai, passando a soma dos tamanhos obtidos.

   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, inputs + motifs, optimization_type, batch))
      return false;

O próximo passo é inicializar a camada convolucional interna de incorporação dos padrões de acordo com os parâmetros recebidos do programa externo.

   if(!cMotifs.Init(0, 0, OpenCL, dimension * window, dimension * step, dimension, units_count,
                                                                           1, optimization, iBatch))
      return false;

Note que o tamanho das incorporações retornadas é igual à dimensionalidade dos dados brutos.

Aqui mesmo, desativamos forçadamente a função de ativação usando o método sobrescrito anteriormente.

   SetActivationFunction(None);
//---
   return true;
  }

Depois disso, finalizamos a execução do método, retornando o resultado lógico da operação ao programa que o chamou.

Após a inicialização do objeto, partimos para a construção dos processos de propagação para frente, que serão implementados no método feedForward. Aqui tudo é bastante direto.

bool CNeuronMotifs::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto dos dados brutos e imediatamente verificamos a validade desse ponteiro. Em seguida, sincronizamos as funções de ativação da camada dos dados brutos e do objeto atual.

   if(NeuronOCL.Activation() != activation)
      SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation());

Essa operação nos permite sincronizar a região de resultados da camada de incorporações com os dados brutos.

E só após concluir essa preparação, realizamos a propagação para frente da camada interna.

   if(!cMotifs.FeedForward(NeuronOCL))
      return false;

Depois disso, concatenamos o tensor das incorporações obtidas com os dados brutos.

   if(!Concat(NeuronOCL.getOutput(), cMotifs.getOutput(), Output, NeuronOCL.Neurons(), cMotifs.Neurons(), 1))
      return false;
//---
   return true;
  }

O tensor concatenado é gravado no buffer de resultados, herdado da classe pai, e encerramos a execução do método, retornando o resultado lógico da operação ao programa que o chamou.

A seguir, veremos os métodos de propagação reversa. Como você deve ter imaginado, esses algoritmos também são simples. No método de distribuição do gradiente de erro calcInputGradients, por exemplo, realizamos apenas uma operação de desconcatenação do buffer de gradientes de erro, herdado da classe pai, distribuindo os valores entre o objeto dos dados brutos e a camada interna.

bool CNeuronMotifs::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(!DeConcat(NeuronOCL.getGradient(),cMotifs.getGradient(),Gradient,NeuronOCL.Neurons(),cMotifs.Neurons(),1))
      return false;
//---
   return true;
  }

No entanto, essa aparente simplicidade requer algumas explicações. Primeiramente, não ajustamos o gradiente de erro passado para os dados brutos e para a camada interna pela derivada da função de ativação dos respectivos objetos. Neste caso, essa operação seria redundante. Isso é possível graças à sincronização do ponteiro da função de ativação do nosso objeto, da camada interna e dos dados brutos, que realizamos durante a construção do método de propagação para frente. Essa operação simples nos permite obter o gradiente de erro já ajustado pela derivada da função de ativação correta no nível dos resultados do objeto. Dessa maneira, realizamos a desconcatenação de um gradiente de erro já corrigido.

O segundo ponto importante é que não repassamos o gradiente de erro da camada interna de extração de padrões para os dados brutos. Curiosamente, isso se deve justamente à natureza da tarefa que estamos resolvendo: a extração de padrões dos dados brutos. Nosso objetivo aqui é encontrar padrões significativos, não "forçar" os dados brutos a se ajustarem aos padrões desejados. No entanto, como é fácil notar, os dados brutos ainda recebem seu gradiente de erro pelo fluxo direto de dados.

E o código completo dessa classe e de todos os seus métodos pode ser consultado no anexo.

2.3 Atenção multiescalar

Mais um "tijolo" que precisamos construir é o objeto de atenção multiescalar. Devo dizer que, talvez, aqui fizemos o maior desvio em relação ao algoritmo original do Molformer. O motivo é que, neste bloco, os autores do framework realizavam o mascaramento de objetos distantes do ponto analisado, além de uma distância determinada. E dessa forma, focavam a atenção apenas em uma área delimitada.

Já em nossa implementação, seguimos um caminho diferente. Em primeiro lugar, em vez do mecanismo de atenção proposto, utilizamos o método de relativa Self-Attention, que analisa não apenas o deslocamento posicional, mas também o contexto. Em segundo lugar, para alterar a escala da atenção, aumentamos o tamanho de um único elemento analisado para dois, três ou quatro elementos da sequência original. Isso pode ser comparado à análise de um gráfico de time frame superior. A implementação da nossa solução é apresentada na classe CNeuronMultiScaleAttention. A estrutura da nova classe é mostrada a seguir.

class CNeuronMultiScaleAttention :  public CNeuronBaseOCL
  {
protected:
   uint              iWindow;
   uint              iUnits;
   //---
   CNeuronBaseOCL    cWideInputs;
   CNeuronRelativeSelfAttention  cAttentions[4];
   CNeuronBaseOCL    cConcatAttentions;
   CNeuronMHAttentionPooling cPooling;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronMultiScaleAttention(void) {};
                    ~CNeuronMultiScaleAttention(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronMultiScaleAttention; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Aqui definimos explicitamente o número de escalas, declarando um array fixo de objetos de atenção relativa. Além disso, na estrutura da classe são declarados mais 3 objetos, cuja finalidade será explicada durante a implementação dos métodos da classe.

Todos os objetos internos são declarados como estáticos, o que nos permite deixar vazios o construtor e o destruidor da classe. A inicialização de todos os objetos declarados e herdados é feita no método Init.

bool CNeuronMultiScaleAttention::Init(uint numOutputs, uint myIndex,
                                      COpenCLMy *open_cl, uint window,
                                      uint window_key, uint units_count,
                                      uint heads,
                                      ENUM_OPTIMIZATION optimization_type,
                                      uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

Nos parâmetros do método, como de costume, recebemos constantes que definem de forma única a arquitetura do objeto a ser criado. E no corpo do método, chamamos diretamente o método de mesmo nome da classe pai. Acredito que não seja necessário repetir que ele já contém os controles e algoritmos de inicialização dos objetos herdados.

Após a execução bem-sucedida do método da classe pai, armazenamos algumas constantes em variáveis internas.

   iWindow = window;
   iUnits = units_count;

Além disso, antes da inicialização dos objetos recém-declarados, vale destacar que, neste ponto, ainda não sabemos o tamanho do tensor dos dados brutos. Muito menos sabemos se seu tamanho é múltiplo das nossas escalas de análise. Aliás, o tensor recebido como dados brutos pode nem ser múltiplo dessas escalas. No entanto, os objetos de atenção em grande escala precisam receber um tensor com tamanho apropriado. Para cumprir esse requisito, criaremos um objeto interno no qual copiaremos os dados brutos e adicionaremos valores nulos nas posições em falta. Antes disso, determinaremos o tamanho necessário do buffer como o maior múltiplo das nossas escalas que seja superior ao tamanho atual.

   uint units1 = (iUnits + 1) / 2;
   uint units2 = (iUnits + 2) / 3;
   uint units3 = (iUnits + 3) / 4;
   uint wide = MathMax(MathMax(iUnits, units1 * 2), MathMax(units2 * 3, units3 * 4));

Em seguida, inicializamos o objeto para copiar os dados brutos com o tamanho necessário.

   int idx = 0;
   if(!cWideInputs.Init(0, idx, OpenCL, wide * iWindow, optimization, iBatch))
      return false;
   CBufferFloat *temp = cWideInputs.getOutput();
   if(!temp || !temp.Fill(0))
      return false;

O buffer de resultados desta camada será preenchido com valores nulos.

O próximo passo é inicializar os objetos internos de atenção em diferentes escalas, mantendo os demais parâmetros.

   idx++;
   if(!cAttentions[0].Init(0, idx, OpenCL, iWindow, window_key, iUnits, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[1].Init(0, idx, OpenCL, 2 * iWindow, window_key, units1, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[2].Init(0, idx, OpenCL, 3 * iWindow, window_key, units2, heads, optimization, iBatch))
      return false;
   idx++;
   if(!cAttentions[3].Init(0, idx, OpenCL, 4 * iWindow, window_key, units3, heads, optimization, iBatch))
      return false;

Aqui vale destacar que, apesar das diferentes escalas dos objetos de atenção, esperamos obter tensores de tamanhos comparáveis na saída. Afinal, todos utilizam essencialmente a mesma fonte de dados brutos. Portanto, para realizar a concatenação dos resultados da atenção, declararemos um objeto com tamanho 4 vezes maior que os dados brutos.

   idx++;
   if(!cConcatAttentions.Init(0, idx, OpenCL, 4 * iWindow * iUnits, optimization, iBatch))
      return false;

E para realizar a média dos resultados da atenção, utilizaremos a classe de pooling baseada em dependências que criamos anteriormente.

   idx++;
   if(!cPooling.Init(0, idx, OpenCL, iWindow, iUnits, 4, optimization, iBatch))
      return false;

Ao final do método de inicialização, substituímos os ponteiros dos buffers de resultados e de gradientes de erro do objeto criado pelos ponteiros correspondentes do buffer da camada de pooling.

   SetActivationFunction(None);
   if(!SetOutput(cPooling.getOutput()) ||
      !SetGradient(cPooling.getGradient()))
      return false;
//---
   return true;
  }

Concluímos o método retornando o resultado lógico da execução das operações ao programa que o chamou.

Note que, nesta classe, não criamos objetos para executar conexões residuais, como nos blocos de atenção discutidos anteriormente. Isso ocorre porque os blocos internos de atenção relativa que utilizamos já possuem conexões residuais. Sendo assim, a média dos resultados de atenção já leva essas conexões em conta. E qualquer operação adicional seria redundante.

Após a inicialização do objeto, passamos à construção dos processos de propagação para frente, que serão implementados no método feedForward.

bool CNeuronMultiScaleAttention::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- Attention
   if(!cAttentions[0].FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método de propagação para frente, como de costume, recebemos um ponteiro para o objeto com os dados brutos, o qual passamos diretamente para o método de mesmo nome do objeto interno de atenção de escala original (unitária). No corpo do método chamado do objeto interno, além das operações principais, também é feita a verificação da validade do ponteiro recebido. Portanto, após a execução bem-sucedida do método da classe interna, podemos utilizar com segurança o ponteiro recebido do programa externo. Na etapa seguinte, transferimos os dados brutos para o buffer da camada interna correspondente. Em seguida, sincronizamos as funções de ativação.

   if(!Concat(NeuronOCL.getOutput(), NeuronOCL.getOutput(), cWideInputs.getOutput(), iWindow, 0, iUnits))
      return false;
   if(cWideInputs.Activation() != NeuronOCL.Activation())
      cWideInputs.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation());

Vale notar que, neste caso, para copiar os dados brutos, usamos o método de concatenação, em cujos parâmetros indicamos duas vezes o ponteiro para o buffer de resultados do objeto de dados brutos. Para o primeiro buffer, especificamos o tamanho da janela dos dados brutos, e para o segundo, indicamos o valor 0. Com esses parâmetros, é evidente que obteremos uma cópia dos dados brutos no buffer de resultados indicado. Aqui, não ocorre a adição de valores nulos para preencher dados ausentes, como foi feito durante a inicialização do objeto.

No entanto, a adição de valores nulos é feita implicitamente. Lembre-se de que, durante a inicialização do objeto interno de dados brutos, o buffer de resultados é preenchido com valores nulos. No processo de treinamento e uso, esperamos receber tensores de dados brutos com tamanho fixo. Portanto, toda vez que copiamos os dados brutos, apenas modificamos os valores dos mesmos elementos, enquanto os demais continuam com valor zero.

Após a formação do objeto expandido dos dados brutos, criamos um laço para executar as operações de atenção multiescalar. No corpo desse laço, chamamos sequencialmente os métodos de propagação para frente dos objetos de maior escala, com o ponteiro do objeto expandido dos dados brutos.

//--- Multi scale attentions
   for(int i = 1; i < 4; i++)
      if(!cAttentions[i].FeedForward(cWideInputs.AsObject()))
         return false;

Os resultados da atenção em todas as escalas são concatenados em um único tensor. É importante destacar que, apesar das diferentes escalas dos dados analisados, na saída obtemos tensores comparáveis, e cada elemento da sequência original permanece em sua posição. Por isso, também concatenamos os tensores no nível dos elementos da sequência original.

//--- Concatenate Multi-Scale Attentions
   if(!Concat(cAttentions[0].getOutput(), cAttentions[1].getOutput(), cAttentions[2].getOutput(),
              cAttentions[3].getOutput(), cConcatAttentions.getOutput(), 
              iWindow, iWindow, iWindow, iWindow, iUnits))
      return false;

Em seguida, também no nível dos elementos da sequência original, realizamos o pooling ponderado dos resultados da atenção multiescalar com base nas dependências.

//--- Attention pooling
   if(!cPooling.FeedForward(cConcatAttentions.AsObject()))
      return false;
//---
   return true;
  }

Ao final do método, retornamos o resultado lógico da execução das operações ao programa que o chamou.

Vale lembrar que, na fase de inicialização do objeto, substituímos os ponteiros para os buffers de resultados e de gradientes de erro. Portanto, os resultados do pooling são imediatamente direcionados para os buffers que fazem a interface de comunicação entre as camadas da rede neural. Dessa forma, omitimos a operação redundante de cópia dos dados.

Os métodos de propagação reversa desta classe eu recomendo que você estude por conta própria. O código completo da classe e de todos os seus métodos está incluído no anexo.

2.4 Montando o framework Molformer

Acima, realizamos um extenso trabalho de construção dos blocos individuais do framework Molformer. Agora, chegou o momento de organizá-los em uma arquitetura completa. Para isso, criaremos uma nova classe chamada CNeuronMolformer. Como objeto pai, utilizaremos a classe CNeuronRMAT, que contém a implementação de um mecanismo de modelo linear simples. A seguir, apresentamos a estrutura da nova classe.

class CNeuronMolformer  :  public CNeuronRMAT
  {
public:
                     CNeuronMolformer(void) {};
                    ~CNeuronMolformer(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key,
                          uint units_count, uint heads, uint layers,
                          uint motif_window, uint motif_step,
                          ENUM_OPTIMIZATION optimization_type, uint batch); //Molformer
   //---
   virtual int       Type(void) override   const   {  return defNeuronMolformer; }
  };

Vale destacar que, diferentemente dos objetos implementados anteriormente, aqui sobrescrevemos apenas o método de inicialização do novo objeto da classe Init. Isso foi possível graças à estrutura linear organizada na classe pai. Agora, basta preenchermos o array dinâmico herdado da classe pai com o conjunto necessário de objetos sequenciais. Todo o algoritmo de interação entre eles já está implementado nos métodos da classe pai.

Nos parâmetros do único método sobrescrito, recebemos uma série de constantes que nos permitem interpretar de forma única a arquitetura do objeto a ser criado, conforme definido pelo usuário.

bool CNeuronMolformer::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                            uint window, uint window_key, uint units_count,
                            uint heads, uint layers,
                            uint motif_window, uint motif_step,
                            ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, window * units_count, optimization_type, batch))
      return false;

E no corpo do método, chamamos diretamente o método de mesmo nome da classe base de camada neural totalmente conectada.

Repare que chamamos o método da camada neural base, e não do objeto pai direto. Isso porque, no corpo do método, vamos criar uma arquitetura completamente nova. Não há necessidade de reaproveitar as decisões arquitetônicas da classe pai.

No passo seguinte, preparamos o array dinâmico onde vamos armazenar os ponteiros dos objetos criados.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);

E então partimos para as operações de criação e inicialização dos objetos necessários. Primeiro, criamos e inicializamos o objeto de extração de padrões. O ponteiro para o novo objeto é adicionado ao array dinâmico.

   int idx = 0;
   CNeuronMotifs *motif = new CNeuronMotifs();
   uint motif_units = units_count - MathMax(motif_window - motif_step, 0);
   motif_units = (motif_units + motif_step - 1) / motif_step;
   if(!motif ||
      !motif.Init(0, idx, OpenCL, window, motif_window, motif_step, motif_units, optimization, iBatch) ||
      !cLayers.Add(motif)
     )
      return false;

Em seguida, criamos variáveis locais para armazenar temporariamente os ponteiros dos objetos, e criamos um laço para criar os blocos internos do codificador (Encoder), cuja quantidade é determinada por uma constante recebida nos parâmetros do método.

   idx++;
   CNeuronMultiScaleAttention *msat = NULL;
   CResidualConv *ff = NULL;
   uint units_total = units_count + motif_units;
   for(uint i = 0; i < layers; i++)
     {
      //--- Attention
      msat = new CNeuronMultiScaleAttention();
      if(!msat ||
         !msat.Init(0, idx, OpenCL, window, window_key, units_total, heads, optimization, iBatch) ||
         !cLayers.Add(msat)
        )
         return false;
      idx++;

No corpo do laço, criamos e inicializamos o objeto de atenção multiescalar. Em seguida, adicionamos um bloco convolucional com conexão residual.

      //--- FeedForward
      ff = new CResidualConv();
      if(!ff ||
         !ff.Init(0, idx, OpenCL, window, window, units_total, optimization, iBatch) ||
         !cLayers.Add(ff)
        )
         return false;
      idx++;
     }

Os ponteiros para os objetos criados são adicionados ao array dinâmico de objetos internos.

É importante observar que, na saída do bloco de atenção multiescalar, obtemos um tensor concatenado dos dados brutos com as incorporações dos padrões, enriquecido com informações sobre as dependências internas. No entanto, a saída da classe deve ser um tensor dos dados brutos enriquecidos. Em vez de simplesmente "descartar" as incorporações dos padrões, usaremos uma função de escalonamento dos dados dentro de cada sequência unitarizada. Para isso, primeiro transpomos os resultados do bloco anterior.

//--- Out
   CNeuronTransposeOCL *transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, idx, OpenCL, units_total, window, optimization, iBatch) ||
      !cLayers.Add(transp)
     )
      return false;
   idx++;

Depois, adicionamos uma camada convolucional que realizará a função de escalonamento de cada sequência unitarizada.

   CNeuronConvOCL *conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, idx, OpenCL, units_total, units_total, units_count, window, 1, optimization, iBatch) ||
      !cLayers.Add(conv)
     )
      return false;
   idx++;

E então retornamos os resultados obtidos ao formato original dos dados.

   idx++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, idx, OpenCL, window, units_count, optimization, iBatch) ||
      !cLayers.Add(transp)
     )
      return false;

Por fim, só nos resta substituir os ponteiros para os buffers de dados e retornar o resultado lógico da execução das operações ao programa que o chamou.

   if(!SetOutput(transp.getOutput()) ||
      !SetGradient(transp.getGradient()))
     return false;
//---
   return true;
  }

Com isso, encerramos a análise das classes de construção do framework Molformer. O código completo das classes apresentadas e de todos os seus métodos está disponível no anexo. Lá também se encontra o código completo de todos os programas utilizados na preparação deste artigo. Cabe destacar desde já que todos os programas de interação com o ambiente e de treinamento dos modelos foram totalmente reutilizados de trabalhos anteriores, sem qualquer modificação. Foram feitas apenas pequenas alterações pontuais na arquitetura do codificador (Encoder) do estado do ambiente, com as quais recomendo que você se familiarize por conta própria. A descrição completa da arquitetura de todos os modelos treinados também está incluída no anexo. Agora, passamos para a parte final deste artigo — o treinamento dos modelos e os testes dos resultados.

3. Testes

Neste artigo, implementamos o framework Molformer com os recursos do MQL5 e agora entramos na etapa final — o treinamento dos modelos e a verificação da política de comportamento treinada do Ator. Seguimos o algoritmo de treinamento descrito em trabalhos anteriores, e treinamos simultaneamente três modelos: Codificador do estado da conta, Ator e Crítico. Codificador analisa a situação do mercado, Ator executa operações de trade com base na política aprendida, e Crítico avalia as ações do Ator e indica ajustes na política de comportamento.

O treinamento é realizado com dados históricos reais de EURUSD, no time frame H1, abrangendo todo o ano de 2023, utilizando parâmetros padrão dos indicadores analisados.

O processo de treinamento é iterativo e inclui atualizações periódicas do conjunto de dados de treinamento.

Para avaliar a eficácia da política aprendida, são utilizados dados históricos de janeiro de 2024. Os resultados do teste são apresentados abaixo.

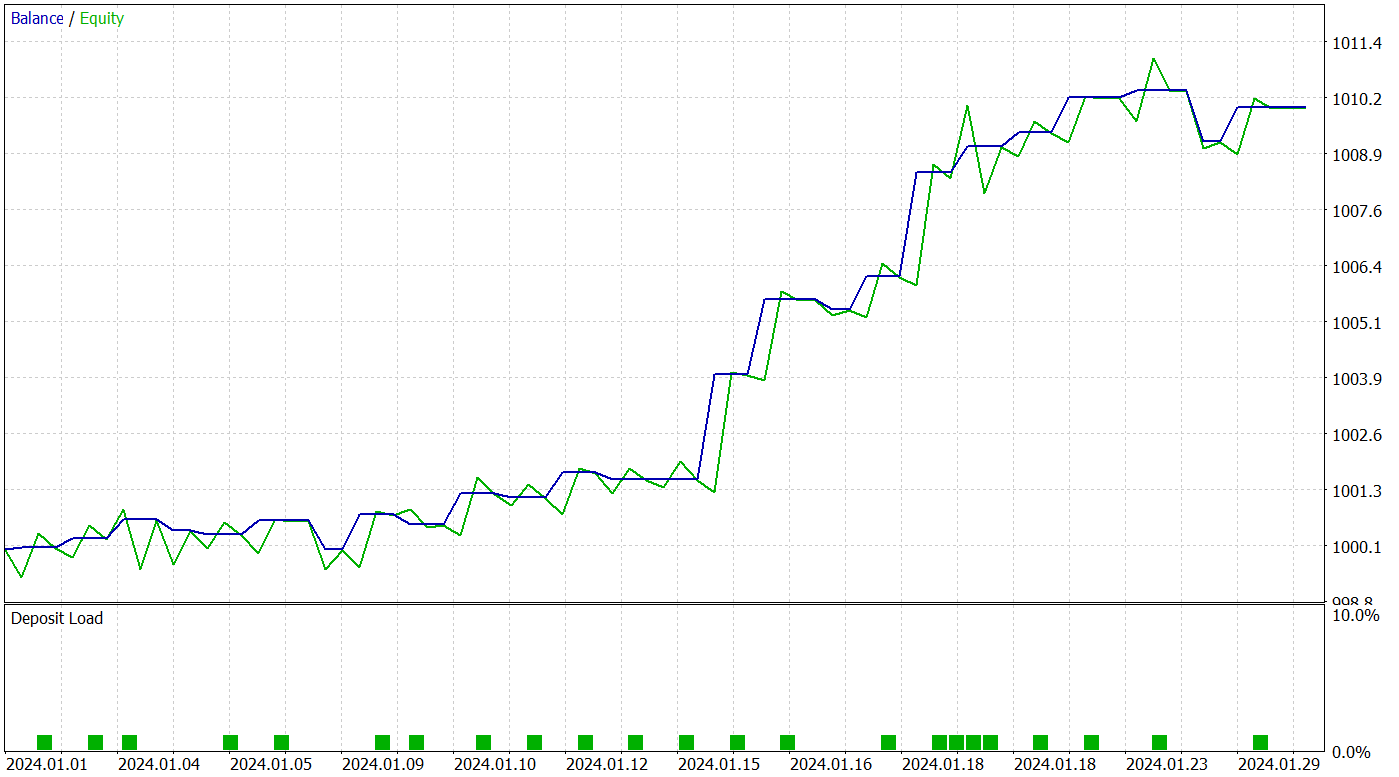
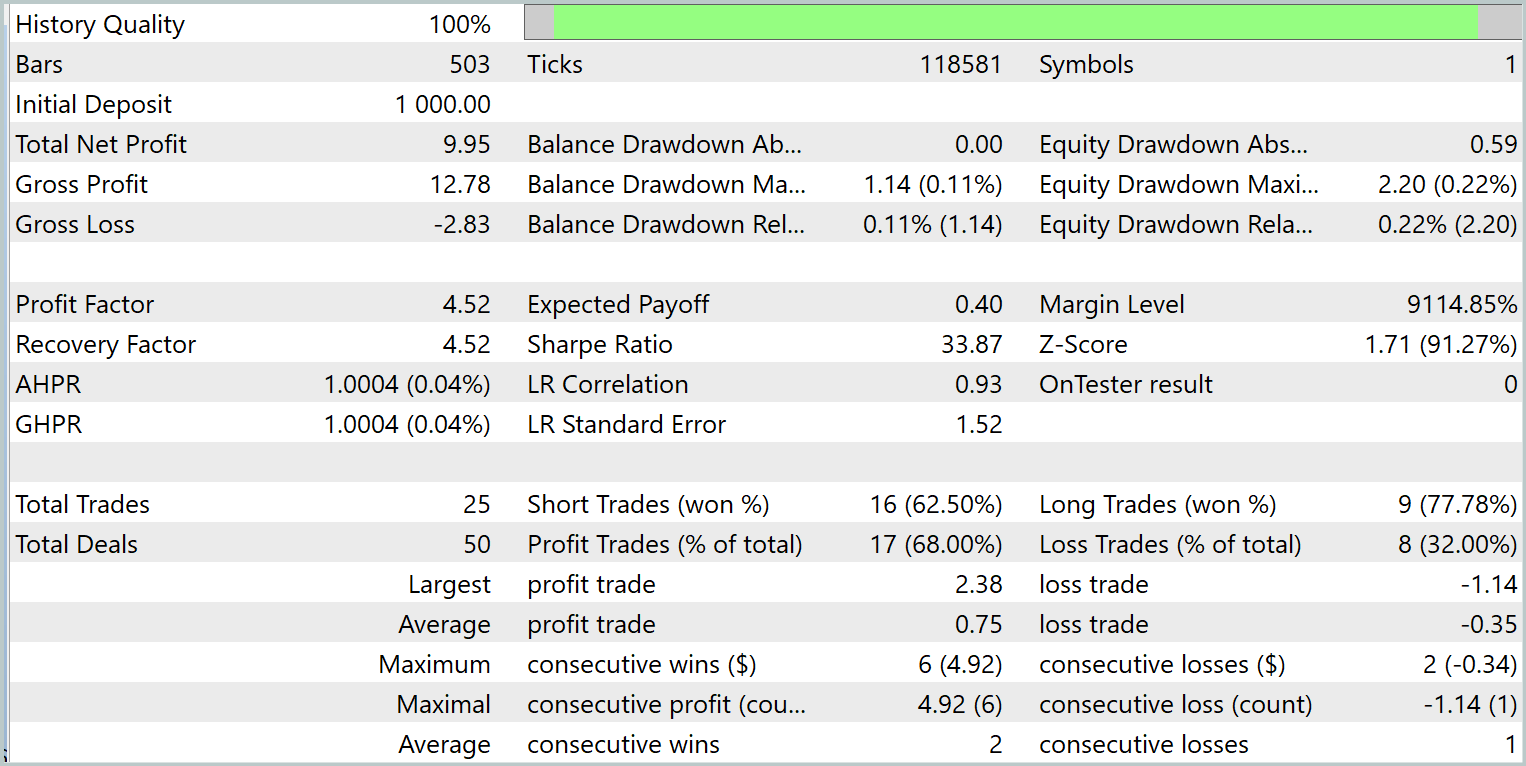
Com base nos dados apresentados, a modelo treinada executou 25 operações de trade durante o período de teste, das quais 17 foram encerradas com lucro. Isso representa 68% do total. Além disso, os lucros médio e máximo das operações vencedoras foram o dobro dos valores correspondentes das operações perdedoras.

O potencial do modelo proposto também é evidenciado pelo gráfico de saldo, que mostra uma tendência clara de crescimento. No entanto, o curto período de teste e o número limitado de operações permitem apenas afirmar que há um potencial promissor.

Considerações finais

O método Molformer representa um avanço significativo na área de análise e previsão de dados de mercado. O uso de grafos de mercado heterogêneos, que incluem tanto ativos individuais quanto suas combinações em forma de padrões de mercado, permite ao Featured Image ao modelo considerar relações e estruturas de dados mais complexas, o que melhora significativamente a precisão na previsão dos movimentos futuros de preço.

Na parte prática deste artigo, implementamos nossa interpretação das abordagens do Molformer utilizando recursos do MQL5. Integrámos as soluções propostas ao modelo e o treinamos com dados históricos reais. Como resultado, obtivemos um modelo capaz de generalizar o conhecimento adquirido para novas situações de mercado e gerar lucro. Isso é comprovado pelos resultados dos testes. Acreditamos que a abordagem proposta pode servir de base para pesquisas e aplicações futuras na área de análise financeira, oferecendo a traders e analistas novas ferramentas para que tomem decisões mais fundamentadas em cenários de incerteza.

Links

• Molformer: Motif-based Transformer on 3D Heterogeneous Molecular Graphs
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA de coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA de coleta de exemplos com o método Real-ORL
3	Study.mq5	Expert Advisor	EA de treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para construção de rede neural
7	NeuroNet.cl	Biblioteca	Biblioteca com código OpenCL