どんな市場でも優位性を得る方法(第5回):FRED EURUSD代替データ
本連載では、増え続ける代替金融データの世界をうまく活用できるようサポートすることを目指しています。ビッグデータの時代を生きる現代の投資家は、どの代替データセットを取引プロセスに組み込むべきかを慎重に判断するための十分なリソースを持ち合わせていないかもしれません。本記事の目的は、どの代替データセットを検討すべきか、また、どのデータセットは使用しない方がよいかを判断するために必要な情報を提供することです。
取引戦略の概要
相関関係は、金融分析アプローチの基本原則です。2つの資産に相関関係がある場合、ポートフォリオを多様化したり、予想される価格変動へのエクスポージャーを最大化したりしようとする投資家にとって、この指標はポートフォリオ構築において有用なツールとなります。
連邦準備制度は、ドルの外国為替価値を総合的に示す一連の指数を維持しています。その中でも特に注目したのは、広義のドル日次指数(NBDD)です。このインデックスは2006年1月に100ポイントの基準値で設定されました。執筆時点では、2008年の景気後退時に約86ポイントという過去最低値を記録し、2022年には約128ポイントの史上最高値を更新しました。このインデックスは2011年後半から強気トレンドを継続しており、現在は約121ポイントで推移しており、過去最高値に近い水準にあります。これは過去最高値に近い値です。
以下のグラフでは、広義のドル指数とEUR/USDペアの為替レートを重ね合わせています。この2つの時系列データの間に明確な関係性を見出すことはほとんどできません。米ドルの為替レートはグラフの下部に平坦な青い線としてほぼ隠れていますが、広義のドル指数は赤い線としてはっきりと表示されています。
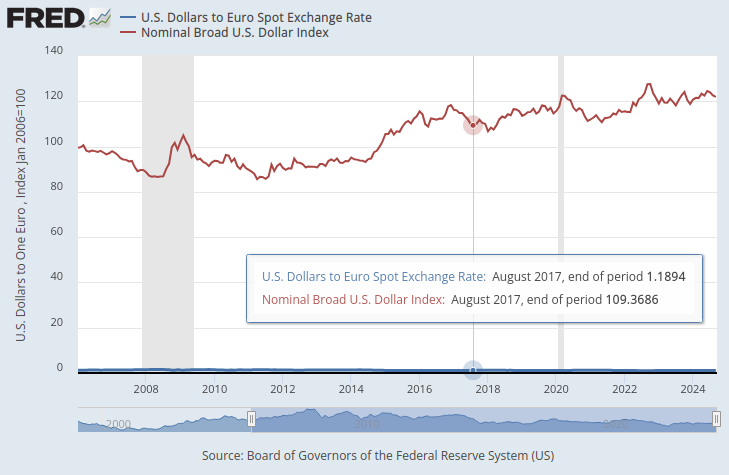
図1:ドル対ユーロのスポット為替レートとドル指数
両方の時系列データが同じスケールであることを確認すると、明らかなパターンが現れます。Y軸を変更して、1年間の時系列データの変化率を記録するようにします。この手順を実行すると、インデックスがEURUSD外国為替レートとほぼ完全な負の相関関係を示していることが明確にわかります。
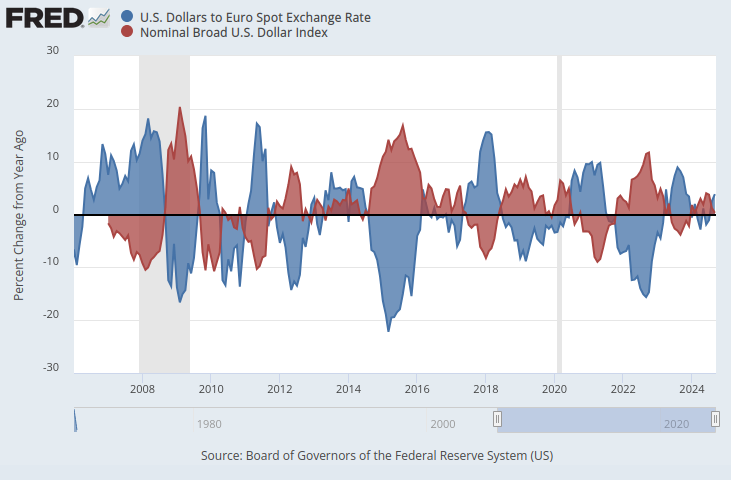
図2:ドル対ユーロのスポット為替レートとドルインデックス(パーセント表示)
これらのデータセットを使用してEURUSDの将来の為替レートを予測する取引戦略をアルゴリズム的に学習する可能性を検討します。完全な負の相関関係を考えると、連邦準備制度経済データベース(FRED)のマクロ経済指標を考慮すると、滞在的に、モデルが為替レートについて学習できる情報が存在する可能性があります。
方法論の概要
提案の妥当性をテストするために、まずMetaTrader 5端末からEURUSDの毎日の過去の為替レートを取得し、そのデータをFRED Python APIから取得した3つのマクロ経済データセットと結合しました。3つのFRED時系列データセットは次のことを記録していました。
- 米国債の金利
- 米国の予想インフレ率
- 広義ドル指数
これにより、AIモデルを構築するための3つのデータセットを作成できました。
- 通常のOHLC市場相場
- 代替FREDデータ
- 最初の2つのスーパーセット
問題となっているすべてのデータセットを統合し、スケールを変換してFREDのWebサイトでおこなった操作を再現したところ、EURUSD為替レートと広義のドル指数の価格の相関レベルはほぼ-0.9であることがわかりました。ほぼ満点です。それだけでなく、広義のドル指数の現在の値と、20日後のEURUSD終値の将来値との相関関係は-0.7であることも確認されました。
視覚化すると、時系列データを驚くほどうまく分離することができ、その精度は、このシリーズの記事でこれまで示したことのないレベルです。比較的長い期間にわたるデータの変化率を使用すると、データを非常にうまく分離できるようです。3D散布図により、データがどの程度適切に分離されているかがさらに検証され、明らかな強気ゾーンと弱気ゾーンを識別することができました。さらに、FREDの公式Webサイトでデータの散布図を作成すると、データの傾向が明確に確認できました。散布図の傾向は、Pythonの通常の高度な分析ツールを使用しなくても明確に定義されました。これにより、2つの時系列データセットによって共有される潜在的な情報があり、それをモデルが学習できる可能性があるという自信が生まれました。
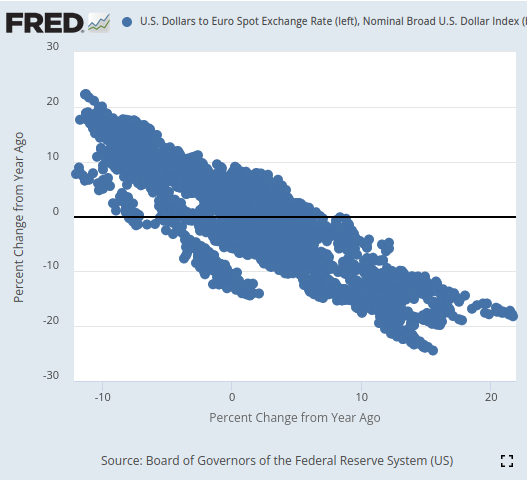
図3:興味のある2つのデータセットの散布図を視覚化する
これまでのところ、これらすべては有望に思えるかもしれませんが、EURUSD為替レートの将来の価値を予測する能力の向上にはつながりませんでした。実際のところ、パフォーマンスは悪化するばかりで、通常の市場相場のみを含む最初のデータセットを使用した方が良かったようです。
3つのデータセットとそれらすべてに共通するターゲットとの関係を学習するために、3つの同一のディープニューラルネットワーク(DNN)回帰モデルを訓練しました。最初のDNNモデルは最も低い誤差率を生成しました。さらに、分析のために選択したFREDデータセットのいずれにも、私たちの特徴選択アルゴリズムは影響を与えなかったようです。挫けることなく、訓練データに過剰適合することなく、訓練データセットを使用してDNNモデルパラメータを調整することに成功しました。これは、未知の検証データでデフォルトのDNNモデルよりも優れたパフォーマンスを示したという事実によって示唆されます。訓練と検証でこれらの決定に到達するために、ランダムシャッフルをおこなわない時系列交差検証を採用しました。
ONNX形式にエクスポートする前に、モデルの残差を検査し、健全性を確認しました。残念ながら、私たちのモデルから観測された残差はひどく誤動作しており、これは私たちのモデルが効果的に学習できなかったことを示している可能性があります。
最後に、モデルをONNX形式にエクスポートし、PythonとMQL5を使用して統合されたAI搭載のエキスパートアドバイザーを構築しました。
データの取得
まず、必要なPythonライブラリをインポートします。
#Import the libraries we need from fredapi import Fred import seaborn as sns import numpy as np import pandas as pd import MetaTrader5 as mt5 import matplotlib.pyplot as plt
次に、資格情報と、FREDから取得する時系列を定義しました。
#Define important variables fred_api = "ENTER YOUR API KEY" fred_broad_dollar_index = "DTWEXBGS" fred_us_10y = "DGS10" fred_us_5y_inflation = "T5YIFR"
FREDにログインします。
#Login to fred
fred = Fred(api_key=fred_api)必要なデータを取得しましょう。
#Fetch the data
dollar_index = fred.get_series(fred_broad_dollar_index)
us_10y = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)シリーズに名前を付けると、後でそれらを結合できるようになります。
#Name the series so we can merge the data dollar_index.name = "Dollar Index" us_10y.name = "Bond Interest" us_5y_inflation.name = "Inflation"
欠落している値があれば、移動平均で埋めます。
#Fill in any missing values dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True) us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True) us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
MetaTrader 5端末からデータを取得する前に、まずそれを初期化する必要があります。
#Initialize the terminal
mt5.initialize()4年間の履歴データを取得したいと考えています。
#Define how much data to fetch amount = 365 * 4 #Fetch data eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount)) eur_usd
時間列を秒形式から実際の日付に変換します。
#Convert the time column eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')
時間列がデータのインデックスであることを確認します。
#Set the column as the index
eur_usd.set_index('time',inplace=True)どのくらい先の将来を予測するかを定義します。
#Define the forecast horizon look_ahead = 20
ここで、予測子とターゲットを指定しましょう。
#Define the predictors predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] ohlc_predictors = ["open","high","low","close","tick_volume"] fred_predictors = ["Dollar Index","Bond Interest","Inflation"] target = "Target" all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
データを結合します。
#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)データにラベルを付けます。
#Define the target target = merged_data.loc[:,"close"].shift(-look_ahead) target.name = "Target"
FRED Webサイトで分析したデータと同様に、年間変化率が表示されるようにデータをフォーマットします。
#Convert the data to yearly percent changes merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100 merged_data = merged_data.merge(target,right_index=True,left_index=True) merged_data.dropna(inplace=True) merged_data
プロット目的でバイナリターゲットを追加します。
#Add binary targets for plotting purposes merged_data["Binary Target"] = 0 merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1
データのインデックスをリセットします。
#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_data探索的データ分析
まず、セントルイス連邦準備銀行のWebサイトで生成したプロットを再作成します。これにより、前処理手順が意図したとおりに実行されたことが検証されます。
#Plotting our data set plt.title("EURUSD Close Against FRED Broad Dollar Index") plt.plot(merged_data.loc[:,"close"]) plt.plot(merged_data.loc[:,"Dollar Index"])
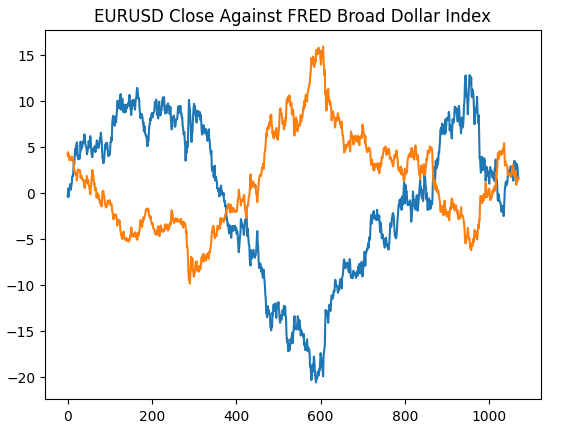
図4:FRED Webサイトでの観察結果をPythonで再現する
それでは、データセット内の相関レベルを分析してみましょう。ご覧のとおり、インフレデータセットは、取得した3つの代替FREDデータセットすべての中で相関レベルが最も弱いです。しかし、残りの2つの代替データセットには大きな可能性があるように見えたにもかかわらず、パフォーマンスの向上は得られませんでした。
#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)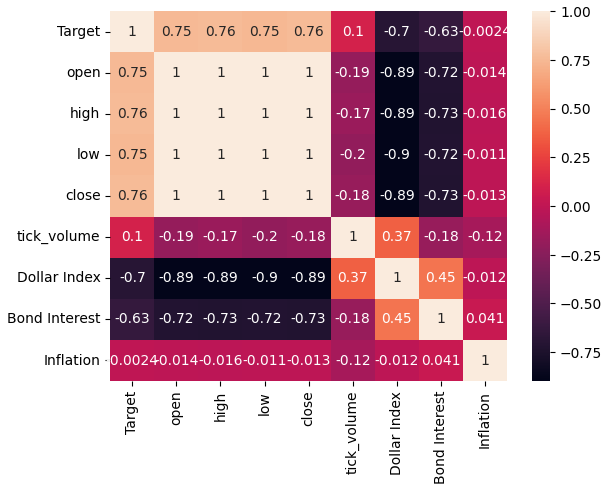
図5:相関ヒートマップ
一度に多数のデータセットを表示する場合、ペアプロットを使用すると、利用可能なすべてのデータ間に存在する可能性のある関係をすばやく確認できます。オレンジ色の点と青色の点が非常によく分離されているのがはっきりとわかります。さらに、このプロットの主対角線に沿ってカーネル密度推定(kde)プロットが実行されます。KDEプロットは、各列内のデータの分布を視覚化するのに役立ちます。小さなセクションに重なり合う2つの丘のような形状が観察されるという事実は、データが大部分で適切に分離されていることを意味します。
sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")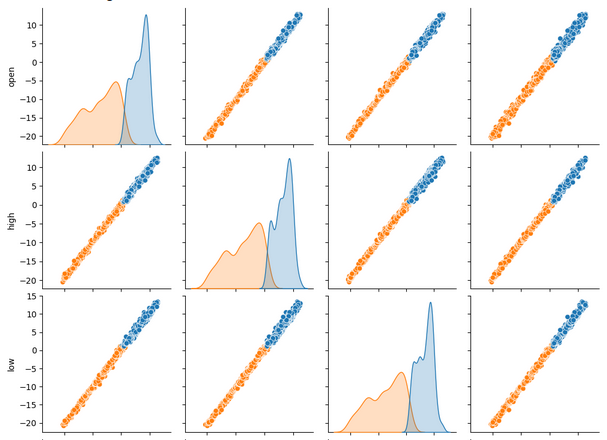
図6:ペアプロットを使用してデータを視覚化する
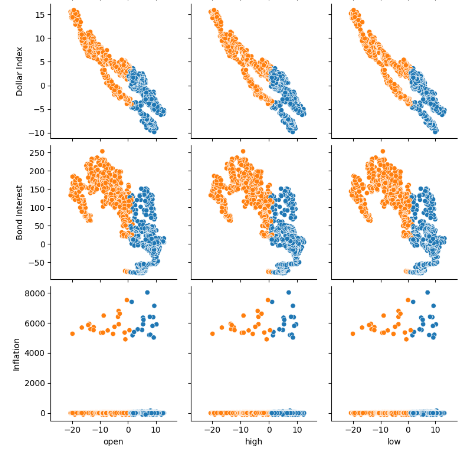
図7:FRED代替データとEURUSDペアとの関係を視覚化する
ここで、x軸とy軸に広義のドル指数と債券金利、z軸にEURUSD終値を使用して3D散布図を作成します。データは重複がほとんどない2つの異なるクラスターに分かれているようです。これはモデルがデータから学習可能な決定境界を示唆しています。残念ながら、私たちはこれをモデルに効果的に公開できなかったと思います。
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"]) ax.set_xlabel("Dollar Index") ax.set_ylabel("Bond Interest") ax.set_zlabel("EURUSD close")
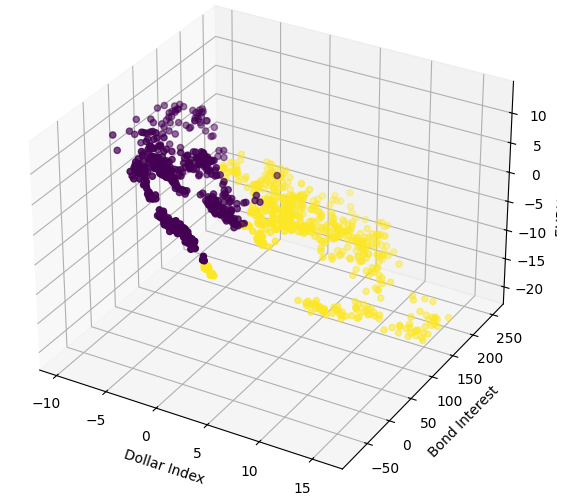
図8:市場データを3Dで可視化する
データモデル化の準備
では、保有する財務データをモデル化する準備をしましょう。まず、モデルの入力とターゲットを定義します。
#Let's define our set of predictors X = merged_data.loc[:,predictors] y = merged_data.loc[:,"Target"]
必要なライブラリをインポートします。
#Import the libraries we need
from sklearn.model_selection import train_test_splitここで、先ほど概説した3つのグループにデータを分割します。
#Partition the data ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)
モデルの交差検証精度を保存するためのデータフレームを作成します。
#Prepare the dataframe to store our validation error validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))
データのモデリング
データをモデル化するために必要なライブラリをインポートしましょう。
#Let's cross validate our models from sklearn.neural_network import MLPRegressor from sklearn.model_selection import cross_val_score
先ほど概説した3つのニューラルネットワークを定義します。
#Define the neural networks ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
各モデルをテストします。
#Let's obtain our cv score ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
交差検証スコアを保存します。
for i in np.arange(0,5): validation_error.iloc[i,0] = ohlc_score[i] validation_error.iloc[i,1] = fred_score[i] validation_error.iloc[i,2] = all_score[i]
検証エラーを視覚化します。
#Our validation error
validation_error| MetaTrader 5データ | FRED代替データ | すべてのデータ |
|---|---|---|
| -0.147973 | -0.79131 | -4.816608 |
| -0.103913 | -2.073764 | -0.655701 |
| -0.211833 | -0.276794 | -0.838832 |
| -0.094998 | -1.954753 | -0.259959 |
| -1.233912 | -2.152471 | -3.677273 |
5つのフォールドすべてにわたる平均パフォーマンスを分析すると、MetaTrader 5からの通常の市場データが最善の選択肢である可能性があることがわかります。
#Our mean performane across all groups
validation_error.mean()| 入力データ | 平均5倍の誤差 |
|---|---|
| MetaTrader 5 | -0.358526 |
| FRED | -1.449818 |
| ALL | -2.049675 |
モデルのパフォーマンスをプロットすると、MetaTrader 5データがより一貫した誤差レベルを生成していることがわかります。
#Plotting our performance
validation_error.plot()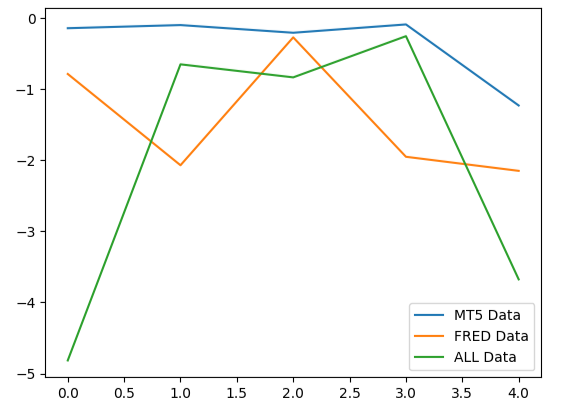
図9:選択する必要があった3つのデータセットによって生成された3つの異なるエラーレベルを視覚化する
MetaTrader 5エラーボックスプロットの潰れた形状は、モデルが一貫したパフォーマンスを通じてスキルを発揮していることを示しているため、望ましいものです。
#Creating box-plots of our performance
sns.boxplot(validation_error)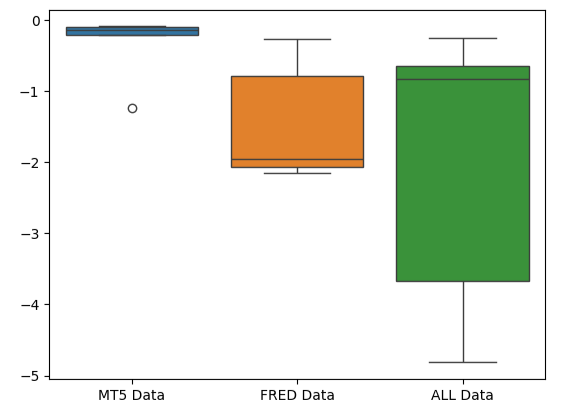
図10:モデルのエラー指標をボックスプロットとして視覚化する
特徴量の重要性
DNNモデルにとってどの機能が最も重要であるかを考えてみましょう。うまくいけば、私たちが選択した代替データが有用であれば、それは私たちの特徴重要度アルゴリズムによってそのように判断されるでしょう。残念ながら、私たちの分析では、MetaTrader 5市場データの変動だけでターゲットをかなりうまく説明できるようです。したがって、FRED時系列には、モデルが保有するデータから推論できなかった追加情報は含まれていませんでした。
まず、必要なライブラリをインポートしましょう。
#Feature importance
from alibi.explainers import ALE, plot_ale累積ローカル効果(ALE)プロットは、各モデル入力がターゲットに与える影響を視覚化するのに役立ちます。ALEプロットは、私たちのような相関性の高いデータで訓練されたモデルを説明できる堅牢な機能を備えているため、人気があります。部分依存性(PD)プロットなどの従来の学術的手法は、相関レベルが強い予測因子を説明する場合にはまったく信頼できませんでした。アルゴリズムの元の仕様は、Daniel W. ApleyとJingyu Zhuによる2016年の研究論文の完全版(こちら)で読むことができます。

図11:ALEアルゴリズムの共同開発者、Daniel W. Apley
エールの説明をDNN回帰モデルに適合させてみましょう。
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])
これで、各予測子がターゲットに及ぼす影響について説明が得られます。ALEプロットは直感的に視覚的に解釈できるため、優れた出発点となります。簡単に言えば、得られたALEプロットが平坦な線である場合、DNNモデルの観点からは、観察中の予測子はターゲットにほとんど影響を与えないか、まったく影響を与えません。同様に、ALEプロットが直線性から離れるほど、モデルが学習したターゲットと予測子の関係は単純な直線関係から遠ざかることになります。
図12の左上隅にある始値と目標のALEプロットは、EURUSDの始値が上昇すると、将来の終値も上昇することをモデルが学習したことを示しています。始値と終値のALEプロットが反対方向にどのように変化するかを観察します。これは、これら2つの予測因子だけで、ターゲットの大きな変動を説明できる可能性があることを示唆している可能性があります。
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)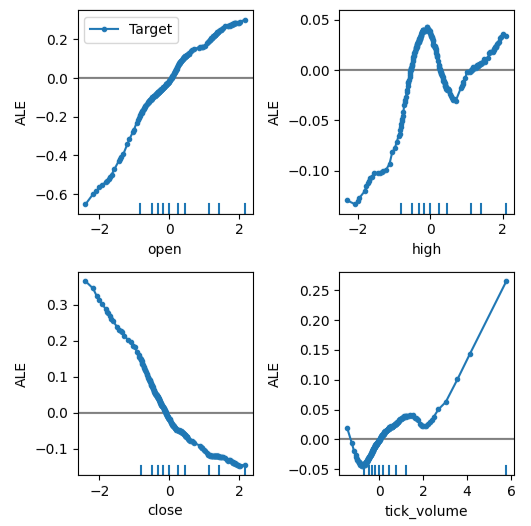
図12:MetaTrader 5市場データでALEプロットを視覚化する
ここで前方選択を実行します。アルゴリズムはヌルモデルから開始し、モデルのパフォーマンスがそれ以上向上しなくなるまで、モデルのパフォーマンスを最も向上させる1つの機能を反復的に追加します。
#Forward selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
モデルを初期化します。
#Reinitialize the model all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
ここで、必要な前方選択オブジェクトを指定する必要があります。このアルゴリズムのインスタンスに、重要と思われる変数をできるだけ多く選択するように指示します。
#Define the feature selector sfs1 = SFS(all_nn, k_features=(1,X.shape[1]), forward=True, scoring='neg_mean_squared_error', cv=5, n_jobs=-1 )
FRED時系列はいずれもアルゴリズムによって選択されませんでした。
#Best features we identified
sfs1.k_feature_names_アルゴリズムの選択プロセスを視覚化できます。プロットは、モデルパラメータが増加するにつれてモデルのパフォーマンスが低下したことを明確に示しています。
#Fit the forward selection algorithm fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')
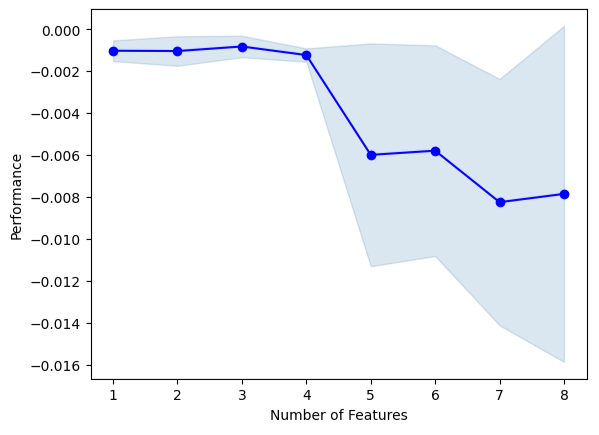
図13:予測子を繰り返し追加しながらモデルのパフォーマンスを視覚化する
パラメータチューニング
ランダムサーチを使用してDNNモデルのパラメータ調整を実行してみましょう。まず、モデルを初期化する必要があります。
#Reinitialize the model model = MLPRegressor(max_iter=500)
ここで、チューニングパラメータを定義します。
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
"early_stopping":[True,False],
"warm_start":[True,False],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)チューニングオブジェクトを適合します。
#Fit the tuner
tuner.fit(train_X,train_y)私たちが見つけた最良のパラメータを見てみましょう。
#The best parameters we found
tuner.best_params_'tol':1e-05,
'solver': 'lbfgs',
'shuffle':True,
'learning_rate_init':0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes':(10, 20, 40, 80),
'early_stopping':True,
'alpha':0.1,
'activation': 'relu'}
より深いパラメータ最適化
SciPyライブラリを使用して、より優れたモデルパラメータを検索してみましょう。最適化プロセスは、子供の頃のかくれんぼのような検索問題として考えることができます。モデルがこれまでに見たことのないデータに対して最良の誤差率を生成するモデルの理想的なパラメータは、連続パラメータのそれぞれに割り当てることができる可能性のある値の無限の空間の中に隠されています。
必要なライブラリをインポートしましょう。
#Deeper optimization from scipy.optimize import minimize from sklearn.metrics import mean_squared_error from sklearn.model_selection import TimeSeriesSplit
時系列分割オブジェクトを定義します。
#Define the time series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
現在のコストを返すデータフレームを作成し、視覚化のためにモデルの進行状況を保存するリストを作成します。
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) algorithm_progress = []
ここでコスト関数を定義します。SciPyの最小化ライブラリは、関数からの出力が最小になるような関数への入力を見つけるためのさまざまなアルゴリズムを提供します。他のすべてのDNNパラメータを一定に保ちながら、訓練データに対するモデルの5倍の誤差レベルの平均を最小化する量として使用します。
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2] ) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Store the algorithm's progress algorithm_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
ルーチンの開始点を定義し、パラメータの境界も指定します。この問題の場合、唯一の制限は、すべてのモデルパラメータが正である必要があるということです。
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100))
モデルパラメータを最適化するために、Truncated Newton Constrained (TNC)アルゴリズムを使用します。打ち切りニュートン法は、境界が適用される大規模な非線形最適化問題を解決するのに適した一連の方法の1つです。SciPyライブラリは、アルゴリズムのC実装へのラッパーを提供します。
#Searching deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
終了が正常に完了したかどうかを確認しましょう。
#The result of our optimization
resultsuccess:False
status:4
fun:0.001911232280110637
x: [ 1.000e-100 1.000e-100 1.000e-100]
nit:0
jac: [ 2.689e+06 9.227e+04 1.124e+05]
nfev:116
最適な入力を見つけるのが難しかったようですので、最適化手順のパフォーマンスを視覚化してみましょう。
#Store the optimal coefficients optimal_weights = result.x optima_y = min(algorithm_progress) optima_x = algorithm_progress.index(optima_y) inputs = np.arange(0,len(algorithm_progress)) #Plot the performance of our optimization procedure plt.scatter(inputs,algorithm_progress) plt.plot(optima_x,optima_y,'ro',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.xlabel("Iterations") plt.ylabel("Training MSE") plt.title("Minimizing Training Error")
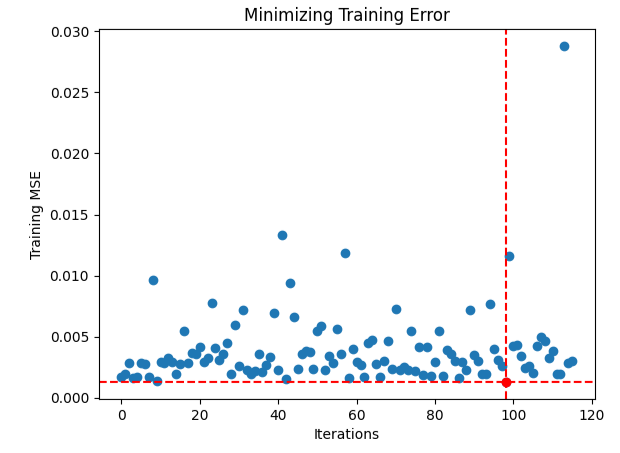
図14:赤い点は、TNCオプティマイザーによって推定された最適な入力値を表す
過剰適合のテスト
3つのモデルすべてを初期化し、訓練セットで訓練して、テストデータでデフォルトモデルを上回るパフォーマンスが得られるかどうかを確認してみましょう。これまでの意思決定プロセスではテストデータを使用していなかったことを思い出してください。
#Testing for overfitting default_nn = MLPRegressor(max_iter=500) #Randomized NN random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] ) #TNC NN tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2] )
各モデルを訓練セットに適合させます。
#Store the models in a list models = [default_nn,random_search_nn,tnc_nn] #Fit the models for model in models: model.fit(train_X,train_y)
検証誤差レベルを保存するデータフレームを作成します。
#Create a dataframe to store our validation error validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))
各モデルをテストし、そのスコアを記録します。
#Let's obtain our cv score default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) #Store the model error in a dataframe for i in np.arange(0,5): validation_error.iloc[i,0] = default_score[i] validation_error.iloc[i,1] = random_score[i] validation_error.iloc[i,2] = tnc_score[i]
検証エラーを見てみましょう。
#Let's see the validation error validation_error
| デフォルトモデル | ランダムサーチ | TNC |
|---|---|---|
| -0.362851 | -0.029476 | -0.054709 |
| -0.323601 | -0.053967 | -0.087707 |
| -0.064432 | -0.024282 | -0.026481 |
| -0.121226 | -0.019693 | -0.017709 |
| -0.064801 | -0.012812 | -0.016125 |
5つのフォールドすべてにわたって平均パフォーマンスを計算すると、ランダムサーチモデルが最善の策であることが明確にわかります。
#Our best performing model
validation_error.mean()| モデル | 平均検証エラー |
|---|---|
| デフォルトモデル | -0.187382 |
| ランダムサーチ | -0.028046 |
| TNC | -0.040546 |
ボックスプロットを作成すると、デフォルトモデルのパフォーマンスがどの程度変化したかがすぐにわかります。カスタマイズされたモデルは、厳しい誤差レベルの範囲内で実行することができ、パラメータ調整の選択に対する自信が高まりました。
#Let's create box-plots sns.boxplot(validation_error)
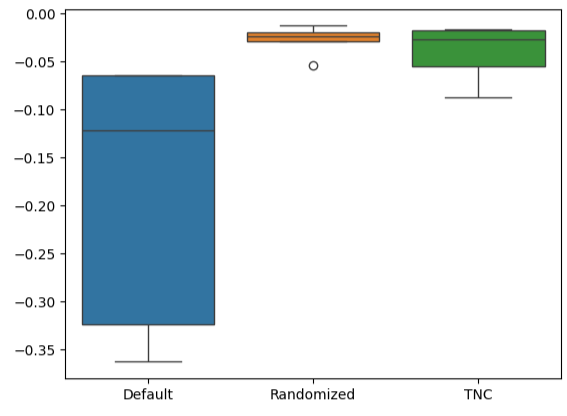
図15:モデルのパフォーマンスをボックスプロットとして視覚化する
交差検証データの折れ線グラフを作成すると、デフォルトのモデルと調整されたモデル間の差異が強調表示されます。デフォルトモデルのパフォーマンスを表す青い線と残りの色付きのプロットの間には、かなりの誤差があることがわかります。
#We can also visualize model performance through a line plot
validation_error.plot()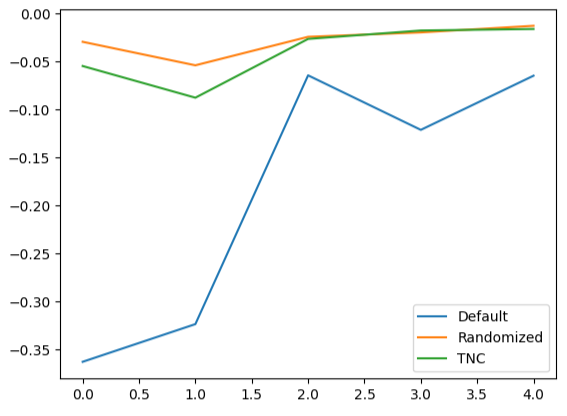
図16:テストデータでさまざまなモデルの5倍のパフォーマンスをプロットする
残差分析
モデルを盲目的に信頼して本番環境に展開することはできません。モデルの残差を検査して、モデルが実際に効果的に学習したことを確認してみましょう。理想的には、関数を完全に近似したモデルでは、残差は平坦な線になります。つまり、モデルの予測にエラーはありません。さらに、これはモデルの予測における誤差の量が変化しないことも意味します。
その結果、モデルのパフォーマンスが理想から遠ざかるほど、理想的な線形および定常残差プロットから観察される歪みが大きくなります。私たちのモデルの残差はさまざまな量の誤差を示し、時には以前の誤差の量と相関していました。これは懸念の原因となる可能性があり、予測子またはターゲットを変換することで対処できる可能性があります。
モデルを初期化しましょう。
#Resdiuals analysis model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
訓練データにモデルを適合させ、テストデータを使用して残差を記録します。
#Fit the model model.fit(train_X,train_y) #Record the residuals residuals = test_y - model.predict(test_X)
残差プロットは理想からは程遠いため、これに対処するには他の前処理手順を検討する必要があるかもしれません。
#Residuals analysis
residuals.plot()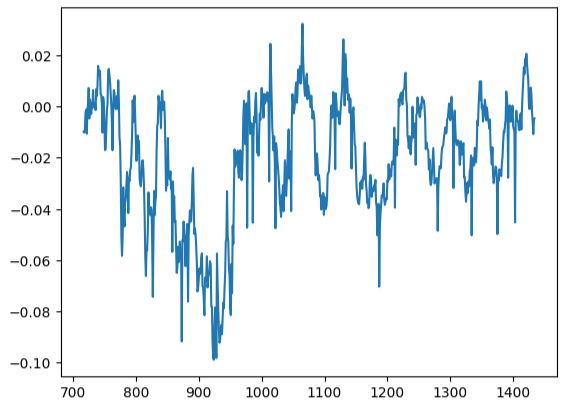
図17:テストデータにおけるモデルの残差の視覚化
自己相関を測定することは、偽の回帰の可能性を検出するための堅牢なアプローチです。残念ながら、モデルの残差もこのテストに合格しませんでしたが、予測子やターゲットをより適切に変換すれば、さらなる強化が得られる可能性があるという指標として機能する可能性があります。
#Autocorrelation plot from statsmodels.graphics.tsaplots import plot_acf acf = plot_acf(residuals,lags=40)
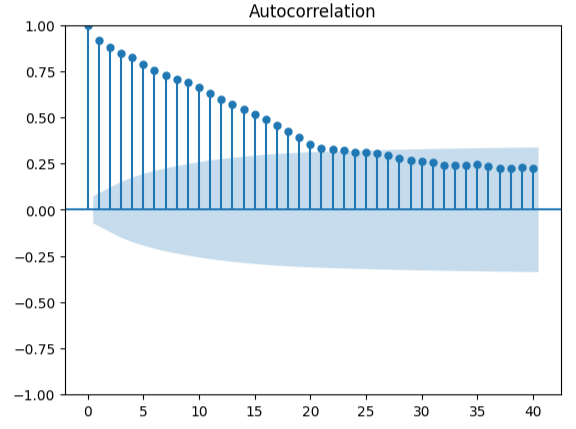
図18:モデルの残差を視覚化する
ONNXへのエクスポートの準備
データをONNX形式にエクスポートする前に、まず各列の平均値と標準偏差をデータフレームに保存します。データを変化率に変換しても改善は得られなかったため、代わりに元の形式のデータを使用して、それをZスコアの計算に使用することに注意してください。
#Prepare to convert the model to ONNX format scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"]) for i in X.columns: scale_factors.loc["mean",i] = merged_data.loc[:,i].mean() scale_factors.loc["std",i] = merged_data.loc[:,i].std() merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i] scale_factors

図19:Zスコアを含むデータフレーム
データをCSV形式で書き出します。
#Save the scale factors to CSV format scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")
ONNXへのエクスポート
ONNXは、開発者がONNX APIをサポートする任意のプログラミング言語で機械学習モデルを構築および展開できるようにするオープンソースプロトコルです。まず必要なライブラリをインポートします。
# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType最後にモデルを初期化します。
#Initialize the model model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
保有するすべてのデータにモデルを適合させます。
# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])モデルの出力形状を定義します。
# Define the input type initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]
モデルのONNXグラフ表現を作成します。
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
ONNXモデルを保存します。
# Save the ONNX model onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")
Netronでモデルを視覚化する
モデルを視覚化することで、仕様に従ってモデルが作成されていることを検証できます。入力と出力の形状が期待どおりであるかどうかを検証します。Netronは、機械学習モデルを視覚化するためのオープンソースライブラリです。始めるにはライブラリをインポートしましょう。
import netron
これで、DNN回帰を簡単に視覚化できるようになりました。
netron.start("FRED EURUSD D1.onnx")
図20:DNN回帰モデルの視覚化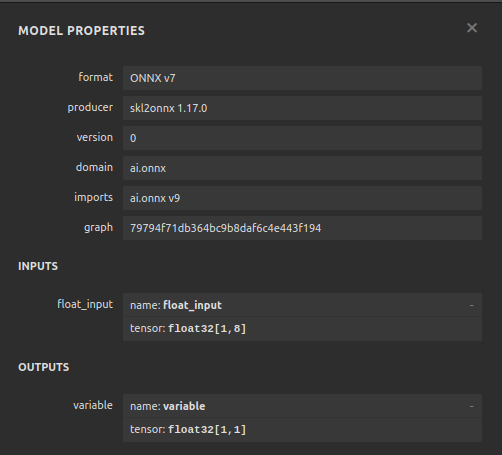
図21:モデルの入力と出力の形状を視覚化する
MQL5での実装
エキスパートアドバイザー(EA)に統合する必要がある最初のコンポーネントはONNXモデルです。EAのリソースとしてONNXファイルを単純に含めます。
//+------------------------------------------------------------------+ //| FRED EURUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/ja/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/ja/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];
次に、ポジションの管理に必要な取引ライブラリをロードします。
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
プログラム全体で必要となるグローバル変数を作成します。
//+------------------------------------------------------------------+ //| Define global variables | //+------------------------------------------------------------------+ long model; double mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349}; double std_values[5] = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997}; vectorf model_output = vectorf::Zeros(1); vectorf model_inputs = vectorf::Zeros(8); int model_sate = 0; int system_sate = 0; double bid,ask;
モデルが初めてロードされるときは、まずONNXモデルをロードして、それが動作するかどうかをテストしてみましょう。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_model()) { //--- We failed to load the ONNX model return(INIT_FAILED); } //--- Test if we can get a prediction from our model model_predict(); //--- Eveything went fine return(INIT_SUCCEEDED); }
モデルがチャートから削除されると、使用しなくなったリソースも解放されます。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we no longer need release_resources(); }
新しい価格を受け取るたびに、現在の市場価格を保存するために割り当てた変数を更新します。同様に、ポジションがない場合は、モデルの指示に従います。一方、すでにポジションを開いている場合は、モデルが反転の可能性について警告し、それに応じてポジションをクローズします。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update our bid and ask prices update_market_prices(); //--- Fetch an updated prediction from our model model_predict(); //--- If we have no trades, follow our model's directions. if(PositionsTotal() == 0) { //--- Our model is predicting price levels will appreciate if(model_sate == 1) { Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = 1; } //--- Our model is predicting price levels will deppreciate if(model_sate == -1) { Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = -1; } } //--- Otherwise Manage our open positions else { if(system_sate != model_sate) { Alert("AI System Detected A Reversal! Closing All Positions on EURUSD"); Trade.PositionClose("EURUSD"); } } } //+------------------------------------------------------------------+
この関数は、現在の市場価格を追跡する変数を更新します。
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
ここで、リソースをリリースする方法を定義します。
//+------------------------------------------------------------------+ //| Release the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(model); ExpertRemove(); }
上記で作成したバッファからONNXモデルを作成する関数を定義しましょう。この関数がいずれかの時点で失敗すると、falseが返され、初期化手順が中断されます。
//+------------------------------------------------------------------+ //| Create our ONNX model from the buffer we defined above | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from the buffer we defined model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model was not illdefined if(model == INVALID_HANDLE) { //--- We failed to define our model Comment("We failed to create our ONNX model: ",GetLastError()); return false; } //---- Define the model I/O shape ulong input_shape[] = {1,8}; ulong output_shape[] = {1,1}; //--- Validate our model's I/O shapes if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape)) { Comment("Failed to define our model I/O shape: ",GetLastError()); return(false); } //--- Everything went fine! return(true); }
これは、モデルから予測を取得する関数です。この関数は、まずEURUSD市場データクオートを取得して正規化し、その後、現在のFRED代替データを読み取るルーチンを呼び出します。
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 5 inputs will be fetched from the market matrix eur_usd_ohlc = matrix::Zeros(1,5); eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } } //+------------------------------------------------------------------+
この関数は、MQL5\Filesディレクトリから FRED代替データを読み取ります。CSVファイルはPythonスクリプトによって毎日更新されることを思い出してください。
//+------------------------------------------------------------------+ //| This function will read in our FRED data | //+------------------------------------------------------------------+ bool read_fred_data(void) { //--- Read in the file string file_name = "FRED EURUSD ALT DATA.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 20) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { model_inputs[5] = (float) value; } if(counter == 5) { model_inputs[6] = (float) value; } if(counter == 7) { model_inputs[7] = (float) value; } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast: ",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } //--- Everything went fine return(true); } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); return false; } //--- Something went wrong return false; }
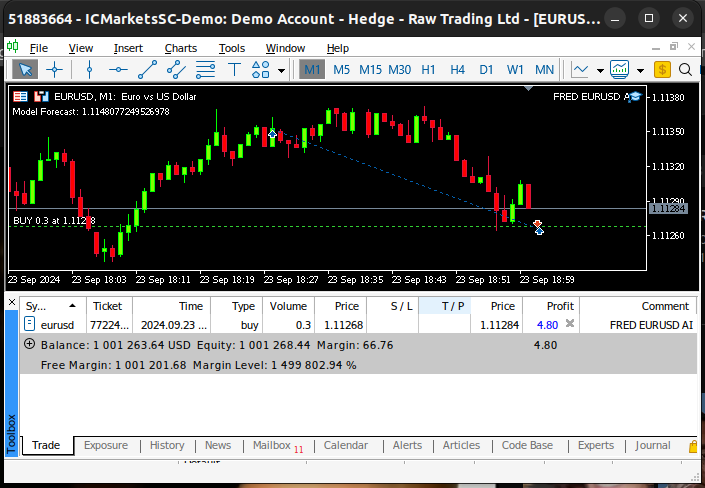
図22:アルゴリズムのフォワードテスト
結論
この記事では、広義の日次ドル指数はEURUSDペアを予測する際にあまり役に立たない可能性があること、あるいは、真の関係を効果的に学習する前に銘柄をさらに変換する必要がある可能性があることを示しました。あるいは、関係性をうまく捉える可能性を最大化するために、より多様なモデルをテストすることも検討できます。サポートベクターマシンなどのモデルは、高次元空間での決定境界の学習を必要とする問題で優れたパフォーマンスを発揮する傾向があります。まだ調査していないデータセットが何十万もあります。しかし残念ながら、今日は市場の他の企業に対して優位に立つことができませんでした。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15949
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 MetaTraderとGoogleスプレッドシートを使用して取引ジャーナルを作成する方法
MetaTraderとGoogleスプレッドシートを使用して取引ジャーナルを作成する方法
 MQL5-Telegram統合エキスパートアドバイザーの作成(第7回):チャート上のインジケーター自動化のためのコマンド解析
MQL5-Telegram統合エキスパートアドバイザーの作成(第7回):チャート上のインジケーター自動化のためのコマンド解析
 データサイエンスとML(第30回):株式市場を予測するパワーカップル、畳み込みニューラルネットワーク(CNN)と再帰型ニューラルネットワーク(RNN)
データサイエンスとML(第30回):株式市場を予測するパワーカップル、畳み込みニューラルネットワーク(CNN)と再帰型ニューラルネットワーク(RNN)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
