在任何市场中获得优势(第五部分):联邦储备经济数据库(FRED)欧元兑美元( EURUSD)可替代数据
在本系列文章中,我们的目标是帮助您在不断增长的可替代金融数据领域中找到方向。生活在大数据时代的现代投资者,可能没有足够的资源来审慎决定应该在交易过程中包含哪些可替代数据集。我们的目标是为您提供所需的信息,帮助您在充分知情的情况下做出决策,判断哪些可替代数据集您可能应该纳入考量,而哪些数据集或许不纳入会更为妥当。
交易策略概述
相关性是金融分析方法中的一个核心基础原则。如果两项资产之间存在相关性,那么寻求分散投资组合风险或最大化其对预期价格变动敞口的投资者,可以明智地利用这一指标来构建其投资组合。
联邦储备系统维护了一系列指数,这些指数作为美元外汇价值的综合衡量指标。在所有可用的指数中,我们特别关注名义广义美元指数(NBDD)。该指数于2006年1月设立,初始值为100点。截至本文撰写时,该指数在2008年经济衰退期间创下约86点的历史新低,并在2022年达到大约128点的历史新高。自2011年底以来,该指数一直处于看涨趋势,目前徘徊在121点左右。这一数值接近其历史高点。
在以下图表中,我们将广义美元指数和欧元兑美元汇率进行了叠加。但几乎不可能在这两个时间序列数据之间看到任何实质性关系。美元汇率几乎被隐藏在图表底部的蓝色水平线中,而广义美元指数则是清晰可见的红色线条。
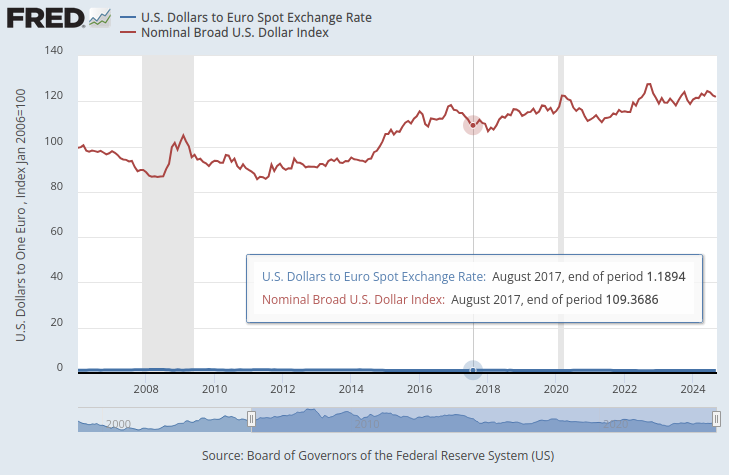
图1:美元兑欧元即期汇率与广义美元指数
如果我们确保这两个时间序列数据在同一尺度上,一个明显的模式就会出现。我们将改变y轴,使其记录时间序列数据在过去一年中的百分比变化。当执行这一步骤时,我们可以清楚地观察到,该指数与欧元兑美元外汇汇率显示出近乎完美的负相关性。
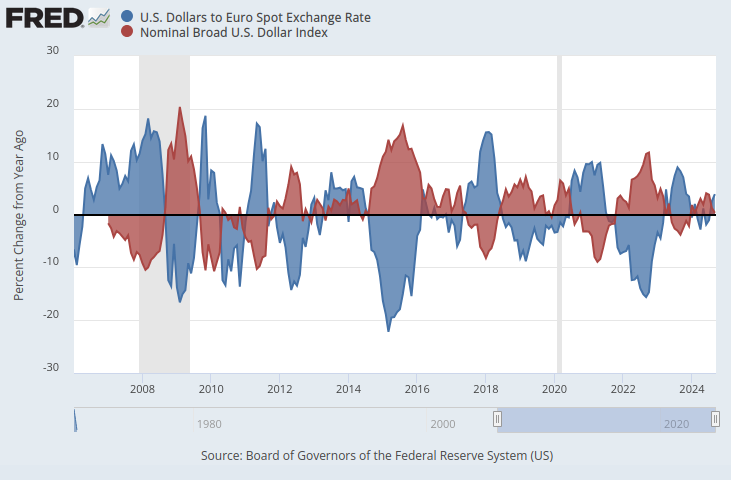
图2:以百分比形式表示的美元兑欧元即期汇率与广义美元指数
我们将探索使用这些数据集算法化学习交易策略的可行性,这些策略可以用来预测欧元兑美元未来的汇率。鉴于近乎完美的负相关性,我们的模型或许能够从FRED提供的宏观经济指标中学习到有关汇率的信息。
方法论概述
为了验证我们的假设,我们首先从MetaTrader 5终端获取欧元兑美元的历史日汇率数据,并将这些数据与我们通过FRED的Python应用程序接口(API)获取的3个宏观经济数据集合并。这3个FRED时间序列数据集记录的是:
- 美国债券利率
- 美国预期通货膨胀率
- 广义美元指数
这使我们能够创建3个数据集来构建我们的人工智能(AI)模型:
- 普通的OHLC市场价格数据。
- 可替代的FRED数据。
- 前两个数据集的超集。
在合并所有相关数据集并转换尺度以复制我们在FRED网站上所做的操作后,我们观察到欧元兑美元汇率与广义美元指数之间的相关性水平接近-0.9。这是一个近乎完美的分数!不仅如此,我们还观察到广义美元指数的当前值与欧元兑美元收盘价20天后的未来值之间的相关性为-0.7。
通过可视化处理,我们能够非常出色地对时间序列数据进行分离,其精细程度令我怀疑在之前此系列文章中是否曾展现过这样的水准。使用相对较长的时间窗口计算数据的百分比变化,似乎能够让我们非常有效地分离数据。我们的3D散点图进一步验证了数据分离得非常好,能够识别出明显的看涨和看跌区域。此外,当我们使用官方FRED网站上的散点图绘制数据时,可以清楚地观察到数据的趋势。即使没有使用我们通常在Python中使用的高级分析工具,散点图中的趋势也定义得很好。这让我们相信,这两个时间序列数据集之间可能共享了一些潜在的信息,我们希望模型能够学习到这些信息。
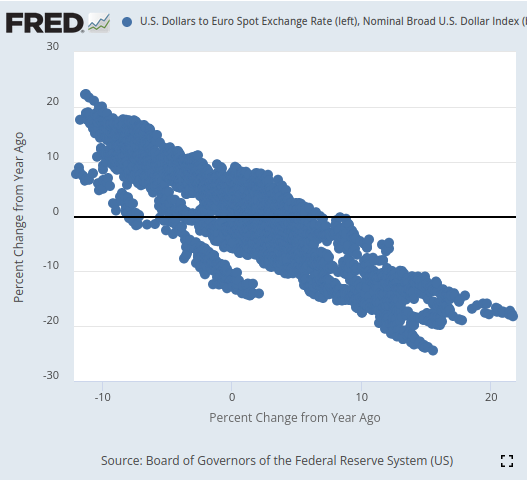
图3:可视化我们感兴趣的两个数据集的散点图
尽管到目前为止,这一切听起来都颇具前景,但就提升我们预测欧元兑美元汇率未来价值的能力而言,这些努力并未转化为实际的成效。事实上,我们的表现变得更糟,或许我们使用仅包含普通市场价格数据的第一个数据集反而会好一些。
我们训练了三个相同的深度神经网络(DNN)回归器,用来学习三个数据集与它们共同的目标之间的关系。第一个DNN模型产生了最低的误差率。此外,在选择用于分析的任何FRED数据集中,我们的特征选择算法似乎对其中任何一个数据集都未表现出特别关注或认可。尽管如此,我们还是成功地使用训练数据集调整了DNN模型的参数,而训练数据也没有过拟合。这表明我们在未见的验证数据上表现优于默认的DNN模型。我们在训练和验证中使用了时间序列交叉验证,而没有随机打乱数据,从而得出了这些结论。
在将模型导出为ONNX格式之前,我们检查了模型的残差,以确保模型处于良好状态。遗憾的是,我们从模型中观察到的残差表现不佳,这可能表明模型未能有效地学习。
最后,我们将模型导出为ONNX格式,并使用Python和MQL5构建了一个集成AI的EA。
获取数据
开始之前,我们首先导入了我们需要的Python库。
#Import the libraries we need from fredapi import Fred import seaborn as sns import numpy as np import pandas as pd import MetaTrader5 as mt5 import matplotlib.pyplot as plt
然后我们定义了证书以及希望从FRED获取的时间序列数据。
#Define important variables fred_api = "ENTER YOUR API KEY" fred_broad_dollar_index = "DTWEXBGS" fred_us_10y = "DGS10" fred_us_5y_inflation = "T5YIFR"
登录FRED。
#Login to fred
fred = Fred(api_key=fred_api)让我们获取所需的数据。
#Fetch the data
dollar_index = fred.get_series(fred_broad_dollar_index)
us_10y = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)为这些序列命名,使我们能够在后续操作中将它们合并。
#Name the series so we can merge the data dollar_index.name = "Dollar Index" us_10y.name = "Bond Interest" us_5y_inflation.name = "Inflation"
用滚动平均值填补任何缺失值。
#Fill in any missing values dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True) us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True) us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
在从我们的MetaTrader 5终端获取数据之前,我们首先需要对其进行初始化。
#Initialize the terminal
mt5.initialize()我们希望获取4年的历史数据。
#Define how much data to fetch amount = 365 * 4 #Fetch data eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount)) eur_usd
将时间列从秒格式转换为实际日期。
#Convert the time column eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')
确保时间列是我们数据的索引。
#Set the column as the index
eur_usd.set_index('time',inplace=True)定义我们想要预测多久之后的未来数据。
#Define the forecast horizon look_ahead = 20
现在,让我们来指定预测变量(自变量)和目标变量(因变量)。
#Define the predictors predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] ohlc_predictors = ["open","high","low","close","tick_volume"] fred_predictors = ["Dollar Index","Bond Interest","Inflation"] target = "Target" all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
合并数据。
#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)标记数据。
#Define the target target = merged_data.loc[:,"close"].shift(-look_ahead) target.name = "Target"
对数据进行格式化处理,使其像我们在FRED网站上分析的数据一样,展示年百分比变化。
#Convert the data to yearly percent changes merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100 merged_data = merged_data.merge(target,right_index=True,left_index=True) merged_data.dropna(inplace=True) merged_data
添加一个二进制目标变量,实现绘图目的。
#Add binary targets for plotting purposes merged_data["Binary Target"] = 0 merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1
重置数据索引。
#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_data探索性数据分析
我们首先将重新创建在圣路易斯联邦储备银行网站上生成的图表,这将验证是否按照预期执行了预处理步骤。
#Plotting our data set plt.title("EURUSD Close Against FRED Broad Dollar Index") plt.plot(merged_data.loc[:,"close"]) plt.plot(merged_data.loc[:,"Dollar Index"])
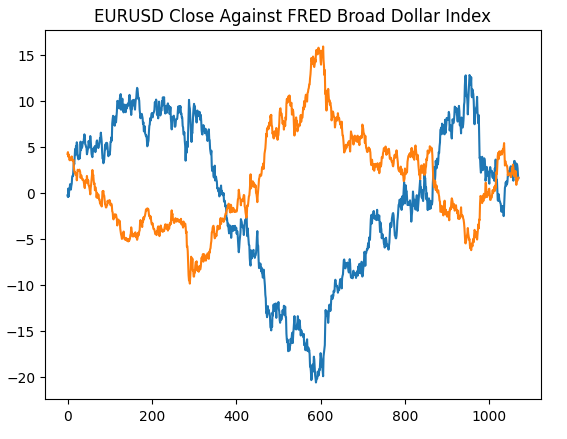
图4:在Python中重现我们在FRED网站上的观察结果
现在让我们分析数据集中的相关性水平。正如我们所观察到的,通货膨胀数据集在获取的3个替代FRED数据集中相关性水平最弱。然而,尽管我们剩下的2个可替代数据集看起来潜力巨大,但并没有获得任何性能提升。
#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)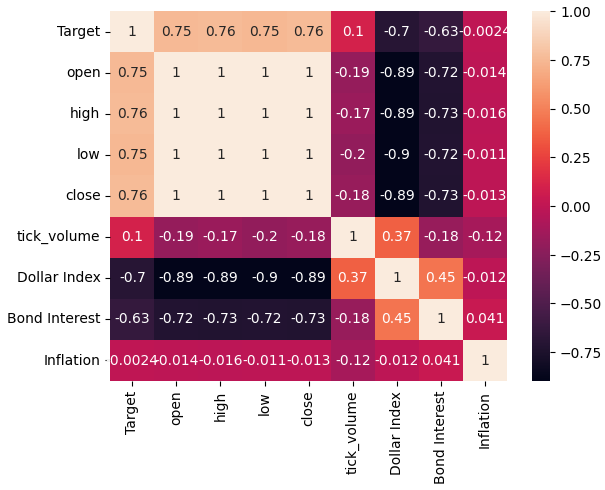
图5:我们的相关性热力图
当同时查看大量数据集时,成对散点图可以帮助我们快速了解所拥有的全部数据之间可能存在的关系。我们可以清楚地看到,橙色和蓝色的点似乎被非常清晰地分隔开来。此外,我们在这个图的主对角线上还有核密度估计(KDE)图。KDE图帮助我们可视化每列数据的分布情况。我们观察到的两个类似山丘形状的部分在小范围内重叠,这意味着数据在很大程度上是很好地分隔开的。
sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")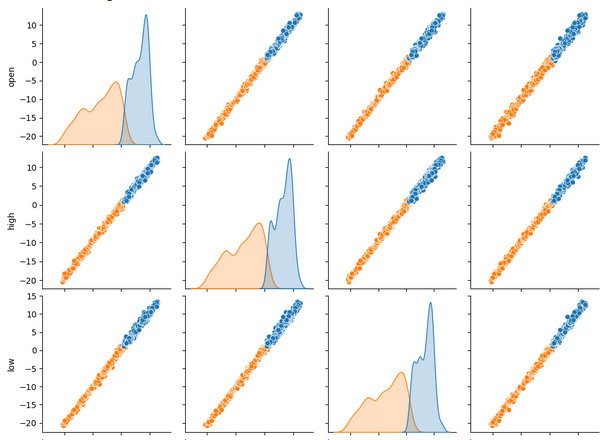
图6:使用成对散点图可视化我们的数据
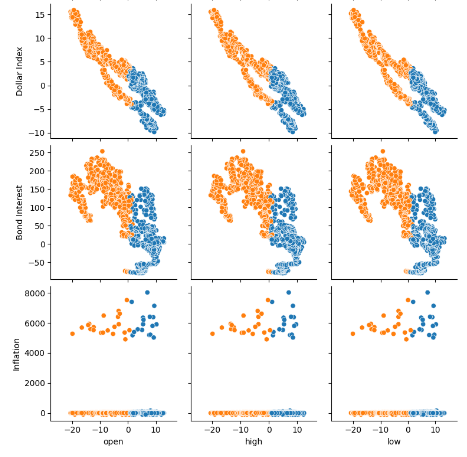
图7:可视化我们的FRED可替代数据及其与欧元兑美元货币对的关系
现在我们将使用广义美元指数和债券利率作为x轴和y轴,欧元兑美元收盘价作为z轴,进行3D散点图绘制。数据似乎分为两个不同的簇,几乎没有重叠。这自然意味着可能存在一个决策边界,我们的模型可以从数据中学习。遗憾的是,我认为未能有效地将这一点传递给我们的模型。
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"]) ax.set_xlabel("Dollar Index") ax.set_ylabel("Bond Interest") ax.set_zlabel("EURUSD close")
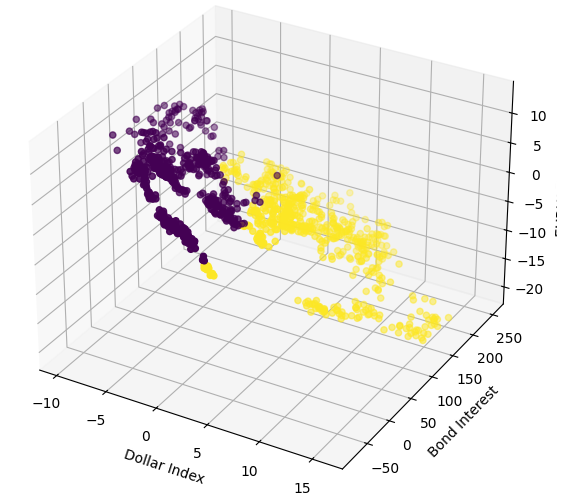
图8:以3D方式可视化我们的市场数据
准备建模数据
现在让我们准备好对金融数据进行建模,我们将从定义模型的输入和目标开始。
#Let's define our set of predictors X = merged_data.loc[:,predictors] y = merged_data.loc[:,"Target"]
导入我们所需的库。
#Import the libraries we need
from sklearn.model_selection import train_test_split现在,我们将把数据分为前面概述的3组。
#Partition the data ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)
创建一个数据结构来存储我们模型的交叉验证准确率。
#Prepare the dataframe to store our validation error validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))
数据建模
让我们导入对数据进行建模所需的库。
#Let's cross validate our models from sklearn.neural_network import MLPRegressor from sklearn.model_selection import cross_val_score
定义我们之前概述的三个神经网络。
#Define the neural networks ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
测试每个模型。
#Let's obtain our cv score ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
存储我们的交叉验证得分。
for i in np.arange(0,5): validation_error.iloc[i,0] = ohlc_score[i] validation_error.iloc[i,1] = fred_score[i] validation_error.iloc[i,2] = all_score[i]
可视化验证误差。
#Our validation error
validation_error| MetaTrader 5数据 | FRED可替代数据 | 全部数据 |
|---|---|---|
| -0.147973 | -0.79131 | -4.816608 |
| -0.103913 | -2.073764 | -0.655701 |
| -0.211833 | -0.276794 | -0.838832 |
| -0.094998 | -1.954753 | -0.259959 |
| -1.233912 | -2.152471 | -3.677273 |
通过对所有5折交叉验证的平均表现进行分析表明,来自MetaTrader 5的普通市场数据可能是我们的最优选择。
#Our mean performane across all groups
validation_error.mean()| 输入数据 | 平均5折误差 |
|---|---|
| MetaTrader 5 | -0.358526 |
| FRED | -1.449818 |
| 全部 | -2.049675 |
当绘制模型的性能时,我们可以观察到MetaTrader 5数据产生了更一致的误差水平。
#Plotting our performance
validation_error.plot()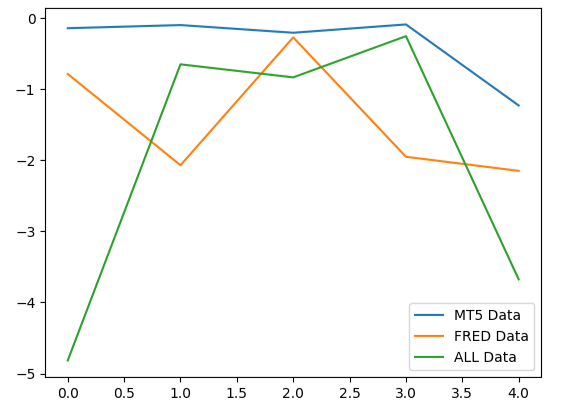
图9:可视化我们选择的三个数据集所产生的三种不同的误差水平
MetaTrader 5误差箱线图的扁平形状是理想的,因为它表明模型通过其一致的表现展示了技能。
#Creating box-plots of our performance
sns.boxplot(validation_error)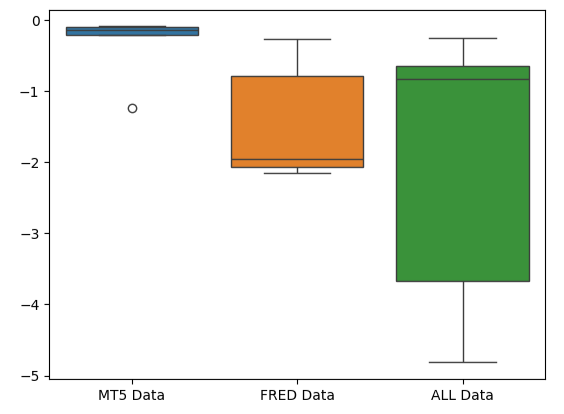
图10:以箱线图的形式可视化我们模型的误差指标
特征的重要性
让我们来分析哪些特征可能对我们的深度神经网络(DNN)模型最重要。希望我们选择的可替代数据是有用的,这样一来,我们的特征重要性算法就会认定其确实如此。遗憾的是,我们的分析表明,MetaTrader 5的市场数据本身似乎就能很好地解释目标变量。因此,我们的模型无法从已有数据中推断出来的任何附加信息,FRED时间序列中都没有包含。
开始之前,让我们导入我们需要的库。
#Feature importance
from alibi.explainers import ALE, plot_ale累积局部效应(ALE)图帮助我们可视化每个模型输入对目标变量的影响。ALE图因其在解释高度相关数据(如我们的数据)上训练的模型方面表现出色而被广泛使用。传统的学术方法,如部分依赖(PD)图,在解释具有强相关性的预测变量时并不可靠。该算法的原始规范可以在丹尼尔·W·阿普利(Daniel W. Apley)和朱静宇(Jingyu Zhu)于2016年发表的完整研究论文中找到,论文链接在这里。

图11:ALE算法的共同创造者丹尼尔·W·阿普利
让我们将ALE解释器拟合到DNN回归器上。
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])
现在我们可以获得每个预测变量对目标影响的解释。ALE图具有直观的可视化解析,使其成为很好的起点。简单来说,如果我们获得的ALE图是一条水平线,那么从DNN模型的角度来看,正在观察的预测变量对目标几乎没有影响。同样地,ALE图离线性越远,我们的模型学习到的目标与预测变量之间的关系就越可能远离简单的线性关系。
图12左上角的开盘价与目标的ALE图表明,随着欧元兑美元开盘价的增加,模型已经学会未来收盘价也会增加。观察开盘价和收盘价的ALE图如何朝相反方向变化。这可能表明,仅这两个预测变量就可能解释目标变量的显著方差。
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)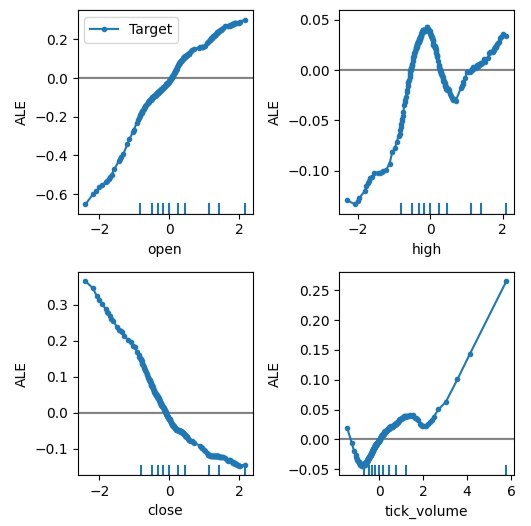
图12:在MetaTrader 5市场数据上可视化我们的ALE图
现在我们将执行正向选择。该算法从一个空模型开始,并逐步添加一个能够最大程度提升模型性能的特征,直到模型性能无法再提升为止。
#Forward selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
初始化模型。
#Reinitialize the model all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
现在我们需要指定想要的正向选择的对象。我们将指使该算法实例选择它认为重要且尽可能多的变量。
#Define the feature selector sfs1 = SFS(all_nn, k_features=(1,X.shape[1]), forward=True, scoring='neg_mean_squared_error', cv=5, n_jobs=-1 )
算法没有选择任何FRED时间序列数据。
#Best features we identified
sfs1.k_feature_names_我们来可视化算法的选择过程。我们的图表清楚地显示出,随着模型参数的增加,模型的性能却在下降。
#Fit the forward selection algorithm fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')
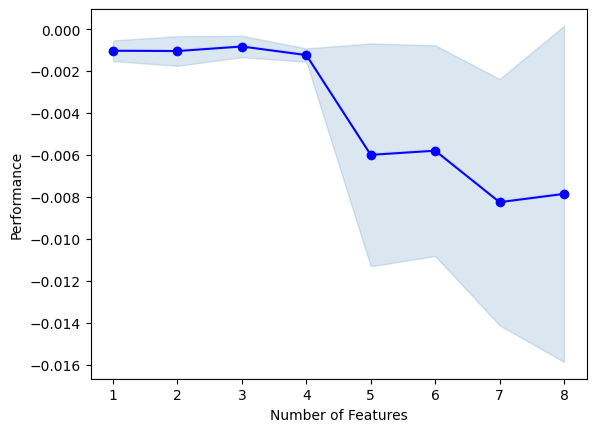
图13:随着我们逐步增加更多的预测变量,进而可视化模型性能
参数调整
让我们使用随机搜索对DNN模型进行参数调整。首先,我们需要初始化模型。
#Reinitialize the model model = MLPRegressor(max_iter=500)
现在我们将定义调优参数。
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
"early_stopping":[True,False],
"warm_start":[True,False],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)安装调优对象。
#Fit the tuner
tuner.fit(train_X,train_y)让我们看一下已找到的最优参数。
#The best parameters we found
tuner.best_params_'tol': 1e-05,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes': (10, 20, 40, 80),
'early_stopping': True,
'alpha': 0.1,
'activation': 'relu'}
更深入的参数优化
让我们使用SciPy库来寻找更好的模型参数。我们可以将优化过程想象成搜索问题,就好像儿时玩的捉迷藏游戏。您看,那些能让我们的模型在未见数据上产生最佳误差率的理想参数,就隐藏在可以为每个连续参数分配的无限可能值的空间中。
让我们导入所需的库。
#Deeper optimization from scipy.optimize import minimize from sklearn.metrics import mean_squared_error from sklearn.model_selection import TimeSeriesSplit
定义一个时间序列分割对象。
#Define the time series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
创建一个数据结构以返回当前成本,并创建一个列表来存储模型的进度以便可视化。
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) algorithm_progress = []
现在,我们将定义成本函数。SciPy的minimize库为我们提供了多种算法,用于找到函数的输入值,这些输入值将使函数的输出达到最小。我们将使用模型在训练数据上的5折交叉验证误差水平的平均值作为需要最小化的量,同时保持所有其他DNN参数不变。
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2] ) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Store the algorithm's progress algorithm_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
让我们为该过程定义起始点,并同时为参数指定界限。针对这个问题,我们唯一的界限就是所有模型参数都应为正数。
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100))
我们将使用截断牛顿约束(Truncated Newton Constrained,简称 TNC)算法来优化模型参数。截断牛顿法是一类适用于解决带边界约束的大型非线性优化问题的方法。SciPy库为我们提供了该算法的一个采用C语言实现的封装接口。
#Searching deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
让我们看一下是否成功终止。
#The result of our optimization
result成功:错误
状态:4
fun: 0.001911232280110637
x: [ 1.000e-100 1.000e-100 1.000e-100]
nit: 0
jac: [ 2.689e+06 9.227e+04 1.124e+05]
nfev: 116
看来我们在寻找最优输入时遇到了困难,那么可视化一下优化过程的性能表现。
#Store the optimal coefficients optimal_weights = result.x optima_y = min(algorithm_progress) optima_x = algorithm_progress.index(optima_y) inputs = np.arange(0,len(algorithm_progress)) #Plot the performance of our optimization procedure plt.scatter(inputs,algorithm_progress) plt.plot(optima_x,optima_y,'ro',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.xlabel("Iterations") plt.ylabel("Training MSE") plt.title("Minimizing Training Error")
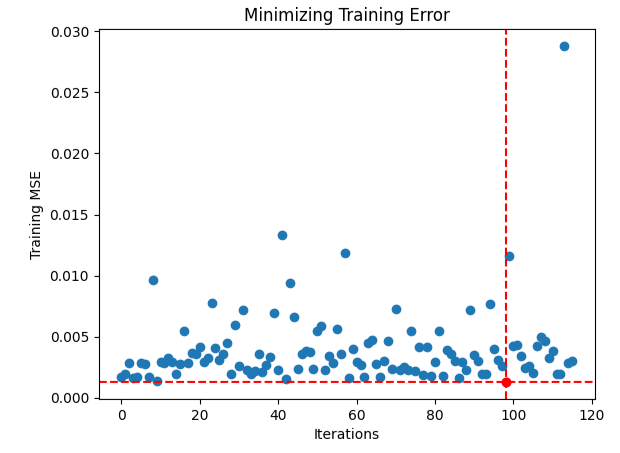
图 14:红色圆点代表由我们的TNC优化器估计的最优输入值
检测过拟合
让我们初始化三个模型,看看是否可以在训练集上对它们进行训练,并在测试数据方面超越默认模型的性能。回想一下,到目前为止,我们在决策过程中尚未使用过测试数据。
#Testing for overfitting default_nn = MLPRegressor(max_iter=500) #Randomized NN random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] ) #TNC NN tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2] )
在训练集上分别拟合每个模型。
#Store the models in a list models = [default_nn,random_search_nn,tnc_nn] #Fit the models for model in models: model.fit(train_X,train_y)
创建一个数据结构来存储我们的验证误差水平。
#Create a dataframe to store our validation error validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))
测试每个模型并记录其得分。
#Let's obtain our cv score default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) #Store the model error in a dataframe for i in np.arange(0,5): validation_error.iloc[i,0] = default_score[i] validation_error.iloc[i,1] = random_score[i] validation_error.iloc[i,2] = tnc_score[i]
让我们来看看验证误差。
#Let's see the validation error validation_error
| 默认模型 | 随机搜索 | TNC |
|---|---|---|
| -0.362851 | -0.029476 | -0.054709 |
| -0.323601 | -0.053967 | -0.087707 |
| -0.064432 | -0.024282 | -0.026481 |
| -0.121226 | -0.019693 | -0.017709 |
| -0.064801 | -0.012812 | -0.016125 |
在计算所有5折交叉验证的平均性能后,很明显可以看出我们的随机搜索模型是最优选择。
#Our best performing model
validation_error.mean()| 模型 | Average Validation Error |
|---|---|
| 默认模型 | -0.187382 |
| 随机搜索 | -0.028046 |
| TNC | -0.040546 |
绘制箱线图可以快速展示默认模型性能的变化范围。我们定制的模型能够保持在严格的误差水平范围内运行,这让我们对调优参数的选择更加有信心。
#Let's create box-plots sns.boxplot(validation_error)
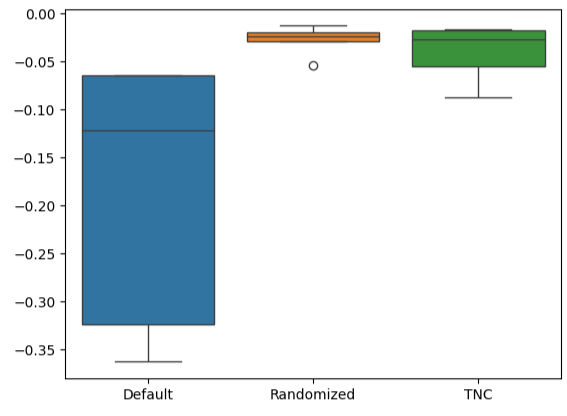
图 15:以箱线图形式可视化我们模型的性能
绘制交叉验证数据的折线图凸显了默认模型与我们调优后的模型之间的差异。我们可以看到,代表默认模型性能的蓝色折线与其他彩色折线之间存在显著的误差。
#We can also visualize model performance through a line plot
validation_error.plot()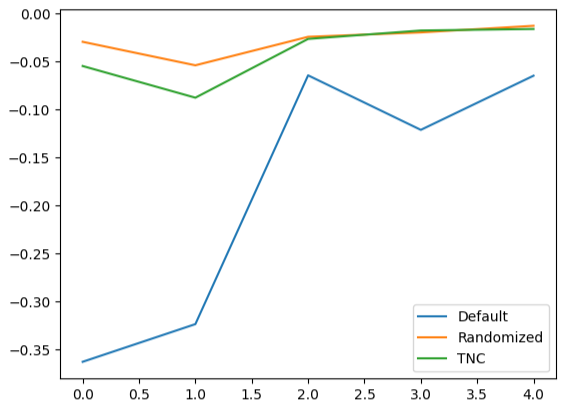
图 16:绘制不同模型在测试数据上的5折交叉验证性能
残差分析
我们不能盲目地相信我们的模型并将其投入生产。让我们通过检查模型的残差来尝试确保模型确实已经有效地学习。理想情况下,一个完美逼近函数的模型将具有一条平坦的残差线。这意味着模型的预测没有误差。此外,这也意味着模型预测中的误差量不会发生变化。
因此,我们的模型性能与理想情况的偏离程度越大,在理想的线性和平稳残差图中观察到的失真就越多。我们的模型残差显示出不同大小的误差,有时这些误差与之前的误差量相关。这可能是令人担忧的原因,或许可以通过转换预测变量或目标变量来解决。
让我们初始化模型。
#Resdiuals analysis model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
在训练数据上拟合模型,然后使用测试数据记录残差。
#Fit the model model.fit(train_X,train_y) #Record the residuals residuals = test_y - model.predict(test_X)
我们的残差图与理想情况相差甚远,可能需要探索其他预处理步骤来解决这一问题。
#Residuals analysis
residuals.plot()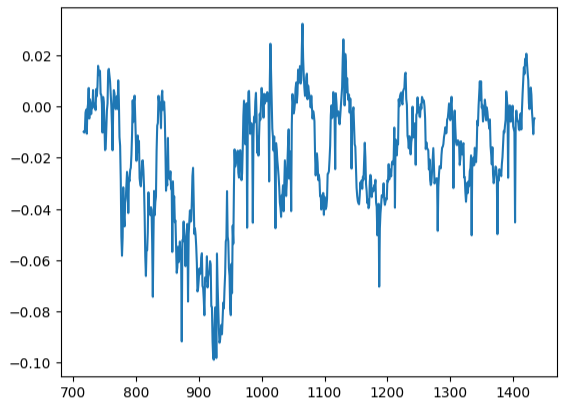
图 17:可视化模型在测试数据上的残差
测量自相关是一种可靠的方法,用于检测可能存在的虚假回归。遗憾的是,我们的模型残差也未能通过这项测试,这或许表明,如果我们能更好地对预测变量或目标变量进行转换,才有可能实现进一步的优化。
#Autocorrelation plot from statsmodels.graphics.tsaplots import plot_acf acf = plot_acf(residuals,lags=40)
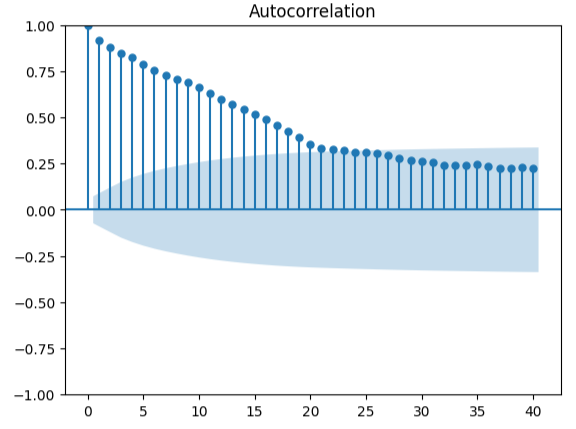
图 18:可视化我们模型的残差
准备导出为ONNX格式
在将数据导出为 ONNX 格式之前,让我们先将每列的均值和标准差存储到一个数据结构中。需要注意的是,由于将数据转换为百分比变化并没有带来任何改进,因此我们将使用数据的原始形式来进行z分数计算。
#Prepare to convert the model to ONNX format scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"]) for i in X.columns: scale_factors.loc["mean",i] = merged_data.loc[:,i].mean() scale_factors.loc["std",i] = merged_data.loc[:,i].std() merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i] scale_factors

图 19:包含我们z分数的数据结构
将数据写入 CSV 格式。
#Save the scale factors to CSV format scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")
导出到ONNX
ONNX 是一种开源协议,它允许开发者使用任何支持 ONNX API 的编程语言来构建和部署机器学习模型。我们将首先导入所需的库。
# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType最后一次初始化模型。
#Initialize the model model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
基于我们现有的全部数据拟合模型。
# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])定义我们模型的输出形状。
# Define the input type initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]
创建我们模型的ONNX图表。
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
保存ONNX模型。
# Save the ONNX model onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")
在Netron中可视化我们的模型
可视化我们的模型将有助于验证其是否按照我们的规范创建。我们希望验证输入和输出的形状是否符合预期。Netron是一个用于可视化机器学习模型的开源库。让我们从导入这个库开始。
导入netron
现在,我们可以轻松地可视化DNN回归器。
netron.start("FRED EURUSD D1.onnx")
图20:可视化我们的DNN回归器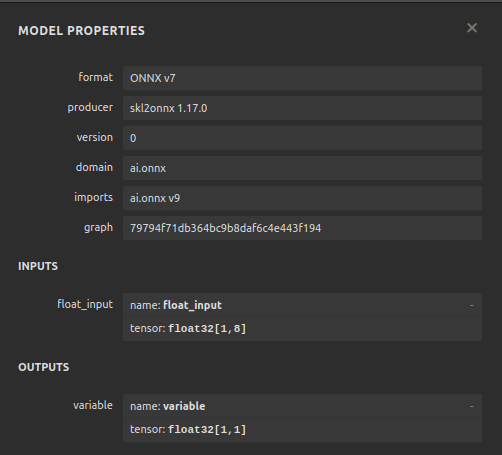
图21:可视化我们模型的输入和输出形状
在MQL5中的实现
我们需要整合到EA中的第一个组件将是ONNX模型。我们简单地将ONNX文件包含在EA的资源中。
//+------------------------------------------------------------------+ //| FRED EURUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];
现在,让我们加载用于管理仓位所需的交易库。
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
创建我们在整个程序中需要用到的全局变量。
//+------------------------------------------------------------------+ //| Define global variables | //+------------------------------------------------------------------+ long model; double mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349}; double std_values[5] = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997}; vectorf model_output = vectorf::Zeros(1); vectorf model_inputs = vectorf::Zeros(8); int model_sate = 0; int system_sate = 0; double bid,ask;
每当首次加载我们的模型时,我们先尝试加载我们的ONNX模型,然后测试其是否能正常工作。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_model()) { //--- We failed to load the ONNX model return(INIT_FAILED); } //--- Test if we can get a prediction from our model model_predict(); //--- Eveything went fine return(INIT_SUCCEEDED); }
如果将模型从图表中移除,我们也将释放不再使用的资源。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we no longer need release_resources(); }
每当接收到新的价格数据时,我们会更新已分配用于存储当前市场价格的变量。同样地,如果我们没有持仓,将遵循模型的指示。另一方面,如果我们已经有持仓,那么将允许模型提醒我们可能出现的反转信号,并据此平仓。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update our bid and ask prices update_market_prices(); //--- Fetch an updated prediction from our model model_predict(); //--- If we have no trades, follow our model's directions. if(PositionsTotal() == 0) { //--- Our model is predicting price levels will appreciate if(model_sate == 1) { Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = 1; } //--- Our model is predicting price levels will deppreciate if(model_sate == -1) { Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = -1; } } //--- Otherwise Manage our open positions else { if(system_sate != model_sate) { Alert("AI System Detected A Reversal! Closing All Positions on EURUSD"); Trade.PositionClose("EURUSD"); } } } //+------------------------------------------------------------------+
该函数将更新我们用于跟踪当前市场价格的变量。
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
现在,我们将定义释放资源的方式。
//+------------------------------------------------------------------+ //| Release the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(model); ExpertRemove(); }
让我们来定义一个函数,该函数负责根据前面创建的缓冲区来新建ONNX模型。如果该函数在任意时间点执行失败,它将返回 false,这样将中断我们的初始化流程。
//+------------------------------------------------------------------+ //| Create our ONNX model from the buffer we defined above | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from the buffer we defined model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model was not illdefined if(model == INVALID_HANDLE) { //--- We failed to define our model Comment("We failed to create our ONNX model: ",GetLastError()); return false; } //---- Define the model I/O shape ulong input_shape[] = {1,8}; ulong output_shape[] = {1,1}; //--- Validate our model's I/O shapes if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape)) { Comment("Failed to define our model I/O shape: ",GetLastError()); return(false); } //--- Everything went fine! return(true); }
这是负责从我们的模型中获取预测结果的函数。该函数将首先获取并标准化欧元兑美元的市场行情数据报价,然后再调用一个负责读取我们当前FRED可替代数据的程序。
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 5 inputs will be fetched from the market matrix eur_usd_ohlc = matrix::Zeros(1,5); eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } } //+------------------------------------------------------------------+
该函数将从MQL5\Files目录中读取我们的FRED可替代数据。回想一下,CSV文件将由我们的Python脚本每天更新。
//+------------------------------------------------------------------+ //| This function will read in our FRED data | //+------------------------------------------------------------------+ bool read_fred_data(void) { //--- Read in the file string file_name = "FRED EURUSD ALT DATA.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 20) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { model_inputs[5] = (float) value; } if(counter == 5) { model_inputs[6] = (float) value; } if(counter == 7) { model_inputs[7] = (float) value; } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast: ",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } //--- Everything went fine return(true); } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); return false; } //--- Something went wrong return false; }
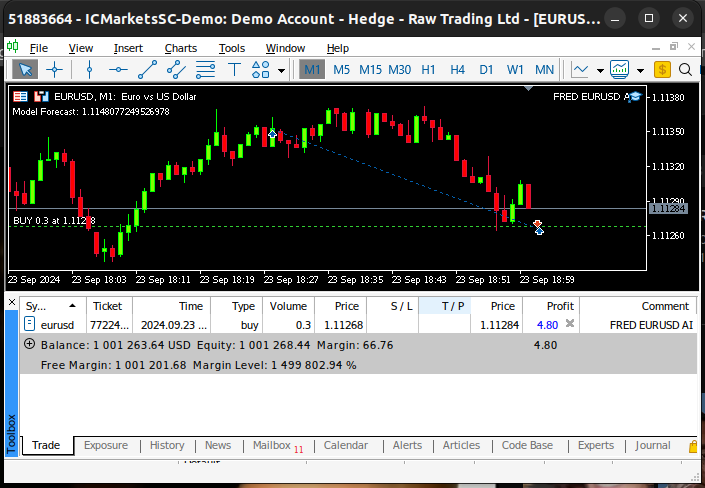
图22:对我们的算法进行前瞻性测试
结论
在本文中,我们展示了名义广义美元指数在预测欧元兑美元货币对时可能并没有明显效果,或者另一种可能是,在能够有效地学习到真实关系之前,该指标可能需要做更多的转换。或许,我们也可以考虑测试更广泛的模型,以最大化捕捉这种关系的可能性。诸如支持向量机(Support Vector Machines)之类的模型,在需要于高维空间中学习决策边界的问题上,往往表现出色。我们还有成千上万的数据集尚未探索。但遗憾的是,至今我们未能在市场上获得优势。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15949
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 美元和欧元指数图表 — MetaTrader 5 服务示例
美元和欧元指数图表 — MetaTrader 5 服务示例
 从基础到中级:BREAK 和 CONTINUE 语句
从基础到中级:BREAK 和 CONTINUE 语句
 您应当知道的 MQL5 向导技术(第 35 部分):支持向量回归
您应当知道的 MQL5 向导技术(第 35 部分):支持向量回归
