Verschaffen Sie sich einen Vorteil gegenüber jedem Markt (Teil V): FRED EURUSD Alternative Daten
In dieser Artikelserie möchten wir Ihnen helfen, sich in der ständig wachsenden Landschaft der alternativen Finanzdaten zurechtzufinden. Der moderne Anleger, der im Zeitalter von Big Data lebt, verfügt möglicherweise nicht über genügend Ressourcen, um sorgfältig zu entscheiden, welche alternativen Datensätze er in seinen Handelsprozess einbeziehen sollte. Unser Ziel ist es, Sie mit den Informationen zu versorgen, die Sie benötigen, um eine fundierte Entscheidung darüber zu treffen, welche alternativen Datensätze Sie möglicherweise in Betracht ziehen sollten und auf welche Sie vielleicht besser verzichten sollten.
Überblick über die Handelsstrategie
Die Korrelation ist ein Grundprinzip des analytischen Ansatzes im Finanzbereich. Wenn zwei Vermögenswerte korreliert sind, können Anleger, die entweder ihr Portfolio diversifizieren oder ihr Engagement in Bezug auf erwartete Preisänderungen maximieren wollen, diese Kennzahl auf intelligente Weise für den Aufbau ihres Portfolios nutzen.
Das Federal Reserve System unterhält eine Sammlung von Indizes, die als zusammenfassende Messgrößen für den Devisenwert des Dollars dienen. Von allen uns zur Verfügung stehenden Indizes interessierte uns besonders der Nominal Broad Dollar Daily Index (NBDD). Der Index wurde im Januar 2006 mit einem Wert von 100 Punkten eingeführt. Zum Zeitpunkt der Erstellung dieses Berichts erreichte der Index während der Rezession 2008 ein Rekordtief von etwa 86 Punkten und erreichte sein Allzeithoch von etwa 128 Punkten im Jahr 2022. Der Index befindet sich seit Ende 2011 in einem Aufwärtstrend und pendelt derzeit um 121 Punkte. Damit liegt er in der Nähe seines Allzeithochs.
In der folgenden Grafik haben wir den Broad Dollar Index und den Wechselkurs des EURUSD-Paares übereinander gelegt. Es ist fast unmöglich, eine wesentliche Beziehung zwischen den beiden Zeitreihen zu erkennen. Der US-Dollar-Wechselkurs ist als flache blaue Linie am unteren Rand des Diagramms fast unsichtbar, während der Broad Dollar Index die deutlich sichtbare rote Linie ist.
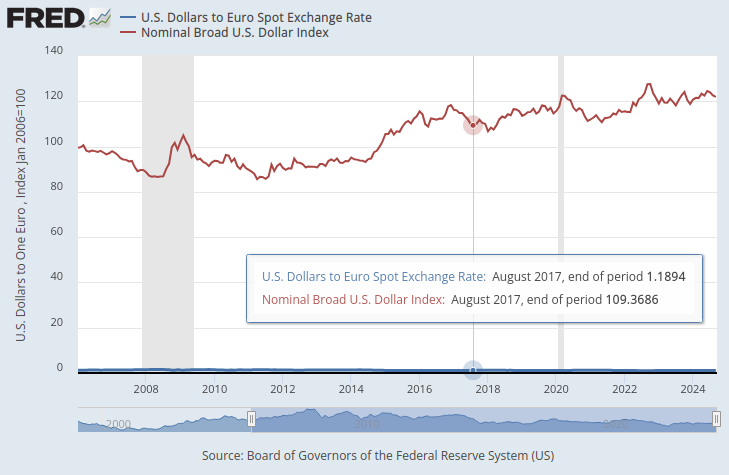
Abb. 1: Der Kassakurs von Dollar zu Euro und der Broad Dollar Index
Wenn wir sicherstellen, dass beide Zeitreihen auf der gleichen Skala liegen, ergibt sich ein offensichtliches Muster. Wir werden unsere y-Achse so ändern, dass sie die prozentuale Veränderung der Zeitreihendaten über ein Jahr erfasst. Wenn wir diesen Schritt durchführen, können wir eindeutig feststellen, dass der Index eine fast perfekte negative Korrelation zum EURUSD-Wechselkurs aufweist.
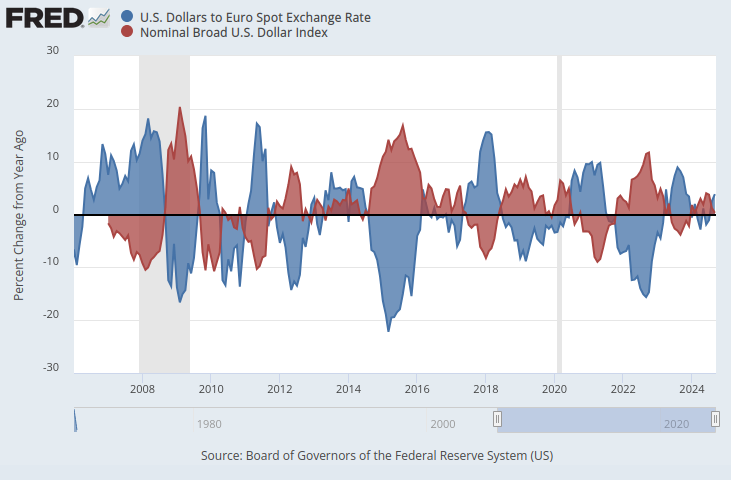
Abb. 2: Der Dollar-Euro-Kassakurs und der Broad Dollar Index in einer Prozentskala
Wir werden untersuchen, ob es möglich ist, eine Handelsstrategie algorithmisch zu erlernen, die diese Datensätze zur Vorhersage des künftigen Wechselkurses des EURUSD nutzt. In Anbetracht der perfekten negativen Korrelation könnte unser Modell aufgrund der makroökonomischen Indikatoren aus der Federal Reserve Economic Database (FRED) möglicherweise einige Informationen über den Wechselkurs erfahren.
Überblick über die Methodik
Um die Gültigkeit unseres Vorschlags zu testen, haben wir zunächst die täglichen historischen Wechselkurse für den EURUSD von unserem MetaTrader 5-Terminal abgerufen und die Daten mit drei makroökonomischen Datensätzen kombiniert, die wir von der FRED Python API abgerufen haben. Die 3 FRED-Zeitreihendaten wurden aufgezeichnet:
- Zinssätze für amerikanische Anleihen
- Erwartete Inflationsraten in den USA
- Broad Dollar Index
So konnten wir 3 Datensätze für die Erstellung unseres KI-Modells erstellen:
- Gewöhnliche OHLC-Marktnotierungen.
- Alternative FRED-Daten
- Eine Obermenge der ersten 2.
Nach der Zusammenführung aller fraglichen Datensätze und der Umstellung der Skalen auf die FRED-Website haben wir festgestellt, dass die Korrelation zwischen den Preisen des EURUSD-Wechselkurses und des Broad Dollar Index fast -0,9 beträgt. Das ist ein fast perfektes Ergebnis! Darüber hinaus haben wir festgestellt, dass die Korrelation zwischen dem aktuellen Wert des Broad Dollar Index und dem 20 Tage in der Zukunft liegenden Wert des EURUSD-Schlusskurses -0,7 beträgt.
Bei der Visualisierung waren wir in der Lage, die Zeitreihendaten bemerkenswert gut zu trennen, und zwar mit einer Finesse, die wir in dieser Artikelserie wohl noch nie gezeigt haben. Es scheint, dass die Verwendung der prozentualen Veränderung der Daten über relativ lange Zeitfenster eine sehr gute Trennung der Daten ermöglicht. Unsere 3D-Streudiagramme bestätigten zudem, wie gut die Daten voneinander getrennt waren, und wir konnten offensichtliche Auf- und Abwärtszonen identifizieren. Darüber hinaus konnten wir anhand von Streudiagrammen der Daten auf der offiziellen FRED-Website eindeutig einen Trend in den Daten erkennen. Der Trend im Streudiagramm war klar definiert, auch ohne dass wir unsere üblichen fortschrittlichen Analysetools in Python verwenden mussten. Dies gab uns die Zuversicht, dass die beiden Zeitreihendatensätze einige potenzielle Informationen gemeinsam haben könnten, die unser Modell hoffentlich lernen kann.
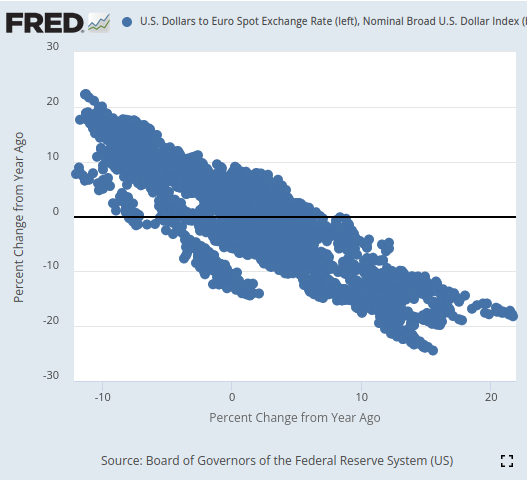
Abb. 3: Visualisierung eines Streudiagramms für die 2 Datensätze, die uns interessieren
So vielversprechend das alles auch klingen mag, nichts davon hat sich in einer verbesserten Leistung bei der Vorhersage des zukünftigen Wertes des EURUSD-Wechselkurses niedergeschlagen. Tatsächlich hat sich unsere Leistung nur verschlechtert, und es scheint, dass wir mit dem ersten Datensatz, der nur gewöhnliche Marktnotierungen enthielt, besser dran waren.
Wir haben 3 identische Deep Neural Network (DNN) Regressoren trainiert, um die Beziehung zwischen unseren 3 Datensätzen und dem gemeinsamen Ziel zu erlernen, das sie alle teilen. Das erste DNN-Modell wies die niedrigste Fehlerquote auf. Darüber hinaus zeigte sich keiner unserer Algorithmen zur Merkmalsauswahl von einem der FRED-Datensätze beeindruckt, die wir für unsere Analyse ausgewählt hatten. Wir ließen uns nicht entmutigen und konnten die Parameter unseres DNN-Modells mithilfe des Trainingsdatensatzes abstimmen, ohne die Trainingsdaten zu stark anzupassen. Darauf deutet die Tatsache hin, dass wir das Standard-DNN-Modell bei ungesehenen Validierungsdaten übertroffen haben. Wir haben die Zeitserien-Kreuzvalidierung ohne zufälliges Mischen verwendet, um diese Entscheidungen in Training und Validierung zu treffen.
Bevor wir unser Modell in das ONNX-Format exportiert haben, haben wir die Residuen unseres Modells überprüft, um sicherzustellen, dass unser Modell in einem guten Zustand ist. Leider waren die Residuen, die wir bei unserem Modell beobachtet haben, stark fehlerhaft, was darauf hindeuten könnte, dass unser Modell nicht effektiv gelernt hat.
Schließlich haben wir unser Modell in das ONNX-Format exportiert und mit Python und MQL5 einen integrierten KI-gestützten Expert Advisor erstellt.
Abrufen der Daten
Um loszulegen, haben wir zunächst die benötigten Python-Bibliotheken importiert.
#Import the libraries we need from fredapi import Fred import seaborn as sns import numpy as np import pandas as pd import MetaTrader5 as mt5 import matplotlib.pyplot as plt
Dann haben wir unsere Anmeldedaten und die Zeitreihen, die wir von FRED abrufen möchten, festgelegt.
#Define important variables fred_api = "ENTER YOUR API KEY" fred_broad_dollar_index = "DTWEXBGS" fred_us_10y = "DGS10" fred_us_5y_inflation = "T5YIFR"
Melden wir uns bei FRED an
#Login to fred
fred = Fred(api_key=fred_api)und holen uns die benötigten Daten.
#Fetch the data
dollar_index = fred.get_series(fred_broad_dollar_index)
us_10y = fred.get_series(fred_us_10y)
us_5y_inflation = fred.get_series(fred_us_5y_inflation)Die Benennung der Serien ermöglicht es uns, sie später zusammenzuführen.
#Name the series so we can merge the data dollar_index.name = "Dollar Index" us_10y.name = "Bond Interest" us_5y_inflation.name = "Inflation"
Wir füllen alle fehlenden Werte mit dem gleitenden Durchschnitt auf.
#Fill in any missing values dollar_index.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True) us_10y.fillna(us_10y.rolling(window=5,min_periods=1).mean(),inplace=True) us_5y_inflation.fillna(dollar_index.rolling(window=5,min_periods=1).mean(),inplace=True)
Bevor wir Daten von unserem MetaTrader 5-Terminal abrufen können, müssen wir es zunächst initialisieren.
#Initialize the terminal
mt5.initialize()Wir möchten 4 Jahre historische Daten abrufen
#Define how much data to fetch amount = 365 * 4 #Fetch data eur_usd = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",mt5.TIMEFRAME_D1,0,amount)) eur_usd
und konvertieren die Zeitspalte vom Sekundenformat in das aktuelle Datum.
#Convert the time column eur_usd['time'] = pd.to_datetime(eur_usd.loc[:,'time'],unit='s')
Wir machen die Zeitspalte zum Index unserer Daten
#Set the column as the index
eur_usd.set_index('time',inplace=True)und legen fest, wie weit in die Zukunft wir vorausschauen möchten.
#Define the forecast horizon look_ahead = 20
Nun bestimmen wir unsere Prädiktoren und Ziele
#Define the predictors predictors = ["open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] ohlc_predictors = ["open","high","low","close","tick_volume"] fred_predictors = ["Dollar Index","Bond Interest","Inflation"] target = "Target" all_data = ["Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"] all_data_binary = ["Binary Target","open","high","low","close","tick_volume","Dollar Index","Bond Interest","Inflation"]
und führen die Daten zusammen.
#Merge our data
merged_data = eur_usd.merge(dollar_index,right_index=True,left_index=True)
merged_data = merged_data.merge(us_10y,right_index=True,left_index=True)
merged_data = merged_data.merge(us_5y_inflation,right_index=True,left_index=True)Kennzeichnung der Daten.
#Define the target target = merged_data.loc[:,"close"].shift(-look_ahead) target.name = "Target"
Wir formatieren die Daten so, dass sie die jährliche prozentuale Veränderung anzeigen, genau wie die Daten, die wir auf der FRED-Website analysiert haben,
#Convert the data to yearly percent changes merged_data = merged_data.loc[:,predictors].pct_change(periods = 365) * 100 merged_data = merged_data.merge(target,right_index=True,left_index=True) merged_data.dropna(inplace=True) merged_data
fügen ein binäres Ziel für die Darstellung hinzu.
#Add binary targets for plotting purposes merged_data["Binary Target"] = 0 merged_data.loc[merged_data["close"] < merged_data["Target"],"Binary Target"] = 1
und setzen den Index der Daten zurück.
#Reset the index
merged_data.reset_index(inplace=True,drop=True)
merged_dataExplorative Datenanalyse
Wir beginnen damit, das Diagramm, das wir auf der Website der St. Louis Federal Reserve erstellt haben, neu zu erstellen, um zu überprüfen, ob wir unsere Vorverarbeitungsschritte wie vorgesehen durchgeführt haben.
#Plotting our data set plt.title("EURUSD Close Against FRED Broad Dollar Index") plt.plot(merged_data.loc[:,"close"]) plt.plot(merged_data.loc[:,"Dollar Index"])
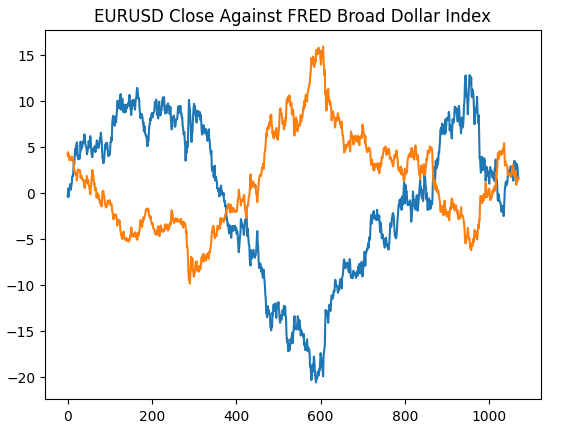
Abb. 4: Nachbildung unserer Beobachtung auf der FRED-Website in Python
Lassen Sie uns nun die Korrelationsniveaus innerhalb unseres Datensatzes analysieren. Wie wir feststellen können, weist der Inflationsdatensatz von allen 3 alternativen FRED-Datensätzen, die wir abgerufen haben, die geringsten Korrelationswerte auf. Wir konnten jedoch keine Leistungsverbesserungen erzielen, obwohl unsere verbleibenden 2 alternativen Datensätze so viel Potenzial zu haben schienen.
#Exploratory data analysis
sns.heatmap(merged_data.loc[:,all_data].corr(),annot=True)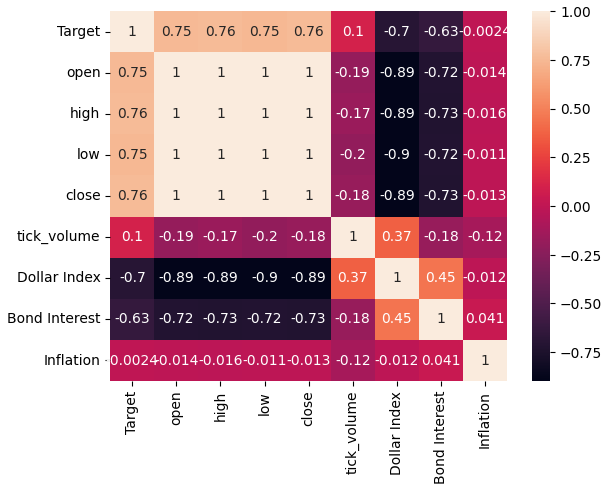
Abb. 5: Unsere Heatmap der Korrelationen
Bei der gleichzeitigen Betrachtung vieler Datensätze können uns Paar-Diagramme helfen, die Beziehungen zwischen allen verfügbaren Daten schnell zu erkennen. Es ist deutlich zu erkennen, dass die orangefarbenen und blauen Punkte bemerkenswert gut voneinander getrennt sind. Darüber hinaus haben wir Kernel-Dichte-Schätzungen (KDE), die entlang der Hauptdiagonale dieses Diagramms verlaufen. KDE-Diagramme helfen uns, die Verteilung der Daten innerhalb jeder Spalte zu visualisieren. Die Tatsache, dass wir zwei hügelartige Formen beobachten, die sich in einem kleinen Abschnitt überschneiden, deutet darauf hin, dass die Daten größtenteils gut voneinander getrennt sind.
sns.pairplot(merged_data.loc[:,all_data_binary],hue="Binary Target")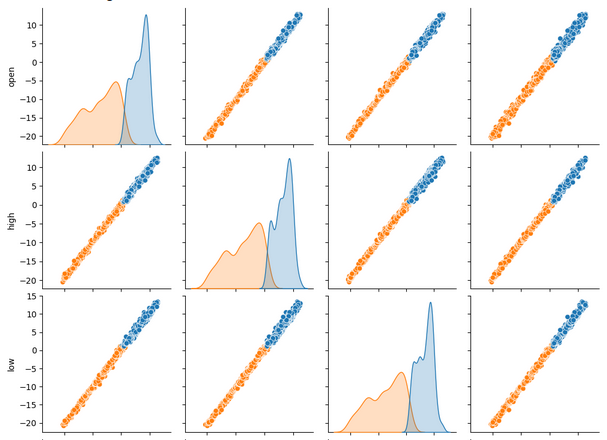
Abb. 6: Visualisierung unserer Daten mit Hilfe von Paar-Diagrammen
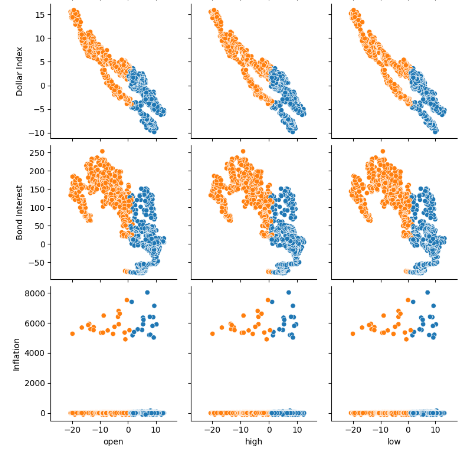
Abb. 7: Visualisierung unserer alternativen FRED-Daten und ihrer Beziehung zu unserem EURUSD-Paar
Wir werden nun 3D-Streudiagramme mit dem Broad Dollar Index und dem Anleihezins auf der x- und y-Achse und dem EURUSD-Schlusskurs auf der z-Achse erstellen. Die Daten scheinen sich in 2 verschiedenen Clustern zu befinden, die sich kaum überschneiden. Dies würde natürlich bedeuten, dass es eine Entscheidungsgrenze geben könnte, die unser Modell aus den Daten lernen könnte. Bedauerlicherweise haben wir es versäumt, dies unserem Modell wirksam zu vermitteln.
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["Dollar Index"],merged_data["Bond Interest"],merged_data["close"],c=merged_data["Binary Target"]) ax.set_xlabel("Dollar Index") ax.set_ylabel("Bond Interest") ax.set_zlabel("EURUSD close")
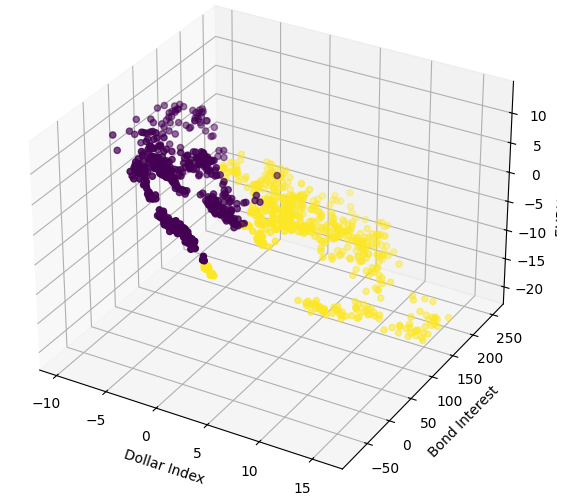
Abb. 8: Visualisierung unserer Marktdaten in 3D
Vorbereiten der Datenmodellierung
Beginnen wir nun mit der Modellierung der uns vorliegenden Finanzdaten, indem wir zunächst unsere Modelleingaben und unser Ziel definieren.
#Let's define our set of predictors X = merged_data.loc[:,predictors] y = merged_data.loc[:,"Target"]
Importieren der benötigten Bibliothek.
#Import the libraries we need
from sklearn.model_selection import train_test_splitNun werden wir unsere Daten in die 3 Gruppen aufteilen, die wir zuvor beschrieben haben.
#Partition the data ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,test_size=0.5,shuffle=False) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,test_size=0.5,shuffle=False) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,test_size=0.5,shuffle=False)
Erstellen wir einen Datenrahmen, um die Genauigkeit der Kreuzvalidierung unseres Modells zu speichern.
#Prepare the dataframe to store our validation error validation_error = pd.DataFrame(columns=["MT5 Data","FRED Data","ALL Data"],index=np.arange(0,5))
Modellierung der Daten
Importieren wir die Bibliotheken, die wir zur Modellierung der Daten benötigen.
#Let's cross validate our models from sklearn.neural_network import MLPRegressor from sklearn.model_selection import cross_val_score
Wir definieren die 3 neuronalen Netze, die wir zuvor skizziert haben,
#Define the neural networks ohlc_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) fred_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
und testen jedes Modell.
#Let's obtain our cv score ohlc_score = cross_val_score(ohlc_nn,ohlc_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) fred_score = cross_val_score(fred_nn,fred_train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) all_score = cross_val_score(all_nn,train_X,train_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1)
Speichern wir unsere Ergebnisse der Kreuzvalidierung
for i in np.arange(0,5): validation_error.iloc[i,0] = ohlc_score[i] validation_error.iloc[i,1] = fred_score[i] validation_error.iloc[i,2] = all_score[i]
und visualisieren den Validierungsfehler.
#Our validation error
validation_error| MetaTrader 5 Daten | FRED Alternative Daten | Alle Daten |
|---|---|---|
| -0.147973 | -0.79131 | -4.816608 |
| -0.103913 | -2.073764 | -0.655701 |
| -0.211833 | -0.276794 | -0.838832 |
| -0.094998 | -1.954753 | -0.259959 |
| -1.233912 | -2.152471 | -3.677273 |
Die Analyse unserer durchschnittlichen Performance über alle 5 Folds hinweg zeigt, dass unsere gewöhnlichen Marktdaten aus dem MetaTrader 5 die beste Wahl sein könnten.
#Our mean performane across all groups
validation_error.mean()| Eingabedaten | Durchschnittlicher 5 Fold-Fehler |
|---|---|
| MetaTrader 5 | -0.358526 |
| FRED | -1.449818 |
| ALLES | -2.049675 |
Wenn wir die Leistung unserer Modelle aufzeichnen, können wir feststellen, dass die MetaTrader 5 konsistentere Fehlerniveaus aufweisen.
#Plotting our performance
validation_error.plot()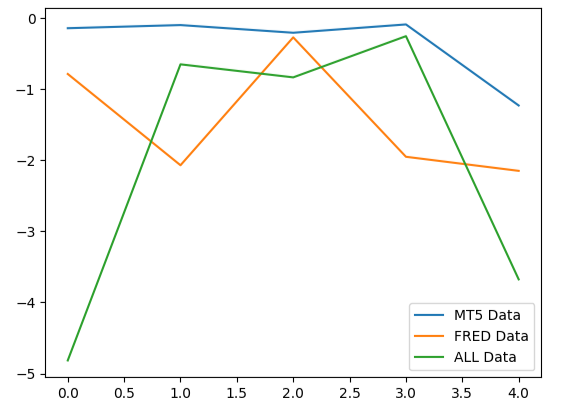
Abb. 9: Visualisierung der 3 verschiedenen Fehlerniveaus, die sich aus den 3 Datensätzen ergeben, aus denen wir wählen mussten
Die flache Form des MetaTrader 5-Fehler-Box-Plots ist wünschenswert, weil sie zeigt, dass das Modell durch seine konsistente Leistung seine Fähigkeiten unter Beweis stellt.
#Creating box-plots of our performance
sns.boxplot(validation_error)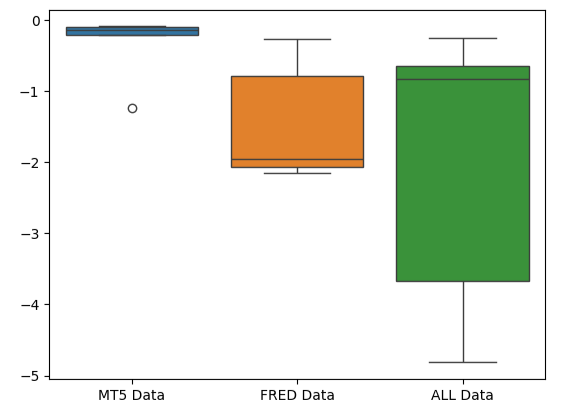
Abb. 10: Visualisierung der Fehlermetriken unseres Modells als Boxplots
Die Bedeutung der Merkmale
Lassen Sie uns überlegen, welche Merkmale für unser DNN-Modell am wichtigsten sein könnten. Hoffentlich sind die von uns ausgewählten alternativen Daten nützlich, dann werden sie von unseren Algorithmen zur Merkmalsgewichtung als nützlich eingestuft. Leider deutet unsere Analyse darauf hin, dass die Schwankungen in den MetaTrader 5-Marktdaten das Ziel allein recht gut zu erklären scheinen. Daher enthielten die FRED-Zeitreihen keine zusätzlichen Informationen, die unser Modell nicht aus den ihm vorliegenden Daten hätte ableiten können.
Für den Anfang importieren wir die benötigten Bibliotheken.
#Feature importance
from alibi.explainers import ALE, plot_aleMit Hilfe von ALE-Diagrammen (Accumulated Local Effects) können wir die Auswirkungen der einzelnen Modelleingaben auf das Ziel visualisieren. ALE-Diagramme sind wegen ihrer robusten Fähigkeit, Modelle zu erklären, die mit stark korrelierten Daten trainiert wurden, wie die unseren, sehr beliebt. Klassische akademische Methoden wie Partial Dependency (PD) Plots waren einfach nicht zuverlässig, wenn es um die Erklärung von Prädiktoren mit starken Korrelationsniveaus ging. Die ursprüngliche Spezifikation des Algorithmus kann in der vollständigen Forschungsarbeit von Daniel W. Apley und Jingyu Zhu aus dem Jahr 2016 kann hier nachgelesen werden.

Abb. 11: Daniel W. Apley, Mitbegründer des ALE-Algorithmus
Passen wir die Erklärungen von ALE an unseren DNN Regressor an.
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["Target"])
Jetzt können wir die Auswirkungen der einzelnen Prädiktoren auf das Ziel erklären. ALE-Plots haben eine intuitive visuelle Interpretation, die sie zu einem guten Ausgangspunkt macht. Einfach ausgedrückt: Wenn das ALE-Diagramm, das wir erhalten, eine flache Linie ist, dann hat der beobachtete Prädiktor aus Sicht unseres DNN-Modells wenig bis gar keinen Einfluss auf das Ziel. Je weiter das ALE-Diagramm von der Linearität entfernt ist, desto mehr hat unser Modell gelernt, dass die Beziehung zwischen dem Ziel und dem Prädiktor von einer einfachen linearen Beziehung abweichen kann.
Das ALE-Diagramm des Eröffnungskurses und des Kursziels (obere linke Ecke von Abb. 12) zeigt uns, dass mit dem Anstieg des Eröffnungskurses des EURUSD das Modell gelernt hat, dass der zukünftige Schlusskurs ebenfalls steigen wird. Beachten Sie, wie die ALE-Diagramme des Eröffnungs- und Schlusskurses in entgegengesetzte Richtungen variieren. Dies könnte darauf hindeuten, dass diese beiden Prädiktoren allein eine signifikante Varianz im Ziel erklären könnten.
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)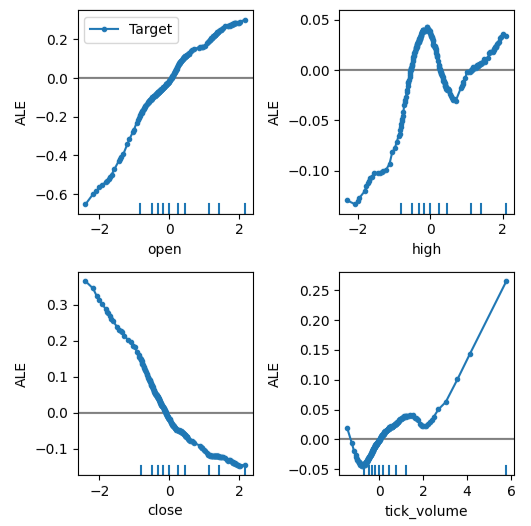
Abb. 12: Visualisierung unserer ALE Plots auf unseren MetaTrader 5 Marktdaten
Wir werden nun eine Vorwärtsselektion durchführen. Der Algorithmus beginnt mit einem Nullmodell und fügt iterativ 1 Merkmal hinzu, das die Leistung des Modells am meisten verbessert, bis die Leistung des Modells nicht weiter gesteigert werden kann.
#Forward selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS from mlxtend.plotting import plot_sequential_feature_selection as plot_sfs
Initialisieren wir das Modell,
#Reinitialize the model all_nn = MLPRegressor(hidden_layer_sizes=(10,20,40),max_iter=500)
Nun müssen wir das gewünschte Forward-Selection-Objekt angeben. Wir werden diese Instanz des Algorithmus anweisen, so viele Variablen auszuwählen, wie er für wichtig hält.
#Define the feature selector sfs1 = SFS(all_nn, k_features=(1,X.shape[1]), forward=True, scoring='neg_mean_squared_error', cv=5, n_jobs=-1 )
Keine der FRED-Zeitreihen wurde von dem Algorithmus ausgewählt.
#Best features we identified
sfs1.k_feature_names_Wir können den Auswahlprozess des Algorithmus visualisieren. Unsere Grafik zeigt deutlich, dass die Leistung unseres Modells mit der Erhöhung der Modellparameter abnimmt.
#Fit the forward selection algorithm fig1 = plot_sfs(sfs1.get_metric_dict(), kind='std_dev')
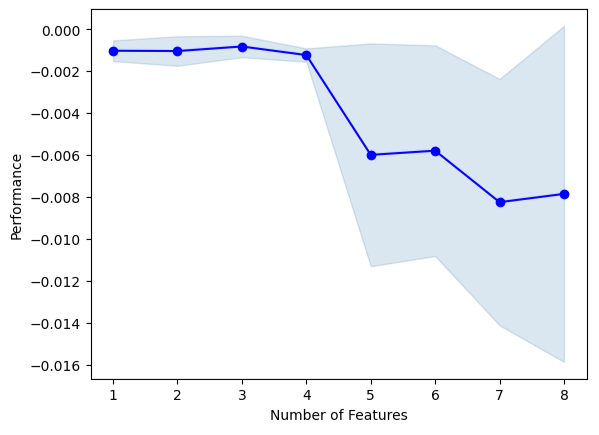
Abb. 13: Visualisierung der Leistung unseres Modells, wenn wir iterativ weitere Prädiktoren hinzufügen
Einstellung der Parameter
Wir wollen die Parameter unseres DNN-Modells mithilfe einer Zufallssuche abstimmen. Zunächst müssen wir unser Modell initialisieren.
#Reinitialize the model model = MLPRegressor(max_iter=500)
Nun werden wir unsere Tuning-Parameter festlegen.
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"hidden_layer_sizes":[(10,20,40),(10,20,40,80),(5,10,20,100),(100,50,10),(20,20,10),(1,5,10,20),(20,10,5,1)],
"early_stopping":[True,False],
"warm_start":[True,False],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
)Passen wir das Abstimmobjekt an.
#Fit the tuner
tuner.fit(train_X,train_y)Sehen wir uns die besten Parameter an, die wir gefunden haben.
#The best parameters we found
tuner.best_params_'tol': 1e-05,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate_init': 0.01,
'learning_rate': 'invscaling',
'hidden_layer_sizes': (10, 20, 40, 80),
'early_stopping': True,
'alpha': 0.1,
'activation': 'relu'}
Tiefergehende Parameter-Optimierung
Wir wollen mit Hilfe der SciPy-Bibliothek nach besseren Modellparametern suchen. Wir können uns Optimierungsprozesse als Suchprobleme vorstellen, fast wie das Versteckspiel in der Kindheit. Die idealen Parameter für unser Modell, die bei Daten, die das Modell noch nicht gesehen hat, die beste Fehlerquote ergeben, sind in dem unendlichen Raum möglicher Werte verborgen, die wir jedem unserer kontinuierlichen Parameter zuweisen könnten.
Importieren wir nun die benötigten Bibliotheken.
#Deeper optimization from scipy.optimize import minimize from sklearn.metrics import mean_squared_error from sklearn.model_selection import TimeSeriesSplit
Definieren wir ein Zeitserien-Split-Objekt
#Define the time series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
und erstellen einen Datenrahmen, um die aktuellen Kosten zurückzugeben, und eine Liste, um den Fortschritt unseres Modells zur Visualisierung zu speichern.
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) algorithm_progress = []
Nun werden wir unsere Kostenfunktion definieren. Die Minimierungsbibliothek von SciPy bietet uns verschiedene Algorithmen, um die Eingaben für eine beliebige Funktion zu finden, die zu einer minimalen Ausgabe der Funktion führen. Wir verwenden den Durchschnitt der 5 Fold-Fehler des Modells auf den Trainingsdaten als die zu minimierende Größe, während wir alle anderen DNN-Parameter konstant halten.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=x[0], tol=x[1], learning_rate_init=x[2] ) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Store the algorithm's progress algorithm_progress.append(current_error_rate.iloc[:,0].mean()) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Legen wir die Ausgangspunkte für die Routine fest und geben wir auch die Grenzen für die Parameter an. Bei diesem Problem bestehen unsere einzigen Grenzen darin, dass alle Modellparameter positiv sein sollten.
#Define the starting point pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]] bnds = ((10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100), (10.00 ** -100,10.00 ** 100))
Wir werden den Algorithmus Truncated Newton Constrained (TNC) verwenden, um unsere Modellparameter zu optimieren. Die verkürzten (truncated) Newton-Methoden sind eine Familie von Methoden, die sich für die Lösung großer nichtlinearer Optimierungsprobleme unter Einhaltung von Grenzen eignen. Die SciPy-Bibliothek bietet uns einen Wrapper für eine C-Implementierung des Algorithmus.
#Searching deeper for parameters result = minimize(objective,pt,method="TNC",bounds=bnds)
Mal sehen, ob wir die Beendigung erfolgreich abgeschlossen haben.
#The result of our optimization
resultsuccess: False
status: 4
fun: 0.001911232280110637
x: [ 1.000e-100 1.000e-100 1.000e-100]
nit: 0
jac: [ 2.689e+06 9.227e+04 1.124e+05]
nfev: 116
Es scheint, dass wir Schwierigkeiten hatten, die optimalen Eingaben zu finden, lassen Sie uns die Leistung unseres Optimierungsverfahrens veranschaulichen.
#Store the optimal coefficients optimal_weights = result.x optima_y = min(algorithm_progress) optima_x = algorithm_progress.index(optima_y) inputs = np.arange(0,len(algorithm_progress)) #Plot the performance of our optimization procedure plt.scatter(inputs,algorithm_progress) plt.plot(optima_x,optima_y,'ro',color='r') plt.axvline(x=optima_x,ls='--',color='red') plt.axhline(y=optima_y,ls='--',color='red') plt.xlabel("Iterations") plt.ylabel("Training MSE") plt.title("Minimizing Training Error")
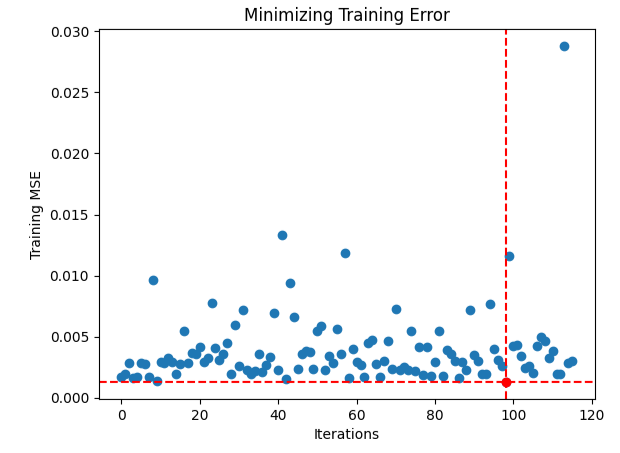
Abb. 14: Der rote Punkt stellt die von unserem TNC-Optimierer geschätzten optimalen Eingabewerte dar
Test auf Überanpassung
Initialisieren wir alle 3 Modelle und sehen, ob wir sie auf dem Trainingsset trainieren und das Standardmodell auf den Testdaten übertreffen können. Wir haben ja die Testdaten in unserem Entscheidungsprozess bisher nicht verwendet haben.
#Testing for overfitting default_nn = MLPRegressor(max_iter=500) #Randomized NN random_search_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] ) #TNC NN tnc_nn = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=result.x[0], tol=result.x[1], learning_rate_init=result.x[2] )
Passen wir jedes der Modelle an die Trainingsmenge an.
#Store the models in a list models = [default_nn,random_search_nn,tnc_nn] #Fit the models for model in models: model.fit(train_X,train_y)
Wir erstellen einen Datenrahmen, um unsere Validierungsfehlerstufen zu speichern.
#Create a dataframe to store our validation error validation_error = pd.DataFrame(columns=["Default","Randomized","TNC"],index=np.arange(0,5))
testen jedes Modell und merken uns seine Punktzahl.
#Let's obtain our cv score default_score = cross_val_score(default_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) random_score = cross_val_score(random_search_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) tnc_score = cross_val_score(tnc_nn,test_X,test_y,scoring='neg_root_mean_squared_error',cv=5,n_jobs=-1) #Store the model error in a dataframe for i in np.arange(0,5): validation_error.iloc[i,0] = default_score[i] validation_error.iloc[i,1] = random_score[i] validation_error.iloc[i,2] = tnc_score[i]
Schauen wir uns den Validierungsfehler an.
#Let's see the validation error validation_error
| Standardmodell | Zufällige Suche | TNC |
|---|---|---|
| -0.362851 | -0.029476 | -0.054709 |
| -0.323601 | -0.053967 | -0.087707 |
| -0.064432 | -0.024282 | -0.026481 |
| -0.121226 | -0.019693 | -0.017709 |
| -0.064801 | -0.012812 | -0.016125 |
Die Berechnung der durchschnittlichen Leistung über alle 5 Fold hinweg zeigt deutlich, dass unser Modell der zufälligen Suche die beste Wahl ist.
#Our best performing model
validation_error.mean()| Modell | Durchschnittlicher Validierungsfehler |
|---|---|
| Standardmodell | -0.187382 |
| Zufällige Suche | -0.028046 |
| TNC | -0.040546 |
Die Erstellung von Boxplots zeigt uns schnell, wie stark die Leistung des Standardmodells variiert. Unsere angepassten Modelle konnten innerhalb einer engen Bandbreite von Fehlern abschneiden, was uns mehr Vertrauen in die Wahl unserer Parameter gab.
#Let's create box-plots sns.boxplot(validation_error)
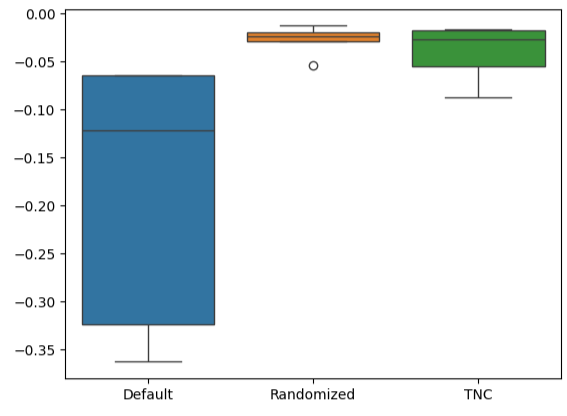
Abb. 15: Visualisierung der Leistung unseres Modells als Boxplots
Die Erstellung von Liniendiagrammen der Kreuzvalidierungsdaten verdeutlicht die Diskrepanz zwischen dem Standardmodell und unseren abgestimmten Modellen. Es ist zu erkennen, dass zwischen der blauen Linie, die die Leistung des Standardmodells darstellt, und den übrigen farbigen Diagrammen eine erhebliche Abweichung besteht.
#We can also visualize model performance through a line plot
validation_error.plot()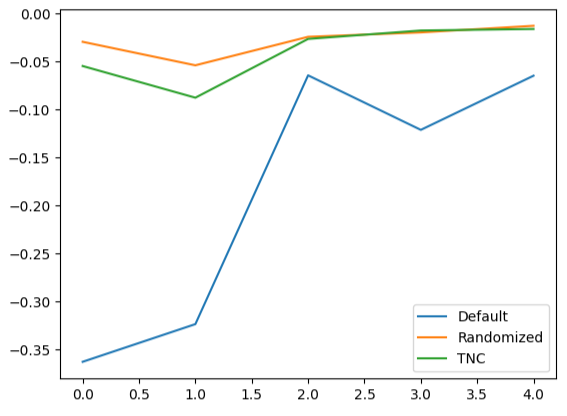
Abb. 16: Darstellung der Leistung von 5 Fold unserer verschiedenen Modelle mit den Testdaten
Analyse der Residuen
Wir können unserem Modell nicht blind vertrauen und es in der Produktion einsetzen. Versuchen wir sicherzustellen, dass unser Modell tatsächlich effektiv gelernt hat, indem wir die Residuen unseres Modells untersuchen. Im Idealfall weist ein Modell, das eine Funktion perfekt approximiert hat, Residuen auf, die eine flache Linie bilden. Das bedeutet, dass die Vorhersage des Modells keinen Fehler enthält. Darüber hinaus bedeutet dies auch, dass sich die Höhe des Fehlers in der Vorhersage des Modells nicht ändert.
Je weiter die Leistung unseres Modells vom Ideal abweicht, desto stärker ist die Abweichung vom idealen linearen und stationären Residuenverlauf. Die Residuen unseres Modells wiesen unterschiedliche Fehlerbeträge auf, die teilweise mit den vorherigen Fehlerbeträgen korrelierten. Dies ist wahrscheinlich besorgniserregend und kann möglicherweise durch eine Änderung des Prädiktors oder des Ziels behoben werden.
Initialisieren wir das Modell,
#Resdiuals analysis model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
passen das Modell an die Trainingsdaten an und erfassen dann die Residuen anhand der Testdaten.
#Fit the model model.fit(train_X,train_y) #Record the residuals residuals = test_y - model.predict(test_X)
Unser Residuen-Diagramm war weit vom Ideal entfernt, und wir müssen möglicherweise andere Vorverarbeitungsschritte untersuchen, um dieses Problem zu lösen.
#Residuals analysis
residuals.plot()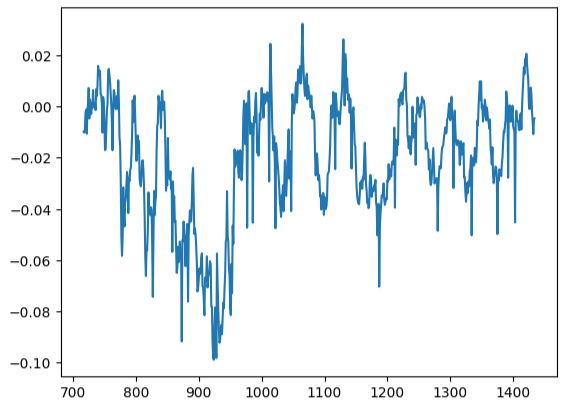
Abb. 17: Visualisierung der Residuen unseres Modells anhand von Testdaten
Die Messung der Autokorrelation ist ein robuster Ansatz zur Aufdeckung möglicher falscher Regressionen. Leider haben unsere Modellresiduen auch diesen Test nicht bestanden und könnten möglicherweise als Indikator dafür dienen, dass wir zusätzliche Verbesserungen erzielen können, wenn wir unsere Prädiktoren oder unser Ziel besser transformieren.
#Autocorrelation plot from statsmodels.graphics.tsaplots import plot_acf acf = plot_acf(residuals,lags=40)
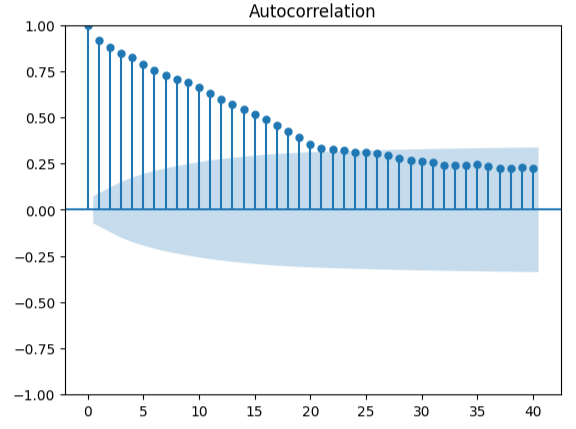
Abb. 18: Visualisierung der Residuen unseres Modells
Vorbereiten des Exports nach ONNX
Bevor wir unsere Daten in das ONNX-Format exportieren können, müssen wir zunächst die Mittelwerte und Standardabweichungen der einzelnen Spalten in einem Datenrahmen speichern. Da wir durch die Umwandlung der Daten in prozentuale Veränderungen keine Verbesserungen erzielen konnten, werden wir die Daten in ihrer ursprünglichen Form verwenden und diese für unsere z-Score-Berechnungen nutzen.
#Prepare to convert the model to ONNX format scale_factors = pd.DataFrame(columns=X.columns,index=["mean","std"]) for i in X.columns: scale_factors.loc["mean",i] = merged_data.loc[:,i].mean() scale_factors.loc["std",i] = merged_data.loc[:,i].std() merged_data.loc[:,i] = (merged_data.loc[:,i] - scale_factors.loc["mean",i]) / scale_factors.loc["std",i] scale_factors

Abb. 19: Unser Datenrahmen mit unseren z-Scores
Wir sichern die Daten im CSV-Format.
#Save the scale factors to CSV format scale_factors.to_csv("FRED EURUSD D1 scale factors.csv")
Exportieren nach ONNX
ONNX ist ein Open-Source-Protokoll, das es Entwicklern ermöglicht, Modelle für maschinelles Lernen in jeder Programmiersprache zu erstellen und einzusetzen, die die ONNX-API unterstützt. Zunächst importieren wir die benötigten Bibliotheken,
# Import the libraries we need
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorTypeinitialisieren das Modells, zum letzten Mal,
#Initialize the model model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"], early_stopping=tuner.best_params_["early_stopping"], warm_start=tuner.best_params_["warm_start"], max_iter=500, activation=tuner.best_params_["activation"], learning_rate=tuner.best_params_["learning_rate"], solver=tuner.best_params_["solver"], shuffle=tuner.best_params_["shuffle"], alpha=tuner.best_params_["alpha"], tol=tuner.best_params_["tol"], learning_rate_init=tuner.best_params_["learning_rate_init"] )
und passen das Modell an alle Daten an, die wir haben,
# Fit the model on all the data we have
model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])Definieren wir die Ausgangsform unseres Modells,
# Define the input type initial_types = [("float_input",FloatTensorType([1,X.shape[1]]))]
erstellen eine ONNX-Darstellung unseres Modells
# Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
und speichern das ONNX-Modell.
# Save the ONNX model onnx.save_model(onnx_model,"FRED EURUSD D1.onnx")
Visualisierung unseres Modells in Netron
Durch die Visualisierung unseres Modells können wir überprüfen, ob es gemäß unseren Spezifikationen erstellt wurde. Wir wollen überprüfen, ob die Eingabe- und Ausgabeformen mit unseren Erwartungen übereinstimmen. Netron ist eine Open-Source-Bibliothek zur Visualisierung von Machine-Learning-Modellen. Lassen Sie uns die Bibliothek importieren, um zu beginnen.
import netron
Jetzt können wir unseren DNN Regressor leicht visualisieren.
netron.start("FRED EURUSD D1.onnx")
Abb. 20: Visualisierung unseres DNN-Regressors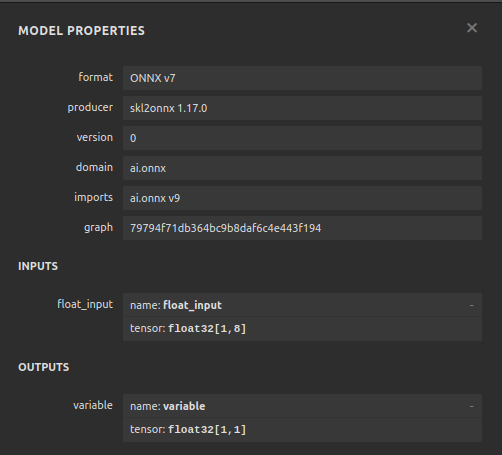
Abb. 21: Visualisierung der Eingabe- und Ausgabeformen unseres Modells
Implementation in MQL5
Die erste Komponente, die wir in unseren Expert Advisor integrieren müssen, ist das ONNX-Modell. Wir werden einfach die ONNX-Datei als Ressource für unseren Expert Advisor verwenden.
//+------------------------------------------------------------------+ //| FRED EURUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\FRED EURUSD D1.onnx" as const uchar onnx_buffer[];
Lassen Sie uns nun die Handelsbibliothek laden, die wir für die Verwaltung unserer Positionen benötigen.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Erstellen von globalen Variablen, die wir in unserem Programm benötigen.
//+------------------------------------------------------------------+ //| Define global variables | //+------------------------------------------------------------------+ long model; double mean_values[5] = {1.1113568153310105,1.1152603484320558,1.1078179790940768,1.1114909337979093,65505.27177700349}; double std_values[5] = {0.05467420688685988,0.05413287747761819,0.05505429755411189,0.054630920048519924,26512.506288360997}; vectorf model_output = vectorf::Zeros(1); vectorf model_inputs = vectorf::Zeros(8); int model_sate = 0; int system_sate = 0; double bid,ask;
Wenn unser Modell zum ersten Mal geladen wurde, sollten wir zunächst versuchen, unser ONNX-Modell zu laden und dann testen, ob es funktioniert.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_model()) { //--- We failed to load the ONNX model return(INIT_FAILED); } //--- Test if we can get a prediction from our model model_predict(); //--- Eveything went fine return(INIT_SUCCEEDED); }
Wenn unser Modell aus dem Diagramm entfernt wird, werden auch die Ressourcen frei, die wir nicht mehr benötigen.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we no longer need release_resources(); }
Immer wenn wir neue Preise erhalten, aktualisieren wir die Variablen, die wir zur Speicherung der aktuellen Marktpreise zugewiesen haben. Wenn wir keine offenen Positionen haben, folgen wir ebenfalls der Richtlinie unseres Modells. Wenn wir hingegen bereits offene Positionen haben, lassen wir unser Modell vor möglichen Umkehrungen warnen und schließen unsere Positionen entsprechend.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update our bid and ask prices update_market_prices(); //--- Fetch an updated prediction from our model model_predict(); //--- If we have no trades, follow our model's directions. if(PositionsTotal() == 0) { //--- Our model is predicting price levels will appreciate if(model_sate == 1) { Trade.Buy(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = 1; } //--- Our model is predicting price levels will deppreciate if(model_sate == -1) { Trade.Sell(0.3,"EURUSD",ask,0,0,"FRED EURUSD AI"); system_sate = -1; } } //--- Otherwise Manage our open positions else { if(system_sate != model_sate) { Alert("AI System Detected A Reversal! Closing All Positions on EURUSD"); Trade.PositionClose("EURUSD"); } } } //+------------------------------------------------------------------+
Diese Funktion aktualisiert unsere Variablen, die die aktuellen Marktpreise festhalten.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
Nun werden wir die Art und Weise festlegen, wie unsere Ressourcen freigegeben werden sollen.
//+------------------------------------------------------------------+ //| Release the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { OnnxRelease(model); ExpertRemove(); }
Definieren wir die Funktion, die für die Erstellung unseres ONNX-Modells aus dem oben erstellten Puffer verantwortlich ist. Wenn diese Funktion zu irgendeinem Zeitpunkt fehlschlägt, wird sie false zurückgeben, was unsere Initialisierungsprozedur unterbricht.
//+------------------------------------------------------------------+ //| Create our ONNX model from the buffer we defined above | //+------------------------------------------------------------------+ bool load_onnx_model(void) { //--- Create the ONNX model from the buffer we defined model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model was not illdefined if(model == INVALID_HANDLE) { //--- We failed to define our model Comment("We failed to create our ONNX model: ",GetLastError()); return false; } //---- Define the model I/O shape ulong input_shape[] = {1,8}; ulong output_shape[] = {1,1}; //--- Validate our model's I/O shapes if(!OnnxSetInputShape(model,0,input_shape) || !OnnxSetOutputShape(model,0,output_shape)) { Comment("Failed to define our model I/O shape: ",GetLastError()); return(false); } //--- Everything went fine! return(true); }
Dies ist die Funktion, die für das Abrufen einer Vorhersage aus unserem Modell verantwortlich ist. Die Funktion holt zunächst EURUSD-Marktdaten ab und normalisiert sie, bevor sie eine Routine aufruft, die für das Lesen unserer aktuellen alternativen FRED-Daten zuständig ist.
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 5 inputs will be fetched from the market matrix eur_usd_ohlc = matrix::Zeros(1,5); eur_usd_ohlc[0,0] = iOpen(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,1] = iHigh(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,2] = iLow(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,3] = iClose(Symbol(),PERIOD_D1,0); eur_usd_ohlc[0,4] = iTickVolume(Symbol(),PERIOD_D1,0); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((eur_usd_ohlc[0,i] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } } //+------------------------------------------------------------------+
Diese Funktion liest unsere alternativen FRED-Daten aus unserem MQL5-Verzeichnis. Die CSV-Datei wird jeden Tag von unserem Python-Skript aktualisiert.
//+------------------------------------------------------------------+ //| This function will read in our FRED data | //+------------------------------------------------------------------+ bool read_fred_data(void) { //--- Read in the file string file_name = "FRED EURUSD ALT DATA.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 20) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { model_inputs[5] = (float) value; } if(counter == 5) { model_inputs[6] = (float) value; } if(counter == 7) { model_inputs[7] = (float) value; } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast: ",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } //--- Everything went fine return(true); } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); return false; } //--- Something went wrong return false; }
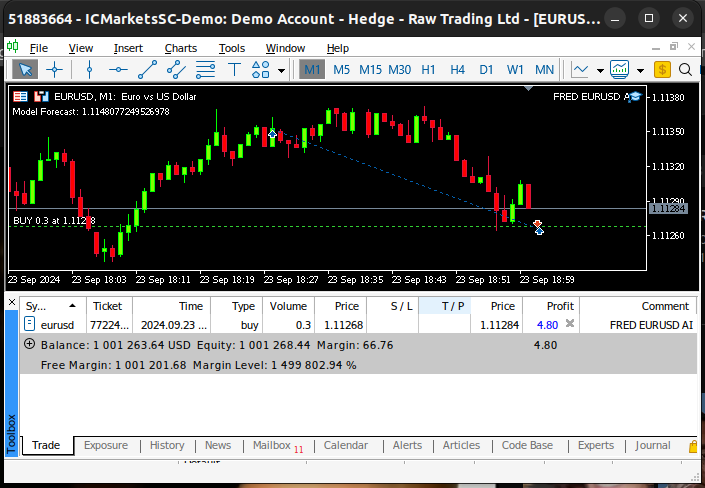
Abb. 22: Vorwärtsprüfung unseres Algorithmus
Schlussfolgerung
In diesem Artikel haben wir gezeigt, dass der nominale breite Tagesindex entweder keine große Hilfe bei der Prognose des EURUSD-Paares ist, oder dass das Symbol mehr Transformationen erfordert, bevor die wahre Beziehung effektiv erkannt werden kann. Alternativ können wir auch eine breitere Palette von Modellen testen, um die Wahrscheinlichkeit zu erhöhen, dass wir die Beziehung gut erfassen können. Modelle wie Support Vector Machines eignen sich besonders gut für Probleme, die das Erlernen einer Entscheidungsgrenze im hochdimensionalen Raum erfordern. Es gibt Hunderttausende von Datensätzen, die wir noch erforschen müssen. Aber leider haben wir heute keinen Vorsprung gegenüber dem Rest des Marktes gewonnen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15949
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wie man ein Handelsjournal mit MetaTrader und Google-Tabellen erstellt
Wie man ein Handelsjournal mit MetaTrader und Google-Tabellen erstellt
 Beispiel eines neuen Indikators und eines Conditional LSTM
Beispiel eines neuen Indikators und eines Conditional LSTM
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 41): Deep-Q-Networks
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 41): Deep-Q-Networks
 Erstellen eines Expert Advisor, der Telegram integriert (Teil 7): Befehlsanalyse für die Automatisierung von Indikatoren auf Charts
Erstellen eines Expert Advisor, der Telegram integriert (Teil 7): Befehlsanalyse für die Automatisierung von Indikatoren auf Charts
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.