Reimaginando Estratégias Clássicas (Parte IX): Análise de Múltiplos Time-Frames (II)

Existem muitos time-frames disponíveis para os traders utilizarem. Para um novo membro da comunidade, ou qualquer pessoa que esteja aprendendo a negociar, a escolha pode ser difícil de fazer. Mesmo traders experientes frequentemente debatem e compartilham pontos de vista diferentes, tentando estabelecer qual time-frame é o mais indicado. Tentaremos responder a essa pergunta de forma objetiva, definindo o time-frame ideal como aquele que minimiza os níveis de erro do nosso modelo de IA.

Na discussão de hoje, prestaremos atenção à distribuição dos resíduos do nosso modelo ao longo de 11 time-frames. Observamos 2 regiões de baixo erro nos time-frames Mensal e de 1 Hora. No entanto, não há um padrão óbvio na distribuição dos níveis de erro do modelo; ele parece atingir um máximo e um mínimo no time-frame de 1 Hora. Antes de podermos responder de forma definitiva à velha pergunta “Qual é o melhor time-frame para usar?”, devemos ter certeza razoável de que a distribuição dos resíduos não muda caso alteremos o mercado. Além disso, no futuro, devemos considerar uma busca exaustiva por todos os time-frames disponíveis.

Visão Geral da Metodologia de Negociação

Embora o padrão criado pelos candles de preço possa parecer muito diferente entre todos os time-frames, há apenas um preço sendo oferecido em todos eles a cada momento. Os traders costumam analisar diferentes time-frames ao mesmo tempo para obter insights sobre o estado atual do mercado. Se a tendência estiver enfraquecendo, provavelmente veremos ações de preço contraditórias em time-frames menores do que aquele usado para abrir nossa negociação. Além disso, esses sinais de fraqueza sempre aparecerão primeiro no time-frame mais baixo, antes de se tornarem perceptíveis nos time-frames mais altos.

De modo geral, a maioria das estratégias que incluem análise de múltiplos time-frames busca compreender o sentimento do mercado a partir de time-frames mais altos. Alguns traders bem-sucedidos procuram pela formação de padrões conhecidos de ação de preço em time-frames maiores, como padrões de candle engolfo de alta. Tradicionalmente, a presença ou ausência desses padrões servia como sinal para traders que buscavam setups de alta probabilidade. Nós desejávamos aprender, de forma algorítmica, qual time-frame nos fornece níveis de erro confiáveis ao prever o par EURUSD.

De certa forma, todos nós entendemos intuitivamente que, quanto mais distante no futuro tentamos prever, mais difícil é a tarefa. Os resultados da nossa análise de hoje desafiam essa crença de forma fundamental. Antes que você possa entender por que estou dizendo isso, ou se essas conclusões são válidas, precisamos primeiro discutir a metodologia empregada.

Visão Geral da Metodologia

Para que nosso teste fosse justo, tivemos que buscar a mesma quantidade de dados de cada período. O fator limitante nesta etapa foi o número de barras disponíveis no período Mensal. Apenas 400 barras de dados mensais correspondem a aproximadamente 33 anos. Existem poucos mercados tão antigos, o que pode enviesar nossa compreensão sobre o melhor período em todos os mercados possíveis. No entanto, para o escopo de nossa discussão, o par EURUSD possui conjuntos de dados ricos nos quais podemos confiar.

Buscamos 400 linhas de cotações mensais no terminal MetaTrader 5. Em seguida, buscamos 400 linhas correspondentes do valor futuro do par EURUSD. Esse processo de 2 etapas foi repetido nos 10 períodos restantes. Para esta análise, selecionei:

1. Semanal
2. Diário
3. H12
   
4. H8
5. H4
6. H1
7. M30
8. M15
9. M5
10. M1
    

Devo admitir que esperava observar fortes níveis de correlação, especialmente entre períodos que estão próximos em termos de periodicidade. No entanto, só houve níveis moderados de correlação em toda a amostra. Os únicos pares de correlação interessantes que podem merecer análise adicional foram:

1. Preço Atual H4 e Preço Futuro H8
2. Preço Atual M1 e Preço Futuro H4
3. Preço Atual M1 e Preço Futuro M5
   

Lembre-se de que nossos dados de entrada tinham 22 colunas; naturalmente, a matriz de correlação que obtivemos era grande e não será exibida na íntegra na nossa discussão. A partir dos nossos dados até o momento, conseguimos criar 11 conjuntos de entradas para serem testados. Após modelar nossos dados, observamos que nossos modelos tiveram melhor desempenho nos time-frames Mensal e de 1 Hora. Esse resultado foi bastante contraintuitivo. Nosso alvo foi de 20 passos no futuro. 20 meses no futuro equivalem a um período de 1 ano e 8 meses. Nosso modelo conseguiu prever as mudanças no preço ao longo de um ano com mais precisão do que prever mudanças no preço em 20 minutos.

Intrigados pelos 2 time-frames de baixo erro, transformamos os dados de preço em retornos periódicos e, em seguida, realizamos testes de causalidade de Granger sobre os retornos. Observamos valores-p significativos que nos sugerem que os retornos horários causavam, no sentido de Granger, os retornos mensais. Esse teste prova que podemos modelar os retornos mensais usando os retornos horários com um modelo VAR (Vector Auto Regression).

Usamos uma biblioteca de Time Series Warping para alinhar e encontrar similaridades entre os dados mensais e horários. Nosso algoritmo conseguiu encontrar muitos pontos de similaridade entre os dados. Isso nos deu confiança em nosso processo de seleção e prosseguimos para ajustar com sucesso os parâmetros do nosso modelo mensal e exportá-lo no formato ONNX.

Por fim, implementei um Expert Advisor que faz previsões dos níveis de preço antecipados no time-frame mensal e, em seguida, executa suas negociações no time-frame horário. O sistema pode alternar entre fechar suas posições com base em reversões previstas por IA ou usando médias móveis. Empregamos análise técnica para cronometrar nossas entradas de posição.

Buscando os Dados que Precisamos

Vamos começar importando a biblioteca do MetaTrader 5 e algumas outras bibliotecas necessárias.

#Import the libraries we need
import pandas as pd
import numpy  as np 
import seaborn as sns
import MetaTrader5 as mt5
from sklearn.model_selection import cross_val_score,train_test_split,TimeSeriesSplit
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

Agora, vamos testar se conseguimos acessar o Terminal.

#Initialize the terminal
mt5.initialize()

Verdadeiro

Vamos definir os time-frames que gostaríamos de testar.

#Declare the time-frames we are interested in
time_frames = [mt5.TIMEFRAME_MN1,
               mt5.TIMEFRAME_W1,
               mt5.TIMEFRAME_D1,
               mt5.TIMEFRAME_H12,
               mt5.TIMEFRAME_H8,
               mt5.TIMEFRAME_H4,
               mt5.TIMEFRAME_H1,
               mt5.TIMEFRAME_M30,
               mt5.TIMEFRAME_M15,
               mt5.TIMEFRAME_M5,
               mt5.TIMEFRAME_M1
              ]

Quantas barras de dados devemos buscar?

#How many bars should we fetch 
fetch = 400

Vamos prever 20 passos no futuro.

#How far into the future should we forecast?
look_ahead = 20

Defina as colunas do nosso DataFrame.

#Create our dataframe
inputs = ["MN","W","D","H12","H8","H4","H1","M30","M15","M5","M1"]

target = []

for i in np.arange(0,len(inputs)):
    target.append(inputs[i] + " Target")

Crie o data-frame que contém nossos preços.

columns = inputs + target

prices = pd.DataFrame(columns=columns,index=np.arange(0,fetch))

Fig 1: Alguns dos insumos em nosso data-frame

Fig 2: Alguns dos alvos em nosso data-frame

Precisamos de um data-frame para armazenar nossos níveis de erro.

#As colunas para o data frame de níveis de erro.
error_columns = []


for i in np.arange(0,len(inputs)):
    error_columns.append(inputs[i])

#Create a dataframe to store our error levels
error_levels = pd.DataFrame(columns=error_columns,index=[0])
test_error_levels = pd.DataFrame(columns=error_columns,index=[0])

Busque os dados de preços que precisamos.

for i in np.arange(0,len(time_frames)):
    print(i)
    prices.iloc[:,i]   = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],look_ahead,fetch)).loc[:,"close"]
    prices.iloc[:,i+10] = pd.DataFrame(mt5.copy_rates_from_pos("EURUSD",time_frames[i],0,fetch)).loc[:,"close"]

Análise Exploratória dos Dados

Vamos analisar os níveis de correlação em nosso data-frame. Observe os fortes níveis de correlação entre os períodos H12 e H8. Quais outros níveis de correlação chamam sua atenção?

fig, ax = plt.subplots(figsize=(15,15)) 
sns.heatmap(prices.corr(),annot=True,ax=ax)

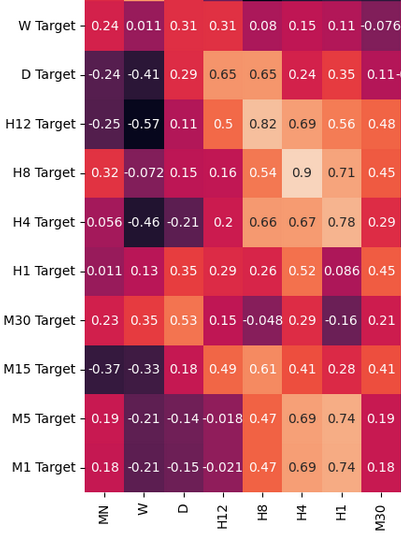
Fig 3: Alguns valores da matriz de correlação que obtivemos

Ao realizar um scatter-plot dos preços de fechamento mensais e semanais, observamos uma tendência pouco clara. Na maior parte, parece que os dados apresentam uma tendência geral de alta.

sns.scatterplot(data=prices,x="MN Close",y="W Close")

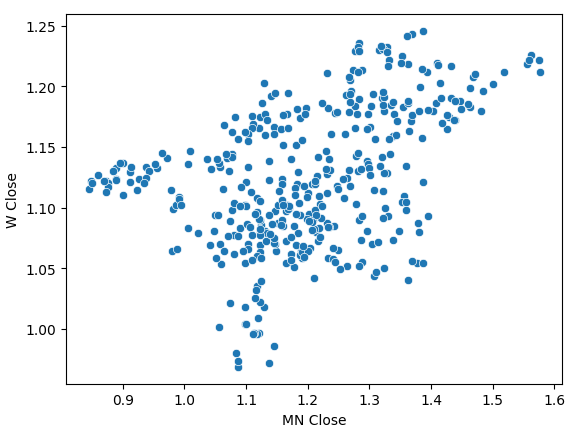
Fig 4: Um scatter plot de nossos preços de fechamento mensais e semanais

Transformamos nossos dados de preços em retornos periódicos e realizamos novamente o scatter plot. Desta vez, uma tendência geral aparece: nossos retornos parecem se agrupar em torno de 0.

sns.scatterplot(data=prices.pct_change(),x="MN Close",y="W Close")

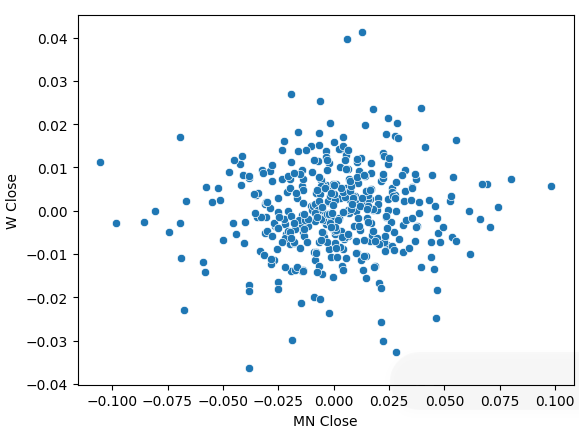
Fig 5: Um scatter plot de nossos retornos em diferentes períodos

Quando realizamos box plots de nossos retornos em diferentes períodos, pudemos observar outra tendência. A variância de nossos retornos diminui à medida que nos afastamos do período mensal em direção a períodos menores. Da mesma forma, o retorno médio em todos os períodos está próximo de 0. Isso também pode ser interpretado como um indicativo de que, se quisermos maximizar os retornos de um portfólio, devemos considerar períodos mais longos.

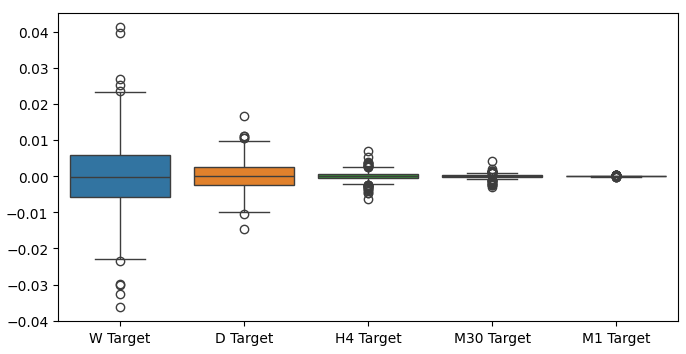
Fig 6: Um box-plot de nossos retornos em diferentes períodos

Preparando para Modelar os Dados

Agora vamos fazer as preparações necessárias para começar a modelar os dados. Primeiro, precisamos criar divisões train-test de nossos dados.

#Create train test splits
X_train_mn,X_test_mn,y_train_mn,y_test_mn      = train_test_split(prices.loc[:,["MN"]],prices.loc[:,"MN Target"],test_size=0.5,shuffle=False)
X_train_w,X_test_w,y_train_w,y_test_w          = train_test_split(prices.loc[:,["W"]],prices.loc[:,"W Target"],test_size=0.5,shuffle=False)
X_train_d,X_test_d,y_train_d,y_test_d          = train_test_split(prices.loc[:,["D"]],prices.loc[:,"D Target"],test_size=0.5,shuffle=False)
X_train_h12,X_test_h12,y_train_h12,y_test_h12  = train_test_split(prices.loc[:,["H12"]],prices.loc[:,"H12 Target"],test_size=0.5,shuffle=False)
X_train_h8,X_test_h8,y_train_h8,y_test_h8      = train_test_split(prices.loc[:,["H8"]],prices.loc[:,"H8 Target"],test_size=0.5,shuffle=False)
X_train_h4,X_test_h4,y_train_h4,y_test_h4      = train_test_split(prices.loc[:,["H4"]],prices.loc[:,"H4 Target"],test_size=0.5,shuffle=False)
X_train_h1,X_test_h1,y_train_h1,y_test_h1      = train_test_split(prices.loc[:,["H1"]],prices.loc[:,"H1 Target"],test_size=0.5,shuffle=False)
X_train_m30,X_test_m30,y_train_m30,y_test_m30  = train_test_split(prices.loc[:,["M30"]],prices.loc[:,"M30 Target"],test_size=0.5,shuffle=False)
X_train_m15,X_test_m15,y_train_m15,y_test_m15  = train_test_split(prices.loc[:,["M15"]],prices.loc[:,"M15 Target"],test_size=0.5,shuffle=False)
X_train_m5,X_test_m5,y_train_m5,y_test_m5      = train_test_split(prices.loc[:,["M5"]],prices.loc[:,"M5 Target"],test_size=0.5,shuffle=False)
X_train_m1,X_test_m1,y_train_m1,y_test_m1      = train_test_split(prices.loc[:,["M1"]],prices.loc[:,"M1 Target"],test_size=0.5,shuffle=False)

Agora armazene essas divisões em listas.

train_X = [
X_train_mn,
X_train_w,
X_train_d,
X_train_h12,
X_train_h8,
X_train_h4,
X_train_h1,
X_train_m30,
X_train_m15,
X_train_m5,
X_train_m1
]

test_X = [
X_test_mn,
X_test_w,
X_test_d,
X_test_h12,
X_test_h8,
X_test_h4,
X_test_h1,
X_test_m30,
X_test_m15,
X_test_m5,
X_test_m1
]

Repita o procedimento acima para os valores-alvo.

train_y = [
y_train_mn,
y_train_w,
y_train_d,
y_train_h12,
y_train_h8,
y_train_h4,
y_train_h1,
y_train_m30,
y_train_m15,
y_train_m5,
y_train_m1,
]

test_y = [
y_test_mn,
y_test_w,
y_test_d,
y_test_h12,
y_test_h8,
y_test_h4,
y_test_h1,
y_test_m30,
y_test_m15,
y_test_m5,
y_test_m1,
]

Valide cada modelo com cross-validation.

#Record our error 
for i in np.arange(0,len(train_X)):
    #Fit the model
    model = LinearRegression()
    cv_score = cross_val_score(model,train_X[i],train_y[i],cv=5)
    error_levels.iloc[0,i] = np.mean(cv_score * -1)
    #Record validation error
    model.fit(train_X[i],train_y[i])
    test_error_levels.iloc[0,i] = mean_squared_error(test_y[i],model.predict(test_X[i]))

Nossos respectivos níveis de erro.

error_levels

MN	W	D	H12	H8	H4	H1	M30	M15	M5	M1
0.719131	3.979435	3.897228	5.023601	5.218168	40.406227	0.196244	18.264356	3.680168	20.331821	3.540946

Vamos visualizar nossa aproximação da distribuição dos resíduos do modelo.

fig, ax = plt.subplots(figsize=(7,4)) 
sns.barplot(error_levels,ax=ax)

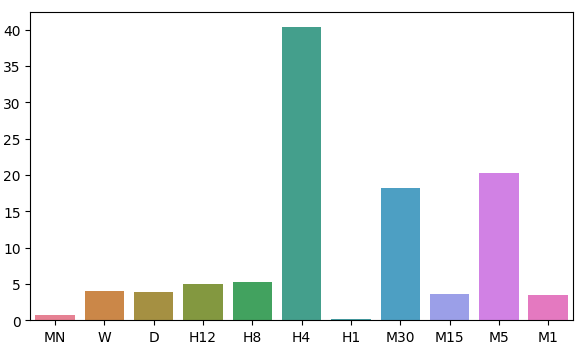
Fig 7: Visualizando os níveis de erro de nosso modelo

Importância das Variáveis

Agora que identificamos nossos períodos ótimos, vamos tentar detectar se pode haver alguma causalidade entre os 2 períodos. Em 1969, Sir Clive Granger propôs um teste para determinar empiricamente se duas séries temporais causavam uma à outra, mesmo em casos em que valores passados de uma série temporal afetavam valores futuros da outra. Simplificando, o teste de Granger é aprovado se conseguirmos defasar os valores de uma série temporal e usá-los para prever o valor futuro da segunda sem uma queda significativa na variância de nossas previsões.

Desde a sua criação, o teste de Granger passou por muitas mudanças e melhorias. Nos tempos modernos, ele é amplamente usado em diversas indústrias, da neurociência às finanças. O uso do teste tem estado no centro de muito debate acadêmico por mais de meio século. Grande parte do problema reside nas suposições de linearidade que são implicitamente feitas pelo teste de Granger. Portanto, se existir uma relação causal verdadeira que seja não linear, o teste de Granger refutará sua existência. Além disso, na prática, o teste é geralmente limitado a problemas bivariados. Ou seja, raramente usamos o teste de Granger em grandes problemas com mais de 2 séries temporais.

Fig 8: O falecido economista britânico Sir Clive Granger

Para começar, vamos primeiro importar a biblioteca statsmodels e então rodar o teste. O teste é realizado em versões defasadas do fechamento de H1. O teste é aprovado se obtivermos valores-p < 0,05, o que aconteceu na primeira defasagem. Todas as defasagens subsequentes falharam no teste e podemos rejeitar que haja qualquer causalidade além da primeira defasagem.

from statsmodels.tsa.stattools import grangercausalitytests

result = grangercausalitytests(prices[['H1 Close','MN Close']].pct_change().dropna(), maxlag=4)

Causalidade de Granger
número de defasagens (sem zero) 1
teste F baseado em ssr: F=4.4913 , p=0.0347 , df_denom=395, df_num=1
teste qui-quadrado baseado em ssr: chi2=4.5254 , p=0.0334 , df=1
teste de razão de verossimilhança: chi2=4.4999 , p=0.0339 , df=1
teste F de parâmetro: F=4.4913 , p=0.0347 , df_denom=395, df_num=1

Causalidade de Granger
número de defasagens (sem zero) 2
teste F baseado em ssr: F=2.2706 , p=0.1046 , df_denom=392, df_num=2
teste qui-quadrado baseado em ssr: chi2=4.5991 , p=0.1003 , df=2
teste de razão de verossimilhança: chi2=4.5727 , p=0.1016 , df=2
teste F de parâmetro: F=2.2706 , p=0.1046 , df_denom=392, df_num=2

A causalidade de Granger normalmente funciona em uma direção. Vamos confirmar isso verificando a causalidade na direção oposta. Nenhum dos valores-p obtidos foi significativo, o que nos tranquiliza de que a causalidade está realmente ocorrendo apenas em uma direção, como esperado.

result = grangercausalitytests(prices[['MN Close','H1 Close']].pct_change().dropna(), maxlag=4)

Causalidade de Granger
número de defasagens (sem zero) 1
teste F baseado em ssr: F=0.0188 , p=0.8909 , df_denom=395, df_num=1
teste qui-quadrado baseado em ssr: chi2=0.0190 , p=0.8905 , df=1
teste de razão de verossimilhança: chi2=0.0190 , p=0.8905 , df=1
teste F de parâmetro: F=0.0188 , p=0.8909 , df_denom=395, df_num=1

Causalidade de Granger
número de defasagens (sem zero) 2
teste F baseado em ssr: F=2.2182 , p=0.1102 , df_denom=392, df_num=2
teste qui-quadrado baseado em ssr: chi2=4.4930 , p=0.1058 , df=2
teste de razão de verossimilhança: chi2=4.4678 , p=0.1071 , df=2
teste F de parâmetro: F=2.2182 , p=0.1102 , df_denom=392, df_num=2

Causalidade de Granger
número de defasagens (sem zero) 3
teste F baseado em ssr: F=1.7310 , p=0.1601 , df_denom=389, df_num=3
teste qui-quadrado baseado em ssr: chi2=5.2863 , p=0.1520 , df=3
teste de razão de verossimilhança: chi2=5.2513 , p=0.1543 , df=3
teste F de parâmetro: F=1.7310 , p=0.1601 , df_denom=389, df_num=3

Causalidade de Granger
número de defasagens (sem zero) 4
teste F baseado em ssr: F=1.4694 , p=0.2108 , df_denom=386, df_num=4
teste qui-quadrado baseado em ssr: chi2=6.0148 , p=0.1980 , df=4
teste de razão de verossimilhança: chi2=5.9694 , p=0.2014 , df=4
teste F de parâmetro: F=1.4694 , p=0.2108 , df_denom=386, df_num=4

O Dynamic Time Series Warping também nos permite encontrar semelhanças entre dois conjuntos de dados de séries temporais. O algoritmo também pode ser usado para alinhar séries de comprimentos diferentes. Nós aplicamos o algoritmo para encontrar pontos de semelhança entre os retornos mensais e horários de nossos dados. O algoritmo realiza essa tarefa minimizando uma função de custo especializada que mede a diferença entre 2 séries. Vamos começar importando as bibliotecas necessárias.

#Let's calculate the simillarities between our time series data
from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis

Agora vamos encontrar as semelhanças entre os retornos.

series_1 = prices["MN Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100
series_2 = prices["H1 Close"].pct_change(periods=1).dropna().reset_index(drop=True) * 100
path = dtw.warping_path(series_1, series_2)
dtwvis.plot_warping(series_1, series_2, path)

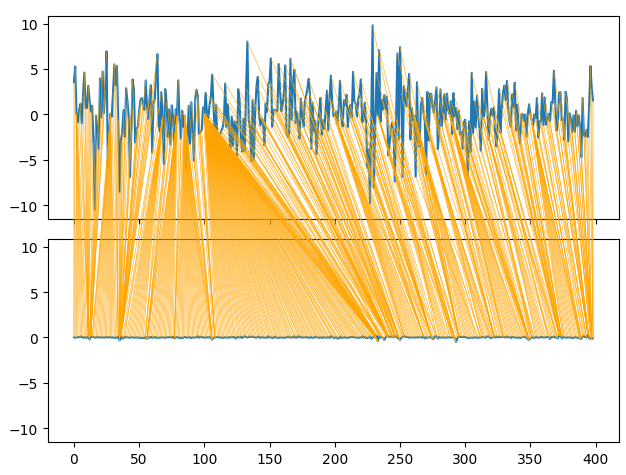
Fig 9: Visualizando as semelhanças entre os retornos mensais e horários

Ajuste de Parâmetros

Agora vamos ajustar os parâmetros de nossa Rede Neural Profunda para superar a performance de referência definida por nossa Regressão Linear. Note que, devido à natureza dos procedimentos de otimização usados para treinar a DNN, os resultados obtidos nesta seção do artigo podem ser difíceis de reproduzir. De fato, eu rodei esse teste 5 vezes e não conseguimos superar o modelo Linear em 2 dos testes.

Importe as bibliotecas necessárias e inicialize o modelo.

#Let's try to outperform our linear regression model
from sklearn.neural_network import MLPRegressor
from sklearn.model_selection import RandomizedSearchCV

#Let's tune our model
model = MLPRegressor(max_iter=500)

Defina o espaço de parâmetros.

#Tuner 
tuner = RandomizedSearchCV(
    model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,0.000000001,0.000000000000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001,0.000000001,0.000000000000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[1,0.1,0.0001,0.000001,100,10000,1000000,1000000000,100,1000],
        "shuffle": [True,False],
        "hidden_layer_sizes":[(1,4),(1,4,5),(1,8,10),(2,5),(8),(10,12),(5,10,4)]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ajuste o tuner.

tuner.fit(X_train_mn,y_train_mn)

Os melhores parâmetros que encontramos.

tuner.best_params_

{'tol': 0.001,
 'solver': 'lbfgs',
 'shuffle': True,
 'learning_rate_init': 1,
 'learning_rate': 'adaptive',
 'hidden_layer_sizes': (2, 5),
 'alpha': 1e-05,
 'activation': 'identity'}

Otimização Mais Profunda

Vamos realizar uma busca mais aprofundada por parâmetros ótimos usando a biblioteca SciPy.

#Deeper optimization
from scipy.optimize import minimize

Crie estruturas de dados para registrar nosso progresso.

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
optimization_progress = []

Defina a função objetivo a ser minimizada. Queremos minimizar o erro quadrático médio (RMSE) do nosso modelo.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=x[0],
                         tol=x[1],
                         learning_rate_init=x[2])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(X_train_mn)):
        #Train the model
        model.fit(X_train_mn.loc[train[0]:train[-1],:],y_train_mn.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(y_train_mn.loc[test[0]:test[-1]],model.predict(X_train_mn.loc[test[0]:test[-1],:]))
    #Record the progress made by the optimizer
    optimization_progress.append(current_error_rate.iloc[:,0].mean())
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Especifique o ponto inicial para o procedimento de otimização e forneça limites amplos para que possamos aproximar a otimização global.

#Define the starting point
pt = [tuner.best_params_["alpha"],tuner.best_params_["tol"],tuner.best_params_["learning_rate_init"]]
bnds = ((0.000000001,10000000000),(0.0000000001,10000000000),(0.000000001,10000000000))

Otimizando nosso modelo de DNN.

#Searchin deeper for parameters
result = minimize(objective,pt,method="TNC",bounds=bnds)

Parece que realizamos a otimização com sucesso.

Resultados

 message: Converged (|x_n-x_(n-1)| ~= 0)
 success: True
  status: 2
     fun: 0.04257403904271943
       x: [ 4.864e-05  1.122e-03  9.999e-01]
     nit: 1
     jac: [ 1.298e+04  1.806e+02 -3.371e+03]
    nfev: 92

Armazene nossos valores ótimos.

optima_y = result.fun
optima_x = optimization_progress.index(optima_y)
inputs = np.arange(0,len(optimization_progress))

Visualize o progresso feito pelo procedimento de Otimização.

plt.scatter(inputs,optimization_progress)
plt.plot(optima_x,optima_y,'s',color='r')
plt.axvline(x=optima_x,ls='--',color='red')
plt.axhline(y=optima_y,ls='--',color='red')
plt.title("Minimizing Training MSE")

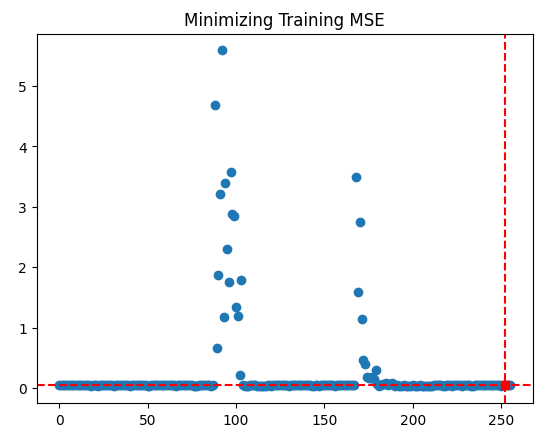
Fig 10: Os resultados do nosso procedimento de otimização TNC

Testando Overfitting

Vamos verificar se realmente conseguimos superar nosso modelo linear padrão.

#Test for overfitting
benchmark = LinearRegression()

default_model = MLPRegressor(max_iter=200)

random_search_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=tuner.best_params_["alpha"],
                         tol=tuner.best_params_["tol"],
                         learning_rate_init=tuner.best_params_["learning_rate_init"],
                         max_iter=200
                        )

lbfgs_model = MLPRegressor(hidden_layer_sizes=tuner.best_params_["hidden_layer_sizes"],
                         activation=tuner.best_params_["activation"],
                         learning_rate=tuner.best_params_["learning_rate"],
                         solver=tuner.best_params_["solver"],
                         shuffle=tuner.best_params_["shuffle"],
                         alpha=result.x[0],
                         tol=result.x[1],
                         learning_rate_init=result.x[2],
                         max_iter=200
                        )

Ajuste os modelos no conjunto de treino.

#Fit the models
benchmark.fit(X_train_mn,y_train_mn)
default_model.fit(X_train_mn,y_train_mn)
random_search_model.fit(X_train_mn,y_train_mn)
lbfgs_model.fit(X_train_mn,y_train_mn)

Faça as preparações para registrar nossas pontuações de validação cruzada.

#Record our cross val scores
models = [benchmark,
          default_model,
          random_search_model,
          lbfgs_model
         ]

val_error = pd.DataFrame(columns=["Linear Reg","Default NN","Random Search NN","TNC NN"],index=[0])

Valide cada modelo com cross-validation.

for i in np.arange(0,len(models)):
    val_error.iloc[0,i] = np.mean(cross_val_score(models[i],X_test_mn,y_test_mn,cv=5,n_jobs=-1)) * -1

Nosso erro de validação mostra claramente que nossa rede neural otimizada por TNC foi a que apresentou melhor desempenho.

val_error

Regressão Linear	NN padrão	Busca Aleatória NN	TNC NN
3.323741	3.987083	3.314776	3.283775

Exportando para formato ONNX

Agora vamos preparar a exportação do nosso modelo para o formato ONNX. ONNX significa Open Neural Network Exchange e é um protocolo de código aberto para representar qualquer modelo de aprendizado de máquina como uma árvore de nós representando cálculos e o fluxo de dados após cada cálculo. O ONNX nos permite construir e usar modelos de aprendizado de máquina em diferentes linguagens de programação, desde que implementem a especificação ONNX.

Importe a biblioteca ONNX para começar.

#Preparing to export to ONNX
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Prepare o modelo.

#Fit the model on all the data we have 
model = MLPRegressor(
 solver= 'lbfgs',
 shuffle= True,
 activation= 'identity',
 learning_rate= 'adaptive',
 hidden_layer_sizes= (2, 5),
 alpha= 4.864e-05,
 tol= 1.122e-03,
 learning_rate_init= 9.999e-01,
)

Ajuste o modelo em todos os dados que temos.

model.fit(prices[["MN Close"]],prices.loc[:,"MN Target"])

Defina o formato de entrada do nosso modelo.

#Define the input types for our ONNX model
initial_types = [("float_input",FloatTensorType([1,1]))]

Crie a representação ONNX do modelo.

# Create the ONNX representation
onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)

Exporte o modelo para o formato ONNX.

# Save the ONNX model
onnx.save_model(onnx_model,"EURUSD MN1 AI.onnx")

Agora vamos visualizar nosso modelo em formato ONNX para garantir que nossas entradas estejam no tamanho correto.

import netron

netron.start("EURUSD MN1 AI.onnx")

Fig 11: Visualizando nosso modelo DNN

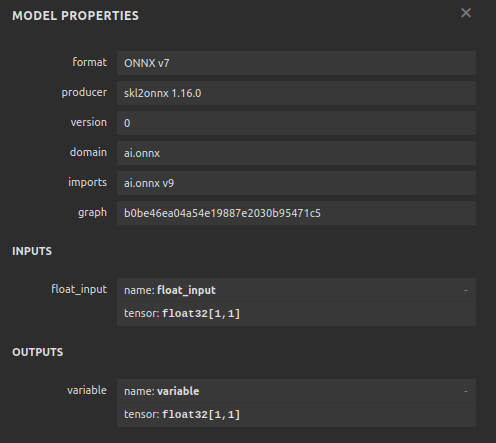
Fig 12: O formato de entrada/saída (I/O shape) do nosso modelo

Implementando em MQL5

Agora queremos implementar nosso algoritmo de trading em MQL5. Desejamos que nosso algoritmo de trading possa alternar entre fechar suas posições usando médias móveis simples e usar previsões de IA. Além disso, queremos orientar nosso modelo de IA utilizando análise técnica. Para começar, primeiro importaremos o modelo ONNX que exportamos acima.

//+------------------------------------------------------------------+
//|                                                EURUSD MTF AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX resources                                          |
//+------------------------------------------------------------------+
#resource "\\Files\\EURUSD MN1 AI.onnx" as const uchar onnx_buffer[];

Agora definiremos nosso enumerador personalizado para especificar como o usuário gostaria de fechar posições.

//+-------------------------------------------------------------------+
//| Define our custom type                                            |
//+-------------------------------------------------------------------+
enum close_type
  {
   MA_CLOSE = 0, // Moving Averages Close
   AI_CLOSE = 1  // AI Auto Close
  };

Vamos criar entradas, para que possamos mudar como nossa aplicação fecha posições e verificar qual abordagem é melhor.

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input close_type user_close_type = AI_CLOSE; // How should we close our positions?

Precisamos importar a classe de negociação (trade class).

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

Crie variáveis globais que precisaremos ao longo de nosso programa.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long    onnx_model;
vectorf model_input  = vectorf::Zeros(1);
vectorf model_output = vectorf::Zeros(1);
double  bid,ask;
int     ma_hanlder;
double  ma_buffer[];
int     bb_hanlder;
double  bb_mid_buffer[];
double  bb_high_buffer[];
double  bb_low_buffer[];
int     rsi_hanlder;
double  rsi_buffer[];
int     system_state = 0,model_state=0;

Quando nossa aplicação estiver sendo carregada, criaremos primeiro nosso modelo ONNX a partir do buffer que criamos anteriormente. Em seguida, atribuiremos nossos manipuladores de indicadores técnicos.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load our ONNX function
   if(!load_onnx_model())
     {
      return(INIT_FAILED);
     }

//--- Load our technical indicators
   bb_hanlder  = iBands("EURUSD",PERIOD_D1,30,0,1,PRICE_CLOSE);
   rsi_hanlder = iRSI("EURUSD",PERIOD_D1,14,PRICE_CLOSE);
   ma_hanlder  = iMA("EURUSD",PERIOD_D1,20,0,MODE_EMA,PRICE_CLOSE);

//---
   return(INIT_SUCCEEDED);
  }

Se nosso Expert Advisor for removido do gráfico, devemos liberar os recursos que não estivermos mais utilizando.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Release the resources we don't need
   release_resources();
  }

Agora, sempre que recebermos preços atualizados, primeiro armazenaremos os novos dados técnicos, faremos uma previsão com nosso modelo e, em seguida, exibiremos estatísticas importantes para o usuário. Se não tivermos posições abertas, seguiremos as previsões do nosso modelo. Caso contrário, seguiremos as entradas do usuário para determinar se devemos manter nossas posições abertas ou fechá-las.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market data
   update_market_data();

//--- Fetch a prediction from our model
   model_predict();

//--- Display stats
   display_stats();

//--- Find a position
   if(PositionsTotal() == 0)
     {
      if(model_state == 1)
         check_bullish_setup();
      else
         if(model_state == -1)
            check_bearish_setup();
     }

//--- Manage the position we have
   else
     {
      //--- How should we close our positions?
      if(user_close_type == MA_CLOSE)
        {
         ma_close_positions();
        }

      else
        {
         ai_close_positions();
        }

     }
  }
//+------------------------------------------------------------------+

Agora vamos definir como nosso sistema de IA deve encerrar suas operações. Se nosso sistema de IA detectar que os níveis de preços irão mudar de maneira que contradiga a posição assumida, encerraremos nossas operações.

//+------------------------------------------------------------------+
//| Close whenever our AI detects a reversal                         |
//+------------------------------------------------------------------+
void ai_close_positions(void)
  {
   if(system_state != model_state)
     {
      Alert("Reversal detected by our AI system,closing open positions");
      Trade.PositionClose("EURUSD");
     }
  }

Por outro lado, se confiarmos na média móvel para fechar nossas posições, então queremos encerrar quaisquer operações de venda se o preço de fechamento estiver acima da média móvel e vice-versa para as operações de compra.

//+------------------------------------------------------------------+
//| Close whenever price reverses the moving average                 |
//+------------------------------------------------------------------+
void ma_close_positions(void)
  {
//--- Is our buy position possibly weakening?
   if(system_state == 1)
     {
      if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0])
         Trade.PositionClose("EURUSD");
     }
//--- Is our sell position possibly weakening?
   if(system_state == -1)
     {
      if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0])
         Trade.PositionClose("EURUSD");
     }
  }

Para abrirmos uma operação, exigiremos primeiro um rompimento das Bandas de Bollinger, seguido de uma confirmação pelo indicador RSI e, por fim, também queremos ver a média móvel no lado correto em relação ao preço.

//+------------------------------------------------------------------+
//| Check bearish setup                                              |
//+------------------------------------------------------------------+
void check_bearish_setup(void)
  {
   if(iClose("EURUSD",PERIOD_D1,0) < bb_low_buffer[0])
     {
      if(50 > rsi_buffer[0])
        {
         if(iClose("EURUSD",PERIOD_D1,0) < ma_buffer[0])
           {
            Trade.Sell(0.3,"EURUSD",bid,0,0,"EURUSD MTF AI");
            system_state = -1;
           }
        }
     }
  }

//+------------------------------------------------------------------+
//| Check bullish setup                                              |
//+------------------------------------------------------------------+
void check_bullish_setup(void)
  {
   if(iClose("EURUSD",PERIOD_D1,0) > bb_high_buffer[0])
     {
      if(50 < rsi_buffer[0])
        {
         if(iClose("EURUSD",PERIOD_D1,0) > ma_buffer[0])
           {
            Trade.Buy(0.3,"EURUSD",ask,0,0,"EURUSD MTF AI");
            system_state = 1;
           }
        }
     }
  }

Essa função atualmente exibirá apenas a previsão do modelo.

//+------------------------------------------------------------------+
//| Display account stats                                            |
//+------------------------------------------------------------------+
void display_stats(void)
  {
   Comment("Forecast: ",model_output[0]);
  }

Obtendo uma previsão de nosso modelo e armazenando-a usando uma flag binária.

//+------------------------------------------------------------------+
//| Fetch a prediction from our model                                |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get inputs
   model_input.CopyRates("EURUSD",PERIOD_MN1,COPY_RATES_CLOSE,0,1);
//--- Fetch a prediction from our model
   OnnxRun(onnx_model,ONNX_DEFAULT,model_input,model_output);
//--- Store the model's prediction as a flag
   if(model_output[0] > model_input[0])
     {
      model_state = -1;
     }
   else
      if(model_output[0] < model_input[0])
        {
         model_state = 1;
        }
  }

Agora vamos especificar a função que liberará os recursos que não precisamos.

//+------------------------------------------------------------------+
//| Release the resources we don't need                              |
//+------------------------------------------------------------------+
void release_resources(void)
  {
   OnnxRelease(onnx_model);
   IndicatorRelease(ma_hanlder);
   IndicatorRelease(rsi_hanlder);
   IndicatorRelease(bb_hanlder);
   ExpertRemove();
  }

Sempre que uma nova cotação de preço chegar, esta função será chamada para atualizar os dados de mercado que temos.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
//--- Update all our technical data
   bid = SymbolInfoDouble("EURUSD",SYMBOL_BID);
   ask = SymbolInfoDouble("EURUSD",SYMBOL_ASK);
   CopyBuffer(ma_hanlder,0,0,1,ma_buffer);
   CopyBuffer(rsi_hanlder,0,0,1,rsi_buffer);
   CopyBuffer(bb_hanlder,0,0,1,bb_mid_buffer);
   CopyBuffer(bb_hanlder,1,0,1,bb_high_buffer);
   CopyBuffer(bb_hanlder,2,0,1,bb_low_buffer);
  }

Por fim, vamos definir a função que criará nosso modelo ONNX a partir do buffer que definimos anteriormente.

//+------------------------------------------------------------------+
//| Load our ONNX model                                              |
//+------------------------------------------------------------------+
bool load_onnx_model(void)
  {
//--- Create the ONNX model from our buffer
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model
   if(onnx_model == INVALID_HANDLE)
     {
      //--- Give feedback
      Comment("Failed to create the ONNX model");
      //--- We failed to create the model
      return(false);
     }

//--- Specify the I/O shapes
   ulong input_shape[] = {1,1};
   ulong output_shape[] = {1,1};

//--- Validate the I/O shapes
   if(!(OnnxSetInputShape(onnx_model,0,input_shape)) || !(OnnxSetOutputShape(onnx_model,0,output_shape)))
     {
      //--- Give feedback
      Comment("We failed to define the correct input shapes");

      //--- We failed to define the correct I/O shape
      return(false);
     }

   return(true);
  }
//+------------------------------------------------------------------+

Fig 13: As entradas do nosso Expert Advisor

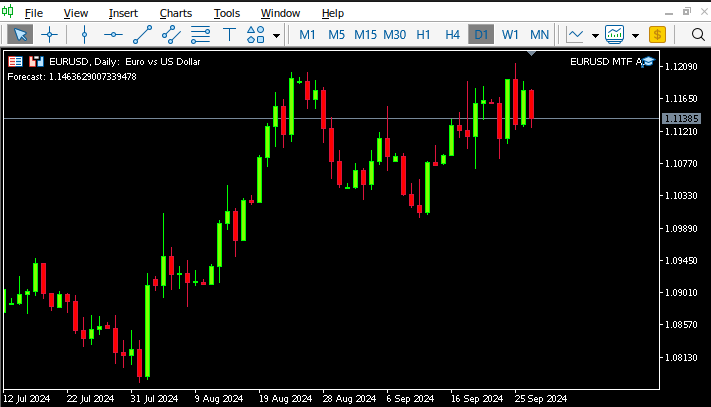
Fig 14: Nosso Expert Advisor em ação

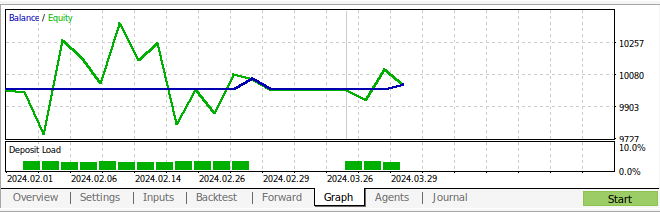
Fig 15: Os resultados do back-testing de nossa estratégia

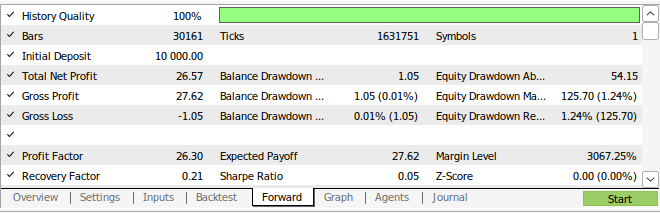
Fig 16: Resultados do walk forward testing da nossa estratégia

Conclusão

Neste artigo, demonstramos que os períodos mensal e horário parecem ser os mais estáveis para prever o par EURUSD. Não podemos afirmar com confiança que isso seja válido para todos os mercados existentes. Da mesma forma, devemos no futuro considerar testar mais períodos possíveis para garantir que não estejamos deixando de lado intervalos de tempo mais adequados. Além disso, há outros ajustes que podemos fazer em nossa abordagem para buscar métricas de erro mais baixas. Por exemplo, podemos nos perguntar se existe uma combinação de períodos de tempo que poderia reduzir ainda mais nossos níveis de erro.