Expert Advisor Auto-Otimizável com MQL5 e Python (Parte VI): Aproveitando o Deep Double Descent

O overfitting em aprendizado de máquina pode assumir muitas formas diferentes. Mais comumente, ocorre quando um modelo de IA aprende demais sobre o ruído nos dados e não consegue fazer generalizações úteis. Isso leva a um desempenho ruim quando avaliamos o modelo em dados que ele nunca viu antes. Muitas técnicas foram desenvolvidas para mitigar o overfitting, mas tais métodos podem ser desafiadores de implementar, especialmente quando você está apenas começando sua jornada. No entanto, um artigo recente, publicado por um grupo de ex-alunos de Harvard, sugere que, em certas tarefas, o overfitting pode ser um problema do passado. Este artigo irá guiá-lo pelo estudo e demonstrar como você pode construir modelos de IA de classe mundial, alinhados com as pesquisas mais avançadas do mundo.

Visão Geral da Metodologia

Existem muitas técnicas usadas para detectar overfitting ao desenvolver modelos de IA. O método mais confiável é examinar os gráficos do erro de teste e do erro de treinamento do modelo. Inicialmente, os dois gráficos podem cair juntos, o que é um bom sinal.. À medida que continuamos treinando nosso modelo, atingiremos um nível ótimo de erro e, uma vez ultrapassado esse ponto, o erro de treinamento continua a cair, mas o erro de teste só piora. Muitas técnicas foram desenvolvidas para remediar esse problema, como o early stopping. O early stopping encerra o procedimento de treinamento se o erro de validação do modelo não mudar significativamente ou continuar a se deteriorar. Depois, os melhores pesos são restaurados, e assume-se que o melhor modelo foi localizado, como na Fig. 1 abaixo.

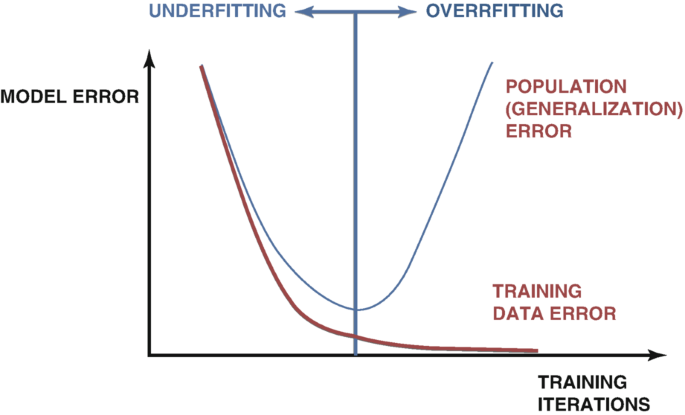
Fig 1: Um gráfico generalizado demonstrando o overfitting na prática

Essas ideias foram abaladas até suas bases por um artigo de 2019 intitulado "Deep Double Descent", cujo link está disponível aqui. O artigo não tenta explicar o fenômeno que demonstra, apenas descreve as características do fenômeno observadas na época da escrita. Em essência, o estudo mostra que, em certos problemas, o erro de teste do modelo cairá a princípio, antes de começar a subir e depois cair dramaticamente uma segunda vez, atingindo novos mínimos antes da convergência final, como demonstrado na Fig. 2 abaixo.

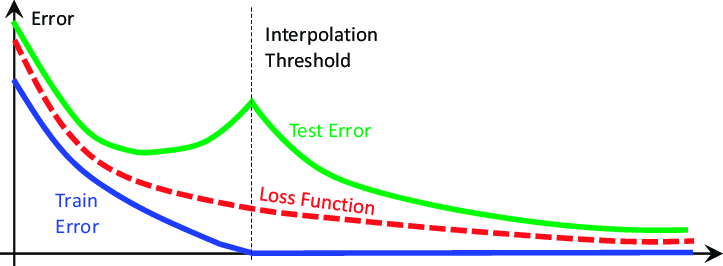
Fig 2: Visualizando o fenômeno do deep double descent

O artigo demonstra que esse fenômeno pode ser conceituado como função de:

1. Os parâmetros do modelo.
2. O número máximo de iterações de treinamento.

Ou seja, se treinarmos continuamente modelos cada vez maiores no mesmo conjunto de dados, observaremos que o erro de teste cairá primeiro, antes de começar a subir, e se continuarmos treinando modelos ainda maiores, veremos o erro de teste cair novamente, para novos mínimos, criando um gráfico de erro semelhante ao da Fig. 2 acima. No entanto, treinar progressivamente modelos cada vez maiores nem sempre é viável devido ao custo computacional. Para nossa discussão, exploraremos o fenômeno do deep double descent como uma função do número máximo de iterações permitidas.

A ideia é que, à medida que permitimos que nosso modelo realize mais iterações de treinamento, seu erro de validação sempre aumentará primeiro, antes de cair para novos mínimos. O tempo necessário para o modelo atingir seu erro máximo e começar a cair varia dependendo de vários fatores, como a quantidade de ruído no conjunto de dados e o tipo de modelo sendo treinado.

Não há explicações amplamente aceitas para o fenômeno, mas até agora, a forma mais simples de entendê-lo é imaginar o double descent como uma função dos parâmetros do modelo.

Imagine que começamos com uma rede neural simples; o modelo provavelmente subajustará (underfitting) nossos dados. Isso significa que seu desempenho poderia melhorar adicionando mais complexidade ao modelo. À medida que aumentamos a complexidade da rede neural, lentamente nos aproximamos de um ponto em que nosso modelo se ajusta exatamente aos dados. No aprendizado de máquina tradicional, aprendemos que o erro de treinamento sempre cairá se tornarmos o modelo mais complexo. Isso é verdade. Mas não é toda a verdade.

Uma vez que nosso modelo é complexo o suficiente para ajustar nossos dados perfeitamente, neste ponto o erro de treinamento é tipicamente um valor muito próximo de 0 e para de cair, mesmo que aumentemos ainda mais a complexidade. Esse é o primeiro golpe contra as ideologias tradicionais do aprendizado de máquina. Esse ponto é comumente chamado de limiar de interpolação. Se continuarmos aumentando a complexidade do modelo além desse limiar, observaremos uma queda notável na acurácia do teste. E, na maioria dos casos, as taxas de erro do modelo cairão para novos mínimos e se estabilizarão ali.

Algoritmos destinados a mitigar o overfitting, como o early stopping, parecem ter nos limitado sem querer. Esses algoritmos sempre encerrarão o treinamento antes de observarmos a segunda descida. Vamos recriar o fenômeno do double descent, para observá-lo independentemente.

Primeiros Passos

Primeiro, precisaremos extrair nossos dados da plataforma MetaTrader 5 usando um script que construímos em MQL5.

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- File name
   string file_name = "Market Data " + Symbol()+  ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);
  }
//+------------------------------------------------------------------+

Para começar, vamos importar primeiro as bibliotecas necessárias.

#Standard libraries
import pandas                  as     pd
import numpy                   as     np
import seaborn                 as     sns
import matplotlib.pyplot       as     plt
from   mpl_toolkits.mplot3d    import Axes3D
from   sklearn.linear_model    import LinearRegression
from   sklearn.neural_network  import MLPRegressor
from   sklearn.metrics         import mean_squared_error
from   sklearn.model_selection import cross_val_score,TimeSeriesSplit

Agora, vamos carregar os dados.

#Read in the data
data = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')

Vamos limpar os dados.

#Clean up the data
data.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)

Remova as colunas desnecessárias.

#Drop columns we don't need
data = data.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
data

Visualizando os dados.

#Plot the close price
plt.plot(data["Close"])
plt.xlabel("Time")
plt.ylabel("Close Price")
plt.title("GBPUSD Daily Close")

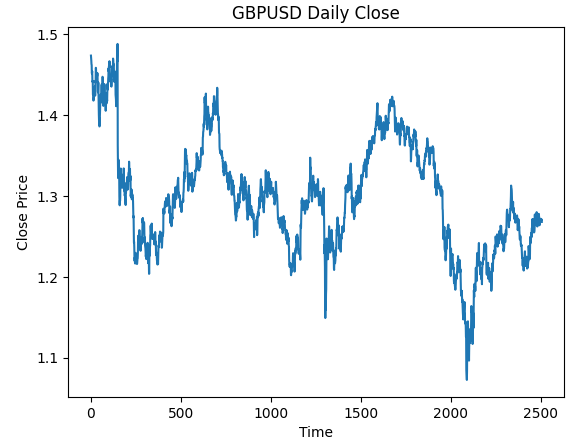
Fig 3: Os dados diários de OHLC do GBPUSD com os quais trabalharemos

Queremos treinar um modelo que preveja os retornos diários do GBPUSD. No entanto, existem 2 variáveis que precisamos escolher:

1. Com que frequência devemos calcular os retornos?
2. Quão longe no futuro devemos prever?

Normalmente, prevemos 1 passo à frente e calculamos os retornos como a diferença entre 2 dias consecutivos. Mas será que isso é realmente o ideal? É sempre o melhor que podemos fazer? Não responderemos a essa pergunta — os próprios dados responderão por nós.

Vamos realizar uma busca em grade (grid search) para os parâmetros de nossos retornos e de nosso horizonte de previsão. Primeiro, precisamos definir um eixo uniforme para ambos os parâmetros.

#Define the input range
x_min , x_max = 2,100 #Look ahead
y_min , y_max = 2,100 #Period

Agora, defina os eixos X e Y.

#Sample input range uniformly
x_axis = np.arange(x_min,x_max,4) #Look ahead
y_axis = np.arange(y_min,y_max,4) #Period

Precisamos criar uma mesh-grid. A mesh-grid são dois arrays bidimensionais individuais que podem ser usados juntos para mapear todas as combinações possíveis de entradas que queremos avaliar.

#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis)

Essa função será usada para limpar o conjunto de dados antes de testarmos a acurácia do modelo com as novas configurações que gostaríamos de avaliar.

#This function will create and return a clean dataframe according to our specifications
def clean_data(look_ahead,period):
    #Create a copy of the data
    temp = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')
    #Clean up the data
    temp.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)
    temp = temp.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
    #Define our target
    temp["Target"] = temp["Close"].shift(-look_ahead)
    #Apply the differencing
    temp["Close"] = temp["Close"].diff(period)
    temp["Open"] = temp["Open"].diff(period)
    temp["High"] = temp["High"].diff(period)
    temp["Low"] = temp["Low"].diff(period)
    temp = temp.dropna()
    temp = temp.reset_index(drop=True)
    return(temp)

Nossa próxima função irá validar cruzadamente o modelo sob as configurações passadas e retornar seu erro de validação cruzada.

#Evaluate the objective function
def evaluate(look_ahead,period):
    #Define the model
    model = LinearRegression()
    #Define our time series split
    tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
    temp = clean_data(look_ahead,period)
    score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv))
    return(score)

Finalmente, precisamos de uma função que registre nossos resultados em um array que tenha o mesmo formato de qualquer uma de nossas mesh-grids.

#Define the objective
def objective(x,y):
    #Define the output matrix
    results = np.zeros([x.shape[0],y.shape[0]])
    #Fill in the output matrix
    for i in np.arange(0,x.shape[0]):
        #Select the rows
        look_ahead = x[i]
        period     = y[i]
        for j in np.arange(0,y.shape[0]):
            results[i,j] = evaluate(look_ahead[j],period[j])
    return(results)

Até agora, implementamos as funções de que precisamos para ver como os níveis de erro do modelo mudam à medida que alteramos o intervalo com o qual calculamos os retornos e até onde no futuro desejamos prever. Primeiro, vamos observar como um modelo simples se comporta quando mudamos esses parâmetros, antes de começarmos a lidar com redes neurais profundas mais complexas.

linear_reg_res = objective(x,y)
linear_reg_res = np.abs(linear_reg_res)

Um gráfico de contorno é comumente usado em geografia para mostrar mudanças de altitude em um terreno. Podemos usar esses gráficos de superfície para encontrar quais pares de parâmetros produzem os menores níveis de erro em nosso modelo de regressão linear simples. As regiões azuis são combinações que produziram baixo erro, enquanto as regiões vermelhas são combinações insatisfatórias. O ponto branco, na região azul-escura do gráfico de contorno, representa as melhores configurações de previsão para nosso modelo de regressão linear.

Como podemos ver no gráfico abaixo, nosso modelo linear simples teria superado facilmente qualquer trader no mercado que estivesse usando o período de retorno clássico de 1 e prevendo 1 passo à frente.

plt.contourf(x,y,linear_reg_res,100,cmap="jet")
plt.plot(x_axis[linear_reg_res.min(axis=0).argmin()],y_axis[linear_reg_res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting GBPUSD Daily Close")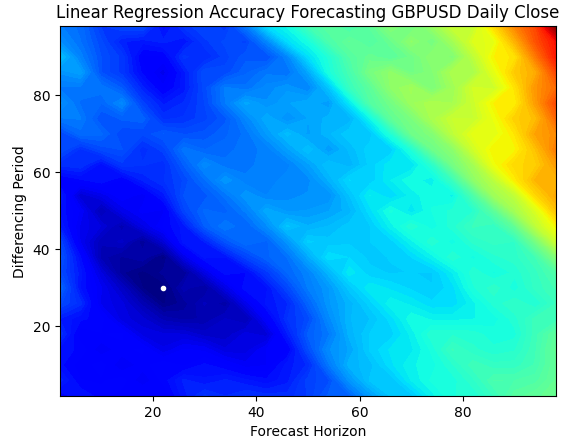

Fig 4: Nosso gráfico de contorno da acurácia da regressão linear prevendo o GBPUSD Diário

Visualizar os resultados em 3D gera uma superfície que nos permite enxergar a relação do modelo com o mercado GBPUSD. O gráfico mostra que, à medida que prevemos mais adiante no futuro, nossas taxas de erro caem até um nível ótimo e começam a subir novamente à medida que continuamos olhando mais para frente. No entanto, a conclusão mais importante é que, para nosso modelo linear, a Fig. 5 abaixo mostra claramente que as melhores entradas estão na faixa de 20 a 40, tanto para o horizonte de previsão quanto para o período de retorno.

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,linear_reg_res,cmap="jet")

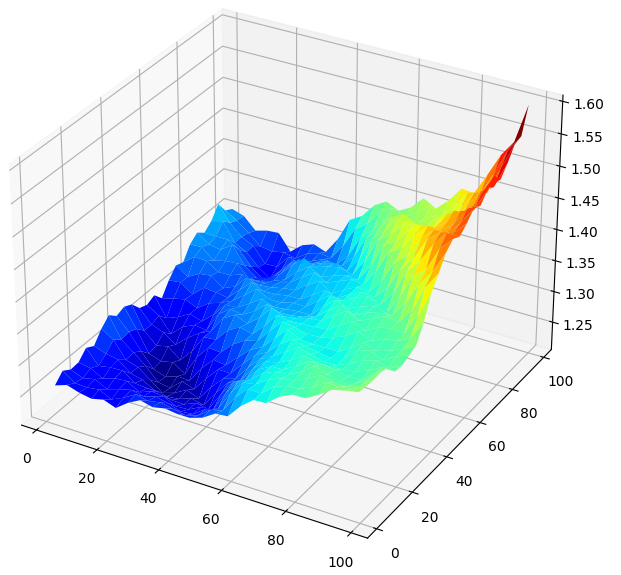
Fig 5: Visualizando o erro do modelo linear ao prever os retornos diários do GBPUSD

Agora que estamos familiarizados com os gráficos de contorno e de superfície, vamos observar como nossa rede neural profunda se comporta quando a usamos para buscar no mesmo espaço de parâmetros.

res = objective(x,y)
res = np.abs(res)

O gráfico de superfície da rede neural é exponencialmente mais complexo de visualizar. As zonas azuis são desejáveis porque representam combinações que produziram baixos níveis de erro. No entanto, repare que zonas vermelhas surgem abruptamente no meio de combinações ótimas. Isso é bastante interessante, não é?

Como duas combinações podem estar tão próximas e ainda assim ter níveis de erro tão diferentes? Isso ocorre em parte devido à natureza dos algoritmos de otimização usados para treinar redes neurais. Se treinássemos esse modelo uma segunda vez, obteríamos um gráfico inteiramente diferente, com um ponto ótimo diferente.

plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")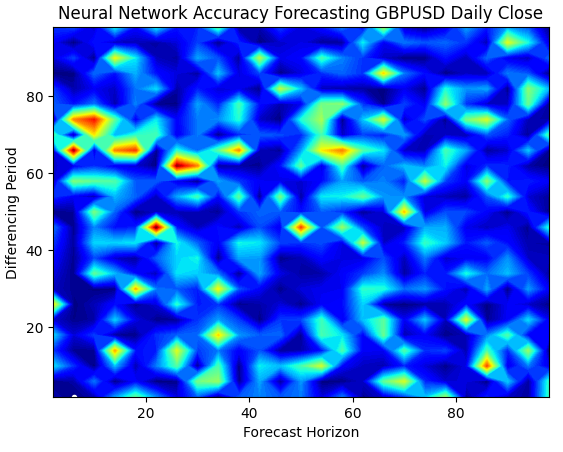

Fig 6: As redes neurais são muito sensíveis às entradas que fornecemos

Ao visualizar o desempenho do modelo em 3D, podemos ver o quão instáveis as redes neurais podem ser. Podemos afirmar com confiança que a rede neural aprendeu efetivamente alguma relação útil? Qual modelo está se saindo melhor até agora? Se abordarmos o problema pela escola de pensamento tradicional, escolheremos o modelo linear simples, porque ele gera gráficos de erro mais suaves — o que pode ser um sinal de maior habilidade — e as taxas de erro voláteis da rede neural poderiam ser vistas como indício de overfitting.

No entanto, essa é uma abordagem clássica de aprendizado de máquina. Pela escola contemporânea, vemos os gráficos de erro da rede neural como indicação de que o modelo ainda não convergiu de fato, e não como indício de overfitting. Em outras palavras, de acordo com o artigo do Double Descent, ainda é cedo para compararmos a rede neural. Vamos tentar provar isso por conta própria, em vez de confiar cegamente em artigos de pesquisa devido à credibilidade de seus autores.

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,res,cmap="jet")

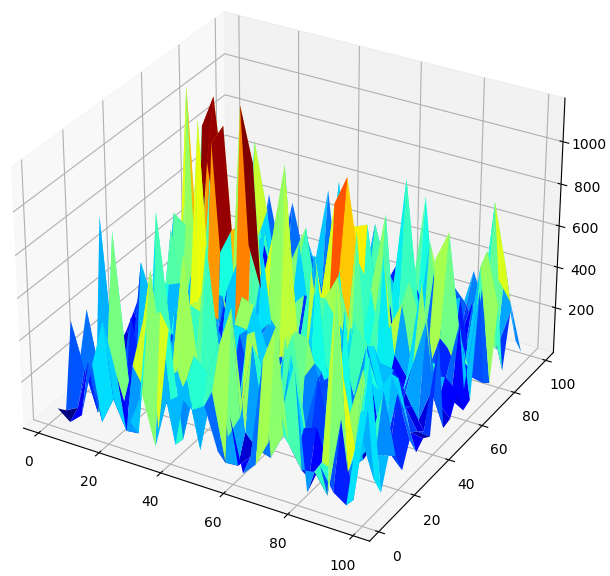
Fig 7: Níveis de erro da rede neural prevendo os retornos diários do GBPUSD

Verificando o Double Descent

Primeiro, aplicaremos os melhores parâmetros que encontramos para calcular os retornos e até onde no futuro devemos prever.

#The best settings we have found so far
look_ahead = x_axis[res.min(axis=0).argmin()]
difference_period = y_axis[res.min(axis=1).argmin()]
data["Target"] = data["Close"].shift(-look_ahead)
#Apply the differencing
data["Close"] = data["Close"].diff(difference_period)
data["Open"] = data["Open"].diff(difference_period)
data["High"] = data["High"].diff(difference_period)
data["Low"] = data["Low"].diff(difference_period)
data.dropna(inplace=True)
data.reset_index(drop=True,inplace=True)
data

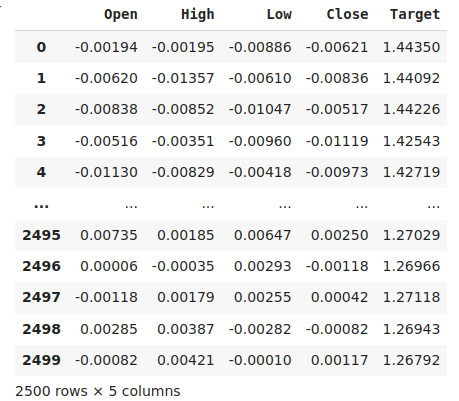
Fig 8: Nossos dados em sua forma atual

Importando as bibliotecas necessárias.

from sklearn.model_selection import train_test_split,TimeSeriesSplit
from sklearn.metrics         import mean_squared_error

Defina o número máximo de epochs. Lembre-se de que o double descent é uma função da complexidade do modelo ou do número máximo de iterações de treinamento. Testaremos isso com uma rede neural simples e variaremos o número máximo de iterações. Nosso número máximo de iterações será progressivo em potências de 2.

max_epoch = 50

Criando um DataFrame para armazenar nossos níveis de erro.

err_rates = pd.DataFrame(columns = np.arange(0,max_epoch),index=["Train","Validation","Test"])

Precisamos configurar nosso objeto de divisão de séries temporais.

tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

Agora realize a divisão train test.

train , test = train_test_split(data,shuffle=False,test_size=0.5)

Validando nosso modelo de forma cruzada, à medida que aumentamos o número máximo de iterações como potências de 2.

for j in np.arange(0,max_epoch):
  #Define our model and measure its error
  current_train_err = []
  current_val_err = []
  model = MLPRegressor(hidden_layer_sizes=(6,5),max_iter=(2 ** j))

  for i,(train_index,test_index) in enumerate(tscv.split(train)):
    #Assess the model
    model.fit(train.loc[train_index,["Open","High","Low","Close"]],train.loc[train_index,'Target'])
    current_train_err.append(mean_squared_error(train.loc[train_index,'Target'],model.predict(train.loc[train_index,["Open","High","Low","Close"]])))
    current_val_err.append(mean_squared_error(train.loc[test_index,'Target'],model.predict(train.loc[test_index,["Open","High","Low","Close"]])))

  #Record our observations
  err_rates.loc["Train",j]      = np.mean(current_train_err)
  err_rates.loc["Validation",j] = np.mean(current_val_err)
  err_rates.loc["Test",j]       = mean_squared_error(test['Target'],model.predict(test.loc[:,["Open","High","Low","Close"]]))

Nossas primeiras 6 iterações mostram como as taxas de erro do modelo mudaram ao passarmos de 1 para 32 iterações de treinamento. Como podemos ver no gráfico abaixo, nosso erro de teste começou caindo, depois começou a subir, antes de formar um fundo mais alto. Nossas taxas de erro de treinamento e validação começaram aumentando antes de cair para um fundo levemente mais alto e depois subirem novamente. No entanto, 32 iterações representam apenas um pequeno intervalo do processo de treinamento. Vamos observar como o restante do processo se desenrola.

plt.plot(err_rates.iloc[0,0:5])
plt.plot(err_rates.iloc[1,0:5])
plt.plot(err_rates.iloc[2,0:5])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

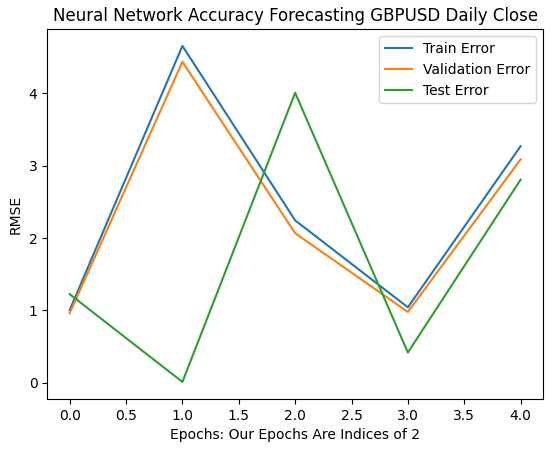
Fig 9: Nossa acurácia de validação de 1 a 32 iterações

À medida que avançamos, agora vemos como as taxas de erro do modelo evoluem no intervalo de 64 a 256. Parece que, após alguma divergência, as taxas de erro finalmente estão convergindo para um mínimo. No entanto, de acordo com o artigo, ainda temos um longo caminho a percorrer.

Vale notar que, por padrão, o scikit-learn instancia redes neurais que executam apenas 200 iterações. Esse número é um pouco menor que 2 elevado à potência 8. E com algoritmos como o early stopping, teríamos ficado presos em ótimos locais enganosos, em algum lugar entre os vales e picos da superfície irregular observada na Fig. 7 acima. 

plt.plot(err_rates.iloc[0,0:9])
plt.plot(err_rates.iloc[1,0:9])
plt.plot(err_rates.iloc[2,0:9])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

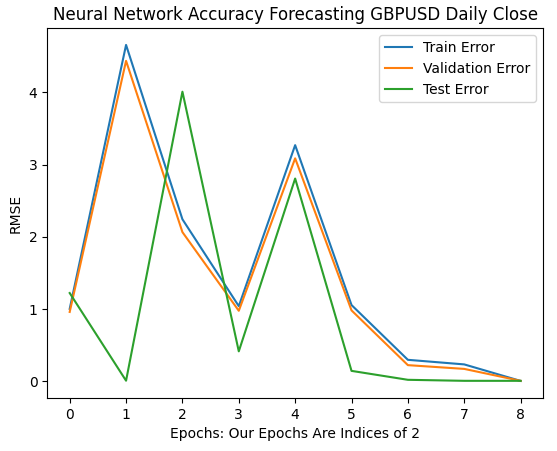
Fig 10: As taxas de erro do modelo começam a convergir

Nossas taxas de erro ótimas foram produzidas quando o modelo pôde executar mais de 1 bilhão de iterações! O número exato é 2 elevado à potência 30. Esse ponto está marcado pela linha vertical vermelha na Fig. 11 abaixo. Normalmente realizamos frações do número ótimo de iterações, por medo de overfitting, o que nos deixa presos em níveis de erro subótimos à esquerda da linha vermelha.

plt.plot(err_rates.iloc[0,:])
plt.plot(err_rates.iloc[1,:])
plt.plot(err_rates.iloc[2,:])
plt.axvline(err_rates.loc["Test",:].argmin(),color='red')
plt.legend(["Train Error","Validation Error","Test Error","Double Descent Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")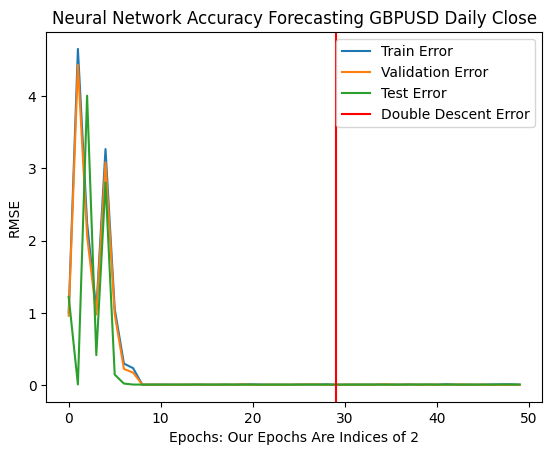

Fig 11: Nossos níveis de erro do double descent estão marcados pela linha vertical vermelha, e à esquerda podemos observar o domínio clássico do aprendizado de máquina tradicional

Otimização da Nossa Rede Neural

Fica claro que há algum mérito no artigo. Em circunstâncias normais, nem sequer consideraríamos permitir inúmeras iterações, por medo de overfitting. Agora podemos otimizar nosso modelo com confiança, sem o medo de superajustar os dados de treinamento.

from sklearn.model_selection import RandomizedSearchCV

Inicializar o modelo.

#Reinitialize the model
model = MLPRegressor(max_iter=(err_rates.loc["Test",:].argmin()))

Vamos definir os parâmetros sobre os quais queremos buscar.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(1,4),(5,8,10),(5,10,20),(10,50,10),(20,5),(1,5),(20,10)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=2**9,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Finalmente, ajuste o objeto tuner.

tuner.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

Os melhores parâmetros que encontramos.

tuner.best_params_

{'warm_start': True,
 'tol': 0.1,
 'solver': 'lbfgs',
 'shuffle': False,
 'learning_rate_init': 1e-06,
 'learning_rate': 'adaptive',
 'hidden_layer_sizes': (5, 8, 10),
 'early_stopping': False,
 'alpha': 1e-05,
 'activation': 'relu'}

Convertendo para ONNX

Agora que criamos nosso modelo, podemos convertê-lo para o formato ONNX. ONNX significa Open Neural Network Exchange, e é um protocolo de código aberto que nos permite criar e implantar modelos de IA em qualquer linguagem de programação que ofereça suporte à especificação da API ONNX. O MQL5 nos permite importar nossos modelos de IA e implantá-los diretamente em nossos terminais. Primeiro, vamos importar as bibliotecas necessárias.

import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Em seguida, ajustaremos nosso modelo com todos os dados disponíveis.

model = tuner.best_estimator_.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

Especifique a forma de entrada (input shape) do seu modelo.

#Define the input shape of 1,4
initial_type = [('float_input', FloatTensorType([1, 4]))]
#Specify the input shape
onnx_model = convert_sklearn(model, initial_types=initial_type)

Salve o modelo ONNX.

#Save the onnx model
onnx.save(onnx_model,"GBPUSD DAILY.onnx")

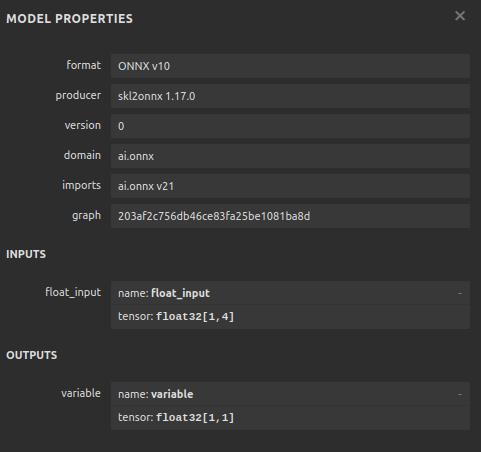
Fig 12: Os parâmetros de entrada e saída do nosso modelo ONNX

 

Implementação em MQL5

Agora podemos começar a implementar nossa estratégia de trading em MQL5. Nossa estratégia será baseada no período Daily. Usaremos uma combinação das Bandas de Bollinger e Médias Móveis para determinar a tendência predominante do mercado.

As Bandas de Bollinger são comumente usadas para identificar ativos sobrecomprados ou sobrevendidos. Normalmente, quando o preço atinge a banda superior, considera-se que o ativo em questão está sobrecomprado. Tipicamente, quando os preços estão sobrecomprados, espera-se que eles caiam e retornem ao nível médio. Nós, porém, usaremos as Bandas de Bollinger de forma seguidora de tendência.

Quando os preços cruzarem acima da linha do meio das Bandas, consideraremos isso um forte sinal de alta (bullish), e o oposto será verdadeiro quando os preços caírem abaixo da linha do meio — tomaremos isso como um forte sinal de venda. Regras de trading tão simples tendem a gerar sinais em excesso, o que pode não ser o ideal. Por isso, filtraremos as flutuações de preço considerando valores de médias móveis em vez da ação do preço em si.

Aplicaremos 2 médias móveis: uma sobre o preço máximo (high) e outra sobre o preço mínimo (low), para criar um canal de médias móveis. Nossos sinais de entrada serão gerados quando ambas as médias móveis cruzarem a linha do meio da Banda de Bollinger e nossa previsão de IA indicar que o preço realmente se moverá naquela direção. 

Finalmente, nossas posições serão encerradas sempre que o canal de médias móveis cruzar novamente a linha do meio da Banda de Bollinger, ou se o canal voltar para dentro das Bandas após ter rompido para fora — o que acontecer primeiro.

Vamos começar primeiro carregando nosso modelo ONNX.

//+------------------------------------------------------------------+
//|                                                    GBPUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load our ONNX file                                               |
//+------------------------------------------------------------------+
#resource  "\\Files\\GBPUSD DAILY.onnx" as const uchar onnx_buffer[];

Em seguida, precisamos carregar a biblioteca Trade para ajudar a gerenciar nossas posições.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

Também precisamos de algumas variáveis globais para os dados que compartilharemos em diferentes partes da aplicação.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
bool   patience = true;
long   onnx_model;
int    bb_handler,ma_h_handler,ma_l_handler;
double ma_h_buffer[],ma_l_buffer[];
double bb_h_buffer[],bb_m_buffer[],bb_l_buffer[];
int    state;
double bid,ask;
vectorf model_forecast = vectorf::Zeros(1);

Nossos indicadores técnicos têm parâmetros de período que queremos que o usuário final possa ajustar conforme as condições de mercado mudem.

//+------------------------------------------------------------------+
//| User Inputs                                                      |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int bb_period = 60;
input int ma_period = 14;

Na primeira vez que nossa aplicação for carregada, inicializaremos os indicadores técnicos antes de carregar o modelo ONNX. Usaremos o buffer ONNX definido no início do programa para criar um modelo a partir dele. A partir daí, validaremos que nosso modelo ONNX está correto e que seus parâmetros de entrada e saída estão alinhados com nossas especificações.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Setup technical indicators
   bb_handler   = iBands(Symbol(),PERIOD_D1,bb_period,0,1,PRICE_CLOSE);
   ma_h_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_HIGH);
   ma_l_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_LOW);
//--- Define our ONNX model
   ulong input_shape [] = {1,4};
   ulong output_shape [] = {1,1};
//--- Create the model
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

   if(onnx_model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to load AI module correctly");
      return(INIT_FAILED);
     }

//--- Validate I/O
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()," Actual shape: ",OnnxGetInputCount(onnx_model));
      return(INIT_FAILED);
     }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()," Actual shape: ",OnnxGetOutputCount(onnx_model));
      return(INIT_FAILED);
     }


//--- Everything was okay
   return(INIT_SUCCEEDED);
  }

Se nossa aplicação de trading não estiver mais em uso, liberaremos os recursos que não estivermos utilizando.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(onnx_model);
   IndicatorRelease(bb_handler);
   IndicatorRelease(ma_h_handler);
   IndicatorRelease(ma_l_handler);
  }

Por fim, sempre que recebermos novas cotações de preços, atualizaremos nossas variáveis globais. A partir disso, o próximo passo dependerá do número de posições abertas: Se nenhuma, buscaremos um sinal de entrada. Caso contrário, verificaremos sinais de saída.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update technical data
   update();

   if(PositionsTotal() == 0)
     {
      patience = true;
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      string direction = model_forecast[0] > iClose(Symbol(),PERIOD_D1,0) ? "UP" : "DOWN";
      Comment("Model Forecast: ",model_forecast[0]," ",direction);
      close_setup();
     }
  }

A função a seguir obterá uma previsão do nosso modelo.

//+------------------------------------------------------------------+
//| Get a prediction from our model                                  |
//+------------------------------------------------------------------+
void model_predict(void)
  {
   double o,h,l,c;
   vector op,hi,lo,cl;
   op.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OPEN,0,3);
   hi.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_HIGH,0,3);
   lo.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_LOW,0,3);
   cl.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_CLOSE,0,3);

   o =  op[2]  - op[0];
   h =  hi[2]  - hi[0];
   l =  lo[2]  - lo[0];
   c =  cl[2]  - cl[0];

   vectorf model_inputs = vectorf::Zeros(4);
   model_inputs[0] = o;
   model_inputs[1] = h;
   model_inputs[2] = l;
   model_inputs[3] = c;

   OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast);
  }

Agora definiremos como nossa aplicação deve encerrar posições. A variável booleana patience será usada para controlar quando a aplicação deve fechar as posições. Se o canal de médias móveis não tiver rompido as Bandas de Bollinger quando nossas posições foram inicialmente abertas, a variável patience será definida como true. Esse valor permanecerá true até que o canal rompa as Bandas. Nesse ponto, a flag patience será alterada para false e, se o canal retornar para dentro das Bandas, nossas posições serão encerradas.

//+------------------------------------------------------------------+
//| Close our open positions                                         |
//+------------------------------------------------------------------+
void close_setup(void)
  {
   if(patience)
     {
      if(state == 1)
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
           {
            patience = false;
           }


         if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
           {
            Trade.PositionClose(Symbol());
           }
        }

      else
         if(state == -1)
           {
            if(ma_h_buffer[0] < bb_l_buffer[0])
              {
               patience = false;
              }

            if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
              {
               Trade.PositionClose(Symbol());
              }
           }
     }

   else
     {
      if((state == -1) && (ma_l_buffer[0] > bb_l_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }

      if((state == 1) && (ma_h_buffer[0] < bb_h_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }
     }

  }

Para considerarmos o setup válido, queremos que o canal de médias móveis esteja completamente de um lado da linha do meio e que nossa previsão de IA concorde com a ação do preço. Caso contrário, simplesmente aguardaremos em vez de perseguir flutuações momentâneas de preço.

//+------------------------------------------------------------------+
//| Check for valid trade setups                                     |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
     {
      model_predict();
      if((model_forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0)))
        {
         if(ma_h_buffer[0] < bb_l_buffer[0])
            patience = false;

         Trade.Sell(0.3,Symbol(),bid,0,0,"GBPUSD AI");
         state = -1;
        }
     }

   if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
     {
      model_predict();
      if(model_forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
            patience = false;

         Trade.Buy(0.3,Symbol(),ask,0,0,"GBPUSD AI");
         state = 1;
        }
     }
  }

Finalmente, precisamos de uma função responsável por atualizar nossas variáveis globais.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update(void)
  {
   CopyBuffer(bb_handler,0,0,1,bb_m_buffer);
   CopyBuffer(bb_handler,1,0,1,bb_h_buffer);
   CopyBuffer(bb_handler,2,0,1,bb_l_buffer);
   CopyBuffer(ma_h_handler,0,0,1,ma_h_buffer);
   CopyBuffer(ma_l_handler,0,0,1,ma_l_buffer);
  }
//+------------------------------------------------------------------+

Agora podemos realizar o backtest de nossa estratégia de trading. Usamos o strategy tester para avaliar nossa aplicação ao longo de aproximadamente 3 anos de dados diários do GBPUSD. Note que, quando construímos nosso modelo de IA, usamos dados diários do mercado entre 2016 e 2024. Portanto, o backtest mostrado abaixo está efetivamente testando nossa estratégia de IA em dados que o modelo já havia visto. Mesmo assim, embora nosso modelo tenha sido exposto aos dados e bem treinado, nosso saldo de conta foi bastante volátil ao longo do tempo.

Isso demonstra que, embora tenhamos treinado bem nosso modelo, modelos de IA não “lembram” o que “aprenderam” no sentido humano. Eles tentam criar uma fórmula que generalize bem os dados. Isso significa que ainda podem cometer erros em dados nos quais já foram treinados.

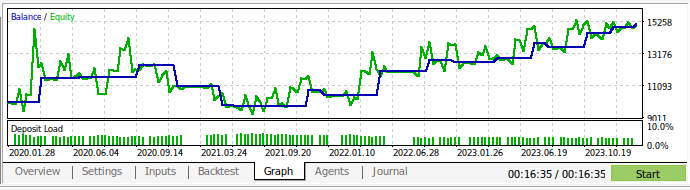
Fig 13: Realizamos o backtest da aplicação em aproximadamente 3 anos de dados diários do GBPUSD

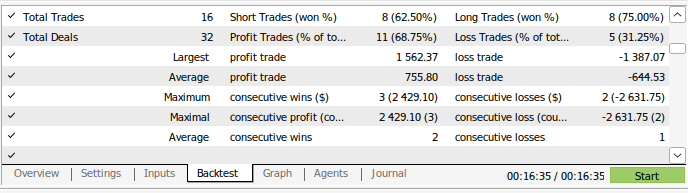
Fig 14: Detalhes do desempenho de trading do nosso modelo

Conclusão

Recapitulando, demonstramos que a aparência de “overfitting” pode, em certas circunstâncias, ser apenas um chamado para maior esforço. A ideologia clássica de superajuste de modelos de IA, até certo ponto, nos manteve presos em níveis de erro subótimos. No entanto, estamos confiantes de que, após a leitura deste artigo, você será capaz de fazer melhor uso dos seus modelos. Lembre-se de que também tínhamos a opção de simplesmente aumentar o número de camadas ocultas no modelo ou treinar um modelo com apenas uma camada, mas aumentar a largura dessa camada. Contudo, treinar modelos tão massivos exigiria uma abordagem completamente diferente, demandando habilidades em computação paralela.

Este artigo forneceu a você uma abordagem computacionalmente barata de treinar um modelo básico de tamanho fixo, utilizando dados diários devido ao pequeno número de linhas que teremos de processar nesse horizonte temporal. Entretanto, para que nossos resultados sejam conclusivos e robustos, talvez precisemos reduzir nosso conjunto de treinamento para metade de seu tamanho — de modo que nosso modelo seja treinado de 2016 a 2020, e todos os dados de 2020 a 2024 não sejam expostos ao modelo durante o treinamento.