Adicionando um LLM personalizado a um robô investidor (Parte 5): Desenvolvimento e teste de uma estratégia de trading com LLM (II) - Configuração do LoRA

Conteúdo

• Conteúdo
• Introdução
• Configuração do ambiente
• Biblioteca peft
• Configuração do LoRA
• Comparação de diferentes métodos de ajuste fino
• Considerações finais

Introdução

No artigo anterior, mostramos como realizar o ajuste fino completo de um modelo GPT-2 pré-treinado com os nossos próprios dados financeiros e avaliamos os resultados gerados pelo modelo. Neste e nos próximos artigos, aprofundaremos a implementação de outros métodos de ajuste fino, apresentando exemplos de código (abordaremos apenas os métodos apresentados no artigo anterior, pois implementar todos seria inviável. Escolheremos apenas alguns dos métodos mais utilizados para implementar). Neste artigo, usaremos o método LoRA como exemplo.

Além disso, temos o desafio de comparar horizontalmente os modelos treinados com esses diferentes métodos de ajuste fino e, então, identificar o modelo mais eficaz para o par de moedas atual (é claro que a eficácia do modelo também pode variar de acordo con las condiciones de mercado, como tendência de alta, tendência de baixa ou mercado lateral). Isso pode nos dar uma indicação mais clara sobre qual método de treinamento de modelo usar na prática para obter os melhores resultados. Naturalmente, numa abordagem mais rigorosa, deveríamos não apenas comparar horizontalmente esses diferentes métodos de treinamento, mas também comparar o desempenho de modelos ajustados para diferentes pares de moedas, usando diferentes métodos de tratamento de dados e de ajuste fino. Embora pareça uma tarefa simples, é extremamente trabalhosa. Pessoalmente, considero que, se quisermos aplicar essa série de métodos à negociação, esse passo é imprescindível. Porém, não pretendo me aprofundar nesse ponto nesta série de artigos, pois acredito que qualquer pessoa pode facilmente expandir essa funcionalidade com base em nossos exemplos. Basta substituir os dados de treinamento por outros pares de moedas e, depois, comparar horizontalmente a eficácia do modelo. É um trabalho meticuloso, mas não difícil.

Nos artigos anteriores, esqueci de apresentar a configuração do ambiente e as dependências das bibliotecas no exemplo de código, o que pode ter causado erros para alguns usuários ao tentarem executar os exemplos devido à ausência de dependências. Nas próximas publicações, fornecerei explicações detalhadas sobre a configuração do ambiente e as dependências utilizadas no código atual para ajudar os leitores a executarem os exemplos com facilidade.

Configuração do ambiente

Abaixo, está o ambiente de trabalho utilizado nos exemplos de código apresentados neste artigo. Naturalmente, isso não significa que o seu ambiente deve ser exatamente igual ao meu. No entanto, caso você enfrente problemas ao executar o código, poderá se basear na minha configuração.

• Sistema operacional: Ubuntu 22.04.5 LTS (ou versão equivalente no WSL)
• Versão do Python: 3.10.14
• Bibliotecas Python necessárias:

1. torch-2.4.1
2. numpy-1.26.3
3. pandas-2.2.3
4. transformers-4.45.1
5. petf-0.13.0
6. matplotlib-3.9.2

Se você não sabe como configurar o ambiente de execução do código, descrevi essa configuração em detalhes em outros artigos da série:

• Usuários com placa de vídeo AMD podem consultar o artigo anterior (Adicionando uma LLM personalizada ao robô de trading (Parte 4): Treinando sua própria LLM com GPU)
• Usuários com placa de vídeo NVIDIA podem consultar o segundo artigo da série (Adicionando uma LLM personalizada ao robô de trading (Parte 2): Exemplo de implantação do ambiente)

Não vou entrar em detalhes sobre isso aqui.

Biblioteca peft

Como já apresentamos o LoRA no artigo anterior, não repetiremos a explicação aqui. Para tornar o processo de ajuste fino mais simples e compreensível, não reproduziremos o exemplo de código original do LoRA. Em vez disso, utilizaremos a biblioteca peft, que é mais simples.

Essa biblioteca python reúne várias configurações de que precisamos, incluindo a classe de configuração de parâmetros do LoRA (LoraConfig), o método de inicialização do modelo com LoRA (get_peft_model), e a classe para carregar um modelo LoRA ajustado (PeftModel).

A seguir, vou apresentar as configurações passo a passo, começando pela classe LoraConfig.

1. Classe LoraConfig

A classe LoraConfig pertence à biblioteca peft e pode ser importada diretamente dela. Depois de importar a classe LoraConfig, é necessário definir os parâmetros de configuração.

Abaixo está a configuração de parâmetros da classe LoraConfig:

• r (`int`):

Dimensão de atenção do LoRA ("posto").

• target_modules (`Optional[Union[List[str], str]]`):

Nomes dos módulos aos quais o adaptador deve ser aplicado. Se este parâmetro for definido, apenas os módulos com os nomes especificados serão substituídos. Se for passada uma string, será feita uma correspondência por expressão regular. Se for passada uma lista de strings, será feita correspondência exata ou será verificado se o nome do módulo termina com alguma das strings fornecidas. Com o valor all-linear, todos os módulos lineares/Conv1D serão selecionados, exceto a camada de saída. Caso contrário, os módulos serão escolhidos com base na arquitetura do modelo. Se a arquitetura for desconhecida, ocorrerá um erro — nesse caso, será necessário especificar os módulos-alvo manualmente.

• lora_alpha (`int`):

Parâmetro alpha para escalonamento do LoRA.

• lora_dropout (`float`):

Probabilidade de dropout para as camadas do LoRA.

• fan_in_fan_out (`bool`):

Defina como True se a camada a ser substituída armazena pesos no formato (fan_in, fan_out). Por exemplo, o GPT-2 utiliza Conv1D, que armazena os pesos nesse formato; portanto, esse parâmetro deve ser definido como True.

• bias (`str`):

Tipo de viés para o LoRA. Os valores possíveis são: none, all ou lora_only. Com os valores all ou lora_only, os vieses correspondentes serão atualizados durante o treinamento. Vale lembrar que isso significa que, mesmo com os adaptadores desativados, o modelo não produzirá as mesmas saídas que o modelo base sem adaptação.

• use_rslora (`bool`):

 Quando True, utiliza-se Rank-Stabilized LoRA, que define o fator de escala do adaptador como lora_alpha/math.sqrt(r), já que foi comprovado que apresenta melhor desempenho. Caso contrário, será usado o valor padrão original lora_alpha/r.

• modules_to_save (`List[str]`):

 Lista de módulos, exceto as camadas dos adaptadores, que devem ser definidos como treináveis e salvos no checkpoint final.

• init_lora_weights (`bool` | `Literal["gaussian", "olora", "pissa", "pissa_niter_[número de iterações]", "loftq"]`):

Define como os pesos das camadas do adaptador serão inicializados. O valor padrão True faz a inicialização padrão da implementação de referência da Microsoft. O valor gaussian ativa a inicialização gaussiana, escalonada conforme o posto do LoRA, aplicada a módulos lineares e camadas. Definir como False resulta numa inicialização totalmente aleatória, o que não é recomendado. loftq é usado para ativar a inicialização LoftQ. olora ativa a inicialização OLoRA. pissa ativa a inicialização adaptação dos principais valores e vetores singulares (Principal Singular values and Singular vectors Adaptation - PiSSA), que converge mais rápido que o LoRA e alcança desempenho superior. Além disso, o PiSSA reduz o erro de quantização em comparação ao QLoRA, promovendo melhorias adicionais. Passar
    pissa_niter_[número de iterações] executa a inicialização PiSSA baseada em Fast-SVD, em que [número de iterações] indica o número de iterações do subespaço para executar o FSVD, devendo ser um número inteiro não negativo. Se for definido como 16, a inicialização de um modelo 7B pode ser concluída em poucos segundos e o desempenho no treinamento será aproximadamente equivalente ao uso do SVD.

• layers_to_transform (`Union[List[int], int]`):

Índices das camadas a serem transformadas. Se for passada uma lista de inteiros, o adaptador será aplicado às camadas com os índices especificados nessa lista. Se for passado um único número inteiro, a transformação será aplicada à camada correspondente a esse índice.

• layers_pattern (`str`):

Nome do padrão de camada, usado apenas se layers_to_transform for diferente de None.

• rank_pattern (`dict`):

 Mapeamento entre nomes de camadas ou expressões regulares e os postos que diferem do valor padrão definido por r.

• alpha_pattern (`dict`):

Mapeamento entre nomes de camadas ou expressões regulares e os valores de alpha que diferem do valor padrão definido por lora_alpha.

• megatron_config (`Optional[dict]`):

Argumentos TransformerConfig para o Megatron. Usado para criar camadas lineares paralelas com LoRA. Pode ser obtido via core_transformer_config_from_args(get_args()). Essas duas funções pertencem ao Megatron. Os argumentos serão usados para inicializar o TransformerConfig do Megatron. Este parâmetro precisa ser especificado se você quiser aplicar o LoRA às camadas ColumnParallelLinear e RowParallelLinear do Megatron.

• megatron_core (`Optional[str]`):

Módulo principal do Megatron, com valor padrão megatron.core.

• loftq_config (`Optional[LoftQConfig]`):

Configuração do LoftQ. Se definido como None, o LoftQ será utilizado para quantizar os pesos dos canais principais e inicializar as camadas. Também será passado init_lora_weights='loftq'. Note que, nesse caso, não se deve passar um modelo já quantizado, pois o LoftQ realiza essa quantização automaticamente.

• use_dora (`bool`):

Ativa a "adaptação de baixo posto com decomposição dos pesos" (Weight-Decomposed Low-Rank Adaptation - DoRA). Esse método separa a atualização dos pesos em duas partes: magnitude e direção. A direção é tratada pela LoRA padrão, enquanto a magnitude é controlada por um parâmetro treinável separado. Isso pode melhorar o desempenho do LoRA, especialmente em postos baixos. Atualmente, o DoRA é compatível apenas com camadas lineares e Conv2D. O DoRA tem um custo maior do que o LoRA puro, por isso é recomendado fundir os pesos para a inferência. Mais informações podem ser encontradas aqui: https://arxiv.org/abs/2402.09353.

• layer_replication (`List[Tuple[int, int]]`):

Cria uma nova pilha de camadas, posicionando as camadas originais do modelo de acordo com os intervalos especificados. Isso permite expandir (ou reduzir) o modelo sem duplicar os pesos da base. Adaptadores LoRA separados serão conectados a cada nova camada.

• runtime_config (`LoraRuntimeConfig`):

Configurações de tempo de execução (que não são salvas nem restauradas).

Acima estão todos os parâmetros da classe LoraConfig. Durante o treinamento real, geralmente não definimos todos os valores, mas apenas alguns parâmetros importantes conforme a necessidade, deixando o restante com os valores padrão. No exemplo utilizado neste artigo, definimos apenas os seguintes parâmetros: lora_alpha=32, lora_dropout=0.1, e deixamos os demais com as configurações padrão. Claro que as configurações apresentadas aqui não são as ideais. Você pode sempre experimentar diferentes combinações de parâmetros para encontrar a configuração ótima.

peft_config = LoraConfig(
                         lora_alpha=32, 
                         lora_dropout=0.1)

2. Função get_peft_model()

A função get_peft_model() também pode ser importada diretamente da biblioteca peft. Precisamos usá-la para carregar nosso modelo GPT-2 como um modelo configurado com base nas especificações definidas, antes do ajuste fino. No exemplo deste artigo, vamos carregar o GPT-2 como um modelo configurado com LoRA.

Da mesma forma, vamos primeiro analisar os parâmetros da função:

• model ([`transformers.PreTrainedModel`]):

Modelo a ser encapsulado.

• peft_config ([`PeftConfig`]):

Objeto de configuração contendo os parâmetros do modelo Peft.

• adapter_name (`str`, `optional`, valor padrão - `default`):

Nome do adaptador incorporado. Se não for especificado, será usado o nome padrão do adaptador (default).

• mixed (`bool`, `optional`, valor padrão - `False`):

Define se diferentes tipos de adaptadores (compatíveis) podem ser misturados.

• autocast_adapter_dtype (`bool`, *optional*):

Define se o tipo do adaptador deve ser convertido automaticamente. O padrão é True. Atualmente, isso apenas converte os pesos do adaptador de float16 ou bfloat16 para float32, pois esse tipo de conversão costuma ser necessário para garantir estabilidade no treinamento, afetando apenas alguns tuners PEFT.

• revision (`str`, `optional`, valor padrão - `main`):

Versão da base do modelo. Se não for especificado, o modelo peft salvo irá carregar a versão principal (main) da base.

Neste exemplo, utilizamos apenas os parâmetros model e peft_config, deixando os demais com os valores padrão. O parâmetro model é usado para passar o modelo GPT-2, enquanto peft_config é utilizado para carregar nossa configuração LoraConfig.

model = get_peft_model(model, peft_config)

3. Classe PeftModel

A classe PeftModel é a classe base da biblioteca peft. Ela pode inicializar qualquer tipo de modelo compatível com essa biblioteca. Precisamos utilizar a classe PeftModel para carregar os parâmetros do LoRA salvos durante o ajuste fino, juntamente com os parâmetros originais do modelo GPT-2 pré-treinado, unificando-os em um único modelo após o treinamento, para então utilizar esse modelo carregado na verificação das saídas. Da mesma forma, vamos primeiro revisar os parâmetros de configuração da classe.

• model ([`~transformers.PreTrainedModel`]) – modelo base Transformer para o Peft.
• peft_config ([`PeftConfig`]) – configuração do modelo Peft.
• adapter_name (`str`, *optional*) – nome do adaptador, por padrão "default".
• autocast_adapter_dtype (`bool`, *optional*):

Define se o tipo do adaptador deve ser convertido automaticamente. O padrão é True. Atualmente, isso apenas converte os pesos do adaptador de float16 ou bfloat16 para float32, pois isso é geralmente necessário para garantir estabilidade no treinamento e afeta apenas alguns tuners PEFT.

• low_cpu_mem_usage (`bool`, `optional`, padrão - `False`):

    Cria pesos de adaptador vazios em um metadispositivo. Útil para acelerar o carregamento.

• Atributos:

    - base_model ([`torch.nn.Module`]) – modelo base Transformer para o Peft.

    - peft_config ([`PeftConfig`]) – configuração do modelo Peft.

    - modules_to_save (`list` de `str`) – lista com os nomes dos submódulos que devem ser salvos ao salvar o modelo.

    - prompt_encoder ([`PromptEncoder`]) – codificador de prompt para Peft ao utilizar [`PromptLearningConfig`].

    - prompt_tokens (`torch.Tensor`) – tokens virtuais de prompt para Peft ao utilizar [`PromptLearningConfig`].

    - transformer_backbone_name (`str`) – nome do backbone Transformer no modelo base ao utilizar [`PromptLearningConfig`].

    - word_embeddings (`torch.nn.Embedding`) – embeddings de palavras no Transformer base ao utilizar [`PromptLearningConfig`].

Ao utilizar a classe PeftModel, usamos diretamente o método de classe PeftModel.from_pretrained(model, peft_model_id) para carregar o modelo. O model é o GPT-2, e peft_model_id são os parâmetros do modelo LoRA que configuramos.

model = PeftModel.from_pretrained(model, peft_model_id)

Observação:

Não utilize low_cpu_mem_usage=True ao criar um novo adaptador PEFT para treinamento.

Configuração do LoRA

Após entendermos como configurar o LoRA usando a biblioteca peft, vamos finalizar nosso exemplo de código.

1. Importação das bibliotecas necessárias

Não há nada de especial aqui. Importamos diretamente as bibliotecas necessárias para o ambiente Python:

import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer
from transformers import TextDataset, DataCollatorForLanguageModeling
from transformers import Trainer, TrainingArguments
import torch
from peft import get_peft_model, LoraConfig, PeftModel

2. Carregamento dos dados e configuração do modelo

Primeiro verificamos se a aceleração por GPU está disponível no ambiente atual, para garantir que ele esteja corretamente configurado. Se você tiver uma GPU disponível, mas ela não estiver sendo usada, deve verificar a configuração do ambiente. Embora seja possível executar a tarefa com a CPU, isso levará muito mais tempo.

dvc = 'cuda' if torch.cuda.is_available() else 'cpu'
print(dvc)

Em seguida, definimos os parâmetros de configuração do LoRA. Esses parâmetros já foram apresentados anteriormente, então vamos utilizá-los diretamente:

model_name_or_path = 'gpt2'
peft_config = LoraConfig(
    lora_alpha=32, 
    lora_dropout=0.1
)

model_name_or_path é o nosso modelo pré-treinado. Em seguida, definimos o caminho onde a versão ajustada do modelo LoRA será salva: peft_model_id.

peft_model_id = f"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}"

Agora vamos carregar o arquivo llm_data.csv. Usaremos os últimos 20 preços de fechamento deste conjunto de dados como entrada, e vamos comparar a saída gerada pelo modelo com os preços de fechamento restantes para verificar a eficácia do modelo.

df = pd.read_csv('llm_data.csv')

Depois disso, precisamos carregar os dados pré-processados do arquivo train.txt (removemos aqui a parte do código que transforma o llm_data.csv em train.txt, já que realizamos essa conversão no artigo anterior e, portanto, não há necessidade de fazê-la novamente). Definimos o tokenizador, o train_dataset e o data_collator. Essa parte é idêntica à do nosso artigo anterior, então não entraremos em detalhes. Leitores interessados podem consultar a publicação anterior.

tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)
train_dataset = TextDataset(tokenizer=tokenizer, file_path="train.txt", block_size=60)
data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)

Também precisamos instanciar TrainingArguments. Aqui, removemos os parâmetros save_steps e save_total_limit. Esses parâmetros servem basicamente para controlar a frequência e quantidade de checkpoints salvos durante o treinamento, mas como no LoRA precisamos salvar apenas os parâmetros LoRA, para evitar conflitos, removemos esses dois parâmetros e adicionamos save_strategy='no', utilizando o método save_model da classe Trainer para salvar o modelo.

training_args = TrainingArguments(
    output_dir=peft_model_id,     
    overwrite_output_dir=True,    
    num_train_epochs=3,     
    per_device_train_batch_size=32,
    save_strategy='no'
)

3. Carregamento e configuração do modelo

Primeiro, carregamos o modelo pré-treinado GPT-2 como HeadModel:

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)

Depois, precisamos combinar os parâmetros ajustados do LoRA com o modelo GPT-2 pré-treinado. Esse processo, que costumava ser bem complexo, agora exige apenas uma linha de código com o uso da função get_peft_model() da biblioteca peft. Essa biblioteca realmente simplificou bastante nosso trabalho.

model = get_peft_model(model, peft_config)

Em seguida, criamos uma instância do Trainer, executamos o ajuste fino e salvamos o modelo. Essa parte não é diferente do código do artigo anterior, por isso não vamos comentá-la em detalhes aqui. Leitores interessados podem consultar a publicação anterior.

trainer = Trainer(
    model=model,
    args=training_args,
    data_collator=data_collator,
    train_dataset=train_dataset
)
trainer.train()
trainer.save_model(peft_model_id)

Vale observar que o modelo salvo com o comando trainer.save_model(peft_model_id) não é mais um modelo completo, ele contém apenas os pesos do LoRA. Durante o ajuste fino com LoRA, os pesos pré-treinados do GPT-2 são congelados, e apenas os pesos do LoRA passam pelo ajuste. Por isso, ao carregar o modelo ajustado, é necessário utilizar o método from_pretrained() da classe PeftModel para recarregar essas duas partes dos pesos em conjunto, garantindo o funcionamento correto do modelo. Não é mais possível usar GPT2LMHeadModel.from_pretrained() para carregar o modelo.

Após o ajuste fino, o modelo será salvo na pasta gpt2_LORA_None no diretório onde está localizado o script de treinamento (como não definimos o parâmetro task_type na classe LoraConfig, esse parâmetro assume por padrão o valor None, por isso o nome da pasta termina com None).

4. Teste do modelo ajustado

Depois do ajuste fino, precisamos carregar o modelo ajustado e gerar as previsões para verificar se ele está funcionando corretamente. Como mencionado anteriormente, o modelo ajustado com LoRA não pode ser carregado usando GPT2LMHeadModel.from_pretrained(), devendo ser usado o método from_pretrained() da classe PeftModel, para carregar simultaneamente o modelo GPT-2 pré-treinado e os pesos do LoRA. Os parâmetros do método PeftModel.from_pretrained() já foram apresentados anteriormente, por isso não vamos repeti-los aqui. Após carregar o modelo, é necessário movê-lo para a GPU (se disponível) e colocá-lo em modo de inferência.

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = PeftModel.from_pretrained(model, peft_model_id)
model.to(dvc)
model.eval()

Em seguida, fazemos a verificação da saída para garantir que o modelo está funcionando corretamente. Esse processo foi descrito no artigo anterior, e a explicação detalhada do código pode ser encontrada lá.

prompt = ' '.join(map(str, df.iloc[:, 1:20].values[-1]))
generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc), 
                                            do_sample=True, 
                                            max_length=200)[0], 
                                            skip_special_tokens=True)
print(f"test the model: {generated}")

Resultado:

teste do modelo: 0.61163 0.61162 0.61191 0.61195 0.61209 0.61231 0.61224 0.61207 0.61187 0.61184 

0.6119 0.61169 0.61168 0.61162 0.61181 0.61184 0.61184 0.6118 0.61176 0.61174 0.61175 0.61169 

0.6119 0.61174 0.6116 0.61144 0.61155 0.61207 0.61192 0.61203 0.61158 0.61202 0.61158 0.61156 

0.61146 0.61196 0.61144 0.656 0.61142 0.61141 0.61137 0.60952 0.611

O código completo do script de ajuste fino está no arquivo lora-tuning.py.

import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer
from transformers import TextDataset, DataCollatorForLanguageModeling
from transformers import Trainer, TrainingArguments
import torch
from peft import get_peft_model, LoraConfig, PeftModel

dvc='cuda' if torch.cuda.is_available() else 'cpu'
print(dvc)
model_name_or_path='gpt2'

peft_config = LoraConfig(
                        #  task_type=None, 
                        #  inference_mode=False, 
                        #  r=8, 
                         lora_alpha=32, 
                         lora_dropout=0.1,
                         )

peft_model_id = f"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}"
df = pd.read_csv('llm_data.csv')

# sentences = [' '.join(map(str, prices)) for prices in df.iloc[:-10,1:].values]
# with open('train.txt', 'w') as f:
#     for sentence in sentences:
#         f.write(sentence + '\n')

tokenizer = GPT2Tokenizer.from_pretrained(model_name_or_path)
train_dataset = TextDataset(tokenizer=tokenizer,
                            file_path="train.txt", 
                            block_size=60)

data_collator = DataCollatorForLanguageModeling(tokenizer=tokenizer, mlm=False)
training_args = TrainingArguments(output_dir=peft_model_id,     
                                  overwrite_output_dir=True,    
                                  num_train_epochs=3,     
                                  per_device_train_batch_size=32,
                                  save_strategy= 'no',   
                                #   save_steps=10_000,    
                                #   save_total_limit=2,
                                #   load_best_model_at_end=True,
                                  )

model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = get_peft_model(model, peft_config)

trainer = Trainer(model=model,
                  args=training_args,
                  data_collator=data_collator,
                  train_dataset=train_dataset,)

trainer.train()

# model.save_pretrained(peft_model_id)
trainer.save_model(peft_model_id)

# config = PeftConfig.from_pretrained(peft_model_id)
model = GPT2LMHeadModel.from_pretrained(model_name_or_path)
model = PeftModel.from_pretrained(model, peft_model_id)
model.to(dvc)
model.eval()

prompt = ' '.join(map(str, df.iloc[:,1:20].values[-1])) 
generated = tokenizer.decode(model.generate(tokenizer.encode(prompt, return_tensors='pt').to(dvc), 
                                            do_sample=True, 
                                            max_length=200)[0], 
                                            skip_special_tokens=True)

print(f"test the model:{generated}")

Os arquivos de dados serão anexados ao final. O arquivo original de dados terá o nome llm_data.csv, e o arquivo de dados pré-processado será train.txt.

Comparação de diferentes métodos de ajuste fino

Após os experimentos com diferentes métodos de ajuste fino, obtivemos novos modelos GPT-2 com características distintas. Isso exige uma comparação entre os resultados e a velocidade de treinamento de cada método, a fim de escolher de forma fundamentada o método mais adequado para a estratégia do EA. Como o modelo GPT-2 pré-treinado não consegue reconhecer nossos dados de entrada, não é necessário incluí-lo na comparação. Assim, neste comparativo, consideramos apenas o ajuste fino completo e o ajuste com LoRA. Claro que nos próximos artigos continuarei apresentando outros métodos para ampliarmos nossas opções.

1. Comparação de eficiência

Primeiramente, precisamos comparar o custo do treinamento. Damos preferência a métodos com alta eficiência e baixo custo de treinamento. Aqui comparamos o tempo de treinamento, o uso de memória e a velocidade de inferência. Embora as diferenças possam ser pequenas em modelos pequenos como o GPT-2, elas se tornam bem significativas ao utilizarmos modelos maiores (como 7B, 13B, 34B ou superiores).

	Tempo de treinamento (seg)	Memória de vídeo (GB)	Tempo de geração (seg)
Configuração do LoRA	69.5605	4.1	1.242877
Ajuste fino completo	101.7946	5.67	0.876525

2. Comparação de precisão

Em relação à precisão, comparamos temporariamente os modelos ajustados por diferentes métodos utilizando as métricas MSE (erro quadrático médio), RMSE (raiz do erro quadrático médio) e NRMSE (erro quadrático médio normalizado). Outros indicadores (como complexidade, robustez e outros) não serão considerados por enquanto.

Em seguida, carregamos os últimos 20 preços de fechamento dos dados originais como entrada, e utilizamos os dados restantes como saída esperada para avaliar os modelos gerados pelos dois métodos de treinamento.

• Dados de entrada: [0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176]
• Preços reais: [0.6119, 0.61197, 0.61201, 0.61242, 0.61237, 0.6123, 0.61229, 0.61242, 0.61212, 0.61197, 0.61201, 0.61213, 0.61212, 0.61206, 0.61203, 0.61206, 0.6119, 0.61193, 0.61191, 0.61202, 0.61197, 0.6121, 0.61211, 0.61214, 0.61203, 0.61203, 0.61213, 0.61218, 0.61227, 0.61226]

Depois carregamos os modelos (o modelo com ajuste fino completo está salvo na pasta gpt2_stock no diretório atual, e o modelo ajustado com LoRA está salvo na pasta gpt2_LORA_None, também no diretório atual) e realizamos a inferência. Com base nos resultados obtidos, calculamos seus valores de MSE, RMSE e NRMSE. Esses códigos já foram apresentados no artigo anterior, então não vamos detalhá-los aqui.

import time
import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer, GPT2Config
from sklearn.metrics import mean_squared_error
import torch
import numpy as np
from peft import PeftModel
import matplotlib.pyplot as plt

# Load dataset
df = pd.read_csv('llm_data.csv')

# Set device (GPU or CPU)
dvc = 'cuda' if torch.cuda.is_available() else 'cpu'

# Define model paths
base_model = 'gpt2'
fine_tuning_path = './gpt2_stock'
lora_tuning_path = './gpt2_LORA_None'

# Initialize tokenizer and models
tokenizer = GPT2Tokenizer.from_pretrained(base_model)
model_fine_tuning = GPT2LMHeadModel.from_pretrained(fine_tuning_path).to(dvc)
model_lora_tuning = GPT2LMHeadModel.from_pretrained(base_model)
model_lora_tuning = PeftModel.from_pretrained(model_lora_tuning, lora_tuning_path).to(dvc)

# Extract input data and true prices
input_data = df.iloc[:, 1:20].values[-1]
true_prices = df.iloc[-1:, 21:].values.tolist()[0]

# Prepare prompt
prompt = ' '.join(map(str, input_data))

Encapsulamos o processo de inferência e o cálculo do MSE, RMSE e NRMSE na função generater(model) e usamos o valor previsto, o MSE, o RMSE e o NRMSE como valores de retorno. Quando utilizamos modelos diferentes para avaliar as saídas, simplesmente passamos o modelo como parâmetro. Vale destacar que a variável true_prices usada em nossa função é uma variável global, e como precisamos modificar seu valor dentro da função, devemos declará-la como global, caso contrário, será exibida uma mensagem de erro.

def generater(model):
    global true_prices
    
    # Set the model to evaluation mode
    model.eval()
    
    # Tokenization and text generation using the model
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_} seconds')
    
    # Process the generated data
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim both lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true_prices and generated_prices lists
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    # Calculate MSE, RMSE, NRMSE metrics
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse
def generater(model):
    global true_prices
    
    # Set the model to evaluation mode
    model.eval()
    
    # Tokenization and text generation using the model
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_} seconds')
    
    # Process the generated data
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim both lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true_prices and generated_prices lists
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    # Calculate MSE, RMSE, NRMSE metrics
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse

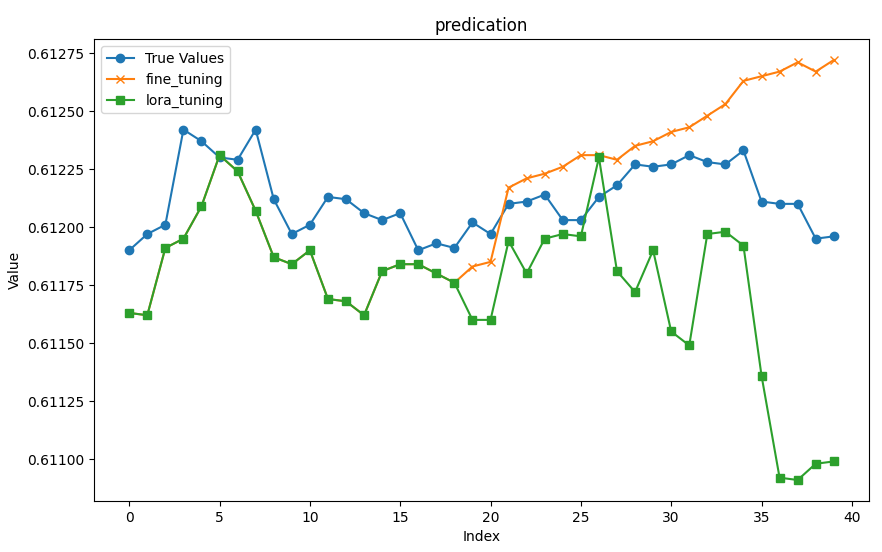
Encapsulamos a visualização do resultado da saída na função plot_(a, b, title):

def plot_(a, b, title):
    # Set up the figure size
    plt.figure(figsize=(10, 6))
    
    # Plot true_prices only if the title is 'prediction'
    if title == 'prediction':
        plt.plot(true_prices, label='True Values', marker='o')
    
    # Plot the fine-tuning and lora-tuning values
    plt.plot(a, label='fine_tuning', marker='x')
    plt.plot(b, label='lora_tuning', marker='s')
    
    # Set the title and labels for the axes
    plt.title(title)
    plt.xlabel('Index')
    plt.ylabel('Value')
    
    # Display the legend and save the plot to a file
    plt.legend()
    plt.savefig(f"{title}.png")

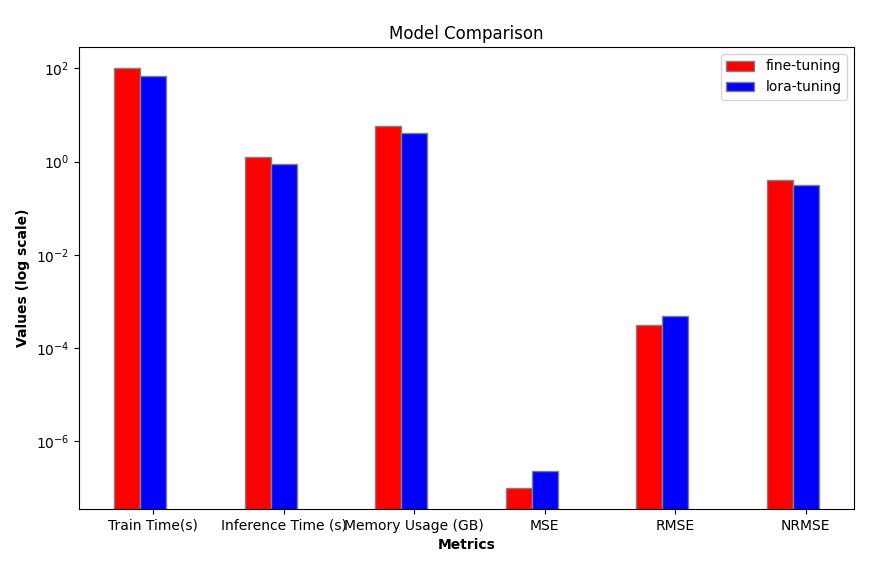
Encapsulamos a eficiência do modelo e os indicadores de avaliação mencionados anteriormente na função groups_chart(a, b, models):

def groups_chart(a, b, models):
    # Define metrics for the chart
    metrics = ['Train Time(s)', 'Inference Time (s)', 'Memory Usage (GB)', 'MSE', 'RMSE', 'NRMSE']
    
    # Set figure size
    plt.figure(figsize=(10, 6))
    
    # Update values for model a and b
    a = [101.7946, 1.243, 5.67, a[1], a[2], a[3]]
    b = [69.5605, 0.877, 4.10, b[1], b[2], b[3]]
    
    # Bar width for each group of bars
    bar_width = 0.2
    
    # Set the positions of the bars
    r1 = np.arange(len(metrics))  # Positions for model a
    r2 = [x + bar_width for x in r1]  # Positions for model b
    
    # Plot bars for both models
    plt.bar(r1, a, color='r', width=bar_width, edgecolor='grey', label=models[0])
    plt.bar(r2, b, color='b', width=bar_width, edgecolor='grey', label=models[1])
    
    # Set log scale for y-axis
    plt.yscale('log')
    
    # Set labels and title
    plt.xlabel('Metrics', fontweight='bold')
    plt.xticks([r + bar_width / 2 for r in range(len(metrics))], metrics)  # Center the x-axis ticks
    plt.ylabel('Values (log scale)', fontweight='bold')
    plt.title('Model Comparison')
    
    # Display legend and save the plot
    plt.legend()
    # plt.show()  # Uncomment to display the plot
    plt.savefig('Comparison.png')

Observação:

O problema aqui é que a escala dos indicadores que estamos medindo não é uniforme, por isso utilizei uma escala logarítmica: plt.yscale('log'). Isso permite lidar de forma eficaz com situações em que o volume dos dados varia significativamente.

Os diferentes modelos executam a inferência individualmente:

fine_tuning_result = generater(model_fine_tuning)
lora_tuning_result = generater(model_lora_tuning)

Resultados da inferência do modelo com ajuste fino completo:

• preços gerados: [0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.61183, 0.61185, 0.61217, 0.61221, 0.61223, 0.61226, 0.61231, 0.61231, 0.61229, 0.61235, 0.61237, 0.61241, 0.61243, 0.61248, 0.61253, 0.61263, 0.61265, 0.61267, 0.61271, 0.61267, 0.61272]
• MSE: 1.0064750000000609e-07
• RMSE: 0.0003172499014972362
• NRMSE: 0.3965623768715889

Resultados da inferência do modelo ajustado com LoRA:

• preços gerados: [0.61163, 0.61162, 0.61191, 0.61195, 0.61209, 0.61231, 0.61224, 0.61207, 0.61187, 0.61184, 0.6119, 0.61169, 0.61168, 0.61162, 0.61181, 0.61184, 0.61184, 0.6118, 0.61176, 0.6116, 0.6116, 0.61194, 0.6118, 0.61195, 0.61197, 0.61196, 0.6123, 0.61181, 0.61172, 0.6119, 0.61155, 0.61149, 0.61197, 0.61198, 0.61192, 0.61136, 0.61092, 0.61091, 0.61098, 0.61099]
• MSE: 2.3278249999999242e-07
• RMSE: 0.00048247538797330626
• NRMSE: 0.3195201244856309

Visualizamos os resultados e salvamos como imagens:

plot_(fine_tuning_result[0],lora_tuning_result[0],title='predication')
groups_chart(fine_tuning_result,lora_tuning_result,models=['fine-tuning','lora-tuning'])

Visualização dos gráficos comparativos:

Observação:

Executei o script várias vezes para testes, e os resultados de cada execução podem variar, por isso os dados e gráficos apresentados aqui são apenas para referência. É totalmente normal se os seus resultados forem diferentes dos meus.

3. Escolha do modelo adequado

Do ponto de vista da eficiência, fica evidente que o ajuste com LoRA é superior ao ajuste fino completo em termos de velocidade de treinamento, velocidade de inferência e uso de memória. Em seguida, comparamos a precisão das inferências. A partir dos nossos gráficos, é possível perceber intuitivamente que os dados de saída dos dois modelos são praticamente idênticos para os 18 primeiros valores previstos, enquanto para os valores seguintes, o erro aumenta gradualmente. As previsões do modelo com ajuste fino completo são, em geral, relativamente estáveis, como indicado pelos valores de NRMSE.

Executei o script test.py várias vezes para verificar se os resultados eram consistentes. Os resultados variaram: NRMSE do modelo ajustado com LoRA era, às vezes, pequeno (em torno de 0,17, muito inferior ao NRMSE do modelo com ajuste fino completo), mas, em outras execuções, era extremamente alto (chegando a 0,76688). O NRMSE do ajuste fino completo permaneceu estável, em torno de 0,4. É importante observar que esses dados não significam necessariamente que o modelo com todos os parâmetros ajustados seja melhor do que o modelo ajustado com LoRA. É bastante provável que o LoRA não tenha convergido com as mesmas configurações de treinamento usadas no ajuste completo. A melhor solução seria configurar uma lógica adequada de parada antecipada (early stopping), com base na perda durante o treinamento, para garantir a convergência do modelo. Essa parte ainda não foi implementada no exemplo de código, mas os leitores interessados podem desenvolvê-la por conta própria.

É claro que diferentes configurações dos parâmetros do modelo também podem afetar seu desempenho. Por isso, uma abordagem mais científica seria encontrar primeiro os parâmetros ideais para a configuração do modelo ou do método de treinamento com o mesmo conjunto de dados e garantir que o modelo esteja convergindo com esses parâmetros. Em seguida, deve-se realizar uma comparação horizontal entre diferentes métodos ou modelos de treinamento e avaliar de forma abrangente os diversos indicadores para escolher o melhor método ou modelo.

O código completo do script de teste está em test.py:

import time
import pandas as pd
from transformers import GPT2LMHeadModel, GPT2Tokenizer, GPT2Config
from sklearn.metrics import mean_squared_error
import torch
import numpy as np
from peft import PeftModel
import matplotlib.pyplot as plt

# Load the dataset
df = pd.read_csv('llm_data.csv')

# Define the device (GPU if available)
dvc = 'cuda' if torch.cuda.is_available() else 'cpu'

# Model paths and base settings
base_model = 'gpt2'
fine_tuning_path = './gpt2_stock'
lora_tuning_path = './gpt2_LORA_None'

# Load the tokenizer and models
tokenizer = GPT2Tokenizer.from_pretrained(base_model)
model_fine_tuning = GPT2LMHeadModel.from_pretrained(fine_tuning_path).to(dvc)
model_lora_tuning = GPT2LMHeadModel.from_pretrained(base_model)
model_lora_tuning = PeftModel.from_pretrained(model_lora_tuning, lora_tuning_path).to(dvc)

# Extract the input data and true prices from the dataset
input_data = df.iloc[:, 1:20].values[-1]
true_prices = df.iloc[-1:, 21:].values.tolist()[0]
prompt = ' '.join(map(str, input_data))

# Function to generate predictions
def generater(model):
    global true_prices
    model.eval()
    
    # Tokenization and text generation
    token = tokenizer.encode(prompt, return_tensors='pt').to(dvc)
    start_ = time.time()
    generated = tokenizer.decode(
        model.generate(token, do_sample=True, max_length=200)[0], 
        skip_special_tokens=True
    )
    end_ = time.time()
    
    print(f'Generate time: {end_ - start_}')
    
    # Processing generated prices
    generated_prices = generated.split('\n')[0]
    generated_prices = list(map(float, generated_prices.split()))
    generated_prices = generated_prices[:len(true_prices)]
    
    # Function to trim lists to the same length
    def trim_lists(a, b):
        min_len = min(len(a), len(b))
        return a[:min_len], b[:min_len]
    
    # Trim the true prices and generated prices
    true_prices, generated_prices = trim_lists(true_prices, generated_prices)
    
    # Output metrics
    print(f"Input data: {input_data}")
    print(f"True prices: {true_prices}")
    print(f"Generated prices: {generated_prices}")
    
    mse = mean_squared_error(true_prices, generated_prices)
    print('MSE:', mse)
    
    rmse = np.sqrt(mse)
    nrmse = rmse / (np.max(true_prices) - np.min(generated_prices))
    
    print(f"RMSE: {rmse}, NRMSE: {nrmse}")
    
    return generated_prices, mse, rmse, nrmse

# Function to plot the comparison between true prices and predictions
def plot_(a, b, title):
    plt.figure(figsize=(10, 6))
    
    if title == 'prediction':
        plt.plot(true_prices, label='True Values', marker='o')
    
    plt.plot(a, label='fine_tuning', marker='x')
    plt.plot(b, label='lora_tuning', marker='s')
    
    plt.title(title)
    plt.xlabel('Index')
    plt.ylabel('Value')
    plt.legend()
    plt.savefig(f"{title}.png")

# Function to generate a bar chart comparing different metrics between models
def groups_chart(a, b, models):
    metrics = ['Train Time(s)', 'Inference Time (s)', 'Memory Usage (GB)', 'MSE', 'RMSE', 'NRMSE']
    plt.figure(figsize=(10, 6))
    
    # Data for the metrics
    a = [101.7946, 1.243, 5.67, a[1], a[2], a[3]]
    b = [69.5605, 0.877, 4.10, b[1], b[2], b[3]]
    
    bar_width = 0.2
    r1 = np.arange(len(metrics))
    r2 = [x + bar_width for x in r1]
    
    # Plotting bars for both models
    plt.bar(r1, a, color='r', width=bar_width, edgecolor='grey', label=models[0])
    plt.bar(r2, b, color='b', width=bar_width, edgecolor='grey', label=models[1])
    
    # Set y-axis to log scale for better visibility of differences
    plt.yscale('log')
    
    plt.xlabel('Metrics', fontweight='bold')
    plt.xticks([r + bar_width for r in range(len(metrics))], metrics)
    plt.ylabel('Values (log scale)', fontweight='bold')
    plt.title('Model Comparison')
    plt.legend()
    plt.savefig('Comparison.png')

# Generate results for both fine-tuned and LORA-tuned models
fine_tuning_result = generater(model_fine_tuning)
lora_tuning_result = generater(model_lora_tuning)

# Plot the prediction comparison
plot_(fine_tuning_result[0], lora_tuning_result[0], title='prediction')

# Generate the comparison chart for the models
groups_chart(fine_tuning_result, lora_tuning_result, models=['fine-tuning', 'lora-tuning'])

Considerações finais

Neste artigo, discutimos como realizar o ajuste fino de um modelo GPT-2 pré-treinado utilizando o método de configuração LoRA e comparamos os métodos de ajuste fino apresentados. Isso nos permite escolher, de maneira mais intuitiva, o método e o modelo de treinamento que melhor se adaptam à nossa estratégia de negociação. Continuaremos explorando outros métodos e aplicando-os ao ajuste fino do modelo GPT-2 pré-treinado, buscando técnicas mais precisas para a nossa estratégia. Embora o resultado final possa estar longe do ideal devido à escala dos parâmetros do modelo GPT-2, o processo para encontrá-lo é o mesmo. Você pode estar se perguntando por que não realizar comparações horizontais entre diferentes modelos. É uma boa pergunta, mas existem muitos modelos disponíveis e, mesmo dentro de um único modelo, é possível encontrar diferentes escalas de parâmetros. Obviamente, não é possível concluir essa tarefa com apenas alguns exemplos simples. Embora não seja complicado, é um processo bastante meticuloso. Por isso, eu sugiro estudar como buscar os melhores resultados entre diferentes modelos com base nos exemplos de métodos apresentados neste artigo.

Você está pronto para continuar explorando? Vejo você no próximo artigo!