
Reimaginando Estratégias Clássicas (Parte VI): Análise de Múltiplos Tempos Gráficos
Introdução
Existem maneiras potencialmente infinitas de um investidor moderno integrar Inteligência Artificial (IA) para aprimorar suas decisões de negociação. Infelizmente, é improvável que você consiga avaliar todas essas estratégias antes de decidir qual estratégia confiar com seu capital suado. Nesta série de artigos, exploraremos estratégias de negociação para avaliar se podemos melhorar a estratégia com IA. Nosso objetivo é apresentar as informações de que você precisa para tomar uma decisão informada sobre se essa estratégia é adequada para o seu perfil de investidor individual.
Visão Geral da Estratégia de Negociação
Neste artigo, revisitamos uma estratégia bem conhecida de análise de múltiplos tempos gráficos. Um grande grupo de traders bem-sucedidos ao redor do mundo acredita que há virtude em analisar mais de um tempo gráfico antes de tomar decisões de investimento. Existem várias variantes diferentes da estratégia. No entanto, todas tendem a sustentar a crença geral de que qualquer tendência identificada em um tempo gráfico superior persistirá em todos os tempos gráficos inferiores.
Por exemplo, se observarmos um comportamento de preço altista no gráfico diário, esperaríamos razoavelmente ver padrões de preço altistas no gráfico horário. Essa estratégia também leva a ideia mais adiante, pois, segundo a estratégia, devemos dar mais peso às flutuações de preço que estão alinhadas à tendência observada no tempo gráfico superior.
Em outras palavras, retornando ao nosso exemplo simples, se observássemos uma tendência de alta no gráfico diário, estaríamos mais inclinados a procurar oportunidades de compra no gráfico horário e tomaríamos relutantemente posições contrárias à tendência observada no gráfico diário.
De maneira geral, a estratégia se desfaz quando a tendência observada no tempo gráfico superior é revertida. Isso geralmente ocorre porque a reversão começa apenas em um tempo gráfico inferior. Lembre-se de que, ao usar essa estratégia, pouca atenção é dada às flutuações observadas em tempos gráficos inferiores que são contrárias ao tempo gráfico superior. Portanto, os traders que seguem essa estratégia geralmente esperam que a reversão seja observada no tempo gráfico superior. Isso pode resultar em uma grande volatilidade nos preços enquanto esperam pela confirmação do tempo gráfico superior.
Visão Geral da Metodologia
Para avaliar os méritos dessa estratégia empiricamente, tivemos que extrair dados significativos de nosso terminal MetaTrader 5. Nosso objetivo neste artigo foi prever o preço de fechamento futuro do EURUSD 20 minutos no futuro. Para atingir esse objetivo, criamos 3 grupos de preditores:
- Informações comuns de preços de abertura, máxima, mínima e fechamento.
- Mudanças nos níveis de preços em tempos gráficos superiores.
- Um superconjunto dos dois conjuntos acima.
Observamos níveis relativamente fracos de correlação entre os dados de preços comuns e as mudanças de preço nos tempos gráficos superiores. Os níveis de correlação mais fortes que observamos foram entre as mudanças de preço no M15 e os níveis de preços no M1, aproximadamente -0,1.
Criamos um grande conjunto de modelos diversos e os treinamos em todos os 3 conjuntos de preditores para observar as mudanças na precisão. Níveis de erro mais baixos foram observados ao usar o primeiro conjunto de preditores, dados de mercado comuns. A partir de nossas observações, parece que o modelo de regressão linear é o melhor desempenho, seguido pelo modelo Gradient Boosting Regressor (GBR).
Como o modelo linear não possui parâmetros de ajuste muito interessantes para nós, selecionamos o modelo GBR como nossa solução candidata, e os níveis de erro do modelo linear se tornaram nossa referência de desempenho. Nosso objetivo agora passou a ser otimizar o modelo GBR para superar o desempenho de referência do modelo linear.
Antes de iniciarmos o processo de otimização, realizamos a seleção de recursos usando o algoritmo de seleção reversa. Todos os recursos relacionados às mudanças de preço em tempos gráficos superiores foram descartados pelo algoritmo, sugerindo possivelmente que a relação pode não ser confiável, ou alternativamente, podemos interpretar isso como se não tivéssemos exposto a associação de forma significativa ao nosso modelo.
Utilizamos um algoritmo de busca randomizada com 1000 iterações para encontrar as configurações ótimas para o nosso modelo GBR. Depois, empregamos os resultados da nossa busca randomizada como ponto de partida para uma otimização local dos parâmetros contínuos do GBR usando o algoritmo Limited Memory Broyden Fletcher Goldfarb And Shanno (L-BFGS-B).
Não conseguimos superar o modelo GBR padrão nos dados de validação, o que pode indicar que estávamos sobreajustando os dados de treinamento. Além disso, também não conseguimos superar o desempenho de referência do modelo linear na validação.
Extração de Dados
Criei um script útil em MQL5 para extrair dados de nosso terminal MetaTrader 5. O script também buscará as mudanças de preço de uma seleção de tempos gráficos superiores e gerará o arquivo no caminho: "MetaTrader 5\MQL5\Files..."
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //---Amount of data requested input int size = 5; //How much data should we fetch? //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void OnStart() { //---File name string file_name = "Market Data " + Symbol() + " multiple timeframe 20 step look ahead .csv"; //---Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= -1;i<=size;i++) { if(i == -1) { FileWrite(file_handle,"Time","Open","High","Low","Close","M5","M15","M30","H1","D1"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i), (iClose(Symbol(),PERIOD_M5,i) - iClose(Symbol(),PERIOD_M5,i+20)), (iClose(Symbol(),PERIOD_M15,i) - iClose(Symbol(),PERIOD_M15,i+20)), (iClose(Symbol(),PERIOD_M30,i) - iClose(Symbol(),PERIOD_M30,i+20)), (iClose(Symbol(),PERIOD_H1,i) - iClose(Symbol(),PERIOD_H1,i+20)), (iClose(Symbol(),PERIOD_D1,i) - iClose(Symbol(),PERIOD_D1,i+20)) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Lendo os Dados
Vamos começar carregando as bibliotecas que precisamos.
import pandas as pd imort numpy as np
Observe que os dados estão indo do presente para o passado distante. Precisamos reverter os dados para que sigam do passado para o presente próximo.
#Let's format the data so it starts with the oldest date market_data = market_data[::-1] market_data.reset_index(inplace=True)
Agora definiremos nosso horizonte de previsão.
look_ahead = 20 Rotulando os dados. Nosso objetivo será o preço de fechamento futuro do EURUSD.
#Let's label the data market_data["Target"] = market_data["Close"].shift(-look_ahead)
Agora, vamos excluir quaisquer linhas com valores ausentes.
#Drop rows with missing values
market_data.dropna(inplace=True)
Análise Exploratória de Dados
Analisando os níveis de correlação.
#Let's see if there is any correlation market_data.iloc[:,2:-1].corr()
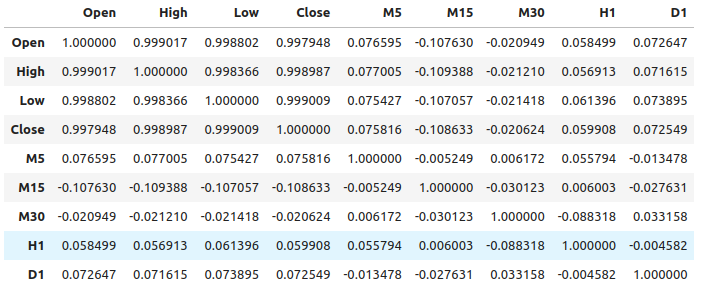
Fig 1: Níveis de correlação entre diferentes tempos gráficos
Como podemos ver, há níveis moderadamente fracos de correlação em nosso conjunto de dados. Observe que correlação não necessariamente prova que existe uma relação entre as variáveis observadas.
A informação mútua é uma medida do potencial que um preditor tem para explicar nosso alvo. Vamos começar considerando uma variável que sabemos que tem um forte potencial de prever o alvo, o preço de abertura.
from sklearn.feature_selection import mutual_info_regression
Agora, como referência, esse é um bom score de informação mútua (MI).
#MI Score for the Open price
print(f'Open price has MI score: {mutual_info_regression(market_data.loc[:,["Open"]],market_data.loc[:,"Target"])[0]}') Agora vejamos a pontuação MI para as mudanças de preço no tempo gráfico M5 em relação ao preço futuro no tempo gráfico M1.
#MI Score for the M5 change in price
print(f'M5 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M5"]],market_data.loc[:,"Target"])[0]}') Nossa pontuação MI é consideravelmente menor, isso significa que talvez não tenhamos exposto a relação de maneira significativa, ou talvez não haja dependência entre os níveis de preço em diferentes tempos gráficos!
#MI Score for the M15 change in price
print(f'M15 change in price has MI score: {mutual_info_regression(market_data.loc[:,["M15"]],market_data.loc[:,"Target"])[0]}') O mesmo ocorre para os tempos gráficos restantes que selecionamos.
Modelando a Relação
Vamos definir nossos preditores e nosso alvo.
#Let's define our predictors and our target ohlc_predictors = [ "Open", "High", "Low", "Close" ] time_frame_predictors = [ "M5", "M15", "M30", "H1", "D1" ] all_predictors = ohlc_predictors + time_frame_predictors target = "Target"
Agora, importamos as bibliotecas que precisamos.
#Import the libraries we need from sklearn.linear_model import LinearRegression from sklearn.linear_model import SGDRegressor from sklearn.ensemble import RandomForestRegressor from sklearn.ensemble import BaggingRegressor from sklearn.ensemble import GradientBoostingRegressor from sklearn.ensemble import AdaBoostRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.svm import LinearSVR from sklearn.neural_network import MLPRegressor from sklearn.model_selection import TimeSeriesSplit,RandomizedSearchCV from sklearn.metrics import root_mean_squared_error from sklearn.preprocessing import RobustScaler
Definimos os parâmetros para o nosso objeto de divisão de séries temporais.
#Define the time series split object gap = look_ahead splits = 10
Agora, vamos preparar nossos modelos e também criar dataframes para armazenar nossos níveis de precisão. Dessa forma, podemos observar a mudança na precisão à medida que alteramos as entradas de nossos modelos.
#Store our models in a list models = [ LinearRegression(), SGDRegressor(), RandomForestRegressor(), BaggingRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), KNeighborsRegressor(), LinearSVR(), MLPRegressor(hidden_layer_sizes=(10,4),early_stopping=True), MLPRegressor(hidden_layer_sizes=(100,20),early_stopping=True) ] #Create a list of column titles for each model columns = [ "Linear Regression", "SGD Regressor", "Random Forest Regressor", "Bagging Regressor", "Gradient Boosting Regressor", "AdaBoost Regressor", "K Neighbors Regressor", "Linear SVR", "Small Neural Network", "Large Neurla Network" ] #Create data frames to store our accuracy ohlc_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) multiple_time_frame_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns) all_accuracy = pd.DataFrame(index=np.arange(0,10),columns=columns)
Agora, vamos preparar os preditores e escalar nossos dados.
#Preparing to perform cross validation
current_predictors = all_predictors
scaled_data = pd.DataFrame(RobustScaler().fit_transform(market_data.loc[:,all_predictors]),columns=all_predictors)
Criar o objeto de divisão de séries temporais.
#Create the time series split object
tscv = TimeSeriesSplit(gap=gap,n_splits=splits)
Agora, realizaremos a validação cruzada. O primeiro loop percorre a lista de modelos que criamos anteriormente, e o segundo loop valida cada modelo por vez.
#First we will iterate over all the available models for i in np.arange(0,len(models)): #First select the model model = models[i] #Now we will cross validate this current model for j , (train,test) in enumerate(tscv.split(scaled_data)): #First define the train and test data train_X = scaled_data.loc[train[0]:train[-1],current_predictors] train_y = market_data.loc[train[0]:train[-1],target] test_X = scaled_data.loc[test[0]:test[-1],current_predictors] test_y = market_data.loc[test[0]:test[-1],target] #Now we will fit the model model.fit(train_X,train_y) #And finally record the accuracy all_accuracy.iloc[j,i] = root_mean_squared_error(test_y,model.predict(test_X))
Nossos níveis de precisão ao usar entradas comuns para nosso modelo.
ohlc_accuracy
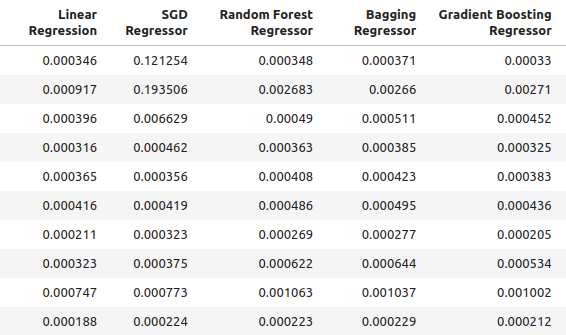
Fig 2: Níveis normais de precisão.
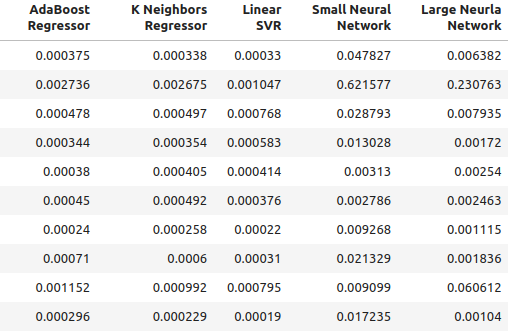
Fig 3: Níveis normais de precisão II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {ohlc_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.00042256332959154886
SGD Regressor had error levels 0.0324320107406244
Random Forest Regressor had error levels 0.0006954883552094012
Bagging Regressor had error levels 0.0007030697054783931
Gradient Boosting Regressor had error levels 0.0006588749449742309
AdaBoost Regressor had error levels 0.0007159624774453208
K Neighbors Regressor had error levels 0.0006839218661791973
Linear SVR had error levels 0.000503277800807813
Small Neural Network had error levels 0.07740701832606754
Large Neural Network had error levels 0.03164056895135391
Nossa precisão ao usar as novas entradas que criamos.
multiple_time_frame_accuracy
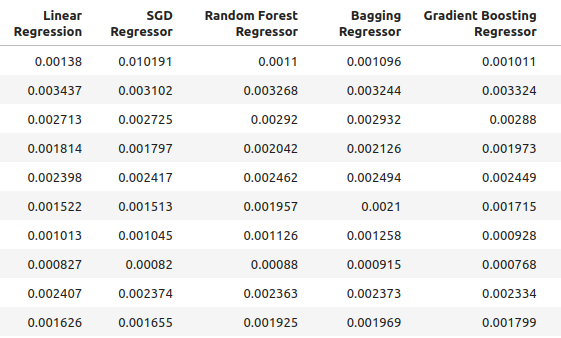
Fig 4: Níveis de precisão da nossa nova abordagem
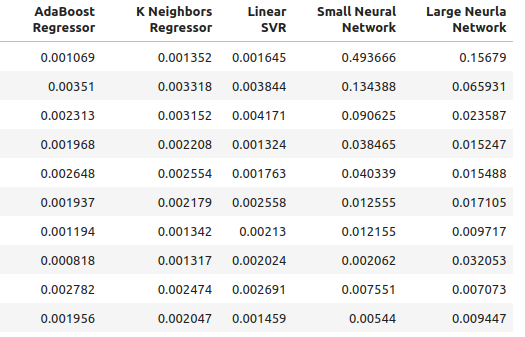
Fig 5: Níveis de precisão da nossa nova abordagem II
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {multiple_time_frame_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.001913639795583766
SGD Regressor had error levels 0.0027638553835377206
Random Forest Regressor had error levels 0.0020041047670504254
Bagging Regressor had error levels 0.0020506512726394415
Gradient Boosting Regressor had error levels 0.0019180687958290775
AdaBoost Regressor had error levels 0.0020194136735787625
K Neighbors Regressor had error levels 0.0021943350208868213
Linear SVR had error levels 0.0023609474919917338
Small Neural Network had error levels 0.08372469596701271
Large Neural Network had error levels 0.035243897461061074
Por fim, vamos observar nossa precisão ao usar todos os preditores disponíveis.
all_accuracy
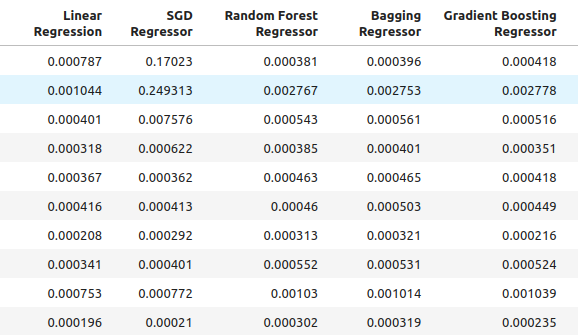
Fig 6: Níveis de precisão ao usar todos os preditores disponíveis.
for i in np.arange(0,ohlc_accuracy.shape[1]): print(f"{columns[i]} had error levels {all_accuracy.iloc[:,i].mean()}")
Linear Regression had error levels 0.00048307488099524497
SGD Regressor had error levels 0.043019079499194125
Random Forest Regressor had error levels 0.0007196920919204373
Bagging Regressor had error levels 0.0007263444909545053
Gradient Boosting Regressor had error levels 0.0006943964783049555
AdaBoost Regressor had error levels 0.0007217149661087063
K Neighbors Regressor had error levels 0.000872811528292862
Linear SVR had error levels 0.0006457525216512596
Small Neural Network had error levels 0.14002618062102
Large Neural Network had error levels 0.06774795252887988
Como podemos ver, o modelo linear foi o de melhor desempenho em todos os testes. Além disso, ele teve o melhor desempenho ao usar dados OHLC comuns. No entanto, o modelo não possui parâmetros de ajuste de interesse para nós. Portanto, selecionaremos o segundo melhor modelo, o Gradient Boosting Regressor (GBR), e tentaremos superar o desempenho do modelo linear.
Seleção de Atributos
Agora vamos ver quais atributos foram mais importantes para o nosso modelo GBR.
#Feature selection from mlxtend.feature_selection import SequentialFeatureSelector as SFS
Selecionar o modelo.
#We'll select the Gradient Boosting Regressor as our chosen model model = GradientBoostingRegressor()
Vamos usar o algoritmo de seleção reversa. Começaremos com um modelo que contém todos os preditores e descartaremos continuamente os atributos um por um. Um atributo será descartado apenas se resultar em uma melhoria no desempenho do modelo.
#Let us prepare the Feature Selector Object sfs = SFS(model, k_features=(1,len(all_predictors)), forward=False, n_jobs=-1, scoring="neg_root_mean_squared_error", cv=10 )
Realizando a seleção de atributos.
#Select the best feature sfs_results = sfs.fit(scaled_data.loc[:,all_predictors],market_data.loc[:,"Target"])
O algoritmo manteve apenas o preço alto e descartou todos os outros atributos.
#The best feature we found
sfs_results.k_feature_names_
Vamos visualizar nossos resultados.
#Prepare the plot fig1 = plot_sfs(sfs_results.get_metric_dict(),kind="std_dev") plt.title("Backward Selection on Gradient Boosting Regressor") plt.grid()
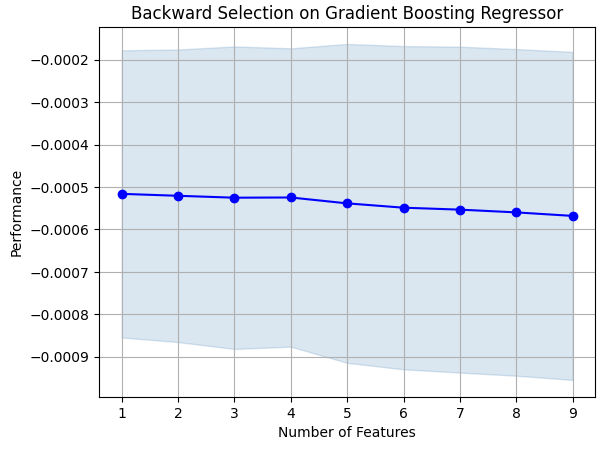
Fig 7: Visualizando o processo de seleção de atributos
Como podemos ver, o tamanho do modelo e os níveis de erro estavam diretamente proporcionais. Ou seja, à medida que nosso modelo aumentava, os níveis de erro também aumentavam.
Ajuste de Parâmetros
Agora vamos realizar o ajuste de parâmetros no nosso modelo GBR. Identificamos 11 parâmetros do modelo que valem a pena ajustar, e permitiremos 1000 iterações do objeto de ajuste antes de terminar o processo de otimização.
#Let us try to tune our model
from sklearn.model_selection import RandomizedSearchCV
Antes de começarmos a ajustar nosso modelo, vamos dividir nossos dados em duas partes. Uma metade será para treinar e otimizar nosso modelo, e a outra metade será usada para validação e testar se há overfitting.
#Before we try to tune our model, let's first create a train and test set train_X = scaled_data.loc[:(scaled_data.shape[0]//2),:] train_y = market_data.loc[:(market_data.shape[0]//2),"Target"] test_X = scaled_data.loc[(scaled_data.shape[0]//2):,:] test_y = market_data.loc[(market_data.shape[0]//2):,"Target"]
Definir o objeto de ajuste.
#Time the process import time start_time = time.time() #Prepare the tuning object tuner = RandomizedSearchCV(GradientBoostingRegressor(), { "loss": ["squared_error","absolute_error","huber"], "learning_rate": [0,(10.0 ** -1),(10.0 ** -2),(10.0 ** -3),(10.0 ** -4),(10.0 ** -5),(10.0 ** -6),(10.0 ** -7)], "n_estimators": [5,10,25,50,100,200,500,1000], "max_depth": [1,2,3,5,9,10], "min_samples_split":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0], "criterion":["friedman_mse","squared_error"], "min_samples_leaf":[0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9], "min_weight_fraction_leaf":[0.0,0.1,0.2,0.3,0.4,0.5], "max_features":[1,2,3,4,5,20], "max_leaf_nodes": [2,3,4,5,10,20,50,90,None], "min_impurity_decrease": [0,1,10,(10.0 ** 2),(10.0 ** 3),(10.0 ** 4)] }, cv=5, n_iter=1000, return_train_score=False, scoring="neg_mean_squared_error" )
Ajustar o modelo GBR.
#Tune the GradientBoostingRegressor tuner.fit(train_X,train_y) end_time = time.time() print(f"Process completed in {end_time - start_time} seconds.")
Vamos ver os resultados da melhor para a pior performance.
#Let's observe the results tuner_results = pd.DataFrame(tuner.cv_results_) params = ["param_loss", "param_learning_rate", "param_n_estimators", "param_max_depth", "param_min_samples_split", "param_criterion", "param_min_samples_leaf", "param_max_features", "param_max_leaf_nodes", "param_min_impurity_decrease", "param_min_weight_fraction_leaf", "mean_test_score"] tuner_results.loc[:,params].sort_values(by="mean_test_score",ascending=False)
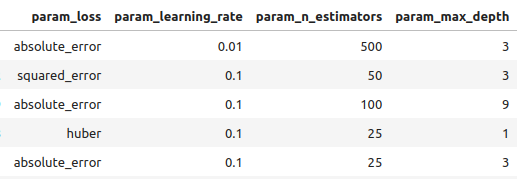
Fig 8: Alguns dos nossos melhores resultados.
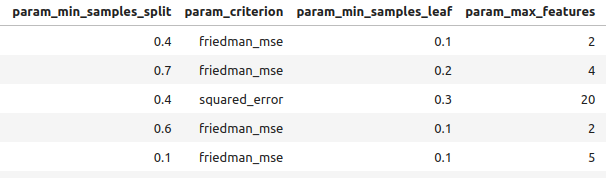
Fig 9: Alguns dos nossos melhores resultados II
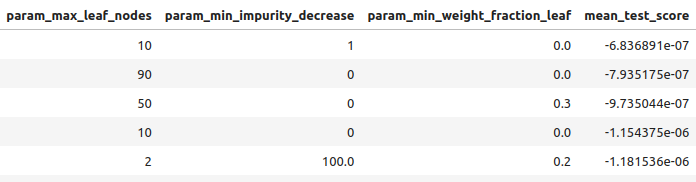
Fig 10: Alguns dos nossos melhores resultados III
Os melhores parâmetros que encontramos.
#Best parameters we found
tuner.best_params {'n_estimators': 500,
'min_weight_fraction_leaf': 0.0,
'min_samples_split': 0.4,
'min_samples_leaf': 0.1,
'min_impurity_decrease': 1,
'max_leaf_nodes': 10,
'max_features': 2,
'max_depth': 3,
'loss': 'absolute_error',
'learning_rate': 0.01,
'criterion': 'friedman_mse'}
Ajuste de Parâmetros Mais Profundo

Fig 11: O logo do SciPy
SciPy é uma biblioteca Python usada para cálculos científicos. SciPy significa Python Científico. Vamos ver se conseguimos encontrar parâmetros ainda melhores. Usaremos a biblioteca SciPy optimize para tentar encontrar parâmetros que melhorem o desempenho do nosso modelo.
#Let's see if we can't find better parameters #We may be overfitting the training data! from scipy.optimize import minimize
Para usar a biblioteca SciPy optimize, precisamos definir uma função objetivo. Nossa função objetivo será a média dos níveis de erro validados cruzadamente que nosso modelo atinge no conjunto de treinamento. Nosso otimizador SciPy buscará coeficientes que reduzam nosso erro de treinamento.
#Define the objective function def objective(x): #Create a dataframe to store our new accuracy current_error = pd.DataFrame(index=[0],columns=["error"]) #x is an array of possible values to use for our Gradient Boosting Regressor model = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=x[0], min_samples_split=x[1], min_samples_leaf=x[2], learning_rate=x[3]) model.fit(train_X.loc[:,:],train_y.loc[:]) current_error.iloc[0,0] = root_mean_squared_error(train_y.loc[:],model.predict(train_X.loc[:,:])) #Record our progress mean_error = current_error.loc[:].mean() #Return the average error return mean_error
Agora, vamos começar o processo de otimização. Observe que alguns parâmetros no modelo GBR não permitem valores negativos, e nosso otimizador SciPy passará valores negativos, a menos que especifiquemos limites para o otimizador. Além disso, o otimizador espera que forneçamos um ponto inicial. Usaremos o ponto final do algoritmo de otimização anterior como ponto de partida para este.
#Let's optimize these parameters again #Fist define the bounds bounds = ((0.0,0.5),(0.3,0.5),(0.001,0.2),(0.001,0.1)) #Then define the starting points for the L-BFGS-B algorithm pt = np.array([tuner.best_params_["min_weight_fraction_leaf"], tuner.best_params_["min_samples_split"], tuner.best_params_["min_samples_leaf"], tuner.best_params_["learning_rate"] ])
Minimizando o erro de treinamento.
lbfgs = minimize(objective,pt,bounds=bounds,method="L-BFGS-B")
Vamos ver os resultados:
lbfgs
success: True
status: 0
fun: 0.0005766670348377334
x: [ 5.586e-06 4.000e-01 1.000e-01 1.000e-02]
nit: 3
jac: [-6.216e+00 -4.871e+02 -2.479e+02 8.882e+01]
nfev: 180
njev: 36
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
Testando para Overfitting
Agora, vamos comparar a precisão dos nossos 2 modelos personalizados com o modelo GBR padrão. Além disso, também vamos observar se superamos o modelo linear.
#Let us now see how well we're performing on the validation set linear_regression = LinearRegression() default_gbr = GradientBoostingRegressor() grid_search_gbr = GradientBoostingRegressor(n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=0, min_samples_split=0.4, min_samples_leaf=0.1, learning_rate=0.01 ) lbfgs_grid_search_gbr = GradientBoostingRegressor( n_estimators=500, min_impurity_decrease=1, max_leaf_nodes=10, max_features=2, max_depth=3, loss="absolute_error", criterion="friedman_mse", min_weight_fraction_leaf=lbfgs.x[0], min_samples_split=lbfgs.x[1], min_samples_leaf=lbfgs.x[2], learning_rate=lbfgs.x[3] )Nossa precisão com o modelo linear.
#Linear Regression
linear_regression.fit(train_X,train_y)
root_mean_squared_error(test_y,linear_regression.predict(test_X)) Nossa precisão com o modelo GBR padrão.
#Default Gradient Boosting Regressor
default_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,default_gbr.predict(test_X)) Nossa precisão com o modelo GBR personalizado por busca aleatória.
#Random Search Gradient Boosting Regressor
grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,grid_search_gbr.predict(test_X)) Nossa precisão ao usar o modelo GBR personalizado por busca aleatória e L-BFGS-B.
#L-BFGS-B Random Search Gradient Boosting Regressor
lbfgs_grid_search_gbr.fit(train_X,train_y)
root_mean_squared_error(test_y,lbfgs_grid_search_gbr.predict(test_X))
Como podemos ver, não conseguimos superar o modelo linear. Além disso, não conseguimos superar o modelo GBR padrão. Portanto, vamos prosseguir com o modelo GBR padrão para fins de demonstração. No entanto, observe que a seleção do modelo linear teria nos dado mais precisão.
Exportando para ONNX
Open Neural Network Exchange (ONNX) é um protocolo que nos permite representar modelos de aprendizado de máquina como um gráfico computacional de nós e arestas. Onde os nós representam operações matemáticas e as arestas representam o fluxo de dados. Ao exportar nosso modelo de aprendizado de máquina para o formato ONNX, seremos capazes de usar nossos modelos de IA dentro do nosso Expert Advisor com facilidade.
Vamos nos preparar para exportar nosso modelo ONNX.
#Falhamos em superar o modelo de regressão linear, em casos como este devemos escolher o modelo linear! #However for demonstrational purposes we'll pick the gradient boosting regressor #Let's export the default GBR to ONNX format from skl2onnx.common.data_types import FloatTensorType from skl2onnx import convert_sklearn import onnx
Agora precisamos escalar nossos dados de uma maneira que possamos reproduzir no MetaTrader 5. A transformação mais simples é simplesmente subtrair a média e dividir pelo desvio padrão.
#We need to save the scale factors for our inputs scale_factors = pd.DataFrame(index=["mean","standard deviation"],columns=all_predictors) for i in np.arange(0,len(all_predictors)): scale_factors.iloc[0,i] = market_data.iloc[:,i+2].mean() scale_factors.iloc[1,i] = market_data.iloc[:,i+2].std() market_data.iloc[:,i+2] = ((market_data.iloc[:,i+2] - market_data.iloc[:,i+2].mean()) / market_data.iloc[:,i+2].std()) scale_factors

Fig 12: Nossos fatores de escala
Definir os tipos de entrada para o nosso modelo ONNX.
#Define our initial types initial_types = [("float_input",FloatTensorType([1,test_X.shape[1]]))]
Ajustando o modelo com todos os dados que temos.
#Fit the model on all the data we have model = GradientBoostingRegressor().fit(market_data.loc[:,all_predictors],market_data.loc[:,"Target"])
Criar a representação ONNX.
#Create the ONNX representation onnx_model = convert_sklearn(model,initial_types=initial_types,target_opset=12)
Salvar o modelo ONNX.
#Now save the ONNX model onnx_model_name = "GBR_M1_MultipleTF_Float.onnx" onnx.save(onnx_model,onnx_model_name)
Visualizando o Modelo
Netron é um visualizador de código aberto para inspecionar modelos de aprendizado de máquina. Atualmente, o Netron oferece suporte a um número limitado de frameworks. No entanto, à medida que o tempo passa e a biblioteca amadurece, o suporte será estendido para diferentes frameworks de aprendizado de máquina.
Importe as bibliotecas que precisamos.
#Import netron so we can visualize the model
import netron
Lançando o Netron.
netron.start(onnx_model_name)
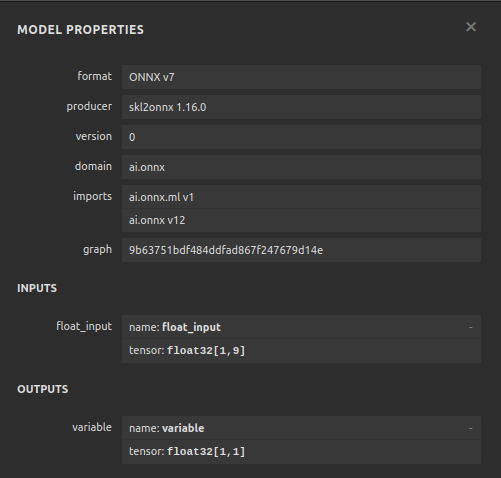
Fig 13: Propriedades do nosso modelo Gradient Boosting Regressor ONNX
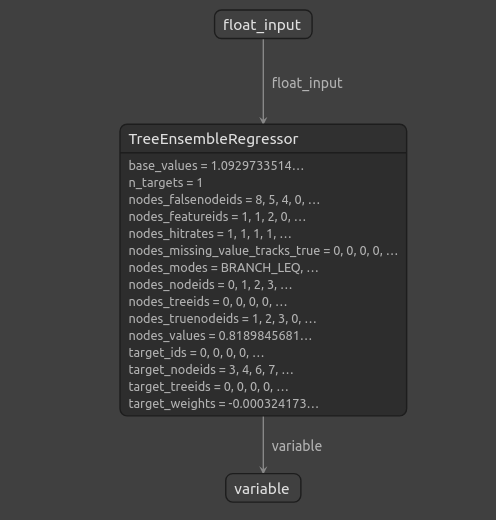 \
\
Fig 14: A estrutura do nosso Gradient Boosting Regressor
Como podemos ver, a forma de entrada e saída do nosso modelo ONNX está onde esperamos, o que nos dá confiança para prosseguir e construir um Expert Advisor em cima do nosso modelo ONNX.
Implementação no MQL5
Para começar a construir nosso Expert Advisor com um módulo de IA integrado, primeiro precisamos carregar o modelo ONNX.//+------------------------------------------------------------------+ //| Multiple Time Frame.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the onnx file | //+------------------------------------------------------------------+ #resource "\\Files\\GBR_M1_MultipleTF_Float.onnx" as const uchar onnx_model_buffer[];
Agora vamos carregar a biblioteca de negociação.
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Vamos definir as entradas que o usuário final pode alterar.
//+------------------------------------------------------------------+ //| Inputs | //+------------------------------------------------------------------+ input double max_risk = 20; //How much profit/loss should we allow before closing input double sl_width = 1; //How wide should out sl be?
Agora, definiremos variáveis globais que serão usadas em todo o nosso programa.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; //Our onnx model double mean_variance[9],std_variance[9]; //Our scaling factors vector model_forecast = vector::Zeros(1); //Model forecast vector model_inputs = vector::Zeros(9); //Model inputs double ask,bid; //Market prices double trading_volume; //Our trading volume int lot_multiple = 20; //Our lot size int state = 0; //System state
Vamos definir funções auxiliares que usaremos ao longo do nosso programa. Primeiro, precisamos de uma função para detectar reversões e alertar o usuário final sobre o perigo à frente que nosso sistema de IA previu. Se nosso sistema de IA detectar uma reversão, fecharemos as posições abertas que temos nesse mercado.
//+------------------------------------------------------------------+ //| Check reversal | //+------------------------------------------------------------------+ void check_reversal(void) { //--- Check for reversal if(((state == 1) && (model_forecast[0] < iClose(Symbol(),PERIOD_M1,0))) || ((state == 2) && (model_forecast[0] > iClose(Symbol(),PERIOD_M1,0)))) { Alert("Reversal predicted."); Trade.PositionClose(Symbol()); } //--- Check if we have breached our maximum risk levels if(MathAbs(PositionGetDouble(POSITION_PROFIT) > max_risk)) { Alert("We've breached our maximum risk level."); Trade.PositionClose(Symbol()); } }
Agora, definiremos uma função para encontrar oportunidades de entrada no mercado. Só consideraremos uma entrada válida se tivermos confirmação de tempos gráficos superiores sobre o movimento. Neste Expert Advisor, queremos que nossas negociações se alinhem com a ação do preço no gráfico semanal.
//+------------------------------------------------------------------+ //| Find an entry | //+------------------------------------------------------------------+ void find_entry(void) { //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bullish momentum if(model_forecast[0] > iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a buy Trade.Buy(trading_volume,Symbol(),ask,(ask - sl_width),(ask + sl_width),"Multiple Time Frames AI"); state = 1; } } //--- Analyse price action on the weekly time frame if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,20)) { //--- We are riding bearish momentum if(model_forecast[0] < iClose(Symbol(),PERIOD_M1,20)) { //--- Enter a sell Trade.Sell(trading_volume,Symbol(),bid,(bid + sl_width),(bid - sl_width),"Multiple Time Frames AI"); state = 2; } } }
Também precisamos de uma função para buscar os preços atuais do mercado.
//+------------------------------------------------------------------+ //| Update market prices | //+------------------------------------------------------------------+ void update_market_prices(void) { ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); }
Nosso modelo ONNX não pode ser usado a menos que padronizemos e normalizemos as entradas. Essa função buscará os fatores de escala que usamos ao treinar nosso modelo ONNX.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ void load_scaling_factors(void) { //--- EURUSD OHLC mean_variance[0] = 1.0930010861272836; std_variance[0] = 0.0017987600829890852; mean_variance[1] = 1.0930721822927123; std_variance[1] = 0.001810556238082839; mean_variance[2] = 1.092928371812889; std_variance[2] = 0.001785041172362313; mean_variance[3] = 1.093000590242923; std_variance[3] = 0.0017979420556511476; //--- M5 Change mean_variance[4] = (MathPow(10.0,-5) * 1.4886568962056413); std_variance[4] = 0.000994902152654042; //--- M15 Change mean_variance[5] = (MathPow(10.0,-5) * 1.972093957036524); std_variance[5] = 0.0017104874192072138; //--- M30 Change mean_variance[6] = (MathPow(10.0,-5) * 1.5089339490060967); std_variance[6] = 0.002436078407827825; //--- H1 Change mean_variance[7] = 0.0001529512146155358; std_variance[7] = 0.0037675774501395387; //--- D1 Change mean_variance[8] = -0.0008775667536639223; std_variance[8] = 0.03172437243836734; }
Definindo a função responsável por buscar previsões do nosso modelo, observe que estamos escalando as entradas antes de passá-las para o nosso modelo ONNX. As previsões são obtidas do modelo usando o comando OnnxRun.
//+------------------------------------------------------------------+ //| Model predict | //+------------------------------------------------------------------+ void model_predict(void) { //--- EURD OHLC model_inputs[0] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[0]) / std_variance[0]); model_inputs[1] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[1]) / std_variance[1]); model_inputs[2] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[2]) / std_variance[2]); model_inputs[3] = ((iClose(Symbol(),PERIOD_CURRENT,0) - mean_variance[3]) / std_variance[3]); //--- M5 CAHNGE model_inputs[4] = (((iClose(Symbol(),PERIOD_M5,0) - iClose(Symbol(),PERIOD_M5,20)) - mean_variance[4]) / std_variance[4]); //--- M15 CHANGE model_inputs[5] = (((iClose(Symbol(),PERIOD_M15,0) - iClose(Symbol(),PERIOD_M15,20)) - mean_variance[5]) / std_variance[5]); //--- M30 CHANGE model_inputs[6] = (((iClose(Symbol(),PERIOD_M30,0) - iClose(Symbol(),PERIOD_M30,20)) - mean_variance[6]) / std_variance[6]); //--- H1 CHANGE model_inputs[7] = (((iClose(Symbol(),PERIOD_H1,0) - iClose(Symbol(),PERIOD_H1,20)) - mean_variance[7]) / std_variance[7]); //--- D1 CHANGE model_inputs[8] = (((iClose(Symbol(),PERIOD_D1,0) - iClose(Symbol(),PERIOD_D1,20)) - mean_variance[8]) / std_variance[8]); //--- Fetch forecast OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
Agora, definiremos uma função para carregar nosso modelo Onnx e definir a forma de entrada e saída.
//+------------------------------------------------------------------+ //| Load our onnx file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the model from the buffer onnx_model = OnnxCreateFromBuffer(onnx_model_buffer,ONNX_DEFAULT); //--- Set the input shape ulong input_shape [] = {1,9}; //--- Check if the input shape is valid if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Alert("Incorrect input shape, model has input shape ", OnnxGetInputCount(onnx_model)); return(false); } //--- Set the output shape ulong output_shape [] = {1,1}; //--- Check if the output shape is valid if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Alert("Incorrect output shape, model has output shape ", OnnxGetOutputCount(onnx_model)); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
Agora podemos definir o procedimento de inicialização do programa. Nosso Expert carregará o arquivo Onnx, carregará os fatores de escala e buscará os dados do mercado.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX file if(!load_onnx_file()) { //--- We failed to load our onnx model return(INIT_FAILED); } //--- Load scaling factors load_scaling_factors(); //--- Get trading volume trading_volume = SymbolInfoDouble(Symbol(),SYMBOL_VOLUME_MIN) * lot_multiple; //--- Everything went fine return(INIT_SUCCEEDED); }
Sempre que nosso programa não estiver em uso, liberaremos os recursos que não precisarmos mais. Liberaremos o modelo Onnx e removeremos o expert advisor do gráfico.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Release the resources we used for our onnx model OnnxRelease(onnx_model); //--- Release the expert advisor ExpertRemove(); }
Sempre que tivermos novos preços sendo oferecidos, primeiro buscaremos uma previsão do nosso modelo e depois atualizaremos os preços do mercado. Se não tivermos uma posição aberta, tentaremos encontrar uma entrada. Caso contrário, se tivermos uma posição que precise ser gerenciada, estaremos atentos a uma possível reversão.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- We always need a prediction from our model model_predict(); //--- Show the model forecast Comment("Model forecast ",model_forecast); //--- Fetch market prices update_market_prices(); //--- If we have no open positions, find an entry if(PositionsTotal() == 0) { //--- Find entry find_entry(); //--- Update state state = 0; } //--- If we have an open position, manage it else { //--- Check if our AI is predicting a reversal check_reversal(); } }
Agora podemos ver nossa aplicação em ação.
Fig 15: Interface do nosso Expert Advisor
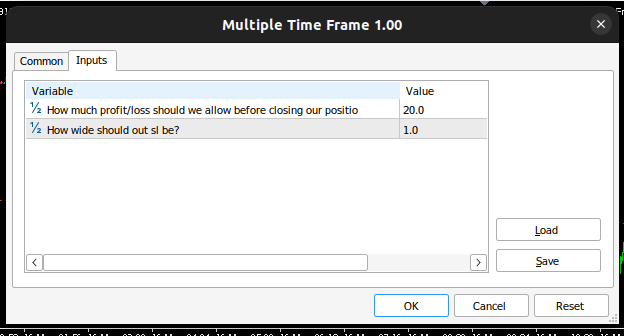
Fig 16: Entradas do nosso Expert Advisor
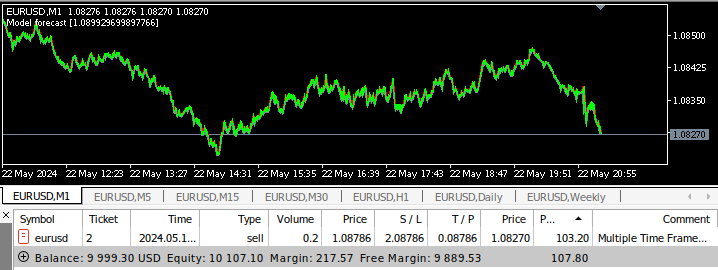
Fig 17: Expert Advisor de Múltiplos Tempos Gráficos sendo testado
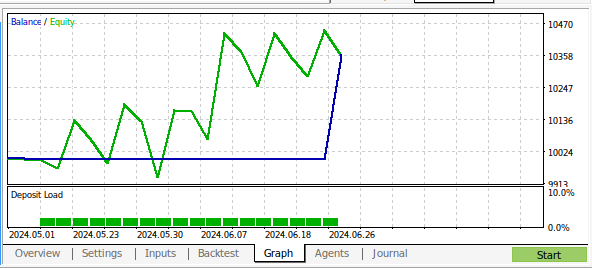
Fig 18: Os resultados do backtest do nosso programa sobre 1 mês de dados M1
Conclusão
Neste artigo, demonstramos que é possível construir um Expert Advisor com IA que analisa múltiplos tempos gráficos. Embora tenhamos obtido níveis de precisão mais altos usando dados OHLC comuns, existem muitas outras opções que não examinamos, por exemplo, não adicionamos nenhum indicador em tempos gráficos superiores. Existem muitas maneiras de aplicar IA na nossa estratégia de negociação, e esperamos que agora você tenha novas ideias sobre as capacidades que podem ser exploradas em sua instalação do MetaTrader 5.
Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/15610
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Integrando o MQL5 com pacotes de processamento de dados (Parte 2): Aprendizado de Máquina e Análise Preditiva
Integrando o MQL5 com pacotes de processamento de dados (Parte 2): Aprendizado de Máquina e Análise Preditiva
 Reimaginando Estratégias Clássicas (Parte V): Análise de Múltiplos Símbolos no USDZAR
Reimaginando Estratégias Clássicas (Parte V): Análise de Múltiplos Símbolos no USDZAR
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos
Técnicas do MQL5 Wizard que você deve conhecer (Parte 33): Kernels de Processos Gaussianos
 Auto-otimização de take-profits e parâmetros do indicador usando SMA e EMA
Auto-otimização de take-profits e parâmetros do indicador usando SMA e EMA
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Obrigado por sua análise detalhada e passo a passo. O resultado é fascinante (e inesperado). Isso significa que devemos testar outros parâmetros também, por exemplo, volume, spread, ação do dia anterior ou isso é mais um ajuste excessivo? Obrigado pelo modelo, agora tenho as ferramentas para verificar por mim mesmo :)